ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 4, с. 506-511

ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ

РАССЕЯНИЕ ПОЛОЖИТЕЛЬНЫХ МЮОНОВ

АТОМАМИ ИНЕРТНЫХ ГАЗОВ

Поступила в редакцию 02.02.2023 г.; после доработки 28.02.2023 г.; принята к публикации 28.02.2023 г.

В настоящей работе методами теории многих тел с использованием комплекса программ АТОМ-М

произведены расчеты сечений упругого и неупругого рассеяния положительных мюонов атомами He и

Ar при малых и средних кинетических энергиях. Для сравнения приводятся также результаты упругого

и неупругого рассеяния позитрона при тех же энергиях. Обсуждается зависимость фаз и сечений

рассеяния от заряда частицы и ее массы, а также от заряда ядра рассеивающего атома.

DOI: 10.31857/S004400272304013X, EDN: EGNOUG

1. ВВЕДЕНИЕ

приближении и решению уравнения Шредингера

с потенциалом Σ. Этот же подход мы используем

Исследование рассеяния положительных мюо-

и при изучении рассеяния мюонов на атомах. Мы

нов на атомах представляет собой важную задачу

определяем собственно энергетическую часть

Σ,

для физики, в частности в теории рассеяния по-

которая является решением интегрального урав-

ложительных частиц изолированными атомами [1].

нения, соответствующего уравнению Шредингера

Взаимодействие положительного мюона с атомом

с потенциалом Σ. Ядро этого уравнения содержит

формально такое же, как и взаимодействие пози-

неприводимую собственно энергетическую часть.

трона, но существенные различия рассеяния этих

Последняя вычисляется в упрощенном приближе-

частиц возникают из-за отличия масс. Вследствие

нии случайных фаз (УПСФ). Для решения за-

большой массы кинетическая энергия вращения

при данном угловом моменте меньше, поэтому

дачи используется разложение волновой функции

следует ожидать большего вклада членов l > 0

налетающего мюона на парциальные волны. При

при малых кинетических энергиях мюона. Сечения

расчетах учитывались четыре парциальные волны

упругого и неупругого рассеяния положительных

l = 0, 1, 2 и 3. Неприводимую собственно энер-

мюонов и позитронов на атомах [2-4] определя-

гетическую часть Σ одночастичной функции Грина

лись нами методами теории многих тел в базисе

удобно разбить на две части: хартри-фоковскую и

функций Хартри-Фока (ХФ) [5, 6], однако неэмпи-

определяемую корреляционным взаимодействием:

рические расчеты упругого и неупругого рассеяния

Σ=Σ^HF +Σ^cor.

(1)

положительных мюонов атомами нам неизвестны.

Собственно энергетическая часть в приближе-

2. МЕТОД РАСЧЕТА

нии Хартри-Фока Σ^HF есть самосогласованное

поле [6, гл. 14], которым атом воздействует на

При изучении рассеяния мюонов на атомах,

рассеиваемый мюон. Волновая функция и фаза

как и ранее для электронов, мы используем ап-

рассеяния δHFl налетающего мюона рассчитыва-

парат квантовой теории многих тел. Как показано

лись в приближении Хартри-Фока [5].

в работе [7], собственно энергетическая часть Σ

одночастичной функции Грина, описывающей рас-

В низшем порядке по Σ^cor сдвиг фаз рассеяния

пространение электрона, совпадает с оптическим

электронной (и мюонной) волны с моментом l по

потенциалом стандартной теории рассеяния. В ре-

сравнению с его хартри-фоковским значением ра-

зультате задача рассеяния сводится к вычислению

вен [4]:

собственно энергетической части в том или ином

Δδl1 (E₁) = -π 〈φν1 |Σ^cor|φν1 〉,

(2)

¹⁾Физико-технический институт им. А.Ф. Иоффе РАН,

где φν1 — волновая функция налетающей частицы

С.-Петербург, Россия.

в приближении Хартри-Фока, E₁ и l₁ — ее энергия

²⁾Институт общей и неорганической химии им. Н.С. Курна-

и орбитальный момент соответственно.

кова РАН, Москва, Россия.

^*E-mail: Larissa.Chernysheva@mail.ioffe.ru

В рамках приближения случайных фаз (ПСФ)

^**E-mail: vgyar@igic.ras.ru

диагональный матричный элемент собственно

506

РАССЕЯНИЕ ПОЛОЖИТЕЛЬНЫХ МЮОНОВ

507

∫



dE^′′

энергетической части для мюона может быть

+ P El |Σ^cor(ω)|E^′′l E^′′l Σ(ω)E′l

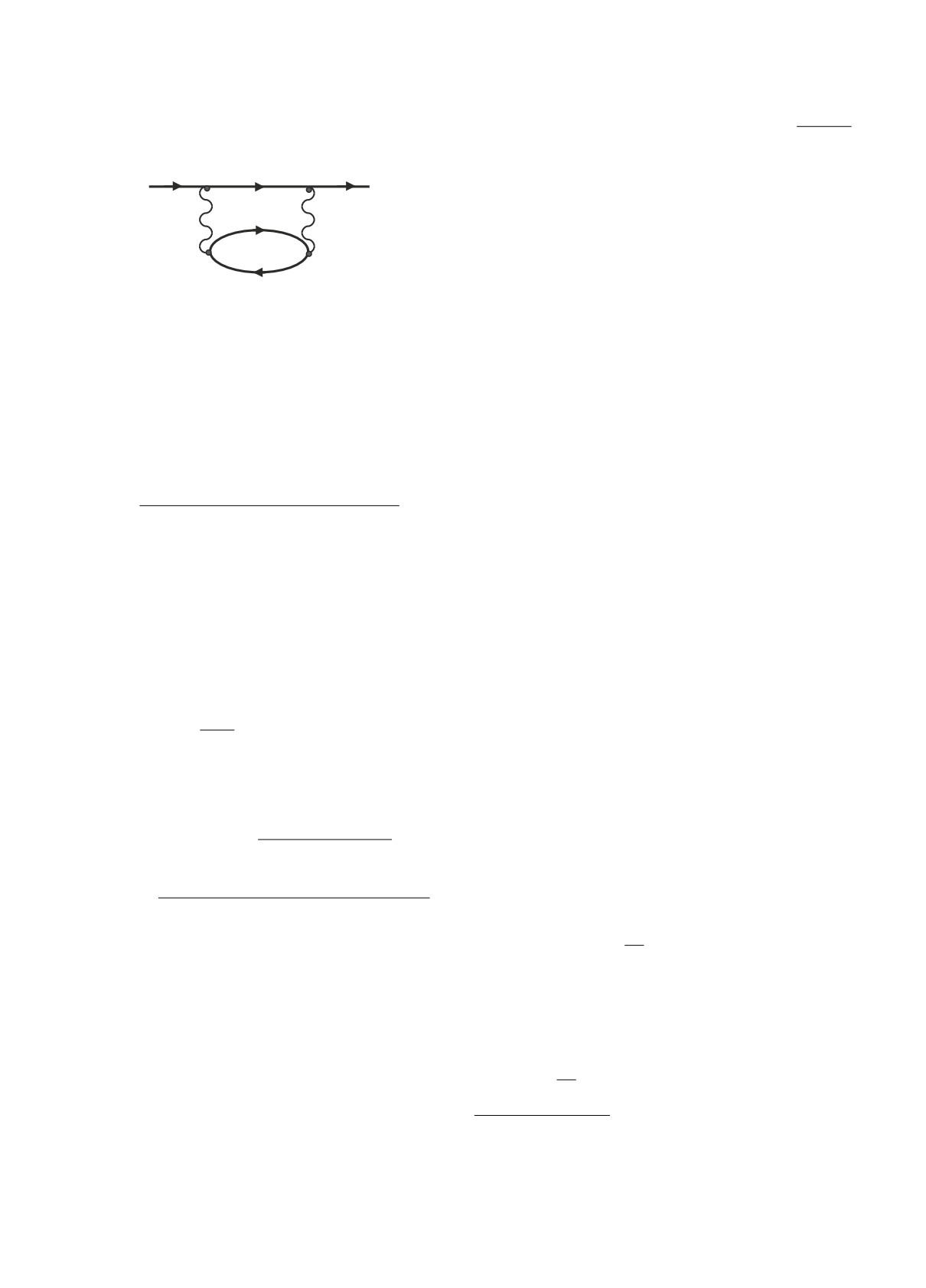
представлен графически следующим образом:

ω-E^′′

∫

Здесь знак P

означает, что интеграл рассматри-

вается в смысле главного значения. Интегрирова-

ние по E^′′ включает суммирование по дискретным

состояниям, в том числе и по занятым (дырочным)

уровням.

Волновые функции в (5) выбираются следую-

щим способом. Налетающий мюон ν₁ описывает-

(3)

ся волновой функцией φ^N , рассчитанной в поле

где волнистая линия обозначает кулоновское взаи-

нейтрального атома. Соответствующим выбором

модействие, а λ — его мультипольность.

волновых функций виртуальных электронов можно

по-разному учесть вклад многоэлектронных кор-

Для расчета этой диаграммы надо всем линиям

реляций, а именно, выбором φN-1ν

(т.е. в поле с

(включая волнистую) сопоставить угловые момен-

ты электронов и мюона (или мультипольность λ

дыркой ν₃) учитывается часть корреляций ПСФ во

взаимодействии между электроном и дыркой.

кулоновского взаимодействия), а каждой волни-

стой линии кулоновского взаимодействия весовой

После того как матричные элементы

множитель [8, 9]

〈ν₁ν₃∥V_λ∥ν₄ν₂〉 получены, уравнение (7) может

быть решено для неприводимой собственно энер-

〈ν₁ν₃∥V_λ∥ν₄ν₂〉 =

(4)

гетической части, через которую выражаются

√

(2l₁ + 1)(2l₂ + 1)(2l₃ + 1)(2l₄ + 1) ×

поправки к фазе рассеяния

⎛

⎞⎛

⎞

[



]

Δδ_l(E) = arctg

-π ψ_El

Σ(E)ψEl

(8)

×⎝l1 λl4⎠⎝l3 λl2⎠Rλ(ν1ν2ν3ν4),

При энергиях, превышающих порог ионизации

атома, выражение для матричного элемента, опре-

где

деляемого (6), становится комплексным, а вместе с

ним становятся комплексными и решение уравне-

∫∞

ния, и поправки к фазе.

R^λ(ν₁ν₂ν₃ν₄) = Pν1 (r)Pν4 (r)dr ×

(5)

Обозначим фазу

δ_l(E) = λ_l(E) + iμ_l(E),

(9)

∫r

r^λ<

где

Pν3 (r^′)Pν2 (r^′)dr^′.

rλ+1

λ_l(E) = δHFl(E) + Re Δδ_l(E),

(10)

Применяя правила графической техники при сум-

μ_l(E) = Im Δδ_l(E),

(11)

мировании моментных диаграмм [8, 9], получаем

∑

где δHFl(E) — фаза волновой функции мюона, ко-

〈ν₁ |Σ^cor (E)| ν₁〉 =

(6)

(2lν1 + 1)(2λ + 1)

торая получается при решении уравнений Хартри-

Фока для мюона в поле атома. Знание фазы (9)

∑

2 〈ν₁ν₃∥V_λ∥ν₄ν₂〉²

позволяет найти как сечения упругого рассеяния

мюона на атоме [9]:

E - Eν2 + Eν3 - Eν4 + iη(1 - 2nν4)

^ν4^,ν2^>F,

ν₃≤F

∑

σ_el =

(2l + 1) ×

(12)

Здесь “2” — результат суммирования по спинам

k²

l=0

в петле (3), νi означает совокупность кванто-

× (cosh 2μ_l - cos 2λ_l) exp(-2μ_l),

вых чисел nl (Eν2 — для непрерывного спектра),

суммирование по ν₃ проводится по занятым (ды-

где k² = 2mEm3), масса мюона m = 207 и энергия

рочным) состояниям, суммирование по ν₄, ν₂ — по

мюона E_m, так и неупругого рассеяния

свободным (частичным) состояниям, в том числе

∑

интегрируется по непрерывному спектру энергий.

σ_in =

(2l + 1) [1 - exp(-4μ_l)] .

(13)

k²

В результате проблема сводится к вычислению

l=0

собственно энергетической части Σ^cor и решению

уравнения

³⁾В статье используется атомная система единиц e = me =



= ℏ = 1, где e— заряд электрона, me — его масса, ℏ —

El Σ(ω)E′l

= El |Σ^cor(ω)| E^′l +

(7)

постоянная Планка.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

508

ЧЕРНЫШЕВА, ЯРЖЕМСКИЙ

Сечение упругого рассеяния, a₂

Сечение неупругого рассеяния, a

100

0.000015

0.00004

s-волна

0.010

p-волна

0.00003

d-волна

s-волна

0.000012

⁺ + He

0.008

f-волна

⁺ + He

p-волна

полное

d-волна

0.00002

0.006

f-волна

0.000009

полное

0.00001

0.004

0.002

0.000006

2000

4000

6000

8000 10 00012 000

2000

4000

6000

8000

10 000

12 000

0.000003

Энергия мюона, эВ

Сечение упругого рассеяния, a₀

Сечение неупругого рассеяния, a₀

1.0

до 2

s-волна

e⁺ + He

p-волна

s-волна

0.8

d-волна

p-волна

f-волна

0.8

d-волна

полное

f-волна

e⁺ + He

0.6

полное

0.6

0.4

0.2

Энергия позитрона, эВ

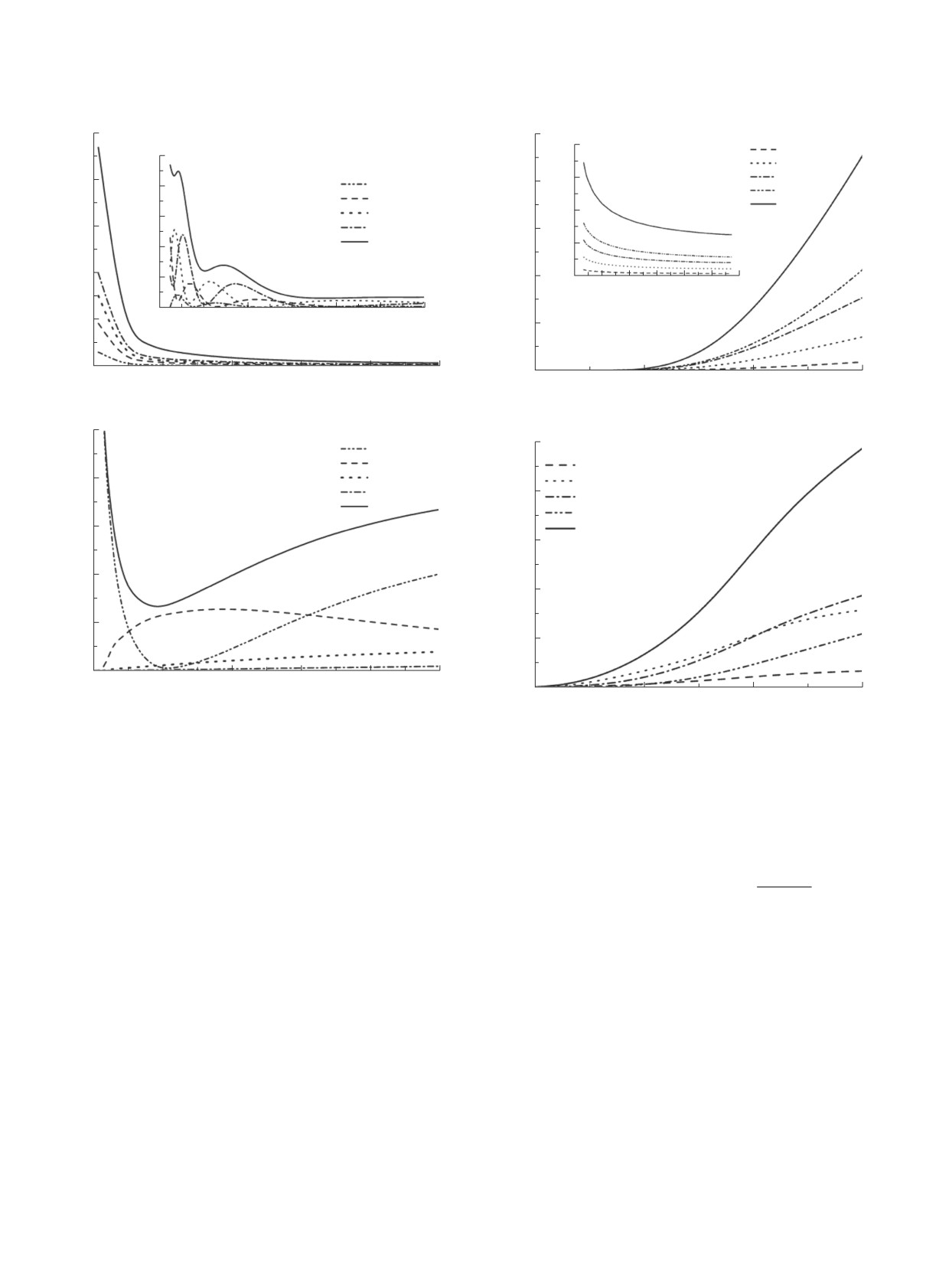
Рис. 1. Сечение упругого рассеяния μ⁺/He и e⁺/He.

Рис.

2. Сечение неупругого рассеяния μ⁺/He и

3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

e⁺/He.

Результаты расчетов сечений упругого и неупру-

гого рассеяния μ⁺/He, e⁺/He, μ⁺/Ar, e⁺/Ar c ис-

рис. 1a). В этом состоит их основное отличие

пользованием программного комплекса АТОМ [6]

от сечений упругого рассеяния e⁺, которые из-за

приведены на рис. 1-4. Расчеты показали, что при

l(l + 1)

наличия центробежного потенциала

, пре-

рассеянии мюонов атомами также, как и при рас-

2mr²

сеянии электронов атомами [10], основной вклад

пятствующего проникновению волновой функции

в фазу рассеяния дают монопольные возбуждения

позитрона в область атома, обращаются в нуль

(λ = 0 в формулах (3)-(6)) электронов валентных

при малых кинетических энергиях (см. рис. 1б).

оболочек. Для сравнения приведены результаты

Сечения неупругого рассеяния мюонов имеют два

расчетов рассеяния позитрона на этих же атомах.

максимума: один в области нескольких сотен эВ,

Эти частицы имеют одинаковый заряд, но разные

а другой в области нескольких тысяч эВ, и по-

массы.

ложение максимума зависит от углового момента

На рис. 1a и 1б приводятся соответственно

парциальной волны.

сечения упругого рассеяния μ⁺/He и e⁺/He. На

На рис. 2a и 2б приведены соответственно се-

врезке рис. 1a — сечения при энергиях в диапазоне

чения неупругого рассеяния μ⁺/He и e⁺/He. На

300-12 000 эВ. Сечения вычислялись для s-, p-,

врезке рис. 2a — сечения при энергиях в диапа-

d-, f-волн. Вклады в сечения упругого рассеяния

зоне 300-12 000 эВ. Наибольший вклад в сечения

μ⁺ парциальных волн l = 0, 1, 2, 3 при малых

неупругого рассечения мюонов на He дает f-волна.

кинетических энергиях не обращаются в нуль (см.

Соотношение между парциальными волнами не

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

РАССЕЯНИЕ ПОЛОЖИТЕЛЬНЫХ МЮОНОВ

509

Сечение упругого рассеяния, a₂

100

0.010

s-волна

p-волна

0.008

⁺ + Ar

d-волна

f-волна

0.006

полное

0.004

0.002

2000

4000

6000

8000

10 000

12 000

14 000

Энергия мюона, эВ

Сечение упругого рассеяния, a₀

до 60

s-волна

p-волна

d-волна

e⁺ + Ar

f-волна

полное

Энергия позитрона, эВ

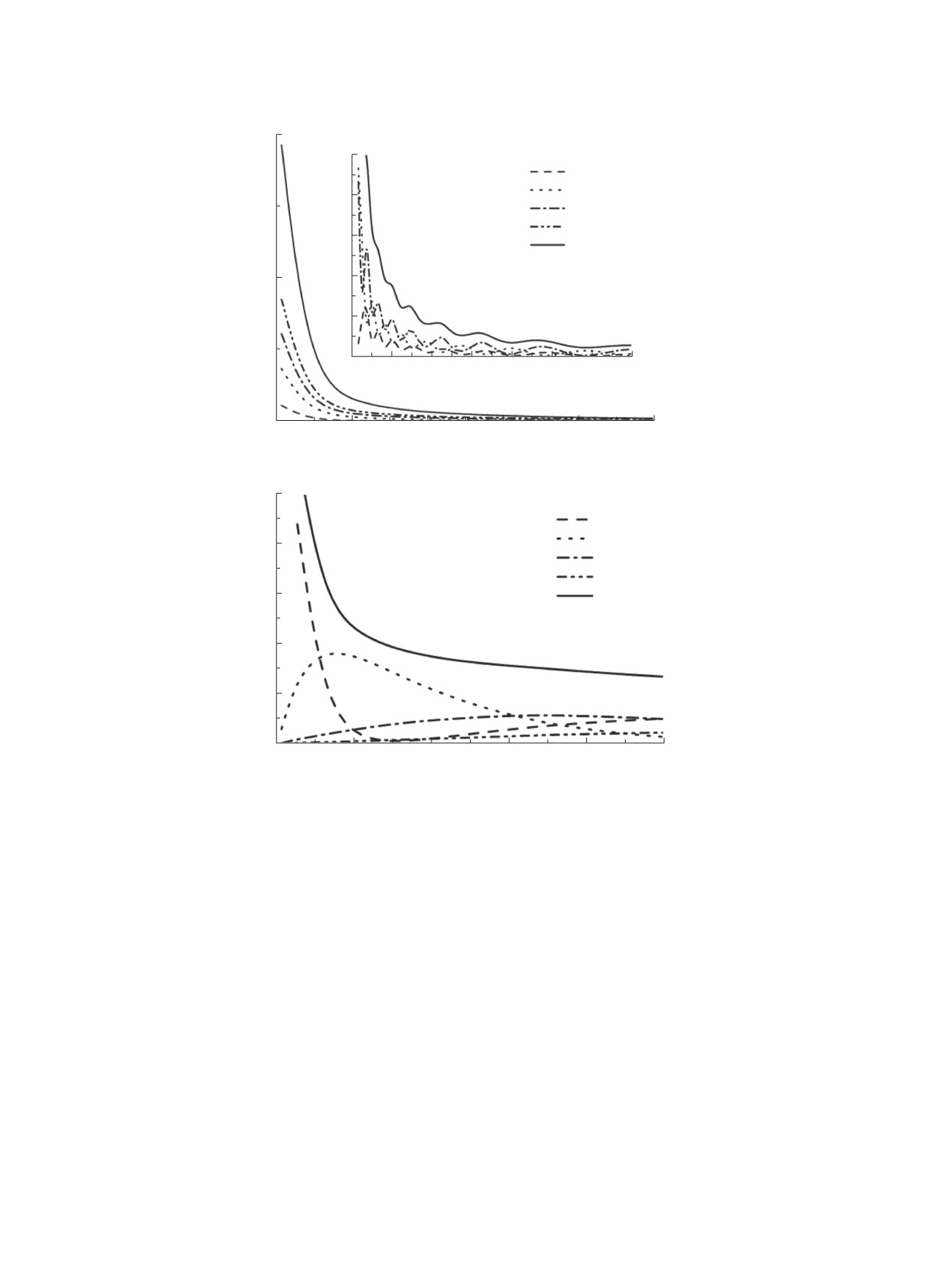
Рис. 3. Сечение упругого рассеяния μ⁺/Ar и e⁺/Ar.

зависит от энергии и приблизительно пропорцио-

мюонов на атоме Ar подобен ходу сечений неупру-

нально величине 2l + 1. В то же время в случае

гого рассеяния на атоме He — соотношения между

позитронов наибольший вклад дают p- и d-волны.

парциальными волнами почти постоянны при из-

менении энергии. Наибольший парциальный вклад

На рис. 3a и 3б мы даем сечения упругого

в рассеяние как мюона, так и позитрона дает f-

рассеяния μ⁺/Ar и e⁺/Ar. На врезке рис. 3a —

волна.

сечения при энергиях в диапазоне 300-14 000 эВ.

Интересно, что осцилляции в сечениях упругого

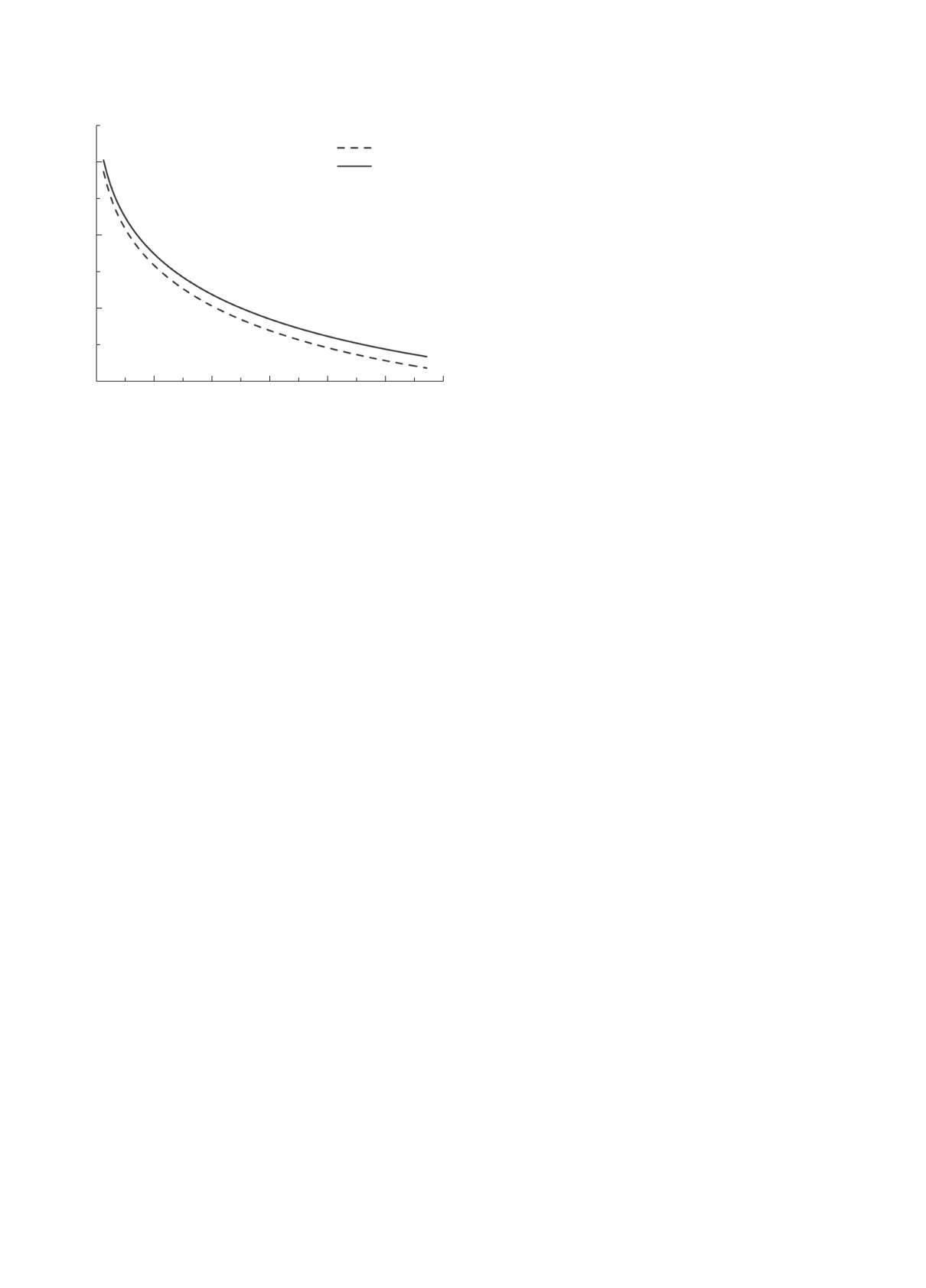
На рис. 5 приведены для сравнения фазы упру-

рассеяния мюонов на атоме Ar сохраняются также

гого рассеяния для p-волны μ⁺/Ar в приближени-

и при больших энергиях (до 14 000 эВ) и наиболь-

ях Хартри-Фока и УПСФ.

ший вклад дает f-волна. В то же время в сечении

Сечения упругого и неупругого рассеяния пози-

упругого рассеяния позитрона на Ar дает вклад s-

тронов хорошо изучены, поэтому интересно рас-

волна.

смотреть отличия в сечении рассеяния мюонов от

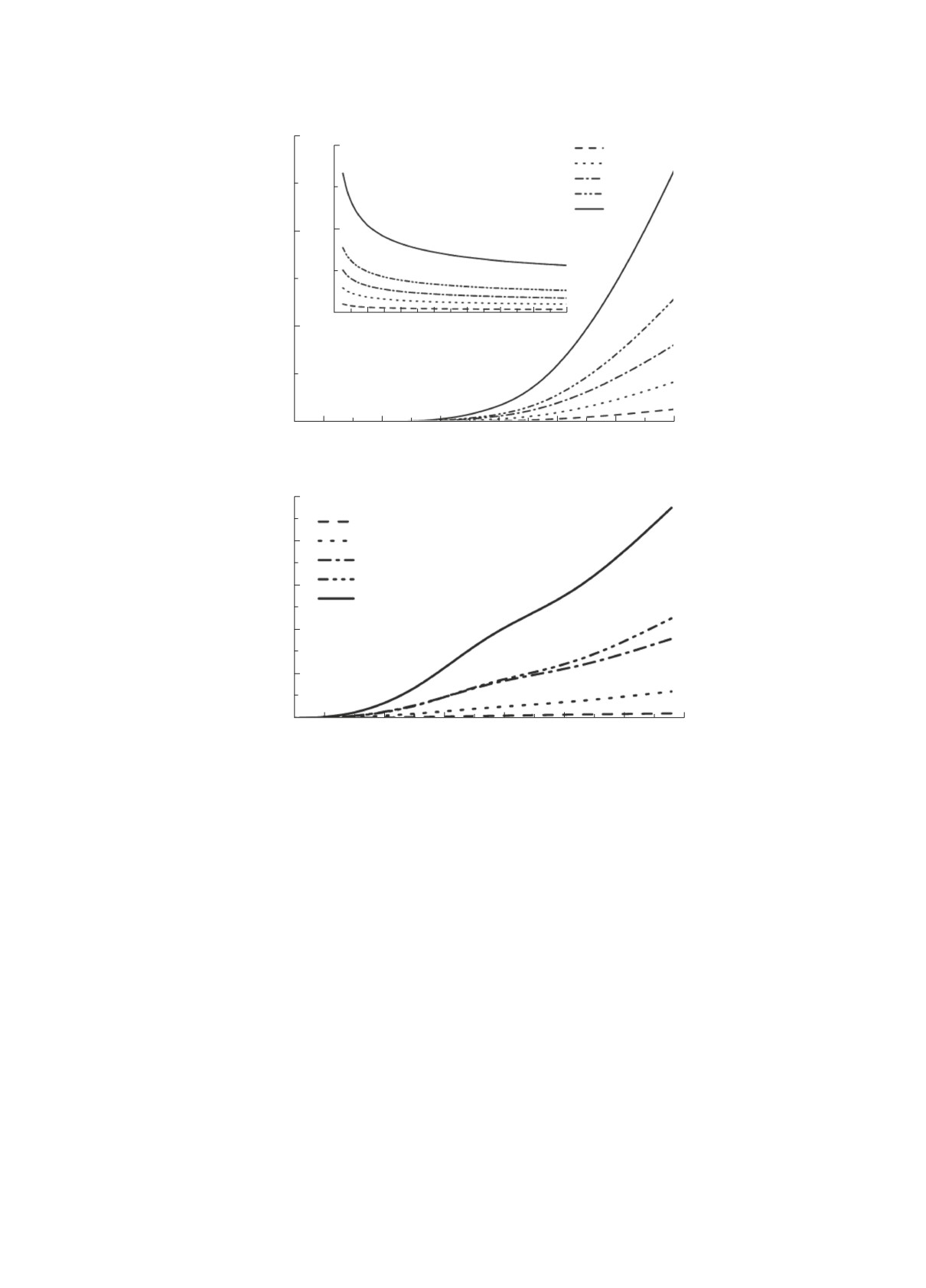
На рис. 4a и 4б приведены сечения неупругого

сечения рассеяния позитронов. Наличие центро-

рассеяния μ⁺/Ar, e⁺/Ar. На врезке рис. 4a —

бежного потенциала, величина которого для пози-

сечения при энергиях в диапазоне 300-12 000 эВ.

трона при l = 1 и r = 1 имеет величину порядка

Ход парциальных сечений неупругого рассеяния

атомной единицы, приводит к тому, что в области

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

510

ЧЕРНЫШЕВА, ЯРЖЕМСКИЙ

Сечение неупругого рассеяния, a₂

0.000006

0.00002

s-волна

p-волна

d-волна

f-волна

⁺ + Ar

полное

0.00001

0.000004

2000

4000

6000

8000

10 000 12 000 14 000

0.000002

Энергия мюона, эВ

Сечение неупругого рассеяния, a₂

s-волна

p-волна

e⁺ + Ar

d-волна

f-волна

полное

Энергия позитрона, эВ

Рис. 4. Сечение неупругого рассеяния μ⁺/Ar и e⁺/Ar.

малых кинетических энергий основной вклад в се-

парциальной волны (см. рис. 1a). Сечения упругого

чение позитрона дает s-волна. В случае μ⁺ цен-

рассеяния μ⁺ на атоме Ar в рассматриваемом

тробежный потенциал примерно в 200 раз мень-

диапазоне (до 14 000 эВ) для всех парциальных

ше и не препятствует проникновению волновой

волн имеют по 5-6 максимумов и минимумов (см.

функции μ⁺ в область атома. Поэтому в случае

рис. 3). В качестве примера на рис. 5 приведена

μ⁺ вклады парциальных волн с l > 0 существенны

фаза упругого рассеяния для p-волны на атоме Ar.

при всех энергиях, начиная от самых малых. При

Из этого рисунка видно, что диапазон изменения

больших энергиях основной вклад в сечения как

фазы соответствует нескольким периодам косину-

e⁺, так и μ⁺ дают парциальные волны с l > 0.

са в формуле (12), что приводит к осцилляционному

Поскольку в знаменателе формулы (12) стоит ве-

характеру зависимости сечения от энергии. Из это-

личина k² = 2mE_m, сечения рассеяния μ⁺ почти

го рисунка видно также, что основной вклад в фазу

на два порядка меньше сечений e⁺. Также важно

дает величина δHFl(E), но при этом вклад много-

отметить, что сечения упругого рассеяния мюонов

во всем диапазоне энергий почти на два порядка

электронных эффектов (см. графическую формулу

превосходят сечения неупругого рассеяния. Сече-

(3)) также весьма существенный. Величины и ха-

ния упругого рассеяния μ⁺ на атоме He имеют по

рактер изменения фаз для остальных парциальных

два максимума для каждой из парциальных волн,

волн аналогичны приведенным на рис. 5 для p-

причем их положения зависят от углового момента

волны.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

РАССЕЯНИЕ ПОЛОЖИТЕЛЬНЫХ МЮОНОВ

511

Фаза, рад

учитываться при расчете эффективной глубины

проникновения мюонов в образец. Зависимость се-

ХФ

чений упругого рассеяния мюонов от кинетической

УПСФ

энергии имеет осциллирующий характер во всем

рассмотренном диапазоне (до 14 000 эВ).

⁺ + Ar

p-волна

СПИСОК ЛИТЕРАТУРЫ

А. О. Вайсенберг, Мю-мезон (Наука, Москва,

1964).

Н. А. Черепков, Л. В. Чернышева, ЯФ 32, 709

(1980).

M. Ya. Amusia, N. A. Cherepkov, L. V. Chernysheva,

and S. G. Shapiro, J. Phys. B 9, 17 (1976).

400

200

400

600

800

1000

1200

M. Ya. Amusia, V. K. Dolmatov, and L. V. Cher-

nysheva, J. Phys. B 54, 185003 (2021).

Энергия мюона, Ry

M. Ya. Amusia and L. V. Chernysheva, Computation

of Atomic and Molecular Processes: Introducing

Рис. 5. Фазы упругого рассеяния μ⁺/Ar (p-волна) в

the ATOM-M Software Suite (Springer Series on

ХФ и УПСФ.

Atomic, Optical, and Plasma Physics, 2021), Vol.

117.

М. Я. Амусья, С. К. Семенов, Л. В. Чернышева,

4. ВЫВОДЫ

АТОМ-М алгоритмы и программы исследова-

Методом Хартри-Фока с применением много-

ний атомных и молекулярных процессов (Наука,

частичной теории возмущений нами рассчитаны

C.-Петербург, 2016).

сечения упругого и неупругого рассеяния μ⁺ и e⁺

J. S. Bell and E. J. Squires, Phys. Rev. Lett. 3, 96

на атомах He и Ar. Результаты расчетов позволяют

(1959).

выявить следующие основные тенденции. Как при

I. Lindgren and J. Morrison, Atomic Many-Body

Theory (Springer, Berlin, 1982).

малых, так и при больших энергиях вклады всех

парциальных волн l = 0, 1, 2, 3 в сечения как

N. F. Mott and H. S. W. Massey, The Theory of

упругого, так и неупругого рассеяния существенны.

Atomic Collisions (Oxford, 1949).

Основной вклад в фазу рассеяния дают моно-

10.

M. Ya. Amusia, L. V. Chernysheva, and V. G.

польные возбуждения (λ = 0 в формулах (3)-(6))

Yarzhemsky, Handbook of Theoretical Atomic

электронов валентных оболочек. Сечения упругого

Physics, Data for Photon Absorption, Electron

рассеяния мюонов почти на два порядка больше

Scattering, and Vacancies Decay (Springer-Verlag,

Berlin, Heidelberg, 2012).

сечений неупругого рассеяния и поэтому должны

SCATTERING OF POSITIVE MUONS BY ATOMS OF INERT GASES

L. V. Chernysheva¹⁾, V. G. Yarzhemsky²⁾

¹⁾ Ioffe Institute, 194021 St. Petersburg, Russia

²⁾ Kurnakov Institute of General and Inorganic Chemistry of RAS, 119991, Moscow, Russia

In the present work, the cross sections of elastic and inelastic scattering of positive muons by He and

Ar atoms at low and medium kinetic energies are calculated by the methods of many-body theory with

the use of the ATOM-M software package. For comparison, the results of elastic and inelastic positron

scattering at the same energies are also given. The dependence of the phases and scattering cross sections

on the charge of the particle and its mass, as well as on the charge of the nucleus of the scattering atom, is

discussed.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023