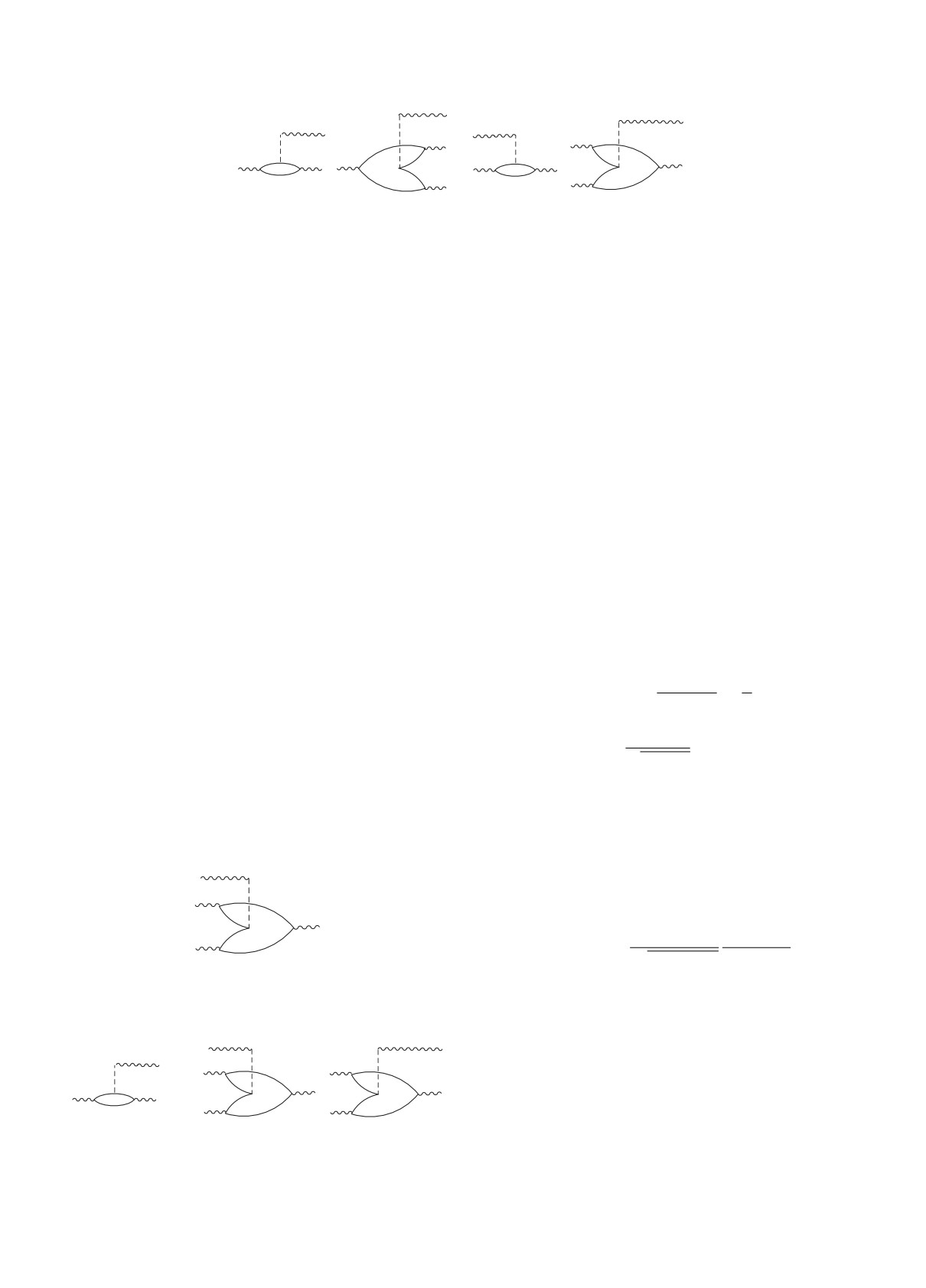ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 4, с. 461-475

ЯДРА

По материалам доклада на “Ядро-2022”

ОСОБЕННОСТИ РОТАЦИОННЫХ ПОЛОС В ТЯЖЕЛЫХ

И СВЕРХТЯЖЕЛЫХ ЯДРАХ. ОПИСАНИЕ СОСТОЯНИЙ

ИРАСТ-ПОЛОСЫ В²⁴⁸Cm

Поступила в редакцию 09.01.2023 г.; после доработки 11.02.2023 г.; принята к публикации 13.02.2023 г.

Представлено дальнейшее развитие расширенной микроскопической версии МВБ за счет рассмот-

рения двухквазичастичных фононов с мультипольностью до J^π = 14⁺. Разработанная теоретическая

схема применена для описания свойств состояний ираст-полосы в²⁴⁸Cm со спинами вплоть до 34⁺.

Данное тяжелое трансактинидное ядро является единственным в этой массовой области ядром, где

измерены значения B(E2) вплоть до спина I^π = 28⁺. Поэтому именно оно и рассматривается в первую

очередь, так как информация по ядру позволяет протестировать представленную теоретическую схему,

опираясь на больший объем экспериментальных данных. Область ядер отличается от более легких

отсутствием эффекта обратного загиба момента инерции от квадрата частоты вращения вплоть до

предельно наблюдаемого в ряде случаев спина I^π = 34⁺. Рассматриваются причины этого эффекта.

Обсуждается ряд особенностей ротационных полос в тяжелых и сверхтяжелых ядрах.

DOI: 10.31857/S0044002723040189, EDN: EGAPWS

1. ВВЕДЕНИЕ

сверхтяжелых ядрах. Поэтому детальное изучение

структуры ядер в области тяжелых и сверхтя-

Изучение свойств тяжелых и сверхтяжелых

желых элементов имеет исключительно важное

ядер в настоящее время является предметом

значение. Большинство тяжелых и сверхтяжелых

первоочередных исследований в ведущих лабо-

ядер являются деформированными, что приводит

раториях [1-18]. Ряд вопросов ядерной физики,

к появлению ротационных полос в их спек-

физики атомов и химии сверхтяжелых элементов

трах. Экспериментальное исследование свойств

остается открытым [7]. Решающее значение в су-

возбужденных уровней ядер, включая изомеры

ществовании сверхтяжелых ядер (Z ≥ 104) имеют

и ротационные полосы, а также теоретический

оболочечные эффекты [1, 5, 7]. Стабилизирующая

анализ соответствующих экспериментальных дан-

роль оболочек в атомных ядрах приводит к суще-

ных позволяют получить важную информацию

ствованию так называемого острова стабильности

о свойствах атомных ядер [9-18]. Эксперимен-

[1, 5, 7] — области сверхтяжелых элементов на

тальная техника, используемая для получения и

карте атомных ядер, причем положение и очер-

изучения тяжелых и сверхтяжелых ядер [1, 8-

тания данного острова чувствительны к деталям

11, 13-17], включает в себя масс-сепараторы и

схемы одночастичных уровней как для протонов,

масс-спектрометры в сочетании с высокочувстви-

так и для нейтронов. Ряд подуровней сферических

тельными детектирующими системами частиц и

орбиталей из области острова стабильности ста-

гамма-излучения. В принципе, экспериментальные

новится доступными [13] для экспериментального

методики можно разделить на два класса. В первом

исследования в деформированных тяжелых и

случае производится измерение гамма-спектров и

спектров конверсионных электронов от распада

¹⁾Государственный университет морского и речного флота

ядер в области мишени с использованием техники

имени адмирала С.О. Макарова, Санкт-Петербург, Рос-

запаздывающих совпадений с выделенными масс-

сия.

сепаратором и соответствующей детектирующей

²⁾ФТИ им. А.Ф. Иоффе, Санкт-Петербург, Россия.

системой продуктами ядерных реакций (например,

³⁾Объединенный институт ядерных исследований, Дубна,

Россия.

с ядрами отдачи), и (или) продуктами распада (на-

^*E-mail: efimov98@mail.ru

пример, с осколками деления ядер отдачи) [13, 16,

^**E-mail: izosimov@jinr.ru

17], а во втором — исследуются спектры альфа-,

461

462

ЕФИМОВ, ИЗОСИМОВ

бета-, гамма-излучений, электронов конверсии при

модах. Примеры описания данного эффекта с по-

распаде из основного или изомерных состояний

мощью бозонного представления различных мод

ядер в фокальной плоскости масс-сепаратора [1-

возбуждений для изотопов Xe, Ba, Ce и ядра¹⁵⁶Dy

4, 8-11, 14, 15]. Экспериментальную информацию

были даны соответственно в работах [21-24]. Об-

о структуре ротационных полос, вплоть до высоких

щим для всех данных ядер является то, что реально

спинов уровней, получают в основном первым

максимальный спин двухквазичастичной пары не

способом [16, 17]. Второй способ, как правило,

превышает значения J^π = 10⁺. Эта пара построена

применим для изучения структуры ядер и изомеров

на одночастичном уровне h11/2. В рассматривае-

с временем жизни, превышающим несколько

мой области ядер в валентной оболочке находятся

микросекунд [1-4, 8-11]. Спектроскопия ядер в

уже два уровня со спином 11/2, это в нейтронной

фокальной плоскости масс-сепаратора позволяет

системе i11/2 и в протонной h11/2. Уровень h11/2

детально исследовать структуру низколежащих

уровней ядер и структуру изомеров.

в протонной системе формально не принадлежит

валентной оболочке, но в силу большого числа бо-

Исследования ротационных полос вплоть до

зонов общее число квазичастиц на нем оказывается

высоких спинов с помощью спектроскопии в об-

максимально возможным и равным 6. При этом

ласти мишени и построение соответствующих схем

энергия квазичастицы существенно понижается.

распада занимают важное место в изучении струк-

Но помимо этого к валентной нейтронной оболочке

туры возбужденных уровней и изомеров в атомных

относится и одночастичное состояние уже со спи-

ядрах [13-18]. Данные о моменте инерции, полу-

ченные из анализа ротационных полос, чувстви-

ном 15/2 — j15/2 и пара нуклонов на этом уровне,

тельны к деталям оболочечной структуры и спари-

образующая возбуждения с моментами вплоть до

ванию, что дает возможность проводить тестирова-

12⁺ и 14⁺. Этот факт требует расширения теорети-

ние теоретических подходов в области тяжелых и

ческой модели, описывающей эффект пересечения

сверхтяжелых ядер [19]. Информация о g-факторе

полос, за счет рассмотрения и двухквазичастич-

изомера, полученная на основании эксперимен-

ных пар с такими высокими спинами. При этом

тальных данных о ротационной полосе, построен-

следует иметь в виду, что успех феноменологии

ной на изомерном состоянии, позволяет установить

в описании состояний ираст-полос до предельно

структуру конфигурации изомера [13]. Исследо-

высоких спинов позволяет считать, что вплоть до

вания структуры ядер в области Z = 100-112 и

этих предельных спинов состояния продолжают

N = 152-162 позволяют отслеживать тенденции

оставаться в значительной степени коллективными

свойств уровней в цепочках изотопов и изотонов,

и не содержат определяющих компонент с высоко-

сопоставлять полученные данные с предсказания-

спиновыми квазичастичными парами.

ми различных теоретических моделей.

Попытка описания ираст-полос для ряда ядер,

Для ряда изотопов Pu, Cm, Fm, No извест-

включая²⁴⁸Cm, была дана в работе [25]. В нашей

ны экспериментальные энергии состояний ираст-

работе описание спектроскопической информации

полос вплоть до спина 32⁺, как в ядре²⁴⁸Cm, и до

дается в терминах элементарных возбуждений, а

34⁺, как в ядре²⁴⁴Pu.

именно фононов различной мультипольности. Для

Анализ зависимости динамических моментов

квадрупольной моды это фононы в приближе-

инерции от квадрата частоты вращения, проведен-

нии Модифицированного Квазичастичного Мето-

ный для ряда трансурановых ядер в [16], показы-

да Случайных Фаз (МКМСФ) [24], когда энер-

вает, что вплоть до предельно измеренных спинов

гия фонона может быть и отрицательной, а мера

не наблюдается обратного загиба (бэкбендинга),

корреляций в основном состоянии — произволь-

кроме единственного ядра²⁴⁴Pu. Отсутствие бэк-

но малой. Фононы с прочими мультипольностями

бендинга означает, что не происходит пересече-

рассматриваются в приближении Тамма-Данкова.

ния основной полосы коллективных состояний и

При этом все фононы формируются в сферическом

состояний, содержащих высокоспиновые квази-

одночастичном базисе, включающем все состоя-

частичные пары. Уникальность указанных полос

ния, волновые функции которых имеют хотя бы за-

соответственно проявляется и в том, что энергии

метную компоненту внутри самого ядра. Описание

полос в четно-четных ядрах для указанных изото-

пов с высокой степенью точности воспроизводятся

сугубо деформированного ядра с использованием

[20] в рамках феноменологии МВБ1. При этом в

сферических ядерных оболочек достигается рас-

смотрением многофононных состояний, что воз-

области более легких ядер для спинов с I^π ≥ 10⁺

расчетные энергии все более и более превышают

можно только через переход от фононов к идеаль-

экспериментальные по мере роста спина. Это нахо-

ным бозонам. Соответствие матричных элементов

дит естественное объяснение через взаимодействие

в бозонном и фононном пространствах позволяет

коллективных состояний с состояниями, постро-

определять параметры бозонной модели. Для па-

енными на высокоспиновых двухквазичастичных

раметров гамильтониана оно представлено в работе

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ОСОБЕННОСТИ РОТАЦИОННЫХ ПОЛОС

463

[24] (см. также ссылки в ней), для параметров E2-

28]. Способ отображения фононных операторов

оператора — в [26].

на бозонные основывается на предположении

замкнутости фононных операторов и их комму-

С полученными таким образом параметрами в

таторов. Замкнутость реализуется через SU(6)-

зависимости от их значений описываются энер-

гии возбуждений как вибрационного, так и рота-

алгебру, а отображение фононных операторов на

ционного характера. Такой подход является уни-

идеальные квадрупольные d-бозоны осуществля-

версальным для описания широкого диапазона

ется таким образом, что их операторы образуют

ядер — от сферических до сильно деформирован-

ту же замкнутую алгебру. Предложено это в

ных, включая переходные.

работе

[27], а несколько подробнее изложено

в статье

[24]. Введение скалярных s-бозонов

Цель настоящей работы заключается в адап-

является здесь чисто формальной процедурой,

тации модели взаимодействующих бозонов для

позволяющей реализовать замкнутость алгебры

описания высокоспиновых состояний ираст-полос

бозонных операторов. Это приводит к бозонному

в тяжелых и сверхтяжелых ядрах. Для этого

гамильтониану

была расширена теоретическая модель, описы-

вающая взаимодействие коллективных состоя-

H_IBM = ε_d n_d + k₁(d⁺ · d⁺ss + H.c.) +

(1)

ний, формирующихся исключительно нижайши-

(

)

ми квадрупольными D-фононами с фононами

+k₂

(d⁺d⁺)⁽²⁾ · ds + H.c.

или квазичастичными парами иной природы, в

1^∑

частности с парами со спинами J^π = 12⁺, 14⁺.

C_L(d⁺d⁺)(L) · (dd)(L),

Учет связи с квазичастичными парами со столь

высокой мультипольностью реализуется впервые.

где H.c. означает эрмитово сопряжение, точка

С помощью разработанной модели нами были

между операторами соответствует скалярному

проанализированы свойства состояний ираст-

произведению, величины ε_d, k₁, k₂, C₀, C₂, C₄

полосы ядра²⁴⁸Cm. В рассматриваемой области

являются параметрами гамильтониана МВБ1.

только для этого ядра в ираст-полосе известны

Все параметры бозонных операторов, включа-

значения B(E2) вплоть до перехода с состояния

ющие операторы электрических квадрупольных

со спином I^π = 28⁺.

переходов, вычисляются на основе процедуры

Марумори [29] через равенство соответствующих

матричных элементов (МЭ) в фермионном и

2. МИКРОСКОПИЧЕСКАЯ ВЕРСИЯ МВБ1

бозонном пространствах. Для получения коррект-

С УЧЕТОМ ВЫСОКОСПИНОВЫХ

ных значений бозонных параметров необходимо

ЭЛЕМЕНТАРНЫХ МОД ВОЗБУЖДЕНИЙ

учитывать связь коллективных, построенных из D-

фононов, и прочих фононов, обозначаемых как B_J

Используемая нами теория для описания ядер-

ных возбуждений с ярко выраженной квадруполь-

с моментами J^π, не превышающими значения 6⁺.

ной коллективностью наиболее подробно была

Учет процессов с б ´ольшими значениями угловых

моментов фононов при вычислении параметров

представлена в [24]. В тяжелых и сверхтяжелых

ядрах нейтроны и протоны заполняют оболочки

гамильтониана (1) является либо несущественным,

82-126, где присутствует одночастичный уровень

либо приводящим к более сложному виду бозон-

с высоким полным спином j15/2, два нуклона на

ного гамильтониана. Учет связи конфигураций,

содержащих как коллективное пространство, так

котором могут дать возбуждения со спинами J^π =

и B_J-фононы, осуществляется в технике теории

= 12⁺ и 14⁺. Поэтому используемая модель требу-

возмущений в варианте Бриллюэна-Вигнера [30].

ет модификации схемы за счет явного расширения

При этом конфигурационное пространство огра-

пространства неколлективных фононов со столь

ничивается компонентами, включающими не более

высокими спинами и соответственно рассмотрения

одного неколлективного фонона.

их взаимодействия со всей совокупностью всех

При описании эффекта пересечения полос

прочих мод возбуждений, включая чисто коллек-

необходимо рассматривать B_J -фононы с более

тивные, сформированные из большой совокуп-

ности одинаковых квадрупольных возбуждений

высокими мультипольностями J^π = 8⁺, 10⁺, а для

с нижайшей энергией и обозначаемые как D-

тяжелых ядер и с J^π = 12⁺, 14⁺. При этом, чтобы

фонон. Одновременное рассмотрение большого

воспроизвести плавный переход в ираст-полосе от

основной полосы к полосе, основанной на высо-

числа фононов, например, больше 8, на фер-

коспиновой двухквазичастичной паре, необходимо

мионном уровне не представляется возможным.

учитывать примеси к коллективным состояниям

Поэтому необходимо от фононного представления

переходить к представлению идеальных бозонов,

фононов B_J с мультипольностями J^π = 2⁺, 4⁺, 6⁺.

для которых точно выполняются коммутационные

При феноменологическом исследовании кол-

соотношения. Делается это в технике МВБ1 [27,

лективных состояний в рамках МВБ1 для ядер,

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

464

ЕФИМОВ, ИЗОСИМОВ

рассматриваемых скорее как деформированные,

обозначаются как

∑

параметр гамильтониана ε_d становится отрица-

n_d(I) = (I|

d+μd_μ|I);

(4)

тельным. Если его рассматривать как однофонон-

ную энергию, то становится очевидным, что для его

описания Квазичастичный Метод Случайной Фазы

P₁(I) =

√

(КМСФ) неприменим, так как он не может дать

Ω(Ω - 1)

как нулевую, так и отрицательную энергию фонона.

× (I|(d⁺ · d⁺ss + s⁺s⁺d · d)|I),

Это возможно в рамках метода Тамма-Данкова,

однако в этом случае не учитываются корреляции в

〈C_L(I)〉 = (I|

(d⁺d⁺)(L) · (dd)(L)|I).

основном состоянии. Поэтому в рассматриваемом

способе определения структуры коллективного ни-

Минимизация функционала (3) по искомым ам-

жайшего квадрупольного D-фонона используется

плитудам осуществляется при выполнении ряда

КМСФ, но с дополнительным условием, что можно

дополнительных условий. Это условия нормировок

уменьшать меру корреляций в основном состоя-

D-фононов, амплитуд бозонных волновых функ-

нии. Это же приводит и к возможности получить

ций |I), амплитуд Боголюбова u и v.

отрицательное значение для однобозонной энергии

Следующие условия не связаны с нормировками

ε_d даже без последующих перенормировок. Таким

функций. Одно из них — это фиксация максималь-

образом, двухквазичастичная структура D-фонона

ного числа бозонов Ω, которое используется при

имеет тот же вид, что и в КМСФ:

построении |I). Условие неизменности Ω при вы-

∑

числении фононных амплитуд (ψ, ϕ) для каждого

D+μ =

√

[ψ₁₂a⁺¹a⁺² +

(2)

21,2;τ=n,p

коллективного состояния приводит к уменьшению

числа квазичастиц на уровнях валентной оболочки

+ ϕ₁₂a2a1]τ(j1j2m1m2|2μ),

и перераспределению фононных амплитуд по вне-

валентным состояниям.

где a⁺(a) — операторы рождения (уничтожения)

Еще одно условие связано с требованием сни-

квазичастиц; 1, 2 обозначают номера одноквази-

жения корреляций в основном состоянии, в чем и

частичных состояний в сферическом базисе; со-

будет помимо прочего заключаться главная идея

стояния1, 2 — сопряженные по времени к 1, 2.

модификации стандартного варианта КМСФ. Вы-

Амплитуды и ψ₁₂, ϕ₁₂ или z⁽⁰⁾ = ψ + ϕ, z⁽¹⁾ = ψ -

полнение этого условия осуществляется введением

- ϕ не зависят от магнитных квантовых чисел и_∑

в минимизируемый функционал слагаемого, регу-

нормированы стандартным образом,

(ψ²¹² -

лирующего величину суммы квадратов ϕ:

1,2;τ

(

)

∑

)(∑

-ϕ²¹²)_τ =

(z⁽⁰⁾¹²z⁽¹⁾¹²)_τ = 1.

1,2;τ

Φ_ϕ = 2χ n_d(I) +

ϕ212τ +

(5)

1,2;τ

Фононные амплитуды ψ, ϕ и параметры Бого-

(

)

)(∑

любова u, v находятся на основе вариационного

χ n_d(I) +

(z⁽¹⁾²¹² + z⁽⁰⁾²

)_τ

принципа из условия минимума энергетического

1,2;τ

функционала

Последнее условие оказалось принципиальным

H_tot = E_vac.q.p. + E(B)0 + (I|H_IBM|I),

(3)

для достижения согласования бозонных средних,

включающего энергию вакуума квазичастиц

амплитуд z(η), u(v) и бозонных амплитуд. Иначе

согласование невозможно.

E_vac.q.p., энергию фононного вакуума E(B)0 и сред-

В результате структура D-фонона опреде-

него значения H_IBM, вычисленного с бозонны-

ляется с использованием довольно сложного

ми волновыми функциями |I) довольно общего

функционала, включающего средние от бозонных

вида, полученными в результате диагонализации

операторов. Если в рамках стандартного КМСФ

бозонного гамильтониана (1) в базисе состояний,

соответствующих неприводимому представлению

решается уравнение HD⁺ = ωD⁺ или 〈DHD⁺〉 -

группы SU(5).

- ω〈DD⁺〉 → min, то множитель Лагранжа ω,

определяемый как ω², является положительной

Таким образом, величина (I|H_IBM|I) явно за-

величиной и трактуется в качестве однобозонной

висит от (ψ, ϕ) и (u, v) через параметры ε_d, k₁,

энергии. В используемом модифицированном ва-

k₂, C₀, C₂, C₄ гамильтониана МВБ1 и неявно

рианте параметр ω не имеет уже такого смысла,

через бозонные волновые функции |I), полученные

а однобозонная энергия, определяемая в качестве

опять с теми же параметрами гамильтониана (1) —

однобозонной энергии ε_d, в ряде случаев, харак-

ε_d, ..., C₄. Средние значения операторов от отдель-

терных для ядер, близких к деформированным,

ных членов гамильтониана по бозонным функциям

оказывается отрицательной.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ОСОБЕННОСТИ РОТАЦИОННЫХ ПОЛОС

465

Выражения для параметров бозонного гамиль-

Во всех описанных случаях расширенная вол-

тониана через амплитуды z(η), u(v) и с учетом

новая функция в фононном представлении имеет

следующий вид:

только D-фононов приведены в работе [24], для

∑

C(0)L — в [31].

Ψ(I) = |ψ_C (I)〉 +

αi1,c₁|(

ψc1 )(I)〉,

(9)

i₁

i₁,c₁

Процессы, приводящие к перенормировке па-

раметров ранее подробнее всего были изложены в

где |ψ_C 〉 есть волновая функция, содержащая су-

работе [24]. Соответствующее взаимодействие, т.е.

перпозицию только D-фононов.

взаимодействие состояний, содержащих только D-

фононы, с состояниями, содержащими дополни-

Конкретная схема перенормировок параметров

тельно один неколлективный B_J -фонон, во втором

гамильтониана приведена в [24], и она остается

порядке приводит к поправкам энергий, а в нашем

неизменной. Зато при изучении пересечения по-

случае — к поправкам параметров бозонного га-

лос необходимо рассмотреть дополнительные моды

мильтониана. При этом, как уже говорилось, рас-

возбуждений и взаимодействие с прочими модами.

сматриваются только неколлективные фононы с

J^π ≤ 6⁺. Помимо перенормировок бозонных пара-

метров данные процессы важны при рассмотрении

2.1. Пересечение полос

связи коллективных состояний с состояниями или

Для описания эффекта пересечения полос

их компонентами, содержащими двуквазичастич-

неколлективные моды возбуждений рассматри-

ные высокоспиновые пары с еще более высокими

ваются явным образом и волновую функцию (9)

спинами с J^π ≤ 10⁺. Как показали полученные

удобнее представить в более развернутом виде, а

оценки, не пренебрежимо малыми оказываются

именно:

матричные элементы трех типов:

|Ψ(I)〉 = α₀ψ_C(I)〉 +

(10)

(I)

〈BJ≤6Dⁿ|H|D+n′ 〉,

(6)

∑

αJ1,c₁B_J

|ψc1 〉 +

(II)

〈BJ=8,10Dⁿ|H|B+J≤6D+n′ 〉,

(7)

J₁=2,4,6,c₁

∑

(III)

〈BJ=12,14Dⁿ|H|B+J=8,10D+n′ 〉.

(8)

αJ2,c₂BJ2|ψc₂ 〉 +

J₂=8,10,c₂

МЭ (I) типа используются для получения поправок

∑

к бозонным параметрам, (I) и (II) — для связи

αJ3,c₃BJ3|ψc₃ 〉,

коллективных состояний, сформированных только

J₃=12,14,c₃

из D-фононных компонент, с состояниями, со-

держащими фермионные пары с J^π ≤ 10⁺. Этого

где с правой стороны вся функция связана в уг-

достаточно для описания коллективных состояний

ловой момент I, суммирование по J означает сум-

и эффекта пересечения полос в ядрах с числом

мирование не только по угловым моментам, но и

нуклонов, меньшим 82. Для более тяжелых ядер,

по всем фононам данной мультипольности. Урав-

нуклоны которых находятся в диапазоне от 84

нение на собственные значения E квазичастично-

го гамильтониана в пространстве представленной

до 124, необходимо рассматривать и совокупность

функции следующее:

матричных элементов (III) типа. При перенор-

мировке параметров бозонного гамильтониана (1)

H|Ψ(I)〉 = E|Ψ(I)〉.

(11)

неколлективные фононы рассматриваются неявно,

Умножая левую сторону этого уравнения на про-

фононы же B_J с J^π > 6⁺ — явно, и бозонная вол-

извольную компоненту, содержащую неколлектив-

новая функция расширяется за счет соответствую-

щих компонент. Так как для описания пересечения

ный фонон B+J|ψci 〉, получаем 〈ψci BJi |H|Ψ(I)〉 =

полос необходимо использовать всю совокупность

= E〈ψciBJi|Ψ(I)〉. Если в этом уравнении не рас-

матричных элементов (I) типа, то вводятся, соот-

сматривать матричные элементы (МЭ), когда фо-

ветственно, идеальные бозоны b_J с J^π ≥ 2⁺. При

ноны B₁ и B₂ находятся в одной группе в соответ-

этом под неколлективными квадрупольными фоно-

ствии с выражением для суммы в (10), то в более

нами понимаются все фононы, кроме нижайшего,

развернутом виде получаем

для которого характерна максимальная коллектив-

α₀〈ψci BJi|H|ψ_C(I)〉 +

ность, за исключением резонансных возбуждений.

При этом следует иметь в виду, что во втором

+ (ω_i + Eci - E)αJi,c_i +

∑

порядке по взаимодействию взаимодействие (I)

^′α_J,c〈ψciBJi|H|B+Jψ_c〉 = 0,

типа использовано для перенормировки бозонных

J,c

параметров.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

466

ЕФИМОВ, ИЗОСИМОВ

∑

где штрих у суммы означает, что в ней отсутствует

β(C, c₂, c₁, J₂, J₁, τ, 7, 9, 4) ×

слагаемое с МЭ 〈ψci BJi |H|B+Jψci〉. Это приводит к

7,9,4;τ

выражению для амплитуд

× ψ(J2)79(n)ψ(J1)94(n^′),

αJi,c_i =

(12)

(

где Jπ1, Jπ2 = 4⁺-14⁺, суммирование по τ означает

α₀〈ψci BJi|H|ψ_C(I)〉 +

суммирование по нейтронам и протонам, ψ(J)12(n) —

(ω_i + Eci - E)

амплитуды неколлективных фононов, которые рас-

)

сматриваются в приближении Тамма-Данкова с

∑

^′α_J,c〈ψciBJi|H|B+Jψ_c〉

учетом только изоскалярного канала взаимодей-

ствия, индексы “1”, “2” означают совокупность

J,c

всех квантовых чисел одночастичных состояний,

Из этого уравнения последовательно получаем все

кроме магнитных; J, n — мультипольность фонона

амплитуды по теории возмущений.

и его номер среди всех существующих в рамках

рассматриваемого одночастичного базиса. Вели-

На первом этапе для Jπ1 = 2⁺, 4⁺, 6⁺

чины γ(. . .) и β(. . .) вычисляются с помощью при-

α₀

αJ1,c₁ = -

(13)

нятого при микроскопическом обосновании МВБ1

(ω₁ + Ec1 - E)

отображения фононов на бозоны. При этом бозон-

× 〈ψc1 BJ1 |H|ψ_C (I)〉.

ный гамильтониан с рассчитываемыми параметра-

ми представлен соотношениями (38)-(44) в работе

На втором этапе для Jπ2 = 8⁺, 10⁺

[24]. Кратко его можно представить в виде

α₀

(14)

αJ2,c₂ =

H_b = H^(0)IBM1 +

(18)

(ω₂ + Ec2 - E)

∑

〈ψc1 BJ1 |H|ψ_C 〉

+ (ω_i + E(b)0)b+ib_i + V⁽¹⁾ + V⁽²⁾ + V⁽³⁾,

(ω₁ + Ec1 - E)

J₁=4,6,c₁

(0)

где H_I

(1) является гамильтонианом МВБ1

× 〈ψc2 BJ2 |H|B+Jψc1 〉.

BM1

с параметрами, определенными только через D-

При этом МЭ 〈ψc1 BJ1=8,10|H|ψC 〉 не рассматри-

фононы, т.е. без учета неколлективных фононов,

вался, как уже говорилось ранее, в силу его мало-

E(b)0 — энергетический сдвиг коллективных со-

сти.

стояний в присутствии хотя бы одного b_i-бозона.

Наконец, на третьем этапе реализуется связь

Следует иметь в виду, что при решении задачи

уже рассмотренных состояний с фононами с муль-

на собственные значения и функции использует-

типольностью Jπ3 = 12⁺, 14⁺:

ся теория возмущений в варианте Бриллюэна-

Вигнера, эффективно отбрасываются те члены

αJ3,c₃ = -

(15)

во втором порядке по взаимодействию, которые

(ω₃ + Ec3 - E)

приводят к перенормировке стандартного гамиль-

∑

αJ2,c₂〈ψc₃ BJ₃ |H|BJ2ψc₂ 〉 =

тониана МВБ1. В этом случае H^(0)IBM1 заменяется

J₂=8,10,c₂

на H_IBM1, т.е. учитывается перенормировка пара-

α₀

∑

метров. Величины ω_i — энергии b_i-бозонов. Не

приводя конкретных выражений для операторов

(ω₃ + Ec3 - E)

(ω₂ + Ec2 - E)

J₂=8,10,c₂

V (1), V ⁽²⁾ и V ⁽³⁾, что сделано в работе [24], отме-

∑

〈ψc1 BJ1 |H|ψ_C 〉

тим, что взаимодействие V⁽¹⁾ содержит бозонные

(ω₁ + Ec1 - E)

операторы (d⁺d)(Ji)s⁺ · b_i, (d⁺(dd)(L)s⁺s⁺)(Ji) ·

J₁=4,6,c₁

· b_i, (d⁺d⁺)(Ji)s · b_i, (d⁺d⁺)(L)d)(Ji) · b_i и эрми-

× 〈ψc2 BJ2 |H|B+J

ψc1 〉〈ψc3 BJ3|H|B+J

ψc2〉.

тово сопряженные к ним. Бозонные параметры

Для фононных МЭ вводим обозначения, которые

при каждом из этих четырех членов типа (I)

соотношения

(6) определяются соответственно

позволяют получить более компактные выражения

для амплитуд:

МЭ 〈D|H|B⁺D⁺〉; 〈D|H|B⁺D⁺D⁺〉; 〈DD|H|B⁺〉;

〈DD|H|B⁺D⁺〉, а их графическое представление

〈ψ_C (I)|H|B+J

(n)ψc1 〉 =

(16)

дано на рис. 1.

∑

= γ(C,c₁,J₁,τ,1,2)ψ(J1)12(n), Jπ1 = 4⁺, 6⁺,

Взаимодействие V⁽²⁾ содержит операторы

1,2;τ

((d⁺d⁺)(L)d⁺)(Ji) · b_iss. Бозонные параметры при

〈ψc2 BJ2 (n)|H|B+J

(n^′)ψc1 〉 =

(17)

них определяются МЭ 〈(DDD)(J)|H|B+J〉, также

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ОСОБЕННОСТИ РОТАЦИОННЫХ ПОЛОС

467

Рис. 1. Графическое изображение матричных элементов взаимодействия D- и B-фононов, соответствующее оператору

V (1). Волнистойлинией обозначается фонон, тонкой линией - квазичастица, вертикальной - взаимодействие.

членами типа (I) соотношения (6), их графическое

задачу через расчет МЭ от различных комбинаций

представление дано на рис. 2. Отличие данных

d-бозонов в пространстве произвольных SU(6)-

членов от всего ряда предыдущих в том, что

функций МВБ1. Конкретно это требует расчета

один B-фонон связан с максимальным числом

бозонных матричных элементов от многобозонных

D-фононов. Таким образом, данный МЭ дает

операторов

прямое взаимодействие коллективного состояния

d⁺, (d⁺d)(L), (d⁺d⁺d⁺)(L), (d⁺d⁺)(L),

(19)

со спином 6⁺ с однофононным состоянием с той

же мультипольностью. Данный МЭ не рассматри-

[d⁺(dd)(L)](λ), [(d⁺d)(L)d](λ).

вается при перенормировке бозонных параметров,

так как члены d⁺d⁺d⁺ddd и d⁺d⁺d⁺dd в бозонном

Их расчет выполнен с помощью однобозонных

гамильтониане не рассматриваются.

генеалогических коэффициентов.

Наконец, V⁽³⁾ комбинируется из (b+ibi2 )(2) ·

Так как решение задачи на собственные значе-

ния и функции осуществляется с помощью теории

· d⁺s, (b+ibi2 )(L) · (d+d+)(L)ss, (b+ibi2 )(L) · (d+d)(L).

возмущений, о чем говорилось выше, то необ-

Бозонные параметры при каждом из этих трех

ходимо произвести суммирование по неколлек-

членов типа (II) и (III) соотношений (7) и

(8)

тивным фононам. Их структура рассматривается

определяются соответственно МЭ 〈DBi1 |H|B⁺〉;_i

в приближении Тамма-Данкова с учетом только

〈DDBi1 |H|B+i〉;

〈DBi1 |H|B⁺D⁺〉, а их графиче-_i

изоскалярных мультипольных сил. В этом случае

ское представление дано на рис. 3.

энергии фононов с мультипольностью J находятся

из уравнения

Единственное отличие в рассматриваемом вза-

имодействии V⁽³⁾ от его же, но в работе [24]

∑

q(J)212

заключается в том, что мультипольность бозонов

F(J)(ω) =

= 0;

(20)

E₁₂ - ω

рассматривается не до 10⁺, а до 14⁺.

1,2;τ

Таким образом, параметры при рассмотрен-

q(J)12 =

√

(-1)l2 ×

ных членах взаимодействия находятся на осно-

2J + 1

ве вычисления МЭ в фермионном пространстве

от квазичастичного гамильтониана по фононным

× 〈1||q(J)||2〉(u₁v₂ + v₁u₂),

функциям с минимальным числом D-фононов, а

где E₁₂ — двухквазичастичная энергия, κ — кон-

учет многофононности переносится на бозонную

станта изоскалярных факторизованных сил, u₁,

v₂ — боголюбовские параметры.

Каждому корню уравнения будет соответство-

вать соответствующая амплитуда фонона

q(J)12

ψ(J)12(n) = -√

(21)

E₁₂ - ω_n

F(J)′(ω_n)

Рис. 2. То же, что на рис. 1, но для оператора V⁽²⁾.

Обозначения как на рис. 1.

Далее производится суммирование по всем фо-

нонам с фиксированной мультипольностью. Дела-

ется это с помощью леммы Жордана и теоремы

о вычетах. В результате получаются выражения

для суммирования произведения амплитуд некол-

B '

лективных фононов. Соответствующие формулы

приведены в Приложении.

Рис. 3. То же, что на рис. 1, но для оператора V⁽³⁾.

Это позволяет для амплитуд α_J,c (13)-(15) с

Обозначения как на рис. 1.

учетом обозначений для МЭ (16) и (17) получить

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

468

ЕФИМОВ, ИЗОСИМОВ

следующие выражения:

пользуются



αJ1,c₁



ω₂(C,c₂,J₂,τ,1,2) =

(25)



(22)

α₀



ωJ1(n) + Ec1 - E

∑

J₁=2,4,6

∑

(n)

1^′,2^′;τ^′

γ(C, c₁, J₁, τ^′, 1^′, 2^′)ψ(J1)1′

′

∑

× γ(C,c₁,J₁,τ,1,2)ψ(J1)12(n),

ωJ1(n) + Ec1 - E

J₁=4,6;c₁;n

1,2;τ

∑



β(C, c₂, c₁, J₂, J₁, τ, 1, 2, 4)ψ(J1 )24(n) =



αJ2,c₂



(23)

α₀



ωJ2(n) + Ec2 - E

∑

1,J1,τ,2,4)

(∑γ(C,c

J₂=8,10

∑

E(J1)24 + Ec1 - E

× ω₂(C,c₂,J₂,τ,1,2)ψ(J2)12(n),

J₁=4,6;c₁

1,2;τ

× β(C,c₂,c₁,J₂,J₁,τ,1,2,4) -



)



∑

αJ3,c₃



^′2^′



(24)

F(J1⁾

(E - Ec1 )

α₀



ωJ3(n) + Ec3 - E

′

+Ec1 -E

1^′,2^′;τ^′

E(J1)1′

J₃=12,14

∑

)

∑

× ω₃(C,c₃,J₃,τ,1,2)ψ(J3)12(n).

β(C, c₂, c₁, J₂, J₁, τ, 1, 2, 4)q(J1 )24

1,2;τ

(J₁)

E₂

+Ec1 -E

Здесь помимо введенных ранее величин γ(. . .) ис-

ω₃(C,c₃,J₃,τ,1,2) =

(26)

∑

(n)∑

1^′,2^′;τ^′

ω₂(C,c₂,J₂,τ^′,1^′,2^′)ψ(J2)1′

′

β(C, c₃, c₂, J₃, J₂, τ, 1, 2, 4)ψ(J2 )24(n) =

ωJ2(n) + Ec2 - E

J₂=8,10;c₂;n

∑

(∑ω₂(C,c₂,J₂,τ,2,4)

β(C, c₃, c₂, J₃, J₂, τ, 1, 2, 4) -

(J₂)

J₂=8,10;c₂

E₂

+Ec2 -E

)

∑

′

∑

β(C, c₃, c₂, J₃, J₂, τ, 1, 2, 4)q(J2 )24

ω₂(C,c₂,J₂,τ^′,1^′,2^′)q(J2)1′

F(J2⁾

(E - Ec2 )

E(J2)

+Ec2 -E

E(J2)24 + Ec2 - E

1^′,2^′;τ^′

1^′2^′

)₂

Осуществляя еще один раз суммирование по

(∑

γ(C, c₁, J₁, τ, 1, 2)q(J1 )12

неколлективным фононам, уравнение на собствен-

E(J1)

-ω₀

1,2;τ

ные значения 〈Ψ|H - E|Ψ〉 = 0 приобретает вид

}

δJ1,2

E_C - E - F₁ - F₂ - F₃ = 0,

(27)

(E - Ec1 - ω₀)F′(J1⁾(ω₀)

где функции F_i имеют следующие выражения:

{

∑

|ω₂(C, c₂, J₂, τ, 1, 2)|²

∑

F₂ =

- (29)

{∑ |γ(C,c₁,J₁,τ,1,2)|2

F₁ =

- (28)

1,2;τ

E(J2)12 + Ec2 - E

(J₁)

J₂=8,10;c₂

E₁

+Ec1 -E

J₁=2,4,6;c₁

1,2;τ

)₂

(∑

)₂

ω₂(C,c₂,J₂,τ,1,2)q(J2)12

(∑

γ(C, c₁, J₁, τ, 1, 2)q(J1 )12

1,2;τ

E(J2)12 + Ec2 - E

(J₁)

E₁

+Ec1 -E

}

1,2;τ

× F(J2)(E - Ec2)

F(J1⁾(E - Ec1

)

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ОСОБЕННОСТИ РОТАЦИОННЫХ ПОЛОС

469

∑

этого достаточно рассматривать переходы между

{∑ |ω₃(C,c₃,J₃,τ,1,2)|2

F₃ =

- (30)

(J₃)

компонентами волновой функции с одинаковыми

J₃=12,14;c₃

1,2;τ

E₁

+Ec3 -E

неколлективными фононами или бозонами, учи-

(∑

тывая действие оператора E2-перехода между

ω₃(C,c₃,J₃,τ,1,2)q(J3)12 )² ×

D-фононными или d-бозонными состояниями.

(J₃)

E₁

+Ec3 -E

1,2;τ

Если ввести более универсальные обозначения

}

для γ(· · · ), ω₂(· · · ), ω₃(· · · ), заменив их на ω(· · · ),

но без индекса, а именно, по правилу, ω(· · · ) =

F(J3⁾(E - Ec3)

= γ(··· ) для J^π = Jπ1 = 2⁺,4⁺,6⁺; ω(··· ) =

= ω₂(··· ) для J^π = Jπ2 = 8⁺,10⁺; ω(··· ) = ω₃(··· )

При вычислении МЭ квадрупольного элек-

трического оператора нас будут интересовать в

для J^π = Jπ3 = 12⁺, 14⁺, то приведенный МЭ E2-

основном переходы вдоль ираст-полосы. Для

переходов будет иметь вид

{

〈Ψ_f |

T (E2)||Ψ_i〉 = α0f α0i

〈ψ(f)C|

T (E2)||ψ(i)C〉 +

(31)

∑

ℜ〈c₁|

T (E2)||c₂〉

ω(C_f , c₁, J, τ, 1, 2)ω(C_i, c₂, J, τ^′, 1^′, 2^′) ×

J=2 c₁(f),c₂(i)

1,2;τ 1^′,2^′;τ^′

}

∑

ψ(J)12(n)ψ(J)1′2′(n)

(ω_J (n) + Ec1 - E_f )(ω_J (n) + Ec2 - E_i)

{

∑

=α0fα0i

〈ψ(f)C|

T (E2)||ψ(i)C〉 +

ℜ〈c₁|

T (E2)||c₂〉 ×

J=2 c₁(f),c₂(i)

[∑

ω(C_f , c₁, J, τ, 1, 2)

ω(C_i, c₂, J, τ, 1, 2)

(J)

E₁

-ε₁

E₁

-ε₂

1,2;τ

(

∑

ω(C_f , c₁, J, τ, 1, 2)q(J)12

∑ ω(C_i,c₂,J,τ^′,1^′,2^′)q(J)1′2′

(ε₁ - ε₂) F(J)(ε1)

E(J)

-ε₁

E(J)

-ε₁

1,2;τ

1^′,2^′;τ^′

1^′2^′

)

∑

ω(C_f , c₁, J, τ, 1, 2)q(J)12

∑ ω(C_i,c₂,J,τ^′,1^′,2^′)q(J)1′2′

F(J)(ε2)

E(J)

-ε₂

E(J)

-ε₂

1,2;τ

1^′,2^′;τ^′

1^′2^′

}

∑

δJ,2

ω(C_f , c₁, J, τ, 1, 2)q(J)12

ω(C_i, c₂, J, τ^′, 1^′, 2^′)q(J)1′2′^]

F′(J)(ω0)(ε1 - ω0)(ε2 - ω0)

(E(J)

-ω₀)

1,2;τ

1^′,2^′;τ^′

(E(J)1′2′^-ω0⁾

где

МЭ только между коллективными компонента-

ε₁ = E_f - Ec1; ε₂ = E_i - Ec2 ;

ми, выраженными через d-бозоны, не затрагивая

⎧

⎫

⎨

⎬

b_J-бозоны. При этом бозонный оператор

T (E2)

I_f

I_i

ℜ = (-1)If+J+Ic2

имеет вид

⎩

⎭

Ic2 J Ic1

(

)₍₂₎

√

T (E2) = e^∗

d⁺s + s⁺d + χE2d⁺d

(32)

(2I_i + 1)(2I_f + 1).

(

)₍₂₎

+e^∗

s⁺(d⁺d)⁽⁰⁾d + d⁺(d⁺d)⁽⁰⁾s

Переходы с неколлективных компонент в коллек-

тивные учитываются при перенормировках эффек-

Микроскопический расчет его параметров с уче-

тивных зарядов [26], что позволяет рассматривать том перенормировок представлен в работе [26].

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

470

ЕФИМОВ, ИЗОСИМОВ

E, МэВ

спаривания определялись по значениям парных

энергий. Мера корреляций в основном состоянии

exp.

248

^∑ϕ²/^∑ ψ2 была принята весьма малой,

coll. 1

coll. 2

равной 0.00225. С данными силовыми константами

th. 1

были произведены расчеты, в результате которых

th. 2

без учета каналов взаимодействия V(2,3) получены

значения параметров H_IBM (1). Следует отметить,

что для рассматриваемого весьма тяжелого ядра

²⁴⁸Cm задача оказывается сильно нелинейной,

что привело к возможности получения различ-

ных параметров гамильтониана. Из возможных

вариантов представлены два, а соответствующие

параметры (1) приведены в табл. 1, из которой

видно, что их различия не слишком велики, а

2 4 6 8 10121416182022242628303234

различия в бозонных энергиях, отмеченных на

I⁺

рис. 4 как “coll.”, весьма заметны. Существенная

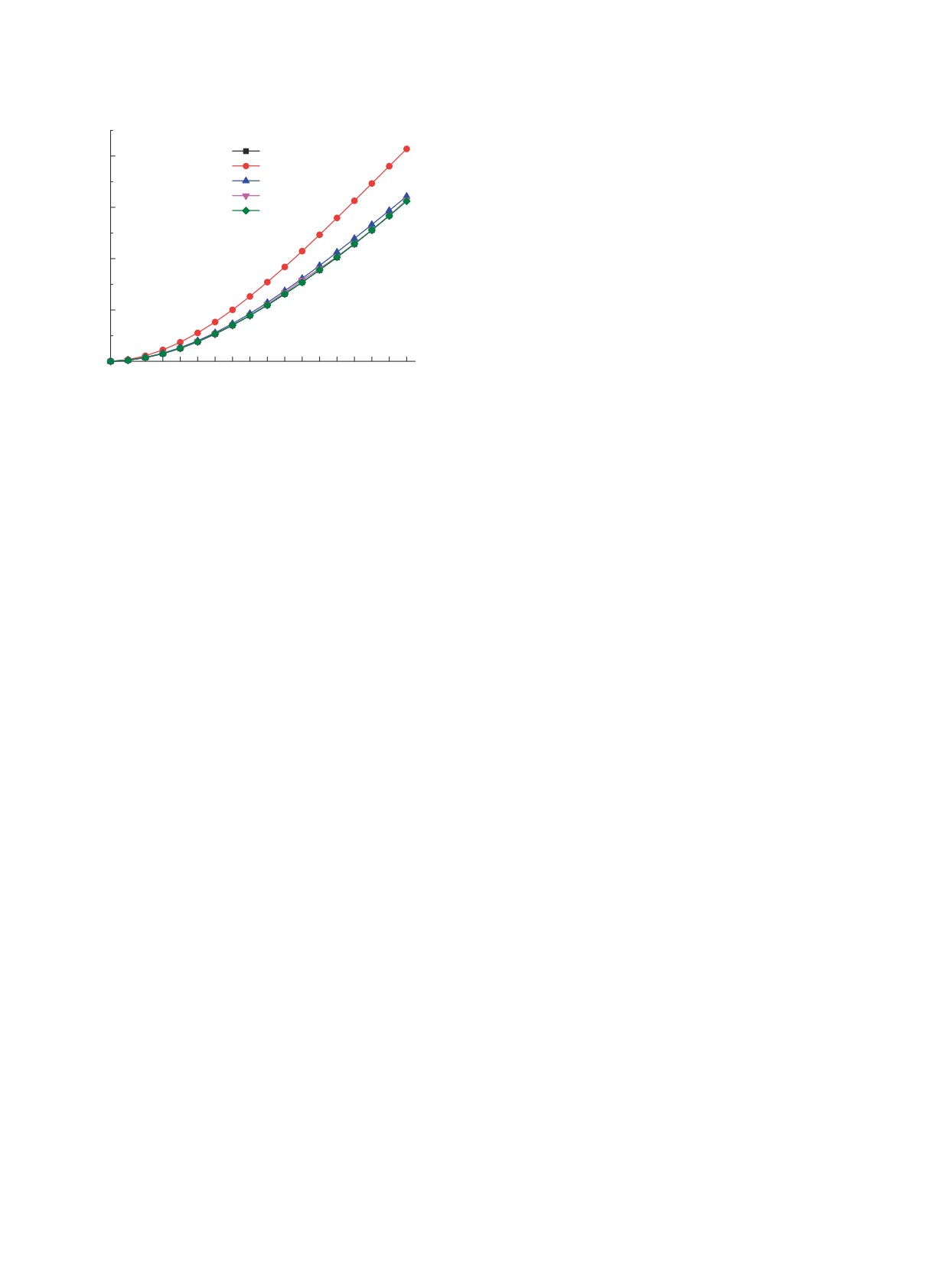
Рис. 4. Энергии состояний ираст-полосы: “coll.1” и

нелинейность задачи коррелирует и со значением

“coll.2” — два варианта расчета без учета каналов

среднего числа квадрупольных бозонов уже в

взаимодействия V⁽²⁾, V⁽³⁾; “th.1”, “th.2” и “exp.” —

основном состоянии, и, как видно из табл. 1, в

теоретические (в двух вариантах расчета) и экспери-

первом варианте оно равно 16.7, а во втором —

ментальные [34] значения (в масштабе рисунка они

15. Причем полное число бозонов равно Ω = 28.

практически сливаются).

Соответственно, это же приводит к существенному

опусканию основного состояния SU(6)-функции

бозонной задачи относительно d-бозонного ваку-

2.2. Результаты расчетов

ума в первом варианте на 25.5 МэВ, во втором —

С единым набором параметров среднего поля

на

25.4. Для двух представленных вариантов

и факторизованных сил рассчитывались как ам-

расчета были взяты различные силовые константы

плитуды D-фононов (2), параметры гамильтониана

спаривания Gn0) и Gp0). В первом варианте это

МВБ1 (1) с учетом перенормировок, так и парамет-

0.0505 и 0.0729 МэВ, во втором — 0.052 и 0.073.

ры расширенного бозонного гамильтониана (18).

Как следует из анализа энергий состояний в

В настоящей работе МЭ квазичастичного

переходных ядрах и как было учтено в работе [35],

остаточного взаимодействия в частично-дырочном

коллективные состояния, построенные на высоко-

и частично-частичном каналах факторизуются

спиновых фононах или бозонах, после пересечения

единым образом в соответствии с [32]. Приведен-

полос могут отличаться в сторону меньшей кол-

ные МЭ мультипольных операторов определяются

лективности. Это проявляется в б ´ольших энергиях

через производную по радиусу от центральной

d-бозонных состояний по сравнению с бозонными

части среднего поля, т.е. q = ∂V (r)/∂rY_J , и

состояниями, которые строятся на фононном ва-

константы G⁽²⁾ = G^τ

и κ(2)ττ′ квад-

кууме или в меньших значениях моментов инер-

τ , Gνπ =0

ции. При этом чем больше коллективность, тем

рупольных факторизованных взаимодействий в

меньше их различия. В силу этого при расчете

частично-частичном (квадрупольное спаривание)

свойств рассматриваемого ядра такое различие от-

и в частично-дырочном каналах. Для сил притя-

носительно энергий возбуждения не учитывалось.

жения приняты знаки констант G⁽²⁾ и κ(2)ττ′ > 0.

Однако следует иметь в виду, что явное присут-

Их значения в реальных расчетах варьируются

ствие высокоспинового двухквазичастичного воз-

относительно оценок, полученных в

[32], и в

буждения, сформированного из уровней среднего

этих единицах равны G⁽²⁾ = 0.625. Оценка для

поля в валентной оболочке, приводит к сокраще-

изовекторной константы через изоскалярную κ₀,

нию конфигурационного пространства, формирую-

полученную там же, равна κ₁ = -0.6κ₀. Это при-

щего амплитуды D-фононов. Если это может слабо

водит к κ_nn = κ_pp = 0.4κ₀; κ_pn = 1.6κ₀ и κ₀ = 1.09.

сказаться на энергиях возбуждения коллективных

Среднее поле принимается в виде сферически-

состояний, то на энергию, формирующую осно-

симметричного потенциала Вудса-Саксона. Его

вание полос, это может сказаться сильнее. Так

параметры взяты из работы [33] и дополнительно

как в работе структура коллективных состояний

не варьировались. Использовался широкий спектр

в присутствии высокоспиновой пары отдельно не

одночастичных состояний, вплоть до резонансных

рассматривалась, то соответствующий сдвиг сле-

состояний, — всего 40 (njl) протонных и столько

дует учитывать как феноменологический параметр

же нейтронных уровней. Константы монопольного

в данной теории. Следует добавить, что учет V (2,3)

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ОСОБЕННОСТИ РОТАЦИОННЫХ ПОЛОС

471

Таблица 1. Параметры H_IBM1 в МэВ, полученные без учета каналов взаимодействия V(2,3); величина n_d есть

среднеечисло бозонов в основном состоянии,т.е. (n_d)_Iπ₌₀+ , максимальное число бозонов Ω = 28,E(0⁺¹) — энергии

основных состояний, полученные с соответствующими параметрами относительно d-бозонного вакуума

Вариант

ε_d

k₁

k₂

C₀

C₂

C₄

n_d

E(0⁺¹)

E(b)0

-0.7651

-0.0388

0.0226

0.0484

0.133

0.0255

16.7

-25.49

-0.83

-0.90503

-0.0354

0.02009

0.1198

0.0843

0.0297

15.0

-25.36

1.95

Таблица 2. Параметры оператора (32) E2-переходов,

от квадрата частоты вращения, что демонстрирует,

e^∗, e∗0 (в e фм²) и χE2 (безразмерен)

насколько тонким является рассмотренный эффект

в данной массовой области.

Вариант

e^∗

χE2

e∗0

Чтобы увидеть различие двух вариантов рас-

чета, на рис. 5 представлены зависимости мо-

9.9939

-0.991

0.0728

ментов инерции от квадрата частоты переходов.

9.3154

-1.0917

0.1473

Экспериментальная кривая обратного загиба не

дает, наблюдается лишь слабый излом. В первом

варианте, несмотря на то, что в соответствии с

канала взаимодействия приводит к сдвигу основно-

рис. 4 имеется удовлетворительное согласие рас-

го состояния, в данном случае — к заметному. Если

чета и эксперимента, проявляется обратный за-

в первом варианте расчета это -1.77, то во втором

гиб, который свидетельствует о том, что первый

-0.68 МэВ. Так как за счет четырехквазичастич-

вариант все же дает пересечение полос. Это же

ных мод, которые не рассматриваются, возможен

подтверждает и бозонный состав волновых функ-

также энергетический сдвиг полос, построенных не

ций, представленный на рис. 6. Хотя, как увидим

на основном состоянии, то вводимый феномено-

ниже, теоретические значения B(E2) при этом

логически сдвиг может быть как отрицательным,

во всей ираст-полосе не имеют заметных спадов.

так и положительным. В гамильтониане (18) он

В этом случае рассмотрение моментов инерции

обозначен как E(b)0 и для первого варианта принят

проявляет себя как исключительно чувствитель-

равным -0.83 МэВ, для второго он, наоборот,

ный инструмент для выявления природы состояний

положителен, а именно 1.95.

ираст-полосы. Следует отметить, что рассмотрение

Для полосы основного состояния в литературе

коллективных состояний в околофермиевской об-

часто используют обозначение g-полосы, которая

ласти в рамках феноменологии МВБ1 [20] приво-

с некоторого спина перестает быть ирастной, а

дит к удовлетворительному описанию ираст-полос

ирастной становится полоса, построенная на вы-

сокоспиновом квазичастичном возбуждении, соот-

ветственно, она называется s-полосой. Для рас-

2J/"², МэВ¹

сматриваемого ядра, в отличие от предыдущих рас-

четов более легких ядер, не вводится ослабление

220

²⁴⁸Cm

связи коллективных и квазичастичных состояний.

На рис. 4 также приведены результаты расчета

200

с учетом V (1,2,3) (взаимодействие V ⁽¹⁾ также вклю-

exp.

чено, несмотря на то, что оно уже учтено при рас-

180

th. 1

th. 2

смотрении перенормировок бозонных параметров,

но во втором порядке по взаимодействию его надо

160

учитывать именно совместно с V(2,3) аналогично

с эффектом интерференции), обозначаемые “th.”.

140

На этом же рисунке приведены экспериментальные

значения — “exp.”, которые по существу совпада-

120

ют с теоретическими значениями в представленном

0.02

0.04

0.06

0.08

0.10

масштабе. Реальное различие не превышает 85 кэВ

(" )2, МэВ2

для первого варианта расчета и 10 кэВ для второго

при I^π < 32⁺. Несмотря на малое различие рас-

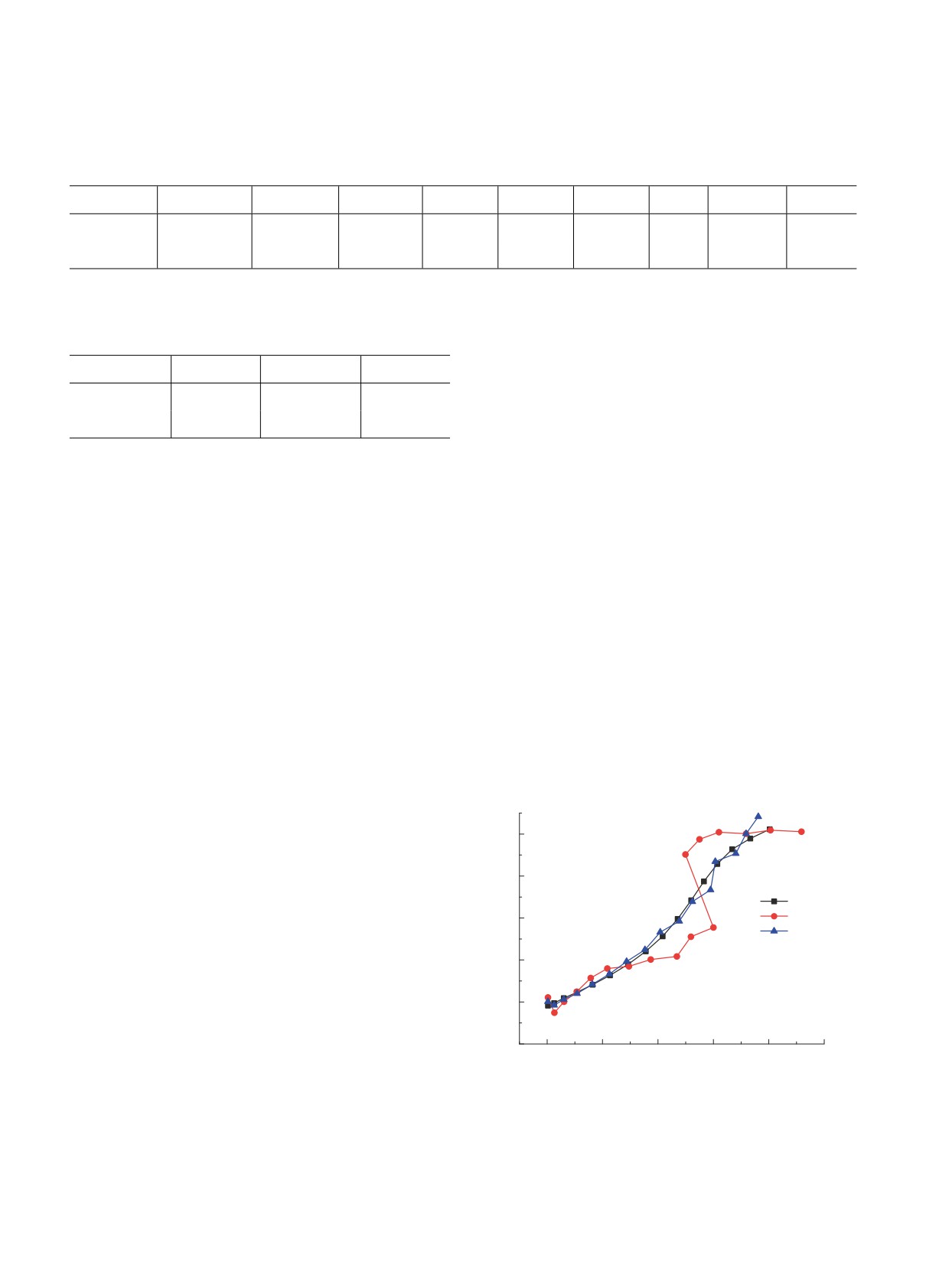
Рис. 5. Зависимость эффективного момента инерции

четных значений энергий от экспериментальных во

от (ℏω)² для ираст-полосы в ядре²⁴⁸Cm по экспери-

втором варианте, тем не менее не воспроизводится

ментальным значениям энергий и для двух вариантов

расчета.

небольшое изменение в наклоне момента инерции

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

472

ЕФИМОВ, ИЗОСИМОВ

Бозонный вклад

моментов инерции, приведенных на рис. 5. Та-

ким образом, можно предположить, что отсутствие

0.75

пересечения полос в рассматриваемой массовой

первый вариант теории

области связано с увеличением энергий состояний,

coll.

0.60

построенных на неколлективных возбуждениях за

b(2)

b(4)

счет сужения конфигурационного пространства,

0.45

b(6)

на котором строятся D-фононные возбуждения.

b(8)

b(10)

Величина данного сдвига, E(b)0, принята равной

0.30

b(12)

1.95 МэВ и может считаться небольшой по срав-

b(14)

нению с E(0⁺¹) = -25.36 МэВ, также приведенной

0.15

в табл. 1. Следует также учитывать малость энер-

гий ираст-полосы. Относительная малость энергий

ираст-полосы при спинах I^π < 34⁺

приводит к

0 2 4 6 8 10121416182022242628303234

тому, что пересечение основной и s-полос может

I⁺

произойти при больших спинах по сравнению с

теми, что известны из эксперимента.

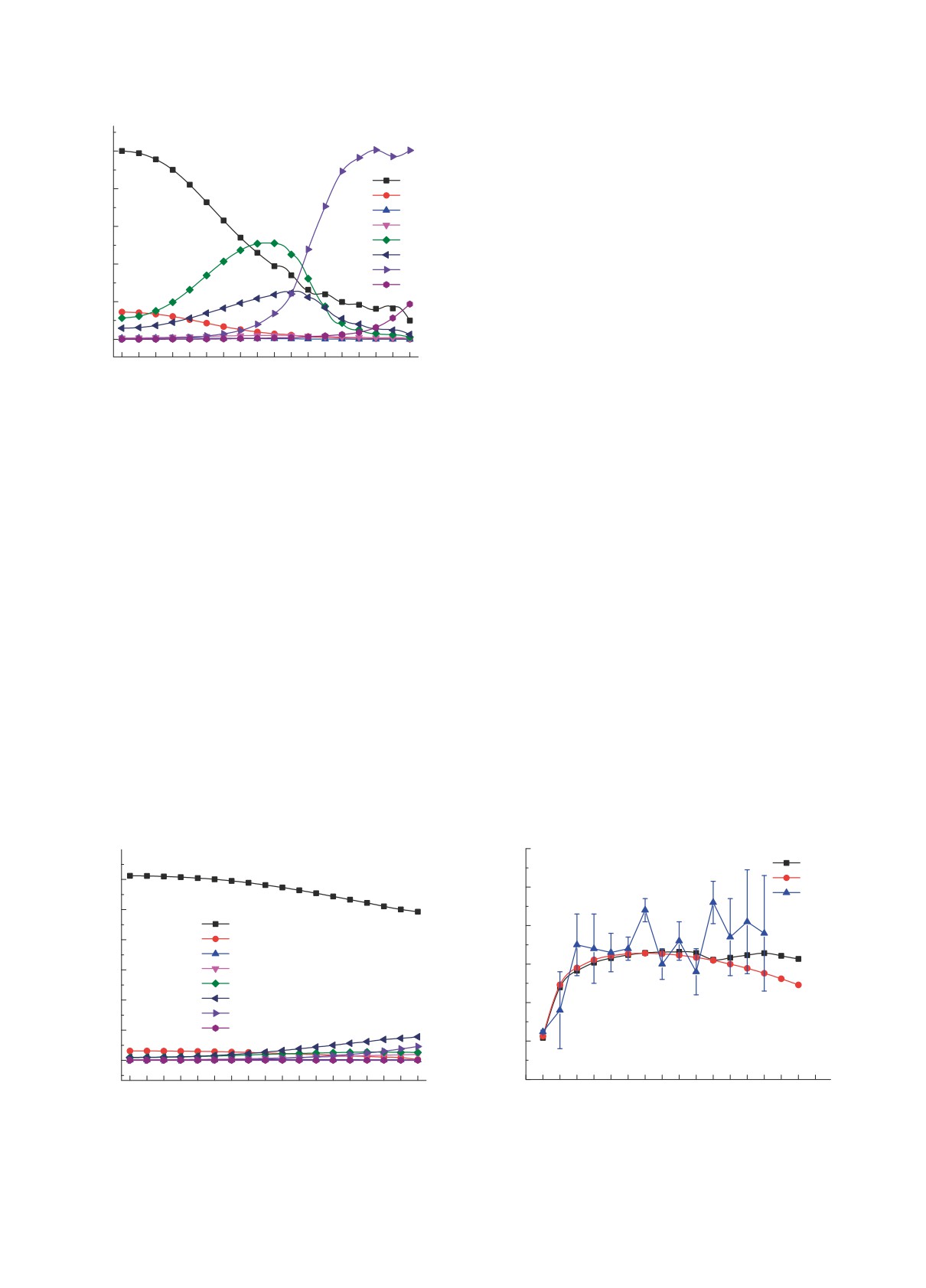
Рис. 6. Бозонный состав волновых функций ираст-

По результатам первого варианта расчета пе-

полос в первом варианте расчета, “coll.” — вклад в

функцию компонент, содержащих только d-бозоны;

ресечение полос, как это видно из рис. 6, осу-

b(J) — вклад от всех компонент, содержащих раз-

ществляется при спинах I^π = 22⁺, 24+ за счет

личные бозоны с фиксированным моментом J, т.е.

замещения, в том числе и чисто коллективной

∑

i₁,c₁

|αJ,i₁,c₁ |², где амплитуды α определяются в (9).

компоненты на компоненту, включающую квази-

частичную пару с моментом именно 12⁺, а не

14⁺. Связано это оказалось с заметным превы-

вплоть до предельно известных спинов. Это мо-

шением МЭ 〈ψc2 BJ2=12|H|BJ1=8,10^ψc1〉надМЭ

жет свидетельствовать о том, что неколлективные

высокоспиновые фононы или квазичастичные пары

〈ψc2 BJ2=14|H|BJ1=10^ψc1〉.

оказывают минимальное влияние на наблюдаемые

Для второго варианта расчета бозонный состав

состояния. Этому соответствует второй вариант

волновых функций представлен на рис. 7. Из него

расчета. Уже расчет энергий только с гамильтони-

видно, что для всех состояний вплоть до спина 32⁺

аном МВБ1 (1) дает значения энергий, близкие к

их природа остается практически чисто коллек-

экспериментальным, а последующий учет высоко-

тивной. Компоненты с высокоспиновыми парами

спиновых мод оказывает не такое большое влия-

начинают быть заметными лишь с состояния с I^π =

ние на результат. Происходит это из-за заметного

= 20⁺, доходя далее до 13%.

сдвига энергий, учитываемого за счет введенного

В работе [36] было отмечено, что только анализ

энергетических спектров не может говорить о при-

параметра E(b)0, приведенного в табл. 1. Именно

роде бэкбендинга и механизме его формирования.

второй вариант дает удовлетворительное описание

B_W(E2; I I

Бозонный вклад

800

248

th. 1

второй вариант теории

0.90

th. 2

700

exp.

0.75

coll.

600

0.60

b(2)

b(4)

b(6)

500

0.45

b(8)

0.30

b(10)

400

b(12)

0.15

b(14)

300

200

0 2 4 6 8 10121416182022242628303234

2 4 6 8 10121416182022242628303234

I⁺

Рис. 7. То же, что и на рис. 6, но для второго варианта

Рис. 8. Теоретическиеи экспериментальные[34] значе-

расчета.

ния вероятностейE2-переходоввнутриираст-полосы.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ОСОБЕННОСТИ РОТАЦИОННЫХ ПОЛОС

473

Необходимо привлекать дополнительные данные.

Для проведения экспериментов в области

К ним, в частности, относятся вероятности пере-

сверхтяжелых ядер крайне важно иметь пред-

ходов между состояниями. Величины B(E2; I →

ставление о свойствах хотя бы нескольких низ-

колежащих уровней в исследуемых ядрах [40].

→ I - 2) представлены на рис. 8, где расчетные

Интерпретация полученных экспериментальных

значения получены без введения эффективных за-

данных требует применения и развития адекватных

рядов [26]. Параметры оператора E2-переходов

теоретических моделей. Развитая в настоящей

(32) приведены в табл. 2.

работе модель позволила успешно описать экспе-

То, что при этом удается воспроизвести аб-

риментальные данные по моментам инерции для

солютные значения B(E2), связано не только с

ядра 248Cm и по величинам B(E2) вплоть до

использованием большого одночастичного базиса,

высоких значений спина уровней ираст-полосы.

но и с учетом эффекта поляризации фононного

Модель является перспективным инструментом

вакуума (см. [26]). Этот эффект вызван примесью к

как для описания, так и для предсказания свойств

фононному вакууму двухфононных состояний DB,

ираст-полос в широкой области атомных ядер,

он существенен при рассмотрении фононов в при-

включая тяжелые и сверхтяжелые ядра.

ближении Тамма-Данкова, но его нет в приближе-

нии КМСФ, а в нашем случае он возникает из-за

ПРИЛОЖЕНИЕ

используемой модификации КМСФ.

Как видно из рис. 8, оба варианта расчета в пре-

Выражения для функции F(J)(ε) (20) и ампли-

делах экспериментальной неопределенности дают

примерно одинаковое качество описания измере-

туд фононов ψ(J)τ12(n) (21) позволяют с помощью

ний. В методическом плане любопытен первый ва-

леммы Жордана и теоремы о вычетах получить

риант тем, что, хотя он дает пересечение полос, но

следующее выражение:

при этом заметного уменьшения значений B(E2) не

∑ψ(J)

происходит.

τ 12

(n)ψ(J)τ′34(n)=

ε-ω_n

По нашему мнению, в рассматриваемом тя-

желом ядре и во всей соответствующей области

реализуется именно то, что дается в описании через

q(J)τ12q(J)τ′34

второй вариант расчета.

(E₁₂ - ε)(E₃₄ - ε)F(J)(ε)

δ₁₃δ₂₄ + (-1)j1-j2+^Jδ₁₄δ₂₃

3. ЗАКЛЮЧЕНИЕ

⁻2δττ′

E₁₂ - ε

Если нижайший фонон именно квадрупольного ти-

В ротационных полосах тяжелых и сверхтя-

па (n = 0) в рассматриваемой сумме не учитывать,

желых ядер может проявляться ряд особенностей

то имеем

[13-17, 37-39]. Одна из них — отсутствие обрат-

ного загиба (бэкбендинга) в зависимости момента

∑

ψ(J)τ12(n)ψ(J)τ′,34(n)=

инерции от квадрата частоты вращения — проана-

ε-ω_n

лизирована в настоящей работе с использованием

n>0

расширенной модели взаимодействующих бозонов.

q(J)τ12

q(J)τ′34

В рамках микроскопической версии МВБ1 с ис-

(E₁₂ - ε) (E₃₄ - ε) F(J)(ε)

пользованием элементарных мод и эффективного

факторизованного взаимодействия на основе сфе-

δ₁₃δ₂₄ + (-1)j1-j2+^Jδ₁₄δ₂₃

−

δ_ττ′

рического одночастичного базиса были проанали-

E₁₂ - ε

зированы свойства состояний ираст-полосы в ядре

²⁴⁸Cm. Выяснена возможная причина отсутствия

q(J)τ12

q(J)τ′34

−

δJ,2.

пересечения полос в данной массовой области.

(E₁₂ - ω₀) (E₃₄ - ω₀)_F (J)^′(ω₀) (ε - ω0)

Включение в модель бозонов с высокими спина-

ми (J^π > 10⁺) позволило существенно расширить

Это позволяет получить необходимые выра-

область применения модели как для описания эф-

жения для суммирования по фононам Тамма-

фектов пересечения полос, так и для его отсутствия

Данкова:



в данной массовой области при довольно высоких

∑



спинах (до I^π ≤ 34⁺). Именно факт отсутствия

ψ(J)τ12(n)ψ(J)τ′1′2′(n)



пересечения полос делает тяжелые и сверхтяжелые

(ω_n - ε₁)(ω_n - ε₂)

n>0

ε₁ = ε₂

ядра, возможно, самым подходящим полигоном, на

котором можно использовать традиционные ядер-

= δ_ττ′δ₁′₁δ₂′₂

ные модели.

(E₁₂ - ε₁)(E₁₂ - ε₂)

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

474

ЕФИМОВ, ИЗОСИМОВ

(

(J)

q_τ

R. Mukhin, J. Piot, et al., Phys. Rev. C 104, 044609

q(J)τ′1′2′

(2021), doi: 10.1103/PhysRevC.104.044609

(ε₁ - ε₂) F(J)(ε₁) (E₁₂ - ε₁) (E₁′₂′ - ε₁)

12.

A. Sobiczewski and K. Pomorski, Prog. Part. Nucl.

(J)

)

q_τ

Phys. 58, 292 (2007).

q(J)τ′1′2′

13.

R.-D. Herzberg and D. M. Cox, Radiochim. Acta 99,

F(J)(ε₂) (E₁₂ - ε₂) (E₁′₂′ - ε₂)

441 (2011).

δJ,2

14.

D. Ackermann and Ch. Theisen, Phys. Scr. 92,

083002 (2017).

F(J)′(ω₀)(ε₁ - ω₀)(ε₂ - ω₀)

15.

D. Ackermann, EPJ Web Conf. 223, 01001 (2019).

(J)

q_τ

16.

R.-D. Herzberg, EPJ Web Conf. 131, 02004 (2016),

q(J)τ′1′2′

(E₁₂ - ω₀) (E₁′₂′ - ω₀)

doi: 10.1051/epjconf/201613102004

17.

Ch. Theisen, P. T. Greenlees, T.-L. Khoo, P. Cho-

wdhuryd, and T. Ishi, Nucl. Phys. A 944, 333 (2015).

∑

ψ(J)τ12(n)ψ(J)τ′1′2′(n)

18.

B. Nerlo-Pomorska, K. Pomorski, P. Quentin, and

= δ_ττ′δ₁′₁δ₂′₂

(ω_n

- ε)²

(E12 - ε)2

J. Bartel, Phys. Scr. 89, 054004 (2014).

n>0

19.

P. T. Greenlees, J. Rubert, J. Piot, et al., Phys. Rev.

(J)

F′(J)(ε)

q_τ

Lett. 109, 012501 (2012).

q(J)τ′1′2′

20.

А. Д. Ефимов, И. Н. Изосимов, ЯФ 84, 421 (2021)

F(J)2(ε) (E₁₂ - ε) (E₁′₂′ - ε)

[A. D. Efimov and I. N. Izosimov, Phys. At. Nucl. 84,

(J)

q_τ

660 (2021)].

q(J)τ′1′2′

21.

А. Д. Ефимов, В. М. Михайлов, Изв. РАН. Сер.

F(J)(ε) (E₁₂ - ε)² (E₁′₂′ - ε)

физ. 82, 1395 (2018) [A. D. Efimov and V. M. Mi-

(J)

khajlov, Bull. Russ. Acad. Sci.: Phys. 82,

1266

q_τ

q(J)τ′1′2′

(2018)].

F(J)(ε) (E₁₂ - ε) (E₁′₂′ - ε)²

22.

А. Д. Ефимов, В. М. Михайлов, Изв. РАН. Сер.

(J)

физ. 83, 1244 (2019) [A. D. Efimov and V. M. Mi-

δJ,2

q_τ

q(J)τ′1′2′

khajlov, Bull. Russ. Acad. Sci.: Phys. 83,

1136

F(J)′(ω₀)(ε - ω₀)² (E12 - ω0) (E1′2′ - ω0)

(2019)].

23.

А. Д. Ефимов, И. Н. Изосимов, ЯФ 84, 298 (2021)

[A. D. Efimov and I. N. Izosimov, Phys. At. Nucl. 84,

СПИСОК ЛИТЕРАТУРЫ

408 (2021)].

1. Ю. Ц. Оганесян, Вестн. РАН 90,

312

(2020)

24.

А. Д. Ефимов, ЯФ 83, 380 (2020) [A. D. Efimov,

[Yu. Ts. Oganessian, Herald Russ. Acad. Sci. 90, 207

Phys. At. Nucl. 83, 651 (2020)].

(2020)].

25.

M. Diebel and U. Mosel, Z. Phys. A 303, 131 (1981).

2. Yu. Ts. Oganessian and V. K. Utyonkov, Nucl. Phys.

26.

А. Д. Ефимов, В. М. Михайлов, Изв. РАН. Сер.

A 944, 62 (2015).

физ. 77, 948 (2013) [A. D. Efimov and V. M. Mi-

3. Yu. Ts. Oganessian, V. K. Utyonkov, N. D. Kov-

khajlov, Bull. Russ. Acad. Sci.: Phys. 77, 862 (2013)].

rizhnykh, et al., Phys. Rev. C 106, L031301 (2022),

27.

D. Janssen, R. V. Jolos, and F. Donau, Nucl. Phys. A

doi: 10.1103/PhysRevC.106.L031301

224, 93 (1974).

4. Yu. Ts. Oganessian, V. K. Utyonkov, D. Ibadullayev,

28.

A. Arima and F. Iachello, Phys. Rev. Lett. 35, 1069

et al., Phys. Rev. C 106, 024612 (2022),

(1975).

https://doi.org/10.1103/PhysRevC.106.024612

29.

T. Marumori, K. Takada, and F. Sakata, Prog. Theor.

5. Yu. Ts. Oganessian, A. Sobiczewski, and G. M. Ter-

Phys. Suppl. 71, 1 (1981).

Akopian, Phys. Scr. 92, 023003 (2017).

30.

Н. Марч, У. Янг, С. Сампантхар, Проблема многих

6. V. Utyonkov, Yu. Ts. Oganessian, S. Dmitriev, et al.,

тел в квантовой механике (Мир, Москва, 1969)

EPJ Web Conf. 131, 06003 (2016).

[N. H. March, W. H. Young, and S. Sampanthar,

7. S. A. Giuliani, Z. Matheson, W. Nazarewicz, et al.,

The Many-Body Problem in Quantum Mechanics

Rev. Mod. Phys. 91, 011001 (2019).

(Cambridge, Univ. Press, 1967)].

8. M. Block, F. Giacoppo, F.-P. Heβberger, and

31.

A. D. Efimov and V. M. Mikhajlov, EPJ Web Conf. 38,

S. Raeder, Riv. Nuovo Cimento 45, 279 (2022).

17005 (2012).

9. M. S. Tezekbayeva, A. V. Yeremin, A. I. Svirikhin,

32.

A. Bohr and B. Mottelson, Nuclear Structure

et al., Eur. Phys. J. A 58, 52 (2022).

(Benjamin, New York, 1975), Vol. 2.

10. K. Hauschild, A. Lopez-Martens, R. Chakma, et al.,

33.

V. I. Isakov, K. I. Erokhina, H. Mach, M. Sanchez-

Eur. Phys. J. A 58, 6 (2022),

Vega, and B. Fogelberg, Eur. Phys. J. A 14, 29 (2002).

https://doi.org/10.1140/epja/s10050-021-00657-8

34.

Brookhaven National Laboratory, National Nuclear

Data Center (online),

11. K. Kessaci, B. J. P. Gall, O. Dorvaux, A. Lopez-

Martens, R. Chakma, K. Hauschild, M. L. Chelnokov,

http://www.nndc.bnl.gov/nndc/ensdf/

V. I. Chepigin, M. Forge, A. V. Isaev, I. N. Izosimov,

35.

A. D. Efimov and V. M. Mikhajlov, Phys. Rev. C 59,

D. E. Katrasev, A. A. Kuznetsova, O. N. Malyshev,

3153 (1999).

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023

ОСОБЕННОСТИ РОТАЦИОННЫХ ПОЛОС

475

36. G.-O. Xu and J.-Y. Zhang, Nucl. Phys. A 343, 189

39. F. P. Heβberger, S. Antalic, B. Suligano, et al., Eur.

(1980).

Phys. J. A 43, 55 (2010).

37. M. Asai, F. P. Heβberger, and A. Lopez-Martens,

40. А. Д. Ефимов, И. Н. Изосимов, Письма в ЭЧАЯ 18,

Nucl. Phys. A 944, 308 (2015).

551 (2021) [A. D. Efimov and I. N. Izosimov, Phys.

38. F. P. Heβberger, Eur. Phys. J. A 53, 75 (2017).

Part. Nucl. Lett. 18, 658 (2021)].

PECULARITIES OF ROTATION BANDS IN HEAVY AND SUPERHEAVY

NUCLEI. DESCRIPTION OF YRAST-BAND STATES IN²⁴⁸Cm

A. D. Efimov1),2), I. N. Izosimov³⁾

¹⁾Admiral Makarov State University of Maritime and Inland Shipping, St. Petersburg, Russia

²⁾Ioffe Physical-Technical Institute, Russian Academy of Sciences, St. Petersburg, Russia

³⁾Joint Institute for Nuclear Research, Dubna, Russia

A further development of the expanded microscopic version of the IBM is presented by considering

two-quasiparticle phonons with multipolarity up to J^π = 14⁺. The developed theoretical scheme is applied

to describe the properties of the yrast-band states in²⁴⁸Cm up to spin 34⁺. This heavy transactinide nucleus

is the only nucleus in this mass region where the values of B(E2) up to spin I^π = 28⁺ are measured. That

is why it is considered foremost, since this information allows us to test the presented theoretical scheme

based on a larger volume of experimental data. The region of transactinide nuclei differs from lighter ones

by the absence of the effect of the back bending in the moment of inertia dependence on the square of the

rotation frequency up to the spin I^π = 34⁺. This article is intended in particular to find out the reason for

this effect. Peculiar properties of the rotation bands in heavy and superheavy nuclei are discussed.

ЯДЕРНАЯ ФИЗИКА том 86

№4

2023