ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 4, с. 476-484
ЯДРА
МОДЕЛЬ МАСС ЯДЕР НА ОСНОВЕ БАЙЕСОВСКОЙ ОЦЕНКИ
ЛОКАЛЬНЫХ РАЗНОСТНЫХ СООТНОШЕНИЙ ЭНЕРГИЙ СВЯЗИ
© 2023 г. К. А. Стопани1)*, Е. В. Владимирова2),
В. В. Негребецкий2), М. В. Симонов2),3), Т. Ю. Третьякова1),2)
Поступила в редакцию 15.02.2023 г.; после доработки 27.02.2023 г.; принята к публикации 28.02.2023 г.
По материалам доклада на "ICPPA-2022”
С помощью метода Монте-Карло цепей Маркова и метода регуляризации Тихонова получены
байесовские оценки значения величины остаточной энергии нейтрон-протонного взаимодействия
Δnp. С использованием этих оценок рассчитана таблица масс ядер с A > 20. Точность сделанных
предсказаний оценивается путем сравнения с экспериментальными данными AME2020 и другими
теоретическими моделями.
DOI: 10.31857/S0044002723040347, EDN: EGCUUV
1. ВВЕДЕНИЕ
GKT в этих работах метод вычисления массовой
таблицы был основан на рекурсивном применении
Модели масс атомных ядер, основанные на
формулы массового соотношения с использова-
феноменологических выражениях, связывающих
нием в качестве начальных значений эксперимен-
массы или энергии связи соседних ядер на NZ-
тально измеренных ядерных масс из баз данных
диаграмме, известны достаточно давно. Массо-
AME. Точность предсказания масс ядер в области,
вая модель, представленная в работе Гарви и
непосредственно примыкающей к области экспе-
Келсона [1] и построенная на базе разностных
риментально измеренных масс, не уступает точно-
соотношений GKL и GKT, связывающих между
сти моделей, основанных на более детальных фи-
собой массы шести соседних ядер, часто приме-
зических принципах [9]. В ряде современных статей
нялась в такой области, как физика нейтронных
рассматриваются новые типы массовых уравнений,
звезд [2]. В публикациях [3-5] было показано,
полученных на основе уравнений GKL и GKT с
что подобные соотношения масс соседних ядер
добавлением неоднородной правой части [10-12].
определяют разностные уравнения в координатах
Очевидно, что в силу присущей локальным мас-
N и Z, являющиеся дискретными аналогами
совым соотношениям принципиальной упрощенно-
дифференциальных уравнений в частных произ-
сти, а также ввиду погрешностей эксперименталь-
водных. Предложенный в [1] метод построения
ного измерения ядерных масс, любое из выше-
модели заключался в нахождении семейства общих
упомянутых массовых уравнений является прибли-
решений разностного уравнения (в этом случае
женным, т.е. неявно включает в себя дополнитель-
однородного) и выборе того решения из семейства,
ное флуктуирующее слагаемое. В настоящей рабо-
которое минимально отклоняется от масс, изме-
те это слагаемое рассматривается как случайная
ренных экспериментально.
величина, аналогичная шуму, и с помощью мето-
дов байесовской статистики производится анализ
В работах [6-8] для построения массовой мо-
поведения случайной составляющей в массовом
дели использовано локальное массовое соотно-
соотношении Δnp, после чего на основе получен-
шение Δnp, определяющее, в соответствии с [3],
ных результатов делаются новые оценки значений
неоднородное разностное уравнение. В отличие от
ядерных масс.
массовых моделей на основе соотношений GKL и
1)Научно-исследовательский институт ядерной физики
2. БАЙЕСОВСКИЕ ОЦЕНКИ
имени Д.В. Скобельцына, Москва, Россия.
ЗНАЧЕНИЙ Δnp
2)Московский государственный университет имени
М.В. Ломоносова, физический факультет, Москва,
Массовое соотношение Δnp определяется сле-
Россия.
дующим выражением:
3)Университет Юстуса Либиха, Гисен, Германия.
*E-mail: kstopani@sinp.msu.ru
Δnp(N,Z) = W(N,Z) - W(N - 1,Z) -
(1)
476
МОДЕЛЬ МАСС ЯДЕР НА ОСНОВЕ БАЙЕСОВСКОЙ ОЦЕНКИ
477
np
, МэВ
3.5
Четные А (четные N, четные Z)
Четные А (нечетные N, нечетные Z)
Нечетные А (нечетные N, четные Z)
3.0
Нечетные А (четные N, нечетные Z)
2.5
2.0
1.5
1.0
0.5
0
0.5
0
50
100
150
200
250
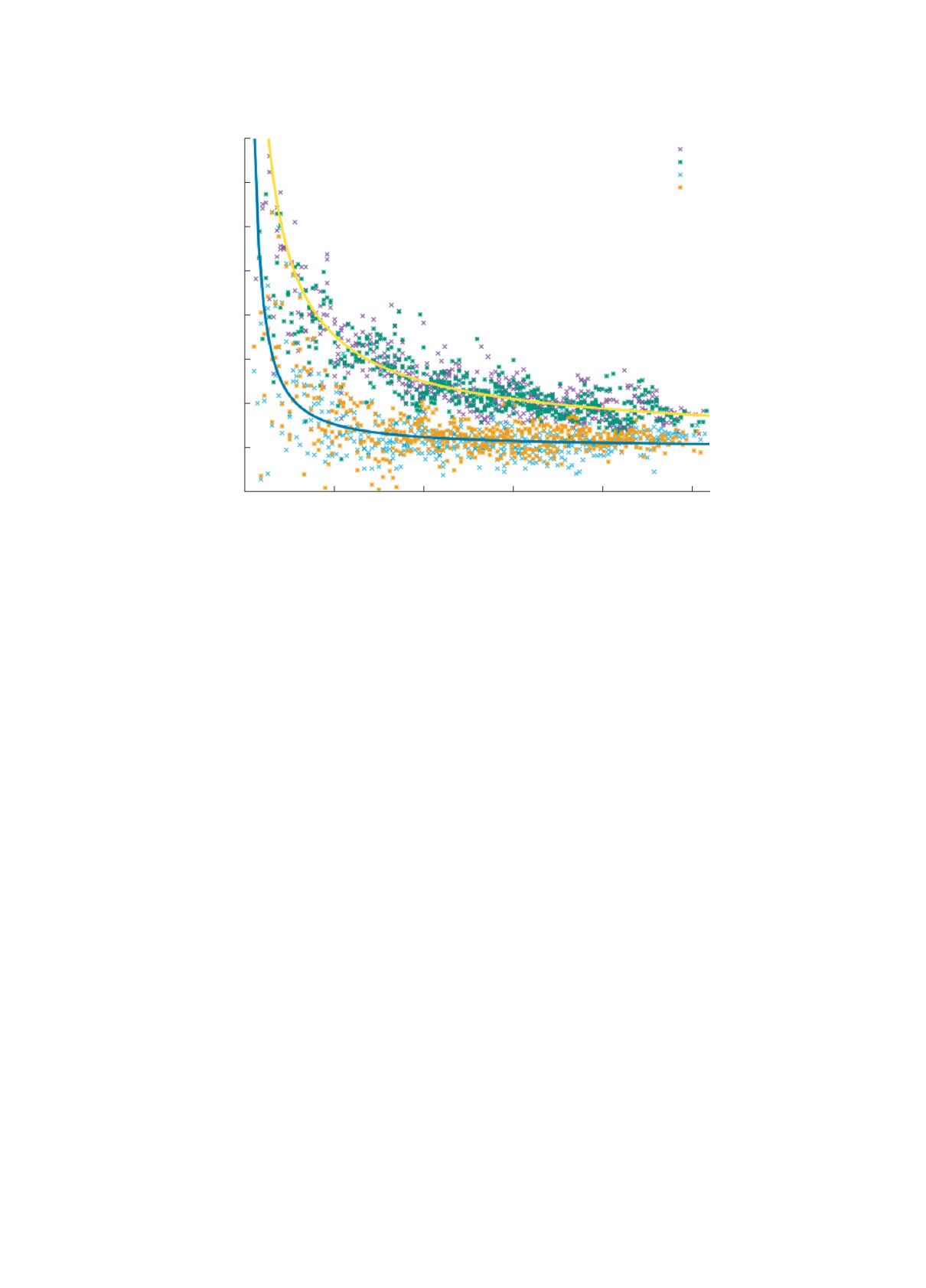
A
Рис. 1. Значения величины Δnp, вычисленные по данным AME2016. Кривые соответствуют аппроксимациям из
работы [8].
- W(N,Z - 1) + W(N - 1,Z - 1),
где Ppost(x|θ) — функция правдоподобия, или ве-
роятность наблюдения данных x при данном зна-
где W (N, Z) — энергия связи ядра (N, Z). Поведе-
чении параметра θ, Pprior(θ) — априорное распре-
ние этой величины на экспериментальных данных
деление, P (x) — маргинальное распределение x,
из библиотеки AME2016 [13] в зависимости от
служащее для нормировки [14]. В подходе байесов-
массового числа A = N + Z показано на рис. 1.
ской статистики использование теоремы Байеса
Видно, что на плоскости (A, Δnp) точки образуют
для оценки статистических характеристик неиз-
две группы, соответствующие четным и нечетным
вестного параметра θ имеет следующую естествен-
значениям A, и при A > 20 в рамках каждой группы
ную интерпретацию: из заранее известной инфор-
точки образуют достаточно однородные области,
мации о θ, содержащейся в априорном распреде-
в которых, благодаря компенсации слагаемых в
лении, и новых данных x извлекается суммарная
выражении (1), практически полностью сглажены
информация о поведении θ в виде апостериорного
эффекты скачков при заполнении оболочек. Это
распределения. В рассматриваемом случае в каче-
свойство и позволило использовать выражение
Δnp для построения массовых таблиц в [3, 6-
стве данных x выступает набор значений {Δnp },
вычисленных на основе экспериментальной базы
8]. В то же время ввиду наличия нескомпенсиро-
ванных проявлений структуры каждого отдельного
данных ядерных масс AME2016, а неизвестным
ядра, а также погрешностей экспериментальных
параметром θ являются интересующие нас в ко-
данных точки на графике отнюдь не сливаются в
нечном счете параметры распределения Δnp. Та-
гладкую функциональную зависимость, а хаоти-
ким образом, для построения байесовской модели
чески распределены в пределах группы. С фор-
необходимо задать вид, который имеют распреде-
мальной точки зрения можно рассмотреть значения
ления, входящие в правую часть выражения (2).
Δnp как случайные величины и воспользоваться
Анализируя характер разброса точек в раз-
методами байесовской статистики для того, чтобы
личных областях рис. 1, можно заключить, что
определить их распределение.
разумным выбором функции правдоподобия будет
Согласно теореме Байеса апостериорное рас-
следующий: при каждом значении A точки Δnp
пределение Ppost(θ|x) случайной величины θ на
имеют нормальное распределение с параметрами
основе данных из наблюдений x вычисляется по
μA и σ2A, а ввиду независимости всех отдельных
формуле
значений Δnp результирующая функция правдопо-
Ppost(θ|x) = P(x|θ)Pprior(θ)/P(x),
(2)
добия является произведением функций плотно-
ЯДЕРНАЯ ФИЗИКА том 86
№4
2023
478
СТОПАНИ и др.
сти вероятности нормального распределения для
для которых оптимальной формой последователь-
каждого Δnp из набора {Δnp }. Таким образом,
ности являются, соответственно, фиксированная
подлежащими оценке неизвестными параметрами
константа и линейная функция. Последний вариант
байесовской модели θ являются совокупности па-
показал наилучшие результаты и был использован
раметров μA и σ2A для каждого A. Для удобства
для проведения расчетов. Таким образом, регуля-
ризующее априорное распределение определяется
функция правдоподобия, а также априорные рас-
выражением
пределения записываются в логарифмическом виде
(
{
})
({
}
{
})
ln Preg2
{μA} ,
σ2A
=
(5)
ln P
Δexpnp
|{μA} ,
σ2A
=
(3)
∑(
[
(
∑
∑
= -τ
(μA - 2μA-2 + μA-4)2 +
1
(
)
=-
ln
2πσ2A
+
)
(
)2
2
A=Amin все Δexpnp,i с данным A
+
σ2A - 2σ2A-2 + σ2A-4
,
(
)2
exp
)]
Δ
-μ
где A принимает значения с шагом 2, и подразуме-
np,i
A
+
вается, что суммирование выполняется сначала для
2σ2
A
четных A, а затем для нечетных, чтобы требова-
ние регулярности выполнялось по-отдельности для
Априорная информация о поведении парамет-
групп Δnp с четными и нечетными A.
ров байесовской модели {μA} и {σ2A} состоит в
В окончательном виде априорное распределение
требовании достаточной плавности поведения их
состоит из Preg2, а также нормирующего апри-
значений как функций массового числа A. Без
орного распределения, рекомендуемого в [16] для
этого требования значения μA и σ2A при каждом
байесовской оценки параметра σ2 нормального
A будут независимыми величинами, и, например,
распределения:
байесовская оценка μA совпадет со средним ариф-
(
{
})
ln Pprior
{μA} ,
σ2A
=
(6)
метическим всех Δnp с данным A по хорошо из-
(
{
})
∑
вестному свойству байесовских оценок параметров
= ln Preg2
{μA} ,
σ2A
-2
ln σA.
нормального распределения. Борьба с физически
A
недостоверными скачками при оценке параметров
является задачей, решаемой методом регуляриза-
Маргинальное распределение P ({Δnp }) опре-
ции Тихонова [15], который обычно формулирует-
деляет плотность вероятности конкретных значе-
ся при использовании в рамках метода наимень-
ний {Δnp } при любой комбинации параметров, и
ших квадратов в виде дополнительного слагаемо-
его нахождение может оказаться затруднительным
го к минимизируемой величине: χ2R = χ2 + τ
∑θ2i,
ввиду необходимости вычисления многомерных ин-
где τ — регуляризационный параметр. По анало-
тегралов. Однако используемый в настоящей ра-
гии регуляризационная составляющая может быть
боте численный метод получения байесовских оце-
определена и в априорном распределении:
нок не зависит от точного указания маргинального
(
{
})
распределения, поэтому можно определить его как
ln Preg1
{μA} ,
σ2A
=
(4)
∑(
)
P ({Δn
(
)2
p }) = const.
= -τ
(μA)2 +
σ2A
,
Параметрами полученной статистической мо-
дели являются 238 пар значений μA и σ2A при
где замена знака +τ на -τ отражает тот факт,
20 ≤ A ≤ 258. Для получения байесовских оценок
что в отличие от χ2R плотность вероятности Preg1
их значений был использован метод Монте-Карло
должна принимать тем меньшие значения, чем
цепей Маркова, суть которого заключается в фор-
менее плавным является регуляризируемый набор
параметров.
мировании равновесной цепи Маркова, значения
которой на каждом шаге распределены в соот-
Пробные расчеты показали, что в рассмат-
ветствии с апостериорным распределением (2), и
риваемом случае выражение
(4) недостаточно
генерации с ее помощью синтетической выборки
эффективно выполняет функцию регуляризации
значений параметров, а сгенерированная выбор-
параметров {μA} и {σ2A}, поскольку, сглаживая
ка в свою очередь используется для получения
их поведение, одновременно приводит к заниже-
байесовских оценок статистических характеристик
нию модуля значений. Поэтому рассматривались
параметров, таких как среднее значение и стан-
также варианты регуляризующего распределе-
дартное отклонение [17]. Для генерации выборки
ния на основе первой τ
∑(θi - θi-1)2 и второй
применялся стандартный алгоритм Метрополиса,
τ
∑((θi - θi-1) - (θi-1 - θi-2))2 дискретных про-
представляющий собой случайное блуждание в
изводных регуляризируемых последовательностей,
пространстве {μA, σ2A}, где вероятность сделать
ЯДЕРНАЯ ФИЗИКА том 86
№4
2023
МОДЕЛЬ МАСС ЯДЕР НА ОСНОВЕ БАЙЕСОВСКОЙ ОЦЕНКИ
479
очередной случайный шаг определяется апостери-
рассчитывались массовые таблицы. В качестве оп-
орным распределением (2). Начальные значения
тимальных τeven,odd были выбраны те значения, при
μA и σ2A для случайного блуждания определя-
которых была минимальной величина ΔRMS65. Их
лись, соответственно, как среднее арифметическое
значения ln τeven = 19 и ln τodd = 7. Соответствую-
щие этим параметрам регуляризации байесовские
и среднеквадратичное отклонения значений {Δnp }
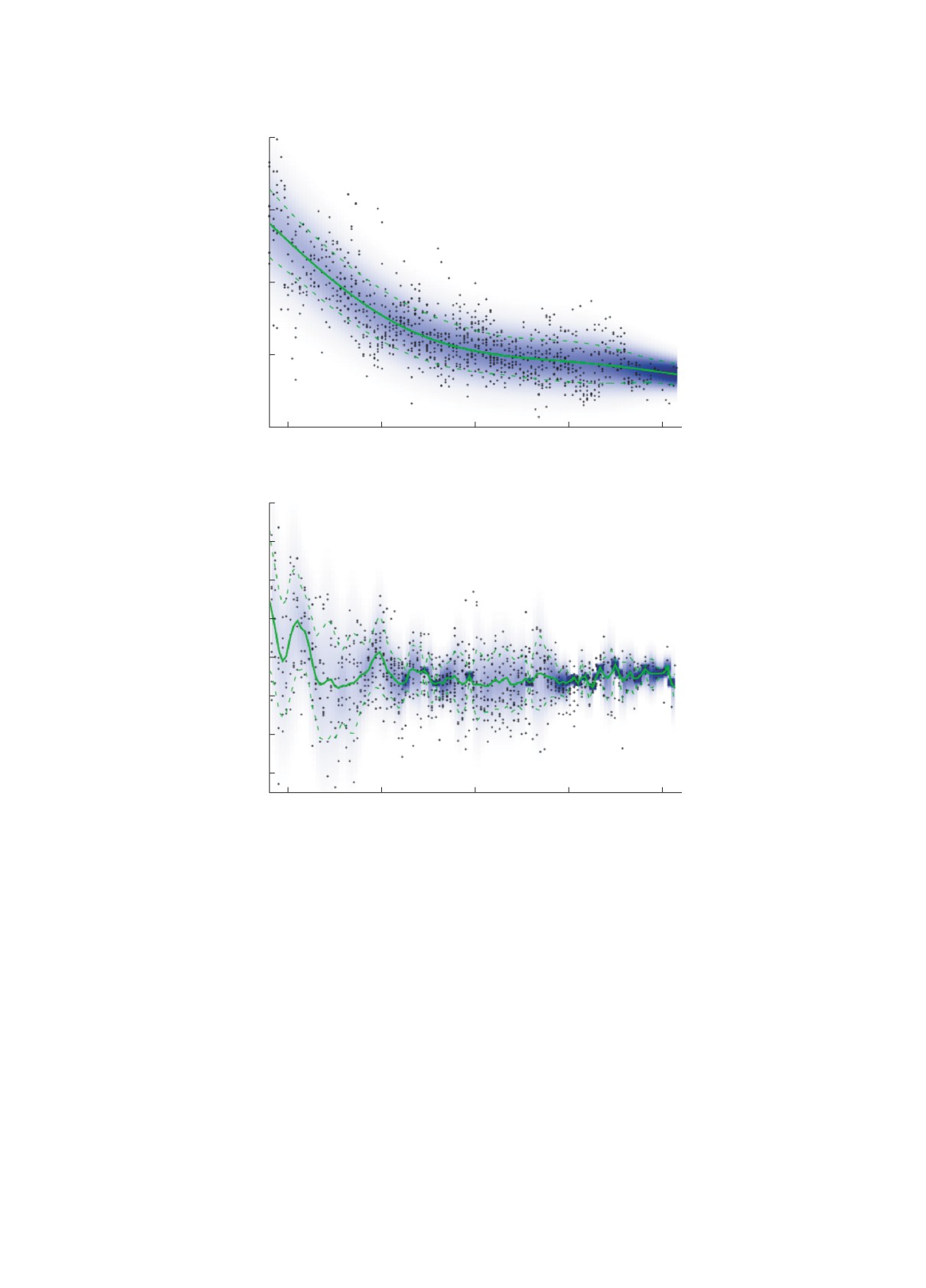
оценки {μ∗A, σ2∗A} показаны на рис. 2. Можно заме-
при данном A. В ходе случайного блуждания пер-
тить, что соответствующее оптимальным оценкам
вые 100 000 сгенерированных точек отбрасывались
поведение величины Δnp для нечетных изотопов
для стабилизации алгоритма, а затем точки запи-
является гораздо менее плавным во всех областях
сывались через каждые 100 шагов для исключения
массовых чисел. Поскольку Δnp представляет со-
корреляции между соседними точками результи-
бой остаточную энергию нейтрон-протонного вза-
рующей выборки. Наконец, вычислялось среднее
имодействия, т.е. разность энергии отделения пары
арифметическое значение и среднеквадратичное
np и энергий отделения двух нуклонов по отдель-
отклонение сгенерированной выборки параметров
ности, то данное поведение при наличии одного
{μA, σ2A}, и полученные величины использовались
непарного нуклона у нечетных ядер представляется
в качестве значения байесовских оценок этих пара-
объяснимым.
метров {μ∗A,σ2∗A} и стандартного отклонения этих
оценок соответственно.
3. СРАВНЕНИЕ С ДРУГИМИ
Используя полученные {μ∗A} в качестве величи-
МАССОВЫМИ МОДЕЛЯМИ
ны Δnp для всех A, по формуле (1) можно рассчи-
Полученные в предыдущем разделе оптималь-
тать значение неизвестной энергии связи ядра по
ные байесовские оценки {μ∗A, σ2∗A} были использо-
трем соседним ядрам, для которых значение энер-
ваны для расчета массовой таблицы на основе экс-
гии связи известно. Полученное при этом значение
периментальных масс из базы данных AME2016. В
энергии связи может быть затем использовано для
таблице 1 приведены значения ΔRMS65, рассчи-
той же цели при вычислении неизвестной энергии
танные по данным ряда теоретических массовых
связи другого ядра, и, таким образом, эта операция
моделей, в сравнении с результатом настоящей
может повторяться в течение нескольких повторе-
работы. Аббревиатурой LMR обозначена массовая
ний цикла, на каждом из которых к области ядер с
модель [8] на основе того же соотношения Δnp, по-
известными энергиями связи на NZ-диаграмме до-
лученная без использования байесовского оцени-
бавляется очередной внешний слой. Для построе-
вания (аппроксимации Δnp, использованные в этой
ния массовой таблицы производилось достаточное
модели, показаны на рис. 1). Модель FRDM(2012)
количество (несколько десятков) циклов итераций,
[18] представляет собой макро-микроскопическую
а затем из массовой таблицы исключались несвя-
занные ядра с отрицательной величиной энергии
модель с многомерной параметризацией формы
отделения частиц и по полученным энергиям связи
ядра и оболочечными поправками Струтинского.
вычислялись массы.
Модель HFB-17 [20] основана на подходе Хартри-
Фока-Боголюбова с использованием потенциа-
Финальной стадией расчета был выбор пара-
ла Скирма. Модель DZ10 [21] основана на ком-
метров регуляризации τ. Вычисления показали,
бинированной массовой формуле Дюфло-Цукера
что вследствие различного поведения Δnp необ-
[22], параметры которой определены по данным
ходимо использовать различные значения τ для
AME2016, а модель DZ10GP [23] по сравнению
четных и нечетных A. Как видно из (6), вели-
с ней была дополнена с помощью метода гаус-
чина параметра регуляризации влияет на форму
совских случайных процессов. Сравнение показы-
зависимости {μ∗A, σ2∗A} от A. При небольших τ
вает, что значение величины ΔRMS65 представ-
в ней могут присутствовать скачки, а в пределе
ленной модели несколько лучше, чем у модели
бесконечно больших значений τ она превращается
LMR без использования байесовского оценивания,
в линейную функцию. Для выбора оптимальных
и заметно превосходит показатели теоретических
τeven и τodd, соответственно, для четных и нечетных
моделей FRDM(2012), HFB-17 и DZ10. Наимень-
A, массовые таблицы вычислялись при различных
шее значение ошибки ΔRMS65 демонстрирует мо-
значениях этих параметров ln τeven,odd = 5-20 с
дель DZ10GP. В этой модели энергия связи ядер
шагом Δ ln τ = 1. Для каждой массовой таблицы,
была представлена в виде суммы двух слагае-
полученной таким способом, вычислялась средне-
мых WDZ10GP(A, Z) = WDZ10(A, Z) + ε(A, Z), т.е.
квадратичная ошибка предсказания масс 65 про-
энергия связи, вычисленная по модели DZ10, кор-
верочных ядер ΔRMS65. Этими ядрами являются
ректируется случайной величиной ε(A, Z), которая
новые ядра, массы которых включены в базу дан-
оценивается с помощью статистического метода
ных AME2020 [18] и отсутствуют в предыдущей
гауссовских процессов и аппроксимирует те ас-
версии AME2016, на основе данных из которой
пекты физической картины, которые не входят в
ЯДЕРНАЯ ФИЗИКА том 86
№4
2023
480
СТОПАНИ и др.
Δnp(A), μ(A)
2.0
а четные А, ln(τ) = 19
1.5
1.0
0.5
0
50
100
150
200
250
Массовое число
Δnp(A), μ(A)
1.0
б нечетные А, ln(τ) = 7
0.8
0.6
0.4
0.2
0
-0.2
-0.4
50
100
150
200
250
Массовое число
Рис. 2. Байесовские оценки параметров распределения Δnp для четных (a) и нечетных (б) ядер. Сплошная кривая —
оценка μA, штриховые кривые отстоят от μA на величину оценки σA, яркость цвета соответствует апостериорному
распределению Δnp.
исходную теоретическую модель. Похожий подход
правки к положенной в качестве основы модели, а,
был с успехом применен в ряде других работ:
напротив, исходно предполагает оцениваемую ве-
например, в [24] для коррекции порога отделения
личину Δnp случайной. Несмотря на такое серьез-
двух нейтронов в микроскопической модели на ос-
ное упрощение, модель тем не менее показывает
нове метода Хартри-Фока-Боголюбова гауссов-
приемлемые результаты.
ским процессом или в [25] для коррекции ядерных
Использованные для оценки точности модели
масс, вычисленных по капельной модели с помо-
65 новых ядер из AME2020 в основном непо-
щью статистического метода радиальных базисных
средственно примыкают на NZ-диаграмме к дан-
функций. Можно отметить, что хотя полученные
ным AME2016. Для того чтобы оценить точность
величины μ∗A также могут рассматриваться как
экстраполяции, на более длинном отрезке была
одномерный гауссовский процесс (см. [26]), все
использована следующая процедура. Из AME2016
же представленный в настоящей работе подход
исключались ядра, находящиеся на ее внешней
не заключается в нахождении статистической по-
границе, по оставшимся данным строилась мас-
ЯДЕРНАЯ ФИЗИКА том 86
№4
2023
МОДЕЛЬ МАСС ЯДЕР НА ОСНОВЕ БАЙЕСОВСКОЙ ОЦЕНКИ
481
660
Fe
655
650
645
а
640
635
МCMC
630
FRDM
HFB
625
DZ10
DZ10GP
LMR
620
75
80
85
90
95
100
Массовое число А
1165
1160
Sn
1155
1150
1145
1140
б
1135
1130
МCMC
FRDM
1125
HFB
DZ10
1120
DZ10GP
LMR
1115
140
145
150
155
160
165
170
175
180
Массовое число А
1430
1420
Eu
1410
1400
в
1390
1380
1370
1360
МCMC
FRDM
1350
HFB
DZ10
1340
DZ10GP
LMR
1330
170
180
190
200
210
220
Массовое число А
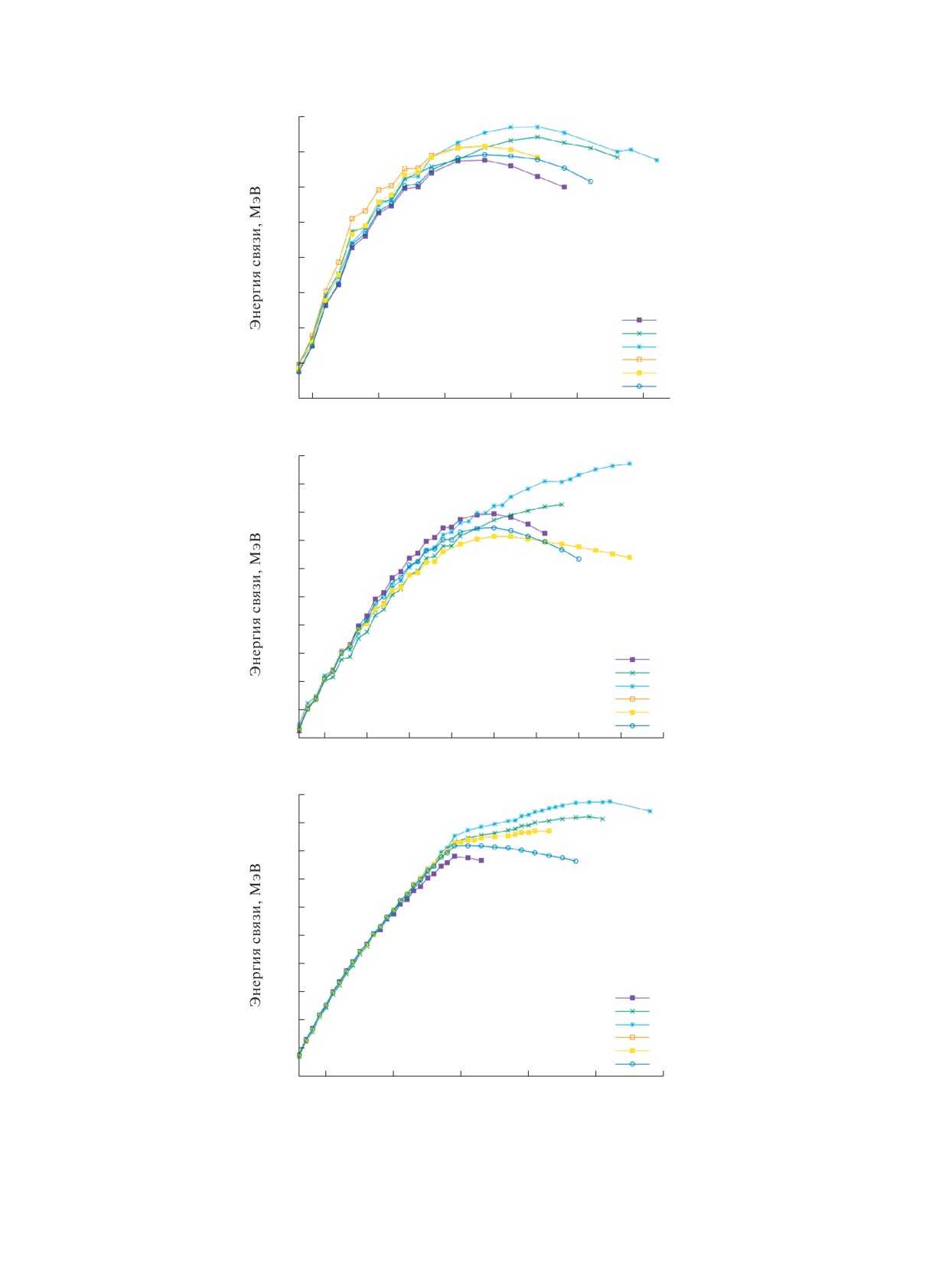
Рис. 3. Значения энергий связи нейтронно-избыточных изотопов Fe (a), Sn (б), Eu (в). MCMC — настоящая работа,
LMR — данные из [8], FRDM — модель [18], HFB — модель [19], DZ10 — модель [20], DZ10GP — модель [21].
ЯДЕРНАЯ ФИЗИКА том 86
№4
2023
482
СТОПАНИ и др.
8
МCMC
FRDM
7
HFB
DZ10
DZ10GP
6
LMR
5
а
4
3
2
1
Fe
0
74
76
78
80
82
84
Массовое число А
4.0
МCMC
FRDM
3.5
HFB
DZ10
DZ10GP
3.0
LMR
2.5
б
2.0
1.5
1.0
Sn
0.5
0
140
145
150
155
Массовое число А
6
5
в
4
3
2
МCMC
FRDM
HFB
1
DZ10
Eu
DZ10GP
LMR
0
170
175
180
185
190
195
Массовое число А
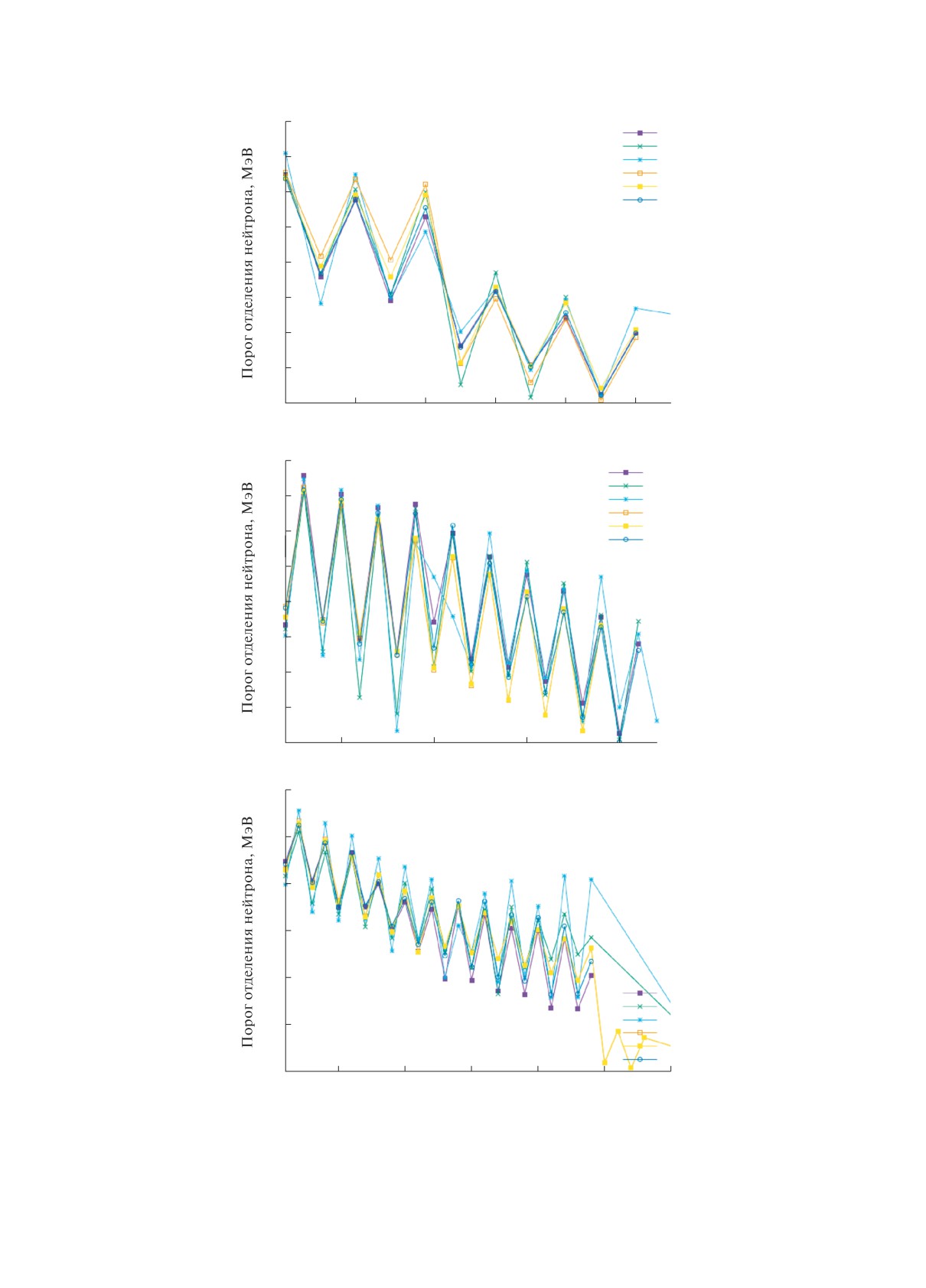
Рис. 4. Значения энергий отделения нейтрона в нейтронно-избыточных изотопах Fe (a), Sn (б), Eu (в). Обозначения
совпадают с рис. 3.
ЯДЕРНАЯ ФИЗИКА
том 86
№4
2023
МОДЕЛЬ МАСС ЯДЕР НА ОСНОВЕ БАЙЕСОВСКОЙ ОЦЕНКИ
483
Таблица 1. Среднеквадратичная ошибка предсказания
где Om — оператор соответствующего разностно-
масс 65 проверочных ядер ΔRMS65 по данным различ-
го выражения, а τ(A, Z) — необязательная правая
ных массовых моделей
часть уравнения. Упомянутые модели удовлетво-
ряют уравнению (7) в каждой точке. В отличие от
Модель
ΔRMS65, кэВ
них массовая таблица в настоящей работе стро-
ится в ходе итерационной процедуры расширения
Настоящая работа
361.9
AME2016, и поэтому разностное уравнение выпол-
LMR [8]
376.5
няется лишь в той части NZ-диаграммы, которая
отсутствовала в AME2016 и была добавлена в
FRDM(2012) [18]
909.2
результате расчета. Следовательно, в рамках ис-
HFB-17 [19]
729.6
ходной статистической модели полученная массо-
вая таблица является математическим ожиданием
DZ10∗ [20]
815.2
ансамбля массовых таблиц, распределение значе-
DZ10GP∗ [21]
289.1
ний Δnp(A) в которых совпадает с распределением
∗ В массовых таблицах DZ10 и DZ10GP отсутствуют ядра
на рис. 1 и одной из которых является реальная
46Mn,50Co,73Rb,211Pa.
массовая таблица с истинными значениями масс
существующих ядер.
совая таблица и вычислялась величина ΔRMS65.
Этот шаг был повторен три раза, после чего из
4. ЗАКЛЮЧЕНИЕ
2498 ядер AME2016 оставалось 1719. При этом
В работе было исследовано статистическое по-
величина ΔRMS65 плавно возрастала от 361.9
ведение величины остаточной энергии нейтрон-
до 367.5 кэВ. Дальнейшее повторение процесса
протонного взаимодействия Δnp и получены бай-
уменьшения объема входных данных было оста-
есовские оценки параметров ее распределения, а
новлено, поскольку не все из 65 проверочных ядер
также на их основе байесовские оценки масс ядер.
были достижимы при экстраполяции по форму-
Главной особенностью модели является просто-
ле (1).
та как исходного массового соотношения, так и
метода вычислений, не требующего сложных ал-
На рис. 3 и 4 показано сравнение вычисленных
горитмов многомерной оптимизации или решения
энергий связи и порогов отделения нейтрона Bn
уравнений. При этом достигаемая точность экстра-
на нейтронно-избыточных изотопах Fe, Sn и Eu
поляции оказывается не хуже, чем у значитель-
вплоть до границы отделения нейтрона (ввиду того,
но более сложных моделей, а также несколько
что представленная модель основана на экстрапо-
превосходит точность предыдущей версии данной
ляции экспериментальных данных AME2016, сле-
модели, не использующей байесовское оценивание.
ва область сравнения ограничена изотопами, для
Байесовская оценка Δnp(A) как функция массово-
которых данные AME2016 отсутствуют). Видно,
го числа для четно-четных и нечетно-нечетных ядер
что при длине дистанции экстраполяции до 10-
демонстрирует значительно более плавное поведе-
20 шагов результаты настоящей работы в целом
ние, чем для нечетных ядер. В последнем случае
согласуются с предсказаниями других моделей, при
наиболее выраженные скачки наблюдаются вблизи
этом расхождение предсказаний различных мо-
A = 60 и A = 100.
делей начинается приблизительно одновременно.
Работа выполнена при поддержке Междисци-
В области наиболее нейтронно-избыточных тяже-
плинарной научно-образовательной школы Мос-
лых ядер с Z > 55 энергии связи, рассчитанные
ковского университета “Фундаментальные и при-
в настоящей работе, оказываются систематически
кладные исследования космоса”.
ниже предсказаний других моделей. Это расхожде-
ние достигает наибольшей величины около 10 МэВ
в области Z > 60, N > 140.
СПИСОК ЛИТЕРАТУРЫ
1. G. T. Garvey, W. J. Gerace, R. L. Jaffe, I. Talmi, and I.
Поскольку μ∗A является байесовской оценкой
Kelson, Rev. Mod. Phys. 41, S1 (1969).
Δnp(A), а в выражение (1) входят лишь опера-
2. С. Шапиро, С. Тьюколски, Чёрные дыры, бе-
ции сложения и вычитания, то полученная с его
лые карлики и нейтронные звёзды, ч. 1 (Мир,
помощью массовая таблица также является бай-
Москва, 1985).
есовской оценкой масс ядер. С другой стороны,
3. J. J ¨anecke and H. Behrens, Phys. Rev. C 9, 1276
как было сказано выше, массовые модели [1, 3-
(1974).
5, 10] получены как точное решение разностного
4. J. J ¨anecke and P. J. Masson, At. Data Nucl. Data
уравнения
Tables 39, 265 (1988).
5. P. J. Masson and J. J ¨anecke, At. Data Nucl. Data
OmM(A,Z) = τ(A,Z),
(7)
Tables 39, 273 (1988).
ЯДЕРНАЯ ФИЗИКА том 86
№4
2023
484
СТОПАНИ и др.
6. Е. В. Владимирова, Б. С. Ишханов, М. В. Симонов,
16. A. Gelman, J. B. Carlin, H. S. Stern, D. B. Dun-
Т. Ю. Третьякова, Уч. записки физ. фак-та Моск.
son, A. Vehtari, and D. B. Rubin, Bayesian
ун-та, 1930409 (2019).
Data Analysis, 3rd ed. (New York, Chapman and
7. E. V. Vladimirova, B. S. Ishkhanov, M. V. Simonov,
Hall/CRC, 2013).
S. V. Sidorov, and T. Yu Tretyakova, Int. J. Mod. Phys.
17. R. M. Neal, Tech. Report CRG-TR-93-1 (University
E 30, 2150025 (2021).
of Toronto, September 1993).
8. E. V. Vladimirova, M. V. Simonov, and T. Yu. Tre-
18. W. J. Huang, M. Wang, F. G. Kondev, G. Audi, and
tyakova, AIP Conf. Proc. 2377, 070003 (2021).
S. Naimi, Chin. Phys. C45, 030002 (2021); M. Wang,
9. D. Lunney, J. M. Pearson, and C. Thibault, Rev. Mod.
W. J. Huang, F. G. Kondev, G. Audi, and S. Naimi,
Phys. 75, 1021 (2003).
Chin. Phys. C 45, 030003 (2021).
10. Z. He, M. Bao, Y. M. Zhao, and A. Arima, Phys. Rev.
19. P. M ¨oller, A. J. Sierk, T. Ichikawa, and H. Sagawa, At.
C 90, 054320 (2014).
Data Nucl. Data Tables 109, 1 (2016).
11. J. L. Tian, N. Wang, C. Li, and J. J. Li, Phys. Rev. C
20. S. Goriely, N. Chamel, and J. M. Pearson, Phys. Rev.
87, 014313 (2013).
Lett. 102, 152503 (2009).
12. Y. Y. Cheng, Y. M. Zhao, and A. Arima, Phys. Rev. C
21. A. Pastore, D. Neill, H. Powell, K. Medler, and
89, 061304 (2014).
C. Barton, Phys. Rev. C 101, 035804 (2020).
13. W. J. Huang, G. Audi, M. Wang, F. G. Kondev,
22. J. Duflo and A. P. Zuker, Phys. Rev. C 52, R23 (1995).
S. Naimi, and X. Xu, Chin. Phys. C 41, 030002
23. M. Shelley and A. Pastore, Universe 7, 131 (2021).
(2017); M. Wang, G. Audi, F. G. Kondev, W. J.
24. L. Neufcourt, Y. Cao, W. Nazarewicz, and F. Viens,
Huang, S. Naimi, and X. Xu, Chin. Phys. C 41,
Phys. Rev. C 98, 034318 (2018).
030003 (2017).
25. N.-N. Ma, H.-F. Zhang, X.-J. Bao, and H.-F. Zhang,
14. А. А. Боровков, Математическая статистика
Chin. Phys. C 43, 044105 (2019).
(Лань, Cанкт-Петербург, 2010).
26. A. Gration and M. I. Wilkinson, Mon. Not. Roy.
15. А. Н. Тихонов, Докл. Акад. Наук СССР 151, 501
(1963).
Astron. Soc. 485, 4878 (2019).
NUCLEAR MASS MODEL BASED ON BAYESIAN ESTIMATES OF LOCAL
DIFFERENCE EXPRESSIONS OF BINDING ENERGIES
K. A. Stopani1), E. V. Vladimirova2), V. V. Negrebetskiy2), M. V. Simonov2),3),
T. Yu. Tretyakova1),2)
1)Skobeltsyn Institute of Nuclear Physics, Moscow, Russia
2)Lomonosov Moscow State University, Faculty of Physics, Moscow, Russia
3)Justus Liebig University, Giessen, Germany
Using the Markov Chain Monte Carlo method and Tikhonov regularization the Bayesian estimates of the
value of the residual neutron-proton interaction energy Δnp were obtained. These estimates are used for
calculation of the nuclear mass table for A > 20. The accuracy of the obtained predictions is evaluated by
comparison with experimental data from AME2020 and other theoretical nuclear mass models.
ЯДЕРНАЯ ФИЗИКА том 86
№4
2023