ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 6, с. 672-680

ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ

ИЗМЕРЕНИЕ ВРЕМЕНИПОДОБНОГО ЭЛЕКТРОМАГНИТНОГО

ФОРМФАКТОРА НЕЙТРОНА НА ДЕТЕКТОРЕ СНД

K. И. Белобородов^1),2), А. В. Бердюгин^1),2), Д. Е. Беркаев¹⁾, А. Г. Богданчиков¹⁾,

А. А. Ботов¹⁾, Т. В. Димова^1),2), В. П. Дружинин^1),2), В. Н. Жабин^1),2), Ю. М. Жаринов¹⁾,

Л. В. Кардапольцев^1),2), А. С. Касаев¹⁾, Д. П. Коврижин¹⁾, И. А. Кооп^1),2),

А. А. Король^1),2), А. С. Купич^1),2), А. П. Крюков¹⁾, А. П. Лысенко¹⁾, Н. А. Мельникова^1),2),

Н. Ю. Мучной^1),2), А. Е. Oбразовский¹⁾, Е. В. Пахтусова¹⁾, К. В. Пугачев^1),2),

С. А. Растигеев¹⁾, Ю. А. Роговский^1),2), С. И. Середняков^1),2)*, З. К. Силагадзе^1),2),

И. К. Сурин¹⁾, Ю. В. Усов¹⁾, А. Г. Харламов^1),2), Ю. М. Шатунов^1),2), Д. А. Штоль¹⁾

Поступила в редакцию 29.06.2023 г.; после доработки 29.06.2023 г.; принята к публикации 29.06.2023 г.

Представлены результаты измерения сечения процесса e⁺e^- → nn и эффективного временипо-

добного формфактора нейтрона. Набор данных проводился в 2020-2021 гг. на e⁺e^--коллайдере

ВЭПП-2000 в диапазоне энергии в системе центра масс от 1891 до 2007 МэВ. Для регистрации

нейтрон-антинейтронных событий использовался универсальный немагнитный детектор СНД. Вы-

деление событий nn производилось системой измерения времени пролета антинейтронов. Величина

измеренного сечения составляет 0.4-0.6 нбн. Нейтронный формфактор в изучаемом диапазоне

энергии изменяется в пределах от 0.3 до 0.2.

DOI: 10.31857/S0044002723060077, EDN: OVHXNC

1. ВВЕДЕНИЕ

угол вылета нейтрона. Полное сечение имеет вид

(

)

4πα²β

σ(s) =

|F (s)|²,

(2)

Внутренняя структура нуклонов описывается

2γ²

электромагнитными формфакторами. Во време-

ниподобной области формфакторы измеряют-

где был введен эффективный формфактор

ся в процессах e⁺e^--аннигиляции в нуклон-

2γ²|G_M (s)|² + |G_E (s)|²

антинуклонные пары. Сечение процесса e⁺e^- →

|F (s)|² =

(3)

2γ² + 1

→ nn зависит от двух формфакторов, электриче-

ского G_E и магнитного G_M :

Значение отношения формфакторов |G_E /G_M | мо-

[

жет быть получено из анализа измеренного распре-

dσ

α²β

|G_M (s)|²(1 + cos² θ) +

(1)

деления по cos θ в уравнении (1). На пороге |G_E | =

dΩ

= |G_M |.

]

|G_E (s)|² sin² θ ,

Последние результаты по времениподобному

γ²

формфактору нейтрона ниже 2 ГэВ были получены

в эксперименте на e⁺e^--коллайдере ВЭПП-2000

где α — постоянная тонкой структуры, s = E², E =

с детектором СНД [1]. В той работе приводится

= 2E_b — энергия в системе центра масс, E_b —

√

список предыдущих измерений. При энергии вы-

энергия пучка в коллайдере, β =

1 - 4m2n/s, γ =

ше 2 ГэВ наиболее точные данные были получе-

= E_b/m_n, m_n — масса нейтрона и θ — полярный

ны на детекторе BESIII [2]. В настоящей работе

приводится измерение сечения процесса e⁺e^- →

¹⁾Институт ядерной физики им. Г.И. Будкера СО РАН,

→ nn и времениподобного формфактора нейтрона

630090, Новосибирск, Россия.

по данным, записанным СНД в 2020—2021 гг., c

²⁾Новосибирский государственный университет, 630090,

Новосибирск, Россия.

интегральной светимостью в 4 раза большей, чем

^*E-mail: S.I.Serednyakov@inp.nsk.su

в предыдущем измерении [1].

672

ИЗМЕРЕНИЕ ВРЕМЕНИПОДОБНОГО ЭЛЕКТРОМАГНИТНОГО ФОРМФАКТОРА

673

e⁺

80 100 см

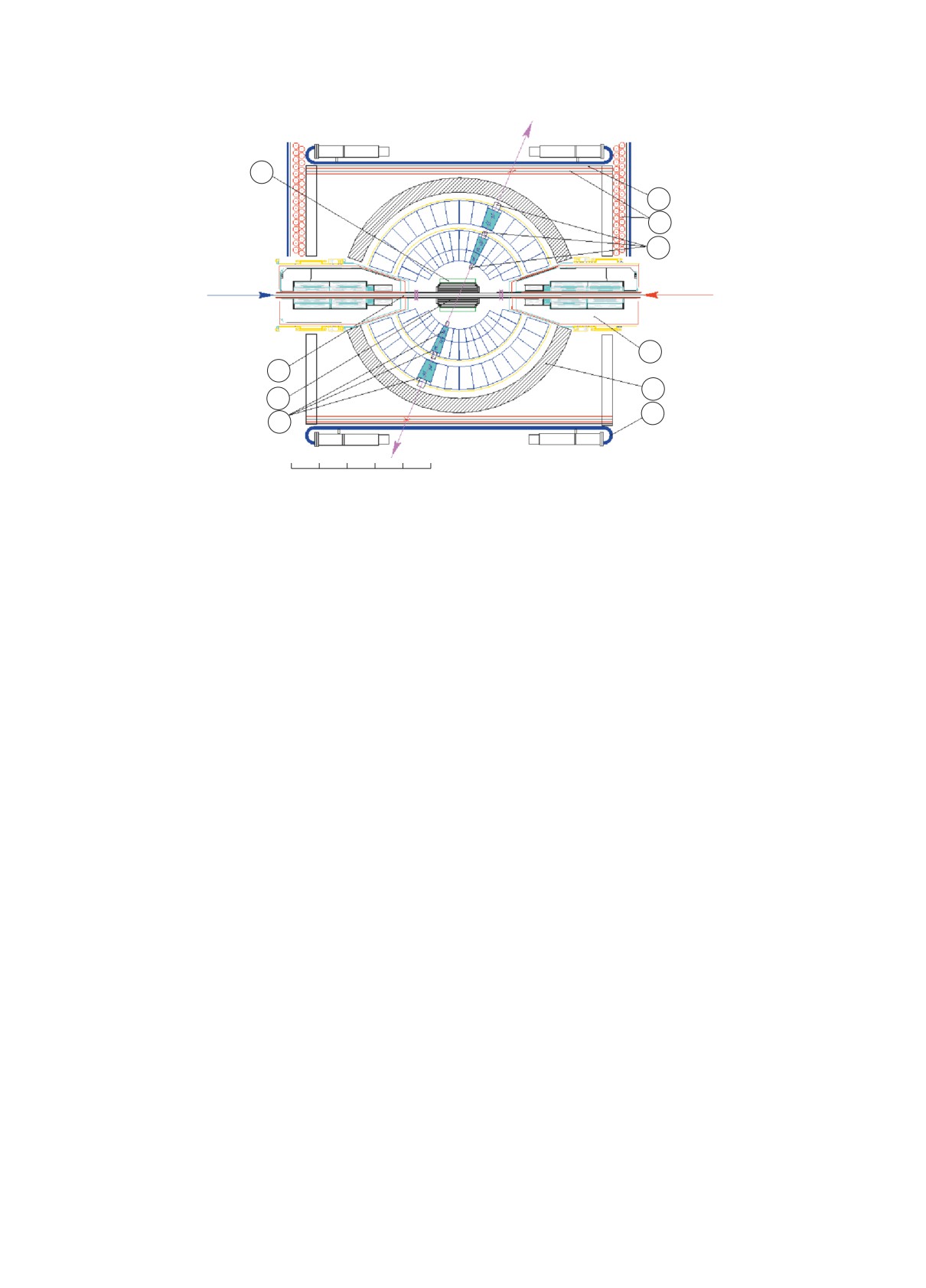
Рис. 1. СНД-детектор, вид вдоль движения пучков: 1 — вакуумная камера, 2 — трековая система, 3 — аэрогелевые

черенковские счетчики, 4 — счетчики NaI(Tl), 5 — вакуумные фототриоды, 6 — железный поглотитель, 7 —

пропорциональные трубки, 8 — стальная пластина, 9 — сцинтилляционные счетчики, 10 — фокусирующие соленоиды

коллайдера.

2. КОЛЛАЙДЕР, ДЕТЕКТОР,

как средневзвешенное время отдельных счетчиков.

ЭКСПЕРИМЕНТ

В качестве веса используется энерговыделение в

счетчике. Временное разрешение калориметра, из-

Электрон-позитронный коллайдер ВЭПП-

меренное по событиям процесса e⁺e^- → γγ, со-

2000 [3] работает в области энергии от порога

ставляет 0.8 нс.

рождения адронов (E = 280 МэВ) до

ГэВ.

Светимость коллайдера выше нуклонного порога

В настоящей работе представлены результаты

при энергии

1.87

ГэВ составляет порядка 5×

анализа данных СНД с интегральной светимостью

× 10³¹ см-2 с-1. На коллайдере установлены два

около 80 пбн-1, записанных в восьми точках по

детектора: СНД и КМД-3.

энергии в интервале 1.891-2.007 ГэВ.

Сферический нейтральный детектор (СНД)

[4] — это немагнитный детектор, включающий

3. УСЛОВИЯ ОТБОРА СОБЫТИЙ

в себя трековую систему, систему черенковских

При рождении пары nn антинейтрон в большин-

счетчиков, сферический электромагнитный кало-

риметр на кристаллах NaI(Tl) и мюонный детектор.

стве случаев аннигилирует в калориметре СНД,

Его схема показана на рис. 1. Калориметр —

образуя пионы, нуклоны, фотоны и другие части-

основная часть детектора, используемая в анализе

цы, которые выделяют в калориметре энергию до

nn. Толщина калориметра составляет

34.7

см

2 ГэВ. Нейтрон из начальной пары nn дает малое

(13.4

радиационных длин). Длина поглощения

энерговыделение в калориметре, особенно на фоне

сигнала от аннигиляции антинейтрона. В данном

антинейтронов в NaI(Tl) изменяется с ростом

энергии от нескольких сантиметров вблизи порога

анализе сигнал от нейтрона не используется. Про-

до 15 см на максимальной энергии [5]. Поэтому

грамма реконструкции событий СНД идентифици-

практически все антинейтроны поглощаются в

рует событие nn как многофотонное.

калориметре.

Основные признаки событий nn — это отсут-

Для измерения времени срабатывания детекто-

ствие заряженных треков и фотонов из центра

ра используется калориметр. Начиная с 2019 г. на

детектора и нарушение баланса импульса в со-

каждом из 1640 счетчиков калориметра установлен

бытии. При выборе условий отбора учитываются

флэш-АЦП [6], измеряющий форму сигнала. При

основные источники фона: космический фон, фон

аппроксимации формы сигнала в счетчике опре-

от процессов e⁺e^--аннигиляции и так называемый

деляется время прихода cигнала и его амплиту-

пучковый фон, возникающий из-за выбывающих из

да. Время прихода события в целом вычисляется

коллайдера электронов и позитронов.

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

674

АЧАСОВ и др.

120

100

t, нс

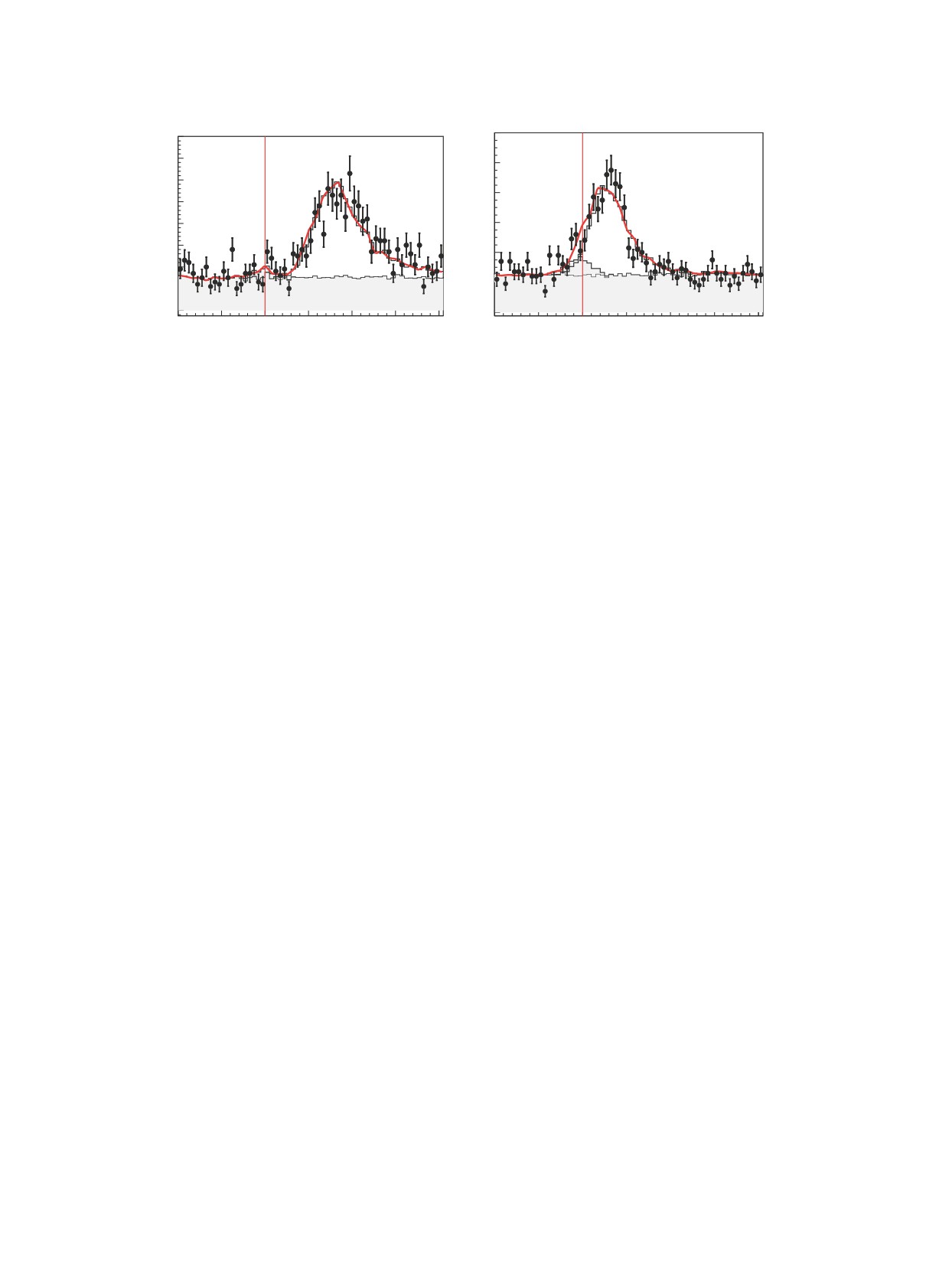
Рис. 2. Временное распределение отобранных событий (точки с ошибками) при энергии E_b = 945 МэВ (а) и E_b =

= 980 МэВ (б). Положение t = 0 соответствует моменту столкновения пучков. Широкий пик справа от нуля — вклад

nn-событий. Тонированная область гистограммы — вклад космического фона (равномерный по времени) и пучкового

фона (пик при t = 0). Сплошная кривая — результат аппроксимации, описывающей вклады эффекта и фона.

Основываясь на специфических особенностях

4. ОПРЕДЕЛЕНИЕ ЧИСЛА ИСКОМЫХ

процесса e⁺e^- → nn и вышеперечисленных фоно-

СОБЫТИЙ

вых процессов, выбранные условия отбора были

Временные спектры для отобранных событий

разделены на три основных группы.

показаны на рис. 2. Нулевое значение времени

В первой группе собраны условия, подавляю-

соответствует моменту столкновения пучков. Вид-

щие фон от событий e⁺e^--аннигиляции, включа-

ны три основных вклада: пик от пучкового и фи-

ющие требование отсутствия заряженных треков в

зического фонов при t = 0, космические события,

событии, ограничение на полный импульс события

равномерно распределенные по времени, и ши-

(p/2E_b > 0.4) и ограничение на поперечный размер

рокий пик от задержанных по времени событий

ливня от фотона с максимальной энергией [7],

nn. Измеренный спектр аппроксимируется суммой

который должен быть шире, чем у фотонов, выле-

этих трех вкладов:

тающих из места встречи пучков.

F (t) = N_nnH_nn(t) + N_csmH_csm(t) +

(4)

Во второй группе находятся условия отбора, ко-

+ N_bkgH_bkg(t),

торые должны подавлять космический фон. Сюда

включено мюонное вето и специальные условия,

где H_nn, H_csm и H_bkg — нормализованные ги-

анализирующие форму распределения энерговы-

стограммы, описывающие временные спектры для

делений в счетчиках калориметра и подавляющие

событий nn, космического фона и суммарного

космические события, преодолевшие мюонное ве-

вклада от пучкового и физического фонов, N_nn,

то [1]. В основном это космические ливни в кало-

N_csm и N_bkg — соответствующие числа событий

риметре.

этих вкладов, которые определяются в результате

В третьей группе содержится ограничение на

аппроксимации. Форма пучкового и физического

энерговыделение в калориметре E_cal > E_b. Это

фонов H_bkg измеряется по событиям, записанным

ограничение практически полностью подавляет

ниже порога рождения nn. Космический спектр

фон от пучков в коллайдере, но при этом эффек-

H_csm измеряется по событиям, в которых срабо-

тивность регистрации событий nn уменьшается на

тала мюонная система, отобранным с понижен-

приблизительно 20%.

ным порогом на энерговыделение в калориметре.

Спектр H_nn вычисляется с помощью моделирова-

Перечисленные выше условия отбора анало-

ния методом Монте-Карло (МС) событий процесса

гичны условиям, используемым в нашей преды-

e⁺e^- → nn.

дущей работе [1]. Единственным отличием явля-

ется отсутствие ограничения на энерговыделение

Сравнение временных спектров в данных и мо-

в третьем слое калориметра СНД. Это увеличи-

делировании для процессов e⁺e^- → γγ и e⁺e^- →

ло эффективность регистрации, хотя и привело к

→ nn показывает, что в данных распределение по

возрастанию космического фона. После наложе-

времени более широкое. Для процесса e⁺e^- →

ния описанных условий отбора для последующего

→ γγ это обусловлено конечным временным раз-

анализа остается около 400 событий на 1 пбн-1

решением системы измерения времени [6], которое

интегральной светимости.

адекватно не моделируется. Поэтому мы проводим

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

ИЗМЕРЕНИЕ ВРЕМЕНИПОДОБНОГО ЭЛЕКТРОМАГНИТНОГО ФОРМФАКТОРА

675

200

150

100

1.0

0.5

1.0

0.5

1.0

cos( )

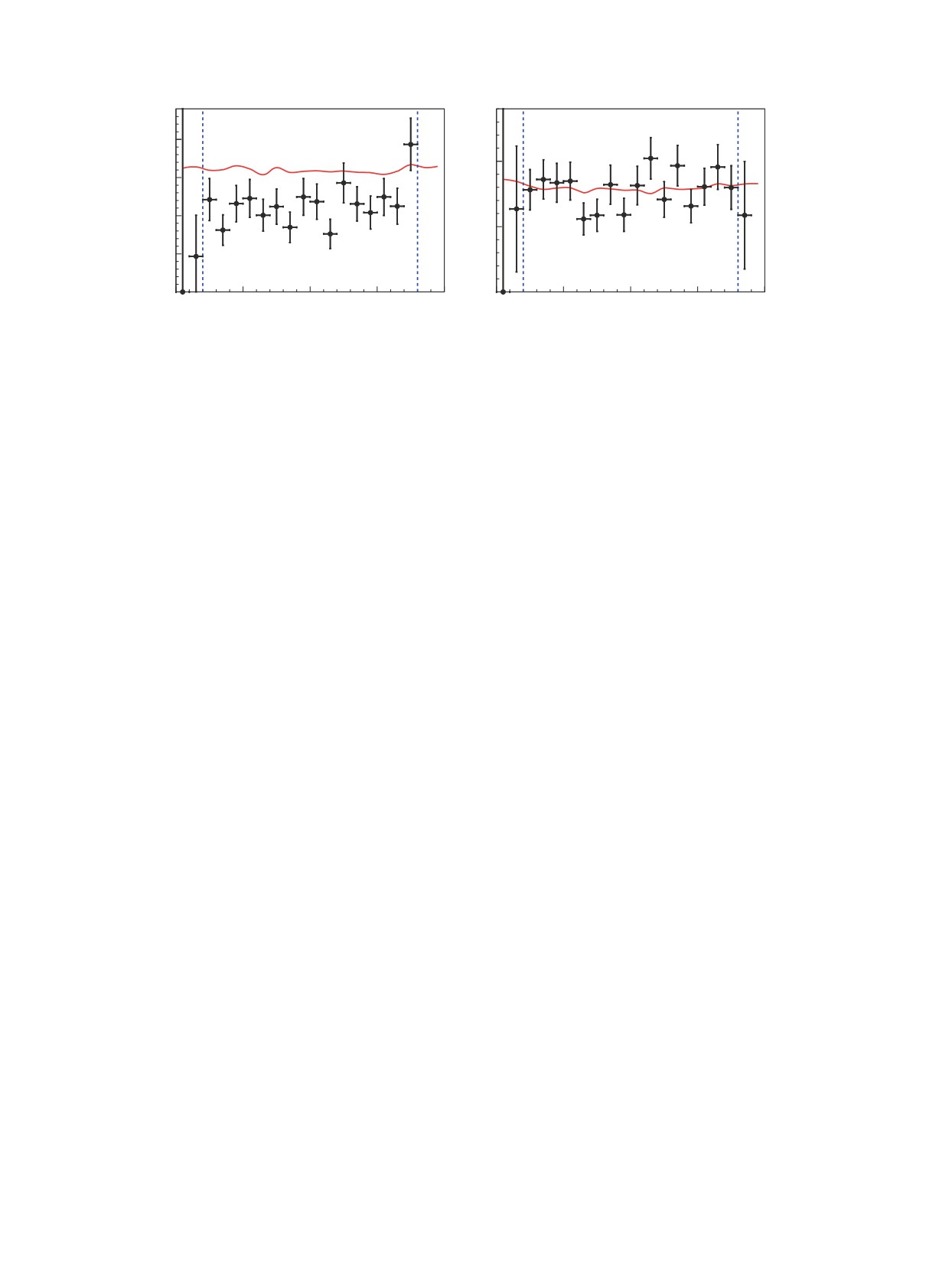
Рис. 3. Распределение по cos θn антинейтрона для данных (точки с ошибками) и моделирования (сплошная кривая) при

энергии E_b = 970 МэВ (а) и E_b = 1000 МэВ (б). Вертикальные линии показывают условия отбора событий.

свертку моделированного спектра с распределени-

что соответствует подавлению числа космических

ем Гаусса с параметром σ_γγ = 0.8 нс. Для событий

событий, прошедших отбор первичного триггера в

процесса e⁺e^- → nn свертка проводится с пара-

электронике детектора, приблизительно в 2 × 10⁴

метром σ_nn = 1.5-2 нс в зависимости от энергии.

раз.

Кроме того, ввиду неудовлетворительного сов-

Числа найденных событий nn при разных энер-

падения формы временного спектра событий nn

гиях приведены в табл. 1. Полное число событий

в моделировании и данных форма H_nn дополни-

около 6000. В табл. 1 приведена только статисти-

тельно корректируется. Несовпадение объясняет-

ческая ошибка аппроксимации. Источником си-

ся использованием в моделировании некоррект-

стематической ошибки в числе событий nn могут

ных значений сечений аннигиляции и рассеяния

быть неопределенности в величине и форме вре-

антинейтронов, а также некорректным распреде-

менного спектра космического и пучкового фонов.

лением продуктов аннигиляции. Была использова-

Вносимая этими источниками ошибка составляет

на следующая простая модель для модификации

15 событий при E_b = 1000 МэВ и менее 8 событий

моделированного распределения. Были построены

при более низких энергиях. Эти значения значи-

временные спектры для моделированных событий,

тельно меньше статистической ошибки в табл. 1 и

в которых первым взаимодействием антинейтрона

в дальнейшем не учитываются.

с веществом детектора было рассеяние (Hsn¯n) или

аннигиляция (Han¯n). Доля событий аннигиляции в

МС составляла около 33%. Аннигиляция дает в ка-

5. РАСПРЕДЕЛЕНИЕ АНТИНЕЙТРОНОВ

лориметре временной спектр, близкий по форме к

ПО ПОЛЯРНОМУ УГЛУ

экспоненциальному, тогда как рассеяние имеет за-

Угол вылета антинейтрона θ_n измеряется по на-

держанное и более широкое временное распреде-

правлению полного импульса события с точностью

ление с неэкспоненциальной формой. Спектр H_nn

около 5^◦. Распределение по cos θ_n эксперимен-

(формула (4)) для аппроксимации строился как

тальных и моделированных событий nn показано

линейная комбинация двух вышеописанных рас-

на рис. 3. Моделирование было выполнено по

пределений H_nn = (1 - α)Hsn¯n + αHan¯n. Параметр

формуле (1) при условии, что G_E = G_M . В этом

α (доля событий аннигиляции) был свободным при

случае в интервале условий отбора 36^◦ < θ_n < 144^◦

аппроксимации. Его значение в данных оказалось

находится около 80% событий nn. Как видно из

большим, чем в моделировании, ≃ 60%, и соответ-

рис. 3, наблюдается согласие между данными и

ственно доля событий рассеяния уменьшилась до

моделированием, что подтверждает правильность

≃ 40%. На рис. 2 видно, что модифицированный

модели углового распределения. Стоит отметить,

таким образом спектр хорошо описывает экспери-

что измеренная в предыдущей работе СНД [1] ве-

ментальные распределения.

личина |G_E /G_M | также не противоречила гипотезе

Получающееся при аппроксимации суммарное

GE = GM .

сечение пучкового и физического фонов σ_bkg со-

ставляет около 7 пбн и слабо зависит от энергии.

6. ЭФФЕКТИВНОСТЬ РЕГИСТРАЦИИ

Главный вклад в σ_bkg дают процессы с нейтраль-

ными каонами: e⁺e^- → K_S K_Lπ⁰, K_S K_Lη и подоб-

Эффективность регистрации ε для событий про-

ные им. Измеренный вклад космического фона в

цесса e⁺e^- → nn в зависимости от энергии в

отобранных событиях составляет около 0.01 Гц,

принятых условиях отбора приведена на рис. 4.

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

676

АЧАСОВ и др.

Таблица 1. Энергия пучка (E_b), интегральная светимость (L), число найденных nn-событий (N_nn), радиационная

поправка (1 + δ), эффективность регистрации (ε), измеренное сечение процесса e⁺e^- → nn (σ), эффективный

формфактор нейтрона (F_n), приведенные ошибки для N и σ — статистические и систематические; для эффек-

тивности регистрации приводится систематическая ошибка; для формфактора F_n приводится квадратичная сумма

статистической и систематической ошибок

E_b, МэВ L, пбн-1

N_nn

1+δ

σ, нбн

F_n

945.5

8.54

676 ± 37

0.746

0.253 ± 0.021

0.420 ± 0.023 ± 0.036

0.322 ± 0.016

950.3

8.86

834 ± 37

0.787

0.246 ± 0.015

0.485 ± 0.022 ± 0.031

0.301 ± 0.012

960.3

8.33

767 ± 35

0.840

0.217 ± 0.013

0.506 ± 0.023 ± 0.032

0.266 ± 0.010

970.8

8.07

718 ± 34

0.870

0.229 ± 0.017

0.447 ± 0.021 ± 0.034

0.230 ± 0.011

968.8

5.51

524 ± 34

0.870

0.186 ± 0.020

0.589 ± 0.039 ± 0.065

0.267 ± 0.017

980.3

7.70

654 ± 37

0.900

0.216 ± 0.018

0.436 ± 0.025 ± 0.038

0.216 ± 0.011

990.4

8.77

624 ± 38

0.920

0.183 ± 0.019

0.422 ± 0.026 ± 0.045

0.204 ± 0.013

1003.5

20.06

1075 ± 50

0.947

0.151 ± 0.014

0.374 ± 0.018 ± 0.035

0.186 ± 0.010

При вычислении эффективности для моделирова-

ния взаимодействия nn с веществом использовал-

ся пакет GEANT4 [8], версия 10.5. Дополнительно

0.30

в моделировании учитывалось излучение фотонов

начальными электронами и позитронами и энерге-

0.25

тический разброс в пучках около 1 МэВ. В моде-

0.20

лировании учитывались неработающие каналы де-

тектора, а также наложения на изучаемые события

0.15

пучкового фона. Для этого во время эксперимента

0.10

с запуском от генератора, синхронизированного с

моментом соударения пучков, записывались спе-

0.05

циальные “события наложений”, которые затем

накладывались на моделированные события. Эф-

1.90

1.92

1.94

1.96

1.98

2.00

фективность регистрации, приведенная на рис. 4,

E, МэВ

скорректирована на разницу между данными и мо-

делированием. Эта поправка обсуждается ниже.

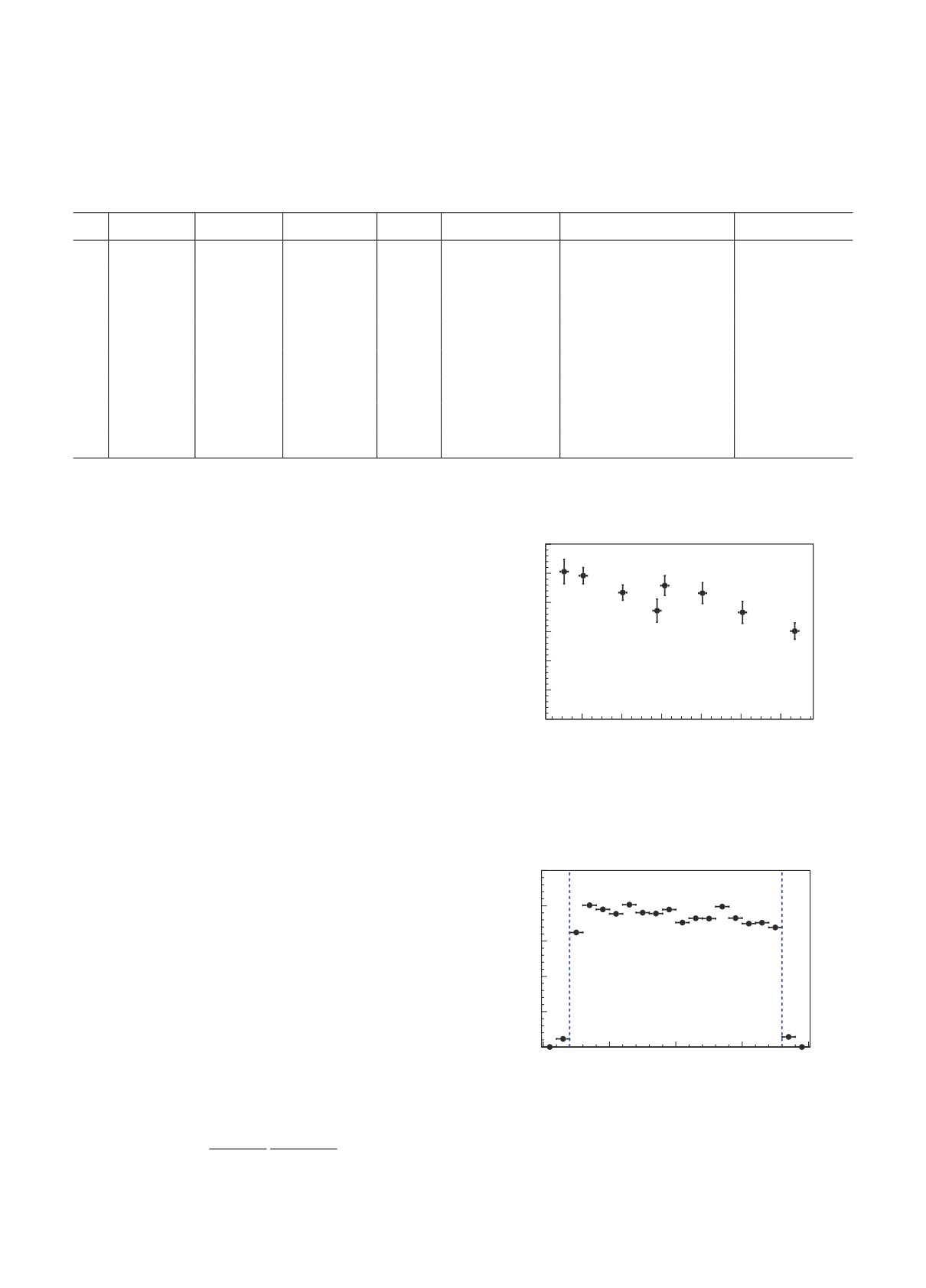
Рис. 4. Эффективность регистрации событий nn после

Численные значения эффективности регистрации

внесения поправок как функция от энергии.

приведены в табл. 1. Уменьшение эффективности

с энергией объясняется энергетической зависимо-

стью параметров отбора, а также увеличением доли

энергии, выходящей за пределы калориметра. На

0.25

рис. 5 представлена угловая зависимость эффек-

0.20

тивности регистрации при энергии 960 МэВ.

Величина эффективности регистрации в приня-

0.15

тых условиях отбора составляет около 20%. Важ-

но выяснить, насколько корректно моделирование

0.10

воспроизводит доли событий, отбрасываемых раз-

0.05

ными условиями отбора. Поправки вычислялись

для трех групп условий отбора, описанных в разд. 3.

Для этого поочередно инвертируются условия от-

1.0

0.5

1.0

бора для групп и далее вычисляются поправки к

cos( )

эффективности регистрации δ_i в каждой из восьми

точек по энергии в следующем виде:

Рис. 5. Эффективность регистрации событий nn, по-

лученная по моделированию, в зависимости от cos θn

n₀

m₀ + m₁

антинейтрона при энергии E_b = 960 МэВ. Вертикаль-

δ=

(5)

n₀ + n₁

m₀

ные линии показывают условия отбора событий.

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

ИЗМЕРЕНИЕ ВРЕМЕНИПОДОБНОГО ЭЛЕКТРОМАГНИТНОГО ФОРМФАКТОРА

677

180

140

160

120

140

100

120

100

t, нс

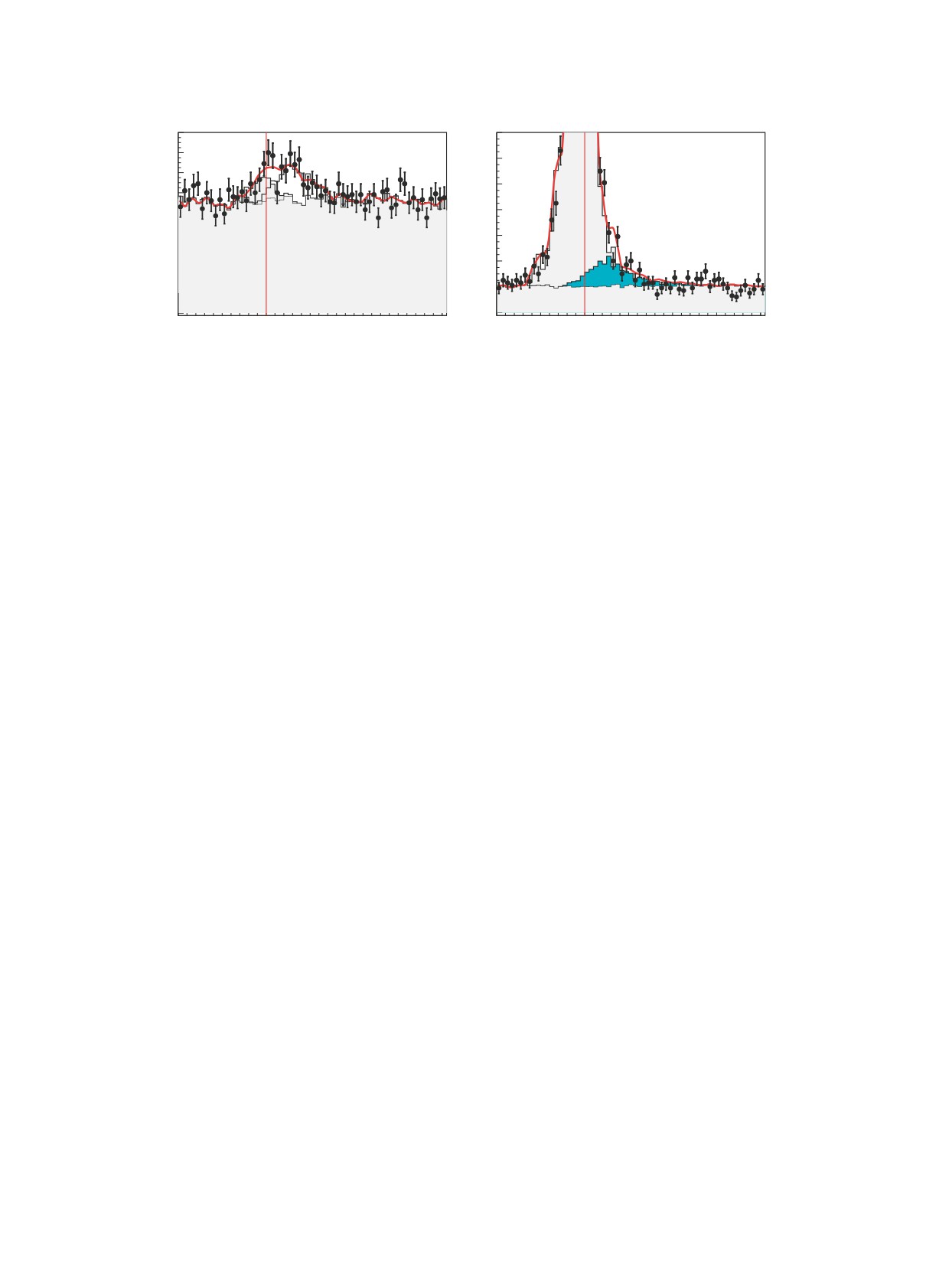
Рис. 6. Временные спектры при инвертированных условиях отбора. а — инвертированные условия второй группы при

E_b = 970 МэВ, б — частично инвертированноеусловиетретьей группы(0.7E_b < E_cal < E_b). Экспериментальныеданные

показаны точками с ошибками. Сплошная кривая — результат аппроксимации данных формулой (4). Светлая тонировка

показывает вклад фона. Темная тонировка на рис. 6б— вклад событий nn.

где n₀ (n₁) — число событий nn в эксперименте,

Дополнительная поправка возникает от части

отобранных со стандартными (инвертированными)

экспериментальных событий, в которых антиней-

условиями. Эти числа определяются при аппрок-

троны прошли через калориметр без взаимодей-

симации временного спектра формулой (4), как

ствия, а также от событий с энерговыделением

описано в разд. 4. Величины m₀ и m₁ относятся к

в калориметре E_cal < 0.7E_b, которые не берутся

соответствующим числам событий в моделирова-

в анализ из-за большого фона и поэтому недо-

нии. Примеры временных спектров с инверсными

ступны для внесения поправок описанным выше

условиями отбора показаны на рис. 6.

способом. Их доля в моделировании составляет

от 1.9% при энергии E_b = 945 МэВ до 8.5% при

В первую группу условий отбора входит тре-

E_b = 1000 МэВ. Ранее (разд. 4) отмечалось, что

бование отсутствия треков заряженных частиц в

для описания формы временного спектра вклад

событии. При изучении инверсного отбора мы до-

процесса рассеяния n в МС следует уменьшить

пускаем наличие одного или нескольких “нецен-

сравнительно с вкладом процесса аннигиляции n

тральных” заряженных треков, имеющих D_xy >

в калориметре в ≃1.5 раза. При таком измене-

> 0.5 см, где D_xy — расстояние между треком и

нии доля событий с E_cal < 0.7E_b в моделировании

осью столкновения пучков. Здесь следует обсудить

уменьшается до 1.4% при E_b = 945 и 5.7% при

возможный фон от родственного процесса e⁺e^- →

E_b = 1000 МэВ. Разница между этими величинами

→ pp. В области энергии E_b > 960 МэВ протоны и

учитывается в качестве дополнительной поправ-

антипротоны дают “центральные” треки в дрейфо-

ки δ_E к эффективности регистрации со 100%-ной

вой камере. События с такими треками отбрасыва-

неопределенностью.

ются условием D_xy > 0.5 см, также как и события

других процессов с заряженными частицами в ко-

Измеренные величины поправок по группам

нечном состоянии. Однако при E_b < 960 МэВ про-

условий отбора δ₁, δ₂, δ₃, a также δ_E и полная

тоны и антипротоны медленные, поэтому они оста-

поправка δ_t = δ₁δ₂δ₃δ_E , вычисленная перемноже-

навливаются в стенке вакуумной камеры коллай-

нием отдельных поправок, приводятся в табл. 2. Из

дера. При этом антипротон аннигилирует с рож-

таблицы видно, что полная поправка δ_t изменяется

дением нескольких заряженных частиц, которые

с энергией в пределах 0.80-1.25, что объясняется

в основном реконструируются как “нецентраль-

сильной зависимостью длины поглощения анти-

ные”. Но и здесь фон от событий pp подавляется

нейтрона в детекторе от энергии.

при аппроксимации временного спектра, так как

максимальное время от столкновения пучков до

Корректированная эффективность регистрации

аннигиляции антипротона даже при E_b = 945 не

получается из эффективности, вычисленной по мо-

превышает 1 нс. Для второй группы условий отбора

делированию, умножением на δ_t. В табл. 1 она

использовались инверсные условия без изменений.

приводится вместе с систематической ошибкой.

Для третьей группы использовалась частичная ин-

В отличие от нашего предыдущего измерения [1],

версия, т.е. изучались события с условием 0.7E_b <

здесь поправки в каждой точке по энергии вычис-

<E_cal <E_b.

ляются независимо.

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

678

АЧАСОВ и др.

Таблица 2. Поправки к эффективности регистрации событий процесса e⁺e^- → nn, описанные в разд. 6 (δ₁, δ₂, δ₃,

δ_E), и полная поправка (δ_t)

E_b, МэВ

δ₁

δ₂

δ₃

δ_E

δ_t

945.5

0.991 ± 0.022

1.292 ± 0.092

0.971 ± 0.038

1.005 ± 0.005

1.249 ± 0.102

950.3

0.977 ± 0.018

1.214 ± 0.062

0.985 ± 0.030

1.009 ± 0.009

1.179 ± 0.072

960.3

9.966 ± 0.019

1.077 ± 0.050

0.992 ± 0.028

1.012 ± 0.012

1.044 ± 0.062

970.8

0.949 ± 0.021

1.198 ± 0.061

0.980 ± 0.050

1.018 ± 0.018

1.134 ± 0.084

968.8

0.958 ± 0.027

1.031 ± 0.080

0.896 ± 0.044

1.018 ± 0.018

0.901 ± 0.097

980.3

0.997 ± 0.031

1.102 ± 0.073

0.986 ± 0.043

1.021 ± 0.021

1.106 ± 0.093

990.4

0.925 ± 0.033

1.131 ± 0.080

0.889 ± 0.041

1.024 ± 0.024

0.952 ± 0.099

1003.5

0.915 ± 0.024

1.065 ± 0.056

0.796 ± 0.028

1.028 ± 0.028

0.797 ± 0.073

7. ИЗМЕРЕННОЕ СЕЧЕНИЕ ПРОЦЕССА

поправка к эффективности регистрации, приведен-

РОЖДЕНИЯ ПАР

ная в табл. 2. Учитываются также погрешности

НЕЙТРОН-АНТИНЕЙТРОН

в измерении светимости (1%) и радиационной по-

правке (2%). На рис. 7 в качестве ошибки приве-

Используя число отобранных nn-событий, ин-

тегральную светимость L и эффективность реги-

дена квадратичная сумма статистической и систе-

страции из табл. 1, можно получить так называемое

матической ошибок. По сравнению с предыдущей

видимое сечение σ_vis(E) = N_nn/Lε. Борновское

работой [1] измеренное сечение имеет примерно в

сечение σ(E) связано с видимым сечением σ_vis(E)

2 раза лучшую статистическую ошибку и в 1.5 раза

следующим образом:

лучшую систематическую ошибку. Кроме того, сле-

дует учесть, что систематические ошибки в разных

σ_vis(E) = σ(E)(1 + δ(E)) =

(6)

точках слабо коррелированы. При максимальной

+∞

∫

энергии E = 2 ГэВ наше сечение согласуется с

= G(E^′, E)dE^′ W (s, x)σ(s(1 - x))dx,

результатом детектора BESIII [2].

-∞

где W (s, x) — функция, описывающая вероятность

излучения фотонов с энергией xE_b начальными

σ, нбн

электронами и позитронами [9], x_max — макси-

0.8

мальная энергия излученного фотона, G(E^′, E) —

SND, This work

0.7

распределение Гаусса, описывающее энергетиче-

SND, (2022)

0.6

BESIII

ский разброс в системе центра масс. В функции

W (s, x) не учитывается вклад поляризации ва-

0.5

куума, поэтому борновское сечение является так

0.4

называемым одетым сечением. Фактор (1 + δ(E))

0.3

учитывает радиационные поправки и энергетиче-

0.2

ский разброс. Этот фактор вычисляется для каж-

дой из восьми энергетических точек, по борнов-

0.1

скому сечению, полученному при аппроксимации

видимого сечения формулой (6). Для энергетиче-

1.88 1.90 1.92 1.94 1.96 1.98 2.00 2.02 2.04 2.06

ской зависимости борновского сечения использу-

E, ГэВ

ется формула (2), в которой формфактор нейтрона

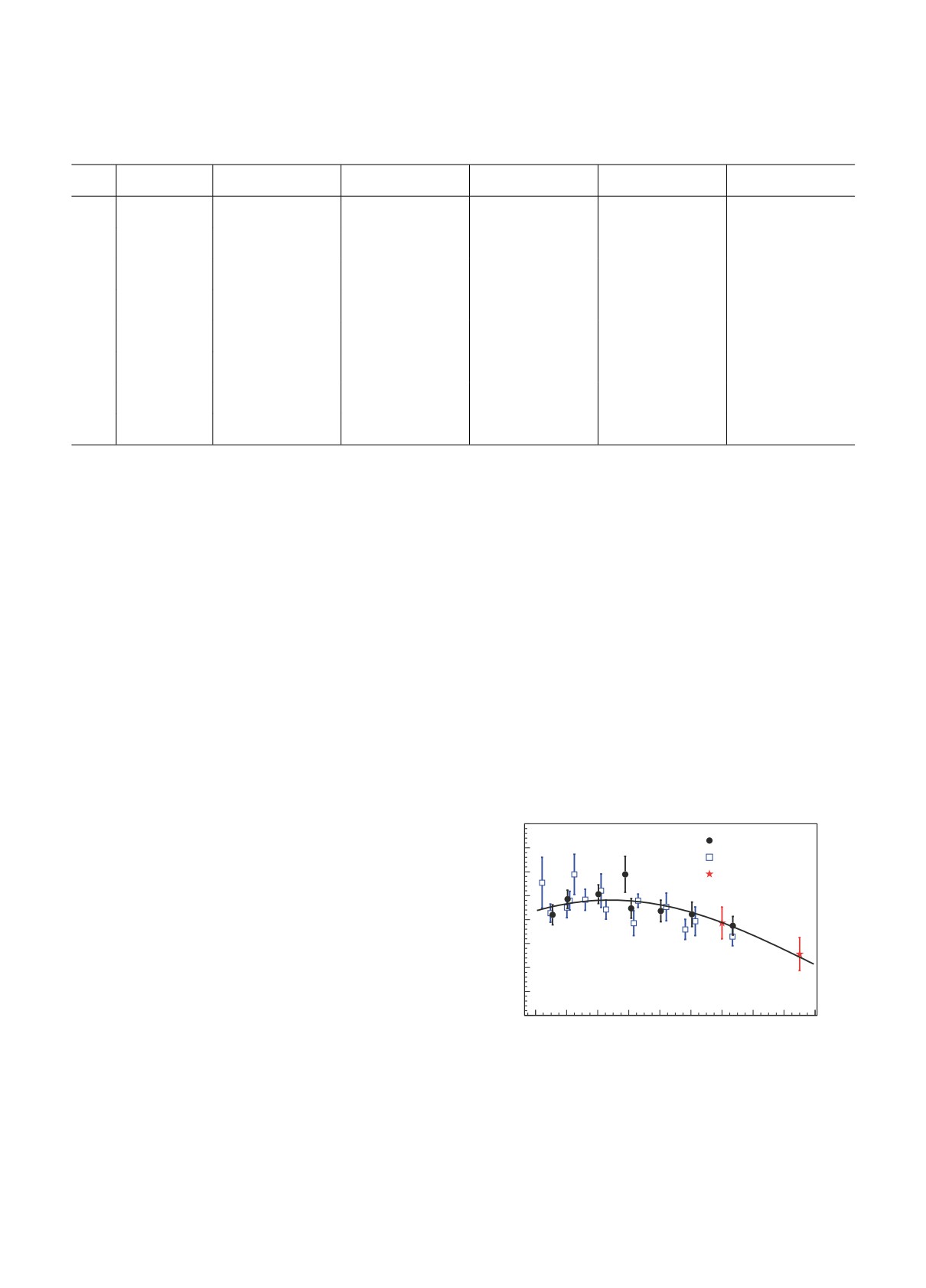
Рис. 7. Измеренное в настоящей работе сечение про-

описывается полиномом второй степени, как это

цесса e⁺e^- → nn в сравнении с предыдущим резуль-

описано в следующем разделе.

татом СНД [1] и результатом детектора BESIII [2].

Измеренное борновское сечение показано на

Сплошная кривая — аппроксимация борновского се-

рис. 7 и приводится в табл. 1. Доминирующий

чения, в которой использовались новые данные СНД и

данные BESIII.

вклад в систематическую ошибку сечения вносит

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

ИЗМЕРЕНИЕ ВРЕМЕНИПОДОБНОГО ЭЛЕКТРОМАГНИТНОГО ФОРМФАКТОРА

679

form factor

0.6

SND, This work

0.5

BESIII

BaBar(pp)

0.4

0.3

0.2

0.1

0.2

0.3

0.4

0.5

0.6

P, ГэВ/c

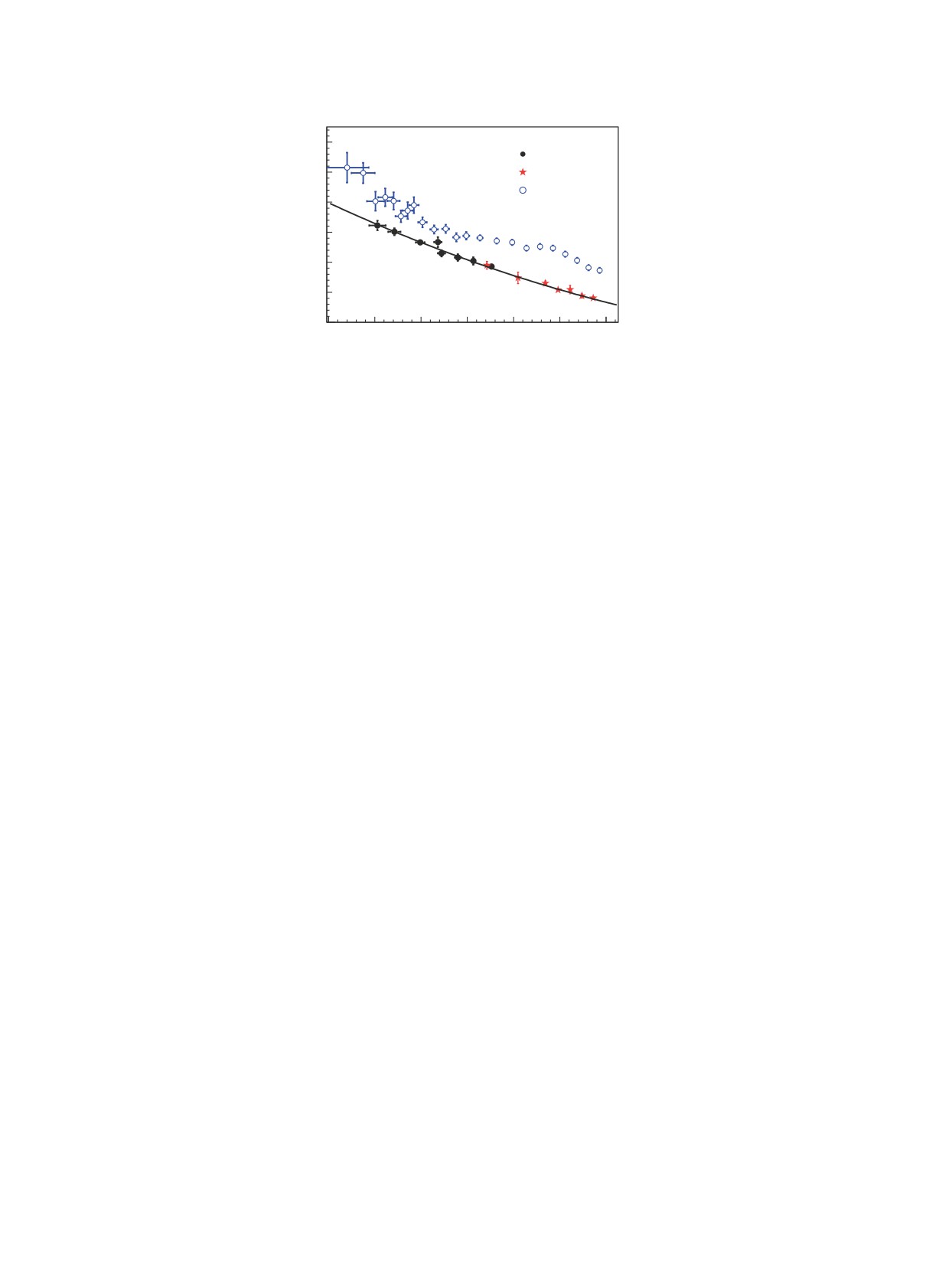
Рис. 8. Времениподобный эффективный формфактор нейтрона, измеренный в настоящей работе (сплошные кружки) и в

эксперименте BESIII [2] (звездочки), как функция импульса нейтрона. Сплошная кривая — результат аппроксимации

квадратичным полиномом. Для сравнения показан эффективный формфактор протона, измеренный в эксперименте

BABAR [10].

8. ЭФФЕКТИВНЫЙ ВРЕМЕНИПОДОБНЫЙ

Данная работа выполнялась по гранту РНФ,

ФОРМФАКТОР НЕЙТРОНА

No. 23-22-00011.

Нейтронный формфактор вычисляется из изме-

ренного сечения, используя формулу (2). Числен-

ные значения формфактора приводятся в табл. 1

СПИСОК ЛИТЕРАТУРЫ

и показаны на рис. 8 вместе с данными BESIII [2]

M. N. Achasov et al. (SND Collab.), Eur. Phys. J. C

и протонным формфактором, измеренным в экспе-

22, 761 (2022);

рименте BABAR [10]. Кривая на рис. 8, аппрокси-

http://doi.org/10.1140/epjc/s10052-022-10696-0

мирующая формфактор — полином второй степени

M. Ablikim et al. (BESIII Collab.), Nat. Phys. 17,

|F_n| = a₀ + a₁p_n + a₂p2n, в котором параметры a_i

1200 (2021);

определены при аппроксимации видимого сечения,

https://doi.org/10.1038/s41567-021-01345-6

а pn — импульс антинейтрона. Получены сле-

P. Yu. Shatunov et al., Part. Nucl. Lett. 13, 995

дующие значения параметров: a₀ = 0.398 ± 0.022,

(2016);

a₁ = -0.713 ± 0.126, a₂ = 0.268 ± 0.166. При про-

http://dx.doi.org/10.1134/S154747711607044X

должении аппроксимирующей кривой к нулевому

M. N. Achasov et al. (SND Collab.), Nucl. Instrum.

импульсу ожидаемое значение нейтронного форм-

Methods A 449, 125 (2000);

фактора на пороге составит a₀ ≃ 0.4. Из рис. 8

http://dx.doi.org/10.1016/S0168-9002(99)01302-9

видно, что протонный формфактор значительно

M. Astrua et al., Nucl. Phys. A 697, 209 (2002);

превышает нейтронный, а их отношение на пороге

http://dx.doi.org/10.1016/S0375-9474(01)01252-0

будет близким к 3/2.

M. N. Achasov et al., JINST 10, T06002 (2015);

http://dx.doi.org/10.1088/1748-

9. ЗАКЛЮЧЕНИЕ

0221/10/06/T06002

Проведен эксперимент по измерению сече-

A. V. Bozhenok et al., Nucl. Instrum. Methods A 379,

ния процесса e⁺e^- → nn на e⁺e^--коллайдере

507 (1996);

ВЭПП-2000 с детектором СНД в области энергии

http://dx.doi.org/10.1016/0168-9002(96)00548-7

от 1891 до 2007 МэВ. Измеренное сечение меняет-

J. Allison et al. (GEANT Collab.), Nucl. Instrum.

ся с энергией в пределах 0.4-0.6 нбн, согласуется с

Methods A 835, 186 (2016);

предыдущим измерением СНД [1], но имеет в 2 раза

https://doi.org/10.1016/j.nima.2016.06.125,

лучшую статистическую точность. При максималь-

https://geant4-data.web.cern.ch/-

ной энергии эксперимента сечение согласуется с

ReleaseNotes/ReleaseNotes4.10.5.html

измерениями детектора BESIII [2]. Эффективный

E. A. Kuraev and V. S. Fadin, Sov. J. Nucl. Phys. 41,

времениподобный формфактор нейтрона извле-

466 (1985).

кается из полученного сечения, используя урав-

10.

J. P. Lees et al. (BABAR Collab.), Phys. Rev. D 87,

нение (2). Формфактор уменьшается с энергией

092005 (2013); Phys. Rev. D 88, 072009 (2013);

от 0.3 до 0.2. По величине формфактор нейтрона

http://dx.doi.org/10.1103/PhysRevD.87.092005

оказывается меньше формфактора протона в этой

области энергии.

http://dx.doi.org/10.1103/PhysRevD.88.072009

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

680

АЧАСОВ и др.

MEASUREMENTS OF THE NEUTRON TIMELIKE ELECTROMAGNETIC

FORM FACTOR WITH THE SND DETECTOR

M. N. Achasov^1),2), A. Yu. Barnyakov^1),2), E. V. Bedarev^1),2), K. I. Beloborodov^1),2),

A. V. Berdyugin^1),2), D. E. Berkaev¹⁾, A. G. Bogdanchikov¹⁾, A. A. Botov¹⁾, T. V. Dimova^1),2),

V. P. Druzhinin^1),2), V. N. Zhabin^1),2), Yu. M. Zharinov¹⁾, L. V. Kardapoltsev^1),2),

A. S. Kasaev¹⁾, D. P. Kovrizhin¹⁾, I. A. Koop^1),2), A. A. Korol^1),2), A. S. Kupich^1),2),

A. P. Kryukov¹⁾, A. P. Lysenko¹⁾, N. A. Melnikova^1),2), N. Yu. Muchnoy^1),2),

A. E. Obrazovsky¹⁾, E. V. Pakhtusova¹⁾, K. V. Pugachev^1),2), S. A. Rastigeev¹⁾,

Yu. A. Rogovsky^1),2), S. I. Serednyakov^1),2), Z. K. Silagadze^1),2), I. K. Surin¹⁾, Yu. V. Usov¹⁾,

A. G. Kharlamov^1),2), Yu. M. Shatunov^1),2), D. A. Shtol¹⁾

¹⁾Budker Institute of Nuclear Physics of Siberian Branch Russian Academy of Sciences,

Novosibirsk, Russia

²⁾Novosibirsk State University, Novosibirsk, Russia

The results of the measurement of the e⁺e^- → nn cross section and effective neutron timelike form factor

are presented. The data taking was carried out in 2020-2021 at the VEPP-2000 e⁺e^- collider in the

center-of-mass energy range from 1891 to 2007 MeV. The general purpose nonmagnetic detector SND is

used to detect neutron-antineutrons events. The selection of nn events is performed using the time-of-flight

technique. The measured cross section is 0.4-0.6 nb. The neutron form factor in the energy range under

study varies from 0.3 to 0.2.

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023