ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 6, с. 727-734
ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ
СВЯЗЬ ДИПОЛЬНЫХ ПОЛЯРИЗУЕМОСТЕЙ ЗАРЯЖЕННЫХ
И НЕЙТРАЛЬНЫХ π-МЕЗОНОВ
© 2023 г. Л. В. Фильков1)*
Поступила в редакцию 27.04.2023 г.; после доработки 23.05.2023 г.; принята к публикации 07.06.2023 г.
Используя факт, что вклад состояний с изоспином I = 0 в разность амплитуд процессов γγ →
→ π+π- и γγ → π0π0 очень мал, проанализированы правила сумм для разности между дипольными
поляризуемостями заряженных и нейтральных пионов как функции параметров σ-мезона. Принимая
во внимание значение киральной теории возмущений для (α1 - β1)π0 = -1.9, получено (α1 - β1)π± =
= 9.4-8.2 для значений параметров σ-мезона в области mσ = 400-550 МэВ, Γσ = 400-600 МэВ,
Γσ→γγ = 0-3 кэВ. Оценка оптимального значения ширины распада σ → γγ дала Γσ→γγ ≲ 0.7 кэВ.
DOI: 10.31857/S0044002723060119, EDN: OTALSW
1. ВВЕДЕНИЕ
полной энергии процесса γ + π± → γ + π±. В
результате было получено (α1 - β1)π± = 13.6 ±
Поляризуемости пионов являются фундамен-
± 2.8 ± 2.4. Этот эксперимент [1] был проведен
тальными структурными параметрами, характери-
зующими поведение пиона во внешнем электро-
при Q2cut < 6 × 10-4 (ГэВ/c)2. События в области
магнитном поле. Дипольные поляризуемости воз-
Q2(2-8) × 10-3 (ГэВ/c)2 были использованы для
никают как O(ν1ν2)-члены в разложении небор-
оценки фона сильных взаимодействий.
новских амплитуд комптоновского рассеяния по
Полученный результат близок к значениям, на-
степеням начальной и конечной энергий фотона ν1
блюденным при радиационном фоторождении пио-
и ν2. В терминах электрической α1 и магнитной
β1 дипольных поляризуемостей соответствующее
нов на протонах (γp → γπ+n) [2] и равным 11.6 ±
± 1.5stat ± 3.0syst ± 0.5mod.
эффективное взаимодействие имеет форму:
(
)
С другой стороны, эти значения отличаются
H(2)eff = -14π
α1E2 + β1H2
(1)
2
от предсказаний киральной теории возмущений
((4.7-6.7) [3]).
Эти параметры даны в единицах 10-4 фм3.
Значения поляризуемостей пиона очень чув-
Эксперимент
Физического
института
ствительны к предсказаниям различных теорети-
им. П. Н. Лебедева по радиационному фото-
ческих моделей. Поэтому аккуратное эксперимен-
рождению на протоне
[4] дал α1π+ = 20 ± 12.
тальное их определение очень важно для исследо-
Это значение имеет большую ошибку, но тем не
вания обоснованности таких моделей.
менее также показывает расхождение с ChPT-
Поляризуемость заряженных пионов была
предсказанием.
впервые экспериментально определена в работе
Результат коллаборации COMPASS [5] для
[1] при анализе процесса рассеяния пионов с
электрической поляризуемости заряженного пиона
высокой энергией в кулоновском поле тяжелых
απ = 2.0 ± 0.6stat ± 0.7syst был получен, также
ядер (π-A → γπ-A′), благодаря эффекту Прима-
изучая рассеяние π--мезона в кулоновском поле
кова. Этот эксперимент был проведен при энергии
тяжелых ядер, предполагая, что α1 = -β1. Это
пионов, равной Ebeam = 40 ГэВ.
значение противоречит результату, полученному в
Поперечное сечение этого процесса имеет
очень похожем эксперименте в Серпухове [1], а
кулоновский пик при Q2 = (pA - p′A)2 = 2Q2min с
также результату работы [2].
шириной, равной
≃6.8Q2min, где Q2min =
(
)2
(
)
COMPASS-эксперимент был проведен с энер-
=
s-μ2
/
4E2beam
, и s обозначает квадрат
гией Ebeam = 190 ГэВ. Для таких значений Ebeam
величина Q2min(COMPASS) должна быть в 22.5 раз
1)Физический институт им. П. Н. Лебедева Российской
меньше, чем Q2min(Serpukhov). В этом эксперимен-
академии наук, Москва, Россия.
*E-mail: filkovlv@lebedev.ru
те [5] авторы рассматривали Q2 ≲ 0.0015 (ГэВ/c)2.
727
728
ФИЛЬКОВ
В работе [6] показано, что интерференция куло-
[21-24] очень неоднозначны и, как было показано в
новской амплитуды с когерентной ядерной ампли-
[15, 17], даже изменение этих полученных значений
тудой важна для 0.0005 ≤ Q ≤ 0.0015 (ГэВ/c)2.
более чем на 100% является еще сравнимо с име-
ющимся коридором ошибок. Поэтому необходимо
В работах [6-8] предполагается, что правиль-
рассмотреть другие дополнительные возможности
ным описанием амплитуды сильных взаимодей-
ствий является модель Глаубера (упругое множе-
определения (α1 - β1)π± .
ственное рассеяние в ядре). Условия и ограничения
Такая информация могла бы быть получена из
приближения Глаубера обсуждаются в классиче-
анализа этих параметров из дисперсионных правил
ской статье о дифракции U. Amaldi, M. Jacob
сумм (д.п.с.). Однако большой вклад в д.п.с. для
и G. Matthiae [9]. При высоких энергиях фазы
(α1 - β1)π± дает σ-мезон, который может быть
сильных взаимодействий становятся комплексны-
очень широким, и это может приводить к дополни-
ми и приобретают дополнительную энергетически
тельным неопределенностям при вычислении д.п.с.
зависимую фазу.
С другой стороны, если мы рассмотрим разни-
Это означает, что при высоких энергиях, а энер-
цу между поляризуемостями заряженных и ней-
гия налетающего пиона COMPASS-эксперимента
тральных пионов Δ ((α1 - β1)) = ((α1 - β1)π± -
180 ГэВ является высокой, фаза сильного взаи-
– (α1 - β1)π0 ), то вклад мезонов с изотопическим
модействия становится комплексной, и суммарная
спином I = 0 в t-канале в эту разницу равен 0
амплитуда требует учета множественного рассея-
[25, 26], когда массы заряженного и нейтральных
ния и будет комплексной, т.е. неизвестные фазы
мезонов равны друг другу. Как результат, модель-
появляются.
ная зависимость (α1 - β1)π± будет существенно
COMPASS-эксперимент должен рассматри-
уменьшена.
вать интерференцию кулоновской и сильных ам-
В настоящей работе мы исследуем DSR для
плитуд. Без реального фита данных невозможно
Δ ((α1 - β1)) как функцию параметров σ-мезона,
оценить эффект модельной зависимости дифрак-
когда массы заряженного и нейтрального пионов
ционного фона [7, 10].
не равны друг другу. Как будет показано, вклад
Поляризуемость заряженных пионов может
σ-мезона оказывается также мал и мы можем
быть так же найдена, изучая процесс γγ →
найти реалистическое ограничение на величину
→ π+π-. Исследование процесса γγ → ππ при
(α1 - β1)π± .
низких и средних энергиях было проведено в
рамках различных теоретических моделей и, в
частности, в рамках дисперсионных соотноше-
2. ДИСПЕРСИОННЫЕ ПРАВИЛА СУММ
ний (д.с.). В работах [11-15] мы анализировали
ДЛЯ ПОЛЯРИЗУЕМОСТЕЙ ПИОНОВ
процессы γγ → π0π0и γγ → π+π-, используя д.с.
с вычитанием для инвариантных амплитуд M++
Мы будем рассматривать амплитуды M++ и
и M+- без разложения на парциальные волны.
M+-. Эти амплитуды не имеют ни кинематических
Вычитательные константы однозначно определя-
сингулярностей, ни нулей [27]. Между амплитудами
лись в этих работах через поляризуемости пионов.
процессов γγ → π+π-, γγ → π0π0 и амплитудами
Значения поляризуемостей были получены из
с изоспинами I = 0 и I = 2 существуют следующие
фита экспериментальных данных процессов γγ →
соотношения:
√
(
)
→ π+π- и γγ → π0π0 в области энергий до 2500
2
1
и 2250 МэВ соответственно. Как результат было
FC =
F0 +
√ F2
,
(2)
3
2
найдено (α1 - β1)π± = 13.0+2.61.9 и (α1 - β1)π0 =
√
)
2(
√
= -1.6 ± 2.2. Этот результат для (α1 - β1)π±
FN =
F0 -
2F2
находится в хорошем согласии со значениями,
3
полученными в работах [1, 2, 4], и противоречит
предсказаниям киральной теории возмущений.
Дипольные поляризуемости (α1 и β1) определя-
ются [14, 28] в результате разложения неборнов-
В работах [16-19] дипольные поляризуемости
ских амплитуд комптоновского рассеяния на пионе
заряженных пионов были определены из анализа
по степеням t при фиксированном s = μ2:
экспериментальных данных процесса γγ → π+π-
√
(
)
в области полной энергии
t < 700 МэВ (где t—
M++
s=μ2,t
= 2πμ (α1 - β1) + O (t) ,
(3)
квадрат полной энергии в γγ с.м. системе).
(
)
π
M±
s=μ2,t
=2
(α1 + β1) + O (t),
Полученные в этих работах результаты близки
μ
к предсказаниям киральной теории возмущений [3,
20]. Однако значения экспериментальных попереч-
где μ2 — масса пиона (разные массы для π0 и π±),
ных сечений процесса γγ → π+π- в этой области
t + s + u = 2μ2.
ЯДЕРНАЯ ФИЗИКА том 86
№6
2023
СВЯЗЬ ДИПОЛЬНЫХ ПОЛЯРИЗУЕМОСТЕЙ
729
Дисперсионные правила сумм для разности ди-
где коэффициент Ch1 может быть оценен, исполь-
польных поляризуемостей были получены в работе
зуя нонет-симметрию [19, 34]:
[13], используя д.с. при фиксированном u = μ2
(6)
Ch1 (1170) ≃ 9Cb1(1235) ≃ 0.45.
без вычитания для амплитуд M++. В этом случае
Редже-полюсная модель позволяет использовать
Как результат получаем Γh1→γπ0 ≃ 1.6845 ±
д.с. без вычитания [27]. Такие д.с. равны:
± 0.44 МэВ.
Недавно было проведено множество работ по
(α1 - β1) =
(4)
изучению σ-мезона (см., например, [35-39]). Сред-
{∫∞
(
)
1
Im M++
t′,u = μ2
dt′
ние значения параметров σ-мезона приведены в
=
+
работе [39]:
2π2μ
t′
4μ2
mσ = 446 ± 6, Γσ/2 = 276 ± 5.
(7)
(
)
}
∫∞
Im M++
s′,u = μ2
ds′
Выражения для мнимых частей резонансных
+
амплитуд приведены в Приложении.
s′ - μ2
4μ2
Кроме вклада σ-, f(980) и f′0(1370)-мезонов мы
учли нерезонансный вклад S-волн с изоспином I =
Как очевидно из (2), вклад изоскалярных мезо-
= 0 и 2, согласно диаграммам на рис. 1.
нов в разность Δ ((α1 - β1)) равен 0 (если массы
Следует отметить, что вершины σ, f(980) и
заряженных и нейтральных мезонов равны). Мы
f′0(1370) мезонных полюсов в дисперсионном при-
будем изучать случай, когда эти массы не равны
ближении включают полную динамику переходов
друг другу.
на массовой поверхности. В этом случае нет необ-
Дисперсионные соотношения в s-канале для за-
ходимости рассматривать прямой и перерассеян-
ряженных пионов насыщались вкладами ρ(770)-,
ный механизмы в отдельности. Согласно условию
b1(1235)-, a1(1260)- и a2(1320)-мезонов, а для
унитарности мнимая часть амплитуды M++ для
π+π- петлевых диаграмм на рис. 1 может быть
π0-мезона вкладами ρ-, ω(782)-, φ-, h1(1170)-
записана как
и b1(1235)-мезонов. В t-канале рассматривались
вклады σ-, f0(980)-, f′0(1370)-мезонов как для
Im M(s)++ = BRe Tπ+π-→ππ,
(8)
заряженных, так и нейтральных пионов.
где B ≡ B (γγ → π+π-) является вкладом борнов-
Кроме того, мы учли нерезонансный S-волновой
ской амплитуды в S-волну γγ → π+π--амплитуды
вклад двух заряженных пионов в t-канале.
и равна:
Параметры ρ-, ω-, φ-, b1- и a2-мезонов да-
(e2 )m2π±
(1 + q/q0)
ны в [29]. Для a1(1260)-мезона мы взяли ma1 =
B=
ln
,
(9)
= 1230 МэВ [29], Γa1 = 425 МэВ (среднее значение
4π t2
1 - q/q0
в [29]), Γa1→γπ± = 0.64 МэВ [30].
где q(q0) есть импульс (энергия) π-мезона. Бор-
Параметры f0(980)- и f′0(1370)-мезонов взяты
новская амплитуда может быть выражена в терми-
нах амплитуд с изоспином I = 0 и I = 2 как
следующим образом:
√
√
f0(980): mf0 = 980 МэВ [29], Γf0 = 70 МэВ
B=
2/3B(I=0) +
1/3B(I=2).
(10)
(среднее значение из
[29]), Γf0→γγ = 0.56 ×
Принимая во внимание, что
×10-3 МэВ, Γf0→ππ = 0.84Γf0
(
)
√
[31], Γf0→K K=
B
γγ → π0π0
=
2/3B(I=0) -
(11)
= 0.16Γf0 ;
√
− 2/
3B(I=2) = 0,
f′0(1370): mf′(1370) = 1430 МэВ, Γf′0(1370) =
0
= 145 МэВ, Γf′
получаем [40]
0
(1370)→γγ = 0.54 × 10-5 МэВ [32],
√
√
Γf′
(1370)→ππ = 0.26Γf′0(1370) [33].
0
B(I=0) =
2/3B, B(I=2) =
1/3B.
(12)
Масса и полная ширина распада h1(1170)-
Амплитуды ππ-рассеяния выражаются через
мезона взяты из [29]: mh1 = 1170 МэВ, Γh1 =
амплитуды в изотопическом пространстве T(I=0) и
= 360 МэВ. Распад h1 → γπ0 еще не был наблю-
T(2) следующим образом:
ден, и мы использовали ширину распада согласно
(
)
работе [19]:
2
1
T(0) +
T(2)
,
(13)
(
)3
Tπ+π-→π+π- =
2
3
2
e
m2h1 - m2
π0
)
Γh1→γπ0 =
Ch1
,
(5)
2(
4π
3m3h1
T(0) - T(2)
Tπ+π-→π0π0 = -
3
ЯДЕРНАЯ ФИЗИКА том 86
№6
2023
730
ФИЛЬКОВ
+
=
+
Born
f0(980)
Рис. 1. S-волновые вклады.
]
Согласно соотношениям (10) и (13) мнимые
(
) qη
-ϵ4θ
t - 4m2η
√
,
части ππ-петель дают вклад в S-волны амплитуды
t
M++ как
√
√
(
)
Im M(s)++
γγ → π0π0
=
(14)
где qk = t/4 - m2k и qη = t/4 - m2η; mk и mη
(
)
4
1
являются массами K и η-мезонов соответственно.
=
BRe T(0) -
T(2)
,
9
2
Параметры в уравнениях (17)-(19) представле-
ны в табл. 1.
(
)
Im M(s)++
γγ → π+π-
=
(15)
Чтобы описать фазовый сдвиг δ20 (t), мы исполь-
(
)
зуем параметризацию [42] в области энергий до
1
=
BRe
4T(0) + T(2)
1.5 ГэВ, предполагая η20 (t) = 1 [43]
9
q
{
}
tan δ20 =
A20 + B20q2 + C20q4 + D20q6
×
(20)
Амплитуды T(0) и T(2) могут быть представлены
q0
как
)
q0
( 4μ2 - s20
Re T(I) =
ηI cos δI0 (t)sin δI0 (t) ,
(16)
×
,
2
q
t-s
0
где
где δI0 (t) — фазовый сдвиг S-волны π-рассеяния с
изоспином I и ηI — неупругость.
A20 = -0.044, B20 = -0.0855/μ2,
Выражение для сдвига фаз δ0 (t) определено,
C20 = -0.00754/μ4,
используя параметризацию работы [41]. При низ-
D20 = 0.000199/μ6, s20 = -11.9/μ2.
ких энергиях t ≲ 4m2k имеем
√
t
μ2
Следует заметить, что вклад петлевой диаграм-
ctg δ00 (t) =
(
)×
(17)
2q
t-12μ2
мы γγ → K+K- → ππ в Δ ((α1 - β1)) очень мал и
{
}
мы не рассматриваем его здесь.
μ
Результаты вычисления вкладов мезонов и ππ-
×
√
+ B0 + B1w (t) + B2w(t)2 + B3w (t)3
,
t
петель (кроме вклада σ-мезона) в д.п.с. (4) для
где
заряженных и нейтральных пионов представлены в
√
√
табл. 2.
t-
4m2k
-t
Параметры q0 и q2 являются вкладами ππ-
w (t) =
√
√
петель с изоспинами I = 0 и I = 2 соответственно.
t+
4m2k - t
и η00 равны 1.
3. ВЫЧИСЛЕНИЯ (α1 - β1)π±
Для энергий 4m2k < t < (1.42 ГэВ)2 мы исполь-
Значения (α1 - β1)π0 были определены при ис-
зуем [41]
следовании процесса γγ → π0π0 в работах [13, 18,
q2k
q4k
19]: -1.6 ± 2.2, -0.6 ± 1.8, -1.25 ± 0.08 ± 0.15.
δ00 (t) = d0 + B
+C
+
(18)
m2k
m4
Эти значения находятся в согласии с пред-
k
сказанием киральной теории возмущений
[44]
(
) q2η
+ Dθ
t - 4m2
,
(α1 - β1)
0
= -1.9 ± 0.2. Поэтому для того
η
m2η
чтобы определить (α1 - β1)π± , мы добавили зна-
[
(
)2
чение (α1 - β1)
0
к результатам вычислений
-qk
qk
q2k
η00 (t) = exp
√
ϵ1 + ϵ2√
+ϵ3
-
(19)
Δ ((α1 - β1)) с помощью д.п.с. при различных
t
t
t
значениях ширины распада σ → γγ, когда масса и
ЯДЕРНАЯ ФИЗИКА том 86
№6
2023
СВЯЗЬ ДИПОЛЬНЫХ ПОЛЯРИЗУЕМОСТЕЙ
731
Таблица 1. Значения коэффициентов в выражениях (17), (19) [41]
B0
7.26 ± 0.23
d0
(227.1 ± 1.3)◦
ϵ1
4.7 ± 0.2
B1
-25.3 ± 0.5
B
(94.0 ± 2.3)◦
ϵ2
-15.0 ± 0.8
B2
-33.1 ± 1.2
C
(40.4 ± 2.9)◦
ϵ3
4.7 ± 2.6
B3
-26.6 ± 2.3
D
(-86.9 ± 4.0)◦
ϵ4
0.38 ± 0.34
Таблица 2. Вклады мезонов и ππ-петель в дисперсионные правила сумм (4) для заряженных и нейтральных пионов
ρ
b1
a1
a2
f0
f′0
q0
q2
π±
-1.14
0.93
1.92
1.98
0.80
0.08
-4.27
0.34
ρ
ω
φ
f0
f′0
h1
q0
q2
π0
-1.42
-11.61
-0.04
0.69
0.08
5.32
-4.26
-1.36
полная ширина распада σ-мезона брались в интер-
масс пионов. Эти правила сумм вычислялись
валах mσ = 400-550 МэВ, Γσ = 400-600 МэВ.
для параметров σ-мезона в интервалах: mσ =
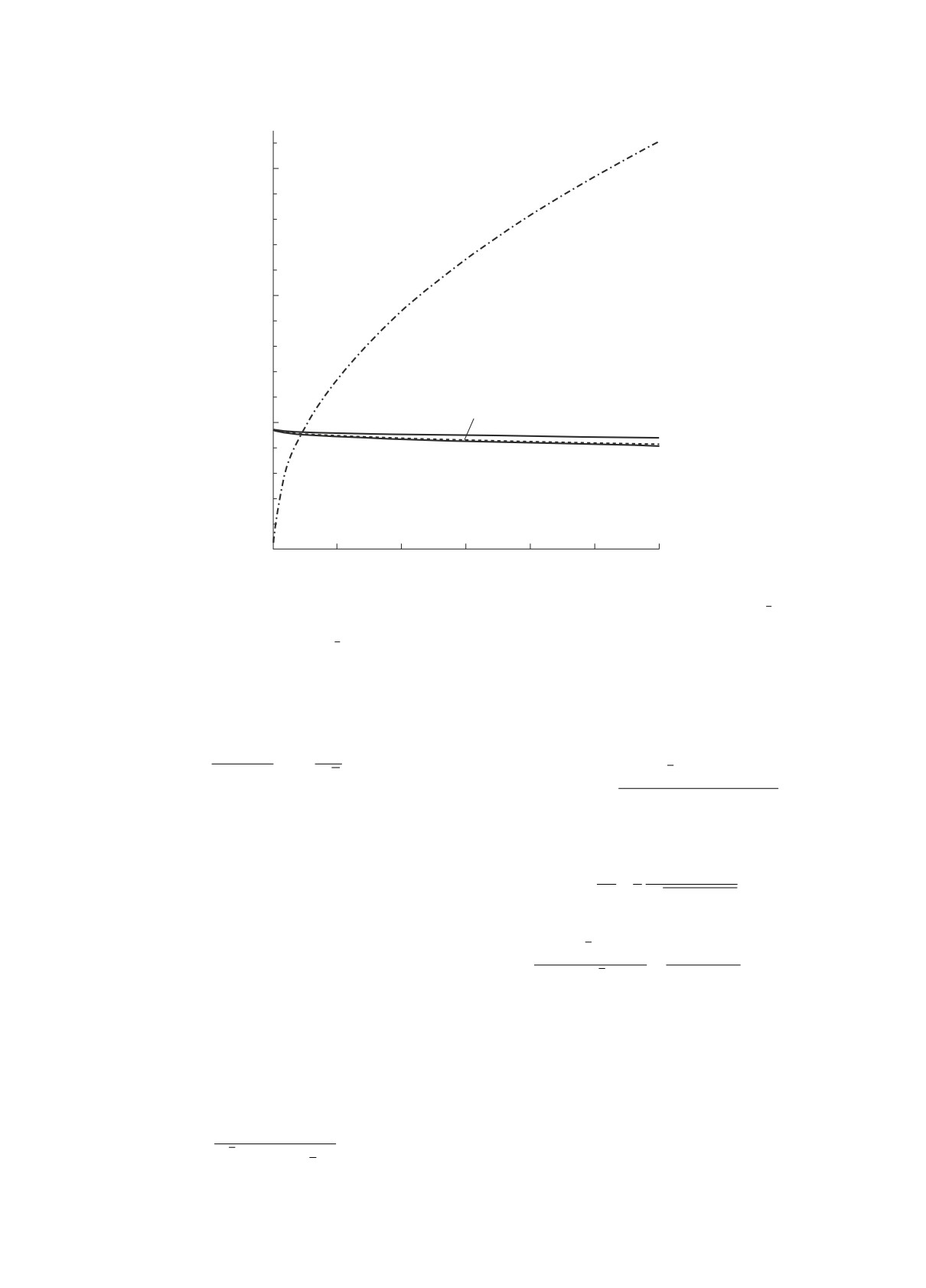
Результаты вычислений представлены на рис. 2.
= 400-550 МэВ, Γσ = 400-600, Γσ→γγ = 0-
√
Кривая
1
соответствует вычислениям с
tσ =
3 кэВ. Для того чтобы определить (α1 - β1)π± , мы
= mσ - i1/2Γσ = 446 - i276. Кривые 2 и 3 соот-
добавили (α1 - β1)
0
= -1.9 к Δ ((α1 - β1)).
ветствуют mσ = 400 МэВ, Γσ = 600 МэВ и mσ =
Полученные значения (α1 - β1)π± слабо зависят
= 550 МэВ, Γσ = 400 МэВ соответственно. Как
от параметров σ-мезона и находятся в пределах
очевидно из этого рисунка, полученные значения
(α1 - β1)π± = 9.4-8.2. Этот результат согласуется
(α1 - β1)π± слабо зависят от массы и полной
с экспериментальными значениями, полученными
ширины распада σ-мезона в рассматриваемой
в работах [1, 2], и противоречит вычислениям в
области. Полученные значения (α1 - β1)π± нахо-
рамках киральной теории возмущений [3].
дятся в пределах 9.5-8.0.
Кроме того, анализ дисперсионных правил сумм
Кривая
4
на рис.
2
является результатом
показал, что значения ((α1 - β1)π± < 15) могут
вычисления дисперсионных правил сумм
(4)
быть получены, если ширина распада Γσ→γγ ≲
для (α1 - β1)π± при mσ = 446 МэВ и Γσ =
≲ 0.7 кэВ. Значения Γσ→γγ ≲ 1 кэВ были ранее
= 552 МэВ, в случае когда не учитывается величи-
также получены в работах [13, 14, 45, 46]. Резуль-
на Δ ((α1 - β1)). Полученные результаты сильно
таты с Γσ→γγ > 1 кэВ приведены в [37, 47].
зависят от ширины распада Γσ→γγ и указывают,
Автор благодарит Т. Валчера, В. Л. Кашеварова
что реалистические значения (α1 - β1)π± могут
и А. И. Львова за полезные обсуждения.
быть получены в рассматриваемом подходе, если
Γσ→γγ ≲ 0.7 кэВ.
Приложение 1
Влияние верхнего предела интегрирования (Λ) в
дисперсионных правилах сумм (4) на результат вы-
числений было изучено. Показано, что результаты
Вклады векторных и псевдовекторных мезонов
(
)
практически не меняются, если Λ больше (6 ГэВ)2.
(ρ, ω, φ, a1и b1) в Im M++
s,u = μ2
вычисляются
В настоящей работе мы проводили интегрирование
с помощью выражения
до (20 ГэВ)2.
(
)
Im M(V)++
s,u = μ2
=
(П.1)
Γ0
4. ЗАКЛЮЧЕНИЯ
= ∓4g2V s(
)2
,
m2V - s
+Γ2
0
Используя факт, что вклад состояний с изоспи-
ном I = 0 в разность Δ ((α1 - β1)) = (α1 - β1)π± -
где mV — масса мезона, знак “+” соответствует
- (α1 - β1)π0 равен 0, когда массы заряженных
вкладу a1- и b1-мезонов и
и нейтральных π-мезонов равны друг другу,
√ (
)3
m2V
mV
мы проанализировали дисперсионные правила
g2V = 6π
×
(П.2)
сумм для этой разницы для реальных значений
s
m2V
-μ2
ЯДЕРНАЯ ФИЗИКА том 86
№6
2023
732
ФИЛЬКОВ
(
)±
1
1
30
4
20
2
10
3
1
0
0.5
1.0
1.5
2.0
2.5
3.0
, кэВ
√
Рис. 2. Зависимость (α1 - β1)π± от Γσ→γγ. Кривые 1, 2 и 3 соответствуют вычислению Δ((α1 - β1)) при
tσ = 446 -
− i276, 400 - i300 и 550 - i200 МэВ соответственно. Кривая 4 является результатом вычисления дисперсионных правил
√
сумм (4) только для (α1 - β1)π± при
tσ = 446 - i276.
(
)
×ΓV→γπD1
m2V
/D1 (s) ,
Тогда легко показать, что мнимая часть ампли-
туды Im Mσ++
(t) вкладов σ-мезона в рассматрива-
(
)3/2
емый процесс может быть представлена как
q2i (s)
m2V
Γ0 =
(
)
(П.3)
(√
)
q2i
m2V
√s×
gσ
t+Ms
Γσ0 (t)
Im Mσ++ (t) =
,
(П.5)
(
)
2
(t - M2σ)2 + (Γσ0 (t))
×D1
m2V
/D1 (s) ΓV .
где
D1
в этих уравнениях связан с центробеж-
[
]1/2
ным потенциалом и равен D1 = 1 + (qir)2 [48],
8π
2
MσΓγγΓσ
r=1
фм — эффективный радиус взаимодей-
gσ =
√
,
(П.6)
ствия, ΓV и ΓV→γπ — полная ширина и шири-
t
3
M2σ - 4μ2
на распада этих мезонов на γπ. Импульсы q2i
(
)
(√
)
(
)1/2
для (ρ, ω, φ, a1 и b1)-мезонов равны
s - 4μ2
/4,
(
)
(
)
Mσ
t+Mσ
t - 4μ2
s - 9μ2
/4,
s - 4m2k
/4, (s - (mρ + μ)2)/4 и
Γσ0 =
√
Γσ. (П.7)
(
)
2
t
M2σ - 4μ2
s - 16μ2
/4 соответственно.
Эти выражения (П.5)-(П.7) могут быть очень по-
лезными для описания скалярных мезонов с боль-
Приложение 2
шими ширинами распада.
Так как K-мезоны дают большой вклад в шири-
Амплитуда вклада скалярного мезона в процесс
ну распада f0(980)-мезона и порог реакции γγ →
γγ → ππ может быть записана как
→K¯ очень близок к массе f0(980)-мезона, мы
gs
T =
√
(П.4)
рассматриваем выражение Флэтта [49] для вклада
t-Ms -i1Γs
2
f0(980)-мезона в процесс γγ → ππ.
ЯДЕРНАЯ ФИЗИКА том 86
№6
2023
СВЯЗЬ ДИПОЛЬНЫХ ПОЛЯРИЗУЕМОСТЕЙ
733
Для t > 4m2k:
10.
L.V. Fil’kov and V. L. Kashevarov, Phys. Part. Nucl.
48, 117 (2017).
Γ0f
0
11.
L. V. Fil’kov and V. L. Kashevarov, in Proceedings
Im Mf0++ = gf0
(
)
,
(П.8)
of the “NSTAR 2007”, Bonn, Germany, 05-08 Sep-
m2f0 - t
2 +Γ2
0f0
tember 2007, p. 179; arXiv:0802.0965 [nucl-th].
12.
L. V. Fil’kov and V. L. Kashevarov, in Proceedings of
где
the 6th Workshop on Chiral Dynamics, 06-10 July
[
(
)1/2
2009, Bern, Switzerland, PoS (CD09) 036; arXiv:
t - 4μ2
Γ0f
= Γf0→ππ
+ (П.9)
0909.4849 [hep-ph].
0
m2 - 4μ2
f0
13.
L. V. Fil’kov and V. L. Kashevarov, Eur. Phys. J. A 5,
(
)1/2 ]
285 (1999).
t - 4m2k
14.
L. V. Fil’kov and V. L. Kashevarov, Phys. Rev. C 72,
+ Γf0→kk
mf0.
035211 (2005).
4m2k - m2
f0
15.
L. V. Fil’kov and V. L. Kashevarov, Phys. Rev. C 73,
035210 (2006).
Для t < 4m2k:
16.
D. Babusci, S. Bellucci, G. Giordano, G. Matone,
([
A. M. Sandorfi, and M. A. Moinester, Phys. Lett. B
Im M++ = gf0Γ0f
m2 - t -
(П.10)
277, 158 (1992).
0
f0
17.
J. F. Donoghue and B. R. Holstein, Phys. Rev. D 48,
(
)1/2
]2
)-1
137 (1993).
4m2k - t
18.
A. E. Kaloshin and V. V. Serebryakov, Z. Phys. C 64,
−
mf0 Γf0→kk
+Γ2
0f0
,
689 (1994).
4m2k - m2
f0
19.
R. Garcia-Martin and B. Moussallam, Eur. Phys. J.
C 70, 155 (2010).
(
)1/2
20.
U. B ¨urgi, Nucl. Phys. B 479, 392 (1997).
t - 4μ2
21.
C. Berger et al. (PLUTO Collab.), Z. Phys. C 26, 199
Γ0f
= Γf0→ππmf0
(П.11)
0
m2 - 4μ2
(1984).
f0
22.
A. Courau et al. (DM1 Collab.), Nucl. Phys. B 271, 1
(1986).
23.
Z. Ajaltoni et al. (DM2 Collab.), Phys. Lett. B 194,
СПИСОК ЛИТЕРАТУРЫ
573 (1987).
1.
Yu. M. Antipov, V. A. Batarin, V. A. Bessubov,
24.
J. Boyer et al. (Mark II Collab.), Phys. Rev. D 42,
N. P. Budanov, Yu. P. Gorin, S. P. Denisov, I. V. Kotov,
1350 (1990).
A. A. Lebedev, A. I. Petrukhin, S. A. Polovnikov,
25.
A. I. L’vov and V. A. Petrun’kin, Preprint of P.N.
V. N. Roinishvili, D. A. Stoyanova, P. A. Kulinich,
Lebedev Physical Institute, No. 170 (1977).
G. V. Mecel’macher, A. G. Ol’shevski, et al.,
26.
L. V. Filkov, I. Guia ¸su, and E. E. Radescu, Phys. Rev.
Phys. Lett. B 121, 445 (1983); Yu. M. Antipov,
D 26, 3146 (1982).
V. A. Batarin, V. A. Bessubov, N. P. Budanov,
27.
H. A. Abarbanel and M. L. Goldberger, Phys. Rev.
Yu. P. Gorin, S. P. Denisov, I. V. Kotov, A. A. Lebedev,
165, 1594 (1968).
A. I. Petrukhin, S. A. Polovnikov, V. N. Roinishvili,
28.
I. Guia ¸su and E. E. Radescu, Ann. Phys. (N.Y.) 122,
D. A. Stoyanova, P. A. Kulinich, G. V. Mecel’macher,
436 (1979).
A. G. Ol’shevski, et al., Z. Phys. C 26, 495 (1985).
2.
J. Ahrens, V. M. Alexeev, J. R. M. Annand,
29.
J. Beringer et al. (PDG Collab.), Phys. Rev. D 86,
H. J. Arends, R. Beck, G. Caselotti, S. N. Cherepnya,
010001 (2012).
D. Drechsel, L. V. Fil’kov, K. F ¨ohl, I. Giller,
30.
M. Zielinski, D. Berg, C. Chandlee, S. Cihangir,
P. Grabmayr, T. Hehl, D. Hornidge, V. L. Kashevarov,
T. Ferbel, J. Huston, T. Jensen, F. Lobkowicz,
M. Kotulla, et al., Eur. Phys. J. A 23, 113 (2005).
T. Ohshima, P. Slattery, P. Thompson, B. Collick,
3.
J. Gasser,M. A. Ivanov, and M. E. Sainio, Nucl. Phys.
S. Heppelmann, M. Marshak, E. Peterson,
B 745, 84 (2006).
K. Ruddick, et al., Phys. Rev. Lett.
52,
1195
4.
T. A. Aibergenov, P. S. Baranov, O. D. Beznisko,
(1984).
S. N. Cherepnija, L. V. Fil’kov, A. A. Nafikov,
31.
V. V. Anisovich, V. A. Nikonov, and A. V. Sarantsev,
Phys. At. Nucl. 65, 1545 (2002).
A. I. Osadchiy, V. G. Raevskiy, L. N. Shtarkov, and
E. I. Tamm, Czech. J. Phys. B 36, 948 (1986).
32.
D. Morgan and M. R. Pennington, Z. Phys. C 48, 623
5.
A. Guskov (COMPASS Collab.), Fizika B 17, 313
(1990).
(2008).
33.
D. V. Bugg, A. V. Sarantsev, and B. S. Zou, Nucl.
6.
G. F ¨aldt and U. Tengblad, Phys. Rev. C 76, 064607
Phys. B 471, 59 (1990).
(2007).
34.
A. I. L’vov and V. A. Petrun’kin, Sov. Physics-
7.
G. F ¨aldt and U. Tengblad, Phys. Rev. C 79, 014607
Lebedev Inst. Reports, No 12 (1985).
(2009); C 87, 029903(E) (2013).
35.
I. Caprini, G. Colangelo, and H. Leutwyler, Phys. Rev.
8.
T. Walcher, Prog. Part. Nucl. Phys. 61, 106 (2008).
Lett. 96, 132001 (2006); hep-ph/0512364.
9.
U. Amaldi, M. Jacob, and G. Matthiae, Ann. Rev.
36.
I. Caprini, Phys. Rev. D 77, 114019 (2008); arXiv:
Nucl. Part. Sci. 26, 385 (1976).
0804.3504.
ЯДЕРНАЯ ФИЗИКА том 86
№6
2023
734
ФИЛЬКОВ
37. B. Moussallam, Eur. Phys. J. C 71, 1814 (2011).
44. S. Bellucci, J. Gasser, and M. E. Sainio, Nucl. Phys.
38. R. Kami ´nski, R. Garcia-Martin, J. R. Pel ´aes, and
B 423, 80 (1994).
J. Ruiz de Elvira, Nucl. Phys. Proc. Suppl. B 234, 253
45. S. Dubni ˇcka, A. Z. Dubni ˇckov ´a, and M. Se ˇcansk ´y,
(2012); arXiv: 1211.2617 [hep-ph].
Acta Phys. Slov. 55, 25 (2005).
39. J. R. Pel ´aez, J. Nebreda, G. Rios, and J. Ruiz de
Elvira, Acta Phys. Polon. Supp. 6, 735 (2013); arXiv:
46. N. N. Achasov and G. N. Shestakov, JETP Lett. 88,
1304.5121 [hep-ph].
295 (2008).
40. M. Boglione and M. R. Pennington, Eur. Phys. J. C
47. M. Hoferichter, D. R. Philips, and C. Schat, Eur.
9, 11 (1999).
Phys. J. C 71, 1743 (2011).
41. R. Garcia-Martin, R. Kami ´nski, J. R. Pel ´aez, J. Ruiz
de Elvira, and F. J. Yndur ´ain, Phys. Rev. D 83, 074004
48. J. M. Blatt and V. F. Weisskopf, Theoretical Nuclear
(2011).
Physics (Springer-Verlag, New York, 1979), pp. 359-
42. A. Schenk, Nucl. Phys. B 363, 97 (1991).
365, 386-389.
43. B. Ananthanarayan, G. Colangelo, J. Gasser, and
H. Leutwyler, Phys. Rep. 353, 207 (2001).
49. S. M. Flatt ´e, Phys. Lett. B 63, 228 (1976).
CONNECTION OF THE DIPOLE POLARIZABILITIES OF CHARGED
AND NEUTRAL π-MESONS
L. V. Fil’kov1)
1)P. N. Lebedev Physical Institute of the Russian Academy of Sciences, Moscow, Russia
Using the fact that the contribution of the states with isospin I = 0 in the difference of the amplitudes
of the processes γγ → π+π- and γγ → π0π0 is very small, the dispersion sum rules for the difference
between the dipole polarizabilities of the charged and neutral pions have been analyzed as a function of
the σ-meson parameters. Then taking into account the current chiral perturbation value of (α1 - β1)π0 =
= -1.9, the value (α1 - β1)π± = 9.4-8.2 has been found for the σ-meson parameter within the region:
mσ = 400-550 MeV, Γσ = 400-600 MeV, Γσ→γγ = 0-3 keV. Estimation of the optimal value of the decay
width σ → γγ has given Γσ→γγ ≲ 0.7 keV.
ЯДЕРНАЯ ФИЗИКА том 86
№6
2023