ЯДЕРНАЯ ФИЗИКА, 2023, том 86, № 6, с. 735-741

ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ПОЛЯ

МОЖНО ЛИ ОЦЕНИТЬ ПАРАМЕТРЫ 2D-ЭВОЛЮЦИИ СИГНАТУРЫ

МЕТРИКИ ПРОСТРАНСТВА С ЭНЕРГИЕЙ ПО КОРРЕЛЯЦИЯМ

АЗИМУТАЛЬНЫХ ХАРАКТЕРИСТИК ЧАСТИЦ?

Поступила в редакцию 12.07.2023 г.; после доработки 12.07.2023 г.; принята к публикации 12.07.2023 г.

Компланарность подстволов в гамма-адронных семействах и так называемый long-range near-side

“ridge”-эффект, обнаруженный CMS Коллаборацией на LHC, могут быть описаны в рамках модели

FANSY 2.0, которая воспроизводит компланарную генерацию наиболее энергичных частиц в адронных

взаимодействиях при сверхвысоких энергиях. Компланарная генерация, в свою очередь, может

объясняться, в частности, гипотезой об эволюции сигнатуры метрики пространственно-временного

континуума, а именно, переходом основного трехмерного состояния в двухмерное (3D ↔ 2D) с ростом

энергии. Предлагается способ экспериментальной проверки этой гипотезы через анализ азимутальных

корреляций частиц, генерируемых во взаимодействиях адронов.

DOI: 10.31857/S0044002723060120, EDN: ORUPJO

1. ВВЕДЕНИЕ

к двум измерениям (3D ↔ 2D) с ростом энергии

[18, 19].

В высокогорных и стратосферных эксперимен-

тах с рентгено-эмульсионными камерами была об-

Коллаборация CMS (LHC) обнаружила при

наружена [1-9] тенденция к компланарности от-

энергии взаимодействия протонов

√s = 7 ТэВ так

носительно изолированных друг от друга наиболее

называемый long-range near-side “ridge”-эффект

энергичных частиц (γ, e^±, h^±) и/или подстволов

(далее “ridge”-эффект) [20], т.е. аномально высо-

кое значение двухчастичной корреляционной функ-

(т.е. развившихся каскадов от вышеупомянутых

частиц) в составе так называемых гамма-адронных

ции R(Δη, Δϕ) = f(S(Δη, Δϕ)/B(Δη, Δϕ)) при

(γ-h) семейств (групп генетически связанных ча-

3 ≲ |Δη| ≤ 4 и |Δϕ| ≈ 0 в событиях с высокой

стиц с высокой (≳5 ТэВ) энергией). Это явле-

(n_ch > 110) множественностью заряженных адро-

ние было первоначально интерпретировано как ре-

нов (h^±) в области |η| < 2.4. Здесь S(Δη, Δϕ)

зультат компланарной генерации наиболее энер-

и B(Δη,Δϕ) — функции сигнала и фона соот-

гичных частиц (КГЧ) с большими поперечными

ветственно, Δη — разность псевдобыстрот адро-

импульсами в плоскости компланарности, pcoplt ≳

нов, Δϕ — разность их азимутальных углов ϕ.

Для функции S(Δη, Δϕ) величины переменных Δη

≳ 1 ГэВ/c [10-12].

и Δϕ вычисляются перебором пар частиц внут-

Идеи, предложенные для объяснения появления

ри одного рассматриваемого взаимодействия. Для

КГЧ при сверхвысоких энергиях, разделяются на

функции B(Δη, Δϕ) величины Δη и Δϕ вычис-

две принципиально разные группы:

ляются для каждой частицы из рассматриваемого

1. ядерно-физические механизмы адронных

взаимодействия поочередно со всеми частицами

взаимодействий, подразумевающие большие pcoplt

другого случайно выбранного взаимодействия.

в плоскости компланарности, и связывающих

Для анализа возможной связи компланарности

эффект с

и “ridge”-эффекта была разработана феноменоло-

1.1. образованием специфических лидирующих

гическая модель FANSY 2.0 [21-24], воспроиз-

систем [13-16];

водящая как традиционную, так и компланарную

1.2. угловым моментом кварк-глюонной струны

генерацию частиц (соответственно версии QGSJ

[17];

[21] и CPG [22]). В модели FANSY

2.0

CPG

максимальная компланарность связана с самыми

2. гипотеза, предполагающая переход размер-

энергичными адронами. При уменьшении быст-

ности пространства на малых масштабах от трех

роты |y| компланарность слабеет и совсем исче-

¹⁾Институт ядерных исследований РАН, Москва, Россия.

зает в центральной кинематической области при

^*E-mail: rauf_m@mail.ru

|y| ≲ y_thr = |y²| - Δy ≈ 2-3, где Δy - параметр.

735

736

МУХАМЕДШИН

При моделировании взаимодействий процесс

рамках 2D-гипотезы степень компланарности ча-

“копланаризации” применяется после розыгрыша

стиц, рожденных в течение того же времени t_int,

взаимодействия в рамках традиционной версии

и частиц, реально существующих в каждый по-

FANSY 2.0 QGSJ. При этом поперечные импульсы

следующий момент времени, может существенно

частиц разворачиваются в сторону случайно вы-

зависеть от развития во времени процессов после-

бранной плоскости компланарности, относительно

довательных распадов тяжелых резонансов в более

которой азимутальные углы поперечных импульсов

легкие частицы.

распределены по Гауссу с σ ∼ σ₀(|y₂/y|)^β . Здесь

Предположим, что по неизвестным нам при-

y₂ — быстрота второй по энергии частицы. При

чинам при энергиях взаимодействия адронов

|y| < |y_thr| ∼ 2-3 эффект отсутствует.

√s ∼ 7 ТэВ имеет место локальный переход

Подчеркнем, что FANSY 2.0 — это модель ad

трехмерного состояния в двухмерное и обратно

hoc, т.е. чисто феноменологическая, поскольку

(3D ↔ 2D). Допустим, что таковыми причинами

ее физические основы остаются неясными. Если

являются, например, очень высокая кратковре-

оставаться в рамках общепринятых концепций, то

менная пространственно-временная плотность

теоретические модели [13-17] почти неизбежно

энергии и/или какие-то релятивистские эффекты.

требуют для описания компланарности большие

Продолжительность времени существования 2D-

значения поперечного импульса pcoplt (что про-

эволюции неизвестна, но она не может быть

тиворечит данным LHC

[25]), иначе придется

меньше t_int. Ниже для удобства используется

предположить уменьшение компонент попереч-

величина τ_2D, отсчет которой начинается от мо-

ного импульса, направленных перпендикулярно

мента генерации прямых частиц, т.е. полное время

плоскости компланарности (что не вписывается

2D-состояния равно сумме t_int + τ_2D. Рассмотрим

экспериментальные возможности оценки этого

в рамки современных представлений). Поэтому с

параметра, имея в виду, что при генерации частиц

феноменологической точки зрения наиболее под-

рождаются как относительно стабильные частицы,

ходящим является предположение об уменьшении

так и резонансы с малыми временами жизни.

размерности пространства с трех до двух [18, 19]

(далее, для краткости, 2D-гипотеза).

Если частицы рождаются в 2D-пространстве,

В настоящей работе не рассматриваются моде-

то они разлетаются компланарно. Резонансы со

ли [13-16], связанные с образованием специфи-

средним временем жизни 〈τ〉 = τ₀γ_L (τ₀ — среднее

ческих лидирующих систем, в частности, дифрак-

время жизни резонанса в покое, γ_L — его Лоренц-

ционных кластеров. Можно только отметить сле-

фактор) могут распадаться как в 2D-пространстве,

дующее: подобные процессы а) не могут детально

если их реальное время жизни τ ≲ τ_2D, так и в 3D-

изучаться на LHC; б) не связаны с эффектами в

пространстве, если τ > τ_2D.

центральной кинематической области, в частности,

Моделирование показывает, что эксперимен-

с “ridge”-эффектом; в) требуют отдельного иссле-

тальная и расчетная функции R(Δη, Δϕ) в области

дования в экспериментах с космическими лучами,

“ridge”-эффекта близки друг к другу при “копла-

поскольку дифракционные процессы играют там

очень важную роль.

наризации” в области быстрот |y| ≳ 3 [22], что

соответствует энергии частиц E ≳ 20 ГэВ. Тогда

Далее будут обсуждаться две важные проблемы

в рамках предположения о справедливости 2D-

для ρ-, ω-, η- и π⁰-мезонов имеем 〈τ〉 ≳ 10-22,

гипотезы. Во-первых, будет рассмотрено, какие

10-21, 10-17 и 10-14 с соответственно. Отметим

экспериментальные данные было бы необходимо, в

только, что распад π⁰-мезонов (последний в це-

идеале, проанализировать для окончательного ре-

почке распадов) должен влиять на наблюдаемую

шения этой проблемы. Во-вторых, попробуем про-

компланарность уже меньше, так как поперечные

анализировать, какие данные, бросающие какой-то

импульсы гамма-квантов относительно направле-

свет на поставленные вопросы, можно получить на

ния движения π⁰-мезонов при их распадах равен

существующих установках на LHC.

∼70 МэВ/c, тогда как, например, поперечные им-

пульсы нейтральных пионов в распаде ρ-мезонов

2. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

равен ∼360 МэВ/c.

И СИГНАТУРА ПРОСТРАНСТВА

В рамках 2D-гипотезы эти величины задают

С экспериментальной точки зрения очень важ-

примерные масштабы временных интервалов, где

ным отличием двух конкурирующих концепций яв-

можно искать какие-то изменения в степени ком-

ляется то, что ядерно-физические механизмы про-

планарности поперечных импульсов различных ти-

текают однократно в течение очень малого про-

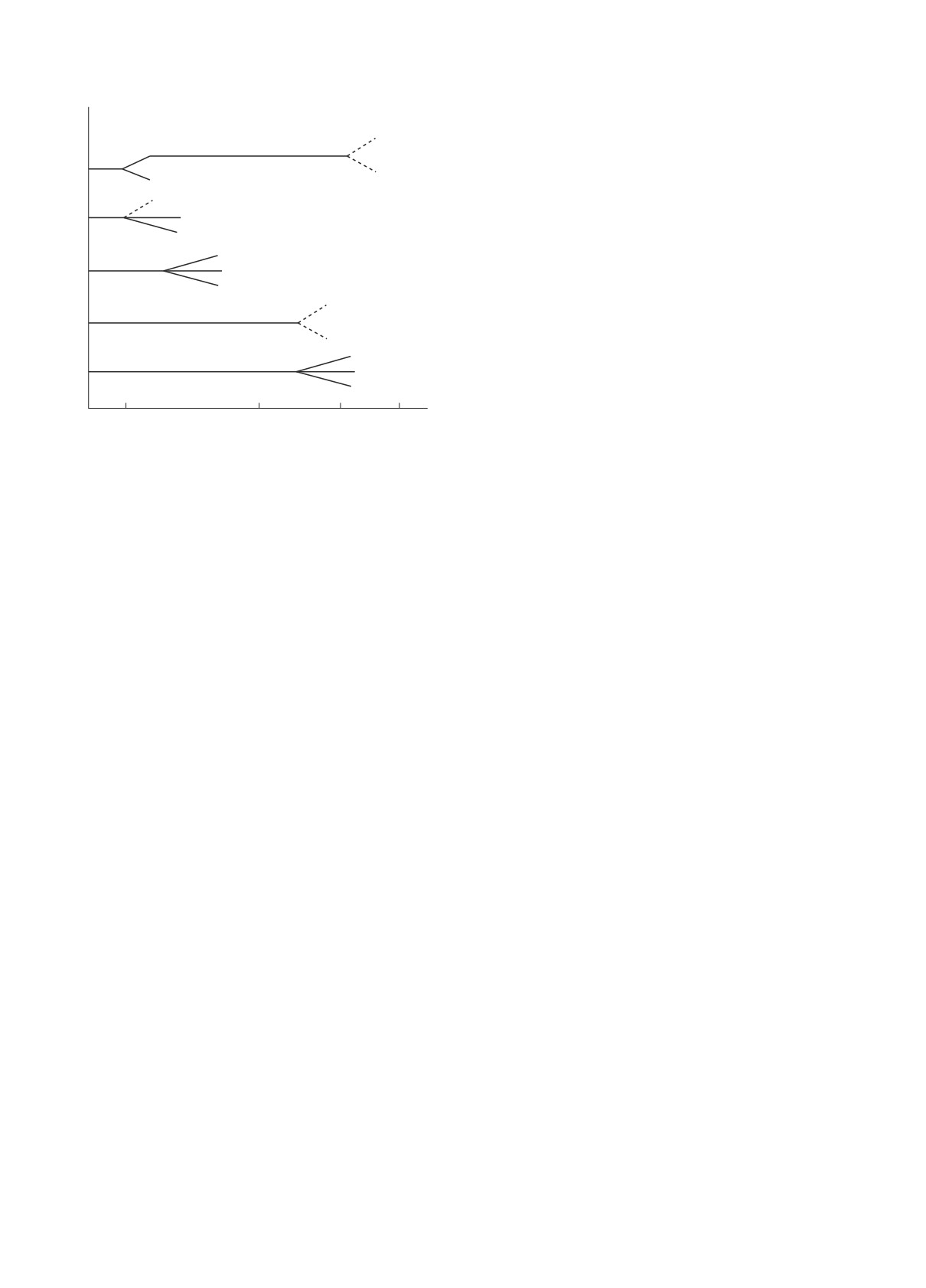
пов частиц. Рисунок 1 иллюстрирует эту карти-

межутка времени, t_int ∼ 2r_p/c ≲ 5 × 10-24 с (r_p —

ну для основных каналов распадов ρ±,0-, ω-, η-

радиус протона, c — скорость света), тогда как в

резонансов и π⁰-мезонов.

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

МОЖНО ЛИ ОЦЕНИТЬ ПАРАМЕТРЫ 2D-ЭВОЛЮЦИИ

737

в широком кинематическом диапазоне (|η, y| ≳ 3,

x_F ≳ 0.01) при сверхвысоких энергиях (в диапа-

зоне LHC), для получения информации о кана-

лах рождения, энергии и импульсах и угловых

характеристиках резонансов; заряженных частиц;

γ-квантов, а также осуществления полного ки-

нематического анализа каждого взаимодействия и

восстановления кинематической истории распадов

нестабильных частиц. Крайне необходимо про-

должить исследование явления компланарности в

космических лучах, где впервые наблюдался этот

феномен. Совместный анализ данных, полученных

на LHC и в космических лучах, может дать очень

интересные и неожиданные результаты.

Таким образом, предлагается следующий алго-

10²²

10¹⁷

10¹⁴

10¹²

ритм действий.

, c

1. Осуществить полный кинематический ана-

Рис. 1. Примерные временные масштабы некоторых

лиз каждого взаимодействия в широком интервале

каналов распадов первичных резонансов (ρ±,0, ω, η) с

быстрот y и/или x_F (до максимально возможных

энергией E ∼ 20 ГэВ и последующих распадов вторич-

значений) вторичных частиц.

ных частиц.

2. Восстановить полную кинематическую исто-

рию распадов всех нестабильных частиц.

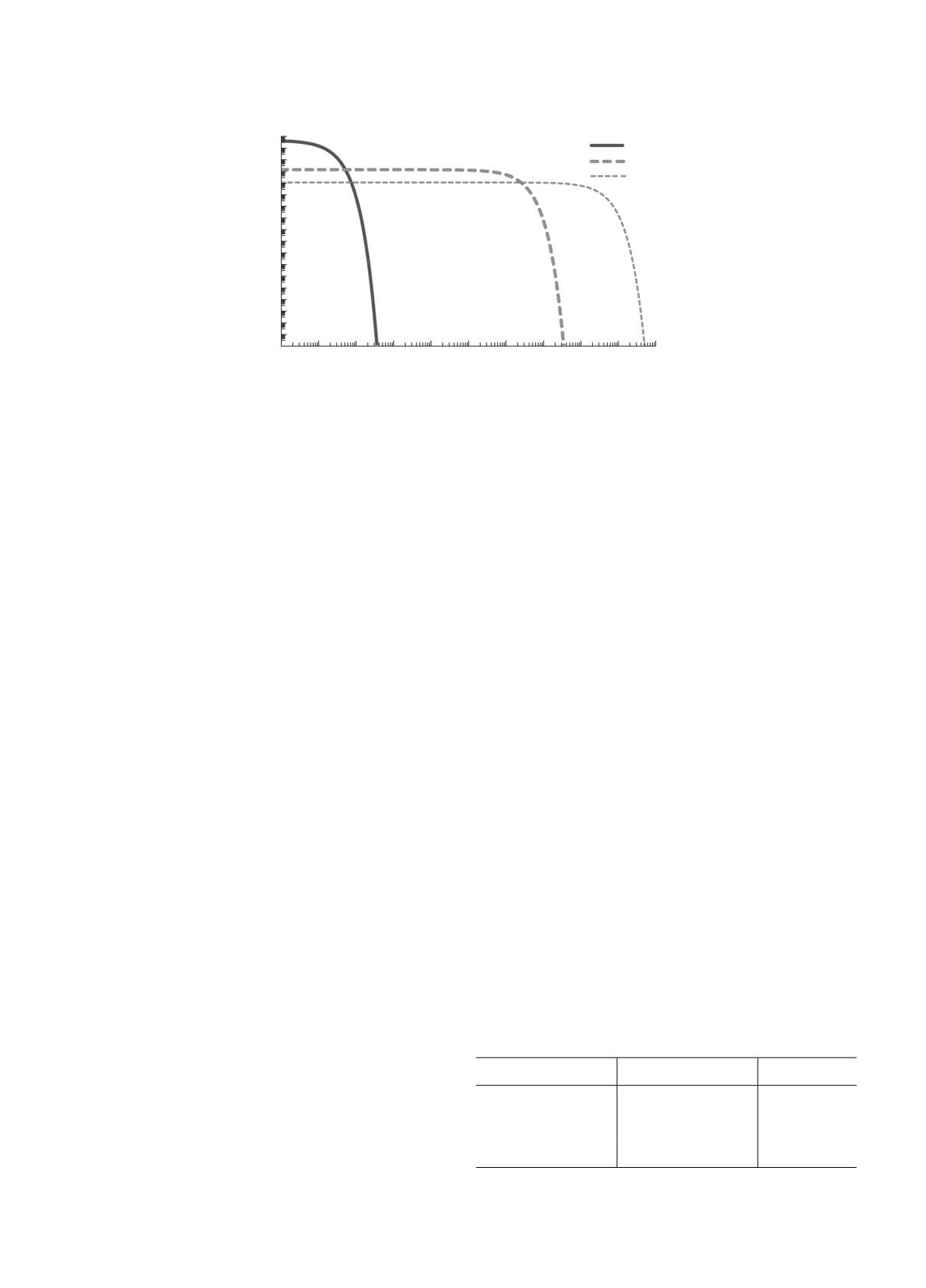
Рисунок 2 показывает временную зависимость

вероятности распада ρ±,0-, η-резонансов и π⁰-

3. Проанализировать степень компланарности

мезонов в покое. Очевидны сильные различия вре-

ρ-, ω-, η-резонансов, π⁰-мезонов, γ-квантов.

мен распадов частиц. Естественно, для движу-

щихся адронов время их распада увеличивается в

Рассмотрим возможные варианты эксперимен-

соответствии с их Лоренц-фактором.

тальных результатов (при выполнении вышеприве-

При различных значениях τ_2D высокую компла-

денных критериях отбора):

нарность могут иметь 1) ρ-, ω-, η-резонансы (и

другие адроны прямой генерации) при τ_2D ≲ 10-22 с;

1. Высокая степень компланарности наблюда-

2) η- и π⁰-мезоны, родившиеся в результате рас-

ется у ρ-мезонов (и других частиц прямой гене-

рации), а у остальных частиц она уже меньше.

пада более тяжелых резонансов при τ_2D ≲ 10-16 с;

3) дополнительно π⁰-мезоны от распада η-мезонов

Отсюда мы имеем 10-23 ≲ τ_2D ≲ 10-22 с.

при τ_2D ≲ 10-14 с; 4) дополнительно γ-кванты

2. Высокая степень компланарности наблюда-

от распада π⁰-мезонов при τ_2D ≳ 10-14 с. Таким

ется также у η-мезонов. Это означает, что 10-17 ≲

образом, при τ_2D ≳ 10-14-10-13 с импульсы всех

≲τ_2D ≲ 10-16 с.

наблюдаемых частиц должны лежать в единой

плоскости компланарности (или, по крайней мере,

3. Высокая степень компланарности наблюда-

в одной из полусфер).

ется у π⁰-мезонов. Это означает, что 10-16 ≲

Отметим, что, в рамках концепции изменения

≲τ_2D ≲ 10-14 с.

размерности пространства, как минимум, первый

случай уже имеет место. На возможность четверто-

4. Наблюдается высокая степень компланар-

го случая намекают характеристики стратосферно-

ности γ-квантов. Это означает, что τ_2D ≳ 10-14 с

го события “JF2af2” [9] с энергией ΣE_γ ≳ 1.4 ПэВ

(что, кстати, существенно больше значения, данно-

и числом частиц n_γ,e± = 38, имеющее экстремаль-

го в обзоре [19]).

ную выстроенность треков вдоль прямой линии.

Вероятность наблюдать подобное событие в ре-

Наконец, можно попытаться искать корреляции

зультате флуктуаций крайне низка (≲10-10) [24].

частиц, рождающихся в двухчастичных распадах и

Для проведения анализа данных с целью про-

разлетающихся строго вперед и назад в с.ц.м. Воз-

верки гипотезы о существовании 3D ↔ 2D процес-

можно, хотя и маловероятно, что это даст какие-

са, необходимы эксперименты по изучению харак-

то указания на существование (3D ↔ 2D ↔ 1D)

теристик генерации и распада энергичных адронов

эволюции сигнатуры метрики.

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

738

МУХАМЕДШИН

d /d

10²⁴

10¹⁸

10¹²

10⁶

10⁰

10⁶

10²⁴

10²²

10²⁰

10¹⁸

10¹⁶

10¹⁴

, c

Рис. 2. Временная зависимость вероятности распада ρ±,0-, η-резонансов и π⁰-мезонов в покое.

3. ПОИСК 2D-ЭВОЛЮЦИИ СИГНАТУРЫ

более точного сравнения экспериментальных дан-

МЕТРИКИ НА LHC

ных и результатов моделирования дополнитель-

но требуется моделирование отклика детекторов и

В данный момент только эксперименты на LHC

других методических проблем.

позволяют исследовать нужную область энергий.

Была начата работа по анализу возможной свя-

Диапазон псевдобыстрот |η| ≲ 2.4, использован-

зи процесса КГЧ с 2D-эволюцией сигнатуры мет-

ный Коллаборацией CMS для анализа “ridge”-

рики. Первые предварительные результаты были

эффекта в pp-взаимодействиях [20], не является

опубликованы в [26]. В настоящей работе при-

оптимальным для анализа эффектов, связанных

ведены более поздние результаты для различных

с компланарной генерацией наиболее энергичных

частиц, основанные на большей статистике и полу-

ченные с помощью уточненных алгоритмов.

частиц. Тем не менее, для анализа возможной связи

процесса КГЧ и “ridge”-эффекта первоначально

Было проведено моделирование двухчастич-

было проведено моделирование в рамках FANSY

ных корреляционных функций R_h±h±(Δη, Δϕ),

2.0 CPG, а именно версии “moderate” [23, 24] (мо-

R_h±γ(Δη,Δϕ) и R_γγ(Δη,Δϕ), полученные для

делирование КГЧ в 3D-пространстве и случайной

пар h^±h^±, h^±γ, γγ соответственно при различных

ориентации всех последующих распадов). Наибо-

значениях τ_2D (от 0 до 10-12 с).

лее важными параметрами процесса “копланари-

Поскольку, с одной стороны, эффективность

зации” поперечных импульсов вторичных частиц

КГЧ в рамках 2D-гипотезы резко возрастает с

являются параметры, определяющие степень ком-

ростом τ_2D, а с другой стороны мы ограничены экс-

планарности, а именно: а) дисперсия отклонения

периментальной величиной “ridge”-эффекта для

азимутального угла адрона от плоскости компла-

пар заряженных частиц, то все расчетные резуль-

нарности σϕ0; б) скорость уменьшения степени

таты необходимо нормировать на данные экспе-

компланарности с уменьшением быстроты адрона,

римента. В настоящей работе сделана нормиров-

определяемая параметром β; в) минимальное зна-

ка на площадь сечения функции R_h±h±(Δη, Δϕ)

чение быстроты y_thr, зависящее от параметра Δy.

(для пар h^±h^±) при |Δη| = 4. Поскольку главны-

Эффективное значение y_thr может быть выбрано

ми критериями будут различия между функциями

только феноменологически. Величины этих пара-

R(Δη, Δϕ) для различных вариантов пар частиц

метров для FANSY 2.0 CPG “moderate” и FANSY

2.0 2D даны в табл. 1.

Таблица 1. Параметры версий “moderate” и “2D” моде-

Было показано [23], что FANSY 2.0 CPG ка-

ли FANSY 2.0

чественно воспроизводит “ridge”-эффект при се-

чении КГЧ-процесса σ_CPG = 42 мбн. На рис. 3a

Параметры

“Moderate”

“2D”

(рис. 7г в [22]) показана экспериментальная функ-

ция R_h±h±(Δη, Δϕ) для пар заряженных частиц, а

Δ_y

4.5

6.0

на рис. 3б (рис. 6 в [23]) показана соответствующая

σϕ0

0.09

0.001

расчетная функция. Оба рисунка демонстрируют

0.82

0.01

“ridge”-эффект в области |Δη| ≳ 3, Δϕ ∼ 0. Для

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

МОЖНО ЛИ ОЦЕНИТЬ ПАРАМЕТРЫ 2D-ЭВОЛЮЦИИ

739

)

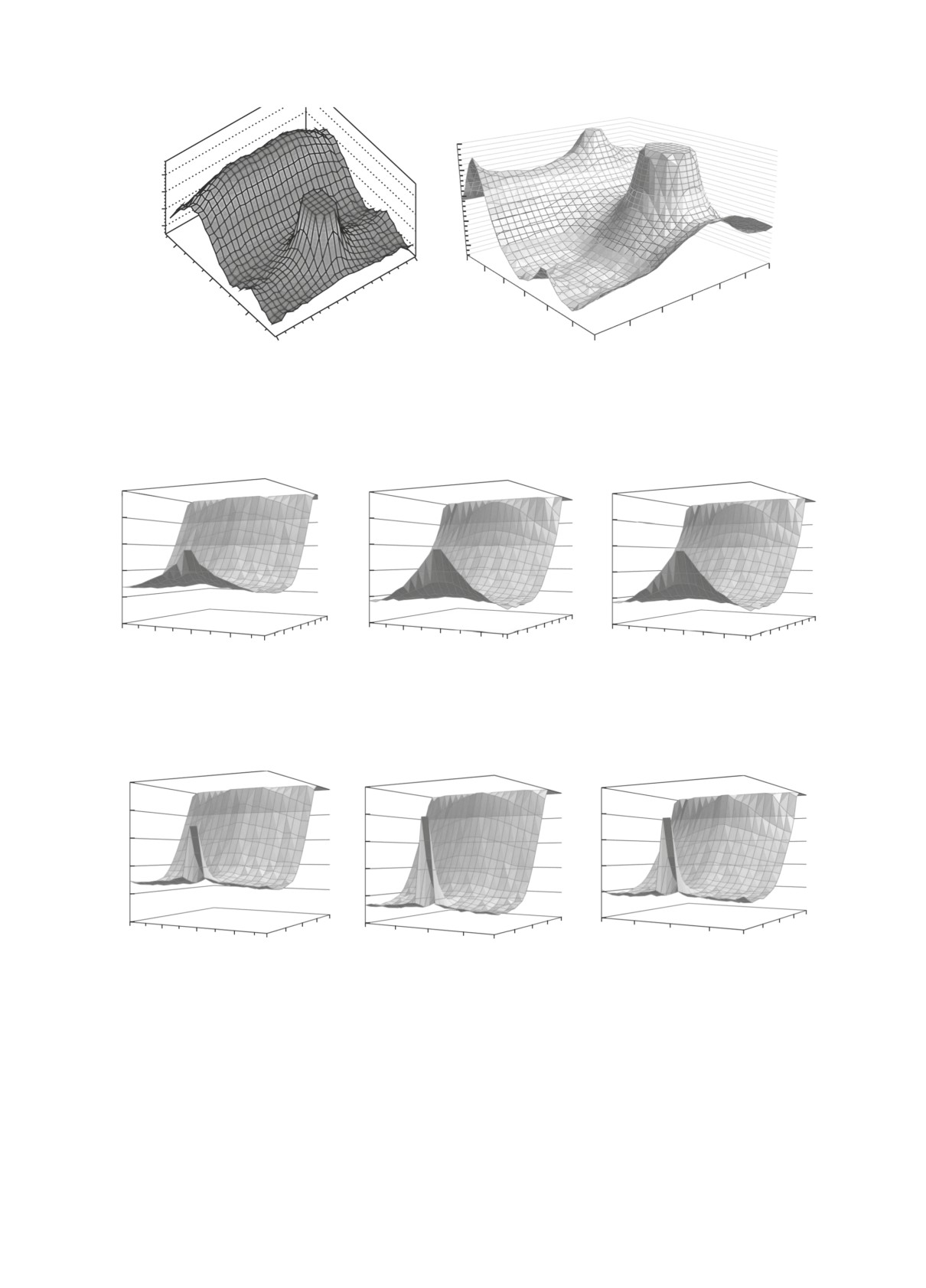
Рис. 3. a — Экспериментальная функция R_h±h±(Δη, Δϕ) для пар заряженных частиц в событиях с высокой множе-

ственностью (рис. 7г в [22]); б — соответствующая функция R_h±h±(Δη, Δϕ), полученная в рамках модели FANSY 2.0

CPG “moderate” при σCPG = 42 мбн (рис. 6 в [23]).

Rh±h±(

)

Rh± (

)

R (

)

Рис. 4. Функции R_h±h±(Δη, Δϕ) (a), R_h±γ (Δη, Δϕ) (б) и Rγγ(Δη, Δϕ) (в), полученные для пар h^±h^±, h^±γ, γγ

соответственно при τ2D = 10-24 с и σ2D = 11.0 мбн.

Rh±h±(

)

Rh± (

)

R (

)

Рис. 5. Функции R_h±h±(Δη, Δϕ) (a), R_h±γ (Δη, Δϕ) (б) и Rγγ(Δη, Δϕ) (в), полученные для пар h^±h^±, h^±γ, γγ

соответственно при τ2D = 10-12 с и σ2D = 2.2 мбн.

при фиксированном значении τ_2D, то используется

h^±γ, γγ соответственно при сечении процесса 2D-

приблизительная нормировка.

эволюции сигнатуры метрики σ_2D = 11 мбн и ее

времени существования τ_2D = 0 с (после компла-

На рис. 4 представлена непосредственно об-

нарной 2D-генерации адронов).

ласть “ridge”-эффекта (|Δη| ≤ 4, -1 < Δϕ < 1)

функций R_h±h±(Δη, Δϕ) (a), R_h±γ(Δη, Δϕ) (б)

На рис. 5 показаны аналогичные функции, по-

и R_γγ(Δη,Δϕ) (в), полученных для пар h^±h^±, лученные при τ_2D = 10-12 с и σ_2D = 2.2 мбн.

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023

740

МУХАМЕДШИН

При τ_2D = 0 (после компланарной генерации

h^±γ-корреляции, пик для γγ-корреляций заметно

адронов) вся последующая цепочка распадов

выше пика для заряженных частиц.

нестабильных частиц, от резонансов до π⁰-

мезонов, происходит в 3D-пространстве. Как ре-

зультат,

пики

функций

R_h±h±(Δη,Δϕ),

СПИСОК ЛИТЕРАТУРЫ

R_h±γ(Δη,Δϕ) и R_γγ(Δη,Δϕ) при Δϕ ≈ 0 доволь-

A. S. Borisov et al. (Pamir Collab), in Proceedings of

но широкие, похожие на пики версии “moderate”

the 4th ISVHECRI Beijing, 1986, p. 4.

[23,

24] (см. рис.

3б) (естественно, с учетом

I. P. Ivanenko and B. L. Kanevsky, JETP Lett. 50,

поправки на значения сечений генерации КГЧ).

2125 (1992).

V. V. Kopenkin, A. K. Managadze, I. V. Rakobolskaya,

При τ_2D = 10-12 с (когда уже распались все

and T. M. Roganova, Phys. Rev. D 52, 2766 (1995).

π⁰-мезоны) имеет место другая картина. Пики ста-

Pamir Collab., Preprint INP MSU, no. 89-67/144

новятся высокими и узкими. Из трех типов кор-

(1989).

реляций самый сильный эффект проявляют h^±γ-

A. S. Borisov, R. A. Mukhamedshin, V. S. Puchkov,

корреляции. Самое главное, что пик при Δϕ ≈ 0

S. A. Slavatinsky, and G. B. Zhdanov, Nucl. Phys. B

для γγ-корреляций заметно выше пика для заря-

(Proc. Suppl.) 97, 118 (2001).

женных частиц. Это сильный маркер, означающий,

L. Xue, Z. Q. Dai, and J. Y. Li, in Proceedings of the

что реальное значение времени существования 2D-

26th ICRC Salt Lake City, 1999, Vol. 1, p. 127.

A. V. Apanasenko, N. A. Dobrotin, L. A. Goncharova,

флуктуации τ_2D ≳ 10-14 с.

K. A. Kotelnikov, and N. G. Polukhina, in

Очевидно, при промежуточных значениях τ_2D

Proceedings of the 15th ICRC Plovdiv, 1977,

соответственно меняются формы и взаимная вели-

Vol. 7, p. 220.

чина пиков.

V. I. Osedlo, I. V. Rakobolskaya, V. I. Galkin,

Напомним, что все вышеизложенные результа-

A. K. Managadze, L. G. Sveshnikova, L. A. Gon-

ты получены в предположении, что процесс КГЧ не

charova, K. A. Kotelnikov, A. G. Martynov, and

имеет отношения к гипотезам [13-16], связанным с

N. G. Polukhina, in Proceedings of the 27th ICRC,

образованием специфических лидирующих систем.

Hamburg, 2001, Vol. 1, p. 1426.

Поскольку подобные процессы не могут изучаться

J. N. Capdevielle, J. Phys. G 14, 503 (1988).

10.

R. A. Mukhamedshin, JHEP 0505, 049 (2005).

на LHC, требуются специальные исследования в

11.

R. A. Mukhamedshin, Nucl. Phys. B (Proc. Suppl.)

экспериментах с космическими лучами, поскольку

196, 98 (2009).

дифракционные процессы играют там очень важ-

12.

А. К. Манагадзе, Р. А. Мухамедшин, Изв. РАН.

ную роль.

Cер. физ. 77, 1573 (2013) [A. K. Managadze and

Для сравнения результатов моделирования с

R. A. Mukhamedshin, Bull. Russ. Acad. Sci.: Phys.

экспериментальными данными необходимо до-

77, 1315 (2013)].

полнительно учесть методические эффекты от-

13.

I. I. Royzen, Mod. Phys. Lett. A 9, 3517 (1994).

клика детектора, искажающие форму функции

14.

J. N. Capdevielle, Nucl. Phys. B (Proc. Suppl.) 175,

R(Δη, Δϕ).

137 (2008).

15.

T. S. Yuldashbaev, Kh. Nuritdinov, and V. M. Chu-

dakov, Nuovo Cimento C 24, 569 (2001).

16.

R. A. Mukhamedshin, Nucl. Phys. B (Proc. Suppl.)

4. ЗАКЛЮЧЕНИЕ

75, 141 (1999).

17.

T. Wibig, hep-ph/0003230.

Детальное исследование азимутальных корре-

18.

L. Anchordoqui, D. C. Dai, M. Fairbairn, G. Land-

ляций резонансов и других частиц, а также цепочек

sberg, and D. Stojkovic, Mod. Phys. Lett. A 27,

их распадов в мезоны и γ-кванты во взаимодей-

1250021 (2012).

ствиях сверхвысоких энергий, может помочь под-

19.

D. Stojkovic, arXiv: 1406.2696v1 [gr-qc].

твердить существование или, как минимум, устано-

20.

The CMS Collab., JHEP 1009, 091 (2010).

вить верхний предел локальной (3D ↔ 2D) эволю-

21.

R. A. Mukhamedshin, Eur. Phys. J. Plus. 134, 584

ции сигнатуры метрики с энергией.

(2019).

Анализ двухчастичных h^±h^±-, h^±γ- и γγ-

22.

R. A. Mukhamedshin and T. Sadykov, J. Phys.: Conf.

корреляций в области |η| ≲ 2.4, |Δη| ≳ 3 может

Ser. 1181, 012089 (2019).

помочь поиску связи азимутальных корреляций с

23.

R. A. Mukhamedshin, Eur. Phys. J. C 82, 155 (2022).

24.

Р. А. Мухамедшин, Изв. РАН. Сер. физ. 85, 534

2D-эволюцией сигнатуры метрики.

(2021) [R. A. Mukhamedshin, Bull. Russ. Acad. Sci.:

При времени существования 2D-эволюции сиг-

Phys. 85, 402 (2021)].

натуры метрики τ_2D ≳ 10-14 с (когда уже распа-

25.

R. A. Mukhamedshin, Eur. Phys. J. C 79, 441 (2019).

лись все π⁰-мезоны) пики функций R_h±h±(Δη, Δϕ),

26.

Р. А. Мухамедшин, Изв. РАН. Сер. физ 87, 962

R_h±γ(Δη,Δϕ) и R_γγ(Δη,Δϕ) при Δϕ ≈ 0 стано-

(2023) [R. A. Mukhamedshin, Bull. Russ. Acad. Sci.:

вятся узкими. Самый сильный эффект проявляют

Phys. 87, 900 (2023)].

ЯДЕРНАЯ ФИЗИКА том 86

№6

2023