Физика Земли, 2022, № 2, стр. 155-160

Изучение вопросов устойчивости геосистем является одним из важных направлений геофизических исследований. Знание причин, влияющих на устойчивость, помогает понимать процессы, происходящие в Земле как с точки зрения прогнозирования опасных разрушительных явлений, так и с точки зрения закономерностей зарождения новых геоструктур в результате возникновения неустойчивости.

В настоящей работе на основе ряда полученных ранее аналитических результатов [Рыжак, 2016; 2019; 2021; Мухамедиев, 2016; Ryzhak, 2017], а также фактических данных о физико-механических параметрах верхних слоев Земли, проведено численное исследование влияния сдвиговой жесткости и модуля объемного сжатия на устойчивость и неустойчивость тяжелых стратифицированных геомассивов, образованных твердыми упругими материалами.

Существующие модели строения геомассивов в тех или иных регионах дают представление о скоростях распространения упругих волн, материальном составе пород и соответствующих им плотностях и упругих параметрах, мощностях слоев и т.д. При этом во многих моделях, в случаях, когда среда в некотором диапазоне глубин предполагается материально однородной, приводятся средние значения упругих параметров и плотностей без учета увеличения плотности геоматериала с глубиной вследствие сжимаемости и увеличения давления под действием силы тяжести. Для ряда традиционных задач геофизики эта информация является вполне достаточной. Однако, как будет видно из дальнейшего, с точки зрения анализа устойчивости того или иного геомассива фактор сжимаемости является очень важным. Заметим, что для среды, образованной любым однородным материалом с определенной зависимостью плотности от давления $\rho = \rho (p)$ и соответствующим модулем объемного сжатия $K(p) = {{\rho (p)} \mathord{\left/ {\vphantom {{\rho (p)} {\frac{{d\rho }}{{dp}}}}} \right. \kern-0em} {\frac{{d\rho }}{{dp}}}}(p)$, плотность возрастает с глубиной $z$ из-за увеличения давления с глубиной под действием силы тяжести:

Проиллюстрируем влияние сжимаемости на распределение плотности по глубине на двух примерах, в каждом из которых среда находится в поле силы тяжести и представляет собой материально однородную сжимаемую жидкость со своим законом объемной упругости.

В обоих примерах ${{K}_{0}}$ и ${{\rho }_{0}}$ – модуль объемного сжатия и плотность в разгруженном состоянии, $\rho $ – плотность в текущем (нагруженном) состоянии, $z$ – глубина в текущем состоянии.

(1) Для сжимаемой жидкости типа Муни–Ривлина с нелинейным упругим законом, задаваемым с помощью упругого потенциала

можно показать, что плотность в нагруженном состоянии линейно нарастает с глубиной по отношению к плотности в разгруженном состоянии (рис. 1а), что задается следующими равенствами:

(2) Для сжимаемой жидкости с упругим соотношением, характеризуемым постоянным модулем объемного сжатия $\left( {dp = {{K}_{0}}\frac{{d\rho }}{\rho }} \right)$, нарастание плотности с глубиной дается следующим равенством (рис. 1б):

Если плотность сжимаемой жидкости в нагруженном состоянии в поле силы тяжести не нарастает с глубиной, то это означает, что жидкость материально неоднородна, и в разгруженном состоянии (в отсутствие силы тяжести) ее плотность убывала бы с глубиной. В работах [Рыжак, 2016; Мухамедиев, 2016; Ryzhak, 2017] было показано, что такая стратификация неоднородной сжимаемой жидкости в поле силы тяжести неустойчива, а устойчивыми являются такие стратификации, где скорость нарастания плотности с глубиной в нагруженном состоянии не меньше, чем для соответствующей материально однородной жидкости, что в терминах распределений механических параметров стратифицированной жидкости в нагруженном состоянии выражается следующим неравенством [Рыжак, 2016; Мухамедиев, 2016; Ryzhak, 2017]:

где: $K(z)$ – модуль объемного сжатия; $\rho (z)$ – плотность; $z$ – глубина.

Таким образом, поскольку для тяжелых сжимаемых жидкостей состояния с постоянным распределением плотности по глубине и, тем более, с убыванием плотности с глубиной неустойчивы, то системы с таким распределением плотности не могут существовать в течение сколько-нибудь длительного времени.

Однако геофизические данные подтверждают факт существования геосистем с инверсией плотности на протяжении длительных периодов времени [Романюк, 2012; Артюшков, 1963; 1963а; Шполянская, 1991], что свидетельствует об их устойчивости. Интуитивно ясно, что устойчивость таких геосистем обеспечивается ненулевой сдвиговой жесткостью материалов, их составляющих, но при этом желательно выяснить степень влияния жесткостных параметров на устойчивость. Таким образом, теоретические исследования вопросов устойчивости и неустойчивости стратифицированных геосистем, характеризующихся как инверсией плотности, так и сдвиговой жесткостью в совокупности со сжимаемостью, являются геофизически актуальными.

Пионерскими исследованиями такого рода явились работы [Дубровский, 1985; 1995], где на физическом уровне строгости была рассмотрена модельная задача об устойчивости системы “литосфера–астеносфера” с инверсией плотности. Строгое аналитическое исследование этой задачи было проведено в работе [Рыжак, 2005], где был выведен энергетический критерий устойчивости/неустойчивости, и на его основе получено необходимое условие устойчивости и оценка основной частоты колебаний такой системы в случае устойчивости.

Результаты, полученные в работе [Рыжак, 2005], были использованы в работах [Рыжак, 2016; Мухамедиев, 2016; Ryzhak, 2017]. В дальнейшем они были использованы также в работах [Рыжак, 2019; 2021], посвященных исследованию тяжелых непрерывно стратифицированных систем, образованных упругими материалами с ненулевой сдвиговой жесткостью. В работах [Рыжак, 2019; 2021] удалось получить аналитически как достаточное условие устойчивости, так и достаточное условие неустойчивости для таких систем.

Для иллюстрации стабилизирующего влияния сдвиговой жесткости приведем полученное в работе [Рыжак, 2019] достаточное условие устойчивости для закрепленного по боковой границе геомассива с зависящими от глубины модулем объемного сжатия $K(z)$ и ненулевым (в отличие от жидкости) модулем сдвига $\mu (z)$:

Сопоставляя неравенства (1) и (2), легко увидеть, что при скорости нарастания плотности с глубиной, удовлетворяющей двойному неравенству:

система, образованная стратифицированной сжимаемой жидкостью, неустойчива, т.к. нарушено условие (1), а система, образованная упругими материалами с ненулевой сдвиговой жесткостью, устойчива, т.к. выполнено условие (2).

Что касается достаточного условия неустойчивости, то оно может быть использовано в задачах геофизики для выявления таких значений сдвиговой жесткости, при которых система будет заведомо неустойчива. Эта информация представляет немалый интерес, так как известно, что упругие параметры геоматериалов могут меняться под действием тех или иных физических причин: изменения температуры, гидрологических условий, давления в результате, например, таяния ледника, высыхания моря, различных техногенных факторов. В ходе таких процессов сдвиговая жесткость геоматериала, упомянутая ранее как важный стабилизирующий фактор, может существенно уменьшаться, в результате чего в изначально устойчивой системе может произойти потеря устойчивости.

Помимо этого, достаточное условие неустойчивости для конкретных существующих стратифицированных геосистем может быть использовано как инструмент уточнения их параметров из соображений устойчивости. В случаях, когда имеются подробные данные о распределениях плотности и упругих модулей в среде (с учетом уплотнения геоматериала из-за возрастания давления с глубиной), соответствующие исследования, основанные на таких данных, могут быть проведены численно.

В данной работе для расчетов используется неравенство, основанное на результатах работы [Рыжак, 2021] и выражающее достаточное условие неустойчивости в терминах жесткостных параметров и геометрических размеров системы.

Пусть область представляет собой параллелепипед с вертикальным размером $l$. Заметим, что если неравенство

выполняется во всей рассматриваемой области, то система устойчива. В случае, если это не так, т.е. для какого-то горизонтального слоя справедливо неравенство: то обретает смысл задача о нахождении при заданных распределениях плотности $\rho (z)$ и модуля объемного сжатия $K(z)$ таких значений сдвиговой жесткости, при которых система будет заведомо неустойчива. Заметим, что при заданном распределении $\rho (z)$ слой, где выполняется неравенство (4), может оказаться разным для различных распределений $K(z)$.

Введем некоторые величины, характеризующие распределения жесткостных и плотностных параметров среды:

где максимум берется по тому слою, где выполняется неравенство (4):

Толщину слоя, где выполняется неравенство

обозначим через $\tilde {l}$ (это именно тот слой, механические параметры которого вносят основной вклад в возможность возникновения неустойчивости системы).

Тогда, с использованием введенных величин $\alpha $, $\theta $, $\tilde {l}$, достаточное условие неустойчивости может быть приведено к следующему виду:

где $\bar {\mu }$ – максимальное значение модуля сдвига геоматериала в слое толщиной $\tilde {l}$. Расчеты, проводимые в работе, сводятся к численному определению величин $\alpha $, $\theta $, $\tilde {l}$, $\bar {\mu }$ и численному исследованию неравенства (5). Исходными для расчетов являются массивы данных, задающие распределения плотности и упругих параметров по глубине.

Приведем результаты вычислений для трех модельных примеров. Для расчетов были использованы представленные в работах [Гарагаш, 2018; Ржевский, 1978; Жарков, 1983; Трофимов, 2005] значения упругих параметров в реально существующих породах.

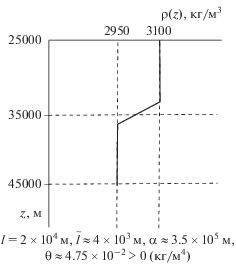
Пример 1. В данном примере принимаемые плотности характерны для глинистых грунтов (рис. 2). Как известно [Трофимов, 2005], физико-механические свойства глинистых грунтов существенно зависят от их дисперсности, пористости, минералогического состава, насыщенности влагой. При постоянном давлении глины изменяют свой объем в зависимости от увлажнения: набухают при увеличении влажности и сжимаются при ее уменьшении. При малой влажности глинистые грунты находятся в твердом состоянии, с увеличением влажности они переходят в пластичное состояние, а при дальнейшем увеличении влажности грунт переходит в текучее состояние, приобретая свойства жидкости. Очевидно, что при переходе из твердого состояния в жидкое вследствие изменения гидрологических условий упругие модули глин испытывают значительные изменения (в особенности сдвиговая жесткость, которая для жидкостей равна нулю). Расчеты в работе выполнены для различных значений упругих параметров, являющихся реалистичными для глинистых грунтов.

Расчеты показывают, что стратифицированная система с заданным распределением плотности $\rho (z)$ в нагруженном состоянии (рис. 2) может быть: 1) устойчивой для любого значения $\mu $, включая сколь угодно малые значения, при достаточно больших значениях $K$ (выполняется неравенство (1), рис. 2, случай а); 2) устойчивой в определенном диапазоне достаточно больших значений $K$ и $\mu $ (выполняется неравенство (2), рис. 2, случай б); 3) неустойчивой при достаточно малых $K$ и $\mu $ (рис. 2, случаи в и г). Сравнение случаев б и в показывает, что при неизменном $K$ система может потерять устойчивость за счет уменьшения $\mu $.

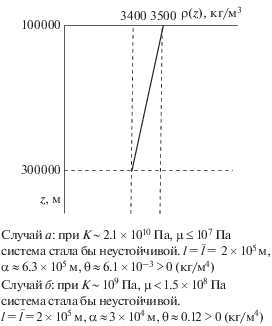
Пример 2. Рассмотрим систему с инверсным распределением плотности в коре Земли, представляющим собой сглаженное распределение, приведенное в работе [Романюк, 2012] для некоторой части рассматриваемого там геомассива (рис. 3). В силу того, что данное распределение имеет место в реально существующем геомассиве, последний представляет собой устойчивую систему, несмотря на наличие инверсии плотности. Устойчивость является следствием достаточно большого значения сдвиговой жесткости слагающих пород, и очевидно, что уменьшение сдвиговой жесткости могло бы повлечь за собой возникновение неустойчивости. Оценить запас устойчивости такой системы, т.е. при известном (для коры Земли) значении модуля объемного сжатия $K \sim {{10}^{{10}}}$ Па и сдвиговой жесткости $\mu \sim {{10}^{{10}}}$ Па, найти такие значения $\mu $, при которых система стала бы заведомо неустойчивой, позволяют вычисления в рамках предложенной в работе методики. Конкретно получено, что для неустойчивости достаточно, чтобы было выполнено неравенство $\mu \leqslant 2 \times {{10}^{4}}$ Па.

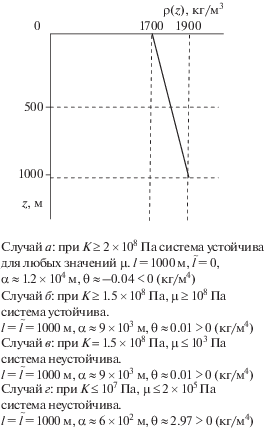
Пример 3. В этом примере использованы данные о распределении плотности в астеносфере, приведенные в работе [Браун, 1984] и характеризующиеся непрерывным и монотонным уменьшением плотности с глубиной (рис. 4). Такое распределение плотности существует и, следовательно, соответствует устойчивости. Расчеты позволили оценить значения упругих параметров $K$ и $\mu $ (представленные на рис. 4, случаи а, б), при которых система стала бы заведомо неустойчивой, т.е. не могла бы существовать в течение сколько-нибудь длительного времени.

Из выполненных расчетов следует, что реальные значения жесткостных параметров геоматериала в астеносфере ($K \sim {{10}^{{10}}}$ Па, $\mu \sim {{10}^{{10}}}$ Па) заведомо выше найденных значений, которые можно назвать “закритическими”.