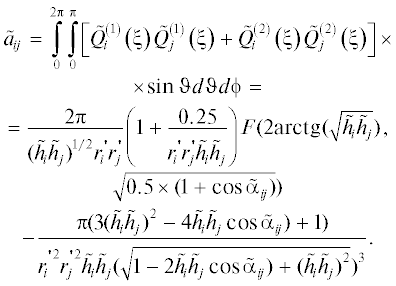Физика Земли, 2022, № 3, стр. 121-135

Аналитические модели физических полей Земли в региональном варианте с учетом эллиптичности

И. Э. Степанова^1, *, А. В. Щепетилов², П. С. Михайлов¹

¹ Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия

² МГУ им. М.В. Ломоносова
г. Москва, Россия

^* E-mail: tet@ifz.ru

Поступила в редакцию 20.11.2021
После доработки 24.12.2021
Принята к публикации 27.12.2021

EDN: GYFYAT
DOI: 10.31857/S0002333722030085

Полный текст (PDF)

Аннотация

Региональный вариант метода линейных интегральных представлений применяется для интерпретации данных об аномальных физических полях Земли. Восстановление элементов поля сводится к решению плохо обусловленных систем линейных алгебраических уравнений с приближенно заданной правой частью. Приводятся результаты математического эксперимента по нахождению аналитического продолжения гравитационного и магнитного полей Земли.

Ключевые слова: гравитационное поле, магнитное поле, трансформация потенциальных полей, аппроксимация.

ВВЕДЕНИЕ

В настоящее время наблюдается стремительный рост объема получаемой различными способами информации о физических полях Земли и других планет Солнечной системы. Данный факт объясняется совершенствованием технологий дистанционного зондирования, увеличением вычислительных мощностей, появлением принципиально новых методов регистрации сигналов. По материалам спутниковой съемки Земли и других планет можно корректировать модели внутреннего строения, изучать эволюцию небесных тел, изучать и прогнозировать глобальные климатические и геофизические процессы, например таяние ледников и временные вариации потенциальных полей. Необходимо принимать во внимание, однако, что вся спутниковая информация нуждается в корректной, математически обоснованной интерпретации. Глубоко залегающие и слабые источники полей при дистанционных исследованиях верифицируются весьма плохо.

Исследователи как в нашей стране, так и за рубежом, применяют различные методы и подходы для решения задач интерпретационного характера (см., например, [Portniaguine,1999; 2002; Arkani-Hamed, 2002; Acuna, 1999]). Особенно популярным становится так называемая “совместная” (или комплексная) инверсия. Предпринимаются попытки восстановления источников сигналов одновременно по данным, к примеру, гравиметрии и градиентометрии [Михайлов и др., 2019; Wang et al., 2019; 2020a; 2020b]. Чрезвычайно важным при обработке аэрокосмических данных становится вопрос об учете формы планеты: сферичности или, при создании более точных аналитических представлений полей, эллиптичности. Трехмерным плотностным моделям Земли посвящено много работ (см., например, [Мартышко и др., 2015; Martyshko et al., 2016]). Для более глубокого понимания геологического строения Земли и других планет весьма актуальным является сравнительный анализ моделей распределения источников поля с учетом сферичности и без такового [Павленкова, 1991; Долгаль, 2015; 2017; Uieda et al., 2015; Schattner et al., 2019].

Целью настоящей работы является улучшение качества аппроксимации потенциальных полей, что особенно актуально, например, для уточнения аналитической модели магнитного поля Марса, предложенной в работе [Gudkova et al., 2021; Salnikov et al., 2021] на основе глобального варианта метода интегральных представлений в рамках структурно-параметрического подхода. Как было указано в работе [Gudkova et al., 2020], магнитное поле Марса отличается от земного как по своей природе (на Марсе нет магнитного динамо), так и по структуре. Спутниковые измерения позволяют сделать вывод о фрагментарной картине остаточного магнитного поля Красной планеты: как будто источники поля группируются в некоторой полосе вблизи экватора и в южном полушарии. При этом достоверно не известно, что послужило причиной “исчезновения” магнитного поля в некоторых областях Марса.

В приведенной выше работе авторов была предложена концепция построения аналитической модели магнитного поля Марса по спутниковым данным на основе комбинированного подхода: модифицированные S-аппроксимации спутниковых измерений строились как в локальной версии метода линейных интегральных представлений [Stepanova et al., 2008], так и в региональной [Stepanova et al., 2009].

В настоящей работе предложены способы улучшения алгоритма аналитического продолжения физических полей вниз, в сторону источников, поскольку данные дистанционного зондирования Земли значительно превалируют над информацией, получаемой благодаря наземным, морским и другим исследованиям.

При разработке уточненной аналитической модели гравитационного и магнитного полей Земли (как и других планет Солнечной системы) можно “двигаться” в двух направлениях:

1) аппроксимационные конструкции строить без учета эллиптичности и топографии, но пространственное распределение элементов гравитационного и магнитного полей, а также все линейные трансформации (включая аналитическое продолжение поля вниз, в область источников) находить уже с учетом особенностей строения планеты;

2) при выборе носителей масс в аппроксимационных построениях учитывать эллиптичность (и рельеф, если позволят вычислительные мощности).

Стоит отметить, что второе направление развития теории интерпретации спутниковых данных представляется весьма перспективным, поскольку точное определение источников гравитационного и магнитного полей очень важно для изучения внутреннего строения небесного тела.

В данной работе предложен способ адаптивной регуляризации обратной задачи по нахождению аналитического продолжения гравитационного и магнитного полей Земли в рамках, в основном, первого подхода. Второй подход применялся нами в несколько редуцированном виде: эллиптичность планеты учитывалась как некоторая весовая функция при постановке вариационной задачи. Кроме того, частичная реализация второго подхода возможна при преобразованиях координат трехмерного пространства, переводящих эллипсоид в сферу. Применение второго подхода в “чистом” виде приводит к необходимости численного интегрирования, что увеличивает время, затрачиваемое на решение обратной задачи, иногда (при высоком разрешении сети наблюдений) – весьма существенно.

ОПИСАНИЕ МЕТОДИКИ

Интегральные представления, как показано в наших предыдущих работах [Stepanova, 2008; Раевский и др., 2015а; 2015б], могут использоваться в трех вариантах построения линейных аналитических аппроксимаций элементов внешних физических полей Земли и планет:

а) глобальном (линейные аналитические аппроксимации строятся для всей Земли);

б) региональном (линейные аналитические аппроксимации строятся для больших по площади территорий – порядка (10⁵–10⁶) км²);

в) локальном (линейные аналитические аппроксимации строятся для небольших по площади территорий – не более 10⁴ км²).

Мы можем приближенно представлять себе Землю как эллипсоид с полуосями a, b, c. Если эллиптичность не учитывается, то планета считается шаром радиуса ${{R}_{0}}$.

Если известны геодезические координаты точки наблюдения, то переход от них к прямоугольным координатам осуществляется по известным формулам [Шимбирев, 1975]:

(1)

$\begin{gathered} X = (N + H)\cos B\cos L, \\ Y = (N + H)\cos B\sin L, \\ Z = ((1 - {{e}^{2}})N + H)\sin B, \\ \end{gathered} $

где: X, Y, Z – пространственные прямоугольные координаты точки, м; B, H, N – геодезические координаты (широта и долгота, рад., высота, м); N – радиус кривизны первого вертикала, м; e – эксцентриситет эллипсоида.

Радиус кривизны первого вертикала и квадрата эксцентриситета эллипсоида вычисляются по формулам:

(2)

$N = \frac{a}{{\sqrt {1 - {{e}^{2}}{{{\sin }}^{2}}B} }},\,\,\,{{e}^{2}} = 2\alpha - {{\alpha }^{2}},$

где: a – большая полуось эллипсоида, м; α – сжатие эллипсоида.

Пусть “идеализированная” Земля есть внутренность эллипсоида с полуосями a, b, c, а реальная Земля трактуется как область, ограниченная кусочно-непрерывной замкнутой поверхностью S, мало отклоняющейся от этого эллипсоида и содержащей его внутри себя. Принимается, что в некоторой (произвольной) совокупности точек ${{x}^{{\left( i \right)}}},$ $i = 1,2,...,N$ на поверхности S заданы приближенные значения гармонической (во внешности сферы) функции $G(x)$, иначе – заданы величины:

(3)

${{f}_{{i,\delta }}} = {{f}_{i}} + \delta {{f}_{i}},\,\,\,\,{{f}_{i}} = G({{x}^{{\left( i \right)}}}).$

Здесь $G\left( x \right)$ имеет следующее интегральное представление:

(4)

$\begin{gathered} G\left( x \right) = \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{\sigma \left( {\vartheta ,\phi } \right)\sin \vartheta d\vartheta d\phi }}{{R\left( {\xi - x} \right)}}} } + \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{w\left( {\vartheta ,\phi } \right)\left\{ {r\cos \vartheta - R} \right\}\sin \vartheta d\vartheta d\phi }}{{{{R}^{3}}\left( {\xi - x} \right)}}} } , \\ R\left( {\xi - x} \right) = {{({{\left| \xi \right|}^{2}} - 2\left| \xi \right|r\cos \vartheta {\kern 1pt} '\,\, + {{r}^{2}})}^{{1/2}}},\,\,\,\,\xi = ({{R}_{0}}\cos \phi \sin \vartheta ,{{R}_{0}}\sin \phi \sin \vartheta ,{{R}_{0}}\cos \vartheta ), \\ x = (r\cos \tilde {\phi }\sin \tilde {\vartheta },r\sin \tilde {\phi }\sin \tilde {\vartheta },r\cos \tilde {\vartheta }),\,\,\,\,\cos \vartheta {\kern 1pt} ' = \sin \vartheta \sin \tilde {\vartheta }\cos (\phi - \tilde {\phi }) + \cos \vartheta \cos \tilde {\vartheta }, \\ \end{gathered} $

В данном случае ${{R}_{0}}$ – средний радиус шарообразной планеты.

Если же необходим учет эллиптичности на этапе построения аппроксимационных конструкций, то вместо (4) справедливо следующее интегральное представление:

(5)

$\begin{gathered} G\left( x \right) = \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{I(\vartheta ,\phi )\sigma \left( {\vartheta ,\phi } \right)\sin \vartheta d\phi d\vartheta }}{{R\left( {\xi - x} \right)}}} } + \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{I(\vartheta ,\phi )w\left( {\vartheta ,\phi } \right)\left\{ {1 - \left[ {\frac{{{{x}_{1}}{{\xi }_{1}}}}{{{{a}^{2}}}} + \frac{{{{x}_{2}}{{\xi }_{2}}}}{{{{b}^{2}}}} + \frac{{{{x}_{3}}{{\xi }_{3}}}}{{{{c}^{2}}}}} \right]} \right\}\sin \vartheta d\vartheta d\phi }}{{{{R}^{3}}\left( {\xi - x} \right)\sqrt {\frac{{\xi _{1}^{2}}}{{{{a}^{4}}}} + \frac{{\xi _{2}^{2}}}{{{{b}^{4}}}} + \frac{{\xi _{3}^{2}}}{{{{c}^{4}}}}} }}} } , \\ R\left( {\xi - x} \right) = {{({{\left| \xi \right|}^{2}} - 2\left| \xi \right|r\cos \vartheta {\kern 1pt} '\,\, + {{r}^{2}})}^{{1/2}}},\,\,\,\,\xi = (a\cos \tilde {\phi }\sin \tilde {\vartheta },b\sin \tilde {\phi }\sin \tilde {\vartheta },c\cos \tilde {\vartheta }), \\ x = (r\cos \tilde {\phi }\sin \tilde {\vartheta },r\sin \tilde {\phi }\sin \tilde {\vartheta },r\cos \tilde {\vartheta }),\,\,\,\cos \vartheta {\kern 1pt} ' = \sin \vartheta \sin \tilde {\vartheta }\cos (\phi - \tilde {\phi }) + \cos \vartheta \cos \tilde {\vartheta }, \\ I(\vartheta ,\phi ) = \sin \vartheta \sqrt {{{a}^{2}}{{b}^{2}}{{{\cos }}^{2}}\vartheta + {{a}^{2}}{{c}^{2}}{{{\sin }}^{2}}\vartheta {{{\sin }}^{2}}\phi + {{b}^{2}}{{c}^{2}}{{{\sin }}^{2}}\vartheta {{{\cos }}^{2}}\phi } . \\ \end{gathered} $

Относительно функций $\sigma $ и $w$ ставится следующая условно вариационная задача:

(6)

$\begin{gathered} \Omega (\sigma ,w) = \int\limits_0^{2\pi } {\int\limits_0^\pi {\left( {\frac{{{{\sigma }^{2}}(\vartheta ,\varphi )}}{{p{{{_{1}^{2}}}_{{}}}}} + \frac{{w_{{}}^{2}(\vartheta ,\varphi )}}{{p_{2}^{2}}}} \right)\sin \vartheta d\vartheta d\varphi } } = \mathop {{\text{min}}}\limits_{\sigma ,w} , \\ {{f}_{{i,\delta }}} = \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{\sigma \left( {\vartheta ,\phi } \right)\sin \vartheta d\vartheta d\phi }}{{R\left( {\xi - x} \right)}}} } + \\ + \,\,\int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{w\left( {\vartheta ,\phi } \right)\left\{ {r\cos \vartheta - R} \right\}\sin \vartheta d\vartheta d\phi }}{{{{R}^{3}}\left( {\xi - x} \right)}}} } , \\ R\left( {\xi - x} \right) = {{({{\left| \xi \right|}^{2}} - 2\left| \xi \right|r\cos \vartheta {\kern 1pt} '\,\, + {{r}^{2}})}^{{1/2}}}, \\ \xi = ({{R}_{0}}\cos \phi \sin \vartheta ,{{R}_{0}}\sin \phi \sin \vartheta ,{{R}_{0}}\cos \vartheta ), \\ x = (r\cos \tilde {\phi }\sin \tilde {\vartheta },r\sin \tilde {\phi }\sin \tilde {\vartheta },r\cos \tilde {\vartheta }), \\ \cos \vartheta {\kern 1pt} ' = \sin \vartheta \sin \tilde {\vartheta }\cos (\phi - \tilde {\phi }) + \cos \vartheta \cos \tilde {\vartheta }, \\ i = 1,2, \ldots ,N, \\ \end{gathered} $

Здесь важно отметить следующий момент. Функции $p_{1}^{2}(\vartheta ,\varphi ),\;p_{2}^{2}(\vartheta ,\varphi )$ характеризуют свойства области задания эквивалентных по внешнему полю носителей масс. В частности, эти функции могут обращаться в нуль на некоторой части поверхности интегрирования. В то же время, выбор указанных функций может представлять собой своеобразный механизм адаптивной регуляризации: элементы матрицы системы линейных алгебраических уравнений (СЛАУ) зависят от этих функций. Таким образом, возникает семейство вариационных задач по определению как неизвестных распределений масс, так и областей задания источников. Подобные постановки относятся к нелинейным обратным задачам, что существенно осложняет процесс поиска решения. Наша методика построения аналитических моделей физических полей Земли может быть описана следующим образом.

Решение вариационной задачи (6) при известных функциях $p_{1}^{2}(\vartheta ,\varphi ),\;p_{2}^{2}(\vartheta ,\varphi )$ эквивалентно решению системы линейных алгебраических уравнений:

(7)

${\text{A}}\lambda = {{f}_{\delta }},\,\,\,\,{{f}_{\delta }} = f + \delta f,$

где вектор ${{f}_{\delta }}$ имеет компоненты ${{f}_{{i,\delta }}}$(см. (1)), а матрица ${\text{A}} = {{{\text{A}}}^{{\text{T}}}} \geqslant 0$ имеет элементы

(8)

$\begin{gathered} {{a}_{{ij}}} = \int\limits_0^{2\pi } {\int\limits_0^\pi {\left[ {p_{1}^{2}Q_{i}^{{\left( 1 \right)}}\left( \xi \right)Q_{j}^{{\left( 1 \right)}}\left( \xi \right) + p_{2}^{2}Q_{i}^{{\left( 2 \right)}}\left( \xi \right)Q_{j}^{{\left( 2 \right)}}\left( \xi \right)} \right]} \times } \\ \times \,\,\sin \vartheta d\vartheta d\phi ,\,\,\,\,\xi = (\vartheta ,\varphi ) \\ \end{gathered} $

в случае интегрального представления (4).

Если учитывается эллиптичность носителя эквивалентных по внешнему полю источников, то элементы матрицы системы линейных алгебраических уравнений (СЛАУ) принимают вид:

(9)

$\begin{gathered} {{a}_{{ij}}} = \int\limits_0^{2\pi } {\int\limits_0^\pi {\left[ {p_{1}^{2}Q_{i}^{{\left( 1 \right)}}\left( \xi \right)Q_{j}^{{\left( 1 \right)}}\left( \xi \right) + p_{2}^{2}Q_{i}^{{\left( 2 \right)}}\left( \xi \right)Q_{j}^{{\left( 2 \right)}}\left( \xi \right)} \right]} \times } \\ \times \,\,I(\vartheta ,\phi )\sin \vartheta d\vartheta d\phi . \\ \end{gathered} $

Для $\sigma $ и $w$ получаем представление:

(10)

$\sigma \left( \xi \right) = p_{1}^{2}\sum\limits_{i = 1}^N {{{\lambda }_{i}}Q_{i}^{{\left( 1 \right)}}\left( \xi \right)} ,\,\,\,\,w\left( \xi \right) = p_{2}^{2}\sum\limits_{i = 1}^N {{{\lambda }_{i}}Q_{i}^{{\left( 2 \right)}}\left( \xi \right)} ,$

где положено:

(11)

$\begin{gathered} Q_{i}^{{\left( 1 \right)}}\left( \xi \right) = \frac{1}{{R(\xi - {{x}^{{\left( i \right)}}})}}, \\ Q_{i}^{{\left( 2 \right)}}\left( \xi \right) = \frac{{\left\{ {1 - \left[ {\frac{{x_{1}^{{(i)}}{{\xi }_{1}}}}{{{{a}^{2}}}} + \frac{{x_{2}^{{(i)}}{{\xi }_{2}}}}{{{{b}^{2}}}} + \frac{{x_{3}^{{(i)}}{{\xi }_{3}}}}{{{{c}^{2}}}}} \right]} \right\}}}{{{{R}^{3}}(\xi - {{x}^{{(i)}}})\sqrt {\frac{{\xi _{1}^{2}}}{{{{a}^{4}}}} + \frac{{\xi _{2}^{2}}}{{{{b}^{4}}}} + \frac{{\xi _{3}^{2}}}{{{{c}^{4}}}}} }}. \\ \end{gathered} $

Если функции $p_{1}^{2}(\vartheta ,\varphi ),\;p_{2}^{2}(\vartheta ,\varphi )$ тождественно на сфере равны 1, то для элементов матрицы СЛАУ получаем следующие выражения:

(12)

$\begin{gathered} {{a}_{{ij}}} = \int\limits_0^{2\pi } {\int\limits_0^\pi {\left[ {Q_{i}^{{\left( 1 \right)}}\left( \xi \right)Q_{j}^{{\left( 1 \right)}}\left( \xi \right) + Q_{i}^{{\left( 2 \right)}}\left( \xi \right)Q_{j}^{{\left( 2 \right)}}\left( \xi \right)} \right]} } \times \\ \times \,\,\sin \vartheta d\vartheta d\phi = \\ = \frac{{2\pi }}{{{{{({{h}_{i}}{{h}_{j}})}}^{{1/2}}}{{r}_{i}}{{r}_{j}}}}\left( {1 + \frac{{0.25}}{{{{r}_{i}}{{r}_{j}}{{h}_{i}}{{h}_{j}}}}} \right)F(2{\text{arctg(}}\sqrt {{{h}_{i}}{{h}_{j}}} ), \\ \sqrt {0.5 \times (1 + \cos {{\alpha }_{i}}_{j})} ) - \\ - \,\,\frac{{\pi (3{{{({{h}_{i}}{{h}_{j}})}}^{2}} - 4{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j}) + 1)}}{{{{r}_{i}}^{2}r_{j}^{2}{{h}_{i}}{{h}_{j}}{{{(\sqrt {1 - 2{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j}) + {{{({{h}_{i}}{{h}_{j}})}}^{2}}} )}}^{3}}}}, \\ \end{gathered} $

где $Q_{i}^{{\left( 1 \right)}}\left( \xi \right)$ и $Q_{i}^{{\left( 2 \right)}}\left( \xi \right)$ определяются выражениями:

(13)

$Q_{i}^{{\left( 1 \right)}}\left( \xi \right) = \frac{1}{{R(\xi - {{x}^{{(i)}}})}},\,\,\,\,Q_{i}^{{\left( 2 \right)}}\left( \xi \right) = \frac{{R - {{r}_{i}}\cos \vartheta _{i}^{'}}}{{{{R}^{3}}(\xi - {{x}^{{(i)}}})}}.$

Здесь ${{h}_{i}} = \frac{{{{R}_{0}}}}{{{{r}_{i}}}},$ ${{h}_{j}} = \frac{{{{R}_{0}}}}{{{{r}_{j}}}},$ а ${{\alpha }_{{ij}}}$ – это угол между векторами ${{x}_{i}}$ и ${{x}_{j}}$. Выражения (12) были получены в предположении, что вектор ${{x}_{i}}$ параллелен оси Oz, в то время как вектор ${{x}_{j}}$ лежит в плоскости zOx (в случае сферы мы всегда можем выбрать такую систему координат, в отличия от эллипсоида). Тогда радиус-векторы i-ой и j-ой точек будут иметь координаты ${{x}_{i}} = ({{r}_{i}},0,0)$и ${{x}_{j}} = ({{r}_{j}}\sin {{\alpha }_{{ij}}},0,{{r}_{j}}\cos {{\alpha }_{{ij}}})$.

Функция $F(\varphi ,k)$ в (12) представляет собой эллиптический интеграл первого рода. Формула (12), как было показано в работе [Страхов, Степанова, 2002], была получена с помощью теоремы сложения для полиномов Лежандра, или, в более общем случае, для полиномов Гегенбауэра, частным случаем которых являются полиномы Лежандра.

Для полиномов Лежандра справедлива формула:

(14)

$\begin{gathered} \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {{{P}_{l}}(\cos {{\theta }_{1}}\cos {{\theta }_{2}} - \sin {{\theta }_{1}}\sin {{\theta }_{2}}\cos {{\varphi }_{2}})d{{\varphi }_{2}} = } \\ = {{P}_{l}}(\cos {{\theta }_{1}}){{P}_{l}}(\cos {{\theta }_{2}}). \\ \end{gathered} $

Замечание. Формулу (14) можно вывести из теоремы сложения для полиномов Гегенбауэра:

$\begin{gathered} \int\limits_0^\pi {C_{l}^{p}\left( {\cos \vartheta \cos \varphi + \sin \vartheta \sin \varphi \cos \psi } \right)} {\kern 1pt} \times \\ \times \,\,C_{k}^{{p - 1/2}}(\cos \psi ){{\sin }^{{2p - 1}}}\psi d\psi = \\ = \frac{{{{2}^{{2k + 2p - 1}}}{{{\left[ {\Gamma (p + k)} \right]}}^{2}}(l - k)!\Gamma (2p + k - 1)}}{{k!\Gamma (2p - 1)\Gamma (l + k + 2p)}} \times \\ \times \,\,C_{{l - k}}^{{p + k}}(\cos \varphi ){{\sin }^{k}}\varphi C_{{l - k}}^{{p + k}}(\cos \vartheta ){{\sin }^{k}}\vartheta . \\ \end{gathered} $

При k = 0 имеем:

$\begin{gathered} \int\limits_0^\pi {C_{l}^{p}\left( {\cos \vartheta \cos \varphi + \sin \vartheta \sin \varphi \cos \psi } \right)} {{\sin }^{{2p - 1}}}\psi d\psi = \\ = \frac{{{{2}^{{2p - 1}}}{{{\left[ {\Gamma (p)} \right]}}^{2}}l!}}{{\Gamma (l + 2p)}}C_{l}^{p}(\cos \varphi )C_{l}^{p}(\cos \vartheta ). \\ \end{gathered} $

Полином Лежандра $P_{l}^{{}}(\cos \varphi )$ – это $C_{l}^{{1/2}}(\cos \varphi )$.

Если записать:

(15)

$\begin{gathered} \frac{1}{{\sqrt {R_{0}^{2} + r_{i}^{2} - 2{{R}_{0}}{{r}_{i}}\cos \vartheta } }} = \frac{1}{{{{r}_{i}}\sqrt {h_{i}^{2} - 2{{h}_{i}}z} + 1}} \equiv \psi ({{h}_{i}},z), \\ z = \cos \vartheta , \\ \end{gathered} $

тогда функция ${{r}_{i}}\psi ({{h}_{i}},z)$ будет производящей функцией для полиномов Лежандра:

(16)

$\psi ({{h}_{i}},z) = \frac{1}{{{{r}_{i}}}}\sum\limits_{m = 0}^\infty {h_{i}^{m}{{P}_{m}}(z)} .$

При интегрировании по сферической поверхности мы получим:

$\begin{gathered} \int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{{\sum\limits_{k = 0}^\infty {h_{i}^{k}{{P}_{k}}(\cos \vartheta )} \sum\limits_{l = 0}^\infty {h_{j}^{l}{{P}_{l}}(\cos {{\vartheta }_{j}})} }}{{{{r}_{i}}{{r}_{j}}}}} } d\varphi d\vartheta = \\ = \frac{{\sum\limits_{m = 0}^\infty {\frac{{4\pi }}{{2m + 1}}{{{({{h}_{i}}{{h}_{j}})}}^{m}}{{P}_{m}}(\cos {{\alpha }_{{ij}}})} }}{{{{r}_{i}}{{r}_{j}}}} \equiv \eta (h),\,\,\,\,h \equiv {{h}_{i}}{{h}_{j}}. \\ \end{gathered} $

Здесь ${{\vartheta }_{j}} = \sin \vartheta \sin {{\alpha }_{{ij}}}\cos \varphi + \cos \vartheta \cos {{\alpha }_{{ij}}}.$ Для $\eta (h)$ в работе [Stepanova, 2009] было выведено дифференциальное уравнение:

(17)

$\eta {\kern 1pt} '(h)h + \frac{1}{2}\eta (h) = \frac{{2\pi }}{{{{r}_{i}}{{r}_{j}}\sqrt {{{h}^{2}} + 1 - 2hz} }},\,\,\,\,z = \cos {{\alpha }_{{ij}}}.$

Интегрируя (17) при начальном условии η(0) = = 2π/r_ir_j, находим:

$\eta (h) = \frac{{2\pi F(2{\text{arctg}}\sqrt h ,k)}}{{{{r}_{i}}{{r}_{j}}\sqrt h }},\,\,\,\,{{k}^{2}} = \frac{{1 + z}}{2}.$

Если вместо сферы поверхностью интегрирования является эллипсоид с полуосями a, b, c (т.е. верно интегральное представление (5) и рассматривается соответствующая вариационная постановка), то следует перейти в пространство других декартовых координат.

А именно, положим:

(18)

$x{\kern 1pt} ' = \frac{x}{a},\,\,\,\,y{\kern 1pt} ' = \frac{y}{b},\,\,\,\,z{\kern 1pt} ' = \frac{z}{c}.$

Эллипсоид с указанными полуосями переходит при такой замене координат в сферу единичного радиуса, а точки наблюдения – в точки штрихованного пространства по формулам (17), внешние по отношению к единичной сфере.

Необходимо отметить, что, безусловно, преобразование (19) не является ортогональным и, по этой причине, расстояния между точками не сохраняются. Если решить вариационную задачу для “штрихованной” единичной сферы, а затем перейти в “нормальное” декартово пространство, то элементы матрицы (12) трансформируются:

(19)

Здесь ${{\tilde {h}}_{i}} = \frac{1}{{r_{i}^{'}}},$ $\tilde {h}_{j}^{'} = \frac{1}{{r_{j}^{'}}},$ $r_{i}^{'} = \sqrt {x_{{1,i}}^{{'2}} + x_{{2,i}}^{{'2}} + x_{{3,i}}^{{'2}}} ,$ $r_{j}^{'} = \sqrt {x_{{1,j}}^{{'2}} + x_{{2,j}}^{{'2}} + x_{{3,j}}^{{'2}}} $, а ${{\tilde {\alpha }}_{{ij}}}$ это угол между векторами $x_{i}^{'}$ и $x_{j}^{'}$.

Таким образом, для успешного построения линейных трансформант гравитационного или магнитного поля в региональном варианте необходимо, в первую очередь, сделать выбор в пользу первого или второго подхода при учете эллиптичности. Если достаточно принять во внимание сферичность Земли, то вариационная постановка обратной задачи геофизики ставится для интегральных представлений сигналов по формулам (3)–(4). При задании координат точек наблюдения необходимо руководствоваться формулами (1)–(2).

В том случае, когда необходимо локализовать (хотя бы в первом приближении) носитель масс, имеет смысл перейти к интегральным представлениям (5)–(6).

Возможен также комбинированный подход: сначала строится более простая (сферическая) аналитическая модель поля, а затем она уточняется в соответствии с изложенным ниже алгоритмом.

Только после того, как построена приемлемая аналитическая аппроксимация исходного элемента гравитационного или магнитного поля, можно переходить к вычислению линейных трансформант поля, в частности, нахождению аналитического продолжения вниз, в сторону источников.

Если резюмировать вышесказанное, то можно предложить следующий алгоритм решения обратной задачи по построению аналитического продолжения вниз гравитационного и магнитного полей:

1. По заданному набору точек наблюдения и заданным начальным приближениям к неизвестным весовом функциям ${{p}_{r}},{\kern 1pt} r = 1,2$, строится модифицированная S-аппроксимация в региональном варианте.

2. Далее осуществляется аналитическое продолжение аппроксимированного поля вниз и вычисляется значение показателя качества решения, который представляет собой отношение эвклидовой нормы разности между теоретическими значениями поля и полученными в результате аппроксимации к норме самого поля.

3. Неизвестные весовые функции меняются по заранее определенному закону, процесс повторяется.

Необходимо отметить, что закон изменения весовых функций может быть определен только эмпирически, ввиду сложности поиска решений нелинейных обратных задач геофизики и того факта, что существует несчетное множество распределений эквивалентных по внешнему полю распределений масс.

Был выбран следующий эмпирический закон изменения весовых функций:

(20)

$p_{1}^{2}(r) = {{(\sqrt r )}^{m}},\,\,\,\,p_{2}^{2}(r) = {{(\sqrt r )}^{n}}.$

Здесь $r = \sqrt {{{{\left( {\xi - {{x}_{0}}} \right)}}^{2}} + {{{\left( {\eta - {{y}_{0}}} \right)}}^{2}} + {{{\left( {\varsigma - {{z}_{0}}} \right)}}^{2}}} ,$ $P = $ $ = \left( {\xi ,\eta ,\varsigma } \right)$ – текущая точка на поверхности, по которой производится интегрирование; $M = \left( {{{x}_{0}},{{y}_{0}},{{z}_{0}}} \right)$ – координата центра масс рассматриваемого набора данных. Показатели степени m и n предполагаются равными целым положительным числам. Весовые функции могут быть заменены масштабирующими множителями в выражениях для элементов матрицы СЛАУ. Таким образом, мы получаем некоторую деформацию исходной матрицы. Физический смысл такая деформация исходной системы линейных алгебраических уравнений имеет в том случае, когда при интегрировании по формулам (2) или (4) весовые функции мало меняются на поверхности носителя масс, и мы можем вынести за знак поверхностного интеграла некоторое среднее значение весовой функции на поверхности носителя (сферы или эллипсоида).

При нахождении S-аппроксимаций, иначе говоря – функций $\sigma \left( \xi \right)$ и $w\left( \xi \right)$, основная вычислительная проблема состоит в нахождении устойчивого приближенного решения (согласованного с имеющейся априорной информацией о векторах f и $\delta f$) системы линейных алгебраических уравнений (7)–(8). В том случае, когда определение формы носителя масс не является целью исследований (т.е. важно найти какое-то эквивалентное по внешнему полю распределение гравитационных или магнитных масс, но дополнительных требований к “качеству” решения обратной задачи не предъявляется), можно считать, что справедливы интегральные представления (3)–(4), а элементы матрицы выражаются через специальные функции по формулам (12).

Сложнее обстоит дело, если форма носителя имеет большое значение для дальнейших процедур в ходе процесса интерпретации данных, т.е. тогда, когда рассматриваются интегральные представления (5)–(6) и соответствующие им вариационные постановки. В отличие от указанного выше случая S-аппроксимаций в региональном варианте без учета эллиптичности Земли, мы не можем выписать аналитические представления искомых элементов матрицы. Для обеспечения высокой точности расчетов была использована кубатурная формула Гаусса [Крылов, Шульгина, 1972]:

(21)

$\begin{gathered} \int\limits_a^b {dx\int\limits_c^d {dy} \int\limits_e^f {g(x,y,z)dz} } \approx \\ \approx \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^l {\sum\limits_{k = 1}^n {{{A}_{i}}{{B}_{j}}{{C}_{k}}g({{x}^{{(i)}}},{{y}^{{(j)}}},{{z}^{{(k)}}})} } } , \\ \end{gathered} $

где А_j, B_j и С_k – коэффициенты квадратурных формул по каждому из направлений x, y, z соответственно (в нашем случае – по $t = \sin \tilde {\vartheta }$ и $\tilde {\varphi }$). Время расчета элементов матрицы для системы из 5000 уравнений (матрица этой системы состоит из 25 000 000 элементов) составляет около 2 ч на Pentium 2.4 ГГц.

Для решения систем (7)–(8) были использованы два метода, предложенные авторами в работах [Stepanova et al., 2020; 2015; Pan et al., 2020; Гудкова и др., 2020]. Мы будем обозначать эти два метода решения систем линейных алгебраических уравнений как БМХР (блочный метод регуляризации Холецкого) и УБМ (усовершенствованный блочный метод). В этих двух методах нахождения устойчивых приближенных решений СЛАУ реализуется механизм адаптивной регуляризации. Сначала решается система уравнений, матрица которой строится по всему набору данных, а затем некоторые блоки матрицы “выключаются” из вычислительного процесса, если соответствующие компоненты вектора решения не оказывают значимого влияния на результат в целом. Многочисленные математические эксперименты на модельных и практических примерах позволяют нам сделать вывод о том, что при интерпретации гравиметрических и магнитометрических данных, в основном, приходится решать СЛАУ, имеющие матрицы с диагональным преобладанием. Во всяком случае, блоки матрицы, в которых “зашита” информация о взаимодействии далеко друг от друга расположенных носителей масс, отличаются существенно меньшим, по сравнению с диагональными, рангом. Таким образом, задавать один и тот же параметр регуляризации для диагональных и внедиагональных блоков нецелесообразно: решение СЛАУ не будет устойчивым к погрешностям в правой части СЛАУ. В БМХР для каждого из блоков матрицы СЛАУ выполняется регуляризация разложения Холецкого, а в УБМ применяются как итерационные алгоритмы для поиска решения, так и прямые (основанные на регуляризации LU-разложения несимметричной матрицы). Блок в СЛАУ может быть и один. Все зависит от качества наборов входных данных, характера рельефа, разрешения и т.п. Автоматически пока определять количество блоков и вектор параметров регуляризации для разных блоков не удается: степень неоднозначности решения обратных задач геофизики очень высока. Мы строим, фактически, метрологические аппроксимации гравитационного и магнитного полей, поскольку нет никакой количественной информации об источниках поля.

АПРОБАЦИЯ АЛГОРИТМОВ И ПРОГРАММ ПОСТРОЕНИЯ S-АППРОКСИМАЦИЙ В РЕГИОНАЛЬНОМ ВАРИАНТЕ С УЧЕТОМ ЭЛЛИПТИЧНОСТИ

Были разработаны программы для построения модифицированных S-аппроксимаций элементов гравитационного и магнитного полей с помощью решения системы (7)–(8). Функция $\frac{{\partial V}}{{\partial r}}$ не является гармонической вне эллипсоида, поэтому формулы (4)–(5) необходимо записать для потенциала гравитационного поля (либо магнитного потенциала, см. [Ягола и др., 2014]), а затем продифференцировать правую и левую часть интегрального представления $V(r)$ по r. Для элементов матрицы (12) вместо $Q_{1}^{{(i)}},Q_{2}^{{(i)}}$ будут фигурировать также производные соответствующих функций по радиусу. Дифференцирование по параметру под знаком интеграла возможно, поскольку интеграл сходится в некоторой внешней по отношению к эллипсоиду области равномерно (расстояние от этой области до границы эллипсоида должно строго положительной величиной $\delta > 0$). Созданные программы были протестированы на некоторых модельных примерах.

Внутри земного шара рассматривалась группа точечных источников (порядка 200–300), создаваемое ими гравитационное поле вычислялось на некотором участке поверхности Земли (протяженностью 1000–1500 км, т.е. рассматривался региональный вариант). Поле такой группы источников (мы располагали источники внутри прямоугольных призм, как это было описано в нашей предыдущей работе [Страхов, Степанова, 2002], аппроксимировалось суммой простого и двойного слоев, распределенных либо на некоторой сфере, либо на поверхности эллипсоида, охватываемого земным шаром (радиус Земли полагался равным 6378 км, полуоси эллипсоида – 6360–6370 км, высотные отметки рельефа не превышали 1–3 км над Землей). В настоящее время вычислительные мощности значительно возросли по сравнению с 2002 г. Поэтому в модельных примерах число точек наблюдений полагалось равным 2000, 5000, 10 000, 20 000, 900 и 4900. Соответствующие модельные примеры мы обозначили как № 1–6. Для примеров № 1–2 были построены аппроксимации без учета эллиптичности (строки 3 и 5 табл. 1) и с учетом эллиптичности (строки 1 и 2 табл. 1).

Таблица 1.

S-aппроксимация гравитационного поля в модельных примерах № 1–6 с помощью суммы простого и двойного слоев (сферический и эллиптический варианты)

№ п/п	№ модельного примера	Кол-во точек (n)	a, b, c или ${{R}_{0}}$, км	Метод решения СЛАУ	${{\sigma }_{{\min }}}$, мГал	${{\sigma }_{{\max }}}$, мГал	$\sigma $₀, мГал	Δ/t
1	1	2000	6365, 6370, 6370	БМХР	0.00015	0.00020	0.00019	1.1е–8 04:02
2	2	5000	6365, 6370, 6370	БМХР	0.00027	0.00032	0.00031	1.3е–8 16:03
3	1	2000	6370	УБМ	0.0001	0.00015	0.00011	1.4е–9 03:06
4	3	10 000	6360, 6365, 6365	УБМ	0.0001	0.00015	0.00012	1.2e–9 38:15
5	2	5000	6370	УБМ	0.001	0.00015	0.00011	1.8e–9 18:07
6	4	20 000	6365, 6370, 6370	УБМ	0.001	0.00015	0.00014	1.5e–9 1:20:14
7	5	900	6365, 6375, 6375	УБМ	0.0005	0.0006	0.0005	1.3e–9 00:01
8	6	4900	6365, 6368, 6368	УБМ	0.0003	0.0004	0.00035	1.6e–8 00:31

Примечание: ${{\sigma }_{0}}^{{}}$ = $\frac{{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}}}{{\sqrt N }}$ – среднеквадратическое отклонение; ${{\sigma }_{{\max }}} = \sqrt {\frac{{\delta _{{\max }}^{2}}}{N}} $, ${{\sigma }_{{\min }}} = \sqrt {\frac{{\delta _{{\min }}^{2}}}{N}} $; Δ = $\frac{{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}}}{{{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}}$ – показатель качества решения; α, β – параметры регуляризации в методе УБМ ; t – время решения СЛАУ в часах и минутах; n – количество пробных решений; a, b, c – полуоси эллипсоида, на котором распределены простой и двойной слои; ${{R}_{0}}$ – радиус сферы в региональном варианте без учета эллиптичности.

Уровень искусственно вносимой (с помощью генератора случайных чисел) помехи в примерах №№ 1–6 составил: от ${{c}^{2}} = {{10}^{{ - 5}}}$ до ${{c}^{2}} = {{10}^{{ - 9}}}$. Результаты решения СЛАУ приведены в табл. 1 для одного из значений помехи из указанного диапазона.

Из табл. 1 следует, что на модельных примерах нам удалось достичь высокой точности решения (показатель качества решения достигает значений порядка $1.2 \times {{10}^{{ - 9}}}$), абсолютная погрешность в мГал составляет 0.00001, на практике такой величины, конечно, добиваться не нужно, но для проверки эффективности метода S-аппроксимаций расчеты для малых значений $\sigma $ проводились.

Для проверки эффективности предлагаемой методики учета эллиптичности Земли был проведен следующий математический эксперимент. В примерах № 1 и 2 поле источников аппроксимировалось не только суммой простого и двойного слоев, распределенных на эллипсоиде с полуосями a = 6365, b = 6370, c = 6370 км, но также и суммой простого и двойного слоев, распределенных на плоскости z = 6300 км. Расчеты проводились с помощью программы БМХР, реализующей блочный метод регуляризации разложения Холецкого. Результаты расчетов совпадают по точности, но в случае S-аппроксимации на плоскости решение получалось за вдвое большее время, нежели указанное в 1 и 4 строках табл. 1.

Весовые функции рассматривались трех типов:

$\begin{gathered} {\text{I}}.\,\,\,\,\,p_{1}^{2}(r) = {{(\sqrt r )}^{m}},\,\,\,\,p_{2}^{2}(r) = {{(\sqrt r )}^{n}},\,\,\,\,m = 1,\,\,\,\,n = 1. \hfill \\ {\text{II}}.\,\,\,\,p_{1}^{2}(r) = {{(\sqrt r )}^{m}},\,\,\,\,p_{2}^{2}(r) = {{(\sqrt r )}^{n}},\,\,\,\,m = 1,\,\,\,\,n = 2. \hfill \\ {\text{III}}{\text{.}}\,\,p_{1}^{2}(r) = {{(\sqrt r )}^{m}},\,\,\,\,p_{2}^{2}(r) = {{(\sqrt r )}^{n}},\,\,\,\,m = 2,\,\,\,n = 2. \hfill \\ \end{gathered} $

Наилучший результат был достигнут для второго типа, и в табл. 1 приводятся показатели качества решения именно для этого случая.

После того, как была построена аналитическая аппроксимация модельного гравитационного поля с тремя типами весовых функций, было выполнено аналитическое продолжение гравитационного поля вниз, на поверхность сферы или эллипсоида. На рис. 1а приводится карта изолиний гравитационного поля, создаваемого группой прямоугольных параллелепипедов на высоте 4 км, модельный пример № 3, N = 10 000. На рис. 1б приводится карта изолиний поля, построенного в результате S-аппроксимации при выборе весовых функций (21) II-го типа.

Рис. 1.

Карты изолиний гравитационного поля модельного примера № 3 (n = 10 000). Исходное поле на высоте 4 км (а) и то же поле, полученное в результате S-аппроксимации (б).

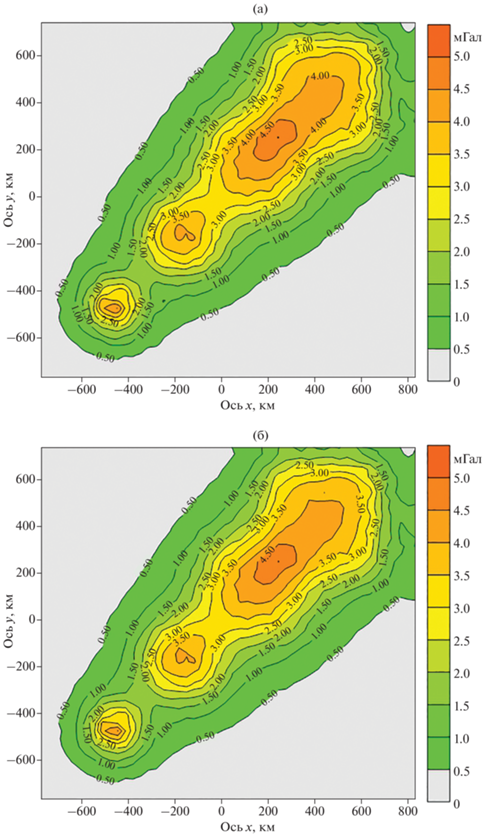
На рис. 2а показано поле, продолженное на уровень геоида в модельном примере № 6. Число точек в наборе полагалось равным 4900. Расчеты для элементов матрицы системы выполнялись по формулам (20): мы “переходили” в дополнительное координатное пространство для учета эллиптичности Земли.

Рис. 2.

Карты изолиний гравитационного поля модельного примера № 6 (n = 4900). Карта изолиний гравитационного поля, полученного в результате S-аппроксимаций (а), и карта изолиний разности между значениями продолженного на поверхность геоида гравитационного поля, полученного в результате S-аппроксимаций, и теоретическими значениями (б).

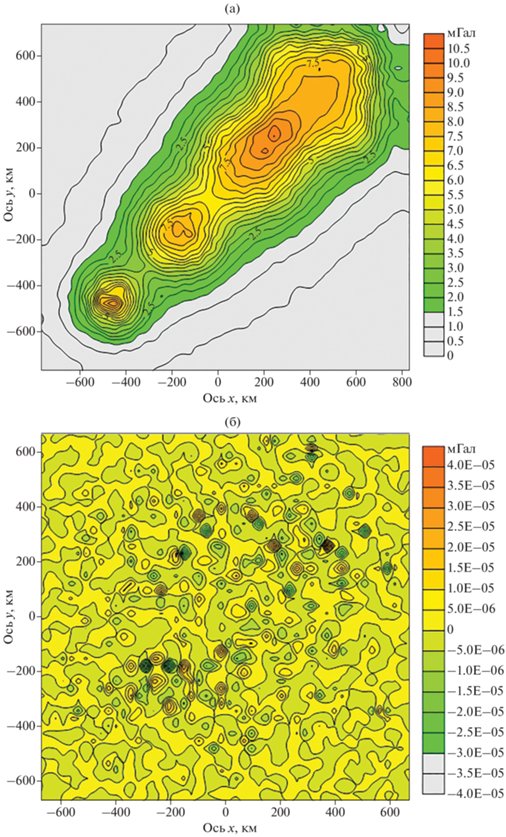
Карта разности между полученными в результате аналитического продолжения и теоретическими значениями поля приведена на рис. 2б.

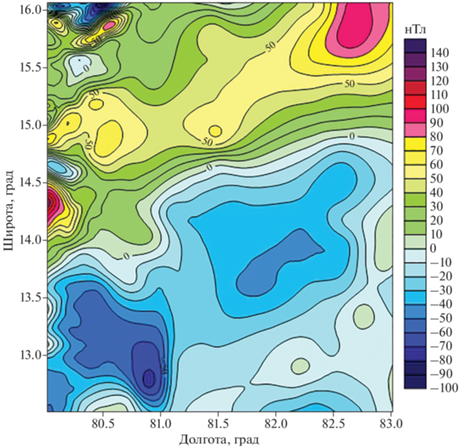
Предлагаемая методика построения аналитических моделей физических полей Земли была апробирована также на реальных данных о магнитном поле в районе Бенгальского залива, полученных с помощью современной глобальной модели EMAG2v3 [Meyer et al., 2017]. Модель EMAG3v3 получена объединением низкочастотных спутниковых данных, в основном представленных сферической моделью MF7, вычисленной по измерениям спутниковой миссии CHAMP в период с 2007 по 2010 гг., с большим объемом инструментальных морских и аэромагнитных съемок. Пространственное разрешение модели составляет 2', и мы выбирали именно такое значение шага дискретизации.

Для расчетов был взят участок магнитного поля модели EMAG2v3 в районе Бенгальского залива, с аномалиями вычисленными на высоте 4 км над уровнем геоида. Размер участка составил 3° × 2°, а значения аномалий поля на участке находится в диапазоне от –133 до 142 нТ. Общее количество данных в узлах регулярной сети составило 11316.

С помощью алгоритма, описанного в предыдущем разделе, была построена модифицированная S-аппроксимация магнитного поля на высоте 4 км над уровнем моря. При этом Земля рассматривалась как эллипсоид вращения с параметрами, указанными в табл. 2. Был применен “редуцированный” подход учета эллиптичности: три типа весовых функций (21) рассматривались для деформации элементов матрицы системы (7)–(8). Координаты точек наблюдения при этом рассчитывались по формулам (1)–(2). Аппроксимированное магнитное поле было продолжено как вниз, на поверхность геоида, так и вверх, на 10 км от уровня моря (т.е. на 6 км от первоначального уровня задания элементов магнитного поля). В настоящей статье исследуется z-компонента магнитного поля (ось z направлена по нормали к эллипсоиду). На рис. 3 показана карта изолиний исходного поля на высоте 4 км.

Таблица 2.

Модифицированная S-аппроксимация магнитного поля в районе Бенгальского залива с помощью суммы простого и двойного слоев (эллиптический вариант)

№ п/п	Кол-во точек (n)	a, b, c, км	Метод решения СЛАУ	${{\sigma }_{{\min }}}$, нТл	${{\sigma }_{{\max }}}$, нТл	$\sigma $₀, нТл	Δ/t
1	11 316	6340, 6340, 6370	УБМ	0.027	0.032	0.0279	0.0004 48:15
2	11 316	6365, 6365, 6370	УБМ	0.0243	0.0272	0.0261	0.0002 42:10

Примечание: ${{\sigma }_{0}}^{{}}$ = $\frac{{\left\| {Ax - {{f}_{\delta }}} \right\|_{E}^{{}}}}{{\sqrt N }}$ – среднеквадратическое отклонение; ${{\sigma }_{{\max }}} = \sqrt {\frac{{\delta _{{\max }}^{2}}}{N}} $, ${{\sigma }_{{\min }}} = \sqrt {\frac{{\delta _{{\min }}^{2}}}{N}} $; Δ = $\frac{{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}}}{{{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}}$ – показатель качества решения; α, β – параметры регуляризации в методе УБМ ; t – время решения СЛАУ в часах и минутах; n – количество пробных решений; a, b, c – полуоси эллипсоида, на котором распределены простой и двойной слои.

Рис. 3.

Карта изолиний магнитного поля в районе Бенгальского залива.

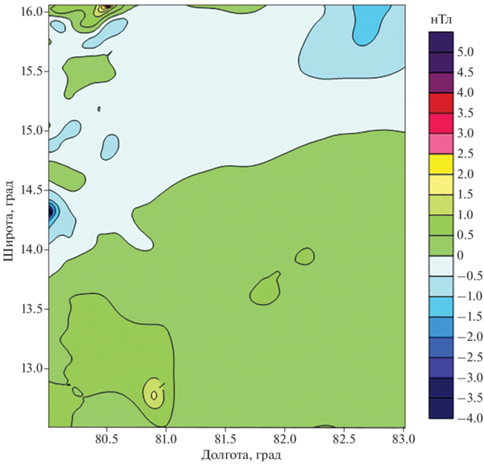
Рис. 4.

Карта разности значений магнитного поля в районе Бенгальского залива и поля, построенного с помощью модифицированных S-аппроксимаций. Весовые функции I типа.

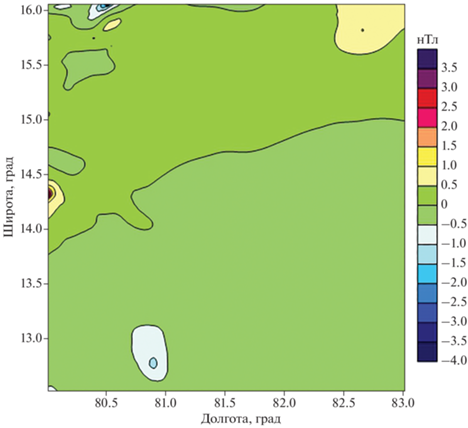
Рис. 5.

Карта изолиний магнитного поля в районе Бенгальского залива, продолженного на высоту 10 км с помощью S-аппроксимаций. Весовые функции II типа.

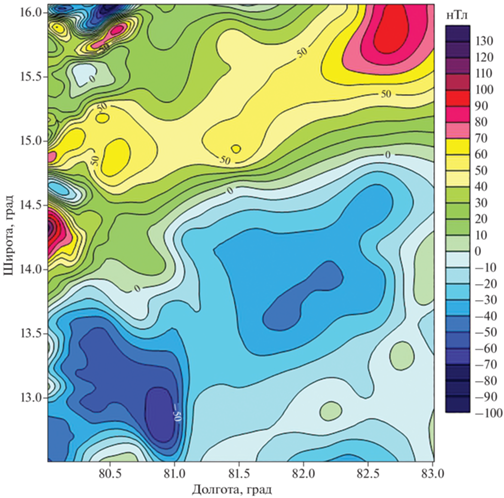
На рис. 4–рис. 6 приводятся результаты аналитического продолжения магнитного поля вверх и вниз. Можно видеть, что предложенная в статье методика не приводит к слишком резкому росту или, наоборот, убыванию значений элемента аномального магнитного поля при изменении высоты точек наблюдения: поле не “распадается”. На картах разностного поля приводятся разности значений между исходным полем и полем, вычисленным с помощью модифицированных S-аппроксимаций на поверхности геоида. В дальнейшем предполагается усовершенствовать предложенную в настоящей работе методику с тем, чтобы можно было находить устйчивое аналитическое продолжение поля как вверх, так и вниз по данным глобальной модели, рассчитанным на уровне геоида и на высоте 4 км. Необходимо отметить, что продолжение поля вниз, в сторону источников, является весьма неустойчивым, соответствующая задача всегда считалась некорректной, и пока нельзя привести примеры совпадения значений магнитного поля на поверхности планет Солнечной системы, измеренных с помощью космических аппаратов, с таковыми, вычисленными согласно существующим моделям. Регуляризирующие алгоритмы нельзя сравнивать по точности полученных приближенных решений обратных задач – заранее невозможно, к сожалению, определить, будет ли тот или иной регуляризирующий оператор приводить к успеху при несущественных изменениях в постановке задачи интерпретации. Некоторые обратные задачи являются нерегуляризируемыми.

Рис. 6.

Карта изолиний разности значений магнитного поля в районе Бенгальского залива, продолженного на высоту 10 км с помощью S-аппроксимаций, и исходных значений поля на высоте 4 км. Весовые функции II типа.

ЗАКЛЮЧЕНИЕ

Предложенный в работе трехступенчатый алгоритм построения аналитических аппроксимаций гравитационного и магнитного полей Земли в региональном варианте модифицированных S-аппроксимаций с учетом эллиптичности позволяет с точностью порядка 5 процентов находить аналитические продолжения полей как вниз, в сторону источников, так и вверх.

Список литературы

Гудкова Т.В., Степанова И.Э., Батов А.В. Модельные оценки плотностных неоднородностей в приповерхностных слоях Марса в зоне установки сейсмометра миссии InSight // Астрон. Вестник. 2020. Т. 54. № 1. С. 18–23.
Долгаль А.С., Симанов А.А., Хохлова В.В. Решение геокартировочных и прогнозно-поисковых геологических задач методом гравиразведки с учетом сферичности Земли // Георесурсы. 2015. Т. 2. № 4(63). С. 56–61.
Долгаль А.С., Бычков С.Г. Оценка различий аномалий силы тяжести для плоской и сферической моделей земли. Международная конференция “Девятые научные чтения Ю.П., Булашевича”. Глубинное строение, геодинамика, тепловое поле Земли, интерпретация геофизических полей. Екатеринбург. 2017. С. 169–173.
Крылов В.И., Шульгина Л.Т. Справочная книга по численному интегрированию. М.: Наука. 1966. 372 с.
Мартышко П.С., Ладовский И.В., Бызов Д.Д. об устойчивых методах интерпретации данных гравиметрии // Докл. РАН. 2016. Т. 471. № 6. С. 725–728.
Мартышко П.С., Мартышко М.П. Уравнения трехмерных обратных задач магниторазведки и алгоритм их решения в класс звездных тел // Уральский геофизический вестник. 2015. № 2(26). С. 50–53.
Михайлов В.О., Тимошкина Е.П., Киселева Е.А., Хайретдинов С.А., Дмитриев П.Н., Карташов И.М., Смирнов В.Б. Проблемы совместной интерпретации временных вариаций гравитационного поля с данными о смещениях земной поверхности и дна океана на примере землетрясения Тохоку-Оки (11 марта 2011 г.) // Физика Земли. 2019. № 5. С. 56–60.
Павленкова Н.И., Егорова Т.П., Старостенко В.И., Козленко В.Г. Трехмерная плотностностная модель литосферы Европы // Физика Земли. 1991. № 4. С. 3–23.
Раевский Д.Н., Степанова И.Э. О решении обратных задач гравиметрии с помощью модифи-цированного метода S-аппроксимаций // Физика Земли. 2015а. № 2. С. 44–54.
Раевский Д.Н., Степанова И.Э. Модифицированный метод S-аппроксимаций. Региональный вариант // Физика Земли. 2015б. № 2. С. 55–66.
Степанова И.Э., Керимов И.А., Раевский Д.Н., Щепетилов А.В. Интерпретация больших объемов данных при решении задач геофизики и геоморфологии с помощью модифицированного метода S-аппроксимаций // Физика Земли. 2017. № 1. С. 123–137.
Степанова И.Э., Керимов И.А., Ягола А.Г. Аппроксимационный подход в различных модификациях метода линейных интегральных представлений // Физика Земли. 2019. № 2. С. 31–47.
Степанова И.Э., Щепетилов А.В., Погорелов В.В., Михайлов П.С. Структурно-параметрический подход при построении цифровых моделей рельефа и гравитационного поля Земли с использованием аналитических S-аппроксимаций // Геофизические процессы и биосфера. 2020. Т. 19. № 2. С. 107–116.
Страхов В.Н. Геофизика и математика. М.: ОИФЗ РАН. 1999. 64 с.
Страхов В.Н., Степанова И.Э. Метод S-аппроксимаций и его использование при решении задач гравиметрии (региональный вариант) // Физика Земли. 2002. № 7. С. 3–12.
Шимбирев Б.П. Теория фигуры Земли. М.: Недра. 1975. 432 с.
Ягола А.Г., Степанова И.Э., Ван Янфей, Титаренко В.Н. Обратные задачи и методы их решения. Приложения к геофизике. М.: Бином. 2014. 214 с.
Acuna M., Connerney J., Ness N., Lin R., Mitchell D., Carlson C., McFadden J., Anderson K., Reme H., Mazelle C., Vignes D., Wasilewski P., Cloutier P. Global distribution of crustal magnetism discovered by the Mars Global SurveyorMAG/ERExperiment // Science. 1999. V. 284. P. 790–793.
Arkani-Hamed J. An improved 50-degree spherical harmonic model of the magnetic field of Mars derived from both high-altitude and low-altitude data // J. Geophysical Research (Planets). 2002. V. 107. P. 5083. https://doi.org/10.1029/2001JE001835
Gudkova T., Stepanova I., Batov A., Shchepetilov A. Modified method S- and R-approximations in solving the problems of Mars’s morphology // Inverse Problems in Science and Engineering. 2021. V. 29. P. 790–804. https://doi.org/10.1080/17415977.2020.1813125
Gudkova T., Stepanova I., Batov A. Density anomalies in subsurface layers of mars: model estimates for the Site of the InSight Mission Seismometer // Solar System Research. 2020. V. 54. P. 15–19. https://doi.org/10.1134/S0038094620010037
Pan L., Quantin C., Tauzin B., Michaut C., Golombek M., Lognonné P., Grindrod P., Langlais B., Gudkova T., Stepanova I., Rodriguez S., Lucas A. Crust heterogeneities and structure at the dichotomy boundary in western Elysium Planitia and Implications for InSight lander // Icarus. 2020. V.338. 113511. https://doi.org/10.1016/j.icarus.2019.113511
Meyer B, Saltus R., Chulliat A. EMAG2v3: Earth Magnetic Anomaly Grid (2-arc-minute resolution). Version 3. NOAA National Centers for Environmental Information. 2017. https://doi.org/10.7289/V5H70CVX
Portniaguine O., Zhdanov M. Focusing geophysical inversion images // Geophysics. 1999. V. 64. P. 874–887.
Portniaguine O., Zhdanov M. 3-D magnetic inversion with data compression and image focusing // Geophysics. 2002. V. 67. P. 1532–1541.
Salnikov A., Stepanova I., Gudkova T., Batov A. Analytical modeling of the magnetic field of Mars from satellite data using modified S-approximations // Doklady Earth Sciences 2021. V. 499. P. 575–579.
Salnikov A.M., Batov A.V., Gudkova T.V., Stepanova I.E. Analysis of the magnetic field data of Mars. The Eleventh Moscow Solar System Symposium (11M-S3), Moscow, Russia, October 5-9, 2020. https://doi.org/0.21046/11MS3-2020
Schattner U., Segev A., Mikhailov V. et al. Magnetic Signature of the Kinneret–Kinarot Tectonic Basin Along the Dead Sea Transform, Northern Israel // Pure Appl. Geophys. 2019. V. 176. P. 4383–4399.
Stepanova I. On the S-approximation of the Earth’s gravity field // Inverse Problems in Science and Engineering. 2008. V. 16. P. 535–544.
Stepanova I., Kerimov I., Raevskiy D., Shchepetilov A. Improving the methods for processing large data in geophysics and geomorphology based on the modified S- and F-approximations // Izvestiya. Physics of the Solid Earth. 2020. V. 54(3). P. 364–378.
Stepanova I., Raevsky D. On the solution of inverse problems of gravimetry // Izvestiya. Physics of the Solid Earth. 2015. V. 51. P. 207–218.
Stepanova I.E. On the S-approximation of the Earth’s gravity field: Regional version // Inverse Problems in Sci. and Eng. 2009. V. 17. V. 8. P. 1095–1111.
Stepanova I.E., Raevskiy D.N., Shchepetilov A.V. Separation of potential fields generated by different sources // Izvestiya. Physics of the Solid Earth. 2020. V. 56. № 3. P. 379–391.
Uieda L., Valéria C.F. Barbosa, Braitenberg C. Tesseroids. Forward-modeling gravitational fields in spherical coordinates // Geophysics. V. 81. № 5 (September–October 2015). P. F41–F48. https://doi.org/10.1190/geo2015-0204.1
Wang Y., Lukyanenko D., Yagola A. Magnetic parameters inversion method with full tensor gradient data // Inverse Problems &Imaging. 2019. V. 13. P. 745–754.
Wang Y., Kolotov I., Lukyanenko D., Yagola A. Reconstruction of magnetic susceptibility using full magnetic gradient data // Computational Mathematics and Mathematical Physics. 2020. V. 60. P.1000–1007.
Wang Y., Leonov A., Lukyanenko D., Yagola A. General Ti-khonov regularization with applications in geoscience // CSIAM Transaction on Applied Mathematics. 2020. V. 1. P. 53–85.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал