Физика Земли, 2022, № 4, стр. 113-134

О методе решения обратной задачи восстановления напряженно-деформированного состояния массива горных пород по данным о естественной трещиноватости

Н. В. Дубиня^1, 2, *, С. А. Тихоцкий^1, 2, **

¹ Московский физико-технический институт (национальный исследовательский университет)
г. Долгопрудный, Россия

² Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия

^* E-mail: dubinya.nv@gmail.com
^** E-mail: sat@ifz.ru

Поступила в редакцию 27.12.2021
После доработки 02.02.2022
Принята к публикации 16.02.2022

EDN: ZRAMCQ
DOI: 10.31857/S0002333722040020

Полный текст (PDF)

Аннотация

В работе рассмотрена задача реконструкции напряженного состояния массива горных пород на основании данных об их естественной трещиноватости. Рассмотрена частная задача восстановления профилей напряжений вдоль ствола скважины по данным о пространственных ориентациях и активности естественных трещин сдвига в породах околоскважинной зон. Развитый в предшествующих работах авторов подход к оценке тектонических напряжений по этим данным рассмотрен с точки зрения особенностей решения обратной задачи. Поставлена задача оптимизации, решаемая в ходе процедуры реконструкции напряженного состояния, и рассмотрены различные методы ее решения. Предложены четыре различных подхода к определению меры соответствия (близости) между наблюдаемыми и модельными характеристиками трещин (далее – мера соответствия), которые могут быть использованы для реконструкции напряжений по данным о трещинах пород околоскважинной зоны. Проведен сравнительный анализ того, как определение меры соответствия влияет на решение обратной задачи. Для этого рассмотрена синтетическая модель трещиноватости, поставлена и решена задача оценки напряженного состояния массива на синтетической модели с использованием различных мер соответствия. Продемонстрировано, что различные определения меры соответствия, использующиеся на практике при реконструкции напряжений по данным о естественной трещиноватости, отличаются между собой как в отношении наличия смещения получаемого решения относительного истинных параметров модели, так и в отношении единственности решения и его устойчивости решения по отношению к зашумлению исходных данных. Сделаны выводы об оптимальности использования тех или иных определений меры соответствия при решении обратной задачи в зависимости от того, какие данные могут быть использованы для анализа естественной трещиноватости.

Ключевые слова: напряженное состояние, естественная трещиноватость, геомеханика месторождений, тектонические напряжения.

1. ВВЕДЕНИЕ

Изучение напряженно-деформированного состояния верхних слоев земной коры остается актуальной, практически значимой задачей. Напряжения и деформации, действующие в горных породах на глубинах до 10 км, должны быть исследованы для того, чтобы решать ряд задач, связанных со строительством, освоением и разработкой месторождений твердых полезных ископаемых и углеводородов.

Среди источников информации о напряженном состоянии верхних слоев земной коры можно выделить скважинные данные. На данный момент существуют различные методы восстановления профилей напряжений по данным геофизических исследований скважин, лабораторных экспериментов и сейсмическим данным (обзор таких методов можно найти в работах [Ljunggren et al., 2003; Dubinya, 2019a]). К наиболее часто используемым методам реконструкции напряжений можно отнести анализ вывалов и трещин растяжения, образующихся при бурении [Zoback et al., 1986; 2003], а также прямые методы измерения минимального горизонтального напряжения, выполняемые при анализе гидроразрыва пласта и тестов на приемистость [Gaarenstroom et al., 1993]. Эти подходы в целом можно отнести к стандартам, использующимся в индустрии добычи нефти и газа [Raaen et al., 2006; Zohreh et al., 2014], однако эти методы обладают рядом ограничений. Помимо практических приложений, развитие методов скважинных оценок напряженного состояния верхних слоев земной коры имеет и фундаментальное значение: согласно современным оценкам [Heidbach et al., 2016], около 15% данных о направлениях действия главных напряжений, имеющихся в мировой карте напряжений World Stress Map, получены по результатам интерпретации данных геофизических исследований скважин. Большая часть этих данных получена именно по данным о вывалах и трещинах растяжения [Zhang, 2013].

Тем не менее, развиваются и альтернативные методы оценки напряженного состояния пород околоскважинной зоны на основании скважинных данных. К таким методам можно отнести: анализ распространения сдвиговых упругих волн в породах со значительной наведенной анизотропией, вызванной сильным различием величин главных напряжений [Sinha et al., 2008; Pistre et al., 2009]; анализ сброшенных деформаций на образцах горных пород [Funato, Chen, 2005; Ito et al., 2013; 2018]; анализ естественной трещиноватости [Ito et al., 2002; Dubinya, Ezhov, 2017].

В основе методов последней группы лежит связь между напряженным состоянием трещиноватых пород околоскважинной зоны и гидравлической проницаемостью естественных трещин. Существует значительное количество исследований, устанавливающих наличие связи между проницаемостью трещиноватой среды и ее текущим напряженно-деформированным состоянием [Sayers, 1990; Barton et al., 1995; Aguilera, 1995; Hickman et al., 1997; Ito, Zoback, 2000; Townend, Zoback, 2000; Rogers, 2002; Rutqvist, Stephansson, 2003; Laubach et al., 2004; Min et al., 2004; Neuman, 2005; Zhang et al., 2007; Agosta et al., 2010; Davidson et al., 2012; Barton et al., 2013; Latham et al., 2013; Kissling et al., 2015]. Некоторые из этих исследований [Barton et al., 1995; Hickman et al., 1997; Ito, Zoback, 2000; Townend, Zoback, 2000; Rogers, 2002; Laubach et al., 2004; Zhang et al., 2007] сфокусированы на флюидопроводимости естественных сдвиговых трещин, находящихся в критическом напряженном состоянии. Согласно концепции критически напряженных трещин, соотношение между нормальным и касательным напряжениями, действующими на поверхности трещины, определяет ее способность проводить флюид: если отношение сдвигового напряжения к нормальному достаточно велико, чтобы допустить скольжение берегов трещины, предполагается, что эта трещина способна служить каналом фильтрации. Трещины с низким отношением сдвигового напряжения к нормальному относятся к нефлюидопроводящим. Изначально эта концепция была предложена на основании детального анализа данных геофизических исследований скважин, расположенных на определенном объекте [Barton et al., 1995]. В дальнейшем наличие связи между флюидопроводящими и критически напряженными трещинами было экспериментально проверено в других областях [Hickman et al., 1997; Ito, Zoback, 2000; Townend, Zoback, 2000], а также подтверждено результатами численного моделирования [Zhang et al., 2007; Barton et al., 2013]. Тем не менее, следует отметить, что критически напряженные сдвиговые трещины могут давать меньший вклад в проницаемость породы по сравнению с трещинами нормального раскрытия [Ligtenberg, 2005], что также подтверждается экспериментальными наблюдениями [Wilbur, Amadei, 1990]. Кроме того, критически напряженные трещины могут оказаться неспособными проводить флюид из-за определенных геологических факторов [Fisher, Knipe, 1998], особенностей истории изменения температуры и напряженного состояния среды [Fisher, Knipe, 2003; Sathar et al., 2012].

На практике концепция критически напряженных трещин используется для предсказания зон повышенной проницаемости при разработке месторождений углеводородов. Результаты геомеханического моделирования могут быть использованы для определения текущего напряженного состояния пород, слагающих месторождение, благодаря чему появляется возможность расчета возможных пространственных ориентаций критически напряженных и, соответственно, флюидопроводящих трещин [Dubinya et al., 2018]. Эти результаты могут быть напрямую использованы для повышения эффективности разработки месторождений, характеризующихся значительным вкладом естественной трещиноватости в фильтрационно-емкостные свойства.

Прогноз количества и пространственных ориентаций критически напряженных трещин для заданного тензора напряжений можно рассматривать как прямую задачу. Может быть сформулирована и обратная задача оценки напряженного состояния по известным данным о критически напряженных трещинах. Такой анализ был предложен в работе [Ito et al., 2002] применительно к задаче реконструкции профилей напряжений вдоль траектории скважины. В этой работе был сформулирован алгоритм решения поставленной обратной задачи: данные геофизических исследований скважин о естественных трещинах в окрестности скважины были использованы для определения того, какие трещины являются флюидопроводящими, а какие – нет. Далее профили напряжений вдоль скважины варьировались, благодаря чему было получено множество классификаций трещин по признаку критического напряженного состояния. Профили напряжений, приводящие к наилучшему соответствию между своей классификацией трещин по признаку критического напряженного состояния и классификацией трещин по признаку флюидопроводимости, полученной по результатам интерпретации геофизических исследований скважин, рассматривались в качестве решения поставленной обратной задачи.

Данная работа посвящена развитию этого подхода. Ясно, что задача реконструкции профилей напряжений по данным о трещиноватости является обратной задачей, при решении которой возникает задача оптимизации, сводящаяся к поиску упомянутого наилучшего соответствия. Решение этой оптимизационной задачи может быть получено с помощью различных методов. При этом ключевым является вопрос выбора меры соответствия (близости) между наблюдаемыми и модельными характеристиками трещин, т.е. целевой функции, подлежащей оптимизации (далее – мера соответствия). В отличие от обратных задач потенциальных полей, в данном случае характеристики трещин имеют либо бинарный (проводящая – не проводящая), либо безразмерный тип и существенно нелинейным образом зависят от параметров напряженного состояния среды. Поэтому использование в качестве меры соответствия традиционных метрик типа эвклидовой невозможно.

В работе рассматриваются четыре различные меры соответствия. Выбор мер соответствия диктуется эмпирическими и практическими соображениями, а получаемая в результате оптимизации целевой функции оценка (т.е., решение обратной задачи) может быть смещенной, т.е. отличаться от истинных значений оцениваемых параметров напряженного состояния. Исследование смещения оценки, получаемой с использованием различных мер соответствия, является одной из целей настоящей работы. Целями исследования также являются выяснение единственности и устойчивости решения и изучение поведения целевой функции в зависимости от принятой меры соответствия.

2. АЛГОРИТМ РЕКОНСТРУКЦИИ НАПРЯЖЕНИЙ ПО ДАННЫМ О ТРЕЩИНОВАТОСТИ

2.1. Концепция критически напряженных трещин

Концепция критически напряженных трещин была предложена в работе [Barton et al., 1995] и активно использовалась во многих исследованиях, связанных с анализом естественной трещиноватости, в частности, при решении задач реконструкции напряжений. Согласно данной концепции, критически напряженной считается естественная трещина сдвига, на поверхности которой действует нормальное σ_n и сдвиговое (касательное) напряжение τ_n, если выполняется следующее условие:

(1)

${{\tau }_{n}} \geqslant \mu {{\sigma }_{n}},$

где μ – коэффициент внутреннего трения породы, содержащей трещину. Коэффициент трения также может быть представлен как тангенс угла внутреннего трения породы φ: μ = tg φ. В рамках используемого подхода каждая трещина рассматривается как элементарная площадка, пространственная ориентация которой определяется компонентами вектора нормали к ней n.

Нормальное и касательное напряжения, действующие на плоскости трещины, могут быть определены, если известна пространственная ориентация нормального вектора n, а также величины и направления главных напряжений элементарного объема среды, в которой присутствует трещина. Здесь и далее главные напряжения σ₁, σ₂ и σ₃ будут считаться положительными, если они являются сжимающими. Будет использовано геомеханическое соглашение о нумерации главных напряжений: σ₁ ≥ σ₂ ≥ σ₃. Также здесь и далее будет рассматриваться модель пороупругости, в рамках которой все напряжения будут рассматриваться как эффективные, то есть равные полным напряжениям за вычетом давления насыщающего породу флюида, корректным образом домноженного на соответствующие коэффициенты тензора пороупругости Био. Величины напряжений, действующих на плоскости трещины, в такой постановке будут определяться как [Jaeger et al., 2007]:

(2)

${{\sigma }_{n}} = {{\sigma }_{1}}{{l}^{2}} + {{\sigma }_{2}}{{m}^{2}} + {{\sigma }_{3}}{{n}^{2}},$

(3)

$\begin{gathered} \tau _{n}^{2} = {{({{\sigma }_{1}} - {{\sigma }_{2}})}^{2}}{{l}^{2}}{{m}^{2}} + {{({{\sigma }_{1}} - {{\sigma }_{3}})}^{2}}{{l}^{2}}{{n}^{2}} + \\ + \,\,{{({{\sigma }_{2}} - {{\sigma }_{3}})}^{2}}{{m}^{2}}{{n}^{2}}, \\ \end{gathered} $

где l, m и n – косинусы углов между нормалью к трещине и направлениями действия главных напряжений σ₁, σ₂ и σ₃ соответственно.

Подстановка выражений (2) и (3) в критерий (1) позволяет определить, является ли трещина известной пространственной ориентации критически напряженной для заданного напряженного состояния. Может быть рассмотрена и обратная задача: если с помощью какого-либо метода установлено, что трещина известной пространственной ориентации является критически напряженной, то ставится вопрос, можно ли на основании этой информации определить напряженное состояние среды? Данная работа посвящена развитию подходов, использующихся для ответа на этот вопрос.

Концепция критически напряженных трещин оказывается удобной для рассмотрения поставленной задачи. В работе [Barton et al., 1995], а также в других работах, указанных во введении, было продемонстрировано, что критически напряженные трещины часто оказываются связанными с флюидопроводящими. Было установлено следующее эмпирическое правило: если для некоторой трещины условие (1) выполняется, то эта трещина будет являться флюидопроводящей при текущих напряжениях. Несмотря на то, что такое правило может быть нарушено из-за особенностей истории изменения состояния среды и ее строения, статистическая связь между критически напряженными и флюидопроводящими трещинами наблюдается для различных регионов. Все представленные далее результаты справедливы тогда, когда критически напряженные трещины являются флюидопроводящими.

Важность этого условия определяется тем, что флюидопроводимость трещин пород околоскважинного пространства, в отличие от их напряженного состояния, может быть определена с помощью методов геофизических исследований скважин [Silva et al., 2003]. В связи с этим можно говорить о том, что существуют методы независимой оценки того, какие трещины являются критически напряженными, а какие нет, благодаря чему могут быть получены данные, необходимые для решения обратной задачи реконструкции напряженного состояния горных пород по данным об их естественной трещиноватости.

2.2. Постановка обратной задачи

Оригинальное решение обратной задачи реконструкции профилей напряжений на основании скважинных исследований трещиноватости было предложено в работе [Ito et al., 2002] в форме поэтапного алгоритма:

I. Рассматриваемый интервал глубин, на котором присутствует информация о естественных трещинах, разбивается на множество интервалов, в каждом из которых присутствует одна трещина.

II. Каждый выделенный интервал глубин характеризуется определенным индексом аномальности, отражающим степень аномальности в данных геофизических исследований скважин, полученных на этом интервале. Аномальность определяется как локальный минимум или максимум в значении того или иного измеряемого геофизического параметра, с амплитудой, превышающей уровень шума. При этом рассматриваются данные геофизических исследований скважин, характеризующие свойства пород околоскважинной зоны, связанные с флюидопроводимостью естественных трещин. Так, в работе [Ito et al., 2002] рассматривался профиль температуры – локальные изменения температуры связывались с наличием флюидопроводящих трещин. Здесь и далее будет использоваться термин “геофизический индикатор”, определяющий произвольные данные геофизических исследований скважин, связанные с флюидопроводимостью естественных трещин: в работе [Ito et al., 2002] в качестве геофизического индикатора рассматривался профиль температуры. Возможны и другие способы анализа флюидопроводимости естественных трещин в породах околоскважинной зоны: так, в работе [Dubinya, Ezhov, 2017] в роли геофизического индикатора выступало присутствие трещины на акустических и электрических микроимиджах – развертках соответствующих свойств пород по полярному углу. Корректный выбор геофизического индикатора для анализа флюидопроводимости естественных трещин в породах околоскважинной зоны важен для решения задачи реконструкции напряжений: если геофизический индикатор выбран некорректно, то и реконструированные напряжения могут оказаться ошибочными. Проблема такого выбора находится за рамками работы: основное внимание уделено математическому описанию проблемы. Любой геофизический индикатор может быть математически проанализирован с одной из двух позиций. С одной стороны, можно ввести бинарный индекс аномальности t_j (определенный для j-го интервала или для j-й трещины), характеризующий наличие или отсутствие аномалии. Наличие аномалии может быть определено как бинарный функционал, действующий на геофизическом индикаторе в окрестности j-й трещины. Простейшим способом задания такого функционала является сравнение индикатора со средним значением: если модуль разницы между величиной геофизического индикатора на глубине трещины и средним значением по интервалу превышает величину шума, то аномалия присутствует (t_j принимается равным единице), в противном случае аномалия отсутствует (t_j принимается равным нулю):

(4)

${{t}_{j}} = \left\{ \begin{gathered} 1,\,\,\,\,{\text{if}}\,\,\,\,\left| {y\left( {{{z}_{j}}} \right) - {{y}_{{mean}}}\left( {{{z}_{j}}} \right)} \right| > {{y}_{{noise}}} \hfill \\ 0,\,\,\,\,{\text{if}}\,\,\,\,\left| {y\left( {{{z}_{j}}} \right) - {{y}_{{mean}}}\left( {{{z}_{j}}} \right)} \right| \leqslant {{y}_{{noise}}} \hfill \\ \end{gathered} \right..$

Здесь y(z) – профиль геофизического индикатора y вдоль траектории скважины как функция от координаты вдоль скважины z (глубины, если скважина вертикальная); z_j – координата j-й трещины; y_mean(z_j) –значение индикатора y в окрестности j-й трещины, осредненное в определенном скользящем окне; y_noise – характерная для индикатора y величина шума. Определение бинарного индекса аномальности (4) было предложено в форме (4) в работе [Ito et al., 2002], где в качестве индикатора y(z) использовался профиль температуры T(z). С другой стороны, индекс аномальности может быть представлен и в небинарной форме: степень аномальности p_j может быть определена для отражения того, насколько серьезный вклад вносит флюидопроводящая трещина в показания геофизического индикатора. Как и в предыдущем случае, для определения степени аномальности может быть рассмотрена измеренная и средняя величина геофизического индикатора, но теперь рассматривается их отношение друг к другу:

(5)

${{p}_{j}} = {{y\left( {{{z}_{i}}} \right)} \mathord{\left/ {\vphantom {{y\left( {{{z}_{i}}} \right)} {{{y}_{{mean}}}\left( {{{z}_{j}}} \right)}}} \right. \kern-0em} {{{y}_{{mean}}}\left( {{{z}_{j}}} \right)}}.$

На втором этапе процедуры реконструкции напряжений, предложенной в работе [Ito et al., 2002], вводится геофизический индикатор и определяется бинарный t_j и небинарный p_j индекс аномальности. Этот индекс рассчитывается для каждой трещины.

III. Для профилей напряжений вводятся упрощающие предположения. В частности, оказывается удобным рассматривать случай линейного роста главных напряжений с глубиной:

(6)

${{\sigma }_{H}}\left( z \right) = az,\,\,\,\,{{\sigma }_{h}}\left( z \right) = bz,\,\,\,\,{{\sigma }_{V}}\left( z \right) = cz.$

Здесь a, b и c – три градиента напряжения, неизменные с глубиной; σ_V, σ_H и σ_h – вертикальное, максимальное горизонтальное и минимальное горизонтальные напряжения соответственно. Предполагается, что эти напряжения являются главными (одна из главных осей тензора напряжений вертикальна). В некоторых случаях вместо градиентов напряжений более удобным оказывается использование соотношений напряжений σ_h/σ_V и σ_H/σ_V, поскольку расчет вертикального напряжения, как правило, не вызывает трудностей:

(7)

${{\sigma }_{H}}\left( z \right) = \frac{{{{\sigma }_{H}}}}{{{{\sigma }_{V}}}}{{\sigma }_{V}}\left( z \right),\,\,\,\,{{\sigma }_{h}}\left( z \right) = \frac{{{{\sigma }_{h}}}}{{{{\sigma }_{V}}}}{{\sigma }_{V}}\left( z \right).$

Если профиль вертикальных напряжений, пространственные ориентации всех естественных трещин в породах околоскважинного пространства, направление действия максимального горизонтального напряжения, а также соотношения напряжений σ_h/σ_V и σ_H/σ_V известны, нормальное и касательное напряжения, действующие на поверхностях каждой трещины, могут быть определены по выражениям (2) и (3).

После этого расчета можно рассмотреть обратную задачу поиска правильной комбинации градиентов или соотношений напряжений. Любая тройка a, b и c или пара σ_h/σ_V и σ_H/σ_V определяет, в соответствии с выражениями (1), (2) и (3), свою классификацию трещин по принципу критической напряженности.

IV. Для каждой трещины и каждого набора градиентов или соотношений напряжений рассматривается “индекс критичности” m_j(σ):

(8)

${{m}_{j}}\left( \sigma \right) = {{\left| {{{\tau }_{n}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\tau }_{n}}} \right|} {{{\sigma }_{n}}}}} \right. \kern-0em} {{{\sigma }_{n}}}}.$

Здесь τ_n и σ_n – рассчитанные сдвиговое и нормальное напряжения, действующие на плоскости j-й трещины для выбранных профилей напряжений. Следует отметить, что также можно ввести бинарный аналог этого индекса k_j(σ) аналогично случаю, рассмотренному выше:

(9)

${{k}_{j}}\left( \sigma \right) = \left\{ \begin{gathered} 1,\,\,\,\,{\text{если}}\,\,\,\,{{\tau }_{n}} \geqslant \mu {{\sigma }_{n}} \hfill \\ 0,\,\,\,\,{\text{если}}\,\,\,\,{{\tau }_{n}} < \mu {{\sigma }_{n}} \hfill \\ \end{gathered} \right..$

Сравнение определений (8) и (9) с условием (1) позволяет заметить, что величина m_j(σ) характеризует степень того, насколько сильно выражено критическое напряженное состояние трещины, тогда как индекс k_j(σ) равен нулю для не критически напряженных трещин и единице для критически напряженных. Следует заметить, что оба индекса зависят от текущего напряженного состояния σ – от соотношений напряжений σ_h/σ_V и σ_H/σ_V или градиентов напряжений a, b и с, выбранных на предыдущем этапе. С другой стороны, индексы аномальности t_j и p_j не зависят от напряженного состояния, так как они напрямую рассчитаны из данных геофизических исследований скважин. Это наблюдение лежит в основе следующего этапа решения задачи реконструкции напряжений по данным о трещиноватости

V. Если соотношения напряжений верные и гипотеза о наличии связи между критически напряженными и флюидопроводящими трещинами справедлива, то между индексами аномальности t_j и p_j с одной стороны и индексами критичности m_j(σ) и k_j(σ) с другой стороны должно существовать соответствие. Здесь и возникает задача оптимизации: необходимо найти такие соотношения между напряжениями, чтобы между критически напряженными и флюидопроводящими трещинами наблюдалось наилучшее соответствие.

Простейшим способом решения этой задачи оптимизации является поиск углов между векторами T, P, M(σ) и K(σ) в N-мерном пространстве (N – общее число трещин на рассматриваемом интервале глубин до его разделения):

(10)

$\begin{gathered} {\mathbf{T}} = \left( {\begin{array}{*{20}{c}} {{{t}_{1}} - {{t}_{a}}} \\ {...} \\ {{{t}_{N}} - {{t}_{a}}} \end{array}} \right),\,\,\,\,{\mathbf{P}} = \left( {\begin{array}{*{20}{c}} {{{p}_{1}} - {{p}_{a}}} \\ {...} \\ {{{p}_{N}} - {{p}_{a}}} \end{array}} \right), \\ {\mathbf{M}}\left( \sigma \right) = \left( {\begin{array}{*{20}{c}} {{{m}_{1}}\left( \sigma \right) - {{m}_{a}}\left( \sigma \right)} \\ {...} \\ {{{m}_{N}}\left( \sigma \right) - {{m}_{a}}\left( \sigma \right)} \end{array}} \right), \\ {\mathbf{K}}\left( \sigma \right) = \left( {\begin{array}{*{20}{c}} {{{k}_{1}}\left( \sigma \right) - {{k}_{a}}\left( \sigma \right)} \\ {...} \\ {{{k}_{N}}\left( \sigma \right) - {{k}_{a}}\left( \sigma \right)} \end{array}} \right), \\ \end{gathered} $

где t_a, p_a, m_a и k_a – осредненные индексы для всего множества трещин:

(11)

$\begin{gathered} {{t}_{a}} = {{\left( {\sum\limits_{j = 1}^N {{{t}_{j}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^N {{{t}_{j}}} } \right)} N}} \right. \kern-0em} N},\,\,\,\,{{p}_{a}} = {{\left( {\sum\limits_{j = 1}^N {{{p}_{j}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^N {{{p}_{j}}} } \right)} N}} \right. \kern-0em} N}, \\ {{m}_{a}}\left( \sigma \right) = {{\left( {\sum\limits_{j = 1}^N {{{m}_{j}}\left( \sigma \right)} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^N {{{m}_{j}}\left( \sigma \right)} } \right)} N}} \right. \kern-0em} N}, \\ {{k}_{a}}\left( \sigma \right) = {{\left( {\sum\limits_{j = 1}^N {{{k}_{j}}\left( \sigma \right)} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^N {{{k}_{j}}\left( \sigma \right)} } \right)} N}} \right. \kern-0em} N}. \\ \end{gathered} $

Каждый из этих векторов может быть рассчитан для любой пары соотношений между напряжениями, выбранными на этапе III. Существуют разные способы определять соответствие между флюидопроводящими и критически напряженными трещинами. В рамках данного этапа работы будут рассматриваться углы между разными парами векторов T, P, M(σ) и K(σ) в качестве кандидатов для мер соответствия, что будет рассмотрено ниже. В любом случае, результатом этого этапа является определенная мера соответствия, характеризующая степень схожести классификаций трещин по признаку флюидопроводимости и критической напряженности, рассчитанная для выбранных соотношений между напряжениями.

VI. Далее выполняется возвращение к этапу III и процедура повторяется для прочих значений соотношений между напряжениями. Соотношения между напряжениями выбираются таким образом, чтобы обеспечить неразрушение породы под действием тектонических напряжений – с полигона напряжений [Zoback et al., 1986] – области в пространстве главных напряжений, ограниченной условием:

(12)

${{\sigma }_{1}} \leqslant {{\sigma }_{3}}\frac{{\sqrt {{{\mu }^{2}} + 1} + \mu }}{{\sqrt {{{\mu }^{2}} + 1} - \mu }} + 2C\frac{1}{{\sqrt {{{\mu }^{2}} + 1} - \mu }},$

где учтена когезия среды C.

VII. Углы между векторами T, P, M(σ) и K(σ) рассчитываются для всех возможных соотношений между напряжениями или градиентов напряжений и проводится поиск глобального максимума меры соответствия. Этот глобальный максимум достигается для напряженного состояния, при котором обеспечивается наилучшее соответствие между критически напряженными трещинами и флюидопроводящими трещинами, выделенными на основании интерпретации результатов геофизических исследований скважин. Соответствующее напряженное состояние рассматривается в качестве решения обратной задачи реконструкции напряжений в породах околоскважинной зоны на основании анализа естественной трещиноватости.

Алгоритм решения поставленной обратной задачи сводится к перечисленным семи этапам. Отдельного внимания заслуживает упомянутая задача оптимизации, решение которой необходимо для определения наилучшего соответствия между флюидопроводящими и критически напряженными трещинами. Прежде всего, необходимо определить численную величину, характеризующую степень соответствия между индексами аномальности t_j и p_j и индексами критичности m_j(σ) и k_j(σ) – далее эта величина будет описываться как мера соответствия. Как было отмечено выше, эта мера может быть введена как угол между двумя векторами в N-мерном пространстве. Всего в данной работе рассмотрено четыре варианта выбора меры соответствия – это было сделано для того, чтобы определить, как наиболее корректно ее вводить с учетом возможных погрешностей в исходных данных (классификации трещин по признаку флюидопроводимости по данным геофизических исследований скважин). Некоторые из этих вариантов использовались раньше [Ito et al., 2002; Dubinya, Ezhov, 2017; Dubinya, 2019b], некоторые предложены в рамках данной работы.

2.3. Меры соответствия

Следует начать с определения меры соответствия R(σ), под которой понимается числовая характеристика, определяющая близость (расстояние) между наблюдаемым и модельным распределением характеристик трещин, т.е. векторами T или P – с одной стороны и K(σ) или M(σ) – с другой стороны. Здесь и далее символ σ обозначает параметры, характеризующие напряженное состояние массива горных пород. Этим символом могут быть обозначены шесть независимых компонент тензора напряжений σ_ij; значения и направления действия главных напряжений для произвольного тензора напряжений; вертикальное σ_V, максимальное горизонтальное σ_H и минимальное горизонтальное σ_h напряжение в случае, когда одна из главных осей тензора напряжений вертикальна; параметры, определяющие профили напряжений в задаче их реконструкции – константы a, b и c в определениях (6) или отношения напряжений σ_H/σ_V и σ_h/σ_V в определениях (7).

Мера соответствия является количественным показателем того, насколько близки друг к другу классификация трещин по признаку флюидопроводимости и критической напряженности при заданных параметрах напряженного состояния σ. Максимум этой меры соответствия достигается при тех параметрах напряженного состояния σ, которые обеспечивают наилучшее соответствие между флюидопроводящими и критически напряженными трещинами. Проблема выбора меры соответствия связана с тем, что отсутствует строгое определение того, как именно для поставленной задачи определяется наилучшее соответствие между двумя классификациями трещин, с учетом неизбежных ошибок и неопределенности при отнесении каждой трещины к тому или иному типу. В значительной степени выбор меры соответствия носит эмпирический характер. Целью данного исследования является поиск такой меры соответствия, которая позволяла бы давать несмещенную единственную оценку напряженного состояния, обладающую наименьшей областью ε-эквивалентных (т.е. эквивалентных при заданном уровне шума во входных данных) решений поставленной обратной задачи. Вместе с тем мера соответствия должна быть практически вычислима на основе имеющихся данных.

Простейшая форма меры соответствия R₁(σ) основана на относительном количестве критически напряженных трещин S_crit [Dubinya, Ezhov, 2017]. В соответствии с определением этой меры, количество трещин, находящихся в критическом напряженном состоянии для истинного напряженного состояния σ, отнесенное к общему количеству трещин на интервале глубин, должно быть равно количеству флюидопроводящих трещин, выделенных в соответствии с геофизическим индикатором, разделенному на общее количество трещин. Мера соответствия для этого случая может быть записана в виде:

(13)

${{R}_{1}}\left( \sigma \right) = 1 - \left| {{{\left( {\sum\limits_{j = 1}^N {{{k}_{j}}\left( \sigma \right)} - \sum\limits_{j = 1}^N {{{t}_{j}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^N {{{k}_{j}}\left( \sigma \right)} - \sum\limits_{j = 1}^N {{{t}_{j}}} } \right)} N}} \right. \kern-0em} N}} \right|.$

Предложенная мера R₁(σ) находятся в пределах от 0 до 1, причем достигает максимума 1 в случае, когда одно и то же количество трещин является критически напряженными и флюидопроводящими.

Мера соответствия R₂(σ) имеет более сложный вид: она основана на попарных сравнениях бинарных индексов t_j и k_j(σ) для всех трещин. Эта мера вводится как угол между векторами T и K(σ) в N-мерном пространстве:

(14)

${{R}_{2}}\left( \sigma \right) = \frac{{\left( {{\mathbf{T}},{\mathbf{K}}\left( \sigma \right)} \right)}}{{\left| {\mathbf{T}} \right| \cdot \left| {{\mathbf{K}}\left( \sigma \right)} \right|}} = \frac{{\sum\limits_{j = 1}^N {{{t}_{j}}{{k}_{j}}\left( \sigma \right)} }}{{\sqrt {\sum\limits_{j = 1}^N {t_{j}^{2}} } \sqrt {\sum\limits_{j = 1}^N {k_{j}^{2}\left( \sigma \right)} } }}.$

Мера соответствия R₂(σ) достигает своего максимума, равного единице, тогда, когда каждая трещина, являющаяся критически напряженной в текущем поле напряжений σ, также является флюидопроводящей. В то же время, все не напряженные критически трещины не способны проводить флюид. Эта мера была использована для реконструкции напряжений по скважинным данным в рамках работы [Dubinya, 2019b]. Можно заметить, что величина R₂(σ) является ковариационной функцией в N-мерном пространстве для векторов T и K(σ).

Следующая мера соответствия R₃(σ) использовалась в работе [Ito et al., 2002]. В отличие от двух предыдущих мер R₁(σ) и R₂(σ), не только наличие критически напряженных трещин, но и индекс критичности принимался во внимание. Предполагалось, что трещина, характеризующаяся высоким отношением сдвигового напряжения, действующего на ее поверхности, к нормальному, внесет больший вклад в аномалию геофизического индикатора, по сравнению с трещиной, для которой отношение τ_n/σ_n лишь немного превосходит μ. В связи с этим в работе [Ito et al., 2002] вместо бинарного индекса K (9) использовался индекс критичности M (8) аналогично определению R₂(σ):

(15)

${{R}_{3}}\left( \sigma \right) = \frac{{\left( {{\mathbf{T}},{\mathbf{M}}\left( \sigma \right)} \right)}}{{\left| {\mathbf{T}} \right| \cdot \left| {{\mathbf{M}}\left( \sigma \right)} \right|}} = \frac{{\sum\limits_{j = 1}^N {{{t}_{j}}{{m}_{j}}\left( \sigma \right)} }}{{\sqrt {\sum\limits_{j = 1}^N {t_{j}^{2}} } \sqrt {\sum\limits_{j = 1}^N {m_{j}^{2}\left( \sigma \right)} } }}.$

Как и в предыдущих случаях, мера должна достигать своего глобального максимума в случае, когда достигается наилучшее соответствие между критически напряженными и флюидопроводящими трещинами. Тем не менее, не следует ожидать, что этот максимум будет равным единице – такое возможно было бы только если бы отношения сдвигового напряжения к нормальному были бы равны единице для всех критически напряженных трещин, тогда как сдвиговые напряжения на всех не критически напряженных трещинах были бы равны нулю.

В рамках данной работы предлагается модифицированная версия этой меры. Можно ожидать, что чем выше отношение сдвигового напряжения на плоскости трещины к нормальному, тем более значительной будет аномалия геофизического индикатора. Таким образом, в предыдущем выражении бинарный индекс T (4) может быть заменен на небинарный индекс P (5):

(16)

${{R}_{4}}\left( \sigma \right) = \frac{{\left( {{\mathbf{P}},{\mathbf{M}}\left( \sigma \right)} \right)}}{{\left| {\mathbf{P}} \right| \cdot \left| {{\mathbf{M}}\left( \sigma \right)} \right|}} = \frac{{\sum\limits_{j = 1}^N {{{p}_{j}}{{m}_{j}}\left( \sigma \right)} }}{{\sqrt {\sum\limits_{j = 1}^N {p_{j}^{2}} } \sqrt {\sum\limits_{j = 1}^N {m_{j}^{2}\left( \sigma \right)} } }}.$

Использование меры соответствия R₄(σ) осложнено необходимостью знания зависимости между отношением напряжений на трещине и степенью выраженности геофизической аномалии. Как было отмечено в работе [Dubinya, 2019b], можно ожидать, что это соотношение может быть нелинейным и зависеть от типа горной породы. Такое соотношение может быть получено по результатам лабораторных экспериментов на образцах породы, детального анализа геофизических данных и численного моделирования.

Перечисленные меры соответствия могут быть использованы для решения обратной задачи реконструкции напряжений: поиска таких параметров напряженного состояния σ, которые обеспечивают достижение глобального максимума выбранной меры в пространстве напряжений, в области, ограниченной условием (12). Можно ожидать, что использование разных мер соответствия может вести к решениям обратной задачи с различными точностями и чувствительностями к зашумлению входных данных: поиск лучшей меры и сравнение полученных решений можно отнести к важным методическим задачам. Для решения этих задач следует рассмотреть область эквивалентных решений и чувствительность результата к зашумлению входных данных. В качестве исходных данных для этого можно использовать синтетическую модель трещин.

Отметим, что все рассматриваемые меры соответствия (целевые функции) нелинейны по отношению к определяемым параметрам напряженного состояния σ, как и сами модельные характеристики трещин M(σ) и K(σ) (см. формулы (8), (9)). Отсюда следует, что рассматриваемая задача не относится к классу задач линейного программирования и при ее решении нельзя использовать обширный класс методов регуляризации, разработанных для линейных обратных задач [Тихонов, Арсенин, 1979]. Что касается возможности отнесения данной задачи к задачам выпуклого программирования, то нелинейный характер мер соответствия затрудняет теоретический анализ данного вопроса. Эмпирическое его исследование составляет одну из задач настоящей работы.

3. РЕКОНСТРУКЦИЯ НАПРЯЖЕНИЙ ПО СИНТЕТИЧЕСКИМ ДАННЫМ

3.1. Синтетическая модель трещиноватости

Исходные данные для решения обратной задачи реконструкции напряженного состояния трещиноватой среды на основании анализа естественной трещиноватости относятся именно к трещинам. К этим данным можно отнести глубину, на которой обнаружена трещина, ее пространственную ориентацию (два угла – угол падения и азимут) и способность трещины проводить флюид. Эта способность связана со значением геофизического индикатора y(z_j), определенным для j-й трещины по результатам интерпретации геофизических исследований скважин на глубине z_j (выражения (4) и (5)). Эти данные используются для определения напряженного состояния σ – отношений напряжений σ_h/σ_V и σ_H/σ_V, – порождающего классификацию трещин в соответствии с признаком критического напряженного состояния. Трещина считается критически напряженной, если нормальное и касательное напряжения, действующие на ее поверхности, удовлетворяют критерию (1). Эти напряжения могут быть найдены по выражениям (2) и (3), если известны направляющие косинусы l и n нормали к трещине в главных осях тензора напряжений. Это означает, что для проверки выполнения критерия (1) достаточно знать величины главных напряжений, направления их действия и пространственную ориентацию рассматриваемой трещины. Здесь и далее будет рассматриваться случай вертикальности одной из главных осей тензора напряжений. Более того, направление действия максимального горизонтального напряжения тоже будет считаться известным: основное внимание уделяется реконструкции величин главных напряжений по данным о трещиноватости. В рамках поставленных условий решением обратной задачи будет являться пара отношений между горизонтальным и вертикальным напряжением σ_h/σ_V и σ_H/σ_V, обеспечивающая наилучшее соответствие между флюидопроводящими и критически напряженными трещинами. Для верификации подхода к решению этой задачи рассматривается модельная трещиноватая среда, подверженная некоторому “истинному” напряженному состоянию. Далее выполняется проверка, может ли информация о естественной трещиноватости быть использована для поиска “истинного” напряженного состояния.

Был рассмотрен массив пород (интервал глубин), в котором все главные напряжения линейно растут с глубиной, максимальное горизонтальное напряжение действует в одном и том же направлении на всем интервале. В этот синтетический массив было помещено 400 естественных трещин, которые были бы обнаружены при бурении в нем вертикальной скважины. Синтезированный массив горных пород был подвергнут трехосному сжатию: были рассмотрены три случая, соответствующие сбросовому, сдвиговому и взбросовому тектоническим режимам.

Для того, чтобы набор трещин являлся достаточно реалистичным, распределение их пространственных ориентаций было определено как распределение Фишера с известным полюсом [Fisher, 1953]:

(17)

${{P}_{{dA}}}\left( \theta \right) = \frac{\kappa }{{4\pi \sinh \left( \kappa \right)}}\exp \left( {\kappa \cdot \cos \theta } \right).$

Здесь P_dA(θ) дает вероятность (в расчете на единицу телесного угла) того, что нормаль к трещине лежит в элементарном угле dA, лежащем на угловом расстоянии θ от истинного среднего направления; θ – отклонение от истинного среднего направления (= 0 для истинного среднего), и κ – параметр кучности: чем выше значение κ, тем более вероятно найти большое отклонение нормали к произвольной трещине и наиболее вероятным направлением. В рамках данной работы параметр кучности принят равным 5.

Математическое ожидание для синтетической модели трещиноватости определяется пространственной ориентацией так называемой оптимально ориентированной трещины – трещины с максимальным значением эквивалентного напряжения по Кулону – разницы между нормальным и касательным напряжениями, действующими на ее поверхности. Для произвольного тензора напряжений нормаль к оптимальной ориентированной трещине определяется как:

(18)

${{{\mathbf{n}}}_{0}} = \alpha {{\sigma }_{1}} + \beta {{\sigma }_{3}}.$

Здесь n₀ – нормаль к плоскости оптимально ориентированной трещины; σ₁ и σ₃ – направления действия максимального и минимального главных напряжений соответственно; α и β – две скалярных безразмерных величины, определяемых из системы:

(19)

$\begin{array}{*{20}{c}} {\alpha = - \sin {\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-0em} 2} - \beta \left( {{{\sigma }_{1}},{{\sigma }_{3}}} \right),} \\ {{{\beta }^{2}} - \beta \frac{{2\left( {A + B + C} \right)\sin {\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-0em} 2}}}{{{{A}^{2}} + {{B}^{2}} + {{C}^{2}}}} + \frac{{3{{{\sin }}^{2}}{\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-0em} 2} - 1}}{{{{A}^{2}} + {{B}^{2}} + {{C}^{2}}}} = 0,} \\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {A = \sigma _{3}^{x} - \sigma _{1}^{x}\left( {{{\sigma }_{1}},{{\sigma }_{3}}} \right)}&{B = \sigma _{3}^{y} - \sigma _{1}^{y}\left( {{{\sigma }_{1}},{{\sigma }_{3}}} \right),} \end{array}} \\ {C = \sigma _{3}^{z} - \sigma _{1}^{z}\left( {{{\sigma }_{1}},{{\sigma }_{3}}} \right).} \end{array}} \end{array}$

Здесь φ – угол внутреннего трения породы (μ = tg φ); $\sigma _{1}^{x}$, $\sigma _{1}^{y}$ и $\sigma _{1}^{z}$ – координаты вектора направления максимального главного напряжения в глобальной системе координат; $\sigma _{3}^{x}$, $\sigma _{3}^{y}$ и $\sigma _{3}^{z}$ – координаты вектора направления минимального главного напряжения в глобальной системе координат. Второе выражение в системе (19) представляет собой квадратное уравнение, имеющее, соответственно, два корня, отвечающие двум системам оптимально ориентированных трещин. Следует отметить, что система (19) не подразумевает необходимости субвертикальности одной из главных осей тензора напряжений и может быть использована для произвольного тензора напряжений.

Для анализа решения обратной задачи в условиях разных тектонических режимов, было рассмотрено три варианта нагружения среды с “истинными” напряжениями. Варианты нагружения были определены в соответствии с тремя тектоническими режимами, допускающими существование критически напряженных трещин для характерного значения трения μ ≈ 0.6.

В качестве первого напряженного состояния был выбран сбросовый тектонический режим, соотношение главных напряжений составляет: σ_V : σ_H : σ_h = σ₁ : σ₂ : σ₃ = 5 : 3 : 1.

В качестве второго напряженного состояния был выбран сдвиговый тектонический режим, соотношение главных напряжений составляет: σ_V : σ_H : σ_h = σ₂ : σ₁ : σ₃ = 3 : 5 : 1.

В качестве третьего напряженного состояния был выбран взбросовый тектонический режим, соотношение главных напряжений составляет: σ_V : σ_H : σ_h = σ₂ : σ₃ : σ₁ = 1 : 7 : 2.

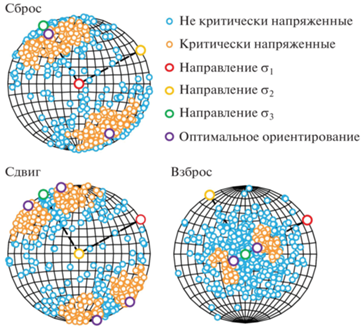
Перечисленные отношения напряжений были использованы для разрешения системы (19) и создания трех синтетических наборов трещин, подчиняющихся распределению (17). После этого пространственная ориентация каждой синтезированной трещины была использована для расчета действующих на ее поверхности напряжений τ_n и σ_n. Эти напряжения были использованы для того, чтобы определить, какие из трещин являются критически напряженными при условиях, указанных выше. Стереограммы, на которых отмечены полюсы к естественным трещинам, показаны на рис. 1. На рисунке показана равновеликая азимутальная проекция Ламберта. Красная точка показывает направление действия максимального главного напряжения σ₁; желтая точка – направление действия промежуточного главного напряжения σ₂; зеленая точка соответствует направлению действия минимального главного напряжения σ₃. Голубыми и оранжевыми точками отмечены нормали к естественным трещинам: оранжевым цветом показаны критически напряженные трещины, голубым – не критически напряженные, в условиях, указанных выше. Фиолетовые точки отмечают направления нормалей к оптимально ориентированным трещинам, рассчитанные по выражению (18) с использованием решения уравнений (19). Черные пунктирные линии показывают направления действия главных напряжений. Во всех трех случаях направление действия максимального горизонтального напряжения считалось одним и тем же.

Рис. 1.

Синтетические стереограммы для рассмотренных тектонических режимов.

Данные по разделению трещин на критически напряженные и некритически напряженные, показанные на рис. 1, используются для верификации алгоритма реконструкции напряжений. Алгоритм можно будет считать верифицированным, если результат решения поставленной задачи (условия, при которых мера соответствия достигает глобального максимума) будет совпадать с “истинными” напряжениями, представленными выше, для каждого из трех рассмотренных случаев.

3.2. Верификация алгоритма реконструкции

Обратная задача реконструкции отношений между главными напряжениями на основании анализа флюидопроводимости естественных трещин была решена для данных, представленных на рис. 1. Эти данные были использованы для того, чтобы рассчитать индексы аномальности t_j и p_j для каждой трещины. Перед тем, как добавлять в рассмотрение зашумление исходных данных, предполагалось, что геофизический индикатор работает идеально, то есть для любой критически напряженной трещины t_j принимался равным единице, а для не критически напряженной – нулю. Небинарный индекс аномальности p_j принимался равным индексу напряженности k_j(σ). Далее исследовалось влияние напряженного состояния на расчетные индексы критичности: эти индексы и соответствующие меры соответствия использовались для всех пар отношений горизонтальных напряжений к вертикальному, удовлетворяющих условию неразрушения (12). Было рассмотрено, достигается ли глобальный максимум меры соответствия при значениях отношений горизонтальных напряжений к вертикальному, равных “истинным”, порождающим классификацию трещин, показанную на рис. 1. Таким образом, синтетические данные были использованы для верификации алгоритма реконструкции напряжений на основании данных о трещиноватости. Кроме того, рассматривалась область эквивалентных решений обратной задачи – для тех случаев, при которых максимум меры соответствия достигается для нескольких значений отношений между напряжениями. Наконец, градиент меры соответствия использовался для анализа устойчивости решения. Семиэтапная процедура реконструкции напряжений была выполнена для данных, показанных на рис. 1. Меры соответствия R₁(σ), R₂(σ), R₃(σ) и R₄(σ) были рассчитаны из возможных отношений между напряжениями σ_h/σ_V и σ_H/σ_V, удовлетворяющих условию (12): для каждой пары отношений индексы критичности k_j(σ) и m_j(σ) рассчитывались по выражениям (8) и (9) с использованием синтезированных пространственных ориентаций трещин и выражений (2) и (3).

Для того, чтобы решить обратную задачу, использовался алгоритм полного перебора: множество возможных значений искомых параметров – соотношений между напряжениями – представляет собой односвязную область в двухмерном пространстве, ограниченную условием (12) и требованием σ_H ≥ σ_h, вытекающим из используемого определения. При использовании коэффициента трения среды µ = 0.6 и величины когезии C = 30 МПа исследуемая область ограничивается четырехугольником, вершины которого имеют в пространстве (σ_h/σ_V, σ_H/σ_V) координаты (0.15, 0.15), (0.15, 1.00), (1.00, 3.65) и (3.65, 3.65). Нижняя граница точности найденного решения при использовании этого алгоритма определяется шагом сканирования по осям. В рамках данной работы был выбран шаг сканирования, равный 0.01. Алгоритм полного перебора в данном случае применяется для того, чтобы иметь возможность исследовать поведение целевой функции на всем допустимом множестве параметров σ, вопросы единственности и устойчивости решения. Вопрос поиска оптимального метода оптимизации выходит за пределы настоящей работы и остается предметом дальнейших исследований. Отметим, что используемый в данной работе алгоритм полного перебора позволяет решать задачу об оценке напряжений без значительных вычислительных затрат: при выбранных параметрах расчет значений четырех мер соответствия для одной реализации системы трещин по всем допустимым (удовлетворяющим условию (12)) напряженным состояниям занимает две минуты при использовании обычного персонального компьютера на базе процессора Intel Core i7 с 4 ГБ оперативной памяти, при реализации алгоритма средствами Visual Basic в программе Microsoft Excel. Уменьшение шага сканирования по осям ведет к росту вычислительных затрат на анализ данных о трещиноватости, однако следует понимать, что на практике при оценке напряжений (например, при анализе скважинных данных) стоит задача анализа всего одного набора данных, то есть достаточно реализовать описанный алгоритм один раз. Кроме того, значительного уменьшения времени на вычисления можно достичь за счет реализации алгоритма с использованием компилируемого языка программирования и программной оптимизации.

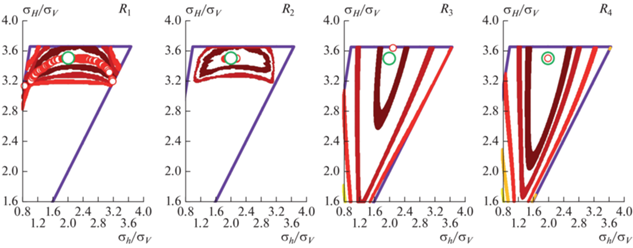
Были проанализированы три тектонических режима. “Истинные” параметры напряженного состояния породили классификацию трещин по признаку флюидопроводимости, индексы аномальности t_j и p_j были рассчитаны по выражениям (4) и (5) в предположении о том, что геофизический индикатор прямо коррелирует с соотношением между касательным и нормальным напряжениями на плоскости трещины при “истинном” напряженном состоянии. Наконец, рассчитанные индексы были использованы для определения значений мер соответствия по выражениям (10), (11) и (13)–(14) для каждого напряженного состояния. Для визуализации результатов были использованы полигоны напряжений [Zoback et al., 1986] – координатные плоскости, по осям которых откладываются отношения горизонтальных напряжений к вертикальному. На таких плоскостях возможные напряженные состояния ограничиваются условием неразрушения (12) и естественным ограничением σ_H ≥ σ_h. На рис. 2– рис. 4 представлены результаты расчета мер соответствия для трех тектонических режимов: сбросовый режим представлен на рис. 2, сдвиговый – на рис. 3, взбросовый – на рис. 4.

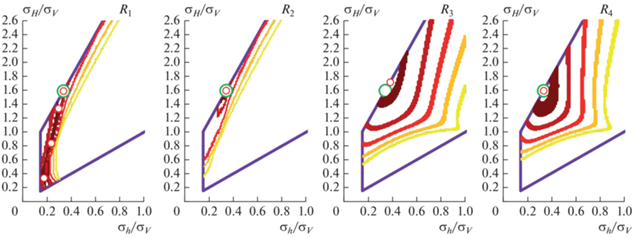
Рис. 2.

Полигоны напряжений для сбросового режима. Фиолетовая линия ограничивает полигон напряжений; сплошные жирные линии – изолинии мер соответствия; красная точка – максимум меры соответствия; зеленая – “истинное” решение.

Рис. 3.

Полигоны напряжений для сдвигового режима. Легенда аналогична рис. 2.

Рис. 4.

Полигоны напряжений для взбросового режима. Легенда аналогична рис. 2.

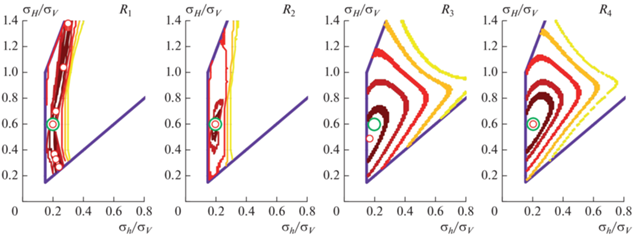
Фиолетовая линия на рис. 2–рис. 4 ограничивает полигон напряжений в соответствии с условием (12). Зеленым цветом показана точка, соответствующая “истинным” отношениям горизонтальных напряжений к вертикальному. Красными точками отмечены напряженные состояния, при которых достигается глобальный максимум соответствующей меры – решение поставленной задачи с использованием выбранной меры соответствия. Сплошные линии оттенков оранжевого представляют собой изолинии постоянных значений меры соответствия: самая темная красная линия соответствует величине меры, составляющей 95% от ее глобального максимума; более светлые линии отражают меньшие значения: более темная красная линия – это изолиния значений R(σ) на уровне 90% от максимума, красная соответствует 80%, оранжевая – 70%, желтая – 60%. Эти изолинии отражают неопределенность и устойчивость решения обратной задачи: чем больше площадь, ограниченная соответствующей линией, тем больше область неопределенности определения напряжений. Формы областей могут быть использованы для понимания сравнительной неопределенности в оценке минимального и максимального горизонтальных напряжений. Далее представлено обсуждение результатов на рис. 2–рис. 4.

Прежде всего, можно заметить, что поставленная обратная задача может не иметь единственного решения. Это особенно ярко проявляется на результатах, полученных с использованием мер соответствия R₁(σ) и R₂(σ). Как следствие, можно говорить о некорректности поставленной обратной задачи. Отдельного внимания заслуживает сравнительный анализ результатов, полученных с использованием различных мер соответствия.

Мера соответствия R₁(σ) не дает возможности единственным образом оценить два горизонтальных напряжения, так как набор различных пар отношений горизонтальных напряжений к вертикальному дает одну и ту же долю критически напряженных трещин. Соответствующий набор параметров напряженного состояния, порождающих долю критически напряженных трещин, равную экспериментально определенной, составляет множество эквивалентности решений обратной задачи. Этот результат в полной мере отвечает практике оценки напряжений с использованием этой меры соответствия для реальных объектов [Ezhov et al., 2017; Dubinya, Ezhov, 2017]: в этих работах было показано, что использование относительного количества критически напряженных трещин позволяет оценивать лишь нелинейную комбинацию двух горизонтальных напряжений, но не каждое из них в отдельности, если в рассмотрение не вводятся дополнительные данные о напряжениях. Следовательно, на плоскости параметров напряженного состояния σ_h/σ_V, σ_H/σ_V множество эквивалентности представляет собой кривую линию, что и видно на рис. 2–рис. 4. Кажущееся распадение множества эквивалентности на дискретный набор точек обусловлено конечным шагом сетки, для которой производился расчет меры соответствия. Очевидно, область эквивалентных решений обратной задачи содержит в себе и “истинное” решение, т.е. несмещенную оценку параметров напряженного состояния среды.

Анализ формы изолиний целевой функции позволяет судить о потенциальной ε-эквивалентности в решении обратной задачи: при наличии ошибок классификации во входных данных доля критически напряженных трещин известна с некоторой погрешностью, следовательно все значения параметров σ, порождающие значения целевой функции близкие к максимуму в пределах погрешности, определяют область ε-эквивалентных решений, т.е. решений, не различимых с практической точки зрения при заданной погрешности ε. Поэтому за оценку области ε-эквивалентных решений можно принять множество пространства параметров, ограниченное изолинией целевой функции заданного уровня. Естественно, множество полностью эквивалентных решений принадлежит области ε-эквивалентности при любом ε.

Интересно, что для меры соответствия R₁(σ) области ε-эквивалентности, ограничиваемые изолиниями целевой функции, отвечающими погрешностям от 10% до 30% (относительно максимума) почти совпадают, т.е. данная мера соответствия слабо чувствительна по отношению к соответствующему увеличению погрешности классификации трещин.

Кроме того, форма изолиний отвечает так называемому “овражному” функционалу с осью, вытянутой на рис. 2 и рис. 3 вдоль вертикальной оси, а на рис. 4 – вдоль горизонтальной оси. Отсюда следует, что использование меры соответствия R₁(σ) для оценки минимального горизонтального напряжения более надежно, чем для оценки максимального горизонтального напряжения для случаев сбросового и сдвигового тектонических режимов, тогда как для взбросового режима ситуация обратна.

Поведение меры соответствия R₂(σ) в целом близко к таковому для меры соответствия R₁(σ), хотя наблюдаются и определенные различия. Видно, что в большинстве случаев у меры R₂(σ) имеется только один глобальный максимум, что позволяет говорить о наличии единственного решения обратной задачи для идеального случая – без ошибок в классификации трещин по признаку флюидопроводимости. В качестве единственного исключения можно отметить случай, показанный для взбросового режима, в котором максимальное значение R₂(σ) было достигнуто для нескольких близких друг к другу напряженных состояний. Важным является тот результат, что максимум меры соответствия R₂(σ) всегда достигается для истинного напряженного состояния, т.е. соответствующая оценка несмещенная, что подтверждает возможность использования этой меры соответствия для оценки напряжений в случае, когда в исходной классификации нет ошибок. Области ε-эквивалентных решений, отвечающих мере соответствия R₂(σ) близки к своим аналогам для меры R₁(σ), т.е. мера R₂(σ) также не слишком чувствительна к возрастанию погрешности в классификации трещин по признаку флюидопроводимости в пределах до 20–30%. Аналогичным образом, для случая недр, находящихся в сбросовом или сдвиговом режиме, более устойчиво определяется минимальное, а для случая взбросового режима – максимальное горизонтальное напряжение.

Поскольку меры соответствия R₃(σ) и R₄(σ) используют небинарные индексы, соответствующие им изолинии целевой функции более гладкие. Хотя поведения решений, получаемых с использованием этих мер близки, следует отметить один важный момент. В то время как у обеих мер соответствия наблюдается по одному глобальному максимуму, этот максимум достигается при “истинном” напряженном состоянии только для R₄(σ). В то же время, максимум меры соответствия R₃(σ) достигается при напряжениях, близких, но не равных “истинным”, т.е. оценка напряженного состояния, получаемая при решении обратной задачи с использованием меры R₃(σ), является смещенной. Этот вопрос заслуживает отдельного внимания. Проведенный анализ показал, что такое несоответствие вызвано отсутствием учета связи между сильными и слабыми аномалиями геофизического индикатора, вызванного, соответственно, сильно и слабо выраженной критической напряженностью трещин. Строго говоря, присутствие большого количества трещин с низким индексом критичности будет оказывать значительное влияние на значение меры соответствия R₃(σ). В то же время, небольшое количество сильно напряженных трещин, с напряжениями, находящимися на плоскости Мора существенно выше критерия (1), не должно оказать сильного влияния на значение меры соответствия R₃(σ). Поскольку R₃(σ) достигает значения, равного единице, только в том случае, когда на всех критически напряженных трещинах действуют равные друг другу по модулю нормальные и касательные напряжения, решение обратной задачи будет соответствовать этому случаю, что приводит к смещению оценки

Последняя мера соответствия R₄(σ) показывает, на первый взгляд, наилучшее поведение: целевая функция имеет единственный глобальный максимум, достигаемый при истинных значения параметров напряженного состояния, т.е. решение обратной задачи единственно и соответствующая оценка σ является несмещенной. Однако для успешного использования этой меры необходимо установить связь между выраженностью аномалии геофизического индикатора (выражение (5)) и соотношением между касательным и нормальным напряжениями (8). В рамках данного теоретического исследования предполагалось, что такая связь уже установлена и подтверждена, причем зависимость между индексами аномальности и критической напряженности линейная. Если такая связь остается справедливой и для реальных данных, можно ожидать, что использование меры R₄(σ) позволит наиболее точно и достоверно реконструировать напряжения по сведениям о естественной трещиноватости. Тем не менее, процесс нахождения и обоснования такой связи может представлять существенные трудности, поскольку требует дополнительных теоретических и экспериментальных исследований влияния критически напряженных трещин на различные физические свойства горных пород и соответствующие геофизические индикаторы (поля).

Отметим, что хотя решение единственно, изолиния целевой функции, отвечающая 90% от максимума (т.е., приблизительно уровню 10% погрешности в данных) ограничивает весьма значительное по площади множество пространства параметров, составляющее множество ε-эквивалентности. Следовательно, даже относительно небольшие погрешности в определении степени “напряженности” трещин по геофизическим индикаторам приводят к практической неразличимости решений, отвечающих существенно различным напряженным состояниям σ. Вкупе со сложностью оценки такой погрешности на практике это делает применение меры R₄(σ) сопряженным со значительными затруднениями.

В заключение отметим, что для всех исследованных мер соответствия целевая функция не является выпуклой на всем множестве допустимых значений σ, как это следует из наблюдаемой на рис. 2–4 формы изолиний. Поэтому данная обратная задача не является задачей выпуклого программирования.

4. АНАЛИЗ УСТОЙЧИВОСТИ

Для того, чтобы проанализировать устойчивость решения рассматриваемой задачи по отношению к зашумлению исходных данных, в анализ был введен параметр зашумления q, характеризующий возможность некорректной классификации трещин в соответствии с геофизическим индикатором. Параметр зашумления q был введен следующим образом: бинарный индекс аномальности t_j для j-й трещины менялся на противоположный с вероятностью q (индекс 1 менялся на 0, индекс 0 менялся на 1); небинарный индекс p_j был умножен на случайную величину, равномерно распределенную на интервале от 1 – q до 1 + q. Для анализа устойчивости решения обратной задачи реконструкции напряжений по данным о трещиноватости, эта задача была решена для исходных данных, зашумленных по законам:

(20)

$\begin{gathered} t_{j}^{{\bmod }}\left( q \right) = \left\{ \begin{gathered} {{t}_{j}}\,\,\,\,{\text{if}}\,\,\,r \geqslant q, \hfill \\ 1 - {{t}_{j}}\,\,\,\,{\text{if}}\,\,\,\,r < q, \hfill \\ \end{gathered} \right. \\ p_{j}^{{\bmod }}\left( q \right) = {{p}_{j}}\left( {1 + \left( {r - \frac{1}{2}} \right)q} \right). \\ \end{gathered} $

Здесь r – случайная величина, равномерно распределенная на промежутке [0; 1]. Модифицированные индексы аномальности $t_{j}^{{\bmod }}$(q) и $p_{j}^{{\bmod }}$(q) порождают классификации трещин по признаку флюидопроводимости, ухудшенные (зашумленные) по сравнению с классификациями, порожденными исходными индексами t_j и p_j. Как следствие, четыре меры соответствия, использованные ранее, также могут зависеть от параметра зашумленности q: R_i = R_i(σ, q), i = 1, 2, 3, 4. Это позволяет численно оценить устойчивость решений обратной задачи, полученных с использованием каждой из этих мер, по отношению к ошибке в классификации трещин по признаку флюидопроводимости, выполненной на основании результатов геофизических исследований скважин.

Для анализа устойчивости были рассмотрены три параметра: расстояние между найденным решением обратной задачи и истинными параметрами напряженного состояния (D(R_i)); значение меры соответствия для истинных напряжений ($R_{i}^{{true}}$); отношение значения меры для истинных значений σ к ее глобальному максимуму (E(R_i)). Эти три параметра были рассчитаны для набора решений обратной задачи, полученных для значений параметра зашумленности от 0 до 50%. Для того, чтобы добиться лучшего понимания устойчивости решения по отношению к зашумлению входных данных, для каждого значения параметра зашумленности проводилось по десять реализаций зашумления – для каждой реализации входные данные модифицировались по выражениям (20) с произвольной величиной r. Эти реализации использовались для расчета минимального, среднего и максимального значений величин D(R_i), $R_{i}^{{true}}$, and E(R_i).

Расстояние от решения до истинного напряженного состояния определялось как:

(21)

$D\left( {{{R}_{i}}} \right) = \frac{{\sqrt {{{{\left( {\sigma _{H}^{{true}} - \sigma _{H}^{{{\text{max}}}}} \right)}}^{2}} + {{{\left( {\sigma _{h}^{{true}} - \sigma _{h}^{{{\text{max}}}}} \right)}}^{2}}} }}{{{{\sigma }_{V}}}}.$

Здесь $\sigma _{H}^{{true}}$ и $\sigma _{h}^{{true}}$ – горизонтальные напряжения, для которых были сформированы исходные данные; $\sigma _{H}^{{{\text{max}}}}$ и $\sigma _{h}^{{{\text{max}}}}$ – горизонтальные напряжения, при которых достигается максимум меры R_i, i, = 1, 2, 3, 4. Это расстояние характеризует абсолютную погрешность в определении напряжений, обусловленную ошибками в изначальной классификации трещин по признаку флюидопроводимости. В случае, когда у обратной задачи наблюдалось несколько эквивалентных решений, из всех возможных расстояний до “истинного” решения выбиралось минимальное.

Расстояния между найденным и “истинным” решениями D(R_i) показаны на рис. 5. Этот и последующие рисунки построены для случая сбросового тектонического режима, для остальных режимов характер зависимостей аналогичен. Пунктирные линии соединяют непосредственно результаты расчетов для разных реализаций (минимальные, средние и максимальные значения расстояний), сплошные линии отображают полученные аппроксимации. Черная линия характеризует максимальное полученное расстояние между полученным и “истинным” решениями, выбранное из всех рассмотренных реализаций (для разных значений r). Темно-серым цветом показано среднее значение расстояния по реализациям, светло-серым – минимальное. Аналогичная цветовая схема будет использована и для анализа значения меры соответствия при “истинных” напряжениях $R_{i}^{{true}}$, и для ее отношения к глобальному максимуму E(R_i).

Рис. 5.

Расстояние между полученным и “истинным” решением обратной задачи с ростом зашумленности исходных данных.

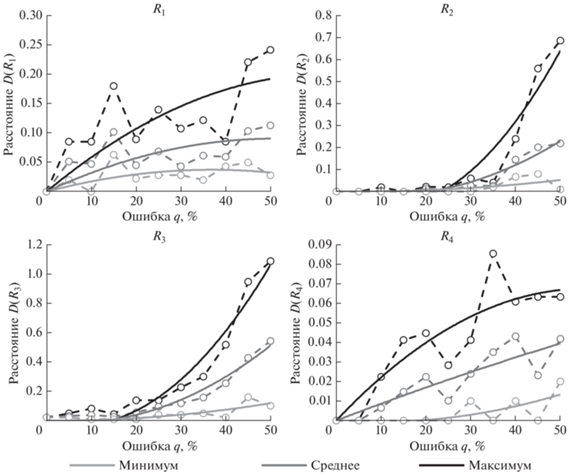
Из результатов, показанных на рис. 5, можно сделать несколько важных выводов. В первую очередь, можно отметить поведение величины D(R₁). В то время, как D(R₂), D(R₃) и D(R₄) характеризуются монотонным ростом расстояния между найденным и “истинным” решениями по мере роста параметра зашумленности, у расстояния D(R₁) (минимальный вариант) существует максимум, достигаемый при определенном параметре зашумленности. При больших значениях параметра зашумленности расстояние D(R₁) начинает уменьшаться с ростом шума. Это явление обусловлено определением (13): вместо того, чтобы попарно сравнивать трещины между собой, использование меры соответствия позволяет лишь сравнивать общую долю критически напряженных и флюидопроводящих трещин. Из выражения (20) следует, что общая доля трещин может оставаться одной и той же для разных значений параметра зашумленности: так, если ровно половина трещин является критически напряженной, величина q = 1 не приведет к изменению доли критически напряженных трещин. Далее, следует отметить, что мера R₄ оказывается самой надежной – диапазон значений D(R₄) значительно меньше диапазонов для других мер (но, как было отмечено ранее, требовательной к установлению связи между аномальностью и выраженностью критической напряженности), поскольку расстояние между полученным и “истинным” решениями обратной задачи в ее случае существенно меньше по сравнению с R₂ и R₃. Наконец, при использовании мер R₂ и R₃ расстояние до истинного решения начинает резко возрастать только при параметре зашумленности, превосходящем 20%. Такая величина приемлема и соответствует типичным ошибкам при интерпретации естественной трещиноватости [Silva et al., 2003].

Второй параметр, использованный для исследования чувствительности решения обратной задачи реконструкции напряжений по отношению к зашумлению исходных данных, был определен как значение меры соответствия при истинных напряжениях:

(22)

${{R}_{i}}^{{true}}\left( {\sigma ,q} \right) = {{R}_{i}}\left( {\sigma _{H}^{{true}},\sigma _{h}^{{true}},q} \right).$

Мера соответствия определяется для напряженного состояния, характеризующегося значениями отношений горизонтальных напряжений к вертикальному, для которых была построена классификация, показанная на рис. 1. На рис. 6 эта величина построена для четырех мер соответствия и набора значений параметра зашумления q. Используется та же легенда, что и на рис. 5: пунктирные линии соответствуют результатам расчетов, сплошные являются аппроксимациями, светло серым цветом отмечено минимальное значение, темно серым – среднее, а черным – максимальное значение меры соответствия для рассмотренных реализаций, отличающихся значением величины r.

Рис. 6.

Значение меры соответствия при “истинных” напряжениях с ростом зашумленности исходных данных.

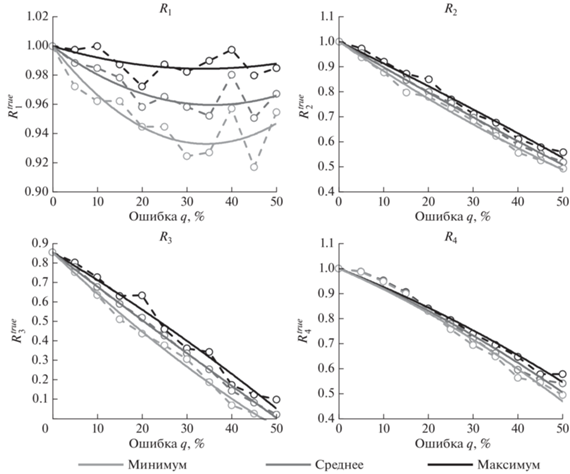
Как и в предыдущем случае, все меры соответствия, за исключением R₁, характеризуются монотонным уменьшением величины $R_{i}^{{true}}$ по мере роста параметра зашумленности. Объяснение этого факта аналогично приведенному выше: при использовании меры R₁ важна только относительная доля критически напряженных и флюидопроводящих трещин, но не их попарное соответствие. Для мер R₂, R₃ и R₄ характерно близкое к линейному падение их значений при “истинных” напряжениях по мере роста параметра зашумленности q. Следует отметить, что величина меры R₃ не равна единице даже для нулевого зашумления, что соответствует обсуждению смещения соответствующей оценки параметров напряженного состояния, получаемой при использовании этой меры соответствия, представленной в предыдущем разделе.

Ясно, что не только абсолютное значение меры соответствия при “истинных” напряжениях уменьшается по мере роста шума: значения мер, рассчитанных для всех прочих напряженных состояний, также уменьшаются. В связи с этим, в анализ чувствительности было введено исследование третьего параметра – отношения E(R_i) значения меры при “истинных” напряжениях к ее абсолютному максимуму. Этот параметр может быть определен как:

(23)

$E\left( {{{R}_{i}}} \right) = \frac{{{{R}_{i}}\left( {\sigma _{H}^{{true}},\sigma _{h}^{{true}}} \right)}}{{\mathop {\max }\limits_{{{\sigma }_{H}},\;{{\sigma }_{h}}} {{R}_{i}}\left( \sigma \right)}} = \frac{{{{R}_{i}}^{{true}}}}{{\mathop {\max }\limits_{{{\sigma }_{H}},\;{{\sigma }_{h}}} {{R}_{i}}\left( \sigma \right)}}.$

Поскольку по определению 0 ≤ R_i(σ_H, σ_h) ≤ ≤ R_i($\sigma _{H}^{{{\text{max}}}},\sigma _{h}^{{{\text{max}}}}$) значение E(R_i) может изменяться в пределах от нуля до единицы. Чем выше величина E(R_i), полученная для определенного параметра зашумленности q, тем меньше неопределенность, возникающая при решении обратной задачи с использованием выбранной меры соответствия. На рис. 7 показаны результаты, полученные для сбросового тектонического режима. Легенда сохраняется аналогичной рис. 5 и рис. 6.

Рис. 7.

Отношение меры соответствия при “истинных” напряжениях к ее глобальному максимуму с ростом зашумленности исходных данных.

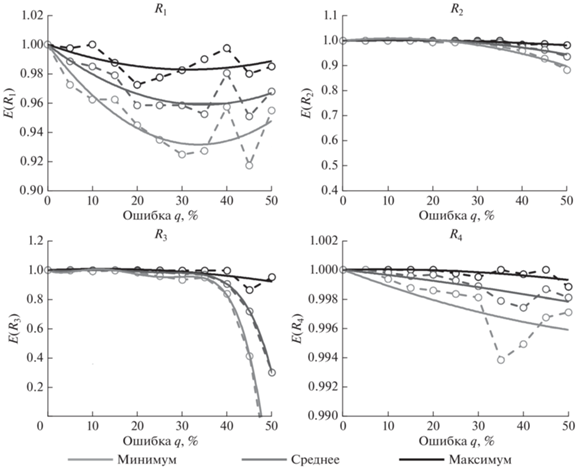
Рис. 7 подтверждает, что хотя у всех мер соответствия, за исключением R₁, наблюдается сходное поведение при рассмотрении ${{R}_{i}}^{{true}}$, то же самое неверно для его нормированного значения. Относительные изменения величин E(R₂) и E(R₃) очень малы для параметров зашумленности, не превосходящих 30%, после чего происходит нелинейное уменьшение этих величин по мере роста q. E(R₄) изменяется существенно меньше и при высоких значениях параметра зашумленности, что еще раз подтверждает преимущества использования меры R₄ с оговоркой о необходимости установления связей между выраженностью критической напряженности трещины и степенью вызванной ее присутствием аномальности геофизического индикатора. ${{R}_{1}}^{{true}}$ и E(R₁) ведут себя сходим образом, поскольку глобальный максимум R₁ остается близким к единице.

Из рис. 5–рис. 7 следует, что высокие значения параметра зашумленности приводят к неустойчивости решения обратной задачи реконструкции напряжений на основании данных о трещиноватости, полученного с использованием любой из рассмотренных мер. Со всех позиций мера соответствия R₄ демонстрирует наилучшие результаты, однако ее использование требует дополнительных исследований, в том числе, специфичных для региона, в котором выполняется реконструкция напряжений. Мера соответствия R₂ демонстрирует схожие с R₄ результаты: хотя точность полученных решений ниже, а чувствительность к погрешностям в исходных данных выше, общие тенденции одни и те же, причем использование меры R₂ не требует установления конкретного вида связи между индексами аномальности и критической напряженности – требуется лишь подтверждение существования такой связи. Несмотря на устойчивое поведение решений, получаемых с использованием меры соответствия R₃, эти решения характеризуются являются смещенными, т.е. не соответствуют истинным значениям напряжений. Наконец, мера R₁ дает решения обратной задачи, чувствительные к зашумлению входных данных.

Представленные результаты позволяют судить об устойчивости решения обратной задачи реконструкции напряжений по данным о трещиноватости по отношению к зашумлению входных данных. Следует отметить, что в рамках данной работы рассматривалась исключительно случайная ошибка в интерпретации данных геофизических исследований скважин с позиций классификации по принципу флюидопроводимости. Наличие в такой классификации систематической ошибки приведет к невозможности корректной реконструкции напряженного состояния пород околоскважинной зоны с использованием разрабатываемого подхода.

5. ВЫВОДЫ

Оценка напряженного состояния верхних слоев земной коры – актуальная и важная задача, решение которой имеет и практическую, и фундаментальную значимость. Разработанные и широко применяемые на практике методы оценки напряжений по скважинным данным имеют ограниченные области применения, в связи с чем, представляется важным развитие альтернативных методов.

Данная работа посвящена одному из этих методов, а именно, реконструкции текущих напряжений на основании анализа естественной трещиноватости. Несмотря на то, что этот метод неоднократно применялся на практике для оценки напряженного состояния массивов горных пород в различных регионах, до сих пор отсутствовало детальное исследование метода решения обратной задачи, возникающей при его применении. При этом разные авторы, реализующие этот подход, используют различные способы определения наилучшего соответствия между критически напряженными и флюидопроводящими трещинами – соответствия, лежащего в основе методов реконструкции напряжений по данным о трещиноватости.

В работе было выполнено систематическое исследование алгоритма реконструкции напряжений на основании скважинных исследований трещиноватости пород околоскважинной зоны. Процедура реконструкции напряжений может быть строго сформулирована следующим образом:

1. Разделение наблюдаемого интервала глубин пласта на интервалы, содержащие по одной естественной трещине;

2. Расчет на каждом интервале коэффициента аномальности показателей геофизических исследований скважины, вызванного присутствием флюидопроводящей трещины. Создание геофизически обоснованной классификации трещин по признаку флюидопроводимости;

3. Выбор модели зависимости напряжений от глубины и определение набора параметров, задающих конкретные профили;

4. Расчет напряжений, действующих на каждой трещине для определенного набора значений параметров напряженного состояния. Создание для каждого такого набора значений, классификации трещин по признаку критической напряженности;

5. Расчет меры соответствия классификаций трещин по признакам флюидопроводимости и критической напряженности для рассматриваемого напряженного состояния;

6. Повтор этапов 4–6 для всех возможных значений параметров, характеризующих напряженное состояние пласта.

Было проведено исследование использования различных способов определения меры соответствия при решении задачи оптимизации: предложено четыре различных меры, проанализированы их преимущества и недостатки.

Представленный алгоритм и предложенные определения меры соответствия были использованы для решения обратной задачи реконструкции напряжений в пласте по данным о его естественной трещиноватости для синтетической модели. Были поставлены цели исследования единственности и несмещенности решения обратной задачи и анализа устойчивости решений, получаемых с использованием разных мер соответствия, к зашумлению исходных данных. Численные эксперименты показали, что предложенный алгоритм действительно может быть использован для восстановления напряженного состояния пласта по данным о его трещиноватости. Предложенные меры соответствия дают возможность получать решения, различающиеся точностью и устойчивостью по отношению к зашумлению исходных данных.

Во всех случаях (для всех исследованных мер соответствия), обратная задача является некорректной по Адамару [Тихонов, Арсенин, 1979], поскольку ее решение неустойчиво. При этом одна из исследованных мер соответствия (R₁(σ) – доля критически напряженных трещин, наиболее часто используемая на практике) приводит также к неединственному решению обратной задачи, при этом множество эквивалентных решений включает истинные значения параметров. Кроме того, обратная задача является нелинейной и, как показало наше исследование, не является также задачей выпуклого программирования. Это делает практически нецелесообразным использование способов регуляризации по Тихонову и иных подходов, широко используемых при решении линейных обратных задач. Вместе с тем, задача является несложной с вычислительной точки зрения, поэтому применение алгоритмов минимизации типа градиентного спуска и пр. в данном случае не требуется, поскольку может быть легко заменено полным перебором значений меры соответствия для всего допустимого множества параметров σ по весьма детальной (с точки зрения потребностей практики) сетке. Такой подход позволяет не только найти решение, отвечающее глобальному максимуму целевой функции, но и исследовать вопросы единственности и устойчивости для каждой конкретной задачи, возникающей в практике.

Отметим, что наиболее удачные определения меры соответствия (порождающие наилучшие результаты на синтетических данных) могут быть использованы на реальных объектах только при условии проведения для конкретных пород специальных исследований связи между выражен-ностью критической напряженности трещин и их влиянием на те или иные свойства пород, которые могут быть измерены с помощью геофизических методов.

Можно отметить важный результат проведенных исследований устойчивости решения обратной задачи по отношению к зашумлению входных данных. В рамках синтетической модели погрешности в интерпретации исходных данных, приводящие к существенным ошибкам в оценке напряжений, оказываются больше, чем реальные погрешности, имеющие место при обработке данных о естественной трещиноватости, в частности, данных геофизических исследований скважин, что свидетельствует о применимости разрабатываемого подхода в реальных условиях.

Полученные в ходе работы результаты позволяют говорить о том, что решения обратной задачи реконструкции напряжений, действующих в массиве горных пород, на основании данных об их естественной трещиноватости действительно могут быть получены после применения описанной процедуры. Выбор меры соответствия между экспериментальными и модельными данными (целевой функции, используемой при решении оптимизационной задачи) в значительной степени определяет область эквивалентных решений поставленной обратной задачи, их устойчивость по отношению к зашумлению исходных данных, а также наличие систематических ошибок в оценке напряжений.

Список литературы

Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука. 1979.
Agosta F., Alessandroni M., Antonellini M., Tondi E., Giorgioni M. From fractures to flow: A field-based quantitative analysis of an outcropping carbonate reservoir // Tectonophysics. 2010. V. 490. № 3–4. P. 197–213. https://doi.org/10.1016/j.tecto.2010.05.005
Aguilera R. Naturally Fractured Reservoirs. 2nd ed. Tulsa: Penn Well Publishing. 1995. 521 p.
Barton C.A., Moos D., Hartley L., Baxter S., Foulquier L., Holl H., Hogarth R. Geomechanically coupled simulation of flow in fractured reservoirs. Proceedings of the 38th Workshop on Geothermal Engineering. Stanford University. California. 11–13 Feb. 2013.
Barton C.A., Zoback M.D., Moos D. Fluid flow along potentially active faults in crystalline rocks // Geology. 1995. V. 23. № 8. P. 683–686. https://doi.org/10.1130/0091-7613(1995)023%3C0683: FFAPAF%3E2.3.CO;2
Davidson J., Siratovich P.A., Wallis I.C., Gravley D.M., McNamara D.D. Quantifying the stress distribution at the Rotokawa Geothermal Field, New Zealand. Proceedings of the 34th New Zealand Geothermal Workshop. Auckland. New Zealand. 19–21 Nov. 2012.
Dubinya N.V. An Overview of Wellbore Methods of Investigating Stress State of the Upper Layers of the Earth’s Crust // Izvestiya, Physics of the Solid Earth. 2019a. V. 55. № 2. P. 311–326. https://doi.org/10.31857/S0002-333720192137-155
Dubinya N.V. Stress state estimation based on local variations of effective elastic moduli caused by presence of critically stressed fractures. Proceedings of the 53rd US Rock Mechanics.Geomechanics Symposium. New York. 23–26 June 2019b. ARMA Conference Paper ARMA 19–139.
Dubinya N., Bayuk I., Tikhotskiy S., Rusina O. Localization and Characterization of Hydraulically Conductive Fractured Zones at Seismic Scale with the Help of Geomecha. Proceedings of the 80th EAGE Conference and Exhibition 2018, Jun 2018. V. 2018. P. 1–5. https://doi.org/10.3997/2214-4609.201800722
Dubinya N.V., Ezhov K.A. In-situ horizontal stress estimation based on the geometrical properties of fractures in well vicinity // Geophysical Research. 2017. V. 18. № 2. P. 5–26. https://doi.org/10.21455/gr2017.2-1
Ezhov K.A., Arsibekov A.A., Dubinya N.V. Application of special well logging techniques for geomechanical model improvement in naturally fractured reservoirs. Proceedings of SPE Russian Petroleum Technology Conference, Moscow, 16–18 October 2017. 2017. SPE Conference Paper SPE-187821-MS.
Fisher R.A. Dispersion on a sphere // Proceedings of the Royal Society A. 1953. V. 217. № 1130. P. 295–305. https://doi.org/10.1098/rspa.1953.0064
Fisher Q.J., Casey M., Harris S.D., Knipe, R.J. Fluid-flow properties of faults in sandstone: the importance of temperature history // Geology. 2003. V. 31. № 11. P. 965–968. https://doi.org/10.1130/G19823.1
Fisher Q.J., Knipe R.J. Fault sealing processes in siliciclastic sediments // Geological Society, London, Special Publications. 1998. V. 147. № 1. P. 117–134. https://doi.org/10.1144/GSL.SP.1998.147.01.08
Funato A., Chen Q. Initial stress evaluation by boring core deformation method. Proceedings of the 34th Symposium on Rock Mechanics. 2005. P. 261–266.
Gaarenstroom L., Tromp R.A.J., de Jong M.C., Brandenburg A.M. Overpressures in the Central North Sea: implications for trap integrity and drilling safety // Geological Society, London, Petroleum Geology Conference Series. 1993. V. 4. № 1. P. 1305–1313. https://doi.org/10.1144/0041305
Heidbach O., Rajabi M., Reiter K., Ziegler M. WSM Team (2016): World Stress Map Database Release 2016. GFZ Data Services. https://doi.org/10.5880/WSM.2016.001
Hickman S., Barton C.A., Zoback M., Morin R., Sass J., Benoit R. In-situ Stress and Fracture Permeability in a Fault-hosted Geothermal Reservoir at Dixie Valley, Nevada // Geothermal Resources Council Transactions. 1997. V. 21. P. 181–189.
Ito T., Funato A., Lin W., Doan M.L., Boutt D.F., Kano Y., Ito H., Saffer D., McNeill L.C., Byrne T., Moe K.T. Determination of stress state in deep subsea formation by combination of hydraulic fracturing in situ test and core analysis: A case study in the IODP Expedition 319 // Journal of Geophysical Research: Solid Earth. 2013. V. 118. № 3. P. 1203–1215. https://doi.org/10.1002/jgrb.50086
Ito T., Fukusawa S., Funato A., Tamagawa T., Tezuka K. A New Method of Stress Measurement Based on Elastic Deformation of Sidewall-Core With Stress Relief During Coring. Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, 17–20 June 2018. 2018. ARMA Conference Paper 18-672.
Ito T., Fujii R., Evans K.F., Hayashi K. Estimation of Stress Profile with Depth from Analysis of Temperature and Fracture Orientation Logs in a 3.6 km Deep Well at Soultz, France. Proceedings of SPE/ISRM Rock Mechanics Conference, Irving, 20–23 October 2002. SPE Conference Paper 78185-MS. https://doi.org/10.2118/78185-MS
Ito T., Zoback M.D. Fracture permeability and in situ stress to 7 km depth in the KTB scientific drillhole // Geophysical Research Letters. 2000. V. 27. № 7. P. 1045–1048. https://doi.org/10.1029/1999GL011068
Kissling W.M., Ellis S.E., McNamara D.D., Massiot C. Modelling fluid flow through fractured rock: Examples using TVZ geothermal reservoirs. Proceedings of the 37th New Zealand Geothermal Workshop, Taupo, New Zealand, 18–20 Nov. 2015.
Jaeger J.C., Cook N.G.W., Zimmermann R.W. Fundamentals of Rock Mechanics. Oxford: Blackwell Publishing. 2007. 488 p.
Laubach S.E., Olson J.E., Gale J.F.W. Are open fractures necessarily aligned with maximum horizontal stress? // Earth and Planetary Science Letters. 2004. V. 222. P. 191–195. https://doi.org/10.1016/j.epsl.2004.02.019
Latham J.P., Xiang J., Belayneh M., Nick H.M., Tsang C.F., Blunt M.J. Modelling stress-dependent permeability in fractured rock including effects of propagating and bending fractures // International J. Rock Mechanics and Mining Sciences. 2013. V. 57. P. 100–112. https://doi.org/10.1016/j.ijrmms.2012.08.002
Ligtenberg J.H. Detection of fluid migration pathways in seismic data: implications for fault seal analysis // Basin Research. 2005. V. 17. P. 141–153. https://doi.org/10.1111/j.1365-2117.2005.00258.x
Ljunggren C., Chang Y., Janson T., Christiansson R. An overview of rock stress measurement methods // International J. Rock Mechanics and Mining Sciences. 2003. V. 40. № 7. P. 975–989. https://doi.org/10.1016/j.ijrmms.2003.07.003
Min K.B., Rutqvist J., Tsang C.F., Jing L. Stress dependent permeability of fractured rock masses: a numerical study // International J. Rock Mechanics and Mining Sciences. 2004. V. 41. P. 1191–210. https://doi.org/10.1016/j.ijrmms.2004.05.005
Neuman S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks // Hydrogeology J. 2005. V. 13. P. 124–147. https://doi.org/10.1007/s10040-004-0397-2
Pistre V., Yan G.R., Sinha B., Prioul R., Vidal-Gilbert S. Determining stress regime and Q factor from sonic data. Proceedings of SPWLA 50th Annual Logging Symposium, The Woodlands, 21–24 June 2009. 2009. SPWLA Conference Paper 2009-23344
Raaen A.M., Horsrud P., Kjorholt H., Okland D. Improved routine estimation of the minimum horizontal stress component from extended leak-off tests // International J. Rock Mechanics and Mining Sciences. V. 43. P. 37–48. https://doi.org/10.1016/j.ijrmms.2005.04.005
Rogers S. Critical stress-related permeability in fractured rocks. Fracture and in situ stress characterization of hydrocarbon reservoirs // Geological Society, London, Special Publications. 2002. V. 209. P. 7–16. https://doi.org/10.1144/GSL.SP.2003.209.01.02
Rutqvist J., Stephansson O. The role of hydromechanical coupling in fractured rock engineering // Hydrogeology J. 2003. V. 11. P. 7–40. https://doi.org/10.1007/s10040-002-0241-5
Sayers C. Stress-induced fluid flow anisotropy in fractured rock // Transport in Porous Media. 1990. V. 5. P. 287–297. https://doi.org/10.1007/BF00140017
Sathar S., Reeves H.J., Cuss R.J., Harrington J.F. The role of stress history on the flow of fluids through fractures // Mineralogical Magazine. 2012. V. 76. № 8. P. 3165–3177. https://doi.org/10.1180/minmag.2012.076.8.30
Silva I., Domingos F., Marinho P., Laronga R., Khan S. Advanced Borehole Image Applications in Turbidite Reservoirs Drilled With Oil Based Mud: A Case Study From Deep Offshore Angola // SPWLA 44th Annual Logging Symposium. 2003. SPWLA-2003-AA.
Sinha B.K., Wang J., Kisra S., Li J., Pistre V., Bratton T., Sanders M., Jun C. Estimation of formation stresses using borehole sonic data. 49th Annual Logging Symposium Proceedings. 2008.
Townend J., Zoback M.D. How faulting keeps the crust strong // Geology. 2000. V. 28. № 5. P. 399–402. https://doi.org/10.1130/0091-7613(2000)28%3C399: HFKTCS%3E2.0.CO;2
Wilbur C., Amadei B. Flow pump measurement of fracture transmissivity as a function of normal stress. Hustrulid W.A., Johnson G.A. (eds.). Rock Mechanics Contributions and Challenges. Rotterdam: Balkema. 1990. P. 621–627.
Zhang J. Borehole stability analysis accounting for anisotropies in drilling to weak bedding planes // International J. Rock Mechanics and Mining Sciences. 2013. V. 60. P. 160–170. https://doi.org/10.1016/j.ijrmms.2012.12.025
Zhang X., Koutsabeloulis N.C., Heffer K. Hydromechanical modelling of critically stressed and faulted reservoirs // AAPG Bulletin. 2007. V. 91. № 1. P. 31–50. https://doi.org/10.1306/08030605136
Zoback M.D., Mastin L., Barton C. In-situ stress measurements in deep boreholes using hydraulic fracturing, wellbore breakouts, and Stonely wave polarization. Proceedings of ISRM International Symposium Proceedings, Stockholm, 31 August–3 September 1986.
Zoback M.D., Barton C.A., Brudy M., Castillo D.A., Finkbeiner T., Grollimund B.R., Moos D.B., Peska P., Ward C.D., Wiprut D.J. Determination of stress orientation and magnitude in deep wells. International J. Rock Mechanics and Mining Sciences. 2003. V. 40. № 7. P. 1,049–1,076. https://doi.org/10.1016/j.ijrmms.2003.07.001
Zohreh M., Junin R., Jeffreys P. Evaluate the borehole condition to reduce drilling risk and avoid potential well bore damages by using image logs // J. Petroleum Science and Engineering. 2014. V. 122. P. 318–330. https://doi.org/10.1016/j.petrol.2014.07.027

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал