Физика Земли, 2022, № 4, стр. 3-18

ВВЕДЕНИЕ

Традиционно считается, что современные деформации разломных зон формируются сдвиговыми перемещениями. В зависимости от характера относительного смещения блоков и угла падения плоскости разломов они делятся на сбросы, взбросы, надвиги, сдвиги и переходные формы (сбросо-сдвиги, сдвиго-сбросы и т.п.). Согласно теории разломообразования Андерсона выделяются три основных типа разломов: сбросы (normal faults), сдвиги (strike-slip faults) и надвиги (reverse faults) [Turcotte, Shubert, 2002]. В соответствии с основами механики деформируемых сред все перечисленные типы разломов относятся к чисто сдвиговым перемещениям бортов.

Однако в механике разрушения существуют три основных механизма трещинообразования (моды разрушения): отрыв, продольный сдвиг и поперечный сдвиг (антиплоская деформация). Таким образом, существуют всего два генетических типа разрушения: отрыв и сдвиг. Поэтому в ряде работ по структурной геологии и геомеханике, кинематика движений по разломам описывается не только сдвигами, но и раздвигами (tensile faults, joints) [Гзовский, 1975; Шерман, 1977; Davis, 1983; Okada, 1985; 1992; Yang, Davis, 1986; Peacock, 2016].

Современные сдвиговые деформации разломных зон повсеместно регистрируются в виде косейсмических и постсейсмических движений в очаговых зонах сильных землетрясений [Кочарян, 2016; Scholz, 2019]. Современные деформации в зонах раздвиговых разломов (tensile faults) в форме локальных оседаний земной поверхности зафиксированы по результатам высокоточных нивелирных наблюдений в сейсмоактивных и нефтегазоносных регионах [Кузьмин, 1999; 2014; 2021а; 2021б]. Важно отметить, что большинство зарегистрированных аномалий относятся к флюидонасыщенным разломам, а кинематика вертикальных смещений представляет собой локальные, симметричные оседания в окрестности разломных зон. Эти аномалии обнаружены практически повсеместно. Главное условие для их идентификации – это наличие сети наблюдений с расстояниями между реперами не более 1 км. В подавляющем большинстве случаев они представлены локальными оседаниями [Кузьмин, 2018а; 2018б].

Из основ механики деформируемой среды следует, что общая деформация состоит из двух составляющих: объемной и сдвиговой. В этом случае любые “не сдвиговые” деформации среды можно считать объемными. С этих позиций наблюдаемые симметричные, локальные оседания или поднятия земной поверхности являются проявлением объемных деформаций разломных зон.

Наличие флюидонасыщенных разломов в существенной мере определяет объемный тип деформирования разломных зон. Естественно, что это требует рассмотрения механизмов формирования аномальных деформаций земной поверхности с использованием модели пороупругой среды. В данной работе представлены результаты анализа ряда аномальных деформаций земной поверхности, которые основаны на представлениях о пороупругих включениях и неоднородностях как модельных аналогов объемного деформирования разломных зон.

МЕХАНИЗМ ФОРМИРОВАНИЯ ОБЪЕМНЫХ ДЕФОРМАЦИЙ РАЗЛОМНЫХ ЗОН НА ОСНОВЕ МОДЕЛЕЙ ПОРОУПРУГИХ ВКЛЮЧЕНИЙ И НЕОДНОРОДНОСТЕЙ

В качестве механизма формирования локальных оседаний земной поверхности, которые возникают в зонах раздвиговых разломов обычно рассматриваются три геомеханические модели: блоковая, дислокационная и индуцированная [Кузьмин, 2019].

Как показывает сравнительный анализ, блоковая модель, где задается горизонтальный раздвиг блоков фундамента и происходит оседание поверхности слоя осадочных пород, не удовлетворяет двум эмпирическим фактам. Она не формирует локальные аномалии. Ширина аномалий зависит от соотношения размеров блоков фундамента и толщины осадочного слоя. Но самое главное – это необходимость, чтобы вариации во времени горизонтальных перемещений блоков соответствовали временному ходу развития локальных приразломных оседаний, а их амплитуды были соизмеримы с амплитудами смещений блоков. А это не наблюдается в результатах измерений. Кроме того, в блоковых моделях не формируются локальные объемные деформации внутри разломных зон.

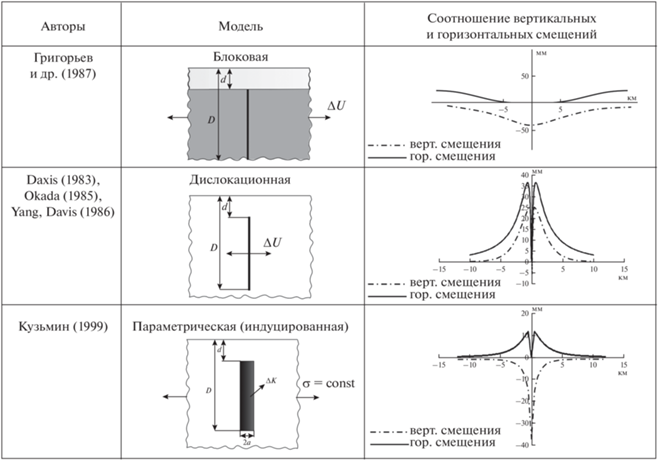
Дислокационная модель достаточно хорошо описывает локальный характер приразломных смещений поверхности. Задаваемые, например, раздвиговые скачки смещений в разломе оказываются вполне соизмеримыми с наблюдаемыми величинами. Однако существенным недостатком дислокационных моделей является отсутствие у них ширины разлома. Кроме этого, морфология и амплитуда аномальных смещений земной поверхности в разломной зоне в дислокационной модели не зависит от характера и интенсивности “региональных” (внешних) условий, в обстановке которых развивается локальная аномалия. Характерной особенностью распределения вертикальных смещений является то, что оседание имеет амплитуду, соизмеримую с амплитудой поднятия. Подобные явления никогда не наблюдались в реальных данных.

Несмотря на то, что блоковая и дислокационные модели формируют симметричные оседания земной поверхности, эти модели нельзя в полной мере отождествлять с объемными деформациями, которые развиваются внутри разломной зоны. Более того, в рамках этих моделей затруднительно описывать флюидонасыщенные разломы. Так, например, в работе [Verma et al., 2017] раздвиговая дислокация помещена в пороупругое полупространство и, следовательно, ее нельзя отождествлять с флюидонасыщенным разломом.

Индуцированная, параметрическая модель основана на том, что локальные деформационные процессы, регистрируемые многократными детальными геодезическими наблюдениями в зонах разломов, обусловлены “внутренними” источниками (вариациями во времени жесткостных параметров разломной зоны), а региональные процессы обеспечивают квазистатический фон приложенных напряжений, характер которых определяет конкретную морфологию аномалий. Важно отметить, что для возникновения наблюдаемых величин аномальных деформаций (5 × 10^–5/год–10^–4/год) достаточно создать условия для изменения во времени всего на несколько первых процентов жесткостных характеристик (упругих модулей) в локальных фрагментах, изначально напряженных, разломных зон. Именно в рамках этой модели возможно естественное обобщение упругой среды на пороупругую.

В большинстве геомеханических моделей, описывающих локальные аномалии деформаций, используется упругое полупространство, которое содержит трехмерную область конечного объема, которая испытывает объемную деформацию – ε₀. При этом поверхность полупространства, которая отождествляется с земной поверхностью считается свободной от напряжения. Эта объемная деформация идентифицируется различными авторами как “трансформационная деформация” или “включение” (“inclusion”) [Eshelby, 1961], “собственная деформация” (“eigenstrain”) [Mura, 1987], “ядро деформации” (nuclei of strain) [Mindlin, Cheng, 1950], “дисторсия” (“distortion”) [Nowacki, 1986]. Общим для всех определений является то, что $~\varepsilon _{{ij}}^{0}$ – это аномальная, по отношению к вмещающей среде, деформация, которая не удовлетворяет условию совместности деформаций. Автор применяет для этой деформации термин дисторсия, который неоднократно применялся в работах V. Nowacki, посвященных неоднородным задачам термоупругости.

Как известно [Eshelby, 1961], оценку аномальных деформации можно провести, либо решая задачу о включении, либо задачу о неоднородности. Основное отличие этих задач состоит в том, что в первом случае внешние нагрузки на полупространство, как правило, отсутствуют. При решении задач о смещениях поверхности полупространства, содержащего неоднородность механических свойств, аномальные деформации формируются в условиях внешней нагрузки. В некоторых частных случаях эти задачи допускают эквивалентные решения, например, в случае изменения во включении объемных модулей [Цуркис, Кузьмин, 2022]. Рассматривая пороупругое включение как модель формирования объемных деформаций разломных зон, можно первоначально использовать модель упругого включения, а затем провести обобщение полученных решений на пороупругое включение. Аналогичным образом можно перевести решение задачи с упругой неоднородностью в решение задачи с пороупругой неоднородностью.

На рис. 2 схематично показано различие между граничными условиями при описании деформации разломной зоны моделями включения и неоднородности.

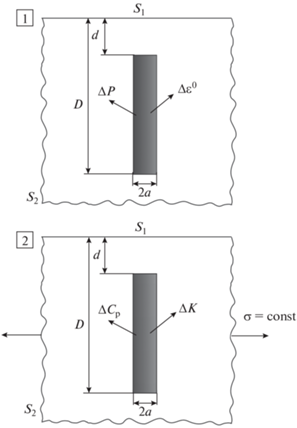
На рисунке обозначены варианты возникновения локальных объемных деформаций для упругих и пороупругих включений и деформаций. В случаях, когда в разломных зонах отсутствует флюид, возникновение аномальных смещений земной поверхности формируется локальными объемными деформациями ${{{{\varepsilon }}}^{0}}$. Когда разломы флюидонасыщенны, объемные деформации формируются изменением порового (пластового) давления $\Delta P$. Аналогично, в задаче упругой неоднородности аномальные объемные деформации возникают при изменениях объемного модуля $\Delta K$. При наличии флюидонасыщенного разлома аномальные объемные деформации внутри активизированного фрагмента разломной зоны происходят при изменении коэффициента поровой сжимаемости $\Delta {{C}_{p}}$. Именно таким образом осуществляется переход от упругих моделей включения и неоднородности к пороупругим.

В линейной теории упругости напряжение ${{\sigma }_{{ij}}}$ связано с деформацией ${{\varepsilon }}_{{ij}}^{~}$ законом Гука: ${{\sigma }_{{ij}}} = $ = ${{C}_{{ijkl}}}{{{{\varepsilon }}}_{{ij}}}$, где ${{C}_{{ijkl}}}$ – тензор упругих модулей. Для изотропной среды закон Гука может быть выражен как:

Здесь: $e = {{{{\varepsilon }}}_{{kk}}}$ – есть объемная деформация; ${{\mu }}$ – модуль сдвига; $K$ – объемный модуль; $\delta _{{ij}}^{~}$ – дельта Кронекера (${{\delta }_{{ij}}} = 1,$ если $i = j,~$ и ${{\delta }_{{ij}}} = 0,~$ если $i \ne j$). Деформация ${{{{\varepsilon }}}_{{ij}}}$ удовлетворяет формуле Коши:

Для квазистатических процессов, когда силами инерции можно пренебречь, напряжение ${{\sigma }_{{ij}}}$ должно удовлетворять условиям равновесия в виде:

где ${{F}_{j}}\left( {x,t} \right)$ есть объемная или массовая сила (body force). Подставляя (1) и (2) в (3) получается уравнение равновесия, выраженное через градиенты смещений:

Формула (1) закона Гука записана с использованием упругих модулей K и ${{\mu }}$. Для удобства осуществления преобразований эта формула может быть записана с использованием упругих модулей ${{\lambda }}$ и ${{\mu }},$ где ${{\lambda }}$ – параметр Ламэ, в виде:

В отличие от формулы (1) в (5) модуль сдвига присутствует при сдвиговой деформации, а параметр Ламэ при объемной. Модули ${{\lambda }}$ и K связаны между собой как ${{\lambda }} = \frac{{3K - 2{{\mu }}}}{3}$.

Для решения задачи использовалась теорема взаимности работ Бетти [Sokolnikoff, 1956], обобщенная для упругих тел с дисторсией [Novacki, 1986]. Если существуют две системы причин (поверхностные ${{T}_{i}}$ и массовые ${{F}_{i}}$ силы, напряжения ${{\sigma }_{{ij}}}$) и следствий (смещения ${{u}_{i}}$ и дисторсии ${{\varepsilon }}_{{ij}}^{0}$), то работа, произведенная силами первой системы на перемещениях и дисторсиях, произведенных второй системой сил, равна работе второй системы сил на перемещениях и дисторсиях, произведенной первой системой сил.

Здесь штрихами отмечены поверхностные и массовые силы, а также напряжения и дисторсии второй системы. Теорема о взаимности работ (6) позволяет вывести методы интегрирования уравнений в перемещениях. С ее помощью можно найти смещение поверхности, вызванное первой системой приложенных сил, по известному решению, которое используется при действии второй системы сил. В данном случае используется метод Майзеля [Maysel, 1941], в котором для нахождения вертикальных смещений поверхности полубесконечного упругого тела в качестве второй системы сил используется известное решение о смещениях, полученных приложением вертикальной точечной нагрузки к поверхности.

В качестве первой системы рассмотрено полубесконечное тело, в котором действуют только дисторсии ${{\varepsilon }}_{{ij}}^{0}$. Пусть массовые силы равны нулю. Представляя, что поверхность тела состоит из двух частей: ${{S}_{1}}$, которая совпадает с земной поверхностью, свободной от напряжений, и ${{S}_{2}}$, которая занимает остальную область и которая закреплена. Таким образом, на ${{S}_{1}}$ отсутствуют нагрузки, а на ${{S}_{2}}$ – смещения. В качестве второй (штрихованной) системы принимается то же тело, свободное от нагрузок на ${{S}_{1}}$ и закрепленное на ${{S}_{2}}$. Предположим далее, что в теле отсутствуют дисторсии (${{\varepsilon }}_{{ij}}^{{'0}} = 0$)), а в точке ξ в направлении оси ${{x}_{k}}$ действует сосредоточенная сила $F_{i}^{'} = {{\delta }}\left( {x - {{\xi }}} \right){{{{\delta }}}_{{ik}}}$. Эта сила вызывает перемещения $u_{i}^{'} = G_{i}^{{\left( k \right)}}\left( {x,{{\xi }}} \right)$, которые должны удовлетворять уравнениям равновесия:

с граничными условиями:

В формулах (7) и (8) $\delta \left( {x - \xi } \right)$ и $G_{i}^{{\left( k \right)}}$ есть функции Дирака и Грина, соответственно. Зная функцию Грина для полупространства, можно вычислить возникающие напряжения $\sigma _{{ij}}^{'}$:

Решение (7) с граничными условиями (8) является типичной задачей статической теорией упругости для тела, в котором отсутствует дисторсия. Применяя к обеим системам причин и следствий теорему взаимности (6), получаем уравнение:

Подставляя граничные условия в (10), получаем выражение, которое связывает смещение поверхности и дисторсию через известное значение функции Грина для напряжений $\sigma _{{ij}}^{{'\left( k \right)}}\left( {x,\xi } \right){\text{:}}$

Таким образом, найдены перемещения ${{u}_{k}}\left( \xi \right)$, выраженные через дисторсии в интегральном виде. Под знаком интеграла стоит известное распределение дисторсии и напряжения $\sigma _{{ij}}^{{'0}}\left( {x,\xi } \right)$, вызванные действием сосредоточенной силы в точке ξ, направленной по оси ${{x}_{k}}$. Учитывая, что для нашей задачи необходимо задавать дисторсию в виде объемной деформации $~{{\varepsilon }}_{{\text{\;}}}^{0}$, $\varepsilon _{{ij}}^{0} = ~\,\,{{\delta }_{{ij}}}{{\varepsilon }^{0}}$. Тогда, учитывая (9), получаем для $u_{k}^{~}\left( \xi \right)$:

Здесь $G_{{j,j}}^{{\left( k \right)}}\left( {x,\xi } \right)$ – функция Грина для смещений.

Если рассматривать только вертикальные смещения $u_{3}^{~}\left( \xi \right)$, то (12) примет вид:

В наиболее компактном виде формулы для тензора Грина от вертикальной сосредоточенной силы, приложенной к поверхности полупространства, имеют вид [Converse, Comninou, 1975]:

где ${{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$ – координаты точки во включении (области дисторсии). Делая для удобства замену переменных (${{\xi }_{1}} - {{x}_{1}} = x$, ${{\xi }_{2}} - {{x}_{2}} = y$, ${{\xi }_{3}} = z$) и осуществляя дифференцирование по соответствующим координатам, можно получить:

Подставляя (14) в (15), получаем формулу для оценки вертикальных смещений поверхности упругого полупространства:

В (16) отсутствует знак минус перед дробью, так как ось z направлена внутрь полупространства. Эту формулу можно использовать и для оценки горизонтальных смещений, если заменить переменную z в числителе подынтегрального выражения на x или y, соответственно. Для получения аналитических формул необходимо проинтегрировать (16) по объему активизированного фрагмента разломной зоны.

Если ввести в рассмотрение среду с пороупругим включением, которое является модельным аналогом флюидонасыщенного разлома, то следуя работам [Goodier, 1937; Geertsma, 1957; Zimmerman, 1991; Wang, 2000], в которых последовательно доказана аналогия между упругими и термоупругими явлениями, а также между термоупругими и пороупругими деформациями, можно показать, что ${{\varepsilon }^{0}} = \frac{{\alpha P}}{{3K}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}m{{C}_{{p~~}}}P$, где: α – коэффициент Био; m – пористость пласта; K – объемный модуль; ${{C}_{{p~~}}}$ – коэффициент объемной сжимаемости пор; ΔP – изменение порового (пластового) давления. Подставляя эти значения в формулу (17) и учитывая, что $K = \frac{{2{{\mu }}\left( {1 + {{\nu }}} \right)}}{{3\left( {1 - 2{{\nu }}} \right)}},~$ получаем окончательную формулу оценки вертикальных смещений поверхности при изменении пластового давления в разломной зоне:

Для геометрического описания разломной зоны цели предлагается, как это делается в геологических и геофизических моделях разломов, использовать вертикальную, протяженную призму как модель разломной зоны (рис. 3).

Из (17) видно, что формулу для вертикальных смещений можно представить в виде произведения двух сомножителей: $~{{U}_{3}} = $ Ph$G{{e}_{3}}$, где: Ph – это физический сомножитель, который характеризует интенсивность смещений, а $G{{e}_{3}}$ – геометрический сомножитель, описывающий морфологию распределения вертикальных смещений в пространстве в зависимости от формы включения (дисторсии).

В работе [Кузьмин, 1999] было обнаружено, что для решения (17) можно использовать гравидеформационную аналогию. Она основана на том, что геометрический сомножитель полностью совпадает с интегральной формулой для вертикального градиента потенциала гравитационного притяжения $W,z = g$:

где: $f$ – гравитационная постоянная; $\Delta \rho $ – изменение плотности. Сравнение (17) и (18) доказывает гравидеформационную аналогию. Тогда можно использовать известное решение теории потенциала для аномалии $\Delta g$ призматического объекта, имеющего аномальную плотность относительно плотности окружающих пород и расположенного на глубине от поверхности полупространства. Это решение можно найти в справочниках и учебниках по гравитационной разведке, например, в работе [Миронов, 1972].

Так, в случае плоской задачи, когда 2в $~ \to \infty $, выражение для вертикальных смещений ${{U}_{3}}$ будет иметь следующее значение:

Ввиду громоздкости формул полное аналитическое выражение для объемной задачи здесь не приводится, но оно также состоит из комбинации функций ln и arctg.

Примечательно, что формулу (19) можно применять не только для описания деформаций разломных зон, но и для моделирования смещений земной поверхности при разработке нефтегазовых пластов. Когда ширина призмы (2a) больше (намного больше) ее толщины (D–d), то это модель разрабатываемого пласта. В случае, когда ширина призмы меньше (намного меньше), чем толщина, то это модель разломной зоны. Поскольку величина объемной деформации является малой величиной, то можно использовать принцип линейной суперпозиции и получить поле смещений в случае, когда месторождение состоит из нескольких пластов. Аналогично, можно построить поле вертикальных смещений от системы разломов, расположенных в пределах одного месторождения.

В работе [Кузьмин, 1999] рассматривалась модель неоднородности, которая использовалась для оценки вертикальных смещений поверхности упругого полупространства, содержащего зону разлома, в которой объемные модули отличаются от модулей окружающей среды. В этой модели также использовалась теорема взаимности и предположение о малых (проценты и первые десятки процентов) относительных изменениях объемного модуля. Диапазон относительных изменений упругости модулей предполагался малым в той же степени, как и предположение о малых деформациях, на котором основана линейная теория упругости.

Как показывают многочисленные наблюдения, локальные оседания в зонах раздвиговых разломов происходят в обстановке квазистатического горизонтального растяжения [Кузьмин, 2014; 2018; 2018а; 2018б]. В этом случае формула для оценки вертикальных смещений в зоне раздвигового разлома выглядит следующим образом:

Здесь $\mathcal{H} = $ $\frac{{\Delta K}}{K}$. При уменьшении $\mathcal{H}$, например, земная поверхность будет оседать, т.к. и в этом случае ось Z направлена вниз и поэтому, если $\mathcal{H} < 0,~$ ${{\sigma }_{{11~}}} < 0$ (растягивающие напряжения), то ${{U}_{3}} > 0$ .

Для обобщения полученной формулы на случай пороупругой неоднородности в нее необходимо ввести пороупругие коэффициенты. Это можно сделать следующим образом. Поскольку изменение во времени объемного модуля К происходит внутри пороупругой среды разломной зоны, то этот модуль характеризует интегральную характеристику пороупругого объема. Тогда, следуя работам [Soltanzadeh et al., 2007; Segall, 2010], можно рассматривать макроскопическое изменение объемного модуля, не привлекая к рассмотрению его микроскопические характеристики. В этом случае К характеризует отношение между приложенным всесторонним эффективным напряжением (давлением) $\Delta {{P}_{{eff}}}$ и относительной объемной деформацией порового пространства $\frac{{{{\Delta }}{{V}_{p}}}}{{{{V}_{p}}}}$, где: ${{V}_{p}}$ – объем порового пространства разломной зоны. Тогда интегральный объемный модуль пороупругой среды можно обозначить ${{K}_{p}}$.

В теории пороупругих сред широко используется величина обратная ${{K}_{p}}$. Она носит название коэффициента сжимаемости порового пространства ${{C}_{p}}$ и выражается формулой (23):

Эффективное давление для горных пород с пористостью больше 5% определяется разностью между всесторонним сжатием и поровым давлением: ${{P}_{{{\text{eff}}}}}$ $ = ~{{P}_{c}}$ $ - {{P}_{p}}$, где ${{P}_{c}}$ есть всестороннее давление. Для условий верхних слоев земной коры всестороннее сжатие равно литостатическому давлению, а поровое давление эквивалентно пластовому.

Анализ формулы (23) показывает, что при снижении пластового давления коэффициент сжимаемости пор будет уменьшаться, а при повышении увеличиваться. Учитывая, что ${{K}_{p}} = \frac{1}{{{{C}_{p}}}}$, при снижении пластового давления объемный модуль будет увеличиваться, а при увеличении ${{P}_{p}}$ уменьшаться. В этом случае локальное оседание в зоне флюидонасыщенного разлома, который находится в состоянии горизонтального квазистатического растяжения, будет наблюдаться при увеличении пластового давления. Эта ситуация кардинальным образом отличается от модели разлома в виде пороупругого включения, в которой увеличение пластового давления приводит к подъему земной поверхности.

АНАЛИЗ ОБЪЕМНЫХ ДЕФОРМАЦИЙ В ЗОНЕ АШХАБАДСКОГО РАЗЛОМА

Практически все исследователи отмечают, что современная геодинамика Туркмено-Иранского сегмента Альпийского складчатого пояса формируется конвергенцией (коллизией) Туранской и Иранской плит. Северной границей области этого взаимодействия является Передовой Копетдагский (Ашхабадский) разлом. Он же является северной границей Копетдага. Копетдаг надвигается на Предгорный прогиб, и Ашхабадский разлом наклонно уходит под Копетдаг. Угол наклона в вертикальной плоскости (угол падения) этого разлома составляет примерно в среднем от 50° до 70° (угол с вертикалью, опущенной вниз – от 20° до 40°) в разных местах его пересечения. Амплитуда вертикальных смещений по разлому достигает 5–7 км. Кроме того, по Ашхабадскому разлому наблюдаются правосторонние горизонтальные смещения, достигающие величины 30 км за неотектонический этап развития [Калугин, 1977; Trifonov, 1978; Allen et al., 2008].

В этом случае, кинематика горизонтальных смещений тектонических структур Туркмено- Иранского сегмента земной коры вдоль меридионального направления должна происходить, на современном этапе, следующим образом. Северо–северо-восточное движение Аравийской плиты приводит к формированию зоны коллизии Иранской и Туранской микроплит, надвигу Копетдага на Туранскую платформу и правому сдвиговому смещению вдоль Ашхабадского разлома.

Если следовать этой схеме и предполагать полную унаследованность современных движений земной коры от прошлых геологических эпох, то существующая система геодеформационных наблюдений, развернутая в центральной части северного Копетдага и имеющая многолетнюю (более 50 лет) историю наблюдений, должна уверенно фиксировать систематический наклон предгорных участков земной поверхности на север–северо-восток по нивелирным данным и постоянное увеличение длин светодальномерных линий, пересекающих Ашхабадский разлом Копетдага под углом 45° и менее [Кузьмин, 2021а].

Однако среднегодовые относительные горизонтальные деформации в зоне Ашхабадского разлома по геодезическим данным оказались равны 2 × 10^–8 /год. Более того, если сравнивать скорости горизонтальных смещений, полученные по светодальномерным и геологическим данным, то по многолетним геодезическим наблюдениям (около 50 лет) скорость правого сдвига по Ашхабадскому разлому в 133 раза меньше, чем по данным геологии (!).

Аналогичные данные получены и по изучению вертикальных смещений земной поверхности методом высокоточного повторного нивелирования. Наблюдения проводились по системе 5 профилей, пересекающих зону Ашхабадского разлома. Длина участка разлома, в пределах которого проводились наблюдения, составляет 80 км. За период наблюдений (58 лет) средняя скорость вертикальных смещений (надвига Копетдага) по Ашхабадскому разлому Копетдага оказалась равна 0.07 мм/год. Если использовать представления о наклоне земной поверхности как горизонтальном градиенте вертикальных смещений, то средняя скорость наклона в зоне Ашхабадского разлома составляет величину 2.5 × 10^–8/год. Столь низкая скорость деформаций (10^–8/год) свидетельствует о том, что среднегодовая скорость изменения региональных напряжений крайне мала. Если полагать, что скорость деформаций линейно пропорциональна скорости приложенных напряжений, то при типичных значениях жесткости среды скорости изменения во времени региональных напряжений будут составлять величины порядка 100 Па/год. Это удивительный результат, если учесть, что оценки скоростей деформаций получены по результатам геодезических наблюдений в сейсмоактивном регионе.

Интересно сопоставить полученные скорости относительных деформаций и наклонов с таким эталонным геодинамическим процессом, как земной прилив. Для географических координат, например, Ашхабада, амплитуда деформаций лунной полусуточной волны М2, которая является доминирующей из всего спектра приливных волн, равна ≈2.3 × 10^–8 для приливных наклонов и 1.6 × 10^–8 для приливных горизонтальных деформаций, соответственно. В этом случае средняя скорость относительных деформаций в сейсмоактивном регионе будет равна или меньше 1–2 амплитуд земноприливных деформаций в год. Это означает, что зона Ирано-Туранского сегмента коллизии Аравийской и Евразийской плит находится в состоянии квазистатического (мягкого) нагружения в течение последних 50 лет. При этом, в зонах разломов неоднократно фиксировались локальные асейсмичные деформационные аномалии со скоростями 10^–5 в год и в Северном Иране [Saberi et al., 2017] и в Южном Туркменистане [Кузьмин, 2014; 2018а; 2018б; 2019].

Для более детального анализа соотношения региональных и локальных процессов в зоне Ашхабадского разлома на рис. 4 представлены результаты многолетних высокоточных нивелирных наблюдений по профилю, пересекающему разлом в районе г. Ашхабада. Профиль разбит на две секции: “блоковую”, расположенную вне зоны разлома, длиной 4 км и “разломную”, организованную непосредственно в разломной зоне и имеющую длину 0.6 км. Частота опроса составляла 1 раз в месяц. Результаты вертикальных превышений переведены в наклоны путем деления на расстояние между реперами.

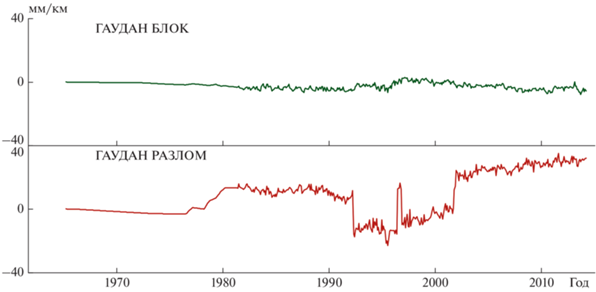
Из графика видно, что на фоне малой величины тренда имеют место знакопеременные вариации движений, которые достигают скоростей порядка 5 × 10^–7 в год для бортовой части и 10^–5 в год для зоны разлома. Отсюда следует, что локальные деформации в разломной зоне происходят в условиях квазистатической (фоновой) нагрузки. Зона разлома проявляет себя автономно, поскольку длительность аномальных периодов деформаций в блоке и разломе не совпадает.

Для исследования пространственного распределения вертикальных смещений земной поверхности на рис. 5 представлены результаты нивелирных наблюдений на этом же профиле, пересекающем Ашхабадский разлом. Расстояние между реперами здесь достигает первых сотен метров, частота измерений – 1 раз в месяц.

На рисунке видно, что в зоне разлома выявляются аномальные смещения (просадки) земной поверхности γ типа с амплитудой порядка 5 мм и шириной – 0.5–1.0 км. Это типичная морфология современной геодинамики разломов, выявленная по многочисленным геодезическим измерениям во многих регионах мира [Кузьмин, 1999; 2019]. Если просуммировать накопившиеся вертикальные смещения и оценить скорость относительных деформаций (наклона), то она будет иметь величину 6 × 10^–5 в год.

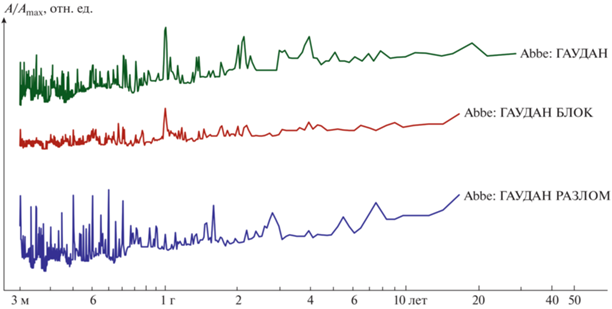
На рис. 6 показаны результаты периодограммного анализа [Кузьмин, Фаттахов, 2021] результатов нивелирования, полученных вдоль всего профиля Гаудан, вдоль блоковой секции и в пределах локальной разломной секции этого профиля. Расчет периодов проводился по специальной программе для обработки временных рядов, разработанной в ИФЗ РАН, WinABD [Дещеревский и др., 2016а; 2016б].

Для исключения “масштабного” эффекта вертикальные смещения реперов были переведены в относительные величины деформаций путем деления на длину соответствующих профилей.

Как следует из рисунка, результаты нивелирования блоковой секции и всего профиля Гаудан (14 км) показывают наличие доминирующей сезонной (годовой) компоненты в спектре вертикальных движений. Периодограмма, полученная по данным нивелирования разломной секции, кардинально отличается. В ней практически отсутствует доминирование годовой гармоники. Наиболее яркие гармоники проявляют себя в области более коротких периодов. Этот факт является дополнительным доказательством в пользу автономного проявления аномальных деформаций в зоне разлома.

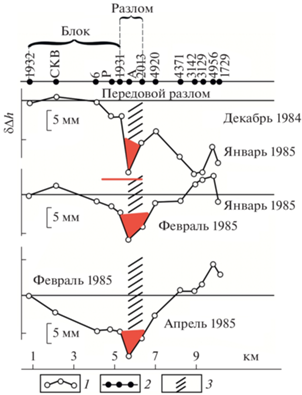
На рис. 7 представлены результаты нивелирования по блоковой и разломной секциям и данные непрерывных наклономерных наблюдений в специально оборудованном помещении, расположенном на глубине 25 м, в котором расположены наклономеры, имеющие чувствительность порядка угловой миллисекунды (5 × 10^–9).

Фактически, проведено сопоставление трех наклономеров, два из которых расположены в бортовых зонах (рис. 7а, 7б), а один – непосредственно в окрестности разломной зоны (рис. 7в). Эти данные были сопоставлены с графиком выпадения атмосферных осадков по данным метеостанции Гауда, расположенной непосредственно в Копетдаге на расстоянии около 30 км к югу от системы наблюдений [Кузьмин, 1999].

Из рис. 7 следует, что результаты нивелирных и наклономерных наблюдений, полученные в бортовых частях по разные стороны разломной зоны хорошо согласуются между собой. Их трендовые вариации незначительны и за неполные девять лет меняются в пределах 0.2–0.3 угловых секунд (порядка 10^–7/год). На фоне практического отсутствия тренда отчетливо прослеживаются годичные (термоупругие) наклоны земной поверхности. Отсюда следует, что в рассматриваемый промежуток времени (порядка 10 лет) не происходили существенные изменения регионального поля напряжений во времени, т.е. активизация во времени регионального эндогенного воздействия была минимальна.

В то же время, как следует из рис. 7в, характер деформирования земной поверхности в приразломной зоне имеет принципиальное отличие. Видно, что временной ход кривой имеет явно выраженный неоднородный характер. Амплитуды аномальных изменений достигают величин 1.5–2.0 угловых секунд (порядка 10^–5), их временная структура содержит колебания с периодами от 3–4 лет до 2–2.5 лет. Очевидно, что имеет место “собственная”, локальная динамика разломной зоны со своей временной структурой и аномально высоким уровнем деформаций.

Самое важное состоит в том, что временная структура деформационного процесса в зоне разлома сильно коррелирует с ходом выпадения атмосферных осадков (рис. 7г), который построен по данным метеостанции “Гаудан”, расположенной в горах, на расстоянии около 40 км к югу от зоны разлома. Анализ гидрогеологической обстановки показал, что областью питания приразломных, глубинных вод являются атмосферные осадки, выпадающие в горах, где и расположена метеостанция. В этом случае периодическое увеличение и уменьшение уровня выпавших осадков в горах, которые инфильтруются в зону разлома, меняет величину порового давления приразломного флюида, что может приводить к деформациям разломной зоны [Кузьмин, 2019].

Необходимо заметить, что за все время инструментальных наблюдений в пределах измерительной сети Ашхабадского геодинамического полигона, не происходили сильные землетрясения. Отдельные сейсмические события с М ≤ 6 происходили, но они не вызывали трендовых изменений в рядах наблюдений. Аномальные деформации, вызванные процессами подготовки этих землетрясений, как правило, носили локальный во времени характер. После реализации сейсмических событий временной ход деформаций восстанавливался на фоновом уровне [Кузьмин, 1999; 2021а].

Формула (17) описывает возникновение аномального смешения при изменении объемной деформации флюидонасыщенной среды разлома при изменении порового давления, обусловленного изменением уровня выпадения атмосферных осадков, а формула (22) – формирование аномальных смещений при изменении объемного модуля, обусловленного динамикой выпадения осадков, когда приложенное региональное напряжение имеет квазистатический характер. Таким образом, на качественном уровне оба механизма могут объяснить высокую корреляцию между вариациями уровня выпадения осадков и аномалиями временного хода вертикальных смещений, измеренных по данным нивелирования разломной секции.

Для определения доминирующего механизма необходимо провести сопоставление формул (17) и (22). Если принять естественное предположение, что в обоих механизмах геометрические параметры разломной зоны совпадают, то геометрические сомножители в обеих формулах идентичны. Это позволяет сравнивать долю вклада каждого из механизмов в формирование локальных смещений на разломе по соотношению физических сомножителей.

Региональное напряженное состояние верхних частей земной коры является растягивающим (по горизонтали), т.к. надвиг Копетдага на Туранскую микролиту формирует Предкопетдагский краевой прогиб, южный склон которого находится в состоянии субгоризонтального растяжения [Сидоров, Кузьмин, 1989].

Анализ результатов многолетних земноприливных наблюдений в зоне Ашхабадского разлома показал, что существуют аномальные изменения амплитуд приливных наклонов. Оценки, проведенные по методу С.М. Молоденского [Молоденский, 1983], показали, что относительные изменения объемного модуля разломной зоны $\mathcal{H}$, которые формируют аномальные изменения амплитуд приливных наклонов, могут изменяться от 1 до 3%. [Кузьмин, 1999].

Принимая для сравнительной оценки типичные значения параметров: ν = 0.25, $m$ = 0.1, ${{C}_{{p~~}}}$ = = 10^–3 1/МПа, ${{\Delta }}P$ = 100 мм водного столба (10³ Па), ${{\mu }}$ = 10⁴ МПа, ${{\sigma }_{{11~}}}$ = 100 МПА, $\mathcal{H}$ = 0.01, можно оценить величины физических сомножителей для задачи с включением (Ph_inc) и неоднородностью (Ph_het). Подставляя значения, получаем, что величина Ph_het превосходит значение Ph_inc примерно в 10³ раз.

Таким образом, доминирующим механизмом, формирующим аномальные смещения в разломной зоне под воздействием атмосферных осадков, являются флуктуации объемного модуля флюидонасыщенной среды, обусловленные вариациями уровня порового давления в разломе, то есть механизм пороупругой неоднородности.

ОБЪЕМНЫЕ ДЕФОРМАЦИИ РАЗЛОМНЫХ ЗОН ПРИ ЭКСПЛУАТАЦИИ ПОДЗЕМНОГО ХРАНИЛИЩА ГАЗА

Подземное хранилище газа (ПХГ) является тестовым объектом, для которого хорошо известна геологическая модель и амплитуда циклического нагружения. Проводя повторные геодезические наблюдения, можно определять деформационную реакцию земной поверхности от изменения пластового давления. В осенне-зимние месяцы происходит отбор газа, а в весенне-летние – закачка. Необходимость строгого контроля герметичности и объемов закачиваемого и отбираемого газа обеспечивает высокую изученность основных параметров ПХГ: геометрические размеры и конфигурация объекта, физические свойства горных пород, амплитуда циклического изменения пластового давления. Специфика эксплуатации ПХГ состоит в том, что в качестве геологического объекта используется либо водоносный пласт, либо истощенное газовое месторождение.

Это подземное хранилище организовано в истощенном пласте газового месторождения. Глубина залегания пласта около 2 км. В процессе эксплуатации газохранилища 2 раза в год производится циклическое воздействие на пласт (закачка и отбор газа). Изменение давления на глубине в период выполненных геодезических измерений составляет 0.8 МПа (отбор) до 1.1 МПа (закачка).

На рис. 8 показаны результаты повторных нивелирных наблюдений вдоль одного из профилей на Степновском подземном хранилище газа, расположенном в Европейской части России [Кузьмин, 2021б]. Нивелирные наблюдения повторяются в среднем через 0.5 года. В интервале между наблюдениями, проводимыми в период отбора газа, общий ход кривой показывает оседание в центральной части газохранилища. В период закачки газа происходит подъем земной поверхности в центральной части профиля.

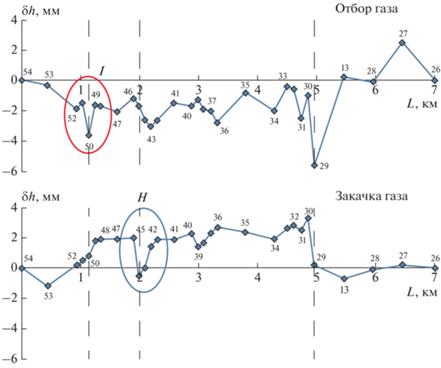
Оценка относительных деформаций вдоль всего профиля (“фоновая” компонента) показывает, что знакопеременные вертикальные смещения земной поверхности равны 1.3 × 10^–6 как в период отбора газа, так и в период закачки. Величина относительных деформаций в зонах разломов изменяется в интервале от 2 × 10^–5 до 8.7 × 10^–5. Таким образом, разломные зоны усиливают циклические деформации при эксплуатации подземного газохранилища почти в 15 раз.

Если обозначить разломы по номерам слева направо, то из рисунка видно, что локальные аномалии, приуроченные к разлому № 1 характеризуются локальным оседанием в период отбора газа и исчезают во время закачки. Разлом № 2 не проявляет себя во время отбора, но отмечается локальным оседанием в период закачки. Локальные смещения в окрестности разлома № 3 ведут себя аналогичным образом. Во время отбора отмечается оседание, а в процессе закачки вновь репер, приуроченный к разлому, оседает. Это означает, что деформационная реакция разломов на циклические нагрузки является нелинейной не только по амплитуде деформаций, но и по знаку аномальных смещений. На всех трех разломах наблюдаются локальные оседания в тот период, когда происходит либо отбор газа, либо закачка.

Результаты нивелирных наблюдений показывают, что при отборе газа происходит оседание всей территории подземного газохранилища и локальные оседания в зонах разломов. Эти процессы хорошо описываются моделью пороупругого включения (17). При закачке газа происходит общее поднятие поверхности и локальные оседания в зонах разломов. Общее поднятие соответствует модели включения, а локальные оседания в зонах разломов в этой модели невозможны. Но, применяя модель пороупругой неоднородности для разломных зон (21), можно адекватно описывать полученные результаты в случае закачки газа.

Данное подземное хранилище газа расположено в истощенном газовом месторождении. Это месторождение характеризуется антиклинальным поднятием. В этом случае верхняя половина изогнутого вверх слоя находится в обстановке субгоризонтального растяжения, а нижняя половина в состоянии сжатия. Как отмечалось выше, при повышении порового давления во флюидонасыщенной среде разломной зоны происходит увеличение коэффициента поровой сжимаемости ${{C}_{{p~~}}}$, а это приводит к снижению величины относительной эффективной жесткости ($\mathcal{H} < 0$), которое формирует локальное оседание под действием горизонтального растяжения $({{\sigma }_{{11~}}} < 0)$, вызванного активизацией изгиба. Это означает, что источники аномалий приурочены к активизированным фрагментам разломных зон, которые расположены выше нейтральной оси изгиба. Происходит формирование деформационных процессов, которые соответствуют различным моделям формирования аномальных деформаций. Например, локальное оседание в зоне первого разлома в период отбора газа соответствует модели пороупругого включения, а просадка на втором разломе в период закачки газа может быть описана моделью пороупругой неоднородности, что отмечено на рисунке.

Как следует из рисунка амплитуды обеих просадок примерно одинаковы. Их ширина также величина, соизмеримая с точностью до расстояния между реперов. Тогда если предположить, что геометрические параметры источников аномалий примерно равны, то справедливость предложенных механизмов будет достоверной, если будут примерно одинаковы и физические сомножители в формулах (17) и (21), которые являются безразмерными величинами.

Принимая для феноменологической оценки ${{\Delta }}P$ = 0.8 МПа, ${{\nu }}$ = 0.25, $m$ = 0.1, ${{C}_{{p~~}}}$ = 10^–3 1/МПа, ${{\mu }}$ = 10⁴ МПа , то физический сомножитель Ph_inc = = 0.9 × 10^–5.

Для оценки физического сомножителя Ph_het необходимо оценить $\mathcal{H}$ и ${{\sigma }_{{11~}}}$ в формуле (17). В работе [Жуков, Кузьмин, 2021] при экспериментах на образцах горных пород-коллекторов ряда газовых месторождений и подземных хранилищ газа показано, что при изменении порового давления на 1 МПа коэффициент поровой сжимаемости ${{C}_{{p~~}}}$ увеличивался, а объемный модуль ${{K}_{p}}$ уменьшался. Относительное изменение объемного модуля $\mathcal{H}$ составило величину порядка 1%.

Для оценки величины горизонтального растяжения ${{\sigma }_{{11~}}}$ можно воспользоваться теорией изгиба тонких пластин, поскольку длина изогнутого пласта намного больше, чем его толщина. Удобные формулы приведены в известной книге [Turcotte, Shubert, 2002]. Из этой теории следует, что напряжения можно приближенно оценить по формуле (24):

где: $H$ – толщина изгибаемого слоя; $L$ – горизонтальный размер подземного газового хранилища; $h$ – амплитуда антиклинального поднятия. Используя (24) и данные о геологическом строении Степновского газохранилища, можно оценить горизонтальное растяжение, которое сформировалось при антиклинальном поднятии за геологический период времени. Оказалось, что ${{\sigma }_{{11~}}} \cong $ 40 МПА. Подставляя эти значения в формулу (17), можно оценить, что Ph_inc = 1.2 × 10^–5.

Таким образом комбинируя модели пороупругого включения и пороупругой неоднородности можно анализировать весь спектр наблюдаемых вертикальных движений земной поверхности.

ЗАКЛЮЧЕНИЕ

Проведенные исследования показали, что локальные деформации земной поверхности формируются не во всей толще разломной зоны, а сосредоточены в ограниченных по размеру активизированных фрагментах. Локальные симметричные оседания и поднятия земной поверхности носят явно не сдвиговый характер, если сдвиговые перемещения понимать в механическом, а не в геологическом смысле.

Разработанные представления о пороупругих включениях и неоднородностях как источниках локальных смещений земной поверхности, доведенные до уровня количественных моделей, позволили провести селекцию механизмов формирования аномальных деформаций в зоне Ашхабадского разлома и определить в качестве доминирующей модели задачу о пороупругой неоднородности прямоугольной формы как модельном аналоге активизированного фрагмента разломной зоны.

Анализ пространственного распределения деформаций земной поверхности на подземном хранилище газа показал, что локальные оседания в зонах разломов возникают как на стадии отбора, так и в период закачки газа. Установлено, что в первом случае аномальные оседания формируются по модели пороупругого включения, а во втором – по модели пороупругой неоднородности. Это означает, что локальные оседания в зоне разлома в период отбора газа линейно связаны с изменением пластового давления.

Формирование аномальных просадок во время закачки газа нелинейно связано с изменением пластового давление. Это является ярким примером индуцированных деформаций разломных зон, когда вариации во времени пороупругих параметров внутри разломной зоны в обстановке внешних квазистатических нагрузок формируют локальное возмущение напряженно-деформированного состояния в окрестности разлома.

Предложенные количественные модели во многом носят феноменологический характер. К сожалению, детальных данных о внутреннем строении разломных зон явно недостаточно для разработки более сложных моделей, учитывающих микроскопические характеристики разломов. По мнению автора, в такой ситуации следует придерживаться строгого соответствия степени детализации модели уровню и качеству эмпирического материала. Усложнение моделей будет осуществляться по мере детализации и увеличения объема эмпирических данных.