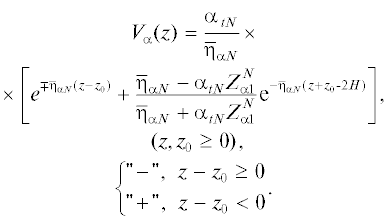Физика Земли, 2022, № 6, стр. 192-204
О расчете фундаментального аффинора Грина для поля в слоистой среде с одноосной электрической и магнитной анизотропией на основе метода В.И. Дмитриева
С. С. Кеоркянц *
Центр геоэлектромагнитных мсследований, филиал Института физики Земли им. О.Ю. Шмидта РАН
г. Троицк, Россия
* E-mail: sourens@mail.ru
Поступила в редакцию 01.10.2021
После доработки 09.03.2022
Принята к публикации 11.03.2022
- EDN: MJOKGQ
- DOI: 10.31857/S0002333722060059
Аннотация
Работа касается проблемы расчетов электромагнитных полей в плоскослоистых средах с одноосной анизотропией электрических и магнитных параметров. Введено понятие фундаментальных аффиноров Грина (ФАГ) электрического (${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }^{{\text{э}}}}$) и магнитного (${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }^{{\text{м}}}}$) типов, вытекающее из определения одноименных векторных потенциалов ${{A}^{{\text{э}}}}$ и ${{A}^{{\text{м}}}}$, и дана их оригинальная трактовка, согласно которой все элементы аффиноров ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }^{{\text{э}}}}$ и ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }^{{\text{м}}}}$ выражены в линейной или линейно-операторной форме через две функции ${{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}$ и ${{g}_{\mu }}$ – фундаментальные решения уравнений типа Гельмгольца с операторами ${{L}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}$ и ${{L}_{\mu }}$, представляющие преобразования Ханкеля (ПХ) 0-го порядка. Прообразы этих ПХ могут быть определены из решения одной общей граничной задачи для спектральной функции (СФ), осуществляемого переходом от исходного линейного дифференциального уравнения 2-го порядка для СФ к уравнению Риккати для связанного с ней спектрального импеданса (СИМ). Сформулированы и реализованы общая стратегия и этапы решения поставленной задачи и приведены окончательные выражения СИМ и СФ для всех возможных случаев расположения точек истока и наблюдения относительно друг друга и границ раздела слоев. Результаты данной работы могут быть использованы для расчетов электромагнитных полей от произвольных электрических и магнитных токов в моделях одноосно анизотропных сред с произвольным количеством слоев и в таких же моделях при наличии в них неоднородностей (с помощью метода интегральных уравнений); при изучении полей в градиентных анизотропных средах путем приближения электромагнитных параметров модели кусочно-постоянными функциями; для изучения эффекта анизотропии тонкослоистых сред при отсутствии анизотропии в каждом отдельном слое.
ВВЕДЕНИЕ
В геофизических исследованиях земной коры широкий интерес представляют задачи изучения электромагнитных полей в моделях слоистых (одномерно неоднородных) сред, включающих локальные неоднородности, то есть тела произвольной формы и размеров, инородные по физическим свойствам относительно вмещающей их среды. Слоистую среду, из которой исключены локальные неоднородности, называют фоновой (background) моделью или моделью - вмещающей среды. Одним из наиболее широко применяемых методов решения прямой задачи электрометрии для описанного выше класса моделей является метод интегральных уравнений (ИУ). Первым и весьма важным этапом при реализации метода ИУ является расчет функции Грина. Для фоновой модели, представляющей плоскослоистую среду, она является аффинором, скалярные элементы которого, как известно, могут быть выражены в виде преобразований Ханкеля 0-го и 1-го порядков либо двойного преобразования Фурье.
Общие основы для расчетов электромагнитных полей гармонического возбуждения в моделях изотропных плоскослоистых сред, включающих неоднородности, с применением методов объемных и граничных ИУ были заложены и развиты в работах В.И. Дмитриева, Е.В. Захарова [Дмитриев, 1969; Захаров, Ильин, 1970; Дмитриев, Захаров, 1987; и др.]. В первой из перечисленных работ [Дмитриев, 1969] было дано определение тензорных функций Грина (ТФГ) электрического и магнитного типов как аффиноров, позволяющих выразить векторные потенциалы, соответственно, электрического или магнитного типов, описывающие поля, порожденные произвольными, одноименными с ними по типу (электрическими или магнитными) объемными токами. Токи распределены в ограниченном объеме плоскослоистой по электромагнитным характеристикам среды. Данные аффиноры можно условно назвать “фундаментальными” аффинорами Грина (ФАГ), соответственно, электрического и магнитного типов, что позволяет отличить их от общепринятого определения аффиноров Грина (АГ), напрямую выражающих полные векторы напряженностей электрического и магнитного полей произвольных источников в виде свертки АГ с вектором плотности электрического или магнитного тока [Фелсен, Мркувиц, 1978; Singer и др., 1997; Avdeev и др., 1997].
Для расчетов скалярных элементов ФАГ, представленных в виде преобразований Ханкеля (ПХ) 0-го и 1-го порядков в работе [Дмитриев, 1969] предложен оригинальный метод аналитического определения прообразов указанных преобразований. Суть метода заключается в представлении прообраза (оригинала) ПХ, который условимся называть спектральной функцией, через вспомогательную функцию (спектральный импеданс), удовлетворяющую дифференциальному уравнению Риккати.
Большой интерес для решения прямых и обратных задач электрометрии представляют модели слоистых анизотропных сред, включающих локальные неоднородности, среди которых наиболее важным частным типом являются модели, где вмещающая плоскослоистая среда является одноосно анизотропной.
Изучению общих свойств элементов ФАГ в средах, одномерно неоднородных в упомянутом выше смысле и одноосно анизотропных (с главной осью $z$), была посвящена работа [Кеворкянц, 2000]. В работе [Кеворкянц, 2007] было дано определение объемных и граничных интегральных уравнений второго рода для модели слоистой одноосно анизотропной среды (модели СОАС), содержащей локальные неоднородности. Логическим завершением упомянутых работ могло бы явиться изложение алгоритма для явных представлений в виде ПХ элементов ФАГ в моделях СОАС с произвольным количеством слоев. Именно решению данной проблемы посвящена настоящая работа. Ниже на основе определения ФАГ, данного в работе [Кеворкянц, 2000], и общей стратегии расчета оригинала ПХ через спектральный импеданс, изложенной в работе [Дмитриев, 1969], дается описание основанного на ней алгоритма расчета элементов ФАГ СОАС с четким логическим обоснованием каждого этапа его реализации. Решение уравнения Риккати для каждого слоя и применение рекуррентных соотношений позволяют, удовлетворяя всем граничным условиям и условиям на бесконечности, определить спектральный импеданс (СИМ), а затем и спектральную функцию в любой точке рассматриваемой модели.
ОБЩЕЕ ОПИСАНИЕ ПОСТАНОВКИ И СТРАТЕГИИ РЕШЕНИЯ ЗАДАЧИ
В качестве модели СОАС для общности будем рассматривать среду с одноосной анизотропией электрических и магнитных параметров, при которой главная ось анизотропии совмещена с осью $z$ системы координат $(x,\,y,\,z)$. Параметры среды, представляющие диагональные тензоры (аффиноры), элементы которых, в общем, кусочно-непрерывные функции от координаты $z$ (градиентная среда), запишем в виде:
(1)
$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } } (z) = \{ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}(z),{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}(z),{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{n}}(z)\} , \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mu } (z) = \{ {{\mu }_{t}}(z),{{\mu }_{t}}(z),{{\mu }_{n}}(z)\} \\ \end{gathered} $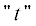 и
и 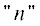 обозначают, соответственно, величины параметров вдоль плоскостей $z = {\text{const}}$ простирания слоев и по нормали к ним.
обозначают, соответственно, величины параметров вдоль плоскостей $z = {\text{const}}$ простирания слоев и по нормали к ним.
Для векторов напряженностей электрического и магнитного полей в СОАС первые два уравнения Максвелла запишутся в виде:
(2)
$rot{\mathbf{H}} = - i\omega \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }{\mathbf{E}} + {\mathbf{J}}_{{{\text{ст}}}}^{{\text{э}}},\,\,\,\,rot{\kern 1pt} {\mathbf{E}} = {\kern 1pt} i\omega \hat {\mu }{\mathbf{H}},$(3)
$\hat {\mu }{\kern 1pt} {\mathbf{H}}\,\,{\text{ = }}rot{\kern 1pt} {{{\mathbf{A}}}^{{\text{э}}}},\,\,\,\,\hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }{\mathbf{E}} = rot{{{\mathbf{A}}}^{{\text{м}}}} + \frac{1}{{i\omega }}{\mathbf{J}}_{{{\text{ст}}}}^{{\text{э}}},$(4)
$\begin{gathered} {\text{ }}rot{\kern 1pt} {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mu } }}^{{ - 1}}}rot{\kern 1pt} {{{\mathbf{A}}}^{{\text{э}}}} - \\ - \,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } } {\kern 1pt} grad\frac{1}{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}}}div({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\nu } }}^{{\text{э}}}}{{{\mathbf{A}}}^{{\text{э}}}}) - {{\omega }^{2}}\hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }{{{\mathbf{A}}}^{{\text{э}}}} = {\mathbf{J}}_{{{\text{ст}}}}^{{\text{э}}}, \\ rot{{{\hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}^{{ - 1}}}rot{{{\mathbf{A}}}^{{\text{м}}}} - \\ - \,\,\hat {\mu }grad\frac{1}{{{{\mu }_{t}}}}div({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\nu } }}^{{\text{м}}}}{{{\mathbf{A}}}^{{\text{м}}}}) - {{\omega }^{2}}\hat {\mu }{{{\mathbf{A}}}^{{\text{м}}}} = {\mathbf{J}}_{{{\text{ст}}}}^{{\text{м}}}, \\ \end{gathered} $Векторы-потенциалы электрического и магнитного типов из (2)–(4) могут быть представлены в виде объемных интегралов от правого скалярного произведения одноименных по типу фундаментального аффинора Грина (ФАГ) и вектора плотности стороннего тока по аналогии с выражениями, приведенными в работе [Дмитриев, 1969]:
(5)
${\mathbf{A}}_{{\text{н}}}^{{{\text{э,м}}}}(P) = \frac{1}{{4\pi }}\int\limits_{{{V}_{0}}} {{{{\hat {G}}}^{{{\text{э,м}}}}}(P,{{P}_{0}}){\mathbf{J}}_{{{\text{ст}}}}^{{{\text{э,м}}}}({{P}_{0}})d{{v}_{{{{P}_{0}}}}}} ,$(6)
${{\hat {G}}^{{{\text{э,м}}}}}(P,{{P}_{0}}) = \left\{ {\begin{array}{*{20}{c}} {g_{t}^{{{\text{э,м}}}}}&0&0 \\ 0&{g_{t}^{{{\text{э,м}}}}}&0 \\ {{{\nabla }_{x}}g_{z}^{{{\text{э,м}}}}}&{{{\nabla }_{y}}g_{z}^{{{\text{э,м}}}}}&{g_{n}^{{{\text{э,м}}}}} \end{array}} \right\},$(7)
${\mathbf{J}}_{{{\text{ст}}}}^{{{\text{э,м}}}}(P,{{P}_{0}}) = \int\limits_{{{V}_{0}}} {\delta (P,{{P}_{0}}){\mathbf{J}}_{{{\text{ст}}}}^{{{\text{э,м}}}}({{P}_{0}})d{{v}_{{{{P}_{0}}}}}} ,$(8a)
$\begin{gathered} \frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{n}}({{z}_{0}})}}{{{{\mu }_{t}}(z)}}g_{n}^{{\text{э}}} \equiv g_{t}^{{\text{м}}} \equiv {{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}(P,{{P}_{{{\kern 1pt} 0}}}), \\ \frac{{{{\mu }_{n}}({{z}_{0}})}}{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}(z)}}g_{n}^{{\text{м}}} \equiv g_{t}^{{\text{э}}} \equiv {{g}_{\mu }}(P,{{P}_{{{\kern 1pt} 0}}}), \\ \end{gathered} $(8b)
$\begin{gathered} {{\Delta }_{t}}g_{z}^{{\text{э}}} = \frac{\partial }{{\partial z}}{{g}_{\mu }} + \frac{{{{\mu }_{t}}{\text{(}}z{\text{)}}}}{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}{\text{(}}{{z}_{0}}{\text{)}}}}\frac{\partial }{{\partial {{z}_{0}}}}{{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}, \hfill \\ {{\Delta }_{t}}g_{z}^{{\text{м}}} = \frac{\partial }{{\partial z}}{{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}} + \frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}{\text{(}}z{\text{)}}}}{{{{\mu }_{t}}{\text{(}}{{z}_{0}}{\text{)}}}}\frac{\partial }{{\partial {{z}_{0}}}}{{g}_{\mu }} \hfill \\ \end{gathered} $(9a)
$\begin{gathered} {{L}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}{{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}} = - 4\pi \delta (P,{{P}_{{{\kern 1pt} 0}}}){{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{n}}({{z}_{0}}), \\ \left[ {{{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}} \right] = \left[ {\frac{1}{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}}}\frac{{\partial {{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}}}{{\partial z}}} \right] = 0, \\ \end{gathered} $(9b)
$\begin{gathered} {{L}_{\mu }}{{g}_{\mu }} = - 4\pi \delta {\kern 1pt} {\kern 1pt} (P,{{P}_{0}}){\kern 1pt} {\kern 1pt} {{\mu }_{n}}({{z}_{0}}), \\ \left[ {{{g}_{\mu }}} \right] = \left[ {\frac{1}{{{{\mu }_{t}}}}\frac{{\partial {{g}_{\mu }}}}{{\partial z}}} \right] = 0, \\ \end{gathered} $(10)
$\begin{gathered} {{L}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}} = {{\Delta }_{t}} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{n}}\frac{\partial }{{\partial {\kern 1pt} z}}\frac{1}{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}}}\frac{\partial }{{\partial z}} + \omega {{{\kern 1pt} }^{2}}{{\mu }_{t}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{n}}, \\ {{L}_{\mu }} = {{\Delta }_{t}} + {{\mu }_{n}}\frac{\partial }{{\partial {\kern 1pt} z}}\frac{1}{{{{\mu }_{t}}}}\frac{\partial }{{\partial z}} + \omega {{{\kern 1pt} }^{2}}{{\mu }_{n}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}} \\ \end{gathered} $Функции ${{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}$ и ${{g}_{\mu }}$ имеют следующее представление в виде ПХ 0-го порядка:
(11)
${{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } ,\mu }}}(P,{{P}_{{{\kern 1pt} 0}}}) = \int\limits_0^\infty {{{J}_{0}}} (\lambda r){{V}_{{{\kern 1pt} \varepsilon ,\mu }}}(\lambda ,z,{\text{ }}{{z}_{0}})\lambda d\lambda ,$(12)
$\begin{gathered} {{\alpha }_{n}}(z)\frac{d}{{dz}}\frac{1}{{{{\alpha }_{t}}(z)}}\frac{{d{{V}_{\alpha }}}}{{dz}} - \eta _{\alpha }^{2}(z){{V}_{\alpha }} = 0, \\ {\text{a}})\left[ V \right] = 0,\,\,\,\,\left[ {\frac{1}{{{{\alpha }_{t}}(z)}}\frac{{d{{V}_{\alpha }}}}{{dz}}} \right] = \left\{ {\begin{array}{*{20}{c}} { - 2}&{(z = {{z}_{0}})} \\ 0&{(z \ne {{z}_{0}})} \end{array}} \right.; \\ {\text{b}})\,\,\mathop {\lim }\limits_{\left| {z - {{z}_{0}}} \right| \to \infty } {{V}_{\alpha }} = 0, \\ \end{gathered} $(13)
$\begin{gathered} {{\eta }_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}(z) = \sqrt {{{\lambda }^{2}} - {{\omega }^{2}}{{\mu }_{t}}(z){{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{n}}(z)} , \\ {{\eta }_{\mu }}(z) = \sqrt {{{\lambda }^{2}} - {{\omega }^{2}}{{\mu }_{n}}(z){{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}(z)} {\kern 1pt} ;\;\,\,\operatorname{R} {{\eta }_{\alpha }}(z) > 0. \\ \end{gathered} $Краевые условия (12) обеспечивают ограниченность ${{V}_{{{\kern 1pt} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } ,\mu }}}(\lambda ,z,{\text{ }}{{z}_{0}})$ для всех $\lambda \in ( - \infty ,\infty )$ и удовлетворение условий на бесконечности для функций ${{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}(r,z,{{z}_{0}})$ и ${{g}_{\mu }}(r,z,{{z}_{0}})$.
Для функций $g_{z}^{{\text{э}}}$ и $g_{z}^{{\text{м}}}$ согласно соотношениям (8b) и (11) следуют представления:
(14)
$\begin{gathered} {{\nabla }_{r}}g_{z}^{{\text{э}}}(M,{{M}_{0}}) = - \int\limits_0^\infty {{{J}_{1}}(\lambda r)} \times \\ \times \,\,{\kern 1pt} \left[ {\frac{d}{{dz}}{{V}_{\mu }}(\lambda ,z,{{z}_{0}}) + \frac{{{{\mu }_{t}}(z)}}{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}({{z}_{0}})}}\frac{d}{{d{{z}_{0}}}}{{V}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}(\lambda ,z,{{z}_{0}})} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} d\lambda , \\ {{\nabla }_{r}}g_{z}^{{\text{м}}}(M,{{M}_{0}}) = - \int\limits_0^\infty {{{J}_{1}}(\lambda r)} {\kern 1pt} \times \\ \times \,\,\left[ {\frac{d}{{dz}}{{V}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}(\lambda ,z,{{z}_{0}}) + \frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}}(z)}}{{{{\mu }_{t}}({{z}_{0}})}}\frac{d}{{d{{z}_{0}}}}{{V}_{\mu }}(\lambda ,z,{{z}_{0}})} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} d\lambda , \\ \end{gathered} $(15)
${{\nabla }_{\xi }}g_{z}^{{{\text{э,м}}}}(M,{{M}_{0}}) = \frac{{\xi - {{\xi }_{0}}}}{r}{{\nabla }_{r}}g_{z}^{{{\text{э,м}}}}(M,{{M}_{0}})\,\,(\xi = x,y).$Учитывая, что все элементы ФАГ (6) обоих типов могут быть выражены через оригиналы ${{V}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}$ и ${{V}_{\mu }}$ функций, соответственно, ${{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}$ и ${{g}_{\mu }}$ (как ПХ 0-го и 1-го порядков), последние можно назвать фундаментальной парой (${{g}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}}$, ${{g}_{\mu }}$) скалярных функций, представляющих решение уравнений типа Гельмгольца и граничных условий соответственно (9a) и (9b).
Известным методом решения задачи (12) является замена искомого решения новой функцией, представляющей собой решение уравнения Риккати [Дмитриев, 1969]. В случае слоисто-анизотропной задачи (12) эта функция представляется в виде выражения:
(16)
$\begin{gathered} {{Z}_{\alpha }}(\lambda ,z,{{z}_{0}}) = \frac{1}{{{{\alpha }_{t}}(z){{V}_{\alpha }}(\lambda ,z,{{z}_{0}})}} \times \\ \times \,\,\frac{{d{{V}_{\alpha }}(\lambda ,z,{{z}_{0}})}}{{dz}}({{\alpha }_{t}} = {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }}_{t}},{{\mu }_{t}}) \\ \end{gathered} $Для удобства дальнейшего изложения, принимая во внимание, что правая часть (16) содержит в числителе производную спектральной функции по $z$, а в знаменателе – ее произведение на параметр среды ${{\alpha }_{t}}$, применим далее к величине ${{Z}_{\alpha }}{\text{(}}\lambda ,z{\text{)}}$, по аналогии с работой [Avdeev et al., 1997], термин “спектральный импеданс” или СИМ.
Из граничной задачи (12) и соотношения (16) следуют уравнение Риккати для спектрального импеданса ${{Z}_{\alpha }}(z)$ как функции переменной $z$:
(17)
$\frac{d}{{dz}}{{Z}_{\alpha }}(z) + {{\alpha }_{t}}(z)Z_{\alpha }^{2}(z) = \frac{{\eta _{\alpha }^{2}(z)}}{{{{\alpha }_{n}}(z)}} = \frac{{\bar {\eta }_{\alpha }^{2}(z)}}{{{{\alpha }_{t}}(z)}},$(18)
$\begin{gathered} {{Z}_{\alpha }}(z + 0) - {{Z}_{\alpha }}(z - 0) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(z \ne {{z}_{0}}), \hfill \\ {{Z}_{\alpha }}({{z}_{0}} + 0) - {{Z}_{\alpha }}({{z}_{0}} - 0) = {{ - 2} \mathord{\left/ {\vphantom {{ - 2} {{{V}_{\alpha }}({{z}_{0}}){\text{ }}}}} \right. \kern-0em} {{{V}_{\alpha }}({{z}_{0}}){\text{ }}}}\,\,\,\,(z = {{z}_{0}}){\kern 1pt} . \hfill \\ \end{gathered} $Во всех приведенных выше соотношениях от (1) до (18) предполагалось, что рассматриваемая модель одноосно анизотропной среды является градиентной, для которой решение задач (12) и (17)–(18) ввиду достаточной своей сложности требует отдельного изучения. В данной работе ниже изложим решение задач (12) и (17)–(18) для модели, электрические и магнитные параметры которой представляют кусочно-постоянные функции $z$. Эту модель далее и будем подразумевать под термином “слоисто-анизотропная”.
В рассматриваемой модели слоисто-анизотропной среды, диэлектрическая и магнитная проницаемости, соответственно, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }_{{t,\,n}}}(z)$ и ${{\mu }_{{t,\,n}}}(z)$ являются константами на интервалах $( - \infty ,{{z}_{1}}]$, $[{{z}_{1}},{{z}_{2}}]$, …, $[{{z}_{{N - 1}}},{{z}_{N}}]$, $[{{z}_{N}},\infty )$ оси $z$, где ${{z}_{1}} < {{z}_{2}} < ... < {{z}_{N}}$ – фиксированные точки на ней, причем, следуя работе [Дмитриев, 1969], принимаем ${{z}_{1}} = 0$. В такой модели, где области $z \leqslant {{z}_{1}} - 0$ и $z \geqslant {{z}_{N}} + 0$ будем считать, соответственно, верхним и нижним полупространствами, интервал $[{{z}_{1}},{{z}_{N}}]$ заполнен слоистой пачкой общей мощностью $H = {{z}_{N}}$, в которой мощность $l$-го слоя равна ${{h}_{l}} = {{z}_{{l + 1}}} - {{z}_{l}}$ ($1 \leqslant l \leqslant N - 1$). Параметры (${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }_{{t,\,n}}}$ и ${{\mu }_{{t,\,n}}}$) верхнего, нижнего полупространств и $l$-го слоя будут обозначены, соответственно, индексами “0”,”N” и “$l$” ($l = 1,2, \ldots ,N - 1$).
Введя следующие обозначения для спектрального импеданса как функции от $z$:
(19)
$\begin{gathered} {{Z}_{{\alpha 1}}}(z) = {{Z}_{\alpha }}(z)\,\,\,\,(z \leqslant {{z}_{0}} - 0), \\ {{Z}_{{\alpha 2}}}(z) = {{Z}_{\alpha }}(z)\,\,\,\,(z \geqslant {{z}_{0}} + 0), \\ \end{gathered} $(20)
$\begin{gathered} {{V}_{\alpha }}({{z}_{0}}) = \frac{{ - 2}}{{{{Z}_{\alpha }}({{z}_{0}} + 0) - {{Z}_{\alpha }}({{z}_{0}} - 0)}} = \\ = \frac{{ - 2}}{{{{Z}_{\alpha }}_{2}({{z}_{0}}) - {{Z}_{{\alpha 1}}}({{z}_{0}})}}. \\ \end{gathered} $Поскольку в рассматриваемой нами модели параметры ${{\alpha }_{t}}$ и ${{\bar {\eta }}_{\alpha }}$ в каждом из упомянутых выше фиксированных интервалов являются по переменной $z$ константами, то уравнение (17), опустив временно порядковый индекс интервала (слоя), запишем в виде:
(21)
$\frac{d}{{dz}}\left( {\ln \frac{{{{\alpha }_{t}}{{Z}_{\alpha }}(z) + {{\Lambda }_{\alpha }}{{\eta }_{\alpha }}}}{{{{\alpha }_{t}}{{Z}_{\alpha }}(z) - {{\Lambda }_{\alpha }}{{\eta }_{\alpha }}}}} \right)dz = 2{{\bar {\eta }}_{\alpha }}dz,$(22)
${{d{{Z}_{\alpha }}(z)} \mathord{\left/ {\vphantom {{d{{Z}_{\alpha }}(z)} {dz}}} \right. \kern-0em} {dz}} = 0,\,\,\,\,\left| z \right| \to \infty .$Из соотношения (21), где далее выполним замену $z$ на символ $\zeta $, обозначающий переменную интегрирования, можно получить решение уравнения (17), проинтегрировав обе стороны (21) по $\zeta $ на отрезке $[{{z}_{{st}}},\,z]$, где ${{z}_{{st}}}$ представляет собой точку ${{z}_{0}}$ или одну из граничных точек интервала $[{{z}_{i}},{{z}_{{i + 1}}}]$, в которой известна величина ${{Z}_{\alpha }}({{z}_{{st}}})$.
Для функции ${{Z}_{\alpha }}(z)$ ниже выделены следующие отрезки, на каждом из которых решается уравнение (21) с учетом определения (19), которое запишем в виде:
(23)
$\begin{gathered} {{Z}_{\alpha }}(\zeta ) = \left\{ \begin{gathered} {{Z}_{{\alpha 1}}}(\zeta )\,\,\,\,(\zeta {\text{ }} \leqslant {{z}_{0}} - 0)\,\,\,\,\zeta \in [{{z}_{0}} - 0,{{z}_{j}}],[{{z}_{j}},{{z}_{{j - 1}}}],{\text{ }}.{\text{ }}.{\text{ }}.{\text{ }},{\text{ }}[{{z}_{{i + 2}}},{{z}_{{i + 1}}}],[{{z}_{{i + 1}}},z] \hfill \\ {{Z}_{{\alpha 2}}}(\zeta )\,\,\,\,(\zeta {\text{ }} \geqslant {{z}_{0}} + 0)\,\,\,\,\zeta \in [{{z}_{0}} + 0,{{z}_{{j + 1}}}],[{{z}_{{j + 1}}},{{z}_{{j + 2}}}],{\text{ }}.{\text{ }}.{\text{ }}.{\text{ }},{\text{ }}[{{z}_{{i - 1}}},{{z}_{i}}],[{{z}_{i}},z] \hfill \\ \end{gathered} \right.. \\ {{z}_{0}} \in [{{z}_{j}},{{z}_{{j + 1}}}],\,\,z \in [{{z}_{i}},{{z}_{{i + 1}}}]. \\ \end{gathered} $ОПРЕДЕЛЕНИЕ СПЕКТРАЛЬНОГО ИМПЕДАНСА
С алгоритмической точки зрения можно выделить следующие три случая расположения точки ${{z}_{0}}$ (на оси ординаты $z$) относительно границ полупространств: 1) z0 ≤ 0; 2) z0 ≥ H; 3) 0 ≤ z0 ≤ H. Все три случая предполагают выполнение следующих трех этапов:
1) определение выражения спектрального импеданса (СИМ) в каждом из полупространств, не содержащих точку ${{z}_{0}}$, с учетом соотношения (16), в котором, как показано ниже, ${{V_{\alpha }^{{ - 1}}d{{V}_{\alpha }}} \mathord{\left/ {\vphantom {{V_{\alpha }^{{ - 1}}d{{V}_{\alpha }}} {dz}}} \right. \kern-0em} {dz}}$ является известной константой; 2) определение выражений СИМ на границах раздела слоев с помощью рекурсивных процедур; 3) получение выражений СИМ в произвольной точке $z$ и в точке $z = {{z}_{0}}$. Заметим, что общей особенностью первых двух случаев расположения точки ${{z}_{0}}$ является возможность представления решения задачи (12) в виде выражений следующего вида:
(24)
$\begin{gathered} {{V}_{\alpha }}(z) = \frac{{{{\alpha }_{{t{\kern 1pt} \nu }}}}}{{{{{\bar {\eta }}}_{{\alpha \nu }}}}}{\kern 1pt} \,\left[ {{{{\text{e}}}^{{ - {\text{sign}}(z - {{z}_{0}}){{{\bar {\eta }}}_{{\alpha \nu }}}(z - {{z}_{0}})}}} + {{R}_{{\alpha \nu }}}{{e}^{{{{{\bar {\eta }}}_{{\alpha \nu }}}(z + {{z}_{0}} - 2{{d}_{\nu }})}}}} \right], \\ \nu = \left\{ \begin{gathered} 0\,\,(z,{{z}_{0}} - 0 \leqslant 0) \hfill \\ N\,\,(z,{{z}_{0}} + 0 \geqslant H) \hfill \\ \end{gathered} \right.,\,\,\,\,{{d}_{0}} = {{z}_{1}} = 0, \\ {{d}_{N}} = {{z}_{N}} = H), \\ \end{gathered} $Ниже изложим по отдельности алгоритмы определения СИМ для каждого из трех случаев, выделяя их общие черты и частные особенности. В каждом из упомянутых случаев поочередно рассматриваются три варианта расположения $z$-координаты точки наблюдения $P(x,y,z)$ относительно границ слоистой пачки, а именно: $z \geqslant H,\,\,0 \leqslant z \leqslant H,\,\,z \leqslant 0$.
Случай I: ${{z}_{0}} < 0$ (то есть ${{z}_{0}} < {{z}_{{j + 1}}} = 0$, при $j = 0$).
Область $z \geqslant H$. Спектральную функцию и СИМ в данном случае, учитывая соотношения (16), (19), удовлетворяя условиям на бесконечности (12b) и (21), запишем в виде:
(25)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}{\text{(}}H{\text{)}}{{e}^{{ - {{\Lambda }_{{\alpha N}}}{\kern 1pt} {{\eta }_{{\alpha N}}}(z - H)}}}, \\ {{Z}_{\alpha }}(z) = - \frac{{{{{\bar {\eta }}}_{{\alpha N}}}}}{{{{\alpha }_{{t{\kern 1pt} N}}}}} = {{Z}_{{\alpha 2}}}(z)\,\,\,\,z \in [H,\infty ). \\ \end{gathered} $Второе из выражений (25), при учете условия непрерывности функции ${{{\text{Z}}}_{\alpha }}(z)$ на границах раздела слоев, приводит к следующему краевому условию для СИМ при $z = H$:
Область $0 \leqslant z \leqslant H$. Выполнив интегрирование уравнения (21) по участку $[{{z}_{{i + 1}}},\;z]$ интервала $[{{z}_{i}},\;{{z}_{{i + 1}}}]$, включающего точку $z$, получаем:
Потенцирование левой и правой частей второго равенства в последнем выражении приводит к соотношению
(26)
$\begin{gathered} {{Z}_{\alpha }}(z) = {{Z}_{{\alpha 2}}}(z) = \frac{{{{{\bar {\eta }}}_{{\alpha i}}}}}{{{{\alpha }_{{t{\kern 1pt} i}}}}} \times \\ \times \,\,\frac{{({{{\bar {\eta }}}_{{\alpha i}}} + {{\alpha }_{{t{\kern 1pt} i}}}Z_{{\alpha 2}}^{{i + 1}}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha {\kern 1pt} i}}}(z - {{z}_{{{\kern 1pt} i + 1}}})}}} - ({{{\bar {\eta }}}_{{\alpha i}}} - {{\alpha }_{{t{\kern 1pt} i}}}Z_{{\alpha 2}}^{{i + 1}})}}{{({{{\bar {\eta }}}_{{\alpha i}}} + {{\alpha }_{{t{\kern 1pt} i}}}Z_{{\alpha 2}}^{{i + 1}}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha {\kern 1pt} i}}}(z - {{z}_{{i + 1}}})}}} + ({{{\bar {\eta }}}_{{\alpha i}}} - {{\alpha }_{{t{\kern 1pt} i}}}Z_{{\alpha 2}}^{{i + 1}})}} \\ ({\text{ }}i{\text{ }} = 1,2, \ldots ,N - 2,N - 1{\text{ }}), \\ \end{gathered} $(27)
$\begin{gathered} Z_{{\alpha 2}}^{l} = {{Z}_{{\alpha 2}}}({{z}_{l}}) = \frac{{{{{\bar {\eta }}}_{{\alpha l}}}}}{{{{\alpha }_{{t{\kern 1pt} l}}}}} \times \\ \times \,\,\frac{{({{{\bar {\eta }}}_{{\alpha l}}} + {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 2}}^{{l + 1}}){{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}}}} - ({{{\bar {\eta }}}_{{\alpha l}}} - {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 2}}^{{l + 1}})}}{{({{{\bar {\eta }}}_{{\alpha l}}} + {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 2}}^{{l + 1}}){{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}}}} + ({{{\bar {\eta }}}_{{\alpha l}}} - {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 2}}^{{l + 1}})}} \\ (l = N - 1,N - 2, \ldots ,2,1;\,\,\,\,{{h}_{l}} = {{z}_{{l + 1}}} - {{z}_{l}}{\text{ }}), \\ \end{gathered} $Область $z \leqslant 0$. Рассмотрим отдельно два интервала $z \in ( - \infty ,\;{{z}_{0}}]$ и $z \in [{{z}_{0}},0]$. Для первого интервала, подставляя выражение (24) для функции ${{V}_{\alpha }}{\text{(}}z{\text{)}}$при $\nu = 0$ и $z \leqslant {{z}_{0}} - 0$ в правую часть (16), получим выражение СИМ и его первой краевой величины в точке $z = {{z}_{0}}$:
(28)
$\begin{gathered} {{Z}_{{\alpha 1}}}(z) = {{Z}_{\alpha }}(z - 0) = {{Z}_{{\alpha 1}}}({{z}_{0}}) = \frac{{{{{\bar {\eta }}}_{{\alpha 0}}}}}{{{{\alpha }_{{t0}}}}}, \\ z \in ( - \infty ,{{z}_{0}}]. \\ \end{gathered} $Второй из интервалов представим как отдельный $i$-ый слой при $i = 0$ с параметрами ${{\alpha }_{{t{\kern 1pt} 0}}}$, ${{\eta }_{{\alpha 0}}}$ и воспользуемся выражением (26), где ${{z}_{{i + 1}}} = {{z}_{1}} = 0$, из которого получим ${{Z}_{\alpha }}(z)$ для ${{z}_{0}} + 0 \leqslant z \leqslant 0$ и, в частности, вторую краевую величину СИМ в точке $z = {{z}_{0}}$:
(29)
$\begin{gathered} {{Z}_{\alpha }}({{z}_{0}} + 0) = {{Z}_{{\alpha 2}}}({{z}_{0}}) = \\ = \frac{{{{{\bar {\eta }}}_{{\alpha 0}}}}}{{{{\alpha }_{{t0}}}}}\frac{{({{{\bar {\eta }}}_{{\alpha 0}}} + {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha 0}}}{{z}_{0}}}}} - ({{{\bar {\eta }}}_{{\alpha 0}}} - {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1})}}{{({{{\bar {\eta }}}_{{\alpha 0}}} + {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha 0}}}{{z}_{0}}}}} + ({{{\bar {\eta }}}_{{\alpha 0}}} - {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1})}}. \\ \end{gathered} $Случай II:${{z}_{0}} > H$ ( то есть z0 ≥ zj , j = N). Определение СИМ в данном случае выполняется по аналогии со случаем I, но при обратном порядке рассмотрения областей расположения точки $z$.
Область $z \leqslant 0$. Спектральная функция и СИМ, определяемый соотношением (16), в данной области представлены выражениями
(30)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}(0){{e}^{{{{{\bar {\eta }}}_{{\alpha 0}}}z}}}{\kern 1pt} ;\,\,\,\,{{Z}_{\alpha }}(z) = {{Z}_{{\alpha 1}}}(z) = \frac{{{{{\bar {\eta }}}_{{\alpha 0}}}}}{{{{\alpha }_{{t0}}}}} \\ z \in ( - \infty ,0], \\ \end{gathered} $(31)
${{Z}_{{\alpha 1}}}( + 0) = {{Z}_{{\alpha 1}}}( - 0) = {{Z}_{{\alpha 1}}}({{z}_{1}}) = Z_{{\alpha 1}}^{1} = \frac{{{{{\bar {\eta }}}_{{\alpha 0}}}}}{{{{\alpha }_{{t0}}}}}.$Область $0 \leqslant z \leqslant H$. Интегрирование уравнения (22) для определения ${{Z}_{\alpha }}(z) = {{Z}_{{\alpha 1}}}(z)$ выполняется на интервалах $[{{z}_{i}},\;z]$ где $z \in [{{z}_{i}},{{z}_{{i + 1}}}]$ с возрастанием индекса $i$ от 1 до $N - 1$ (то есть ${{z}_{i}}$ от ${{z}_{1}}$ к ${{z}_{{N - 1}}}$), что приводит к соотношениям:
(32)
$\begin{gathered} {{Z}_{{\alpha 1}}}(z) = \\ = \frac{{{{{\bar {\eta }}}_{{\alpha i}}}}}{{{{\alpha }_{{ti}}}}}\frac{{({{{\bar {\eta }}}_{{\alpha i}}} + {{\alpha }_{{ti}}}Z_{{\alpha 1}}^{i}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha i}}}(z - {{z}_{i}})}}} - ({{{\bar {\eta }}}_{{\alpha i}}} - {{\alpha }_{{t{\kern 1pt} i}}}Z_{{\alpha 1}}^{i})}}{{({{{\bar {\eta }}}_{{\alpha i}}} + {{\alpha }_{{ti}}}Z_{{\alpha 1}}^{i}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha i}}}(z - {{z}_{i}})}}} + ({{{\bar {\eta }}}_{{\alpha i}}} - {{\alpha }_{{t{\kern 1pt} i}}}Z_{{\alpha 1}}^{i})}}. \\ \end{gathered} $Выражение (32) при $z = {{z}_{{i + 1}}}$ после замены в нем символа $i$ на $l$образует вместе со вторым из соотношений (30) следующую рекурсивную схему :
(33)
$\begin{gathered} Z_{{\alpha 1}}^{1} = \frac{{{{{\bar {\eta }}}_{{\alpha 0}}}}}{{{{\alpha }_{{t0}}}}},\,\,\,\,Z_{{\alpha 1}}^{{l + 1}} = \frac{{{{{\bar {\eta }}}_{{\alpha l}}}}}{{{{\alpha }_{{tl}}}}} \times \\ \times \,\,\frac{{({{{\bar {\eta }}}_{{\alpha l}}} + {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 1}}^{l}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}}}} - ({{{\bar {\eta }}}_{{\alpha l}}} - {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 1}}^{l})}}{{({{{\bar {\eta }}}_{{\alpha l}}} + {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 1}}^{l}){\kern 1pt} {{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}}}} + ({{{\bar {\eta }}}_{{\alpha l}}} - {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 1}}^{l})}} \\ (l = 1, \ldots ,N - 1), \\ \end{gathered} $Область $z \geqslant H$. Для данной области раздельно рассматриваются два интервала.
Первый интервал – это ${{z}_{N}} = H \leqslant z \leqslant {{z}_{0}} - 0$, который будем рассматривать как интервал, занимаемый дополнительным ($N$-м) слоем мощностью $h = {{z}_{0}} - {{z}_{N}}$, обладающим теми же параметрами, что и полупространство $z \geqslant H$ в реальной модели. Второй интервал– это область $z \in [{{z}_{0}},\;\infty )$. Тогда согласно (32) для $i = N$, функция ${{Z}_{\alpha }}(z) = {{Z}_{{\alpha 1}}}(z)$ для интервала ${{z}_{N}} \leqslant z \leqslant {{z}_{0}} - 0$ при учете того, что ${{z}_{N}} = H$, запишется в виде выражения вида (32) с заменой индекса $i$на $N$, из которого при переходе к пределу $z\, \to \,{{z}_{0}}$ следует ее первая краевая величина:
(34)
$\begin{gathered} {{Z}_{\alpha }}({{z}_{0}} - 0) = {{Z}_{{\alpha 1}}}({{z}_{0}}) = \frac{{{{{\bar {\eta }}}_{{\alpha N}}}}}{{{{\alpha }_{{tN}}}}} \times \\ \times \,\,\frac{{({{{\bar {\eta }}}_{{\alpha N}}} + {{\alpha }_{{t{\kern 1pt} N}}}Z_{{\alpha 1}}^{N}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha N}}}({{z}_{0}} - H)}}} - ({{{\bar {\eta }}}_{{\alpha N}}} - {{\alpha }_{{t{\kern 1pt} N}}}Z_{{\alpha 1}}^{N})}}{{({{{\bar {\eta }}}_{{\alpha N}}} + {{\alpha }_{{tN}}}Z_{{\alpha 1}}^{N}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha N}}}({{z}_{0}} - H)}}} + ({{{\bar {\eta }}}_{{\alpha N}}} - {{\alpha }_{{t{\kern 1pt} N}}}Z_{{\alpha 1}}^{N})}} \\ (H \leqslant z \leqslant {{z}_{0}} - 0), \\ \end{gathered} $Для $\infty \geqslant z \geqslant {{z}_{0}} + 0$ используем выражение (24) для спектральной функции, где $\nu = N$, которое при его подстановке в (16) приводит к выражению для СИМ при $z \geqslant {{z}_{0}} + 0$ и для его краевой величины на границе полупространства $z \geqslant H$:
(35)
$\begin{gathered} {{Z}_{\alpha }}(z) = {{Z}_{\alpha }}({{z}_{0}} + 0) = {{Z}_{{\alpha 2}}}({{z}_{0}}) = - \frac{{{{{\bar {\eta }}}_{{\alpha N}}}}}{{{{\alpha }_{{t\,N}}}}}, \\ z \in [{{z}_{0}},\infty ). \\ \end{gathered} $Случай III: ${{z}_{j}} < {{z}_{0}} < {{z}_{{j + 1}}},\,\,1 \leqslant j \leqslant N - 1$ (то есть $0 < {{z}_{0}} < H$).
В указанной области определения параметра ${{z}_{0}}$ функция ${{V}_{\alpha }}(\lambda ,z,{{z}_{0}})$ при $z \notin \left[ {0,H} \right]$ имеет представления, удовлетворяющие условию на бесконечности:
(36)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}(0){{{\text{e}}}^{{{\kern 1pt} {{{\bar {\eta }}}_{{\alpha 0}}}z}}},\,\,\,\,z \in ( - \infty ,0]; \\ {{V}_{\alpha }}(z) = {{V}_{\alpha }}(H){{{\text{e}}}^{{ - {\kern 1pt} {{{\bar {\eta }}}_{{\alpha N}}}(z - H)}}},\,\,\,\,z \in [H,\infty ), \\ \end{gathered} $(37)
$\begin{gathered} {{Z}_{{\alpha 1}}}(z) = {{Z}_{{\alpha 1}}}( + 0) = {{Z}_{{\alpha 1}}}( - 0) = Z_{{\alpha 1}}^{1} = \frac{{{{{\bar {\eta }}}_{{\alpha 0}}}}}{{{{\alpha }_{{t0}}}}}{\text{ }}, \\ z \in ( - \infty ,0], \\ \end{gathered} $(38)
$\begin{gathered} {{Z}_{{\alpha 2}}}(z) = {{Z}_{{\alpha 2}}}(H - 0) = {{Z}_{{\alpha 2}}}(H + 0) = \\ = Z_{{\alpha 2}}^{N} = - \frac{{{\kern 1pt} {{{\bar {\eta }}}_{{\alpha N}}}}}{{{{\alpha }_{{tN}}}}}{\text{ }},\,\,\,\,z \in [H,\infty ). \\ \end{gathered} $Правые части (37) и (38) представляют краевые условия для дифференциального уравнения (21) при $z \in [0,H]$ на интервалах, соответственно, $0 \leqslant z \leqslant {{z}_{0}} - 0$ и ${{z}_{0}} + 0 \leqslant z \leqslant H$. Процедуру определения СИМ для указанных интервалов приведем ниже.
a) $0 \leqslant z \leqslant {{z}_{0}} - 0$. Выражение (21) интегрируется по отрезку $[{{z}_{i}},\;z]$ интервала $[{{z}_{i}},{{z}_{{i + 1}}}]$, что позволяет получить СИМ в произвольной точке $z \in [{{z}_{i}},{{z}_{{i + 1}}}]$ в виде (32), где далее после перехода к пределу $z \to {{z}_{{i + 1}}}$ и замены символа $i$ на $l$, получаем рекурсивную процедуру вида (33) для определения $Z_{{\alpha 1}}^{{l + 1}}$$(l = 1,2, \ldots ,j - 1)$ с начальным элементом $Z_{{\alpha 1}}^{1}$, заданным согласно (37). Из выражения (32), положив в нем $i = j$, получим краевую величину СИМ в точке $z = {{z}_{0}}$ :
(39)
$\begin{gathered} {{Z}_{\alpha }}({{z}_{0}} - 0) = {{Z}_{{\alpha 1}}}({{z}_{0}}) = \frac{{{{{\bar {\eta }}}_{{\alpha j}}}}}{{{{\alpha }_{{tj}}}}} \times \\ \times \,\,\frac{{({{{\bar {\eta }}}_{{\alpha j}}} + {{\alpha }_{{tj}}}Z_{{\alpha 1}}^{j}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha j}}}({{z}_{0}} - {{z}_{j}})}}} - ({{{\bar {\eta }}}_{{\alpha j}}} - {{\alpha }_{{tj}}}Z_{{\alpha 1}}^{j})}}{{({{{\bar {\eta }}}_{{\alpha i}}} + {{\alpha }_{{t{\kern 1pt} i}}}Z_{{\alpha 1}}^{j}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha j}}}({{z}_{0}} - {{z}_{j}})}}} + ({{{\bar {\eta }}}_{{\alpha j}}} - {{\alpha }_{{tj}}}Z_{{\alpha 1}}^{j})}}. \\ \end{gathered} $b) ${{z}_{0}} + 0 \leqslant z \leqslant H$.Интегрирование выражения (21) по отрезку $[{{z}_{{i + 1}}},\;z]$ произвольного интервала $[{{z}_{i}},\;{{z}_{{i + 1}}}\;]$ ($j + 1 \leqslant i \leqslant N - 1$) приводит к выражению вида (26) для СИМ в точке$z$.
В полученном выражении, переходя к пределу $z \to {{z}_{i}}$ и заменив символ $i$ на $l$, получим рекурсивную схему вида (27) для определения$Z_{{\alpha 2}}^{l}$ ($l = N - 1,N - 2, \ldots ,j + 1$) с начальным элементом $Z_{{\alpha 2}}^{N}$, а переход к пределу $z \to {{z}_{0}}$ с заменой индекса $i$ на $j$ приводит к краевой величине СИМ :
(40)
$\begin{gathered} {{Z}_{\alpha }}({{z}_{0}} + 0) = {{Z}_{{\alpha 2}}}({{z}_{0}}) = \frac{{{{{\bar {\eta }}}_{{\alpha j}}}}}{{{{\alpha }_{{tj}}}}} \times \hfill \\ \times \,\,\frac{{({{{\bar {\eta }}}_{{\alpha j}}} + {{\alpha }_{{tj}}}Z_{{\alpha 2}}^{{j + 1}}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha {\kern 1pt} j}}}({{z}_{0}} - {{z}_{{{\kern 1pt} j + 1}}})}}} - ({{{\bar {\eta }}}_{{\alpha j}}} - {{\alpha }_{{tj}}}Z_{{\alpha 2}}^{{j + 1}})}}{{({{{\bar {\eta }}}_{{\alpha j}}} + {{\alpha }_{{tj}}}Z_{{\alpha 2}}^{{j + 1}}){{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha {\kern 1pt} j}}}({{z}_{0}} - {{z}_{{j + 1}}})}}} + ({{{\bar {\eta }}}_{{\alpha j}}} - {{\alpha }_{{tj}}}Z_{{\alpha 2}}^{{j + 1}})}}. \hfill \\ \end{gathered} $ОПРЕДЕЛЕНИЕ СПЕКТРАЛЬНОЙ ФУНКЦИИ
Преобразуя соотношение (16) в уравнение:
запишем его решение в следующем виде:(41)
$\begin{gathered} {{V}_{\alpha }}(z) = V_{\alpha }^{0}\exp \left[ {\int\limits_{{{z}_{{st}}}}^z {{{\alpha }_{t}}(\zeta ){{Z}_{{\alpha {\kern 1pt} s}}}(\zeta )d\zeta } } \right]; \\ s = \left\{ \begin{gathered} 1\,\,\,\,(z \leqslant {{z}_{0}}) \hfill \\ 2\,\,\,\,(z \geqslant {{z}_{0}}), \hfill \\ \end{gathered} \right. \\ \end{gathered} $Для удобства расчетов выражения (41) интегрирование выполняется по интервалам:
(42)
${\text{при}}\,\,z \leqslant {{z}_{0}}{\kern 1pt} :\,\,[{{z}_{0}},{{z}_{j}}],[{{z}_{j}},{{z}_{{j - 1}}}], \ldots ,[{{z}_{{i + 2}}},{{z}_{{i + 1}}}][{{z}_{{i + 1}}},z]\,\,\,\,(j \geqslant i \geqslant 1),$(43)
$\begin{gathered} {\text{при}}\,\,{\kern 1pt} z > {{z}_{0}}:[{{z}_{0}},{{z}_{{j + 1}}}],[{{z}_{{j + 1}}},{{z}_{{j + 2}}}], \ldots ,[{{z}_{{i - 1}}},{{z}_{i}}],[{{z}_{i}},z]\,\,\,{\kern 1pt} (j \leqslant i \leqslant N); \\ {{z}_{i}} \leqslant z \leqslant {{z}_{{i + 1}}},\,\,\,\,{{z}_{j}} \leqslant {{z}_{0}} \leqslant {{z}_{{j + 1}}}\,\,\,\,(i,j = 1,2, \ldots ,N - 1){\text{:}} \\ \end{gathered} $(44)
$\begin{gathered} \int\limits_{{{\zeta }_{{\text{s}}}}}^{{{\zeta }_{{\text{f}}}}} {{{\alpha }_{{tl}}}(\zeta )Z_{\alpha }^{l}(\zeta )d\zeta = {{{\bar {\eta }}}_{{\alpha j}}}\int\limits_{{{\zeta }_{{\text{s}}}}}^{{{\zeta }_{{\text{f}}}}} {\frac{{A_{{\alpha \nu }}^{l}{\kern 1pt} {{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha j}}}(\zeta - z{\kern 1pt} ')}}} - B_{{\alpha \nu }}^{l}}}{{A_{{\alpha \nu }}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha j}}}(\zeta - z{\kern 1pt} ')}}} + B_{{\alpha \nu }}^{l}}}{\kern 1pt} {\kern 1pt} d\zeta {\kern 1pt} ,} } \\ v = \left\{ \begin{gathered} 1,\,\,\,\,z \leqslant {{z}_{0}} - 0,\,\,\,\,{{\zeta }_{{\text{f}}}} \leqslant {{\zeta }_{{\text{s}}}}, \hfill \\ l = j,j - 1, \ldots ,i + 1,i \hfill \\ \hfill \\ 2,\,\,\,\,z \geqslant {{z}_{0}} + 0,\,\,\,\,{{\zeta }_{{\text{f}}}} \geqslant {{\zeta }_{{\text{s}}}} \hfill \\ l = i,i - 1, \ldots ,j + 1,j \hfill \\ \end{gathered} \right., \\ \end{gathered} $(45)
$A_{{\alpha 1}}^{l} = {{\bar {\eta }}_{{\alpha l}}} + {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 1}}^{l},\,\,\,\,B_{{\alpha 1}}^{l} = {{\bar {\eta }}_{{\alpha l}}} - {{\alpha }_{{tl}}}Z_{{\alpha 1}}^{l};$(46)
$A_{{\alpha 2}}^{j} = {{\bar {\eta }}_{{\alpha l}}} + {{\alpha }_{{t{\kern 1pt} l}}}Z_{{\alpha 2}}^{{l + 1}},\,\,\,\,B_{{\alpha 2}}^{l} = {{\bar {\eta }}_{{\alpha l}}} - {{\alpha }_{{tl}}}Z_{{\alpha 2}}^{{l + 1}}.$Верхнее и нижнее выражения в правой части (44') тождественны независимо от того, какая из величин ${{\zeta }_{s}}$ и ${{\zeta }_{{\text{f}}}}$ больше или меньше, но такая их запись является более удобной для окончательного представления спектральной функции ${{V}_{\alpha }}(z,\lambda )$.
Вывод упомянутых выше представлений функции ${{V}_{\alpha }}$ для трех возможных случаев: 1 – ${{z}_{0}} < 0$; 2 – ${{z}_{0}} > H$ и 3 – $0 < {{z}_{0}} < H$ приводится ниже.
Случай I: ${{z}_{0}} < 0$. В этом случае величина ${{Z}_{{\alpha 1}}}({{z}_{0}})$ определяется из выражения (28), а ${{Z}_{{\alpha {\kern 1pt} 2}}}({{z}_{0}})$ – из (29), где $Z_{{\alpha {\kern 1pt} 2}}^{1}$ определяется через $Z_{{\alpha {\kern 1pt} 2}}^{N}$ с помощью рекуррентной процедуры (27) с учетом непрерывности ${{Z}_{\alpha }}(z)$ при $z = {{z}_{i}}$ (${{z}_{0}} \ne {{z}_{i}}$). Вычитая (28) из (29) и подставляя результат в правую часть (20), получим после несложных преобразований
Из сравнения последнего соотношения с выражением (24) при $z = {{z}_{0}}$, где полагаем $\nu = 0,\,\,{{d}_{0}} = 0$, получаем выражение
(47)
$\begin{gathered} {{V}_{\alpha }}(z) = \frac{{{{\alpha }_{{t0}}}}}{{{{{\bar {\eta }}}_{{\alpha 0}}}}} \times \\ \times \,\,\left[ {{{e}^{{ - {{\eta }_{{\alpha 0}}}{\kern 1pt} {\text{sign}}{\kern 1pt} (z - {{z}_{0}})}}} + \frac{{{{{\bar {\eta }}}_{{\alpha 0}}} + {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1}}}{{{{{\bar {\eta }}}_{{\alpha 0}}} - {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1}}}{{{\text{e}}}^{{{{{\bar {\eta }}}_{{\alpha 0}}}(z + {{z}_{0}})}}}} \right]. \\ ({{z}_{0}},z \leqslant 0), \\ \end{gathered} $Как видно из (47) выражение для ${{V}_{\alpha }}{\text{(z)}}$на границе $z = 0$ слоистой пачки имеет вид:
(48)
$\begin{gathered} {{V}_{\alpha }}(0) = \frac{{{{\alpha }_{{t0}}}}}{{{{{\bar {\eta }}}_{{\alpha 0}}}}}{\kern 1pt} \,\left[ {1 + \frac{{{{{\bar {\eta }}}_{{\alpha 0}}} + {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1}{\kern 1pt} {\kern 1pt} }}{{{{{\bar {\eta }}}_{{\alpha 0}}} - {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1}}}} \right]{{{\text{e}}}^{{{{{\bar {\eta }}}_{\alpha }}{{z}_{0}}}}} = \\ = \frac{{2{{\alpha }_{{t0}}}{{e}^{{{{{\bar {\eta }}}_{\alpha }}{{z}_{0}}}}}}}{{{{{\bar {\eta }}}_{{\alpha 0}}} - {{\alpha }_{{t0}}}Z_{{\alpha 2}}^{1}}}\,\,\,\,({{z}_{0}} < 0). \\ \end{gathered} $Теперь, подставив выражение (48) вместо множителя $V_{\alpha }^{0}$ в правую часть (41), выражения (26) и (27) под знак интеграла по интервалу $[0,\;z]$ в экспоненте правой части (41), получим при обозначениях (46) следующие представления функции ${{V}_{\alpha }}{\text{(z)}}$ для любых значений $z$ из области $z \geqslant 0$:
(49)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}(0)\exp \left[ {\left( {{{\delta }_{i}}\sum\limits_{l = 1}^{i - 1} {{{{\bar {\eta }}}_{{\alpha l}}}} \int\limits_{{{z}_{l}}}^{{{z}_{{l + 1}}}} {\frac{{A_{2}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}(\zeta - {{z}_{{l + 1}}})}}} - B_{2}^{l}}}{{A_{2}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}(\zeta - {{z}_{{l + 1}}})}}} + B_{2}^{l}}}d\zeta } } \right) + {{{\bar {\eta }}}_{{\alpha i}}}\int\limits_{{{z}_{i}}}^z {\frac{{A_{2}^{i}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha i}}}(\zeta - {{z}_{{{\kern 1pt} i + 1}}})}}} - B_{2}^{i}}}{{A_{2}^{i}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha i}}}(\zeta - {{z}_{{{\kern 1pt} i + 1}}})}}} + B_{2}^{i}}}d\zeta } } \right] = \\ = {{V}_{\alpha }}(0)\exp \left[ { - \left( {\sum\limits_{l = 1}^{i - 1} {{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}} } \right) - {{{\bar {\eta }}}_{{\alpha i}}}(z - {{z}_{i}})} \right]\,\left[ {\prod\limits_{l = 1}^{i - 1} {\frac{{A_{2}^{l} + B_{2}^{l}}}{{A_{2}^{l}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}}}} + B_{2}^{l}}}} } \right]\frac{{A_{2}^{i}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha i}}}({{z}_{{{\kern 1pt} i + 1}}} - z)}}} + B_{2}^{i}}}{{A_{2}^{i}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha i}}}h{{{\kern 1pt} }_{i}}}}} + B_{2}^{i}}} \\ ({{\delta }_{1}} = 0,\,\,\,\,{{\delta }_{i}} = 1;\,\,\,\,i = 2, \ldots ,N - 1),\,\,\,{{z}_{0}} \leqslant 0,\,\,\,z \in [{{z}_{i}},{{z}_{{i + 1}}}] \subset [0,H]), \\ \end{gathered} $(50)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}(0)\exp \left[ {\left( {\sum\limits_{l = 1}^{N - 1} {{{{\bar {\eta }}}_{{\alpha l}}}} \int\limits_{{{z}_{l}}}^{{{z}_{{l + 1}}}} {\frac{{A_{2}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}(\zeta - {{z}_{{l + 1}}})}}} - B_{2}^{l}}}{{A_{2}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}(\zeta - {{z}_{{{\kern 1pt} + 1}}})}}} + B_{2}^{l}}}d\zeta } } \right) - {{{\bar {\eta }}}_{{\alpha N}}}(z - H)} \right] = \\ = {{V}_{\alpha }}(0)\exp \left[ { - \left( {\sum\limits_{l = 1}^{N - 1} {{{{\bar {\eta }}}_{{\alpha l}}}} {{h}_{l}}} \right) - {{{\bar {\eta }}}_{{\alpha N}}}(z - H)} \right]\prod\limits_{l = 1}^{N - 1} {\frac{{A_{2}^{l} + B_{2}^{l}}}{{A_{2}^{l}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}}}} + B_{2}^{l}}}} \\ ({{z}_{0}} \leqslant 0,\,\,\,\,z \geqslant H). \\ \end{gathered} $Случай II:${{z}_{0}} > H$ (то есть ${{z}_{0}} > {{z}_{N}}$). В этом случае, подставляя разность величин СИМ ${{Z}_{{\alpha 2}}}({{z}_{0}})$ – из (35) и ${{Z}_{{\alpha 1}}}({{z}_{0}})$ из (34) в знаменатель выражения (20), получим после несложных преобразований краевую величину спектральной функции:
(52)
${{V}_{\alpha }}({{z}_{N}}) = \frac{{{{\alpha }_{{{\kern 1pt} tN}}}}}{{{{{\bar {\eta }}}_{{\alpha N}}}}}\frac{{2{{{\bar {\eta }}}_{{\alpha N}}}{{{\text{e}}}^{{ - {{{\bar {\eta }}}_{{\alpha N}}}({{z}_{0}} - H)}}}}}{{{{{\bar {\eta }}}_{{\alpha N}}} + {{\alpha }_{{tN}}}Z_{{\alpha 1}}^{N}}} = {{V}_{\alpha }}(H).$Подставив выражение (52) вместо множителя $V_{\alpha }^{0}$ в правую часть (41) и выражения (32) и (33) под знак интеграла в экспоненте в (41) с начальной и конечной точками интегрирования, соответственно, $\zeta = H$и $\zeta = z$, получим при обозначениях (45) следующие представления функции ${{V}_{\alpha }}{\text{(}}z{\text{)}}$ для значений $z \leqslant H$:
Применение интегральных формул (44) и (44') к показателям экспоненты в правой части каждого из двух последних соотношений приводит к следующим выражениям:
(53)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}(H) \times \\ \times \,\,\exp \left[ { - \left( {\sum\limits_{l = N - 1}^{i + 1} {{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}} } \right) - {{{\bar {\eta }}}_{{\alpha i}}}({{z}_{{i + 1}}} - z)} \right] \times \\ \times \,\,\left( {\prod\limits_{l = N - 1}^{i + 1} {\frac{{A_{1}^{l} + B_{1}^{l}}}{{A_{1}^{l} + B_{1}^{l}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{{{\kern 1pt} l}}}}}}}}} } \right)\frac{{A_{1}^{i} + B_{1}^{i}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha i}}}(z - {{z}_{{{\kern 1pt} i}}})}}}}}{{A_{1}^{i} + B_{1}^{i}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha i}}}{{h}_{i}}}}}}} \\ ({{z}_{0}} \geqslant H,\,\,z \in [{{z}_{i}},\,\,{{z}_{{i + 1}}}] \subset [0,\,H{\kern 1pt} ]), \\ \end{gathered} $(54)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}(H) \times \\ \times \,\,\exp \left[ {\left( { - \sum\limits_{l = N - 1}^1 {{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}} } \right) + {{{\bar {\eta }}}_{{\alpha 0}}}z} \right]\prod\limits_{l = N - 1}^1 {\frac{{A_{1}^{l} + B_{1}^{l}}}{{A_{1}^{l} + B_{1}^{l}{{{\text{e}}}^{{ - 2\eta {{h}_{l}}}}}}}} \\ {\text{ }}({{z}_{0}} \geqslant H,z \leqslant 0). \\ \end{gathered} $Случай III: ${{z}_{j}} \leqslant {{z}_{0}} \leqslant {{z}_{{j + 1}}},\,\,1 \leqslant j \leqslant N - 1$ (то есть $0 \leqslant {{z}_{0}} \leqslant H$).
Область $z \notin (0,\;H)$. В данном случае величина спектральной функции в указанной области определяется выражениями (36), а СИМ – выражениями и граничными условиями (37) для $z \leqslant {\text{0}}$ и (38) для $z \geqslant H$. Величины спектральной функции на границах полупространств – ${{V}_{\alpha }}(0),\,\;{{V}_{\alpha }}(H)$ определяются предельными переходами в ее выражении для $z \notin [0,\;H]$, процедура получения которого приводится ниже.
a) $0 \leqslant z \leqslant {{z}_{0}} - 0$. Выражение (21) интегрируется по отрезку $[{{z}_{i}},\;z]$ интервала $[{{z}_{i}},\;{{z}_{{i + 1}}}]$, что позволяет получить СИМ в произвольной точке $z \in [{{z}_{i}},\;{{z}_{{i + 1}}}]$ в виде (32):
Подставив выражения (32') и (33') в подынтегральное выражение экспоненты в (41), где ${{z}_{{st}}} = {{z}_{0}}$, и, разбив участок интегрирования на интервалы в соответствии с (42), получим следующие соотношения:
(55)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}({{z}_{0}})\exp \left[ {\int\limits_{{{z}_{0}}}^z {{{\alpha }_{t}}(\zeta ){{Z}_{{\alpha {\kern 1pt} s}}}(\zeta )d\zeta } } \right] = \\ = {{V}_{\alpha }}({{z}_{0}})\left\{ {\int\limits_{{{z}_{0}}}^{{{z}_{{\text{f}}}}} {\frac{{A_{{\alpha 1}}^{j}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha j}}}(\zeta - {{z}_{j}})}}} - B_{{\alpha 1}}^{j}}}{{A_{{\alpha 1}}^{j}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha j}}}(\zeta - {{z}_{j}})}}} + B_{{\alpha 1}}^{j}}}d\zeta } + } \right. \\ + \,\,\alpha \sum\limits_{l = j - 1}^{i + 1} {\left[ {\int\limits_{{{z}_{{l + 1}}}}^{{{z}_{l}}} {\frac{{A_{{\alpha 1}}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}(\zeta - {{z}_{l}})}}} - B_{{\alpha 1}}^{l}}}{{A_{{\alpha 1}}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}(\zeta - {{z}_{l}})}}} + B_{{\alpha 1}}^{l}}}d\zeta } } \right]} \,\, + \\ \left. { + \,\,\beta \int\limits_{{{z}_{{i + 1}}}}^z {\frac{{A_{{\alpha 1}}^{i}{{e}^{{2{{{\bar {\eta }}}_{{\alpha i}}}(\zeta - {{z}_{i}})}}} - B_{{\alpha 1}}^{i}}}{{A_{{\alpha 1}}^{i}{{e}^{{2{{{\bar {\eta }}}_{{\alpha i}}}(\zeta - {{z}_{i}})}}} + B_{{\alpha 1}}^{i}}}d\zeta } } \right\}, \\ \end{gathered} $b) ${{z}_{0}} + 0 \leqslant z \leqslant H$. Выражение (21) интегрируется по отрезку $[{{z}_{{i + 1}}},\;z]$ интервала $[{{z}_{i}},\;{{z}_{{i + 1}}}]$, что позволяет получить СИМ в произвольной точке $z \in [{{z}_{i}},{{z}_{{i + 1}}}]$ в виде (26):
По аналогии с (55), подставив выражения (26') и (27') в правую часть (41), где далее участок интегрирования разобьем на интервалы в соответствии с (43), получим выражение:
(56)
$\begin{gathered} {{V}_{\alpha }}(z) = {{V}_{\alpha }}({{z}_{0}})\left\{ {{{{\bar {\eta }}}_{{\alpha j}}}\int\limits_{{{z}_{0}}}^{{{z}_{{\text{f}}}}} {\frac{{A_{{\alpha 2}}^{j}{\kern 1pt} {{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha j}}}(\zeta - {{z}_{{j + 1}}})}}} - B_{{\alpha 2}}^{j}}}{{A_{{\alpha 2}}^{j}{\kern 1pt} {\kern 1pt} {{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha j}}}(\zeta - {{z}_{{j + 1}}})}}} + B_{{\alpha 2}}^{j}}}{\kern 1pt} {\kern 1pt} d\zeta } + } \right. \\ + \,\,\alpha \sum\limits_{l = j + 1}^{i - 1} {\;\left[ {{{{\bar {\eta }}}_{{\alpha l}}}\int\limits_{{{z}_{l}}}^{{{z}_{{l + 1}}}} {\frac{{A_{{\alpha 2}}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}(\zeta - {{z}_{{l + 1}}})}}} - B_{{\alpha 2}}^{l}}}{{A_{{\alpha 2}}^{l}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha l}}}(\zeta - {{z}_{{l + 1}}})}}} + B_{{\alpha 2}}^{l}}}d\zeta } } \right]} + \\ \left. {\,\, + \beta {{{\bar {\eta }}}_{{\alpha i}}}\int\limits_{{{z}_{i}}}^z {\frac{{A_{{\alpha 2}}^{i}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha i}}}(\zeta - {{z}_{{i + 1}}})}}} - B_{{\alpha 2}}^{i}}}{{A_{{\alpha 2}}^{i}{{{\text{e}}}^{{2{{{\bar {\eta }}}_{{\alpha i}}}(\zeta - {{z}_{{i + 1}}})}}} + B_{{\alpha 2}}^{i}}}d\zeta } } \right\}{\text{ }} \\ j \leqslant i \leqslant N - 1,\,\,\,\left\{ \begin{gathered} i = j,\,\,\,\,{{z}_{{\text{f}}}} = z,\,\,\,\,\alpha = 0,\,\,\,{\kern 1pt} \beta = 0 \hfill \\ \left. \begin{gathered} i = j + 1 \hfill \\ i > j + 1{\kern 1pt} \hfill \\ \end{gathered} \right\}{{z}_{{\text{f}}}} = {{z}_{{j + 1}}}{\kern 1pt} \left\{ \begin{gathered} \alpha = 0,\,\,\beta = 1 \hfill \\ {\kern 1pt} \alpha = 1,\,\,{\kern 1pt} \beta = 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.. \\ \end{gathered} $Преобразуя интегралы в выражениях (55) и (56) с помощью интегральной формулы (44'), получим после несложных преобразований следующие окончательные представления ${{V}_{\alpha }}$:
(57)
$\begin{gathered} {\text{a)}}\,\,\,\,0 \leqslant z \leqslant {{z}_{0}} - 0,\,\,\,\,{{V}_{\alpha }}(z) = {{V}_{\alpha }}({{z}_{0}}) \times \\ \times \,\,\exp \left[ { - {{{\bar {\eta }}}_{{\alpha j}}}({{z}_{0}} - {{z}_{{\text{f}}}}) - \alpha \sum\limits_{l = j - 1}^{i + 1} {{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}} - \beta {{{\bar {\eta }}}_{{\alpha i}}}({{z}_{{i + 1}}} - z)} \right] \times \\ \times \,\,\frac{{A_{{\alpha 1}}^{j} + B_{{\alpha 1}}^{j}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha j}}}({{z}_{{\text{f}}}} - {{z}_{j}})}}}}}{{A_{{\alpha 1}}^{j} + B_{{\alpha 1}}^{j}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha j}}}({{z}_{0}} - {{z}_{j}})}}}}} \times \\ \times \,\,\left[ {\sum\limits_{l = j - 1}^{i + 1} {{{{\left( {\frac{{A_{{\alpha 1}}^{l} + B_{{\alpha 1}}^{l}}}{{A_{{\alpha 1}}^{l} + B_{{\alpha 1}}^{l}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}}}}}}} \right)}}^{\alpha }}} } \right]{{\left( {\frac{{A_{{\alpha 1}}^{i} + B_{{\alpha 1}}^{i}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha i}}}(z - {{z}_{i}})}}}}}{{A_{{\alpha 1}}^{i} + B_{{\alpha 1}}^{i}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha i}}}{{h}_{i}}}}}}}} \right)}^{\beta }} \\ {\text{ }}{{z}_{{\text{f}}}} = \left\{ \begin{gathered} z\,\,i = j \hfill \\ {{z}_{j}}\,\,i < j \hfill \\ \end{gathered} \right.;\,\,\,\,\alpha = \left\{ \begin{gathered} 1\,\,i < j - 1 \hfill \\ 0\,\,i \geqslant j - 1 \hfill \\ \end{gathered} \right.,\,\,\,\,\beta = \left\{ \begin{gathered} 1\,\,i \leqslant j - 2 \hfill \\ 0\,\,i > j - 2 \hfill \\ \end{gathered} \right.; \\ \end{gathered} $(58)
$\begin{gathered} {\text{b}})\;\;\;{{z}_{0}} + 0 \leqslant z \leqslant H,\,\,\,\,{{V}_{\alpha }}(z) = {{V}_{\alpha }}({{z}_{0}}) \times \hfill \\ \times \,\,\exp \left\{ { - \left[ {{{{\bar {\eta }}}_{{\alpha j}}}({{z}_{{\text{f}}}}\,\, - {{z}_{0}}) + \alpha \sum\limits_{l = j + 1}^{i - 1} {{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}} + \beta {{{\bar {\eta }}}_{{\alpha l}}}(z - {{z}_{i}})} \right]} \right\} \times \hfill \\ \times \,\,\frac{{A_{{\alpha 2}}^{j}{\kern 1pt} {{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha j}}}({{z}_{{j + 1}}} - {{z}_{{\text{f}}}})}}} + B_{{\alpha 2}}^{j}}}{{A_{{\alpha 2}}^{j}{\kern 1pt} {\kern 1pt} {{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha j}}}({{z}_{{j + 1}}} - {{z}_{0}})}}} + B_{{\alpha 2}}^{j}}}{{\left( {\frac{{A_{{\alpha 2}}^{l} + B_{{\alpha 2}}^{l}}}{{A_{{\alpha 2}}^{l}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha l}}}{{h}_{l}}}}} + B_{{\alpha 2}}^{l}}}} \right)}^{\alpha }} \times \hfill \\ \times \,\,{{\left( {\frac{{A_{{\alpha 2}}^{i}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha i}}}({{z}_{{i + 1}}} - z)}}} + B_{{\alpha 2}}^{i}}}{{A_{{\alpha 2}}^{i}{{{\text{e}}}^{{ - 2{{{\bar {\eta }}}_{{\alpha i}}}{{h}_{i}}}}} + B_{{\alpha 2}}^{i}}}} \right)}^{\beta }} \hfill \\ j \leqslant i \leqslant N - 1,\,\,\,\,\left\{ \begin{gathered} i = j,\,\,\,{{z}_{{\text{f}}}} = z,\,\,\,\alpha = 0,\;\,{\kern 1pt} \beta = 0 \\ \left. \begin{gathered} i = j + 1 \hfill \\ i > j + 1{\kern 1pt} \hfill \\ \end{gathered} \right\}{{z}_{{\text{f}}}} = {{z}_{{j + 1}}}{\kern 1pt} \left\{ \begin{gathered} \alpha = 0,{\kern 1pt} \,\,\beta = 1 \hfill \\ \alpha {\kern 1pt} = 1,{\kern 1pt} \,\,\beta = 1 \hfill \\ \end{gathered} \right. \\ \end{gathered} \right.. \hfill \\ \end{gathered} $В представлениях (57) и (58) используется множитель ${{V}_{\alpha }}({{z}_{0}})$, который рассчитывается с помощью выражения (20), путем подстановки в него величин СИМ, определенных выражениями (32′) для $z = {{z}_{0}} - 0$ и (26') для $z = {{z}_{0}} + 0$, где $i = j$, которые принимают вид:
ЗАКЛЮЧЕНИЕ
Дано определение фундаментальных аффиноров Грина (ФАГ) магнитного и электрического типов, представляющих одноименные векторные потенциалы, в слоистой среде с одноосной анизотропией магнитной и комплексной диэлектрической проницаемостей. Все элементы ФАГ обоих типов представлены через пару фундаментальных скалярных функций – функцию электрического и функцию магнитного типов (ФЭТ и ФМТ), с которыми они связаны линейно напрямую или через прообразы преобразований Ханкеля (ПХ) 1-го порядка. Прообразы ФЭТ и ФМТ условно названы спектральными функциями (по спектру значений параметра интегрирования в выражениях ПХ), соответственно, СФЭТ и СФМТ.
Граничные задачи слоисто-анизотропной среды для СФЭТ и СФМТ однотипны и могут быть сформулированы в виде одной общей задачи, для решения которой использован метод В.И. Дмитриева, основанный на сведении ее к дифференциальному уравнению Риккати и граничным условиям для спектрального импеданса (СИМ), введенного через спектральную функцию. Для определения СИМ ко всем случаям расположения точек истока и наблюдения относительно друг друга и границ слоев сформулирована общая стратегия, изложен алгоритм его реализации и приведены конечные результаты (явные выражения СИМ, а затем спектральной функции, удовлетворяющие условиям на бесконечности).
Изложенный в данной работе результат может быть использован для расчетов электромагнитных полей произвольных источников в одноосно анизотропных средах с произвольным количеством слоев при наличии в них неоднородностей (с помощью метода интегральных уравнений) или без них; при изучении полей в градиентных средах путем приближения функций электропроводности, диэлектрической и магнитной проницаемостей кусочно-постоянными функциями; при изучении эффекта анизотропии тонкослоистых сред при отсутствии анизотропии в каждом отдельном слое.
Список литературы
Дмитриев В.И. Э. Электромагнитные поля в неоднородных средах. М.: изд-во МГУ. 1969. 311 с.
Дмитриев В.И., Захаров Е.В. Интегральные уравнения в краевых задачах электродинамики. Изд-во Московского университета. 1987. 168 с.
Дмитриев В.И., Захаров Е.В. Метод интегральных уравнений в вычислительной электродинамике. М.: МАКС Пресс. 2008. 316 с.
Захаров Е.В., Ильин И.В. Интегральные представления электромагнитных полей в неоднородной слоистой среде // Изв. АН СССР. Сер. Физика Земли. 1970. № 8. С. 62–71.
Кеворкянц С.С. К определению тензорных функций Грина электродинамической задачи слоисто-анизотропной среды // Физика Земли. 2000. № 10. С. 84–92.
Кеворкянц С.С. Объемные и граничные интегральные уравнения второго рода в задачах дифракции на ограниченном теле, помещенном в слоисто-анизотропную среду // Физика Земли. 2007. № 3. С. 4–10.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. В 3 т. Т.1. Элементарные функции. (2-е изд., исправ.) М.: ФИЗМАТЛИТ. 2002. 632 с. ISBN 5-9221-0323-7.
Фелсен Л., Мркувиц Н. Излучение и рассеяние волн. Т. 1. М.: изд-во “МИР”. 1978. 547 с.
Avdeev D.B., Kuvshinov A.V., Pankratov O.V., Newman G.A., High-Performance Three-Dimensional Electromagnetic Modelling Using Modified Neumann Series. Wide-Band Numerical Solution // J. geomagnetism and geoelectricity. 1997. V. 49. № 11–12. P. 1519–1539.
Singer B.Sh., Fainberg E.B. Fast and Stable Method for 3-D Modelling of Electromagnetic Field // Exploration Geophysics. 1997. V. 28. P. 130–135.
Дополнительные материалы отсутствуют.
Инструменты
Физика Земли