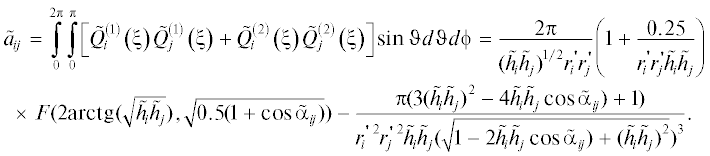Физика Земли, 2023, № 2, стр. 20-35
Аналитические модели зависящих от времени физических полей Земли в локальном варианте
И. Э. Степанова 1, *, А. В. Щепетилов 2, П. С. Михайлов 1
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
2 МГУ им. М.В. Ломоносова
г. Москва, Россия
* E-mail: tet@ifz.ru
Поступила в редакцию 05.03.2022
После доработки 13.04.2022
Принята к публикации 14.04.2022
- EDN: FBJBEN
- DOI: 10.31857/S0002333722060138
Аннотация
Предложена новая методика аналитического описания зависящих от времени сигналов различной природы на основе локальной и региональной версий метода линейных интегральных представлений в пространствах различных размерностей. Обратная задача по нахождению источников поля редуцируется к решению плохо обусловленных систем линейных алгебраических уравнений с приближенно заданной правой частью. Приводятся результаты математического эксперимента по нахождению элементов нестационарных гравитационного и магнитного полей Земли.
ВВЕДЕНИЕ
За последние 10–20 лет объем информации о физических полях и топографии Земли увеличился на несколько порядков. Благодаря различным спутниковым миссиям непрерывным потоком поступают данные о планетах Солнечной системы, при этом орбиты космических аппаратов фактически “заметают” некоторые области трехмерного пространства, обеспечивая, таким образом, достаточно высокую степень разрешения съемки. Как уже было отмечено в нашей предыдущей работе [Степанова и др., 2020], материалы дистанционного зондирования Земли и других небесных тел используются при уточнении теории внутреннего строения нашей планеты и ей подобных, незаменимы при прогнозировании глобального изменения климата и изучении разнообразных геофизических процессов.
В наше время, однако, “простой”, если можно так выразиться, интерпретацией геофизических и геодезических данных, равно как и решением различных задач синтеза с помощью Искусственного интеллекта ограничиться нельзя.
Модели физических полей и топографии должны быть скорректированы с учетом быстро меняющихся огромных массивов данных об этих сигналах. При этом акцент должен быть сделан на разные подходы при интерпретации трендовых составляющих полей и высокочастотных компонент измеряемых (фиксируемых с помощью аппаратуры) сигналов. Поскольку источники, эквивалентные по внешнему полю, определяются всегда неоднозначно, нужно попытаться сформулировать единые критерии отбора оптимальных в некотором смысле распределений масс при исследовании аналогичных математических постановок.
Такой тезис, на первый взгляд, кажется парадоксальным, поскольку локальные аномалии гравитационного (магнитного, теплового и т.п.) поля, как правило, “индивидуальны”: у каждой имеется свой собственный, отличный от других, “портрет”. Но можно объединить отдельные аномалии в группы и подгруппы и назвать такие множества “классами” и “подклассами” объектов, а операции над такими объектами отнести к соответствующим классам отображений – подобно тому, как это делается в математической теории категорий и в программных средах (языках) объектного программирования. К такому выводу авторы настоящей работы пришли на основании многолетнего опыта в решении различных линейных и нелинейных обратных и некорректных задач математической геофизики.
При интерпретации геофизических данных применяются различные методы и подходы (см., например, [Portniaguine, 1999; 2002; Arkani-Hamed, 2002; Acuna, 1999; Михайлов и др., 2019; Wang et al., 2019; Долгаль, 2015; 2017; Uieda et al., 2015; Schattner et al., 2019]).
Восстановление источников сигнала по информации об элементе поля и его градиенте [Wang et al., 2020a; 2020b] представляется нам особенно перспективным.
Магнитное поле Земли не является стационарным, наличие у нашей планеты магнитного динамо обуславливает весьма сложный характер взаимодействия внутреннего магнитного поля с солнечным ветром, представляющим собой потоки заряженных частиц.
В работах авторов, посвященных применению метода линейных интегральных представлений для решения некорректных обратных задач геофизики, ранее не рассматривались постановки для уравнений второго порядка параболического и гиперболического типов. Между тем, возможности указанного метода не ограничиваются уравнениями Лапласа и Пуассона, которым, как известно, удовлетворяют компоненты гравитационного, электрического, магнитного и т.д. полей при определенных условиях. Для того, чтобы восполнить этот “пробел”, мы попытались в настоящей работе предложить аппроксимационную конструкцию для математического моделирования магнитного поля Земли, в которой в явном виде будет учитываться время. Необходимо подчеркнуть, что вне источников поля (т.е. вне внешнего жидкого ядра Земли и других космических объектов, обладающих внутренним генератором магнитного поля) методика разложения сигналов в ряд по сферическим гармоникам, представления в виде интегралов Фурье, вейвлетов и т.п. [Фрик и др., 2020; Титов и др., 2020; Казанцев, 2019] вполне допустимы и могут хорошо “работать” при решении задач анализа и синтеза. Но адекватное реальности моделирование магнитного поля Земли невозможно получить без учета магнитогидродинамических соотношений [Reshetnyak, 2015]. Поэтому актуальной, на наш взгляд, является проблема нахождения устойчивых приближенных решений системы уравнений магнитной гидродинамики, в которой для магнитного поля могут считаться справедливыми некоторые интегральные представления. Мы, таким образом, получаем некоторую систему обыкновенных дифференциальных уравнений, которой удовлетворяет поле скоростей космических частиц – солнечного ветра. Аналогичным образом можно описывать потоки заряженной жидкости (плазмы) и внутри планет. Первым шагом на пути такого моделирования полей является учет времени в качестве независимой переменной (или параметра модели, поскольку при построении решений уравнений в частных производных продуктивным является метод спуска по одной из переменных, от которых эти решения зависят [Владимиров, 1981]).
В наших предыдущих работах мы показали, что глобальный вариант метода линейных интегральных представлений в рамках структурно-параметрического подхода может применяться для построения аналитического продолжения магнитного поля Марса вниз, в сторону источников [Gudkova et al., 2020; 2021; Salnikov et al., 2021]. На Марсе динамо в настоящее время отсутствует, и спутниковые данные свидетельствуют о фрагментарной картине остаточной намагниченности на Красной планете. Как мы уже отмечали в приведенных выше работах, причина исчезновения магнитного поля Марса не установлена.
В настоящей работе мы предприняли попытку аппроксимации аномального магнитного поля Земли в районе Японского моря, согласно данным модели EMAG2v3 [Meyer et al., 2017]. Модель EMAG3v3 получена объединением низкочастотных спутниковых данных, в основном представленных сферической моделью MF7, вычисленной по измерениям спутниковой миссии CHAMP в период с 2007 по 2010 гг., с большим объемом инструментальных морских и аэромагнитных съемок. Пространственное разрешение модели составляет 2', и мы выбирали именно такое значение шага дискретизации при постановке математического эксперимента.
Аппроксимации магнитного поля строились с помощью комбинированной методики, включающей в себя региональный вариант метода модифицированных S-аппроксимаций с учетом эллиптичности и математическую модель поля в трехмерном декартовом пространстве, зависящую от времени в качестве параметра.
Поскольку данные дистанционного зондирования Земли (а тем более, других космических объектов) значительно превышают по объему информацию, полученную каким-либо другим способом, необходимо учитывать особенности топологии планеты при создании аналитических моделей физических полей и топографии. Поэтому при интерпретации гравиметрических и магнитометрических данных в глобальном и региональном масштабах нам представляется целесообразным учет эллиптичности планеты в той или иной степени.
Представление Земли в виде полупространства при решении интерпретационных задач существенно упрощает как математические выкладки, так и вычислительные алгоритмы. При разработке нового варианта метода линейных интегральных представлений для решения нестационарных задач (возникающих при описании физических процессов, описываемых уравнениями в частных производных параболического и гиперболического типов) желательно, на наш взгляд, начать рассмотрение постановок в прямоугольных координатах. Впоследствии результаты можно будет перенести на случай произвольной системы координат.
ОПИСАНИЕ МЕТОДИКИ
Мы неоднократно подчеркивали в предыдущих работах [Stepanova, 2008; Раевский и др., 2015а; 2015б], что локальные интегральные представления элементов физических полей и других сигналов строятся для небольших по площади территорий: не более 104 км2, в отличие от глобальных (линейные аналитические аппроксимации строятся для всей Земли) или региональных (линейные аналитические аппроксимации строятся для больших по площади территорий – порядка (105–106) км2) [Stepanova, 2009].
В данной работе будут рассматриваться зависящие от времени физические поля и другие сигналы в декартовой системе координат – можно полагать, что мы ограничиваемся пока только локальным вариантом ввиду сложности задачи аналитического описания нестационарного поля в глобальном масштабе. Однако такой подход не ограничивает общности: в принципе, можно решать и глобальные задачи в общеземной системе координат. Но тогда эквивалентные по внешнему полю источники окажутся принадлежащими слишком абстрактному классу объектов. С математической точки зрения это – упрощение, некая идеализация, нулевое приближение к решению нелинейной обратной задачи [Ягола и др., 2014]. И такое решение имеет право на существование, поскольку при изучении планет строятся, как правило, метрологические аппроксимации полей: количественная информация об источниках совершенно не доступна [Страхов, Степанова, 2002]. В работе [Степанова и др., 2019] мы предложили применять для интерпретации данных гравимагниторазведки метод линейных интегральных представлений повышенной размерности. При таком подходе, как показал математический эксперимент, особенности векторных полей выявляются с большей степенью точности при построении метрологических аппроксимаций.
Если эллиптичность не учитывается, то планета считается шаром радиуса ${{R}_{0}}$.
В том случае, когда эллиптичность нужно учитывать, Земля представляется в виде эллипсоида с полуосями a, b, c.
Если известны геодезические координаты точки наблюдения, то декартовы можно выразить через геодезические по известным формулам [Шимбирев, 1975]:
(1)
$\begin{gathered} X = (N + H)\cos B\cos L, \\ Y = (N + H)\cos B\sin L, \\ Z = ((1 - {{e}^{2}})N + H)\sin B, \\ \end{gathered} $Радиус кривизны первого вертикала и квадрата эксцентриситета эллипсоида вычисляются по формулам:
(2)
$N = \frac{a}{{\sqrt {1 - {{e}^{2}}{{{\sin }}^{2}}B} }},\,\,\,\,{{e}^{2}} = 2\alpha - {{\alpha }^{2}},$“Идеализированную” Землю будем считать внутренностью эллипсоида с полуосями a, b, c, а реальную Землю представим как область, ограниченную кусочно-непрерывной замкнутой поверхностью S, мало отклоняющейся от этого эллипсоида и содержащей его внутри себя. Предположим, что в некоторой (произвольной) совокупности точек ${{x}^{{\left( i \right)}}},i = 1,2,...,N,$ на поверхности S заданы приближенные значения гармонической (во внешности эллипсоида) функции $G(x)$:
(3)
${{f}_{{i,\delta }}} = {{f}_{i}} + \delta {{f}_{i}},\,\,\,\,{{f}_{i}} = G({{x}^{{\left( i \right)}}}).$Здесь $G\left( x \right)$ имеет следующее интегральное представление:
(4)
$\begin{gathered} G\left( x \right) = \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{I(\vartheta ,\phi )\sigma \left( {\vartheta ,\phi } \right)\sin \vartheta d\phi d\vartheta }}{{R\left( {\xi - x} \right)}}} } + \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{I(\vartheta ,\phi )w\left( {\vartheta ,\phi } \right)\left\{ {1 - \left[ {\frac{{{{x}_{1}}{{\xi }_{1}}}}{{{{a}^{2}}}} + \frac{{{{x}_{2}}{{\xi }_{2}}}}{{{{b}^{2}}}} + \frac{{{{x}_{3}}{{\xi }_{3}}}}{{{{c}^{2}}}}} \right]} \right\}\sin \vartheta d\vartheta d\phi }}{{{{R}^{3}}\left( {\xi - x} \right)\sqrt {\frac{{\xi _{1}^{2}}}{{{{a}^{4}}}} + \frac{{\xi _{2}^{2}}}{{{{b}^{4}}}} + \frac{{\xi _{3}^{2}}}{{{{c}^{4}}}}} }}} } , \\ R\left( {\xi - x} \right) = {{({{\left| \xi \right|}^{2}} - 2\left| \xi \right|r\cos \vartheta {\kern 1pt} '\,\, + {{r}^{2}})}^{{1/2}}},\,\,\,\,\xi = (a\cos \tilde {\phi }\sin \tilde {\vartheta },b\sin \tilde {\phi }\sin \tilde {\vartheta },c\cos \tilde {\vartheta }), \\ x = (r\cos \tilde {\phi }\sin \tilde {\vartheta },r\sin \tilde {\phi }\sin \tilde {\vartheta },r\cos \tilde {\vartheta }),\,\,\,\,\cos \vartheta {\kern 1pt} ' = \sin \vartheta \sin \tilde {\vartheta }\cos (\phi - \tilde {\phi }) + \cos \vartheta \cos \tilde {\vartheta }, \\ x = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right),\,\,\,\,\xi = \left( {{{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}} \right),\,\,\,I(\vartheta ,\phi ) = \sin \vartheta \sqrt {{{a}^{2}}{{b}^{2}}{{{\cos }}^{2}}\vartheta + {{a}^{2}}{{c}^{2}}{{{\sin }}^{2}}\vartheta {{{\sin }}^{2}}\phi + {{b}^{2}}{{c}^{2}}{{{\sin }}^{2}}\vartheta {{{\cos }}^{2}}\phi } . \\ \end{gathered} $Относительно функций $\sigma $ и $w$ ставится следующая условно вариационная задача:
(5)
$\begin{gathered} \Omega (\sigma ,w) = \int\limits_0^{2\pi } {\int\limits_0^\pi {\left( {\frac{{{{\sigma }^{2}}(\vartheta ,\varphi )}}{{p_{1}^{2}}} + \frac{{w_{{}}^{2}(\vartheta ,\varphi )}}{{p_{2}^{2}}}} \right)\sin \vartheta d\vartheta d\varphi } } = \mathop {{\text{min}}}\limits_{\sigma ,w} , \\ G\left( {{{x}^{{(i)}}}} \right) = \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{I(\vartheta ,\phi )\sigma \left( {\vartheta ,\phi } \right)\sin \vartheta d\phi d\vartheta }}{{R\left( {\xi - {{x}^{{(i)}}}} \right)}}} } + \int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{I(\vartheta ,\phi )w\left( {\vartheta ,\phi } \right)\left\{ {1 - \left[ {\frac{{x_{1}^{{(i)}}{{\xi }_{1}}}}{{{{a}^{2}}}} + \frac{{x_{2}^{{(i)}}{{\xi }_{2}}}}{{{{b}^{2}}}} + \frac{{x_{3}^{{(i)}}{{\xi }_{3}}}}{{{{c}^{2}}}}} \right]} \right\}\sin \vartheta d\vartheta d\phi }}{{{{R}^{3}}\left( {\xi - {{x}^{{(i)}}}} \right)\sqrt {\frac{{\xi _{1}^{2}}}{{{{a}^{4}}}} + \frac{{\xi _{2}^{2}}}{{{{b}^{4}}}} + \frac{{\xi _{3}^{2}}}{{{{c}^{4}}}}} }}} } , \\ R\left( {\xi - {{x}^{{(i)}}}} \right) = {{({{\left| \xi \right|}^{2}} - 2\left| \xi \right|{{r}^{{(i)}}}\cos {{\vartheta }^{{(i)}}}^{'} + {{({{r}^{{(i)}}})}^{2}})}^{{1/2}}}\,\,\,\,,\xi = (a\cos \phi \sin \vartheta ,b\sin \phi \sin \vartheta ,c\cos \vartheta ), \\ {{x}^{{(i)}}} = ({{r}^{{(i)}}}\cos {{{\tilde {\phi }}}^{{(i)}}}\sin {{{\tilde {\vartheta }}}^{{(i)}}},{{r}^{{(i)}}}\sin {{{\tilde {\phi }}}^{{(i)}}}\sin {{{\tilde {\vartheta }}}^{{(i)}}},{{r}^{{(i)}}}\cos {{{\tilde {\vartheta }}}^{{(i)}}}), \\ \cos {{\vartheta }^{{(i){\kern 1pt} '}}} = \sin \vartheta \sin {{{\tilde {\vartheta }}}^{{(i)}}}\cos (\phi - {{{\tilde {\phi }}}^{{(i)}}}) + \cos \vartheta \cos {{{\tilde {\vartheta }}}^{{(i)}}}, \\ {{x}^{{(i)}}} = \left( {x_{1}^{{(i)}},x_{2}^{{(i)}},x_{3}^{{(i)}}} \right),\,\,\,\,\xi = \left( {{{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}} \right),\,\,\,i = 1...N, \\ I(\vartheta ,\phi ) = \sin \vartheta \sqrt {{{a}^{2}}{{b}^{2}}{{{\cos }}^{2}}\vartheta + {{a}^{2}}{{c}^{2}}{{{\sin }}^{2}}\vartheta {{{\sin }}^{2}}\phi + {{b}^{2}}{{c}^{2}}{{{\sin }}^{2}}\vartheta {{{\cos }}^{2}}\phi } . \\ \end{gathered} $Функции $p_{1}^{2}(\vartheta ,\varphi ),\;p_{2}^{2}(\vartheta ,\varphi )$ в вариационной постановке (5) должны отражать свойства области задания эквивалентных по внешнему полю носителей масс. В частности, эти функции могут принимать заданные значения на границе области, внутри или вне которой нужно найти распределение элементов поля. В то же время, сами указанные функции могут быть неизвестными, и их определение можно сравнить с механизмом адаптивной регуляризации: элементы матрицы системы линейных алгебраических уравнений (СЛАУ), к решению которой редуцируется вариационная постановка (5), зависят от $p_{1}^{2}(\vartheta ,\varphi ),\;p_{2}^{2}(\vartheta ,\varphi )$ . Можно рассмотреть, таким образом, некоторое семейство вариационных задач по определению как неизвестных распределений масс, так и областей задания источников. Подобные вариационные постановки относятся к нелинейным обратным задачам, что существенно осложняет процесс поиска решения. Наша методика построения аналитических моделей зависящего от времени магнитного поля Земли может быть описана следующим образом.
Решение вариационной задачи (5) при известных функциях $p_{1}^{2}(\vartheta ,\varphi ),\;p_{2}^{2}(\vartheta ,\varphi )$ эквивалентно решению системы линейных алгебраических уравнений [Страхов, Степанова, 2002] :
где вектор ${{f}_{\delta }}$ имеет компоненты ${{f}_{{i,\delta }}}$, а матрица ${\text{A}} = {{{\text{A}}}^{{\text{T}}}} \geqslant 0$ имеет элементы(7)
${{a}_{{ij}}} = \int\limits_0^{2\pi } \begin{gathered} \int\limits_0^\pi {\left[ {p_{1}^{2}Q_{i}^{{\left( 1 \right)}}\left( \xi \right)Q_{j}^{{\left( 1 \right)}}\left( \xi \right) + p_{2}^{2}Q_{i}^{{\left( 2 \right)}}\left( \xi \right)Q_{j}^{{\left( 2 \right)}}\left( \xi \right)} \right]} \times \\ \times \,\,I(\vartheta ,\phi )\sin \vartheta d\vartheta d\phi \\ \end{gathered} .$Для $\sigma $ и $w$ получаем представление:
(8)
$\sigma \left( \xi \right) = p_{1}^{2}\sum\limits_{i = 1}^N {{{\lambda }_{i}}Q_{i}^{{\left( 1 \right)}}\left( \xi \right)} ,\,\,\,\,w\left( \xi \right) = p_{2}^{2}\sum\limits_{i = 1}^N {{{\lambda }_{i}}Q_{i}^{{\left( 2 \right)}}\left( \xi \right)} ,$(9)
$\begin{gathered} Q_{i}^{{\left( 1 \right)}}\left( \xi \right) = \frac{1}{{R\left( {\xi - {{x}^{{\left( i \right)}}}} \right)}}, \\ Q_{i}^{{\left( 2 \right)}}\left( \xi \right) = \frac{{\left\{ {1 - \left[ {\frac{{x_{1}^{{(i)}}{{\xi }_{1}}}}{{{{a}^{2}}}} + \frac{{x_{2}^{{(i)}}{{\xi }_{2}}}}{{{{b}^{2}}}} + \frac{{x_{3}^{{(i)}}{{\xi }_{3}}}}{{{{c}^{2}}}}} \right]} \right\}}}{{{{R}^{3}}\left( {\xi - {{x}^{{(i)}}}} \right)\sqrt {\frac{{\xi _{1}^{2}}}{{{{a}^{4}}}} + \frac{{\xi _{2}^{2}}}{{{{b}^{4}}}} + \frac{{\xi _{3}^{2}}}{{{{c}^{4}}}}} }}. \\ \end{gathered} $Если функции $p_{1}^{2}(\vartheta ,\varphi ),\;p_{2}^{2}(\vartheta ,\varphi )$ тождественно на сфере равны 1, то для элементов матрицы СЛАУ получаем следующие выражения:
(10)
$\begin{gathered} {{a}_{{ij}}} = \\ = \int\limits_0^{2\pi } {\int\limits_0^\pi {\left[ {Q_{i}^{{\left( 1 \right)}}\left( \xi \right)Q_{j}^{{\left( 1 \right)}}\left( \xi \right) + Q_{i}^{{\left( 2 \right)}}\left( \xi \right)Q_{j}^{{\left( 2 \right)}}\left( \xi \right)} \right]\sin \vartheta d\vartheta d\phi } } = \\ = \frac{{2\pi }}{{{{{({{h}_{i}}{{h}_{j}})}}^{{1/2}}}{{r}_{i}}{{r}_{j}}}}(1 + \frac{{0.25}}{{{{r}_{i}}{{r}_{j}}{{h}_{i}}{{h}_{j}}}})F(2{\text{arctg}}(\sqrt {{{h}_{i}}{{h}_{j}}} ), \\ \sqrt {0.5(1 + \cos {{\alpha }_{i}}_{j})} ) - \\ - \,\,\frac{{\pi (3{{{({{h}_{i}}{{h}_{j}})}}^{2}} - 4{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j}) + 1)}}{{{{r}_{i}}^{2}r_{j}^{2}{{h}_{i}}{{h}_{j}}{{{(\sqrt {1 - 2{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j}) + {{{({{h}_{i}}{{h}_{j}})}}^{2}}} )}}^{3}}}}, \\ \end{gathered} $где $Q_{i}^{{(1)}}(\xi )$ и $Q_{i}^{{(2)}}(\xi )$ определяются выражениями:
(11)
$Q_{i}^{{(1)}}(\xi ) = \frac{1}{{R(\xi - {{x}^{{(i)}}})}},\,\,\,\,Q_{i}^{{(2)}}(\xi ) = \frac{{R - {{r}_{i}}\cos \vartheta _{i}^{'}}}{{{{R}^{3}}(\xi - {{x}^{{(i)}}})}}.$Здесь ${{h}_{i}} = \frac{{{{R}_{0}}}}{{{{r}_{i}}}},\,\,{{h}_{j}} = \frac{{{{R}_{0}}}}{{{{r}_{j}}}}$ , а ${{\alpha }_{{ij}}}$ – это угол между векторами ${{x}_{i}}$ и ${{x}_{j}}$. Выражения (10) были получены в предположении, что вектор ${{x}_{i}}$ параллелен оси Oz, в то время как вектор ${{x}_{j}}$ лежит в плоскости zOx (в случае сферы мы всегда можем выбрать такую систему координат, в отличие от эллипсоида). Тогда радиус-векторы i-ой и j-ой точек будут иметь координаты ${{x}_{i}} = ({{r}_{i}},0,0)$ и ${{x}_{j}} = ({{r}_{j}}\sin {{\alpha }_{{ij}}},\,\,0,{{r}_{j}}\cos {{\alpha }_{{ij}}})$.
Функция $F(\varphi ,k)$ в (10) представляет собой эллиптический интеграл первого рода.
Если вместо сферы поверхностью интегрирования является эллипсоид с полуосями a, b, c (т.е. верно интегральное представление (4) и рассматривается соответствующая вариационная постановка), то следует перейти в пространство других декартовых координат.
А именно, положим:
(12)
$x{\kern 1pt} ' = \frac{x}{a},\,\,\,\,y{\kern 1pt} ' = \frac{y}{b},\,\,\,\,z{\kern 1pt} ' = \frac{z}{c}.$Эллипсоид с указанными полуосями переходит при такой замене координат в сферу единичного радиуса, а точки наблюдения – в точки штрихованного пространства по формулам (12), внешние по отношению к единичной сфере.
Преобразование (12) не является ортогональным и, по этой причине, расстояния между точками не сохраняются. Если решить вариационную задачу для “штрихованной” единичной сферы, а затем перейти в “нормальное” декартово пространство, то элементы матрицы (10) принимают вид:
Здесь ${{\tilde {h}}_{i}} = \frac{1}{{r_{i}^{'}}},$ $\tilde {h}_{j}^{'} = \frac{1}{{r_{j}^{'}}},$ $r_{i}^{'} = \sqrt {x_{{1,i}}^{{'2}} + x_{{2,i}}^{{'2}} + x_{{3,i}}^{{'2}}} ,$ $r_{j}^{'} = \sqrt {x_{{1,j}}^{{'2}} + x_{{2,j}}^{{'2}} + x_{{3,j}}^{{'2}}} $, а ${{\tilde {\alpha }}_{{ij}}}$ – это угол между векторами $x_{i}^{'}$ и $x_{j}^{'}$.
Таким образом, для построения линейных трансформант гравитационного или магнитного поля в региональном варианте с учетом эллиптичности можно решить СЛАУ с элементами матрицы, выражающимися по формулам (13).
Безусловно, при таком подходе невозможно учесть все топологические особенности планеты, но представление элементов матрицы СЛАУ в аналитическом виде существенно упрощает процесс нахождения устойчивого приближенного решения обратной задачи. Как видно из выражений (12) и (13), время в таких моделях никак не фигурирует.
При задании пространственных координат точек наблюдения необходимо руководствоваться формулами (1)–(2), связывающими геодезические (или сферические) и декартовы координаты точки наблюдения в общеземной системе координат.
Нестационарность магнитного поля может учитываться по-разному: все определяется конкретной постановкой. В последние 10–20 лет для интерпретации данных о магнитных полях Земли и планет особенно популярным среди зарубежных исследователей стал так называемый метод сингулярных магнитных диполей (ESD) [Whaler et al., 2005; Langlais et al., 2004]. Существует также вариант указанного метода с зависящими от времени компонентами вектора намагниченности [Oliveira et al., 2015]. При этом авторы выбирали наиболее простую форму зависимости – линейную.
В общем случае, поведение магнитного поля планеты (как внешнего, так и внутреннего) определяется из решения достаточно сложной системы уравнений магнитной гидродинамики [Арнольд, Хесин, 2007]:
(14)
$\begin{gathered} \frac{{\partial{ \bar {v}}}}{{\partial t}} = - \left( {\bar {v},\nabla \bar {v}} \right) + \left[ {\bar {B},{\text{rot}}\bar {B}} \right] - \nabla p, \\ \frac{{\partial{ \bar {B}}}}{{\partial t}} = - \left\{ {\bar {v},\bar {B}} \right\} + \nu \Delta \bar {B}, \\ {\text{div}}\bar {v} = 0,\,\,\,\,{\text{div}}\bar {B} = 0. \\ \end{gathered} $В (14): $\bar {v}(\bar {r},t),\;\bar {B}(\bar {r},t)$ - соответственно поле скоростей и магнитная индукция как функции радиус-вектора и времени; $\nabla p$ – градиент давления в среде; $\Delta $ – оператор Лапласа. Квадратные скобки означают векторное произведение двух векторов, а фигурные скобки – это скобка Пуассона двух векторных полей, определяемая как:
Для нахождения приближенного решения системы (14) необходимо заменить дифференциальные операторы их конечно-разностными аналогами. Помимо этого, необходимо учесть граничные и начальные условия, которым удовлетворяют поля (они являются вектор-функциями трех пространственных координат и времени).
Если мы интерпретируем данные о магнитном поле планеты, полученные в результате дистанционного зондирования, то система (14) (или подобная ей) должна учитывать взаимодействие внутреннего (достаточно сильного) поля с магнитным полем, создаваемым потоком заряженных частиц (солнечного ветра), если же нас интересует сам процесс генерации динамо, то поле скоростей в (14) – это поток раскаленной жидкости в ядре.
В обоих случаях поле скоростей и магнитное поле связаны между собой, и “отделить” одну вектор-функцию от другой не представляется возможным.
Целью настоящей работы, как это уже подчеркивалось во Введении, является построение такой математической модели магнитного поля Земли по данным наблюдений, которая могла бы быть полезна при изучении и уточнении внутреннего строения как нашей планеты, так и других космических объектов.
Поэтому мы разработали комбинированную методику интерпретации данных магниторазведки. Кратко последовательность действий в рамках этой методики можно описать следующим образом:
1) по данным наблюдений о магнитном поле в региональном масштабе строится аналитическая модель вектора магнитной индукции (или модуля вектора) в рамках регионального варианта модифицированных S-аппроксимаций с учетом эллиптичности. Весовые функции в вариационной постановке (5) при этом могут подбираться с учетом конкретной постановки и имеющейся априорной информации о возможных источниках поля (геологическом строении региона и т.п.);
2) по построенной в соответствии с рекомендациями п.1 аналитической модели магнитного поля в изучаемом регионе определяются начальные, граничные и другие условия (вектор-функции), которые необходимы для нахождения распределения значений магнитного поля в верхнем полупространстве (если считать Землю нижним полупространством в декартовых координатах) в произвольный момент времени. Время на данном этапе создания комбинированной методики интерпретации магнитных данных считается параметром задачи.
Две составляющие аналитической модели магнитного поля могут показаться избыточными, на первый взгляд. Однако магнитное поле, как мы уже подчеркивали, не может, в общем случае, рассматриваться как решение уравнения Лапласа (в области, не занятой магнитными массами) или Пуассона (в коре планеты, но не в ядре при наличии магнитного динамо).
Можно ограничиться, безусловно, и одной из двух компонент новой математической модели поля в рамках модифицированных S-аппроксимаций, но сочетание двух составляющих обеспечивает более гибкий подход к вычислению линейных трансформант: аналитическому продолжению магнитного поля вверх или вниз.
Опишем теперь, как строится вторая “компонента” математической модели магнитного поля Земли. В настоящей работе мы полагаем, что время – это некий непрерывно меняющийся от нуля до бесконечности параметр модели . Параметр ${{a}^{2}}$ можно считать достаточно большим: если ${{a}^{2}} \to \infty $, то решение приведенного ниже уравнения параболического типа будет стремиться к решению уравнения Лапласа. Ну, а в случае системы (14) указанный параметр связан с коэффициентом магнитной вязкости (магнитным числом Рейнольдса), но мы пока не рассматриваем решение системы (14) в целом.
Как известно, метод спуска по одной из независимых переменных [Владимиров, 1981] позволяет получить решение краевой задачи в пространстве N переменных, если найдено соответствующее решение в N + 1-ом пространстве. Поэтому переход от вектор-функции, зависящей от трех пространственных переменных, к вектор-функции в четырехмерном пространстве (четвертая координата – это время) нам кажется оправданным при построении метрологических аппроксимаций элементов физических полей и топографии.
Если считать Землю (или другую планету) нижним полупространством, ограниченным плоскостью ${{x}_{3}} = 0$ в декартовой системе координат (${{x}_{1}}~{{x}_{{2,}}}~{{x}_{3}}$), то решение первой краевой задачи для уравнения теплопроводности (или диффузии, важно – уравнения параболического типа с постоянными коэффициентами в верхнем полупространстве) можно записать в следующем виде:
(15)
$\begin{gathered} \frac{{\partial{ \bar {B}}}}{{\partial t}} = {{a}^{2}}\Delta \bar {B},\,\,\,\,0 < t < + \infty ,\,\,\,\, - \infty < {{x}_{1}} < + \infty , \\ - \infty < {{x}_{2}} < + \infty ,\,\,\,\,0 < {{x}_{3}} < + \infty , \\ \bar {B}({{x}_{1}},{{x}_{2}},0,t) = \bar {\Psi }({{x}_{1}},{{x}_{2}},t), \\ \bar {B}({{x}_{1}},{{x}_{2}},{{x}_{3}},0) = {{{\bar {B}}}_{0}}({{x}_{1}},{{x}_{2}},{{x}_{3}}). \\ \bar {B}\left( {{\mathbf{x}},t} \right) = \frac{1}{{{{{(2a\sqrt \pi )}}^{3}}}}\int\limits_0^\infty {d{{\xi }_{3}}\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{2}}} } \int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{1}}} {{{\bar {B}}}_{0}}({\mathbf{\xi }}) \times \\ \times \,\,\left\{ {\frac{{\exp ( - {{{{{\left| {{\mathbf{x}} - {\mathbf{\xi }}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{\mathbf{x}} - {\mathbf{\xi }}} \right|}}^{2}}} {(4{{a}^{2}}t)}}} \right. \kern-0em} {(4{{a}^{2}}t)}}}}{t} - \frac{{\exp ( - {{{{{\left| {{\mathbf{x}} + {\mathbf{\xi }}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{\mathbf{x}} + {\mathbf{\xi }}} \right|}}^{2}}} {(4{{a}^{2}}t)}}} \right. \kern-0em} {(4{{a}^{2}}t)}}}}{t}} \right\} + \\ + \,\,\frac{{{{x}_{3}}}}{{{{{(2a\sqrt \pi )}}^{3}}}}\int\limits_0^t {d\tau \int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{2}}} } \times \\ \times \,\,\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{1}}} \bar {\Psi }({\mathbf{\xi }})\left\{ {\frac{{\exp ( - {{{{{\left| {{\mathbf{x}} - {\mathbf{\xi }}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{\mathbf{x}} - {\mathbf{\xi }}} \right|}}^{2}}} {(4{{a}^{2}}(t - \tau ))}}} \right. \kern-0em} {(4{{a}^{2}}(t - \tau ))}}}}{{{{{(t - \tau )}}^{{3/2}}}}}} \right\}, \\ \left| {{\mathbf{x}} - {\mathbf{\xi }}} \right| = {{({{({{x}_{1}} - {{\xi }_{1}})}^{2}} + {{({{x}_{2}} - {{\xi }_{2}})}^{2}} + {{({{x}_{3}} - {{\xi }_{3}})}^{2}})}^{{1/2}}}, \\ {\mathbf{\xi }} = ({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}),\,\,\,\,{\mathbf{x}} = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right). \\ \end{gathered} $Формула (15) получена с помощью нечетного продолжения фундаментального решения уравнения теплопроводности во всем пространстве на нижнее полупространство (см., например, [Будак и др., 1980]). Решение неоднородного уравнения теплопроводности во всем пространстве имеет вид:
(16)
$\begin{gathered} \frac{{\partial{ \bar {B}}}}{{\partial t}} = {{a}^{2}}\Delta \bar {B} + \bar {f},\,\,\,\,0 < t < + \infty ,\,\,\,\, - \infty < {{x}_{1}} < + \infty , \\ - \infty < {{x}_{2}} < + \infty ,\,\,\,\, - \infty < {{x}_{3}} < + \infty , \\ \bar {B}\left( {{\mathbf{x}},t} \right) = \frac{1}{{{{{(2a\sqrt \pi )}}^{3}}}}\int\limits_0^t {d\tau } \int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{3}}\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{2}}} } \times \\ \times \,\,\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{1}}} \bar {f}({\mathbf{\xi }},\tau )\left\{ {\frac{{\exp ( - {{{{{\left| {{\mathbf{x}} - {\mathbf{\xi }}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{\mathbf{x}} - {\mathbf{\xi }}} \right|}}^{2}}} {(4{{a}^{2}}t)}}} \right. \kern-0em} {(4{{a}^{2}}t)}}}}{t}} \right\} \\ \left| {{\mathbf{x}} - {\mathbf{\xi }}} \right| = {{({{({{x}_{1}} - {{\xi }_{1}})}^{2}} + {{({{x}_{2}} - {{\xi }_{2}})}^{2}} + {{({{x}_{3}} - {{\xi }_{3}})}^{2}})}^{{1/2}}}, \\ {\mathbf{\xi }} = ({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}),\,\,\,{\mathbf{x}} = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right). \\ \end{gathered} $Представления решения краевой задачи (15) или уравнения относительно вектор-функции $\bar {B}({\mathbf{x}},t)$ (16) позволяют нам применить метод линейных интегральных представлений [Страхов, Степанова, 2002] в локальном варианте, когда Земля представляется в виде нижнего полупространства, а компоненты магнитной индукции известны в верхнем полупространстве.
В случае уравнения параболического типа основные моменты метода интегральных представлений требуют уточнений и пояснений.
Обратимся к формуле (15) и попробуем сформулировать задачу по поиску минимума некоторого функционала, опираясь на соотношения (5). Вариационные постановки, возникающие при применении различных версий метода линейных интегральных представлений, предполагают наличие у минимизируемой по норме ${{L}_{2}}({{M}_{r}})$ функции (функций, вектор-функций и т.п.) определенных свойств гладкости. Здесь ${{L}_{2}}({{M}_{r}})$ – гильбертово пространство интегрируемых с квадратом функций в областях задания источников поля ${{M}_{r}},\;r = 1,...,R.$
Если вектора магнитной индукции удовлетворяют уравнениям параболического типа, то интеграл по времени от произведения мощности источника и функции Грина для всего пространства берется от нуля до того момента времени, в который было осуществлено измерение сигнала (t, например). Для уравнения Лапласа мы всегда ставили вариационные задачи при фиксированном наборе множеств ${{M}_{r}},~r = 1, \ldots ,R.$ Мы предлагаем определять неизвестную мощность источников из решения следующей вариационной постановки:
(17)
$\begin{gathered} \frac{{\partial{ \bar {B}}}}{{\partial t}} = {{a}^{2}}\Delta \bar {B} + \bar {f},\,\,\,\,0 < t < + \infty ,\,\,\,\, - \infty < {{x}_{1}} < + \infty , \\ - \infty < {{x}_{2}} < + \infty ,\,\,\,\, - \infty < {{x}_{3}} < + \infty , \\ \frac{1}{{{{{(2a\sqrt \pi )}}^{3}}}}\int\limits_0^{ + \infty } {d\tau } \int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{3}}\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{2}}\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{1}}} {{{\bar {f}}}^{2}}(\xi ,\tau )} } = \mathop {\min }\limits_{f(\xi ,\tau )} , \\ \bar {B}\left( {{{{\mathbf{x}}}_{i}},{{t}_{i}}} \right) = \frac{1}{{{{{(2a\sqrt \pi )}}^{3}}}}\int\limits_0^{{{t}_{i}}} {d\tau } \int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{3}}\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{2}}} } \times \\ \times \,\,\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{1}}} \bar {f}(\xi ,\tau )\left\{ {\frac{{\exp ( - {{{{{\left| {{{{\mathbf{x}}}_{i}} - {\mathbf{\xi }}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{{{\mathbf{x}}}_{i}} - {\mathbf{\xi }}} \right|}}^{2}}} {(4{{a}^{2}}({{t}_{i}} - \tau ))}}} \right. \kern-0em} {(4{{a}^{2}}({{t}_{i}} - \tau ))}}}}{{({{t}_{i}} - \tau )}}} \right\}, \\ \left| {{\mathbf{x}} - {\mathbf{\xi }}} \right| = {{({{({{x}_{1}} - {{\xi }_{1}})}^{2}} + {{({{x}_{2}} - {{\xi }_{2}})}^{2}} + {{({{x}_{3}} - {{\xi }_{3}})}^{2}})}^{{1/2}}}, \\ {\mathbf{\xi }} = ({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}),\,\,\,{\mathbf{x}} = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right). \\ \end{gathered} $Решением вариационной задачи (17) будет служить функция:
(18)
$\begin{gathered} \bar {f}({\mathbf{x}},t) = \sum\limits_{j = 1}^N {{{\lambda }_{j}}} \frac{{\exp ( - {{{{{\left| {{\mathbf{x}} - {{{\mathbf{x}}}_{j}}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{\mathbf{x}} - {{{\mathbf{x}}}_{j}}} \right|}}^{2}}} {(4{{a}^{2}}({{t}_{j}} - t)}}} \right. \kern-0em} {(4{{a}^{2}}({{t}_{j}} - t)}})}}{{{{{({{t}_{j}} - t)}}^{{3/2}}}}}, \\ \left| {{\mathbf{x}} - {\mathbf{\xi }}} \right| = {{({{({{x}_{1}} - {{\xi }_{1}})}^{2}} + {{({{x}_{2}} - {{\xi }_{2}})}^{2}} + {{({{x}_{3}} - {{\xi }_{3}})}^{2}})}^{{1/2}}}, \\ {\mathbf{\xi }} = ({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}),\,\,\,{\mathbf{x}} = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right). \\ \end{gathered} $Для элементов матрицы, соответствующей СЛАУ, получим выражения:
(19)
${{a}_{{ij}}} = \frac{{\sqrt \pi a}}{{\left| {{{{\mathbf{x}}}_{{\mathbf{i}}}} - {{{\mathbf{x}}}_{{\mathbf{j}}}}} \right|}}\left\{ {\Phi \left( {\frac{{\left| {{{{\mathbf{x}}}_{{\mathbf{i}}}} - {{{\mathbf{x}}}_{{\mathbf{j}}}}} \right|}}{{2a({{t}_{i}} - {{t}_{j}})}}} \right) - \Phi \left( {\frac{{\left| {{{{\mathbf{x}}}_{{\mathbf{i}}}} - {{{\mathbf{x}}}_{{\mathbf{j}}}}} \right|}}{{2a({{t}_{i}} + {{t}_{j}})}}} \right)} \right\},$При решении вариационных задач, основанных на соотношениях (15), можно считать, что функция $\frac{{\partial {{V}_{a}}\left( x \right)}}{{\partial {{x}_{3}}}}$, гармоническая в полупространстве x3 > –H (или ${{x}_{3}} < H$ ) и связанная с потенциалом аномального магнитного поля ${{V}_{a}}(x)$, имеет следующее интегральное представление:
(20)
$\begin{gathered} \frac{{\partial {{V}_{a}}({\mathbf{x}})}}{{\partial {{x}_{3}}}} = \frac{{{{x}_{3}}}}{{{{{(2a\sqrt \pi )}}^{3}}}} \times \\ \times \,\,\int\limits_0^t {d\tau \int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{2}}\int\limits_{ - \infty }^{ + \infty } {d{{\xi }_{1}}} \bar {\Psi }({\mathbf{\xi }})\left\{ {\frac{{\exp ( - {{{{{\left| {{\mathbf{x}} - {\mathbf{\xi }}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{\mathbf{x}} - {\mathbf{\xi }}} \right|}}^{2}}} {(4{{a}^{2}}(t - \tau ))}}} \right. \kern-0em} {(4{{a}^{2}}(t - \tau ))}}}}{{{{{(t - \tau )}}^{{3/2}}}}}} \right\}} } , \\ \left| {{\mathbf{x}} - {\mathbf{\xi }}} \right| = {{({{({{x}_{1}} - {{\xi }_{1}})}^{2}} + {{({{x}_{2}} - {{\xi }_{2}})}^{2}} + {{({{x}_{3}} + H)}^{2}})}^{{1/2}}}, \\ {\mathbf{\xi }} = ({{\xi }_{1}},{{\xi }_{2}},H),\,\,\,{\mathbf{x}} = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right). \\ - \infty < {{x}_{1}} < + \infty ,\,\,\, - \infty < {{x}_{2}} < + \infty ,\,\,\,0 < {{x}_{3}} < + \infty . \\ \end{gathered} $Здесь интегрирование выполняется по плоскости, на которой в данный момент времени находятся источники нестационарного поля (${{x}_{3}} = - H$).
Представим неизвестную в (20) функцию в следующем виде:
(21)
$\begin{gathered} \psi ({{\xi }_{1}},{{\xi }_{2}},\tau ) = \frac{1}{{{{{\left( {2a\sqrt \pi } \right)}}^{3}}}}\sum\limits_{j = 1}^N {{{\lambda }_{j}}} \left( {x_{3}^{{(j)}} + H} \right)\frac{{\exp \left( { - {{\left( {{{{(x_{1}^{{(j)}} - {{\xi }_{1}})}}^{2}} + {{{(x_{2}^{{(j)}} - {{\xi }_{2}})}}^{2}} + {{{\left( {x_{3}^{{(j)}} + H} \right)}}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{(x_{1}^{{(j)}} - {{\xi }_{1}})}}^{2}} + {{{(x_{2}^{{(j)}} - {{\xi }_{2}})}}^{2}} + {{{\left( {x_{3}^{{(j)}} + H} \right)}}^{2}}} \right)} {(4{{a}^{2}}(\tau + {{t}_{j}}))}}} \right. \kern-0em} {(4{{a}^{2}}(\tau + {{t}_{j}}))}}} \right)}}{{{{{(\tau + {{t}_{j}})}}^{{5/2}}}}}, \\ \left| {{\mathbf{x}} - {\mathbf{\xi }}} \right| = {{({{({{x}_{1}} - {{\xi }_{1}})}^{2}} + {{({{x}_{2}} - {{\xi }_{2}})}^{2}} + {{({{x}_{3}} - {{\xi }_{3}})}^{2}})}^{{1/2}}},\,\,\,\,{\mathbf{\xi }} = ({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}),\,\,\,\,{\mathbf{x}} = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right). \\ \end{gathered} $В этом случае задача о нахождении неизвестной функции $\psi (\tau ,{{x}_{1}},{{x}_{2}})$ сводится к определению вектора $\lambda = ({{\lambda }_{1}}, \ldots {{\lambda }_{N}})$.
Мы получаем характерную для постановок в рамках метода линейных интегральных представлений СЛАУ (систему линейных алгебраических уравнений):
в которой А есть (N × N) – матрица со свойством и элементами ${{a}_{{pq}}},\,\,1 \leqslant p,\,\,q \geqslant N$:(24)
${{\tilde {a}}_{{ij}}} = \frac{{\left( {x_{3}^{{(j)}} + x_{3}^{{(i)}} + 2H} \right)}}{{{{{\left( {2a\sqrt \pi } \right)}}^{3}}}}\left\{ {\frac{{\exp \left( { - {{\left( {{{{(x_{1}^{{(j)}} - x_{1}^{{(i)}})}}^{2}} + {{{(x_{2}^{{(j)}} - x_{2}^{{(i)}})}}^{2}} + {{{\left( {x_{3}^{{(j)}} + x_{3}^{{(i)}} + 2H} \right)}}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{(x_{1}^{{(j)}} - x_{1}^{{(i)}})}}^{2}} + {{{(x_{2}^{{(j)}} - x_{2}^{{(i)}})}}^{2}} + {{{\left( {x_{3}^{{(j)}} + x_{3}^{{(i)}} + 2H} \right)}}^{2}}} \right)} {(4{{a}^{2}}({{t}_{i}} + {{t}_{j}}))}}} \right. \kern-0em} {(4{{a}^{2}}({{t}_{i}} + {{t}_{j}}))}}} \right)}}{{{{{({{t}_{i}} + {{t}_{j}})}}^{{5/2}}}}}} \right\},$Нахождение адекватной реальной геофизической практике аналитической аппроксимации исходного элемента магнитного поля позволяет вычислять линейные трансформанты поля, особенно это важно при построении аналитического продолжения поля.
Можно подытожить вышесказанное о комбинированной методике нахождения аналитических моделей магнитного поля следующим образом.
1) По заданному набору точек наблюдения в трехмерном пространстве и заданным начальным приближениям к неизвестным весовым функциям ${{p}_{r}},{\kern 1pt} r = 1,2$, строится модифицированная S-аппроксимация в региональном варианте. Декартовы координаты при этом связаны с геодезическими соотношениями (1)–(2).
2) По найденному распределению эквивалентных по внешнему магнитному полю источников, распределенных на поверхности нескольких обобщенных сфер (см. формулы (13)) осуществляется аналитическое продолжение аппроксимированного поля в некоторую область трехмерного пространства. При этом вычисляется значение показателя качества решения, который представляет собой отношение эвклидовой нормы разности между теоретическими значениями поля и значениями, полученными в результате аппроксимации, к норме самого поля.
3) Весовые функции меняются в соответствии с определенным исследователем правилом, процесс повторяется до тех пор, пока не будет достигнута необходимая точность.
4) Значения магнитного поля в некоторой области трехмерного пространства, вычисленные на предыдущих шагах алгоритма, принимаются за начальные и граничные значения зависящей от времени вектор-функции, которая является решением трехмерного однородного (или неоднородного) уравнения параболического типа. Для указанной вектор-функции ставится вариационная задача – в рамках локальной версии метода интегральных представлений в трехмерном пространстве с зависимостью от времени – по нахождению источников масс, распределенных либо на семействе плоскостей трехмерного пространства (если рассматривается начально-краевая задача для уравнения теплопроводности), либо на некоторой дискретной сети точек (если принимается, что вектор-функция представляет собой решение уравнения параболического типа во всем пространстве).
Мы вынуждены констатировать на данном этапе разработки новой методики интерпретации магнитных данных, что закон изменения весовых функций может быть определен только эмпирически, ввиду сложности поиска решений нелинейных обратных задач геофизики и того факта, что существует несчетное множество эквивалентных по внешнему полю распределений масс.
При проведении тестовых расчетов был выбран следующий эмпирический закон изменения весовых функций:
Здесь: $r = \sqrt {{{{\left( {\xi - {{x}_{0}}} \right)}}^{2}} + {{{\left( {\eta - {{y}_{0}}} \right)}}^{2}} + {{{\left( {\varsigma - {{z}_{0}}} \right)}}^{2}}} ,$ $P = \left( {\xi ,\eta ,\varsigma } \right)$ – текущая точка на поверхности, по которой производится интегрирование; $M = \left( {{{x}_{0}},{{y}_{0}},{{z}_{0}}} \right)$ – координата центра масс рассматриваемого набора данных. Показатели степени m и n предполагаются равными целым положительным числам.
При нахождении S-аппроксимаций, иначе говоря – функций $\sigma \left( \xi \right)$ и $w\left( \xi \right)$, основная вычислительная проблема состоит в нахождении устойчивого приближенного решения (согласованного с имеющейся априорной информацией о векторах f и $\delta f$) системы линейных алгебраических уравнений (7)–(8).
Для решения систем (6), (7), (13) и (22)–(24) мы применили два метода, предложенные авторами в работах [Stepanova et al., 2020; Pan et al., 2020; Gudkova et al., 2020; Salnikov et al., 2020; 2021]. Первый из методов решения, плохо обусловленных СЛАУ, мы будем обозначать как БМХР (блочный метод регуляризации Холецкого), а второй – как УБМ (усовершенствованный блочный метод). В основе указанных методов лежит механизм адаптивной регуляризации. Сначала решается система уравнений, матрица которой строится по всему набору данных, а затем некоторые блоки матрицы “выключаются” из вычислительного процесса, если соответствующие компоненты вектора решения не оказывают значимого влияния на результат в целом. Мы протестировали оба метода на большом числе модельных и практических примеров, созданных по материалам гравимагниторазведки. В основном, при интерпретации гравиметрических и магнитометрических данных приходится решать СЛАУ, имеющих матрицы с диагональным преобладанием. Блоки матрицы, в которых содержится информация о взаимодействии далеко друг от друга расположенных носителей масс, отличаются существенно меньшим, по сравнению с диагональными, рангом. Поэтому можно сделать однозначный вывод о нецелесообразности выбора одного и того же параметра регуляризации для диагональных и внедиагональных блоков плохо обусловленной системы линейных алгебраических уравнений. В БМХР для каждого из блоков матрицы СЛАУ выполняется регуляризация разложения Холецкого, а в УБМ применяются как итерационные алгоритмы для поиска решения, так и прямые (основанные на регуляризации LU-разложения несимметричной матрицы). Усовершенствованный блочный метод позволяет решать систему и с единственным блоком. Автоматически выбор количества блоков матрицы и вектора параметров регуляризации пока не осуществляется ввиду высокой степени неустойчивости приближенных решений обратных линейных (а тем более, нелинейных) обратных задач геофизики. На данный момент возможны исключительно метрологические аппроксимации гравитационного и магнитного полей, поскольку количественная информация об источниках полей отсутствует.
АПРОБАЦИЯ АЛГОРИТМОВ И ПРОГРАММ НОВОЙ КОМБИНИРОВАННОЙ МЕТОДИКИ ПОСТРОЕНИЯ АНАЛИТИЧЕСКИХ МОДЕЛЕЙ МАГНИТНОГО ПОЛЯ ПО ДАННЫМ МОДЕЛИ EMAG3V3 В РАЙОНЕ ЯПОНСКОГО МОРЯ
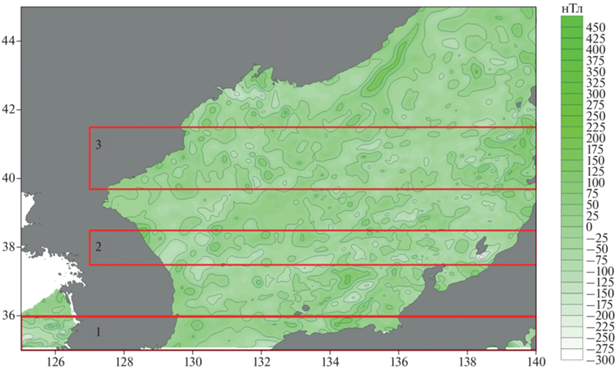
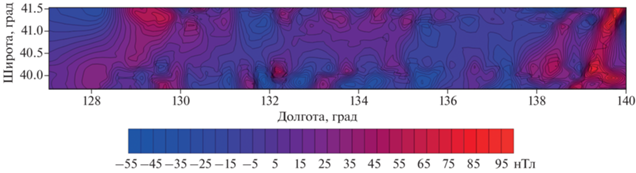
В работе [Родников и др., 2014] приводится сравнительно подробное описание морфологических особенностей магнитного поля в районе Японского моря. В юго-западной части Японского моря аномалии имеют субширотный характер и северо-западное и субмеридиональное простирание. В южной части моря наблюдается слабоинтенсивное знакопеременное поле, при этом аномалии магнитного поля достигают 300 нТл. В юго-западной части интенсивность аномалий не превосходит в среднем 100 нТл, иногда встречаются значения 300 нТл. Восточная часть Японского моря отличается слабоинтенсивными аномалиями до ±50 нТл, однако отрицательные локальные аномалии порой достигают значений 200 нТл. Как указывают авторы [Родников и др., 2014], существенного различия в структуре поля районов, непосредственно примыкающих к северной части о. Хонсю и удаленных от него, не отмечается. Здесь встречаются высокочастотные полосовые аномалии субширотного и северо-восточного простираний, амплитуда которых составляет ≥400 нТл. Положительным аномалиям можно поставить в соответствие массивы неогеновых и четвертичных вулканических пород. На северной оконечности острова преобладают отрицательные аномалии интенсивностью –400 нТл преимущественно меридионального простирания. Для примыкающих к северной части острова Хонсю участках северо-западной части Тихого океана можно отметить отрицательные (–400 нТл) и положительные (+200 нТл) линейные аномалии северо-восточного простирания.
Карта аномалий магнитного поля в районе Японского моря изображена на рис. 1 (согласно модели EMAG3v3).
Мы выбрали для тестирования новой методики полигон, размеры которого составили 12° по широте и 12° по долготе. Полигон был разбит на три подобласти по широте с целью выявления “сильных” и “слабых” мест нового алгоритма интерпретации магнитных данных. Для каждой из трех подобластей были сформированы по два массива точек наблюдения: один массив включал в себя значения географических координат и значения модуля аномального магнитного поля на уровне моря согласно модели EMAG3v3, а второй – отсортированные по значениям модуля магнитной индукции точки). В таблице 1 первые три строки соответствуют массивам первого типа, а последние три строки – второго типа. На первом этапе построения математической модели магнитного поля мы применили региональный вариант модифицированного метода S-аппроксимаций с указанными в предыдущем разделе статьи весовыми функциями.
Таблица 1.
Региональная S-aппроксимация магнитного поля в районе Японского моря с учетом эллиптичности
| № | N | a, b, c, км | Метод решения СЛАУ |
${{\sigma }_{{\min }}}$ нТесл |
${{\sigma }_{{\max }}}$ нТесл |
${{\sigma }_{0}}$ нТесл |
Δ/t |
|---|---|---|---|---|---|---|---|
| 1 | 5000 | 6365, 6370, 6370 |
БМХР | 0.015 | 0.020 | 0.018 | 1.2е–4 05:13 |
| 2 | 10 000 | 6365, 6370, 6370 |
БМХР | 0.027 | 0.032 | 0.031 | 1.5е–4 40:02 |
| 3 | 20000 | 6365, 6370, 6370 |
УБМ | 0.0001 | 0.00015 | 0.00012 | 1.7е–9 1:53:45 |
| 4 | 5000 | 6365, 6370, 6370 |
УБМ | 0.0001 | 0.00015 | 0.00012 | 1.8e–9 18:07 |
| 5 | 10 000 | 6365, 6370, 6370 |
УБМ | 0.0001 | 0.00015 | 0.00011 | 1.6e–9 45:13 |
| 6 | 20 000 | 6365,
6370, 6370 |
УБМ | 0.00001 | 0.000015 | 0.000014 | 2.1e–16 3:14:02 |
Примечания: ${{\sigma }^{{}}}$ = $\frac{{\left\| {Ax - {{f}_{\delta }}} \right\|_{E}^{{}}}}{{\sqrt N }}$ – среднеквадратическое отклонение; ${{\sigma }_{{\max }}} = \sqrt {\frac{{\delta _{{\max }}^{2}}}{N}} $; ${{\sigma }_{{\min }}} = \sqrt {\frac{{\delta _{{\min }}^{2}}}{N}} $; Δ = $\frac{{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}}}{{{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}}$- показатель качества решения; t– время в часах, минутах и секундах.
Магнитное поле аппроксимировалось суммой простого и двойного слоев, распределенных на поверхности эллипсоида, охватываемого земным шаром, (радиус Земли полагался равным 6378 км, полуоси эллипсоида – 6358–6370 км).
Результаты решения СЛАУ приведены в табл. 1; в последнем столбце этой таблицы содержатся значения показателя качества решения (фактически – относительной погрешности) и время, за которое была достигнута заранее заданная точность решения.
Весовые функции рассматривались трех типов:
Наилучший результат был достигнут для второго типа, и в табл. 1 приводятся показатели качества решения именно для этого случая.
Следует отметить, что результат решения СЛАУ (системы линейных алгебраических уравнений) зависит от конкретной постановки, и поэтому не представляется возможным дать рекомендации относительно выбора типа весовых функций в произвольном случае.
В таблице 1 показаны результаты первого этапа алгоритма для всех наборов тестовых данных. На рисунках мы решили показать аппроксимированное и исходное поле для некоторых примеров, поскольку прослеживается одна и та же тенденция: чем больше разброс координат в тестовом наборе, тем выше качество аппроксимации даже при четырехкратном увеличении числа неизвестных (с 5000 неизвестных до 20 000).
Шаг дискретизации в модели EMAG3v3 равен 2 мин, при выполнении расчетов мы задавали такой же.
После того, как была построена аналитическая аппроксимация модельного гравитационного поля с тремя типами весовых функций, было выполнено аналитическое продолжение магнитного поля вверх, на высоту 4 км.
На рис. 2а приводится карта изолиний магнитного поля в северной подобласти исследуемого региона, N = 10 000. На рис. 2б приводится карта изолиний поля, построенного в результате S-аппроксимации при выборе весовых функций (25) II-го типа.
Рис. 2.
(а) – Карта изолиний магнитного поля в северной подобласти исследуемого региона, N = 10 000; (б) – карта изолиний поля, построенного в результате S-аппроксимации при выборе весовых функций (25) II-го типа.
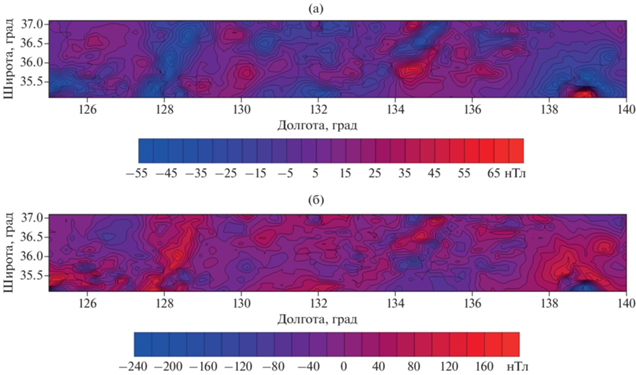
На рис. 3а показано поле южной подобласти. Число точек в наборе полагалось равным 10 000.
Рис. 3.
(а) – Магнитное поле южной подобласти, N = 10000, массив отсортирован; (б) – карта разности между полученными в результате аналитического продолжения на высоту 4 км и теоретическими значениями поля; весовые функции III типа; массив отсортирован.
Карта разности между полученными в результате аналитического продолжения на высоту 4 км и теоретическими значениями поля приведена на рис. 3б. Весовые функции III типа.
На рис. 4 приводится карта изолиний аппроксимированного магнитного поля с учетом эллиптичности при N = 20 000 (здесь N – число точек наблюдений, по которым строится аппроксимация) для южной подобласти, массив данных был отсортирован по возрастанию значений модуля аномального магнитного поля. Весовые функции II типа.
Рис. 4.
Карта изолиний аппроксимированного магнитного поля с учетом эллиптичности при N = 20 000 для южной подобласти, массив данных был отсортирован по возрастанию значений модуля аномального магнитного поля, весовые функции II типа.
После того, как для каждой из подобластей была построена модифицированная S-аппроксимация магнитного поля на уровне моря и на высоте 4 км, мы перешли ко второму этапу алгоритма. Мы поставили задачу (21)–(24) для каждого из описанных выше наборов данных о поле. Время можно ввести в функцию, зависящую лишь от пространственных координат, следующим образом (безусловно, предлагаемая далее конструкция не должна ограничивать общность: если известны компоненты вектора магнитной индукции в реальные моменты времени, то время будет независимой переменной в системе дифференциальных уравнений, заданной в некоторой области пространства и на некотором временном интервале). Будем считать, что воображаемое время связано с координатами точки наблюдения следующим образом: ${{t}_{i}} = \frac{{{{{\left| {{{x}^{{\left( i \right)}}}} \right|}}^{2}}}}{{{{a}^{2}}}}$. В числителе здесь подразумевается квадрат расстояния от точки наблюдения до начала координат. Мы полагали ${{a}^{2}}$ равным 1000, однако такой подход не ограничивает общности. Если бы вместо уравнения параболического типа фигурировало волновое уравнение, то ${{a}^{2}}$ имело бы физический смысл квадрата скорости. В нашем представлении – это величина, характеризующая гипотетическую теплопроводность (скорее, рассеяние магнитного поля благодаря наличию вязкости). Подчеркнем, что на данном этапе разработки новой математической модели магнитного поля $~{{a}^{2}}$ рассматривается как параметр; обратная к $~{{a}^{2}}$ величина может считаться малым параметром, нулевое значение этого малого параметра соответствует “классической” постановке для уравнения Лапласа в области, не занятой магнитными массами. В принципе, каждой точке на регулярной или нерегулярной сети наблюдений можно сопоставить временной параметр произвольным образом. Если у всех точек временные координаты одинаковы, это может означать, что задано некоторое начальное распределение векторного поля. А впоследствии происходит процесс диффузии (или переноса гипотетического тепла) в пространстве и во времени. При генерации магнитного поля в недрах планеты или при взаимодействии внутреннего поля планеты с потоком заряженных частиц зависимость полей от времени определяется уравнением Эйлера, системой уравнений Максвелла и уравнением состояния среды. Мы предлагаем такую модель поля именно исходя из вида уравнений магнитной гидродинамики. Слишком простая, линейная, зависимость вектора намагниченности от времени могла рассматриваться ранее, но в настоящее время возникли новые вызовы, обусловленные стремительным ростом объемов получаемой в результате дистанционного зондирования Земли и других планет Солнечной системы информации.
Значения магнитного поля считались известными в сети точек на уровне моря и на высоте 4 км. По этим значениям мы определяли функцию ${{\Psi }}\left( {{{\tau }},{{{{\xi }}}_{1}},{{{{\xi }}}_{2}}} \right).$
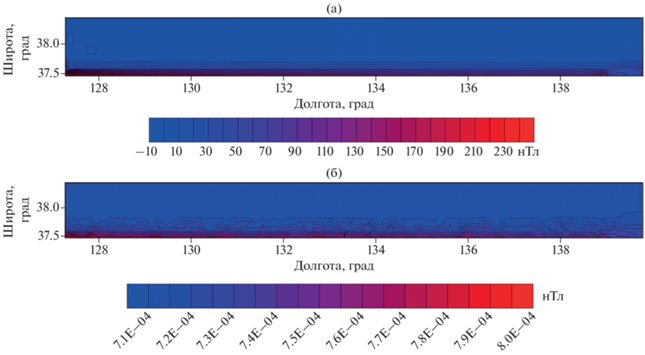
На рис. 5 показано поле, аппроксимированное на втором этапе поля южной подобласти; N = 10 000; массив данных отсортирован. Параметр, играющий роль времени, был искусственно введен в постановку. Значения “времени” в i-ой точке определялись как: ${{t}_{i}} = \frac{{{{{\left| {{{x}^{{\left( i \right)}}}} \right|}}^{2}}}}{{{{a}^{2}}}}$. Параметр ${{a}^{2}}~$ полагался равным 1000.
Рис. 5.
Поле, аппроксимированное на втором этапе поля южной подобласти; N = 10 000; массив данных отсортирован.
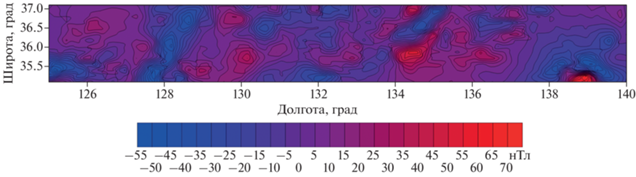
В табл. 2 приводятся результаты аппроксимации магнитного поля для трех подобластей в районе Японского моря с помощью зависящего от времени варианта локальных модифицированных S-аппроксимаций.
Таблица 2.
Модифицированная S-аппроксимация магнитного поля в районе Японского моря с учетом зависимости от времени (локальный вариант)
| № | N | Метод решения СЛАУ |
${{\sigma }_{{\min }}}$, нТесл |
${{\sigma }_{{\max }}}$, нТесл |
$\sigma $0, нТесл |
Δ/t |
|---|---|---|---|---|---|---|
| 1 | 5000 | УБМ | 0.02 | 0.03 | 0.024 | 0.00010 12:18 |
| 2 | 10 000 | УБМ | 0.02 | 0.03 | 0.026 | 0.00014 36:25 |
| 2 | 20 000 | УБМ | 0.02 | 0.03 | 0.028 | 0.0002 59:17 |
Примечания: ${{\sigma }^{{}}}$ = $\frac{{\left\| {Ax - {{f}_{\delta }}} \right\|_{E}^{{}}}}{{\sqrt N }}$ – среднеквадратическое отклонение; ${{\sigma }_{{\max }}} = \sqrt {\frac{{\delta _{{\max }}^{2}}}{N}} $, ${{\sigma }_{{\min }}} = \sqrt {\frac{{\delta _{{\min }}^{2}}}{N}} $; Δ=$\frac{{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}}}{{{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}}$ – показатель качества решения; t – время в часах, минутах и секундах. Значения полуосей a, b, c равны для всех примеров в этой таблице 6365, 6370, 6370 км соответственно.
Результаты расчетов на тестовых примерах показывают, что оба этапа комбинированной методики позволяют сохранить “естественный” характер магнитного поля: не наблюдается слишком резкого роста или убывания значений модуля аномального магнитного поля при изменении высоты точек наблюдения, т.е. поле не “распадается”.
На картах разностного поля приводятся разности значений между исходным полем и полем, вычисленным с помощью модифицированных S-аппроксимаций на поверхности геоида. Дальнейшие исследования будут направлены на разработку устойчивых алгоритмов продолжения поля как вверх, так и вниз, в сторону источников с тем, чтобы добиться согласования новой комбинированной методики интерпретации магнитных данных и существующих моделей глобального и аномального магнитных полей Земли. Продолжение поля вниз, в сторону источников, является всегда сильно неустойчивым, пока авторам настоящей работы не удалось найти примеры успешного решения некорректной задачи по аналитическому продолжению вниз магнитных полей планет, измеренных с помощью космических аппаратов, ни в отечественной, ни в зарубежной литературе.
ЗАКЛЮЧЕНИЕ
В работе предложена новая комбинированная методика интерпретации данных о магнитных полях планет, включающая в себя построение региональных модифицированных S-аппроксимаций с учетом эллиптичности и локальных аппроксимаций нестационарного поля, являющегося решением некоторого уравнения параболического типа с постоянными коэффициентами. Разработаны основные положения метода линейных интегральных представлений применительно к зависящим от времени дифференциальным операторам, что имеет принципиальное значение при решении многих обратных задач математической геофизики.
Список литературы
Арнольд В.И., Хесин Б.А. Топологические методы в гидродинамике. М.: изд-во “МЦНМО”. 2007. 393 с.
Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по уравнениям математической физики. М.: Наука. 1980. 684 с.
Владимиров В.В. Уравнения математической физики. М.: Наука. 1981. 512 с.
Долгаль А.С., Симанов А.А., Хохлова В.В. Решение геокартировочных и прогнозно-поисковых геологических задач методом гравиразведки с учетом сферичности Земли // Георесурсы. 2015. Т. 2. № 4(63). С. 56–61.
Долгаль А.С., Бычков С.Г. Оценка различий аномалий силы тяжести для плоской и сферической моделей земли. Международная конференция “Девятые научные чтения Ю.П., Булашевича”. Глубинное строение, геодинамика, тепловое поле Земли, интерпретация геофизических полей. Екатеринбург. 2017. С. 169–173.
Казанцев С.Г., Кардаков В.Б. Полоидально-тороидальное разложение соленоидальных векторных полей в шаре // Сибирский журн. индустриальной математики. 2019. Т. 22. № 3. С. 74–95.
Михайлов В.О., Тимошкина Е.П., Киселева Е.А., Хайретдинов С.А., Дмитриев П.Н., Карташов И.М., Смирнов В.Б. Проблемы совместной интерпретации временных вариаций гравитационного поля с данными о смещениях земной поверхности и дна океана на примере землетрясения Тохоку-Оки (11 марта 2011 г.) // Физика Земли. 2019. № 5. С. 56–60.
Раевский Д.Н., Степанова И.Э. О решении обратных задач гравиметрии с помощью модифи-цированного метода S-аппроксимаций // Физика Земли. 2015а. № 2. С. 44–54.
Раевский Д.Н., Степанова И.Э. Модифицированный метод S-аппроксимаций. Региональный вариант // Физика Земли. 2015б. № 2. С. 55–66.
Родников А.Г., Забаринская Л.П., Рашидов В.А., Сергеева Н.А. Геодинамические модели глубинного строения регионов природных катастроф активных континентальных окраин. М.: Научный мир. 2014. 172 с.
Степанова И.Э., Керимов И.А., Ягола А.Г. Аппроксимационный подход в различных модификациях метода линейных интегральных представлений // Физика Земли. 2019. № 2. С. 31–47.
Страхов В.Н., Степанова И.Э. Метод S-аппроксимаций и его использование при решении задач гравиметрии (региональный вариант) // Физика Земли. 2002. № 7. С. 3–12.
Степанова И.Э., Щепетилов А.В., Погорелов В.В., Михайлов П.С. Структурно-параметрический подход при построении цифровых моделей рельефа и гравитационного поля Земли с использованием аналитических S-аппроксимаций // Геофизические процессы и биосфера. 2020. Т. 19. № 2. С. 107–116.
Титов В.В., Степанов Р.А., Соколов Д.Д. Переходные режимы винтового динамо // Журнал экспериментальной и теоретической физики. 2020. Т. 157. № 10. С. 849–857.
Фрик П.Г, Соколов Д.Д, Степанов Р.А. Вейвлет-анализ пространственно-временной структуры физических полей // Успехи физических наук. 2021. Т. 191.
Шимбирев Б.П. Теория фигуры Земли. М.: Недра. 1975. 432 с.
Ягола А.Г., Степанова И.Э., Ван Янфей, Титаренко В.Н. Обратные задачи и методы их решения. Приложения к геофизике. М.: Бином. 2014. 214 с.
Acuna M., Connerney J., Ness N., Lin R., Mitchell D., Carlson C., McFadden J., Anderson K., Reme H., Mazelle C., Vignes D., Wasilewski P., Cloutier P. Global distribution of crustal magnetism discovered by the Mars Global SurveyorMAG/ERExperiment // Science. 1999. V. 284. P. 790–793.
Arkani-Hamed J. An improved 50-degree spherical harmonic model of the magnetic field of Mars derived from both high-altitude and low-altitude data // J. Geophysical Research (Planets). 2002. V. 107. P. 5083. https://doi.org/10.1029/2001JE001835
Gudkova T., Stepanova I., Batov A., Shchepetilov A. Modified method S- and R-approximations in solving the problems of Mars’s morphology // Inverse Problems in Science and Engineering. 2021. V. 29. P. 790–804. https://doi.org/10.1080/17415977.2020.1813125
Gudkova T., Stepanova I., Batov A. Density anomalies in subsurface layers of mars: model estimates for the Site of the InSight Mission Seismometer // Solar System Research. 2020. V. 54. P. 15–19. https://doi.org/10.1134/S0038094620010037
Langlais B., Purucker M.E., Mandea M. Crustal magnetic field of Mars // J. Geophys. Res. 2004. V. 109. P. E02008. https://doi.org/10.1029/2003JE002048
Meyer B, Saltus R., Chulliat A. EMAG2v3: Earth Magnetic Anomaly Grid (2-arc-minute resolution). Version 3. NOAA National Centers for Environmental Information. 2017. https://doi.org/10.7289/V5H70CVX
Oliveira J.S., Langlais B., Pais M.A., Amit H. A modified equivalent source dipole method to model partially distributed magnetic field measurements, with application to Mercury // J. Geophysical Research Planets. 2015. V. 120. P. 1075–1094. https://doi.org/10.1002/2014JE004734
Pan L., Quantin C., Tauzin B., Michaut C., Golombek M., Lognonné P., Grindrod P., Langlais B., Gudkova T., Stepanova I., Rodriguez S., Lucas A. Crust heterogeneities and structure at the dichotomy boundary in western Elysium Planitia and Implications for InSight lander // Icarus. 2020. V.338. P. 113511. https://doi.org/10.1016/j.icarus.2019.113511
Portniaguine O., Zhdanov M. Focusing geophysical inversion images // Geophysics. 1999. V. 64. P. 874–887.
Portniaguine O., Zhdanov M. 3-D magnetic inversion with data compression and image focusing // Geophysics. 2002. V. 67. P. 1532–1541.
Reshetnyak M.Yu. Spatial Spectra of the geomagnetic Field in the Observations and Geodynamo Models // Izvestiya, Physics of the Solid Earth. 2015. V. 51. № 3. P. 354–361.
Reshetnyak M.Yu. Inverse problem in Parker’s dynamo // Russian J. Earth Sciences. V. 15. P. ES4001. https://doi.org/10.2205/2015ES000558.2015
Salnikov A.M., Batov A.V., Gudkova T.V., Stepanova I.E. Analysis of the magnetic field data of Mars. The Eleventh Moscow Solar System Symposium (11M-S3). Moscow. Russia. October 5-9. 2020. https://doi.org/0.21046/11MS3-2020
Salnikov A., Stepanova I., Gudkova T., Batov A. Analytical modeling of the magnetic field of Mars from satellite data using modified S-approximations // Doklady Earth Sciences. 2021. V. 499. P. 575–579.
Schattner U., Segev A., Mikhailov V., Rybakov V, Lyakhovsky V. Magnetic Signature of the Kinneret–Kinarot Tectonic Basin Along the Dead Sea Transform, Northern Israel // Pure Appl. Geophys. 2019. V. 176. P. 4383–4399.
Stepanova I. On the S-approximation of the Earth’s gravity field // Inverse Problems in Sci. and Eng. 2008. V. 16. P.535–544.
Stepanova I.E. On the S-approximation of the Earth’s gravity field: Regional version // Inverse Problems in Sci. and Eng. 2009. V. 17. № 8. P. 1095–1111.
Stepanova I., Kerimov I., Raevskiy D., Shchepetilov A. Improving the methods for processing large data in geophysics and geomorphology based on the modified S- and F-approximations // Izvestiya Physics of the Solid Earth. 2020. V. 16. P. 1095–1111.
Uieda L., Valéria C. F. Barbosa, Braitenberg C. Tesseroids. Forward-modeling gravitational fields in spherical coordinates // Geophysics. 2015. V. 81. № 5. F41–F48. https://doi.org/10.1190/geo2015-0204.1
Wang Y., Lukyanenko D., Yagola A. Magnetic parameters inversion method with full tensor gradient data // Inverse Problems &Imaging. 2019. V. 13. P. 745–754.
Wang Y., Kolotov I., Lukyanenko D., Yagola A. Reconstruction of magnetic susceptibility using full magnetic gradient data // Computational Mathematics and Mathematical Physics. 2020. V. 60. P.1000–1007.
Wang Y. Leonov A. Lukyanenko D. Yagola A. General Tikhonov regularization with applications in geoscience // CSIAM Transaction on Applied Mathematics. 2020. V. 1. P. 53–85.
Whaler K. A., Purucker M.E. A spatially continuous magnetization model for Mars // J. Geophys. Res. 2005. V. 110. P. E09001. https://doi.org/10.1029/2004JE002393
Дополнительные материалы отсутствуют.