Физика Земли, 2023, № 5, стр. 3-12
Теория безгистерезисной остаточной намагниченности однодоменных зерен
В. П. Щербаков 1, *, Н. К. Сычева 1, **
1 Геофизическая обсерватория “Борок” Института физики Земли им. О.Ю. Шмидта РАН
п. Борок, Ярославская область, Россия
* E-mail: shcherbakovv@list.ru
** E-mail: sycheva@borok.yar.ru
Поступила в редакцию 04.04.2023
После доработки 26.04.2023
Принята к публикации 28.04.2023
- EDN: VZWAMH
- DOI: 10.31857/S0002333723050095
Аннотация
Предложен новый подход к решению кинетических уравнений, описывающий процесс образования безгистерезисной остаточной намагниченности (ARM), который позволил на два порядка ускорить численный расчет процесса образования ARM для одноосных ориентированных невзаимодействующих однодоменных частиц, при этом практически не уступая в точности строгому численному решению. Из результатов расчетов следует, что восприимчивость ARM целиком определяется величиной параметра коэрцитивности частицы$~g = {{{{\mu }_{0}}m{{B}_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}m{{B}_{0}}} {2kT}}} \right. \kern-0em} {2kT}}$. Выполнено сравнение данных предыдущих приближенных расчетов величины ARM с представленными здесь точными результатами и показано, что расхождение между точными данными и приближенными оценками растет с ростом g, но остается относительно небольшим, в пределах 23%. Предложенный алгоритм быстрого расчета кинетических уравнений позволяет с физической строгостью проанализировать методику псевдо-Телье оценки палеонапряженности для ансамбля однодоменных частиц, что предполагается сделать в последующих работах.
ВВЕДЕНИЕ
Безгистерезисная остаточная намагниченность (ARM) представляет собой лабораторный вид остаточной намагниченности, используемый в магнетизме горных пород и палеомагнетизме для оценки состава, концентрации, коэрцитивного спектра и доменного состояния (ДС) магнитных минералов в природных образцах [Stacey, Banerjee, 1965; Shaw, 1974; Dunlop, Özdemir, 1997; Egli, Lowrie, 2002]. ARM cоздается путем действия на образец переменного магнитного поля типичной частоты 0.05–1 кГц, уменьшающейся до нуля амплитуды в течение 10–100 с при одновременном наложении постоянного поля смещения Bdc, которое, собственно и приводит к возникновению ненулевой остаточной намагниченности. В частности, ARM используется при попытках оценки палеонапряженности древнего геомагнитного поля по методу, описанному в работе [Shaw, 1974], методом псевдо-Телье [Tauxe et al., 1995; de Groot et al., 2013; 2014; 2015; 2016; Paterson et al., 2016]. Идея метода псевдо-Телье состоит в том, что ARM можно рассматривать как аналог естественной остаточной намагниченности (NRM), и аналогия между методами Телье и псевдо-Телье состоит в том, что в обоих методах замена NRM (ARM) происходит ступенчато. Разница же заключается в том, что в методе Телье для разрушения NRM и ее постепенного замещения частичными TRM (pTRM) используется последовательность нагревов, а метод псевдо-Телье основан на последовательном замещении NRM частичными АRМ (pARM) путем приложения к образцу переменного поля AF возрастающей амплитуды. Таким образом, может быть построена диаграмма псевдо-Араи (потеря TRM vs прироста pARM) в полной аналогии с диаграммой Араи (потеря TRM vs прироста pTRM).
Однако проблема состоит в том, что коэффициент kARM пропорциональности ARM внешнему полю B не совпадает с соответствующим коэффициентом kTRM для TRM [Sugiura, 1979; Tauxe et al., 1995]. Соответственно, метод псевдо-Телье считается относительным, в отличие от исходного метода Телье, который был разработан для получения абсолютной палеонапряженности. Однако проблема понимания свойств диаграммы псевдо-Араи еще более сложна. Как известно, линейность диаграммы Араи (в идеальных условиях, то есть когда и NRM, и замещающие ее pTRM имеют термоостаточную природу, и при этом в ходе эксперимента Телье не происходит магнитоминералогических изменений) обеспечивается законами Телье независимости и аддитивности pTRM. Соответственно, при практическом применении метода Телье это подразумевает одинаковую (термостаточную) природу TRM и pTRM. Но если мы имеем дело не с TRM, а, например, с термохимическим намагничиванием (TCRM), то линейность диаграмм Араи–Нагата может быть нарушена [Щербаков и др., 2020; Грибов и др., 2021]. То же справедливо и для метода псевдо-Телье, где физическая природа разрушающейся TRM и приобретаемой pARM различна, что также может привести к нелинейным псевдо-Араи диаграммам.
Таким образом, корректное описание свойств АRМ и pАRМ, как и их пошагового разрушения AF убывающей амплитуды является ключевой задачей для построения теории метода псевдо-Телье. Фундаментальным препятствием на этом пути является то обстоятельство, что строгая теория приобретения ARM отсутствует даже для однодоменных (ОД) зерен. В своем исследовании этой проблемы автор работы [Wohlfart, 1964] отметил, что “для отдельной частицы процесс происходит следующим образом: если первая пиковая амплитуда переменного поля достаточно велика, намагниченность частицы также изменяется. Однако, когда разница между напряженностями переменного и постоянного полей становится слишком низкой, намагниченность больше не меняется на противоположную. Когда же переменное поле падает до нуля (за чем следует уменьшение до нуля постоянного поля Bdc), то частица приобретает остаточную намагниченность в направлении Bdcнезависимо от его величины. Следовательно, начальная безгистерезисная восприимчивость бесконечна”. Чтобы избежать такого физически неприемлемого результата, автор работы [Wohlfart, 1964] предположил, что конечные значения начальной восприимчивости обеспечиваются магнитостатическим взаимодействием частиц ансамбля. Это объяснение было явно неудовлетворительным, и позже в работе [Jaep, 1969] было показано, что изолированная частица на самом деле обладает конечной восприимчивостью, если учесть тепловые флуктуации. Позже были предложены ОД-теории ARM, основанные на анализе кинетических уравнений, подтвердившие конечность восприимчивости ARM [Щербаков, Щербакова, 1977; Walton, 1990; Egli, Lowrie, 2002]. Хотя точные аналитические решения этих уравнений могут быть легко записаны в квадратурах, они плохо поддаются численному вычислению из-за их сложной структуры с двойным интегрированием быстро осциллирующих функций. По этой причине авторами цитированных работ были представлены лишь приближенные решения с неопределенными ошибками результатов.
Но для обоснования (или критики) методики псевдо-Телье требуются строгие оценки отношения TRM/ARM, что может быть достигнуто только путем вывода точных соотношений между этими двумя видами остаточных намагниченностей, по крайней мере, для ОД частиц. Что касается TRM, то нами ранее была развита строгая теория ее образования на основе решения соответствующих кинетических уравнений [Shcherbakov et al., 2021]. В принципе, аналогичный подход может использоваться и для решения проблемы описания процесса приобретения ARM – и такие попытки неоднократно предпринимались в прошлом [Щербаков, Щербакова, 1977; Walton, 1990; Egli, Lowrie, 2002]. Однако, как уже говорилось выше, сложность этой проблемы заключается в том, что кинетические уравнения для ARM оказываются намного сложнее для численного решения, нежели те, что описывают образование TRM. Здесь нами предлагается новый подход к расчету кинетических уравнений для ARM, который позволил резко ускорить численный расчет процесса ее образования, при этом практически не уступая в точности строгому численному решению. Оговоримся, что для упрощения анализа ограничимся в этой работе случаем невзаимодействующих одноосных ориентированных частиц, когда внешнее магнитное поле B параллельно (либо антипараллельно) вектору легкой оси частицы l.
КИНЕТИЧЕСКОЕ УРАВНЕНИЕ И ЕГО РЕШЕНИЕ
Кинетическое уравнение для процесса релаксации магнитного момента m между двумя минимумами (ниже обозначаемыми индексами 1 и 2) имеет вид:
(1)
$\begin{gathered} \frac{{dy}}{{dt}} = - \lambda \left( t \right)\left[ {y - \mu \left( t \right)} \right],\,\,\,\,\lambda \left( t \right) = {{A}_{{1,2}}}\left( t \right) + {{A}_{{2,1}}}\left( t \right), \\ \mu \left( t \right) = \frac{{{{A}_{{1,2}}}\left( t \right) - {{A}_{{2,1}}}\left( t \right)}}{{{{A}_{{1,2}}}\left( t \right) + {{A}_{{2,1}}}\left( t \right)}}. \\ \end{gathered} $Здесь y – вероятность того, что вектор магнитного момента частицы m ориентирован параллельно вектору легкой оси l. Примем для определенности, что состояние 1 совпадает с положением вектора магнитного момента m параллельно направлению Bdc. Согласно работе [Brown, 1962] кинетические коэффициенты для одноосных ориентированных частиц имеют вид:
(2)
$\begin{gathered} {{A}_{{1,2}}} = {{f}_{0}}\sqrt {\frac{g}{\pi }} ~\left[ {1 - {{{\left( {\frac{B}{{{{B}_{0}}}}} \right)}}^{2}}} \right]\left( {1 + \frac{B}{{{{B}_{0}}}}} \right)\exp \left( { - \frac{{\Delta {{E}_{{1,2}}}}}{{kT}}} \right), \\ {{A}_{{2,1}}} = {{f}_{0}}\sqrt {\frac{g}{\pi }} ~\left[ {1 - {{{\left( {\frac{B}{{{{B}_{0}}}}} \right)}}^{2}}} \right]\left( {1 - \frac{B}{{{{B}_{0}}}}} \right)\exp \left( { - \frac{{\Delta {{E}_{{2,1}}}}}{{kT}}} \right). \\ \end{gathered} $Здесь f0 ~ 109 с–1 – характерная частота попыток преодоления потенциального барьера; B0 – критическое поле перемагничивания зерна; параметр коэрцитивности $g = {{{{\mu }_{0}}m{{B}_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}m{{B}_{0}}} {2kT}}} \right. \kern-0em} {2kT}}$. Для дальнейшего важно, что этот параметр всегда >25, поскольку при меньших $g$ зерно является суперпарамагнитным при комнатной температуре Tr и, соответственно, не вносит вклада в ARM при временах, бóльших времени релаксации частиц [Neel, 1955]. Высота потенциального барьера между двумя антипараллельными позициями (обозначаемыми индексами 1 и 2) есть:
(3)
$\begin{gathered} \Delta {{E}_{{1,2}}} = ~~\frac{{{{\mu }_{0}}m{{B}_{0}}}}{2}~{{\left( {1 + \frac{B}{{{{B}_{0}}}}} \right)}^{2}},\,\,\,\Delta {{E}_{{2,1}}} = ~~\frac{{{{\mu }_{0}}m{{B}_{0}}}}{2}~{{\left( {1 - \frac{B}{{{{B}_{0}}}}} \right)}^{2}}, \\ \left| B \right| < {{B}_{0}}. \\ \end{gathered} $При создании ARM :
(4)
$B = {{B}_{{{\text{af}}}}}\alpha \left( t \right)\sin \left( {{{2\pi t} \mathord{\left/ {\vphantom {{2\pi t} {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}} \right) + {{B}_{{{\text{dc}}}}},$Процесс приобретения ARM проходит в двух временных масштабах. Быстрый масштаб отвечает периоду t0 ≈ 0.02 с, в течение которого при достаточно высокой амплитуде AF происходит циклическое перемагничивание m. Но поскольку амплитуда AF медленно, с характерным временем a ~ 10 с затухает, то ослабевшее AF-поле в какой-то момент времени становится не в состоянии перемагничивать частицу из одного положения в другое, ее магнитный момент m “замораживается” и происходит образование ARM. В дальнейшем для определенности положим α(t) = 1 – t/a. Тогда, вводя безразмерные время τ = 2t/t0 и безразмерные поля b(τ) = B(τ)/B0, haf = Baf/B0 и h = Bdc/B0, получаем вместо (1) и (2):
(6)
$\begin{gathered} {{A}_{{1,2}}}\left( \tau \right) = (1 - {{b}^{2}})\left( {1 + b} \right)\exp \left[ {q - g{{{\left[ {1 + b\left( \tau \right)} \right]}}^{2}}} \right], \hfill \\ {{A}_{{2,1}}}\left( \tau \right) = (1 - {{b}^{2}})\left( {1 - b} \right)\exp \left[ {q - g{{{\left[ {1 - b\left( \tau \right)} \right]}}^{2}}} \right]. \hfill \\ \end{gathered} $Здесь q = $\ln \left( {{{f}_{0}}{{t}_{0}}\sqrt {{g \mathord{\left/ {\vphantom {g \pi }} \right. \kern-0em} \pi }} } \right)$.
(7)
$b\left( \tau \right) = h + {{h}_{{{\text{af}}}}}\left( {1 - {\tau \mathord{\left/ {\vphantom {\tau n}} \right. \kern-0em} n}} \right)\sin \left( {\pi \tau } \right),$При f0 = 109 с–1 и t0 = 0.02 с имеем $q\left( g \right) = 15.55 + {{\ln \left( g \right)} \mathord{\left/ {\vphantom {{\ln \left( g \right)} 2}} \right. \kern-0em} 2}$. Это выражение для q будет использоваться в дальнейших расчетах.
Отметим, что при образовании полной ARM Baf = B0, поэтому ниже в этом разделе мы положим haf = 1. Из (6) скорость приближения к равновесию $\lambda \left( \tau \right) = (1 - {{b}^{2}})\{ \left( {1 + b} \right)$$\exp \left[ {q - g{{{\left( {1 + b} \right)}}^{2}}} \right]\,\, + $ $ + \left( {1 - b} \right)\exp \left[ {q - g{{{\left( {1 - b} \right)}}^{2}}} \right]$, что можно представить в более компактном виде:
(8)
$\begin{gathered} \lambda \left( \tau \right) = 2(1 - {{b}^{2}})\left[ {{\text{ch}}\left( {2gb} \right) - b{\text{sh}}\left( {2gb} \right)} \right] \times \\ \times \,\,\exp \left[ {q - g(1 + {{b}^{2}})} \right] = \\ = 2{{(1 - {{b}^{2}})}^{{3/2}}}{\text{ch}}\left[ {2gb - s\left( b \right)} \right]\exp \left[ {q - g(1 + {{b}^{2}})} \right]. \\ \end{gathered} $Здесь $s\left( b \right)\, = \,{\text{arcsh}}\left( {\frac{b}{{\sqrt {1\, - \,{{b}^{2}}} }}} \right)$. Поскольку A1,2(τ) –A2,1(τ) = $ = 2\left[ {{\text{sh}}\left( {2gb} \right) + b{\text{ch}}\left( {2gb} \right)} \right] = 2{{(1 - {{b}^{2}})}^{{3/2}}}{\text{sh}}\left[ {2gb - s\left( b \right)} \right]$ $\exp \left[ {q - g(1 + {{b}^{2}})} \right]$, соответственно,
(9)
$\begin{gathered} \mu \left( \tau \right) = \tanh \left\{ {2gb\left( \tau \right) - s\left[ {b\left( \tau \right)} \right]} \right\} = \\ = \tanh \left\{ {\frac{{{{\mu }_{0}}mB}}{{kT}} - s\left[ {b\left( \tau \right)} \right]} \right\}. \\ \end{gathered} $Выражение (9) очень близко к выражению для намагниченности суперпарамагнитных частиц, возникающей при приложении внешнего поля B, но вместе с тем отличается от нее наличием члена s(b), который возникает здесь из-за присутствия предэкспоненциального множителя $1 \pm {B \mathord{\left/ {\vphantom {B {{{B}_{0}}}}} \right. \kern-0em} {{{B}_{0}}}}$ в (3), имеющего разный знак по отношению к A1 и A2, что отражает разную глубину минимумов 1 и 2.
Общее решение (5) есть
(10)
$\begin{gathered} y\left( \tau \right) = y\left( 0 \right)\lambda \left( x \right)\mu \left( x \right)\exp \left[ { - f\left( \tau \right)} \right] + \\ + \,\,\int\limits_0^\tau {\exp [ - f\left( \tau \right) + f\left( x \right)]dx} , \\ \end{gathered} $Примеры численного решения уравнения (10) представлены на рис. 1.
Рис. 1.
Графики функции y(τ) при различной величине параметра коэрцитивности: (а) $g = 100$; (б) $g = 200$; (в) $g = 400$; (г) $g = 800$.
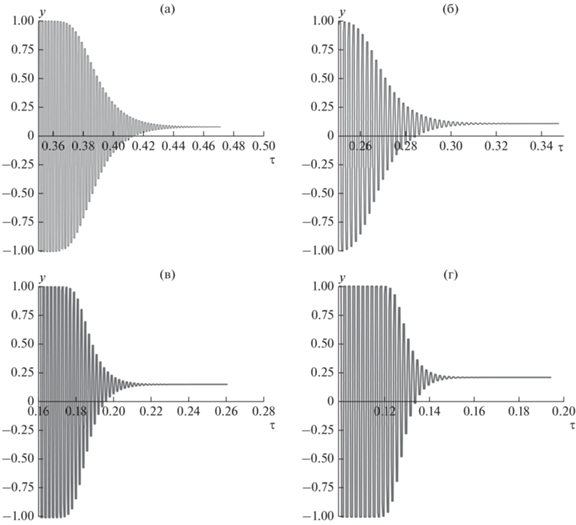
Отметим, что при низких τ, вплоть до интервала, где начинается блокировка магнитного момента, график y(τ) практически повторяет график µ(τ), но с некоторой задержкой момента перемагничивания во времени (рис. 2), обусловленного тем, что амплитуда переменного поля должна вырасти до необходимой величины, обеспечивающей преодоление потенциального барьера (с учетом дополнительного воздействия термофлуктуаций) между двумя состояниями. Соответственно, и величина намагниченности ансамбля зерен при этом всюду близка к полному насыщению. Физически такое поведение обусловлено тем, что низкие τ соответствуют высокой амплитуде AF, так что магнитный момент зерна заведомо насыщается сразу же после переворота.
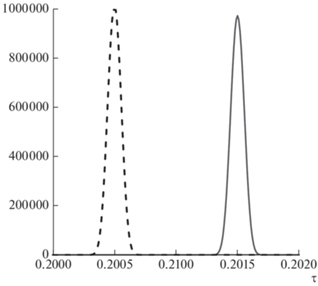
Рис. 2.
Сплошная линия – фрагмент графика функции y(τ) на интервале 0.357 < τ < 0.361; пунктирная линия – фрагмент графика функции µ(τ), $g$ = 100, a = 1000, h = 0.001.
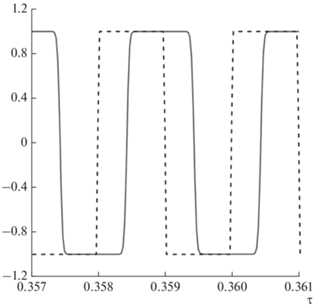
В заключение этого раздела отметим, что в литературе [Walton, 1990; Egli, 2003] обсуждался вопрос о зависимости между периодом переменного поля и величиной ARM, которая в значительной мере определяется временем релаксации ОД частиц. Наши расчеты показали, что в интересующем нас диапазоне периодов от 0.1 до 0.001 с зависимость между периодом переменного поля и величиной ARM носит логарифмический характер и приводит к изменениям в величине ARM не более, чем на несколько процентов. Поэтому в данной работе мы сочли возможным пренебречь этой зависимостью.
СХЕМА БЫСТРОГО РАСЧЕТА ВЕЛИЧИНЫ ARM
Получение каждой кривой на рис. 1 потребовало несколько дней непрерывного счета на компьютере. Как уже говорилось во Введении, причина таких сложностей состоит в необходимости двукратного интегрирования быстро осциллирующих функций и столь большая громоздкость расчетов делает подобный прямолинейный подход непрактичным для детального анализа свойств ARM и, в особенности, расчета диаграмм псевдо-Араи. К счастью, уравнения (10) и (11) обладают свойством, которое позволяет свести задачу только к однократному интегрированию практически без потери точности численного решения.
Kак видно из рис. 2, практически везде с высокой точностью выполняется равенство µ(t) = ±1. Формально это свойство следует из того, что неравенство $2gb \gg 1$ выполняется практически при всех $g$ и τ, за исключением очень узких областей вблизи точек τ = 0, 1, 2 и т. д, (здесь sin(π×t) обращается в нуль), а также на самой последней стадии процесса приобретения ARM, когда амплитуда AF близка к нулю, то есть при τ → n. В подтверждение этого тезиса на рис. 3 построены графики y(τ) и µ(τ) при невысокой величине параметра $g$ = 30 и на самой заключительной стадии процесса приобретения ARM (в данном примере на интервале τ = (800, 804)). Тем не менее, равенство µ(τ)= ±1 с высокой точностью соблюдается и здесь. Мы специально подчеркиваем это обстоятельство, поскольку, как будет показано ниже, именно оно дает возможность построить быструю и эффективную схему численного расчета функции y(τ).
Рис. 3.
(а) – График функции y(τ); (б) – фрагмент графика функции µ(τ) на интервале τ = (0.8, 0.804); $g$ = 30, a = 1000, h = 0.001.
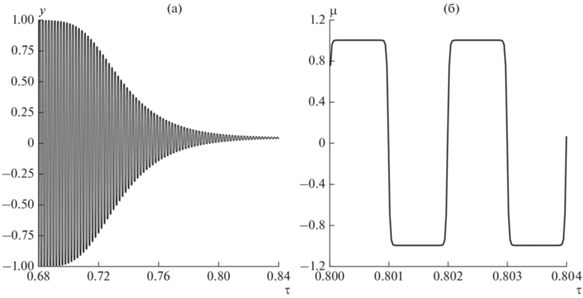
Действительно, рассмотрим некоторый интервал i < τ < i + 1, на котором µ(τ) = (–1)i– 1. Тогда:
(12)
$\begin{gathered} \int\limits_{i - 1}^\tau {\exp \left[ { - f\left( \tau \right) + f\left( x \right)} \right]} \,\lambda \left( x \right)\mu dx = \\ = ~\mu \exp \,\,\left[ { - f\left( \tau \right)} \right]\int\limits_{f\left( {i - 1} \right)}^{f(\tau )} {\exp (f)df} = \\ = \mu \left\{ {1 - \exp \left[ { - f\left( \tau \right) + f\left( {i - 1} \right)} \right]} \right\} = \\ = \mu \left\{ {1 - \exp \left[ { - \int\limits_{i - 1}^\tau {\lambda \left( x \right)} dx} \right]} \right\}. \\ \end{gathered} $Здесь принято во внимание, что λ(x) = df/dx. Соответственно, уравнение (8) на интервале принимает вид:
(13)
$\begin{gathered} y(\tau ) = y\left( {i - 1} \right)\exp \left[ { - z\left( {\tau ,i - 1} \right)} \right] + \\ + \,\,{{( - 1)}^{{i - 1}}}\left\{ {1 - \exp \left[ { - z\left( {\tau ,i - 1} \right)} \right]} \right\}~. \\ \end{gathered} $Здесь введено обозначение $z\left( {\tau ,i - 1} \right) = $ $ = \int_{i - 1}^\tau {\lambda \left( x \right)dx} $. Очевидно, уравнение (13) можно рассматривать как рекуррентное соотношение для реализации расчета функции y(τ) последовательно для интервалов i < τ < i + 1, i = 0, 1, 2 …, n и получить решение задачи на всем интервале t = (0, a). Результаты этих расчетов показали их практическую идентичность с теми, что выполнялись прямым численным интегрированием (рис. 1). Для иллюстрации этого положения на рис. 4 нами приведен фрагмент графика функции y(τ), полученный как по точной формуле (10), так и с помощью приближенного выражения (13). Из сравнения этих кривых видно практически полное согласие обоих способов вычисления, но при этом расчет одной кривой на рис. 1, требующий двукратного интегрирования по формуле (10) на требовал не менее суток, в то время как расчет такой же кривой по формуле (13) занимал не более 10–20 мин, то есть выигрыш во времени составляет примерно два порядка величины. Расчет производился на компьютере с центральным процессором, представленным двумя процессорами Intel Xeon Gold 6226 с базовой частотой 2.70 GHz, числом ядер/потоков 12/24.
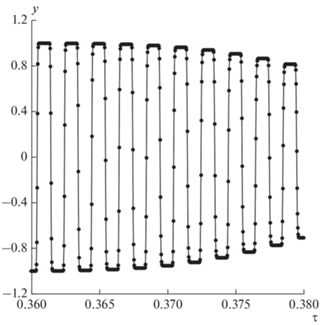
Рис. 4.
Сплошная линия – график функции y(τ), рассчитанный по точной формуле (10), кружки представляют результаты расчета функции y(τ) согласно аппроксимации (13); $g$ = 100, h = 0.001, a = 1000.
ДИСКУССИЯ
Хотя представленный выше алгоритм (13) решения кинетических уравнений (5) позволяет быстро и с достаточной степенью точности описать процессы приобретения ARM в ОД частицах, для широкой аудитории желательно иметь простое приближенное выражение для интенсивности ARM, которое было бы легко получить и интерпретировать из наглядных физических соображений. В этой связи напомним, что в литературе уже известны приближенные выражения для ARM, полученные ранее в работах [Щербаков, Щербакова, 1977; Walton, 1990; Egli, Lowrie, 2002] методом Лапласа (что в данном случае сводится к оценке интегралов (9) методом перевала). Однако этот метод принципиально не способен описать детальное поведение намагниченности y(τ) (типа того, что представлено на рис. 1 и рис. 4), а представляет лишь возможность оценить конечную величину ARM [Walton, 1990], либо получить дифференциальное уравнение для средних по периоду значений y(τ) [Щербаков, Щербакова, 1977; Egli, Lowrie, 2002]. Ниже мы даем относительно простой способ получения такого рода приближений, пренебрегая строгостью математических манипуляций, приобретая взамен физическую прозрачность полученных выражений. Особо отметим, что на основе развитых выше численных методов мы теперь можем строго оценить точность приближенных решений, что имеет самостоятельную ценность.
Для начала опустим в выражениях (3) для кинетических коэффициентов A1 и A2 предэкспоненциальные множители (1 – b2)(1 ± b ) как несущественные. Далее отметим, что при малом внешнем постоянном поле h, удовлетворяющем условию $2gh$ < 1 эти коэффициенты можно записать в виде:
(14)
$\begin{gathered} {{A}_{{1,2}}} \approx \exp \left\{ {q - g{{{\left[ {1 + h + \alpha \left( t \right)\sin \left( {\pi \tau } \right)} \right]}}^{2}}} \right\} \\ \approx \exp \left\{ {q - g{{{\left[ {1 + \alpha \left( t \right)\sin \left( {\pi \tau } \right)} \right]}}^{2}}} \right\} \times \\ \times \,\,\left\{ {1 - 2gh\left[ {1 + \alpha \left( t \right)\sin (\pi \tau )} \right]} \right\} \\ \,{{A}_{{2,1}}} \approx \exp \left\{ {q - g{{{\left[ {1 - \alpha \left( t \right)\sin (\pi \tau )} \right]}}^{2}}} \right\} \\ \times \,\,\left\{ {1 - 2gh\left[ {1 - \alpha \left( t \right)\sin (\pi \tau )} \right]} \right\}. \\ \end{gathered} $Для дальнейшего кинетическое уравнение (1) удобнее представить в виде
(15)
$\frac{{dy}}{{dt}} = - [{{A}_{{1,2}}}\left( t \right) + {{A}_{{2,1}}}\left( t \right)\left] {y + [{{A}_{{1,2}}}\left( t \right) - {{A}_{{2,1}}}\left( t \right)} \right].$Напомним, что параметр $g$ в (14) всегда >25, составляя величину ~102–103. В силу этого частота перехода частиц A1(τ) + A2(τ) из одного состояния в другое имеет острый максимум в окрестности значений τ = i + 1/2, как это проиллюстрировано на рис. 5.
Рис. 5.
Зависимость величины кинетических коэффициентов A1,2 (кривая 1, сплошная линия) и A2,1 (кривая 2, пунктир) от времени τ, $g$ = 200, h = 0, a = 1000.
Именно это обстоятельство и дает возможность применить метод Лапласа для оценки интегралов (11), как это было сделано в работах [Щербаков, Щербакова, 1977; Walton, 1990; Egli, Lowrie, 2002], но мы здесь воспользуемся указанным свойством только для того, чтобы попросту проигнорировать быстро осциллирующий множитель sin(2πτ) в выражениях для кинетических коэффициентов A1 и A2 и записать (15) в виде :
(16)
$\begin{gathered} \frac{{dy}}{{d\tau }} \propto - \exp \left[ {q - g{{{\left( {1 - {{h}_{{{\text{af}}}}}} \right)}}^{2}}} \right]\left[ {y - 2gh\left( {1 - {{h}_{{{\text{af}}}}}} \right)} \right] = \\ = - \exp \left[ {q - g{{{\left( {\frac{\tau }{n}} \right)}}^{2}}} \right]\left( {y - 2gh\frac{\tau }{n}} \right). \\ \end{gathered} $Знак пропорциональности вместо знака равенства здесь поставлен потому, что при принятых приближениях мы заведомо теряем какие-то множители в коэффициентах. Отметим, что при таком упрощении под функцией y(τ) следует понимать просто ее среднюю величину по периоду, поскольку все изменения y(τ) внутри периода игнорируются. Тем не менее, несмотря на столь радикальные упрощения, этот эмпирический подход приводит к тому же результату, что и более детальный анализ, основанный на реальном усреднении коэффициентов уравнения (16) по периодам с применением метода Лапласа [Щербаков, Щербакова, 1975; Egli, Lowrie, 2002]. Действительно, на первой стадии процесса, то есть при высокой haf, что соответствует малым τ/n, частота переходов ${\text{exp}}\left[ {q - g{{{\left( {{\tau \mathord{\left/ {\vphantom {\tau n}} \right. \kern-0em} n}} \right)}}^{2}}} \right]$ очень велика и поэтому единственным способом сохранить величину левой части уравнения (16) dy/dτ в разумных пределах (<1), является приравнивание нулю выражения $y - {{2gh\tau } \mathord{\left/ {\vphantom {{2gh\tau } n}} \right. \kern-0em} n}$ в правой части этого уравнения. Отсюда усредненная по периодам намагниченность:
Подчеркнем, что выражение (17) линейно по полю h. Как следует из вывода этой формулы, линейность обеспечивается условием $2gh < 1$. Физически это означает, что при обычно используемой в экспериментах интенсивности внешнего поля Bdc ≈ (0.05–0.1) мТ (то есть h = Bdc/Ms ≈ 10–3) для обеспечения линейной зависимости ARM(Bdc) величина параметра коэрцитивности $g = {{{{\mu }_{0}}m{{B}_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}m{{B}_{0}}} {2kT}}} \right. \kern-0em} {2kT}}$ не должна превышать 500. Принимая здесь T = Tr = 300 K, найдем, что критические поля перемагничивания B0 для зерен типичного ОД размера от 30 до 80 нм не должны превышать 200 и 10 мТ, соответственно.
При росте τ/n и соответствующем спаде амплитуды haf частота переходов частиц из одного состояния в другое $\exp \left[ {q - g{{{\left( {{\tau \mathord{\left/ {\vphantom {\tau n}} \right. \kern-0em} n}} \right)}}^{2}}} \right]$ резко замедляется, и при $q \ll g{{\left( {{{{\tau }} \mathord{\left/ {\vphantom {{{\tau }} n}} \right. \kern-0em} n}} \right)}^{2}}$ она становится близка к нулю, что означает блокировку состояния магнитного момента частицы. Соответственно, условие $q = g{{\left( {{\tau \mathord{\left/ {\vphantom {\tau n}} \right. \kern-0em} n}} \right)}^{2}}$ можно принять за условие блокировки, откуда :
Уравнения (17) и (18) полностью соответствуют выражениям, полученным более строгим методом в работе [Щербаков, Щербакова, 1975]. Такие же, в сущности, соотношения выведены и в статьях [Walton, 1990; Egli, Lowrie, 2002], хотя там они имеют более сложный вид ввиду дополнительных параметров их моделей, касающихся гистерезисных свойств частиц.
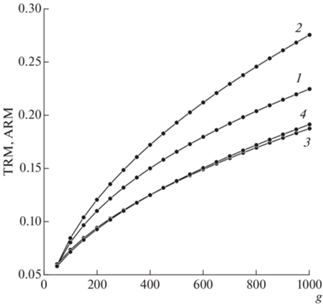
Сравнение результатов расчета по формуле (18) (кривая 2) с точными вычислениями по алгоритму (13) (кривая 1) приведено на рис. 6. Как мы видим, приближение (18) (кривая 2) удовлетворительно отображает точное решение (кривая 1).
Рис. 6.
Сравнение зависимостей интенсивности ARM($g$), рассчитанной по алгоритму (13) (кривая 1) и по приближенной формуле (18) (кривая 2). Сравнение зависимостей интенсивности TRM($g$), рассчитанной по точному решению [Shcherbakov et al., 2021] (кривая 3) и по приближенной формуле (19) (кривая 4). Во всех расчетах принято h = 0.001.
Что касается TRM, то ее величину можно оценить довольно просто [Нагата, 1965]. Образование TRM идет через блокировку суперпарамагнитной намагниченности частиц при охлаждении зерен. Блокировка происходит, когда время релаксации ${{t}_{r}}\sim f_{0}^{{ - 1}}\exp \left[ {{{m{{H}_{c}}} \mathord{\left/ {\vphantom {{m{{H}_{c}}} {\left( {2kT} \right)}}} \right. \kern-0em} {\left( {2kT} \right)}}} \right]$ данной частицы становится порядка времени опыта 100 с. Отсюда получаем известное условие блокировки ${{10}^{2}}\sim f_{0}^{{ - 1}}\exp \left[ {{{m{{H}_{c}}} \mathord{\left/ {\vphantom {{m{{H}_{c}}} {\left( {2kT} \right)}}} \right. \kern-0em} {\left( {2kT} \right)}}} \right]{{|}_{{T = {{T}_{b}}}}}$ или ${{\left. {{{m{{H}_{c}}} \mathord{\left/ {\vphantom {{m{{H}_{c}}} {\left( {2kT} \right)}}} \right. \kern-0em} {\left( {2kT} \right)}}} \right|}_{{T = {{T}_{b}}}}} = $ $\ln \left( {{{f}_{0}}{{t}_{r}}} \right) = {{q}_{{TRM}}} \approx 25$ [Нагата, 1965]. Это соотношение можно переписать в виде ${{q}_{{TRM}}} = g{{\left( {{{{{j}_{{sb}}}} \mathord{\left/ {\vphantom {{{{j}_{{sb}}}} {{{j}_{{sr}}}}}} \right. \kern-0em} {{{j}_{{sr}}}}}} \right)}^{2}}\left( {{{{{T}_{r}}} \mathord{\left/ {\vphantom {{{{T}_{r}}} {{{T}_{b}}}}} \right. \kern-0em} {{{T}_{b}}}}} \right)$, где js(T) – приведенная спонтанная намагниченность, jsr = js(Tr), а jsb = = js(Tb). Подставляя это выражение в формулу для намагниченности изолированной суперпарамагнитной частицы y(Tb) = m(mB/kBT) при температуре блокировки Tb, получим:
(19)
$TRM = 2{{q}_{{TRM}}}B\left( {{{{{j}_{{sr}}}} \mathord{\left/ {\vphantom {{{{j}_{{sr}}}} {{{j}_{{sb}}}}}} \right. \kern-0em} {{{j}_{{sb}}}}}} \right).$Множитель ${{{{j}_{{sr}}}} \mathord{\left/ {\vphantom {{{{j}_{{sr}}}} {{{j}_{{sb}}}}}} \right. \kern-0em} {{{j}_{{sb}}}}}$ появился здесь ввиду роста m(T) при охлаждении частицы от Tb до Tr. Как видно из кривых 3 и 4 на рис. 7, в этом случае наблюдается превосходное согласие между точным решением и приближенным выражением для TRM, в отличие от того, что наблюдается для ARM (кривые 1 и 2). Такое различие связано с тем, что при образовании TRM при высоких температурах намагниченность y(T), действительно, практически не отличается от суперпарамагнитной, равной m(mB/kBT) [Shcherbakov et al., 2021], а ее блокировка происходит почти мгновенно, то есть в интервале температур всего несколько градусов. Соответственно, простая формула (19) дает результат, очень близкий к величине, полученной точным расчетом кинетического уравнения [Shcherbakov et al., 2021]. В то же время процесс блокировки ARM тянется на довольно значительный интервал изменения амплитуды AF (рис. 5), к тому же функция y(T) испытывает быстрые осцилляции, прежде чем ее величина стабилизируется. Все это и ведет к некоторой разнице между точным и приближенным решениями (рис. 6).
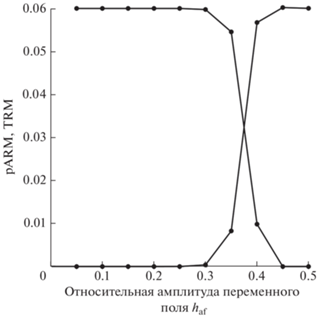
Рис. 7.
Кривые приобретения pARM и разрушения TRM в зависимости от относительной амплитуды AF, $~g = 50,~\,\,a = 1000,\,\,~h = 0.001$.
Приняв для простоты, что магнитная анизотропия частиц обусловлена анизотропией формы, так что B0(T) = B0(0)js(T), найдем:
(20)
$~\frac{{TRM}}{{ARM}} = \frac{{{{q}_{{TRM}}}}}{{\sqrt {qg} }}\frac{{{{j}_{{sr}}}}}{{{{j}_{{sb}}}}} = \sqrt {\frac{{{{q}_{{TRM}}}}}{q}} \sqrt {\frac{{{{T}_{r}}}}{{{{T}_{b}}}}} ~.$Откуда при q = qTRM имеем ${{TRM} \mathord{\left/ {\vphantom {{TRM} {ARM}}} \right. \kern-0em} {ARM}} = \sqrt {{{{{T}_{r}}} \mathord{\left/ {\vphantom {{{{T}_{r}}} {{{T}_{b}}}}} \right. \kern-0em} {{{T}_{b}}}}} $, соотношение, которое было получено ранее в работах [Jaep, 1969; Щербаков, Щербакова, 1977]. При Tr = 300 K и Tb ≈ 600–850 K TRM/ARM ≈ 0.6–0.7 < 1. Это неравенство, однако, полностью противоречит экспериментам, которые свидетельствуют об обратном соотношении между ARM и TRM. Действительно, как показали авторы работ [Борисова, Шолпо, 1985; Paterson et al., 2016], выполнившие ряд экспериментов на природных образцах вулканитов разного генезиса и возраста и показавшими, что в среднем TRM/ARM ≈ 2.7. Автор работы [Sugiura, 1979] выполнил ряд экспериментов по созданию ARM и TRM на искусственных образцах, содержащих ОД частицы в разной объемной концентрации с и показал, что отношение TRM/ARM изменяется от 7.34 при с = 2.3% до 1.19 при с = 2 ×10–4%. Зависимость TRM/ARM от с он связал с ролью магнитостатического взаимодействия между ОД частицами, интенсивность которого падает с уменьшением концентрации, что и ведет к падению восприимчивости как ARM, так и TRM.
Если принять гипотезу о решающей роли магнитостатического взаимодействия в формировании отношения TRM/ARM, то при сравнении теории и эксперимента следует ориентироваться на результат, полученный для наиболее разбавленной магнитной фракции с = 2 ×10–4%, когда энергия магнитостатического взаимодействия и, соответственно, отношение TRM/ARM минимальны. В этой связи обратим внимание на то, что в рамках строгой теории ARM отношение TRM/ARM изменяется в пределах (0.83–1) (рис. 6). А эта оценка уже гораздо ближе к экспериментальным значениям, доложенным в работе [Sugiura, 1979] для с = 2 ×10–4%. Это обстоятельство говорит в пользу гипотезы о том, что обсуждаемое здесь различие между теорией и экспериментом можно отнести к роли магнитостатического взаимодействия, однако, этот вопрос требует серьезных дополнительных исследований. Дело в том, что для обоснованных сравнений теории и эксперимента необходимо обобщить развитую здесь теорию на ансамбль неориентированных частиц, поскольку как в природе, так и в эксперименте мы имеем дело именно с такими образцами. Однако это обобщение не выглядит тривиальным, поскольку при поле B, направленным под углом к легкой оси, зависимость величины барьера от интенсивности B уже не имеет квадратичную форму типа (3) и вообще не описывается алгебраическим выражением [Victora, 1989].
В завершение этого раздела коснемся вопроса расчета методики псевдо-Телье. Очевидно, что для этого следует, прежде всего, построить алгоритмы приобретения pARM и разрушения TRM при приложении к образцу переменного поля AF возрастающей амплитуды haf. Это достаточно легко сделать, рассчитывая кривые y(τ) при ненулевом h и последовательном увеличении haf. Такой же алгоритм применяется и для расчета разрушения NRM с той лишь разницей, что в этом случае следует положить h = 0, а в формуле (13) принять z(0) = TRM. Пример таких расчетов для зерна с параметром $g = 50$ продемонстрирован на рис. 7.
Далее, для построения диаграммы псевдо-Телье TRM(haf) vs pARM(haf) следует рассчитать подобные кривые приобретения pARM и разрушения TRM для достаточно представительного набора параметров v и B0, характеризующих частицу и определяющих величину параметра последующим суммированием этих кривых. Однако, выполнение таких расчетов также имеет смысл лишь после того, как настоящее исследование будет обобщено на случай неориентированных частиц, что и предполагается сделать в нашей следующей работе.
ЗАКЛЮЧЕНИЕ
Описан процесс образования безгистерезисной остаточной намагниченности для одноосных ориентированных невзаимодействующих однодоменных частиц на основе строгого расчета кинетических уравнений. Из результатов расчетов следует, что восприимчивость ARM целиком определяется величиной параметра коэрцитивности частицы$~g = {{{{\mu }_{0}}m{{B}_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}m{{B}_{0}}} {2kT}}} \right. \kern-0em} {2kT}}$. Выполнено сравнение результатов предыдущих приближенных расчетов величины ARM с представленными здесь точными данными и показано, что расхождение между точными данными и приближенными оценками растет с ростом $g$, но остается относительно невысоким, в пределах 23%. Предложен алгоритм быстрого расчета этих уравнений, позволяющий в дальнейшем проанализировать методику псевдо-Телье для ансамбля невзаимодействующих ОД частиц.
Список литературы
Борисова Г.П., Шолпо Л.Е. О возможности статистических оценок палеонапряженности геомагнитного поля // Изв. АН СССР. Сер. Физика Земли. 1985. № 7. С. 71–79.
Грибов С.К., Щербаков В.П., Цельмович В.А., Афиногенова Н.А. Свойства термохимической остаточной намагниченности, образованной при медленном лабораторном охлаждении титаномагнетитсодержащих базальтовых образцов от различных температур, и результаты применения к ней методики Телье // Физика Земли. 2021. № 6. С. 107–121. https://doi.org/10.31857/S0002333721060016
Нагата Т. Магнетизм горных пород. М.: Мир. 1965. 348 с.
Щербаков В.П., Грибов С.К., Афиногенова Н.А., Цельмович В.А. Однофазное окисление ферримагнитных зерен как причина L-образной формы диаграмм Араи–Нагата // Физика Земли. 2020. № 5. С. 70–80. https://doi.org/10.31857/S0002333720050105
Щербаков В.П., Щербакова В.В. О магнитостатическом взаимодействии в системе однодоменных зерен // Изв. АН СССР. Сер. Физика Земли. 1975. № 9.
Щербаков В.П., Щербакова В.В. К расчету термоостаточной и идеальной намагниченностей ансамбля взаимодействующих однодоменных зерен // Изв. АН СССР. Сер. Физика Земли. 1977. № 6. С. 69–83.
Brown W.F. Thermal fluctuation of a single-domain particle // Phys. Rev. 1963. V. 130. P. 1677–1686.
de Groot L.V., Biggin A.J., Dekkers M.J., Langereis C.G., Herrero-Bervera E. Rapid regional perturbations to the recent global geomagnetic decay revealed by a new Hawaiian record // Nat. Commun. 2013. V. 4. https://doi.org/10.1038/ncomms3727
de Groot L.V., Dekkers M.J., Visscher M., ter Maat G.W. Magnetic properties and paleointensities as function of depth in a Hawaiian lava flow // Geochem. Geophys. Geosyst. 2014. V. 15. P. 1096–1112.
de Groot L.V. et al. High paleointensities for the Canary Islands constrain the Levant geomagnetic high // Earth planet. Sci. Lett. 2015. V. 419. P. 154–167.
de Groot L.V., Pimentel A., Di Chiara A. The multi-method paleointensity approach applied to volcanics from Terceira: full-vector geomagnetic data for the past 50 kyr // Geophys. J. Int. 2016. V. 206(1). P. 590–604.
Dunlop D., Ozdemir O. Rock magnetism. Fundamentals and frontiers. Cambridge University Press. 1997. 573 p.
Egli R., Lowrie W. Anhysteretic remanent magnetization of fine magnetic particles // Journal of Geophysical Research. 2002. V. 107. № B10. P. 2209, https://doi.org/10.1029/2001JB000671
Jaep W.F. Anhysteretic magnetization of an assembly of single-domain Particles // J. Appl. Phys. 1969. V. 40. P. 1297– 1298.
Néel L. Some theoretical aspects of rock-magnetism // Advances in Physics. 1955. V. 4(14). P. 191–243. https://doi.org/10.1080/00018735500101204
Paterson G.A., Heslop D., Yongxin P. The pseudo-Thellier palaeointensity method: new calibration and uncertainty estimates // Geophys. J. Int. 2016. V. 207. P. 1596–1608. https://doi.org/10.1093/gji/ggw349
Shaw J. A new method of determining the magnitude of the paleomagnetic field // Geophys. J. R. Astron. Soc. 1974. V. 39. P. 133–141.
Shcherbakov V.P., Lhuillier F., Sycheva N.K. Exact Analytical Solutions for Kinetic Equations Describing Thermochemical Remanence Acquisition for Single-Domain Grains: Implications for Absolute Paleointensity Determinations // JGR Solid Earth. 2021. V. 126. № 5. P. 1–24. https://doi.org/10.1029/2020JB021536
Stacey F.D., Banerjee S.K. The physical principles of the rock magnetism. Elsevier, Amsterdam. 1974. 195 p.
Sugiura N. ARM, TRM, and magnetic interactions: concentration dependence // Earth Planet. Sci. Lett. 1979. V. 42. P. 451–455.
Tauxe L., Pick T., Kok Y.S. Relative paleointensity in sediments: A pseudo-Thellier approach // Geophys. Res. Lett. 1995. V. 22. P. 2885–2888.
Victora R.H. Predicted time dependence of the switching field for magnetic materials // Phys. Rev. Lett. 1989. V. 63. P. 457–460.
Walton D. A theory of anhysteretic remanent magnetization of singledomain grains // J. Magn. Magn. Mater. 1990. V. 87. P. 369–374.
Wohlfarth E.P. A review of the problem of fine-particle interactions with special reference to magnetic recording // J. Appl. Phys. 1964. V. 35. P. 783–790.
Дополнительные материалы отсутствуют.
Инструменты
Физика Земли


