Известия РАН. Энергетика, 2019, № 1, стр. 123-134

Сообщения об универсальных алгоритмах релейной защиты и о разработке на их основе свободных от уставок (setting-less) защит с унифицированными характеристиками появились в недавнее время [1–5]. Убежденность в возможности ее решения основывалась на способности цифровой техники соединять разнородную информацию о наблюдаемом объекте, а именно к результатам наблюдения в текущем режиме добавлять результаты наблюдения в предшествующем режиме и анализировать информацию, полученную наблюдением, совместно с априорной информацией о структуре и параметрах объекта [6, 7]. Но это не более чем концепция решения. Немаловажны детали: форма представления априорной информации, критерии разграничения вероятных состояний объекта, виды замеров, в которые преобразуются наблюдаемые величины. Возможные ответы на подобные вопросы обсуждались в работах [8, 9], где предложено задавать априорную информацию в форме преобразователя, называемого алгоритмической моделью объекта. Вопросы унификации характеристик индикатора повреждения объекта на базе его алгоритмической модели при этом практически не затрагивались. Цель настоящей статьи – поиск ответа на этот вопрос применительно к индикатору повреждения в линии электропередачи.

Классификация наблюдаемых режимов. Разграничение режимов определяется характером задачи, стоящей перед наблюдателем. Анализируя протекающие процессы, наблюдатель подразделяет их на переходные, установившиеся или, быть может, свободные, если пассивный объект отключен от источников. Регистрируя процессы, наблюдатель относит их к предшествующему и к текущему режимам, определяет момент смены одного другим и имеет возможность ввести в рассмотрение модельный чисто аварийный режим [10], для чего определяет вектор аварийных составляющих наблюдаемых величин ${{\underline {\mathbf{V}} }_{{{\text{а в }}}}} = {{\underline {\mathbf{V}} }_{{{\text{т к }}}}} - {{\underline {\mathbf{V}} }_{{{\text{п д }}}}},$ где ${{\underline {\mathbf{V}} }_{{{\text{т к }}}}}$ и ${{\underline {\mathbf{V}} }_{{{\text{п д }}}}}$ – векторы величин, наблюдаемых в текущем и предшествующем режимах.

С точки зрения наблюдателя, идентифицирующего состояние объекта, режимы подразделяются на две группы. На контролируемые режимы ($\alpha $-режимы) надлежит реагировать с высокой чувствительностью и заданным быстродействием, а на альтернативные им режимы ($\beta $-режимы) вовсе не реагировать – требование селективности действия релейной защиты. В свою очередь альтернативные режимы подразделяются на две подгруппы – аварийные ${{\beta }_{f}}$-режимы и нормальные ${{\beta }_{n}}$-режимы. На ${{\beta }_{f}}$-режимы, возможно, отреагирует другой наблюдатель или тот же, но с выдержкой времени. Группа $\alpha $-режимов образует совместно с подгруппой ${{\beta }_{f}}$-режимов объединенную группу аварийных $\alpha {{\beta }_{f}}$-режимов.

Требование селективности означает, что тот из $\alpha $-режимов, который при имеющейся информации невозможно отличить от какого-либо из $\beta $-режимов, признается физически нераспознаваемым. Отсюда вытекает правило: идентификацию $\alpha $-режимов необходимо предварить отстройкой от $\beta $-режимов. Аналогично, идентификацию $\alpha {{\beta }_{f}}$-режимов, решающую задачу пуска релейной защиты, надлежит предварять отстройкой от нормальных ${{\beta }_{n}}$-режимов. Заметим, что для обеспечения селективности защиты отстройку от ${{\beta }_{n}}$-режимов достаточно дополнить отдельной отстройкой от аварийных ${{\beta }_{f}}$-режимов.

Критерии разграничения режимов. Каждая из трех задач идентификации режимов требует отдельного рассмотрения: отстройка от ${{\beta }_{f}}$-режимов, отстройка от ${{\beta }_{n}}$-режимов и идентификация наблюдаемого состояния объекта как $\alpha $-режима. Решение каждой из трех задач основывается на критерии принадлежности режима к тому или иному типу. Насколько известно, первое упоминание о подобном критерии встречается в материалах шведского отделения (г. Вастерас) компании АББ. Там введено понятие “общий критерий повреждения (general fault criteria)”, которое в нашей терминологии относится к отстройке от нормальных режимов ${{\beta }_{n}}.$ Развитие терминологии связано с процедурой локализации однотипных режимов [8, 9]. Локализация, способствующая отстройке от режимов определенного типа, совершается на плоскости комплексного замера. Локализуемое множество режимов отображается в виде компактной области. Чем заметнее область отображения $\beta $-режимов будет смещена относительно области отображения $\alpha $-режимов, тем эффективнее локализация $\beta $-режимов. При идеальной локализации области отображений $\alpha $- и $\beta $-режимов вовсе не должны пересекаться. Введем следующую классификация критериев для разграничения $\alpha $- и $\beta $-режимов: критерий селективности – для локализации ${{\beta }_{f}}$-режимов, критерий функционирования – для локализации ${{\beta }_{n}}$-режимов, критерий КЗ – для идентификации $\alpha $-режимов.

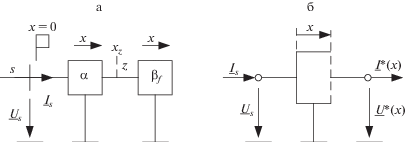
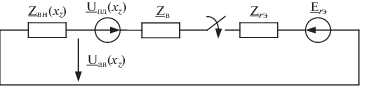
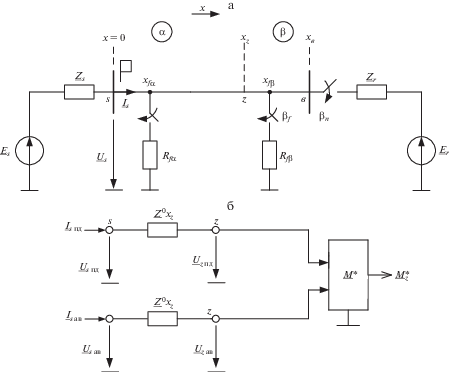
Критерий селективности. Рассмотрим электрическую сеть, в которой причины возникновения $\alpha $- и $\beta $-режимов разнесены в пространстве. На рис. 1 – ${{\underline U }_{s}},$ ${{\underline I }_{s}}$ – наблюдаемые величины, $s$ – место наблюдения, $z$ – граница перехода от $\alpha $-режимов к ${{\beta }_{f}}$-режимам; $\alpha $ и $\beta $ – обозначения, относящиеся еще и к тем частям объекта, повреждения которых создают режимы соответствующего типа (рис. 1а). Алгоритмическая модель, будучи структурным элементом релейной защиты, преобразует входные величины ${{\underline U }_{s}},$ ${{\underline I }_{s}}$ в величины $\underline U {\text{*(}}x{\text{),}}$ $\underline I {\text{*(}}x{\text{)}}$ – напряжение и ток в произвольном месте объекта с координатой $x$ (рис. 1б), прогнозируемые в предположении, что объект не поврежден.

Предположение может не соответствовать действительности, следовательно, выходные величины алгоритмической модели $\underline U {\text{*(}}x{\text{),}}$ $\underline I {\text{*(}}x{\text{)}}$ нельзя отождествлять с соответствующими напряжением и током $\underline U {\text{(}}x{\text{),}}$ $\underline I {\text{(}}x{\text{)}}$ реального объекта. Данное обстоятельство отражено звездочками в обозначениях выходных величин алгоритмической модели.

Критерий селективности призван подсказать наблюдателю, как не принять замыкания в модуле $\beta $ за повреждение модуля $\alpha .$ Воспользуемся с этой целью замером, сформированным из выходных напряжений алгоритмической модели в чисто аварийном и предшествующем режимах

На границе зоны при $x* = {{x}_{z}}$

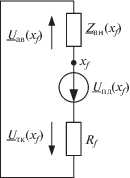
Рассмотрим предпосылки, ведущие к замеру (1), отображаемому на комплексной плоскости $\underline M .$ Пусть ${{x}_{f}}$ – координата места КЗ. Источником чисто аварийного режима является напряжение ${{\underline U }_{{{\text{п д }}}}}{\text{(}}{{x}_{f}}{\text{),}}$ действующее как ЭДС эквивалентного генератора с внутренним сопротивлением ${{\underline Z }_{{{\text{в н }}}}}{\text{(}}{{x}_{f}}{\text{)}} = {{Z}_{{{\text{в н }}}}}{\text{(}}{{x}_{f}}{\text{)}}\,{\text{exp}}\,j{{\varphi }_{{{\text{в н }}}}}{\text{(}}{{x}_{f}}{\text{)}}$ и нагрузкой ${{R}_{f}}$ – переходным сопротивлением КЗ (рис. 2). Для $RL$-цепи справедливо неравенство

которое становится равенством только при металлическом КЗ. В других местах объекта, в частности в месте ${{x}_{z}},$ неравенство напряжений усугубляется

При КЗ в модуле $\beta $ алгоритмическая модель адекватна объекту, т.е. при ${{x}_{f}} > {{x}_{z}}$ неравенство (3) распространяется на величины алгоритмической модели

откуда для модуля замера (1)

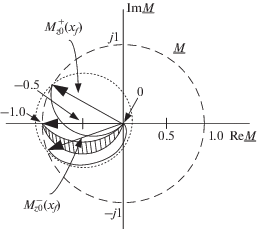
Неравенство (4) локализует множество ${{\beta }_{f}}$-режимов в круге единичного радиуса на плоскости $\underline M ,$ представляя критерий селективности в нулевом приближении. На рис. 3 граничная окружность показана пунктирной линией.

Критерий (3), очевидно, избыточен, так как не учитывает фазовых соотношений, складывающихся при формировании замера (1). Выясним, какую часть круга единичного радиуса занимают отображения этого замера. При КЗ в любом месте ${{x}_{f}} > {{x}_{z}}$ замер описывается уравнением круговой диаграммы, следующим из схемы на рис. 2

где ${{M}_{{z0}}}{\text{(}}{{x}_{f}}{\text{)}}$ – хорда круговой диаграммы, равная замеру ${{\underline M }_{z}}{\text{(}}{{x}_{f}}{\text{)}}$ при металлическом КЗ, ${{\lambda }_{f}} = {{{{R}_{f}}} \mathord{\left/ {\vphantom {{{{R}_{f}}} {{{Z}_{{{\text{в н }}}}}{\text{(}}{{x}_{f}}{\text{)}}}}} \right. \kern-0em} {{{Z}_{{{\text{в н }}}}}{\text{(}}{{x}_{f}}{\text{)}}}}{\kern 1pt} \geqslant 0.$

При КЗ в месте $z\left( {{{x}_{f}} = {{x}_{z}}} \right),$ где ${{\underline M }_{{z0}}}{\text{(}}{{x}_{z}}{\text{)}} = - 1,$

Зависимость (6) при изменении ${{\lambda }_{z}}$ от нуля до бесконечности описывает на плоскости $\underline M $ дугу окружности радиуса ${1 \mathord{\left/ {\vphantom {1 {(2\sin {{\varphi }_{z}})}}} \right. \kern-0em} {(2\sin {{\varphi }_{z}})}}$ с центром, расположенным на вертикали ${\text{Re}}\,\underline M = - 0.5$ в точке ${\text{Im}}\,\underline M = j\,0.5\,{\text{ctg}}\,{{\varphi }_{{{\text{в н }}}}}{\text{(}}{{x}_{z}}{\text{)}}{\text{.}}$ Дуга опирается на хорду ${{\underline M }_{{z0}}}{\text{(}}{{x}_{z}}{\text{)}} = - 1$ (рис. 3).

В системе без потерь угол внутреннего сопротивления ${{\varphi }_{{{\text{в н }}}}}{\text{(}}{{x}_{f}}{\text{)}} = 90^\circ $ вне зависимости от места КЗ. В реальной системе этот угол зависит от места КЗ, изменяясь при вариации пассивных параметров в пределах ${\text{70}}^\circ ...{\text{80}}^\circ .$ Как следствие, дуги (6) образуют сегмент, располагающийся в третьей четверти (заштрихован на рис. 3).

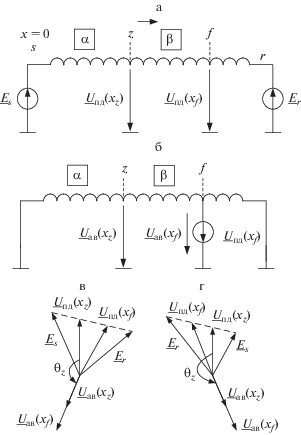
Рассмотрим далее годограф (5) при ${{x}_{f}} > {{x}_{z}}.$ Его положение определяется хордой ${{\underline M }_{{z0}}}{\text{(}}{{x}_{f}}{\text{)}}{\text{.}}$ По мере удаления места ${{x}_{f}} > {{x}_{z}}$ от границы $z,$ вектор ${{\underline M }_{{z0}}}{\text{(}}{{x}_{f}}{\text{)}}$ все более поворачивается относительно исходного положения ${{\underline M }_{{z0}}}{\text{(}}{{x}_{z}}{\text{)}} = - 1.$ Основное влияние на положение хорды оказывает разность фаз напряжений предшествующего режима в граничной точке $z$ и в месте КЗ ${{x}_{f}}.$ Возьмем для примера двухпроводную линию без потерь с углом передачи $\delta = {\text{arg}}\left( {{{{{{\underline E }}_{s}}} \mathord{\left/ {\vphantom {{{{{\underline E }}_{s}}} {{{{\underline E }}_{r}}}}} \right. \kern-0em} {{{{\underline E }}_{r}}}}} \right)$ (рис. 4) и рассмотрим случай металлического КЗ при $\delta > 0$ и $\delta < 0.$ При $\delta > 0$ (прямая передача мощности) напряжение ${{\underline U }_{{{\text{п д }}}}}{\text{(}}{{x}_{z}}{\text{)}}$ опережает напряжение ${{\underline U }_{{{\text{п д }}}}}{\text{(}}{{x}_{f}}{\text{)}}$ (рис. 4в), и соответствующая хорда $\underline M _{{z0}}^{ + }{\text{(}}{{x}_{f}}{\text{)}}$ смещается во второй квадрант (рис. 3). Обратная передача мощности приводит к противоположному эффекту – напряжение ${{\underline U }_{{{\text{п д }}}}}{\text{(}}{{x}_{z}}{\text{)}}$ отстает от ${{\underline U }_{{{\text{п д }}}}}{\text{(}}{{x}_{f}}{\text{)}}$ (рис. 4г), вследствие чего хорда $\underline M _{{z0}}^{ - }{\text{(}}{{x}_{f}}{\text{)}}$ на этот раз смещается в третий квадрант. В итоге критерий селективности в своем следующем приближении приводит к унифицированной характеристике дистанционной защиты в виде окружности, которая окаймляет круговую область в левой части первоначального круга (рис. 3). Центр унифицированной характеристики располагается в точке $\underline M = - 0.5,$ а радиус несколько превышает 0.5. Этот малый круг охватывает начало координат $\underline M = 0$ и, что особенно важно, точку $\underline M = - 1$ вместе со всеми круговыми диаграммами коротких замыканий в модуле $\beta .$

Критерий КЗ. В отличие от критерия селективности, локализующего $\beta $-режимы, критерий КЗ призван подтверждать принадлежность наблюдаемого режима к множеству $\alpha $-режимов. Для этой цели подходит замер

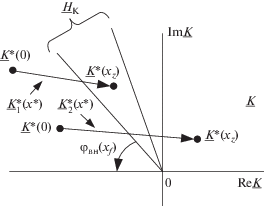
на основе которого создается инструментарий распознавания места КЗ – характеристика места КЗ $\underline K {\text{(}}{{x}_{f}}{\text{)}}$ и координатный годограф $\underline K {\text{*(}}x{\text{)}}$ [11]. Характеристика места КЗ следует из модели эквивалентного генератора (рис. 2) а координатный годограф формируется из выходных величин алгоритмической модели (рис. 1б) при изменении координаты $x* = 0...{{x}_{z}}$ в пределах модуля $\alpha $ (рис. 1а).

Зависимость (8) при изменении ${{\lambda }_{f}}$ в пределах от нуля до бесконечности и фиксированном угле ${{\varphi }_{{{\text{в н }}}}}{\text{(}}{{x}_{f}}{\text{)}}$ отображается лучом на комплексной плоскости $\underline K .$ В системе с малыми потерями значение ${{\varphi }_{{{\text{в н }}}}}{\text{(}}{{x}_{f}}{\text{)}}$ располагается в узком диапазоне углов. Таким образом, область отображения значений $\underline K {\text{(}}{{x}_{f}}{\text{)}}$ – сегмент ${{\underline H }_{K}},$ концентрирующий в себе пучок лучей (8) (рис. 5). Критерий распознавания КЗ в модуле $\alpha $ формулируется следующим образом: если наблюдается $\alpha $-режим, то координатный годограф $\underline K {\text{*(}}x*{\text{)}}$ соприкоснется с сегментом ${{\underline H }_{K}}.$ Иллюстрацией служат годограф $\underline K _{1}^{*}{\text{(}}x{\text{),}}$ вошедший в сегмент, но не покинувший его пределы, и годограф $\underline K _{2}^{*}{\text{(}}x{\text{),}}$ пересекающий сегмент (рис. 5).

Критерий функционирования. Коль скоро замер $\underline M $ обеспечивает локализацию аварийных режимов ${{\beta }_{f}},$ естественно предположить, что он в состоянии обеспечить и локализацию нормальных режимов ${{\beta }_{n}}.$ Рассмотрим режимы включения нагрузки, в общем случае активной. На рис. 6 нагрузка представлена эквивалентным генератором с внутренним сопротивлением ${{\underline Z }_{{r{\text{э }}}}}$ и ЭДС ${{\underline E }_{{r{\text{э }}}}},$ а электрическая сеть представлена относительно конца зоны своим эквивалентным генератором с внутренним сопротивлением ${{\underline Z }_{{{\text{в н }}}}}{\text{(}}{{x}_{z}}{\text{)}}$ и ЭДС ${{\underline U }_{{{\text{п д }}}}}{\text{(}}{{x}_{z}}{\text{)}}{\text{.}}$ Эквивалентные генераторы разделены сопротивлением ${{\underline Z }_{{\text{в }}}}.$

В условиях синхронного включения ЭДС ${{\underline E }_{{r{\text{э }}}}}$ и напряжение ${{\underline U }_{{{\text{п д }}}}}{\text{(}}{{x}_{z}}{\text{)}}$ взаимосвязаны. Допустим, они совпадают по величине и смещены по фазе на угол $\gamma ,$ значения которого располагаются в ограниченном диапазоне

В структуре по рис. 6 отношение составляющих напряжения

определится следующим соотношением между параметрами схемы

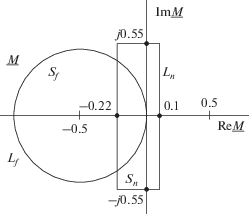
Область отображений замера (11) при вариации параметров (12), (13), ограниченная двумя дугами и двумя отрезками прямых, вписывается в прямоугольник с тремя ограничивающими точками ${{m}_{{11}}}$ и ${{m}_{{12}}}$ на оси вещественных и $ \pm j{{m}_{2}}$ на оси мнимых (рис. 7). Координату ${{m}_{{11}}}$ определим из (12) полагая $\gamma = 0$ и $\theta = 0{\text{:}}$

а координаты ${{m}_{{11}}}$ и ${{m}_{2}}$ определим из (13) – при $\theta = 0$ и ${{\gamma }_{{{\text{max}}}}}{\text{:}}$

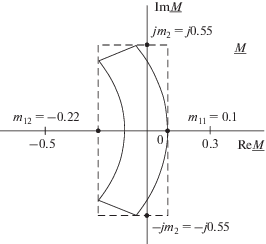
В диапазоне изменения параметров ${{\lambda }_{{{\text{min}}}}} = {\text{0}}{\text{.9,}}$ ${{\lambda }_{{{\text{max}}}}} = {\text{1}}{\text{.1,}}$ ${{\eta }_{{{\text{max}}}}} = 1,$ ${{\gamma }_{{{\text{max}}}}} = 30^\circ $ из (14)–(16) следуют оценки координат:

Индикация КЗ посредством блокировки альтернативных режимов. Воспользуемся для иллюстрации общих положений имитационной моделью линии электропередачи по рис. 8а, в которой координата ${{x}_{z}}$ совпадает с протяженностью защищаемой зоны, а координата ${{x}_{{\text{в }}}}$ – с длиной линии. Место $z$ разделяет электропередачу на $\alpha $- и $\beta $-модули. Алгоритмическую модель однородной линии (рис. 8б) составляет единственный элемент ${{\underline Z }^{0}}x,$ где ${{\underline Z }^{0}}$ – удельное сопротивление линии, $x = 0..{{x}_{{\text{в }}}}.$ В составе имитационной модели имеются элементы с фиксированными и с варьируемыми параметрами. Значения фиксированных параметров: ${{\underline Z }^{0}} = 0.1 + j \times 0.4\,\,{\text{О м /к м ,}}$ ${{x}_{{\text{в }}}} = 100\,\,{\text{к м ,}}$ ${{x}_{z}} = 80\,\,{\text{к м }}{\text{.}}$ Варьируемые параметры подразделяются на аварийные ${{R}_{f}},$ ${{x}_{f}}$ и нормальные – углы $\delta $ или $\gamma $ в зависимости от типа режима, а также пассивные параметры ${{\underline Z }_{s}} = {{Z}_{s}}\,{\text{exp}}\,j\,{{\varphi }_{s}},$ ${{\underline Z }_{r}} = {{Z}_{r}}\,{\text{exp}}\,j\,{{\varphi }_{r}}$ и отношение модулей ЭДС $k = {{{{E}_{s}}} \mathord{\left/ {\vphantom {{{{E}_{s}}} {{{E}_{r}}}}} \right. \kern-0em} {{{E}_{r}}}}{\text{.}}$ Здесь ${{x}_{{f\alpha }}} = 0\,..{{x}_{z}},$ ${{x}_{{f\beta }}} = {{x}_{z}}\,..{{x}_{{\text{в }}}},$ ${{R}_{{f\beta }}} = 0\,..\infty .$ Кроме того, приняты следующие диапазоны изменения варьируемых параметров: ${{R}_{{f\alpha }}} = 0\,..100\,\,{\text{О м ,}}$ ${\text{arg}}\left( {{{{{E}_{s}}} \mathord{\left/ {\vphantom {{{{E}_{s}}} {{{E}_{r}}}}} \right. \kern-0em} {{{E}_{r}}}}} \right) = \delta = - 30^\circ ...30^\circ $ (для режимов $\alpha $ и ${{\beta }_{f}}$) и ${\text{arg}}\left( {{{{{{\underline E }}_{s}}} \mathord{\left/ {\vphantom {{{{{\underline E }}_{s}}} {{{{\underline E }}_{r}}}}} \right. \kern-0em} {{{{\underline E }}_{r}}}}} \right) = \gamma = - 60^\circ ...60^\circ $ (для режимов ${{\beta }_{n}}$), $k = {{{{E}_{s}}} \mathord{\left/ {\vphantom {{{{E}_{s}}} {{{E}_{r}}}}} \right. \kern-0em} {{{E}_{r}}}} = {\text{0}}{\text{.9}}...{\text{1}}{\text{.1,}}$ ${{\underline Z }_{s}} = 1...10\,\,{\text{О м ,}}$ ${{\varphi }_{s}} = 75^\circ ...85^\circ ,$ ${{\underline Z }_{r}} = 1...10\,\,{\text{О м ,}}$ ${{\varphi }_{r}} = 75^\circ ...85^\circ .$

Пусть ${\mathbf{x}}$ – вектор варьируемых параметров имитационной модели; ${\mathbf{x}} \in G,$ где $G$ – область его определения. Соответственно, ${{{\mathbf{x}}}_{\alpha }} \in {{G}_{\alpha }},$ ${{{\mathbf{x}}}_{{\beta f}}} \in {{G}_{{\beta f}}}$ – в $\alpha $- и ${{\beta }_{f}}$-режимах, ${{{\mathbf{x}}}_{{\beta n}}} \in {{G}_{{\beta n}}}$ – в ${{\beta }_{n}}$-режимах. Введем отдельное обозначение вектора нормальных варьируемых параметров имитационной модели, объединяющего все параметры, кроме углов $\delta $ или $\gamma {\text{:}}$

В таком случае векторы режимов примут вид:

Унифицированные характеристики блокировок от режимов ${{\beta }_{f}}$ и ${{\beta }_{n}}$ приведены на рис. 9, где ${{L}_{f}}$ и ${{L}_{n}}$ – обозначения характеристик как граничных линий блокирующих областей ${{S}_{f}}$ и ${{S}_{n}}.$

Входные величины алгоритмической модели, поступающие от имитационной модели, являются функциями варьируемых параметров последней. Зависимость переходит к замеру, формируемому из выходных величин алгоритмической модели (рис. 8б). Замер $\underline M _{z}^{*}$ в режиме КЗ является функцией $\underline M _{z}^{*}{\text{(}}{\mathbf{x}}{\text{),}}$ а в нормальном режиме $\underline M _{z}^{*}{\text{(}}{{{\mathbf{x}}}_{{\beta n}}}{\text{)}}{\text{.}}$

Условия блокирования индикатора принимает форму соответствий, объединенных операцией ИЛИ:

где ${{\delta }_{{{\text{б л }}}}}$ – логический сигнал блокировки.

Распознающая способность алгоритма защиты линии электропередачи оценивается по результатам обработки коротких замыканий в защищаемой зоне. Оценкой служит объектная характеристика, говорящая о чувствительности к переходному сопротивлению ${{R}_{{f\alpha }}}$ при коротком замыкании в месте ${{x}_{{f\alpha }}}$ [7, 8]. Оптимизационная процедура определяет максимальное значение из тех значений ${{R}_{{f\alpha }}},$ которые ранее были подвергнуты минимизации на множестве нормальных параметров. Условиями поиска экстремального значения переходного сопротивления является отображение замера $\underline M _{z}^{*}$ вне соответствующих областей ${{S}_{f}}$ и ${{S}_{n}}.$ Процедура поиска условного экстремума выглядит следующим образом

с ограничениями

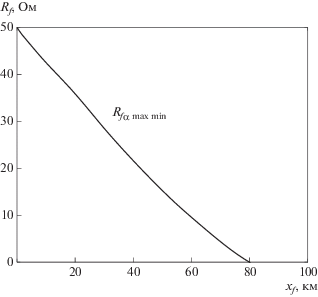
На рис. 10 приведен результат выполнения процедуры (18)–(20) применительно к имитационной модели электропередачи по рис. 8а с использованием алгоритмической модели по рис. 8б. Полученный результат сопровождается дополнительной проверкой блокировок альтернативных режимов:

а также проверкой критерия КЗ в зоне защиты с применением координатного годографа $\underline K {\text{*(}}x*{\text{)}}$ на основе замера (9) и процедуры, иллюстрация которой дана на рис. 5.