Известия РАН. Энергетика, 2019, № 4, стр. 136-148
О численно-аналитическом расчете температурного поля полуограниченного тела при линейном начальном распределении температур
А. К. Соколов *
Ивановский государственный энергетический университет им. В.И. Ленина
Иваново, Россия
* E-mail: sokolov@bjd.ispu.ru
Поступила в редакцию 11.05.2019
После доработки 01.08.2019
Принята к публикации 12.08.2019
Аннотация
Предложено математическое описание температурного поля полуограниченного тела (неограниченной пластины при числе Фурье Fo < 0.05), получено аналитическое решение дифференциального уравнения теплопроводности для интервала времени Δτ при граничных условиях второго рода и линейном начальном распределении температур по сечению тела. Дано описание алгоритма численно-аналитического расчета температурного поля при радиационно-конвективном теплообмене и теплофизических свойствах материала, зависящих от температуры. Приведены примеры расчета нагрева для одного интервала времени Δτ на калькуляторе и температурных полей пластин из кирпича и стали пока температурное возмущение не распространилось на всю толщину пластины. Выполнена оценка погрешности расчета, которая для принятых условий не превышала 1%. Предложенная методика расчета наглядна и проста, так как использует только алгебраические формулы, которые не сложно запрограммировать, например в Microsoft Excel.
В начальной стадии одностороннего нестационарного нагрева или охлаждения неограниченной пластины толщиной 0 ≤ хп ≤ Rп ее температура изменяется только в поверхностном слое толщиной R, величина которого с течением времени увеличивается. В остальной части тела толщиной Rп − R температура может оставаться неизменной. Пока температурное возмущение не распространится на все тело его температурное поле принято считать полуограниченным.
Полуограниченными телами можно считать ограждения теплоэнергетических установок, элементы оборудования при изменении условий теплообмена с внешней средой или другими телами в начальный период времени.
Как правило, именно в этот период значительно изменяется интенсивность теплообмена, а в поверхностном слое возникают большие градиенты температур, которые вызывают термические напряжения, приводящие к разрушению материалов. Следовательно, необходимость совершенствования методов расчета температурных полей в полуограниченных телах представляется актуальной задачей, решение которой позволит прогнозировать величины термических напряжений, разрабатывать безопасные режимы разогрева (охлаждения) конструкций и более точно определять количество теплоты аккумулированной ограждениями при смене погодных условий.
Имеющиеся в литературе [1–3] аналитические решения имеют ограниченную область применения, так как не позволяют учесть реальные условия теплообмена: динамику температуры внешней среды (газов), радиационный перенос, зависимость теплофизических характеристик от температуры и др.
Численные методы расчета температурных полей более универсальны, но требуют весьма трудоемких вычислений. Для снижения трудоемкости расчетов весьма актуально создание и исследование численно-аналитических методов для моделирования температурных полей тел, некоторые из них описаны в работах [4–13].
В статьях [10, 11] был предложен метод расчета температурных полей в полуограниченных телах в форме неограниченной пластины при начальном условии Тн(х, τ = 0) = = const, основанный на математических описаниях и алгоритмах расчета температурных полей тел простой формы, предложенных в работах [8, 9].
В данной работе предлагается развитие метода [11] для расчета температурного поля полуограниченного тела с учетом более сложных начальных условий, которые описываются линейной функцией.
Алгоритм расчета по сравнению с [11] изменится, так как потребуется учитывать температурное поле в непрогретом слое пластины 0 ≤ хп ≤ Rп – R и поток теплоты на поверхности хп = 0.
Расчет процесс нагрева будет заключаться в следующем. Время нагрева пока R ≤ Rп разделяется на ряд расчетных интервалов времени Δτ. Распределение температур по сечению тела в конце каждого расчетного интервала времени Δτ аппроксимируется степенной функцией, параметры которой определяются по аналитическим выражениям, полученным решением линейной системы уравнений, которые описывают начальное и граничные условия температурного поля, а также балансы теплоты. Благодаря заранее полученным приближенным аналитическим решениям для расчетного интервала времени Δτ, решение дифференциального уравнения теплопроводности с частными производными сводится к решению обыкновенного дифференциального уравнения численным методом.
Процедура расчета включает вычисление простых алгебраических выражений (не содержит рядов и специальных функций), поэтому будет понятна и доступна теплоэнергетикам, которые не имеют специальной физико-математической подготовки. Все расчеты в статье, выполнены с помощью Microsoft Excel.
Рассмотрим математическое описание температурного поля ограждения или конструктивного элемента энергетической установки в виде неограниченной пластины толщиной Rп, которую в начале нагрева можно считать полуограниченным телом.
Примем, что начальное распределение температур пластины толщиной Rп, м, описывается линейной функцией
(1)
${{T}_{{\text{н}}}}\left( {{{x}_{0}}} \right) = {{b}_{0}} + {{b}_{1}}{{x}_{{{\text{п\;}}}}}~,\,\,\,\,0 \leqslant {{x}_{{\text{п}}}} \leqslant {{R}_{{\text{п}}}},$(2)
$\frac{{\partial T}}{{\partial {{x}_{{\text{п}}}}}}\left( {0,\tau } \right) = {{b}_{1}} = {{{{q}_{0}}\left( {{{x}_{{\text{п}}}} = 0} \right)} \mathord{\left/ {\vphantom {{{{q}_{0}}\left( {{{x}_{{\text{п}}}} = 0} \right)} \lambda }} \right. \kern-0em} \lambda },$(3)
$\frac{{\partial T}}{{\partial X}}\left( {X = 1} \right){\lambda \mathord{\left/ {\vphantom {\lambda R}} \right. \kern-0em} R} = q\left( \tau \right){\text{\;}},\,\,\,\,0 \leqslant X \leqslant 1{\text{\;}},\,\,\,\,X = {x \mathord{\left/ {\vphantom {x R}} \right. \kern-0em} R},$Примем, что распределение температур в поверхностном слое толщиной R в момент времени τi+ 1 аппроксимируется функцией [8–10]
(4)
$T\left( X \right) = {{a}_{0}} + {{a}_{1}}X + {{a}_{2}}{{X}^{n}},\,\,\,\,0 \leqslant X \leqslant 1,$(5)
${{T}_{{\text{н}}}}\left( {{{x}_{{\text{п}}}},\tau } \right) = {{b}_{0}} + {{b}_{1}}{{x}_{{\text{п}}}}{\text{\;\;}},\,\,\,\,{\text{\;}}0 < {{x}_{{\text{п}}}} < {{R}_{{\text{п}}}} - R.$Рис. 1.
Координаты и распределение температур в пластине толщиной Rп для моментов времени τ = 0 (сплошная линия) и τ > 0 (линия с маркером).
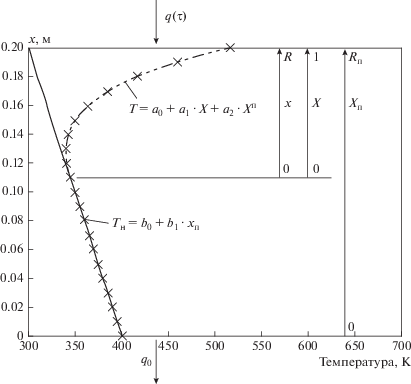
Температура Тн(хп = 0, τ) и градиент температур на поверхности хп = 0 останутся неизменными. На рис. 1 приведены обозначения координат и математическое описание распределение температур в пластине толщиной Rп для двух моментов времени.
Система с двумя текущими координатами хп и х, где 0 ≤ х ≤ R и 0 ≤ хп ≤ Rп, отличается от той, которая обычно применяется при описании температурного поля полуограниченного тела. Для полуограниченного тела обычно используется одна координата 0 ≤ х < ∞, где х = 0 на поверхности теплообмена.
Принятая система координат пластины позволит, не изменяя расчетные формулы использовать их для описания температурного поля пластины, когда тело прогреется на всю толщину пластины (до хп = х = 0) и учесть теплообмен с другой стороны пластины по методу [8, 9].
Величина R будет изменяться во времени. Для конца каждого расчетного интервала значение R можно рассчитать по числу Фурье ΔFo = aΔτi/R2
(6)
$R = \sqrt {{{a\Delta \tau } \mathord{\left/ {\vphantom {{a\Delta \tau } {\Delta {\text{Fo}}}}} \right. \kern-0em} {\Delta {\text{Fo}}}}} .$Число Фурье следует принимать постоянным для всех расчетных моментов времени пока R < Rп, где a − температуропроводность, м/с2, τ − текущее время, с. Для конца интервала i + 1 τ = τi+ 1 = τi + ∆τi.
Величина числа ΔFo будет зависеть от динамики потока теплоты на поверхность тела q. Значение ΔFo должно соответствовать условию ΔFo ≡ min(R), при котором T(x = = 0, τ) = Тн(хп = Rп − R, τ).
Величину ΔFo можно оценить по решению дифференциального уравнения теплопроводности для полуограниченного тела. При q = const ΔFo можно принять по номограмме [3] ΔFo ≈ 0.04. В инженерных расчетах принято считать, что ΔFo ≈ 0.05.
Для расчета распределения температур в конце расчетного интервала времени τi+ 1 = = τi + ∆τi по формуле (4) необходимо определить коэффициенты а0, а1, а2 и показатель степени n.
Формулы для вычисления коэффициентов a0, a1, а2 и показателя степени n можно получить, используя следующие уравнения.
1. Граничное условие, уравнение (3), которое для конца интервала времени при х = R и Х = 1 с учетом выражения (4) примет вид
(3а)
$\frac{{\partial T}}{{\partial X}}\left( {X = 1} \right){\lambda \mathord{\left/ {\vphantom {\lambda R}} \right. \kern-0em} R} = \left( {{{a}_{1}} + n{{a}_{2}}{{X}^{{n - 1}}}} \right){\lambda \mathord{\left/ {\vphantom {\lambda R}} \right. \kern-0em} R} = {{q}_{{\text{к}}}},$Из (3а) можно выразить коэффициент n или a2 для момента времени τi+ 1
(7)
$n = {{\left( {{{{{q}_{{\text{к}}}}R} \mathord{\left/ {\vphantom {{{{q}_{{\text{к}}}}R} {\lambda - {{a}_{1}}}}} \right. \kern-0em} {\lambda - {{a}_{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{{q}_{{\text{к}}}}R} \mathord{\left/ {\vphantom {{{{q}_{{\text{к}}}}R} {\lambda - {{a}_{1}}}}} \right. \kern-0em} {\lambda - {{a}_{1}}}}} \right)} {{{a}_{2}}}}} \right. \kern-0em} {{{a}_{2}}}},$(8)
${{a}_{2}} = {{\left( {{{{{q}_{{\text{к}}}}R} \mathord{\left/ {\vphantom {{{{q}_{{\text{к}}}}R} {\lambda - {{a}_{1}}}}} \right. \kern-0em} {\lambda - {{a}_{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{{q}_{{\text{к}}}}R} \mathord{\left/ {\vphantom {{{{q}_{{\text{к}}}}R} {\lambda - {{a}_{1}}}}} \right. \kern-0em} {\lambda - {{a}_{1}}}}} \right)} n}} \right. \kern-0em} n}.$2. Уравнение баланса теплоты с учетом (1) в плоскости Х = 0 и хп = Rп − Ri + 1
Потоки теплоты в (9) с учетом (1) и (4) можно записать в виде
(11)
$q\left( {X = 0} \right) = {{\lambda \left( {{{a}_{1}} + n{{a}_{2}}{{X}^{{n - 1}}}} \right)} \mathord{\left/ {\vphantom {{\lambda \left( {{{a}_{1}} + n{{a}_{2}}{{X}^{{n - 1}}}} \right)} {{{R}_{{i + 1}}}}}} \right. \kern-0em} {{{R}_{{i + 1}}}}}$3. Уравнение равенства температур в плоскости Х = 0 и хп = Rп − Ri + 1
температуры для которого выразим из (1) и (4)(15)
${{T}_{{\text{н}}}}\left( {{{x}_{{\text{п}}}} = {{R}_{{\text{п}}}} - R} \right) = {{b}_{0}} + {{b}_{1}}\left( {{{R}_{{\text{п}}}} - R} \right)$4. Уравнение баланса теплоты для прогретого слоя толщиной R для интервала времени Δτi+ 1в конечных разностях, которое запишем в следующем виде:
(17)
$\left( {{{T}_{{{\text{ср}},~\,i + 1}}} - {{T}_{{{\text{ср,}}\,{\text{ни}}}}}} \right)c{{R}_{{i + 1}}} = \left( {{{q}_{{{\text{ср}}}}} - {{q}_{{\text{н}}}}} \right){{\tau }_{{i + 1}}},$Величина Tср, ни в начале расчетного интервала времени τi должна определяться по температуре для конца предыдущего интервала времени Тср,i по формуле
(18)
${{T}_{{{\text{ср,}}\,{\text{ни}}}}} = {{{{T}_{{{\text{ср}},~\,i}}}{{R}_{i}}} \mathord{\left/ {\vphantom {{{{T}_{{{\text{ср}},~\,i}}}{{R}_{i}}} {{{R}_{{i + 1}}}}}} \right. \kern-0em} {{{R}_{{i + 1}}}}} + {{{{T}_{{{\text{н}},\,~{\text{ср}},\,~i + 1}}}\left( {{{R}_{{i + 1}}} - {{R}_{i}}} \right)} \mathord{\left/ {\vphantom {{{{T}_{{{\text{н}},\,~{\text{ср}},\,~i + 1}}}\left( {{{R}_{{i + 1}}} - {{R}_{i}}} \right)} {{{R}_{{i + 1}}}}}} \right. \kern-0em} {{{R}_{{i + 1}}}}}.$Обратим внимание, что Tср,i − среднемассовая температура в конце i-го интервала времени относится к слою Ri, а среднемассовая температура в начале i + 1 интервала времени Tср, ни − к расчетному слою Ri + 1 (см. уравнение баланса теплоты (17)). Поэтому на i + 1 интервале времени значение среднемассовой температуры в начале i + 1 интервала времени Tср, ни должно определяться с учетом Tср, i и температуры непрогретой части слоя (Ri + 1 − Ri), которая равна Tн, ср,i+ 1.
Выражение для расчета среднемассовой температуры непрогретого слоя 0 ≤ хп ≤ Rп − Ri в конце интервала Тн, ср, i+ 1 можно получить интегрированием (5)
(19)
${{T}_{{{\text{н}},\,{\text{ср}},\,i + 1}}} = \int\limits_{{{x}_{{n,\,i + 1}}}}^{{{x}_{{n{\text{,}}i}}}} {\left( {{{b}_{0}} + {{b}_{1}}{{x}_{{\text{п}}}}} \right)d{{x}_{{\text{п}}}}} = {{{{b}_{0}} + \left[ {\frac{{{{b}_{1}}}}{2}\left( {x_{{{\text{п}},i}}^{2} - x_{{{\text{п}},\,i + 1}}^{2}} \right)} \right]} \mathord{\left/ {\vphantom {{{{b}_{0}} + \left[ {\frac{{{{b}_{1}}}}{2}\left( {x_{{{\text{п}},i}}^{2} - x_{{{\text{п}},\,i + 1}}^{2}} \right)} \right]} {\left( {{{x}_{{{\text{п}},i}}} - {{x}_{{{\text{п}},\,i + 1}}}} \right)}}} \right. \kern-0em} {\left( {{{x}_{{{\text{п}},i}}} - {{x}_{{{\text{п}},\,i + 1}}}} \right)}},$Значение среднемассовой температуры слоя Ri + 1 в конце интервала Тср, i + 1 определится интегрированием (4) [8, 9]
(20)
${{T}_{{{\text{ср}},~\,i + 1}}} = \int\limits_0^1 {T\left( X \right)dX} = {{{{a}_{0}} + {{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{0}} + {{a}_{1}}} 2}} \right. \kern-0em} 2} + {{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {\left( {n + 1} \right)}}} \right. \kern-0em} {\left( {n + 1} \right)}}.$С учетом (20) уравнение баланса теплоты (17) запишется в виде
(21)
${{{{a}_{0}} + {{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{0}} + {{a}_{1}}} 2}} \right. \kern-0em} 2} + {{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {\left( {n + 1} \right)}}} \right. \kern-0em} {\left( {n + 1} \right)}} - {{T}_{{{\text{ср}}\,{\text{нп}}}}} = {{\left[ {\left( {{{q}_{{{\text{ср}}}}} - {{q}_{0}}} \right)\frac{{\Delta \tau }}{{cR}}} \right]}_{{i + 1}}},$(22)
${{q}_{{{\text{ср}},i + {\text{ }}1}}} = {\text{ }}\left( {{{q}_{{{\text{н}},i + {\text{ }}1}}} + {{q}_{{{\text{к}},i + {\text{ }}1}}}} \right)/2.$Из уравнения (21) выразим коэффициент а2
где(24)
$\Delta T = {{T}_{{{\text{ср,}}\,{\text{ни}}}}} + \left[ {\left( {{{q}_{{{\text{ср}}}}} - {{q}_{0}}} \right)\frac{{\Delta \tau }}{{c{{R}_{{i + 1}}}}}} \right] - {{a}_{0}} - {{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} 2}} \right. \kern-0em} 2}.$С учетом выражения (7) формулу (24) для расчета n представим в виде
(25)
${{a}_{2}} = \Delta T\left[ {{{\left( {\frac{{{{q}_{{\text{к}}}}{{R}_{{i + 1}}}}}{\lambda } - {{a}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{{q}_{{\text{к}}}}{{R}_{{i + 1}}}}}{\lambda } - {{a}_{1}}} \right)} {{{a}_{2}} + 1}}} \right. \kern-0em} {{{a}_{2}} + 1}}} \right]$(26)
${{a}_{2}} = \frac{{\Delta T}}{2} + \sqrt {\frac{{\Delta T}}{4} + \Delta T\left( {\frac{{{{q}_{{\text{к}}}}{{R}_{{i + 1}}}}}{\lambda } - {{a}_{1}}} \right)} .$Отметим, что при ΔТ < 0 коэффициент а2 следует рассчитывать по формуле (8), задавая n = 4.
Зная коэффициент а2, показатель степени n можно определить по формуле (7).
Таким образом, по довольно простым формулам (12), (16) и (26) можно определить а1, а0, а2 и n по формуле (7), рассчитать распределение температур в конце расчетного интервала времени τi+ 1 по (4).
Сравнительно простые формулы (12), (16), (26) и (7) − это аналитическое решение дифференциального уравнения теплопроводности при граничных условиях второго рода для интервала времени Δτi+ 1 при известных значениях Tср, ни и Тн(хп = Rп − R).
Расчет температур поверхности Т1,i+ 1 = Т(Х = 1, τi+ 1) и среднемассовой температуры в конце интервала времени Тср,i+ 1 можно выполнить по формулам
которые получены из (4) при Х = 1 и из выражения (20).Для первого интервала среднемассовая температура Tср, ни в слоя толщиной R1 начале интервала (i = 0) определится из начальных условий по формуле (19) при Ri = 0 = 0 и xп,i = Rп − R0 = Rп.
Для последующих интервалов i > 1 значение Tср, ни найдется с учетом изменения размера прогретого слоя по формуле (18) с учетом (19).
Расчет распределений температур в последующие моменты времени τi+ 1 = τi + Δτ можно выполнять с помощью известных процедур решения обыкновенных дифференциальных уравнений, например, методов Эйлера, Эйлера-Коши, Рунге-Кутта, ломаных и др.
Для заданной функции q(τ), расчет по описанным выше формулам не вызовет серьезных затруднений, так как будет проводиться по простым алгебраическим выражениям. Однако для сопряженной задачи теплообмена система уравнений для расчета а1, а0, а2 и n будет нелинейной.
Обратим внимание, что в формулу (26) для расчета а2 с учетом (24) входят q0(хп) и средний поток теплоты qср,i+ 1, который можно определить по потокам теплоты в начале qн,i+ 1 и конце qк,i+ 1 интервала времени по (22).
Величина q0(хп) зависит от начальных условий и легко находится по (10).
В начале расчета температур на интервале Δτi+ 1 имеются известные данные только для вычисления потока теплоты в начале интервала qн,i+ 1 по известной температуре поверхности Т1,i. Температура поверхности Х = 1 Т1,i+ 1 = Т(Х = 1, τi+ 1) и величина потока теплоты в конце интервала времени qк,i+ 1 неизвестны, поэтому их значения приходиться принимать приближенно. При расчете по методу Эйлера принимается, например, условие qср,i+ 1 ≈ qк,i+ 1 ≈ qн,i+ 1.
Для материалов с низкой теплопроводностью (кирпича, тепловой изоляции) и металлов при интенсивном теплообмене характерна высокая скорость роста температуры обогреваемой поверхности, которая приводит к резкому изменению потока теплоты в пределах расчетного интервала времени. В таких условиях задание qср,i+ 1 ≈ qк,i+ 1 ≈ qн,i+ 1 вызывает значительные погрешности расчета или приводит к абсурдным результатам.
В работах [8, 10] предложена оригинальная методика для оценки значений температуры поверхности (Х = 1) Т1,i+ 1 и qк,i+ 1. Методика основана на допущении постоянства в пределах Δτi+ 1 приведенного коэффициента теплообмена.
Модифицируем ее для данного математического описания.
Рассмотрим процедуру получения первого приближения температуры поверхности $Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}}.$
Поток теплоты q на поверхность Х = 1 в расчетные моменты времени в общем случае может зависеть от температур газов Тг(τ), коэффициентов радиационного σ, Вт/(м2 · К4), и конвективного αк, Вт/(м2 · К), теплообмена.
Запишем выражение для приведенного коэффициента теплообмена в начале расчетного интервала
(29)
${{\alpha }_{{{\text{пр, н}}}}} = {{q}_{{{\text{н}},i + {\text{ }}1}}}/\left( {{{T}_{{{\text{г}},{\text{ н}},i}}} - {{T}_{{1,i}}}} \right),$(30)
${{q}_{{{\text{н}},\,i + {\text{1}}}}} = \sigma \left[ {T_{{\text{г}}}^{4}({{\tau }_{i}}) - T_{{1,i}}^{4}} \right] + \alpha [{{T}_{{\text{г}}}}(\tau ) - {{T}_{{1,i}}})].$Выразим первое приближение для потока теплоты в конце i+1 интервала через приведенный коэффициент теплообмена и неизвестную пока температуру поверхности в конце интервала $Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}}$
(31)
$q_{{{\text{к}},\,i + {\text{1}}}}^{{\text{п}}} = {{\alpha }_{{{\text{пр}}}}}\left( {{{T}_{{{\text{г}},\,{\text{к}},\,i + {\text{1}}}}} - Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}}} \right).$Используя выражения (27) и (28) запишем разность температур $Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}}$ и Тср,i+ 1 с учетом формулы(8) для а2
(32)
$T_{{1,~\,i + 1}}^{1} = {{T}_{{{\text{ср}},~\,i + 1}}} + {{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} 2}} \right. \kern-0em} 2} + \left[ {{{\left( {\frac{{q_{{{\text{к}},\,~i + 1}}^{1}{{R}_{{i + 1}}}}}{\lambda } - {{a}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{q_{{{\text{к}},\,~i + 1}}^{1}{{R}_{{i + 1}}}}}{\lambda } - {{a}_{1}}} \right)} {\left( {n + 1} \right)}}} \right. \kern-0em} {\left( {n + 1} \right)}}} \right].$Из уравнения баланса теплоты (17) получим формулу для Тср,i+ 1 и подставим ее в (32). Преобразовав (32) с учетом (17) получим выражение для расчета первого приближения температуры $Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}},$ которую используем для расчета первого приближение для потока теплоты в конце i + 1 интервала по формуле (31):
(33)
$T_{{1,\,i + 1}}^{1} = \frac{{{{T}_{{{\text{ср}},\,{\text{ни}}}}} + \left[ {{{{\alpha }}_{{{\text{пр}},\,{\text{н}}}}}{{T}_{{{\text{г}},\,i + 1}}} + {{q}_{{{\text{н}},\,i + 1}}} - 2{{q}_{0}}} \right]w + {{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} 2}} \right. \kern-0em} 2} + {{{\alpha }}_{{{\text{пр}},\,{\text{н}}}}}{{T}_{{{\text{г}},\,i + 1}}}\frac{{{{R}_{{i + 1}}}}}{{{\lambda }\left( {{{n}^{1}} + 1} \right)}}}}{{1 + {{{\alpha }}_{{{\text{пр}},\,{\text{н}}}}}\left[ {w + \frac{{{{R}_{{i + 1}}}}}{{{\lambda }\left( {{{n}^{1}} + 1} \right)}}} \right]}},$Величина $Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}}$ является приближенной, так как коэффициент αпр, н справедлив не для всего интервала, а только для его начала. Значение показателя степени nп для первого интервала времени следует принять, например nп = 3. Для второго и последующих этапов его величину можно принять по предыдущему интервалу времени. Исследования показали, что задание nп для первого интервала времени в диапазоне 3 < nп < 6 и 0.03 < Fo < 0.07 практически не отражается на результатах расчета температуры поверхности тела Т(1, τ).
По известной температуре $Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}}$ можно рассчитать приближенное значение потока теплоты в конце интервала qк,i+ 1 по формуле (31), используя $Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}}$ и другие параметры теплообмена соответствующие τi+ 1. По qн,i+ 1 и qк,i+ 1 можно вычислить средний для интервала времени поток теплоты qср,i+ 1 (см. (22)). Далее определить а0, а1 и показатель степени n и по функции (4), рассчитать распределение температур в конце расчетного интервала времени T(X) или Т1,i+ 1. и Тср,i+ 1 по (27), (28).
В некоторых случаях значение Т1,i+ 1 можно уточнять простыми итерациями, используя его в качестве следующего приближения вместо T1, н,i+ 1 при расчете αпр по (20).
Для снижения трудоемкости расчета от расчета $Т_{{{\text{1}},\,i + {\text{1}}}}^{{\text{п}}}$ можно отказаться, когда потоки теплоты незначительно различаются в пределах Δτ, то есть когда qср,i+ 1 ≈ qн,i+ 1 ≈ ≈ qк,i+ 1. Это возможно для металлов или для тел с низкой теплопроводностью, когда слабо изменяется интенсивность теплообмена.
Рассмотрим пример расчета нагрева материала пластины (с = 1.5 × 106; λ = 0.8; a = = 5.333 × 10–7; R = 0.2) со стороны xп = Rп = 0.2 в среде Тг = 600, α = 60 при начальном распределении температур Тн(xп) = 400–500xп (b0 = 400, b1 = –500) (функция Тн(xп) показана на рис. 1).
Определим параметры температурного поля в конце i = 1 периода нагрева.
Примем i = 0; n1 = 3; Ri = 0 = 0; Fо = 0.05; Δτ1 = τ1 = 10; Тг = 600.
Рассчитаем глубину прогрева по формуле (6)
Определим диапазон интегрирования для расчета средней температуры Тср, ни слоя R1 = 0.01033 в начале интервала времени xп, 0 = 0.2; xп, 1 = 0.2 − 0.01033 = 0.1897 и ее значение
Потоки теплоты в xп, 1q0 = λb1 = 0.8(–500) = –400 и на поверхности x = R (X = 1) в начале интервала qн = 60(600 – 300) = 18000.
Приведенный коэффициент теплообмена αпр = α = 60 и комплекс w1
Первое приближение для температуры поверхности в конце интервала времени
Первое приближение потока теплоты в конце первого интервала Δτ
Средний поток теплоты на интервале Δτ1
Коэффициент а0 = 400 + (–500) × 0.1897 = 305.16.
Величина ΔТ по (24)
Коэффициент а2 по (26)
Показатель степени n по формуле (7)
Температура поверхности Т1,i+ 1 (x = R, X = 1 и xп = Rп)
(Значение Т1,i+ 1 отличается от первого приближения на 358.7 – 351.1 = 7.6 К.)
Средние температуры прогретого слоя ${{R}_{1}}$ в конце интервала Δτ
Параметры в начале второго интервала τ2 = 20, Δτ2 = 20 – 10 = 10, i = 1
Описанная процедура повторяется для следующих интервалов времени, пока R < Rп.
Результаты расчета для времени 0 ≤ τ ≤ 3600 с, пока R < Rп, приведены на рис. 2–4.
Рис. 2.
Динамика температур газа (Тг), поверхности хп = Rп (Т1), средних температур прогретого слоя (ТсR) и всей пластины (ТсПл).
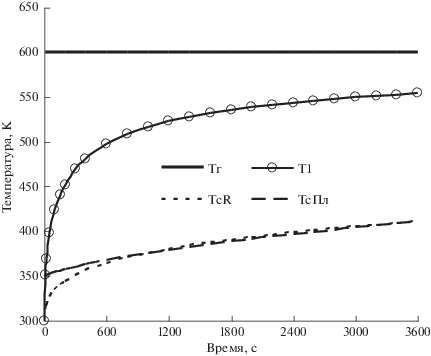
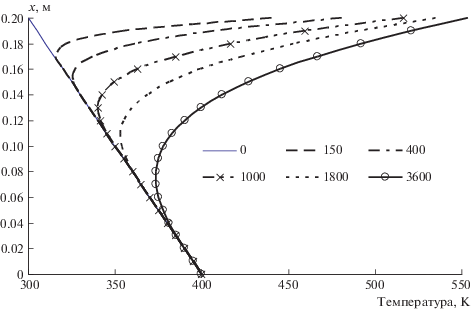
Рис. 4.
Распределения температур по толщине пластины в моменты времени τ = 0, 150, 400, 1000, 1800 и 3600 с.
На рис. 2 показана динамика температур газа, поверхности хп = Rп, средних температур прогретого слоя и всей пластины.
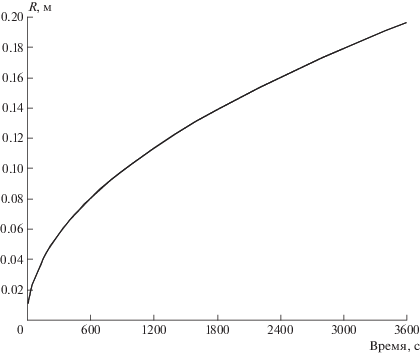
На рис. 3. Показана динамика изменения глубины R прогрева пластины.
По рис. 2 и 3 можно сделать вывод, что для принятых условий, после прогрева пластины наполовину толщины R > Rп и τ > 900 с средние температуры прогретого слоя и всей пластины становятся практически равными.
На рис. 4 показаны распределения температур по толщине пластины, рассчитанные по формулам (1) и (5) для нескольких моментов времени.
Рассмотрим результаты расчета радиационно-конвективного нагрева (α = 40, σ = = 4 × 10–8, Тг(τ) = 900 = const) стальной пластины Rп = 0.2, свойства которой зависят от температуры (коэффициент теплопроводности λ = 63.41 – 0.03256Т, температуропроводность а = 18.1 × 10–6 – 1.34 × 10–8Т). Начальные распределения температур Тн(xп) = b0 + b1xп задавались для двух вариантов:
• 1 – b0 = 400, b1 = –500 (внешний нагрев со стороны хп = 0);
• 2 – b0 = 300, b1 = +500 (внешнее охлаждение со стороны хп = 0).
Величина ΔFo принималась равной 0.051, а Δτ = 15 с.
Обратим внимание, что величины а в (6) и λ в (3), (7), (8) рассчитывались по Т(Х = 1, τ), а λ в (10) – по температуре Тн(xп = Rп – R).
На рис. 5 показана динамика температур поверхности хп = Rп, средней температуры всей пластины для двух вариантов задания начальных условий.
Рис. 5.
Динамика температур поверхности (Т1) хп = Rп средней температуры всей пластины (Тср) при внешнем нагреве со стороны хп = 0 (–500) и внешнем охлаждении со стороны хп = 0 (+500).
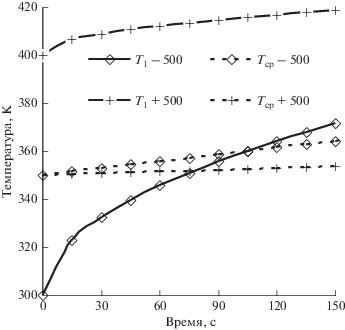
На рис. 5 видно, начальное распределение температур оказывает значительное влияние на скорость роста температуры поверхности.
При внешнем нагреве со стороны хп = 0 Т1 увеличилась за 150 с на 70 К, а при охлаждении – только на 20 К.
При тех же условиях, но при температуре газа Тг(τ) = 600 = const, температуры Т1 и Тср пластины даже снижались при нагреве с верху (хп = Rп) и охлаждении с низу (хп = 0). В этом случае величина ΔТ < 0 (см. (25)) и расчет а2 выполнялся по формуле (8) и n = 4. При n = 3 и n = 5 погрешность расчета увеличивалась, но не более чем на 5 К.
Отметим, что при тех же условиях теплообмена были выполнены расчеты методом конечных разностей. Расхождений результатов не превышало 1%.
ВЫВОДЫ
Предложено решение дифференциального уравнения теплопроводности для полуограниченного тела при начальном условии заданном линейной функцией и граничных условиях второго рода для интервала времени. Описан алгоритм расчета температурного поля численно-аналитическим методом при радиационно-конвективном теплообмене и теплофизических свойствах материала, зависящих от температуры. Приведены результаты расчета пластин из кирпича и стали. Выполнена оценка погрешности расчета, которая для рассмотренных условий теплообмена составляла ~1%.
Список литературы
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Кудинов В.А., Карташов Э.М., Калашников В.В. Аналитические решения задач тепломассопереноса и термоупругости для многослойных конструкций. Учеб. пос. для втузов. М.: Высшая школа, 2005. 340 с.
Пехович А.И., Жидких В.М. Расчеты теплового режима твердых тел. Л.: Энергия, 1968. 304 с.
Лисиенко В.Г., Волков В.В., Маликов Ю.К. Улучшение топливоиспользования и управление теплообменом в металлургических печах. М.: Металлургия, 1988. 230 с.
Котенев В.И. Приближенный метод решения задач нестационарнарной теплопроводности // Известия АН СССР. Энергетика и транспорт. 1989. № 3. С. 111–116.
Губинский В.И. Развитие численно-аналитических методов решения задач теплообмена // Труды междунар. конф. “Экология и теплотехника − 1996". Днепропетровск: Изд-во ГМАУ, 1996. С. 76–78.
Кудинов В.А., Стефанюк Е.В. Задачи теплопроводности на основе определения фронта температурного возмущения. Известия РАН. Энергетика. 2008. № 4. С. 122–138.
Соколов А.К. Численно-аналитический метод расчета температурных полей многослойных пластин в начальной стадии нагрева // Изв. РАН Энергетика. 2009. № 1. С. 138–151.
Соколов А.К. Математическое моделирование нагрева металла в газовых печах: Научное издание. ФГБОУВПО “Ивановский государственный энергетический университет им. В.И. Ленина”. Иваново, 2011. 396 с. ISВN.
Соколов А.К., Сергашев Е.В., Якубина О.А. Численно-аналитический метод расчета температурного поля полуограниченного тела, аппроксимированного степенными функциями / Вестник ИГЭУ. ФГБОУВПО “Ивановский государственный энергетический университет им. В.И. Ленина”. 2015. Вып. 1. С. 59–64.
Соколов А.К., Якубина О.А. Численно-аналитический метод расчета температурного поля полуограниченного тела с использованием показательных функций / Вестник ИГЭУ. ФГБОУВПО “Ивановский государственный энергетический университет им. В.И. Ленина”. 2016. Вып. 2. С. 44–50.
Kudinov V.A. Analytical solution of the Stefan problem with account for the ablation and the temperature-disturbance front / V.A. Kudinov, A.V. Eremin, I.V. Kudinov // Journal of Engineering Physics and Thermophysics. 2012. № 1(85). P. 1441–1452.
Еремин А.В., Стефанюк Е.В., Абишева Л.С. Идентификация источника теплоты на основе аналитического решения задачи теплопроводности / Известия высших учебных заведений. Черная металлургия. 2016. Т. 59. № 5. С. 339–346.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика