1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2023

Известия РАН. Механика твердого тела, 2023, № 3, стр. 106-122

УПРАВЛЕНИЕ ДИНАМИЧЕСКИМИ ПАРАМЕТРАМИ ПЛОСКОЙ БАЛОЧНОЙ КОНСТРУКЦИИ ПОСРЕДСТВОМ ВЫБОРА ЗАКРЕПЛЕНИЙ

И. В. Кудрявцев a, *, В. А. Иванов b, Н. В. Суходоева a, О. И. Рабецкая a, c, А. Е. Митяев a

a Сибирский федеральный университет
Красноярск, Россия

b Общество с ограниченной ответственностью “Борус“
Красноярск, Россия

c Сибирский государственный университет науки и технологий имени академика М.Ф. Решетнева
Красноярск, Россия

* E-mail: ikudryavcev@sfu-kras.ru

Поступила в редакцию 08.07.2022
После доработки 18.08.2022
Принята к публикации 24.08.2022

Полный текст (PDF)

Аннотация

В данной работе предлагается методика обоснованного выбора схемы закрепления, вида опор и их жесткости для плоских балочных конструкций осесимметричного поперечного сечения с целью обеспечения заданных значений первой частоты собственных изгибных колебаний и первой критической нагрузки с учетом действия продольных сил и изменения температуры. Методика основана на известных положениях теории колебаний балок, теории устойчивости по Эйлеру и использует в качестве критерия выбора схемы закрепления коэффициенты опор, которые предварительно нормируются для достижения сопоставимых значений. Выбранная схема обеспечивает заданное значение первой собственной частоты колебаний, величину первой критической температуры или одновременно оба условия работоспособности. Согласно разработанной методике выполнены сравнительные расчеты плоской стержневой конструкции методом конечных элементов, которые показали хорошую сходимость результатов по всем контролируемым параметрам. Предложенный подход может быть использован при проектировании опорного закрепления плоских балочных конструкций различного назначения для обеспечения их динамического поведения.

Ключевые слова: балка, опора, жесткость, колебания, частота, продольная сила, устойчивость, коэффициент опор

Введение. Динамическое поведение балочных конструкций, во многом определяется спектром их собственных частот изгибных колебаний, в котором наиболее опасной обычно является первая собственная частота. Изменение температуры балки приводит к появлению продольных сил, которые смещают спектр собственных частот изгибных колебаний в сторону меньших значений, и они могут достигать опасной резонансной области вплоть до потери устойчивости конструкции.

Существующие аналитические методы расчета свободных колебаний [1–17] и устойчивости [18–22] балочных конструкций обычно ограничиваются рассмотрением отдельных балок с уже заданными условиями закрепления и нагружения. В этом случае задача сводится к дифференциальным уравнениям в частных производных с заданными граничными условиями. Решение такой математической задачи хорошо известно и сводится к поиску собственных векторов и собственных значений для некоторой, полученной после ряда математических преобразований, системы линейных алгебраических уравнений. Получить решение такой задачи обычно возможно только на основе численных методов на ЭВМ. Сложность получения решения таких задач привела к разработке прикладных методов расчета и различных справочников по колебаниям и устойчивости, которые позволяют инженерам-проектировщикам рассчитывать наиболее распространенные модели элементов конструкций при простых условиях закреплений без необходимости составления дифференциальных уравнений и их решения [23–27]. При этом практически вся литература по колебаниям и устойчивости многоопорных балок также основана на проверочном подходе с оценкой динамических параметров плоских балочных конструкций с заданными опорами, без возможности их проектного расчета и обоснования требований к закреплениям.

Однако перед инженером-проектировщиком обычно стоит именно обратная задача: для заданной протяженной конструкции необходимо определить, какие опоры, с какой жесткостью и с каким шагом необходимо установить, чтобы получить требуемые значения собственных частот колебаний и величин критических нагрузок. Для выхода из ситуации в работе предлагается использовать готовые известные решения задач колебаний и устойчивости в виде справочных коэффициентов опор при различных условиях закрепления многоопорной балочной конструкции.

Нормирование значений коэффициентов опор позволило получить единый критерий выбора схемы расстановки опор, а аппроксимация коэффициентов квадратичными функциями позволило учесть жесткость опор. В результате, в данной работе на основе известных аналитических зависимостей теории колебаний и теории устойчивости балок предложена методика, позволяющая выполнять с достаточной для инженерных расчетов точностью обоснованный выбор схемы закрепления плоских многоопорных балочных конструкций, которая обеспечит требуемые значения первой частоты собственных колебаний и первой критической силы или температуры.

1. Динамическое состояние плоских балочных конструкций. Существует огромное многообразие протяженных балочных конструкций и способов их закрепления, что затрудняет обоснованный выбор их закреплений. В данной работе рассматриваются балочные конструкции, состоящие из отдельных протяженных прямых и криволинейных участков с осесимметричной формой поперечного сечения, лежащих в одной плоскости. Предполагается, что все участки имеют идентичную продольную и изгибную жесткость, жесткости всех промежуточных опор равны, расстояния между ними одинаковы, что распространено на практике, поскольку соответствует критериям рациональной конструкции. Геометрия участков соответствует общим требованиям теории изгиба стержней, а в случае тонкостенного поперечного сечения толщина стенки считается достаточной для исключения локальной потери устойчивости формы поперечного сечения, что выполняется при условии [28]:

(1.1)
${l \mathord{\left/ {\vphantom {l D}} \right. \kern-0em} D} \geqslant 10,\quad {D \mathord{\left/ {\vphantom {D t}} \right. \kern-0em} t} \geqslant 10$
где l – длина участка; D – наружный диаметр; t – толщина стенки.

Из всего спектра собственных частот и критических нагрузок протяженной балочной конструкции наиболее опасными обычно являются первая собственная частота изгибных колебаний  f1, и первая критическая сила Pcr1  (или температура ΔТcr1). В этом случае условие работоспособности конструкции примем в виде:

(1.2)
${{f}_{1}} \geqslant \left[ {{{f}_{1}}} \right],\quad {{P}_{{cr1}}} \geqslant \left[ {{{P}_{{cr1}}}} \right]\quad {\text{или}}\quad \Delta {{T}_{{cr1}}} \geqslant \left[ {\Delta {{T}_{{cr1}}}} \right]$
где [f1] – допустимое значение первой собственной частоты; [Pcr1] – допустимая величина критической силы; [ΔТcr1] – допустимое изменение критической температуры.

Принятые ограничения на геометрию конструкции (1.1) приводят к тому, что форма колебаний на первой собственной частоте и первая форма потери устойчивости будут соответствовать поперечному изгибу балки в направлении наименьшей жесткости. В соответствии с этим, рассмотрим уравнения динамического состояния для прямых и изогнутых участков плоской балочной конструкции с учетом действия продольной силы.

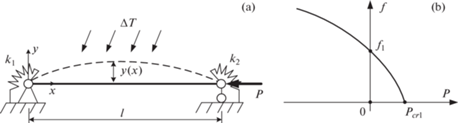
1.1. Прямые участки. Свободные колебания прямого участка балки с упругим шарнирным закреплением и при действии продольной силы Р (рис. 1,а) описываются уравнением [1–6]:

(1.3)
$EJ\frac{{{{\partial }^{4}}y}}{{\partial {{x}^{4}}}} + P\frac{{{{\partial }^{2}}y}}{{\partial {{x}^{2}}}} + m\frac{{{{\partial }^{2}}y}}{{\partial {{t}^{2}}}} = 0$
где y = y(x, t) – функция прогиба; E – модуль Юнга; J – момент инерции сечения; m – удельная масса, m = ρS, где ρ – плотность; S – площадь поперечного сечения; Р – продольная сила.

Рис. 1.

Расчетная схема прямого участка.

Решение уравнения (1.3) для первой частоты собственных колебаний при отсутствии продольной силы имеет вид:

(1.4)
${{f}_{1}} = \frac{{{{\alpha }^{2}}}}{{2\pi {{l}^{2}}}} \cdot \sqrt {\frac{{EJ}}{m}} $
где α = α(k1, k2) – коэффициент опор при колебаниях, учитывающий способ закрепления участка.

Влияние сжимающей продольной силы Р на значение первой частоты собственных колебаний определяется по формуле Галефа [29–32]:

(1.5)
${{f}_{{1\left( {P < > 0} \right)}}} = {{f}_{{1\left( {P = 0} \right)}}} \cdot \sqrt {1 - \frac{P}{{{{P}_{{cr1}}}}}} $
где f1(P<>0) – первая частота свободных колебаний при действии продольной силы Р;

f1(P= 0) – первая частота свободных колебаний при отсутствии продольной силы Р;

Pcr1 – первая критическая сила.

Выражение для первой критической силы найдем из решения уравнения устойчивости для этого же прямого участка с идентичными граничными условиями (рис. 1,а):

(1.6)
$EJ\frac{{{{\partial }^{4}}y}}{{\partial {{x}^{4}}}} + P\frac{{{{\partial }^{2}}y}}{{\partial {{x}^{2}}}} = 0$

Решение задачи устойчивости (1.6) для первой критической нагрузки имеет вид:

(1.7)
${{P}_{{cr1}}} = \frac{{{{\pi }^{2}}EJ}}{{{{\mu }^{2}} \cdot {{l}^{2}}}}$
где μ = μ(k1, k2) – коэффициент опор при потере устойчивости.

По принципу суперпозиции разложим продольную силу Р на две компоненты:

(1.8)
$P = {{P}_{{\Delta T}}} + {{P}_{F}} = {{\alpha }_{t}} \cdot \Delta T \cdot ES + {{P}_{F}}$
где РΔТ  – температурное усилие; PF – сила; αt – коэффициент температурного расширения.

Подставим выражения (1.4, 1.7 и 1.8) в уравнение (1.5) и получим зависимость первой частоты собственных колебаний прямого участка от температурного, силового воздействия, а также способа закрепления в виде общего условия работоспособности:

(1.9)
${{f}_{1}} = {{\left( {\frac{\alpha }{{\pi l}}} \right)}^{2}} \cdot \sqrt {\frac{1}{{4m}}[{{\pi }^{2}}E{{J}_{z}} - {{\mu }^{2}} \cdot {{l}^{2}} \cdot \left( {{{\alpha }_{t}} \cdot \Delta T \cdot ES + {{P}_{F}}} \right)]} \geqslant \left[ {{{f}_{1}}} \right]$

При возрастании нагрузки (1.8), первая собственная частота колебаний прямого участка будет снижаться вплоть до нуля, что соответствует динамическому критерию потери устойчивости (рис.1,б). Таким образом, условие (1.10) соответствует одновременному выполнению обоих критериев работоспособности (1.2): обеспечение минимального значения первой собственной частоты колебаний и устойчивости участка.

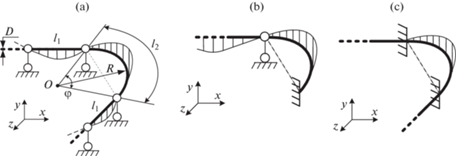
1.2. Криволинейные участки. Расчет криволинейных участков сложнее из-за широкой вариативности геометрии и ее нелинейного влияния на получаемое решение [33–36]. Другой особенностью динамики криволинейных участков является их склонность к образованию, совместно со смежными участками, сложных изгибно-крутильных мод колебаний на более низких частотах, чем у соседних прямых участков. Упростить данную задачу возможно путем установки промежуточных опор по границам криволинейных участков и принятия ряда ограничений на их геометрию. Будем рассматривать криволинейные участки, изогнутые по дуге окружности с углом охвата до 180°, у которых главные оси лежат в плоскости дуги. Соотношения размеров криволинейных участков соответствует условиям (1.1), к которым добавляется условие на отношение поперечного размера сечения участка к радиусу его изгиба (рис. 2,а):

(1.10)
$R{\text{/}}D \geqslant 10$
где D – поперечный размер; R – радиус дуги.

Рис. 2.

Изгибные колебания криволинейного участка.

Принятые ограничения упрощают решение за счет разделения мод колебаний и создают условия для изгибной формы колебаний криволинейного участка на первой собственной частоте. В научной литературе предлагаются сложные зависимости [24, 26, 33–36] для расчета криволинейных участков, которые непригодны для предлагаемой методики. Поэтому нами была проведена серия расчетов криволинейных участков осесимметричного поперечного сечения с соотношениями размеров:

(1.11)
$R{\text{/}}D = 10 \ldots 100,\quad {{l}_{2}}{\text{/}}D = 10 \ldots 100$
с целью упрощения указанных зависимостей и контролем роста погрешности не более 5…7%. В результате были получены упрощенные выражения (1.12), которые определяют первую собственную частоту изгибных колебаний криволинейных участков для углов дуги до 180° при различных условиях закрепления (рис. 2).

(1.12)
$\begin{gathered} {{f}_{{1a}}} = {{\left( {1 - \frac{{{{R}^{3}}{{\varphi }^{3}}}}{{4.86l_{1}^{3}}}} \right)}^{2}} \cdot \frac{{1.57}}{{l_{1}^{2}}}\sqrt {\frac{{EJ}}{m}} ,\quad {{f}_{{1b}}} = \frac{{2.45 - 0.32 \cdot \varphi }}{{{{\varphi }^{2}} \cdot {{R}^{2}}}} \cdot \sqrt {\frac{{EJ}}{m}} \\ {{f}_{{1c}}} = \frac{{3.6 - 0.2 \cdot \varphi }}{{{{\varphi }^{2}} \cdot {{R}^{2}}}} \cdot \sqrt {\frac{{EJ}}{m}} \\ \end{gathered} $

Шарнирно опертый криволинейный участок, в отличие от других способов закреплений на рис. 2, обладает возможностью движения как жесткого целого, вращаясь в шарнирных опорах. В составе протяженной многоопорной конструкции такой участок неподвижен за счет его присоединения к смежным прямым участкам, для которых он становится дополнительной нагрузкой, понижающей исходное значение их первой собственной частоты. Поэтому выражение для  f1a (1.12) фактически определяет первую собственную частоту прямых участков, соединенных с криволинейным (рис. 2,а). Значение же изгибной собственной частоты колебаний криволинейного участка при принятых допущениях и ограничениях на длину всегда будет не ниже, чем для прямых участков.

Одним из принятых в методике допущений является условие равножесткости всех участков, которое выразим через длину прямых и криволинейных участков. Приравняв выражения для первых собственных частот колебаний прямого (1.4) и криволинейного (1.12) участков для случаев закреплений с заделкой (рис. 2,b,c) получаем следующие соотношения:

(1.13)
$l_{{2b}}^{{}} = l_{{1b}}^{{}}\sqrt {1 - 0.056 \cdot \varphi } \,,\quad l_{{2c}}^{{}} = l_{{1c}}^{{}}\sqrt {1 - 0.13 \cdot \varphi } $

Криволинейный участок с шарнирными опорами всегда будет локально понижать значение первой собственной частоты смежных прямых участков. Ограничивая это понижение частоты допустимой величиной, например, 5…10%, и также приравнивая выражения для первых собственных частот колебаний прямого и криволинейного участков, получаем условие на длину дуги в виде:

(1.14)
${{l}_{{2a}}} = \left( {0.5...0.6} \right){{l}_{{1a}}}$

Зная длину криволинейного участка и угол его дуги, можно найти требуемый радиус кривизны, при котором будет обеспечено условие равножесткости:

(1.15)
$R = {{l_{2}^{{}}} \mathord{\left/ {\vphantom {{l_{2}^{{}}} \varphi }} \right. \kern-0em} \varphi }$

Выполнение вышеуказанных условий (1.13–1.15) обеспечивает равную жесткость и частоту колебаний прямых и криволинейных участков. Если же выбрать меньшую длину дуги или ее радиус, то жесткость криволинейного участка будет выше, чем у прямых участков и его можно исключить из рассмотрения в составе плоской балочной многоопорной конструкции, так как такая геометрия заведомо обеспечивает выполнение условий работоспособности (1.2).

Устойчивость криволинейных участков не рассматривается, поскольку при действии продольной силы изогнутая геометрия позволяет им весьма свободно деформироваться в широком диапазоне и условие устойчивости для них теряет смысл.

Далее используем полученные решения применительно к созданию методики обоснованного выбора многоопорного закрепления составных плоских балочных конструкций.

2. Методика выбора схемы закрепления. Расчет собственных частот колебаний и критической нагрузки связан с коэффициентами опор α и μ в выражениях (1.4, 1.7), которые определяются только условиями закрепления и обычно используются для проверочных расчетов путем их выбора из справочников для конструкции с заданными закреплениями. Рассмотрим постановку и решение обратной задачи: управление первой собственной частотой колебаний и первой критической нагрузкой многоопорной конструкции с помощью обоснованного выбора требуемой схемы закрепления через коэффициенты опор.

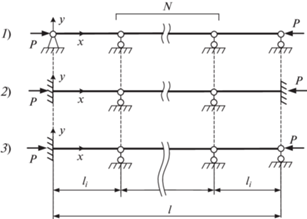
2.1. Выбор базовых схем расстановки опор. С учетом принятых ранее допущений рассмотрим три базовые схемы закрепления плоских балочных конструкций (рис. 3). Считаем, что жесткость криволинейных участков в этих схемах эквивалентна прямым участкам и отдельно их не рассматриваем.

Рис. 3.

Базовые схемы закрепления многоопорной балочной конструкции.

Длина каждого пролета равна:

${{l}_{i}} = {l \mathord{\left/ {\vphantom {l {\left( {N + 1} \right)}}} \right. \kern-0em} {\left( {N + 1} \right)}}$
где l – длина всей конструкции; li – длина пролета; N – число промежуточных опор.

Значения коэффициентов опор α и µ для первых собственных частот колебаний и первых критических сил для каждой схемы взяты из справочников [23–27] и приведены в табл. 1.

Таблица 1.

Исходные значения коэффициентов опор

№ схемы Коэф- фициент Число промежуточных опор N
0 1 2 3 4 5 6 7 8 9 10
1 α π
µ 1
2 α 4.730 3.927 3.557 3.393 3.310 3.260 3.230 3.210 3.196 3.186 3.180
µ 0.5 0.699 0.814 0.879 0.917 0.939 0.954 0.964 0.971 0.977 0.978
3 α 3.927 3.393 3.261 3.210 3.186 3.173 3.164 3.159 3.156 3.153 3.151
µ 0.7 0.879 0.939 0.964 0.977 0.983 0.988 0.99 0.992 0.994 0.996

Набор базовых схем можно изменять в соответствии со спецификой исследуемых конструкций, а значения коэффициентов опор для них рассчитать или взять из справочников.

2.2. Критерий выбора схемы закреплений. Условия работоспособности (1.2) плоской балочной конструкции основывается на выражении (1.9), в которое входят два неравнозначных коэффициента опор α и μ, что затрудняет однозначный выбор требуемой схемы закрепления. Для получения единого критерия выбора схемы закрепления выполним нормирование исходных значений коэффициентов опор (табл. 1) по отношению к коэффициентам опор абсолютно свободной прямолинейной балки:

(2.1)
$\alpha {\kern 1pt} ' = {{\left( {\frac{{\alpha \cdot \left( {N + 1} \right)}}{\pi }} \right)}^{2}},\quad \mu {\kern 1pt} ' = {{\left( {\frac{{N + 1}}{\mu }} \right)}^{2}}$

Полученные значения нормированных коэффициентов опор сведены в табл. 2.

Значения нормированных коэффициентов опор окажутся очень близкими друг к другу в пределах каждого варианта закрепления (табл. 2). Принимая условие их равенства, получаем критерий выбора схемы закрепления в виде минимально допустимого значения коэффициента опор:

(2.2)
${{\alpha }_{{\min }}} = \alpha {\kern 1pt} ' = \mu {\kern 1pt} '$
Таблица 2.

Нормированные значения коэффициентов опор

№ схемы Коэф- фициент Число промежуточных N
0 1 2 3 4 5 6 7 8 9 10
1 α' 1 4 9 16 25 36 49 64 81 100 121
μ' 1 4 9 16 25 36 49 64 81 100 121
2 α' 2.267 6.250 11.54 18.66 27.75 38.77 51.80 66.82 83.83 102.8 124.0
μ' 4 8.187 13.58 20.71 29.73 40.83 53.84 68.87 85.91 104.8 126.5
3 α' 1.563 4.666 9.697 16.71 25.72 36.72 49.70 64.71 81.75 100.7 121.7
μ' 2.041 5.177 10.21 17.22 26.19 37.26 50.20 65.30 82.31 101.2 122.0

Подставив равенство (2.2) в условие работоспособности (1.9), получаем квадратное уравнение, решение которого дает требуемое значение критерия выбора схемы закреплений:

(2.3)
$\min \left( {\alpha {\kern 1pt} ',\;\mu {\kern 1pt} '} \right) \geqslant {{\alpha }_{{\min }}} = {{С}_{P}} + \sqrt {С_{P}^{2} + \frac{{4m{{{\left[ {{{f}_{1}}} \right]}}^{2}}{{l}^{4}}}}{{{{\pi }^{2}}EJ}}} $
где CP – коэффициент учета влияния продольной силы Р, определяется как:

(2.4)
${{C}_{P}} = \frac{{{{l}^{2}}}}{{2{{\pi }^{2}}EJ}}\left( {{{\alpha }_{t}} \cdot \Delta T \cdot ES + {{P}_{F}}} \right)$

Получаем, что для обоснованного выбора схемы закрепления необходимо из табл. 2 выбрать такую базовую схему и число промежуточных опор, для которых значения коэффициентов опор α' и μ' будут не меньше, чем рассчитанное значение по формуле (2.3).

Нормирование коэффициентов опор по зависимостям (2.1) теперь устанавливает удобную прямую зависимость для первой собственной частоты колебаний, критической силы и критической температуры от новых значений коэффициентов опор, которые принимаю вид:

(2.5)
${{f}_{1}}\left( P \right) = \frac{{\alpha {\kern 1pt} '}}{{{{l}^{2}}}} \cdot \sqrt {\frac{1}{{4m}}\left( {{{\pi }^{2}}EJ - \frac{{{{l}^{2}}}}{{\mu {\kern 1pt} '}} \cdot \left( {{{\alpha }_{t}} \cdot \Delta T \cdot ES + {{P}_{F}}} \right)} \right)} \geqslant \left[ {{{f}_{1}}} \right]$
(2.6)
${{P}_{{cr1}}}\left( P \right) = \frac{{\mu {\kern 1pt} 'E}}{{{{l}^{2}}}} \cdot \left( {{{\pi }^{2}}J - \frac{{4{{l}^{4}}{{{\left[ {{{f}_{1}}} \right]}}^{2}}m}}{{\alpha {\kern 1pt} {{'}^{2}}E}}} \right) + {{P}_{F}}$
(2.7)
$\Delta {{T}_{{cr1}}} = \frac{1}{{{{\alpha }_{t}} \cdot ES}} \cdot \left[ {\mu {\kern 1pt} '\left( {\frac{{{{\pi }^{2}}EJ}}{{{{l}^{2}}}} - \frac{{4m{{l}^{2}}{{{\left[ {{{f}_{1}}} \right]}}^{2}}}}{{\alpha {\kern 1pt} {{'}^{2}}}}} \right) - {{P}_{F}}} \right]$

Выбранная, согласно критерию (2.3), схема закрепления будет обеспечивать одновременное выполнение всех условий работоспособности (1.2) плоской многоопорной балочной конструкции, в чем можно убедиться, проверив их фактические значения по зависимостям (2.5–2.7).

2.3. Жесткость промежуточных опор. Изложенный выше метод выбора закреплений имеет недостаток, заключающийся в дискретности значений коэффициентов опор, что не позволяет, например, точно настроить конструкцию на требуемую первую собственную частоту колебаний или первую критическую нагрузку. Одним из способов решения этой проблемы является введение во все опоры такой жесткости, чтобы коэффициенты опор приняли требуемые значения и согласно уравнению (2.5) обеспечили необходимое значение первой собственной частоты колебаний. Существующие методы учета жесткости опор [37–43] неприемлемы для инженерных расчетов многоопорной конструкции из-за своей сложности и необходимости численного решения. Поэтому используем другой подход, основанный на аппроксимации зависимостей коэффициентов опор от жесткости и аналитического решения разрешающего уравнения.

2.3.1. Учет жесткости опор. Нахождение требуемой жесткости опор необходимо начинать с определения по формуле (2.3) требуемого значения критерия αmin и выбора такой базовой схемы и числа промежуточных опор, для которых значения коэффициентов опор α' и µ' будут несколько меньше, чем требуется по этому условию. Недостаточное значение коэффициентов опор будет скомпенсировано жесткостью опор, в качестве которой примем относительную величину С, определяемую как отношение жесткости опоры к изгибной жесткости единицы длины балки (рис. 1,а):

$C = k\frac{{{{l}_{i}}}}{{EJ}}$
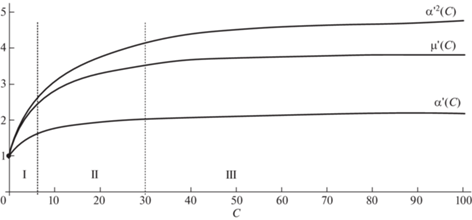
где k – абсолютная жесткость опоры (Н*м).

Появление жесткости в опорах приводит к нарушению условия (2.2), поскольку при увеличении жесткости значения нормированных коэффициентов опор α'(С) и µ'(С) будут нелинейно и не равнозначно увеличиваться (рис. 4). Следовательно, подход, основанный на выражениях (2.2–2.4) в этом случае неприемлем. Кривые α'(С) и µ'(С) на рис. 4 построены по зависимостям (2.1) на основе аппроксимирующих функций для коэффициентов опор α(С) и µ(С), получение которых изложено в работе [44].

Рис. 4.

Зависимости нормированных значений коэффициентов опор от жесткости.

Применяя такую же квадратичную аппроксимацию и разделение диапазона жесткости опор на зоны, получим аппроксимирующие функции для нормированных коэффициентов опор в виде:

(2.8)
$\alpha {\kern 1pt} '\left( C \right) = {{a}_{1}} \cdot {{C}^{2}} + {{a}_{2}} \cdot C + {{a}_{3}};\quad \mu {\kern 1pt} '\left( C \right) = {{b}_{1}} \cdot {{C}^{2}} + {{b}_{2}} \cdot C + {{b}_{3}}$

Коэффициенты аппроксимирующих функций (2.8) определялись методом наименьших квадратов [45] и приведены в табл. 3, погрешность составляет менее 4.8%.

Таблица 3.

Коэффициенты аппроксимирующих функций

Зона C Коэффициенты функции α'(С) Коэффициенты функции µ'(С)
а1 а2 а3 b1 b2 b3
I 0…10 –0.00746 0.1496 1 –0.0162 0.346 1
II 10…100 –1E–4 0.0158 1.602 –2.4E–4 0.0372 2.49
III 100…1000 –2E–07 3.04E-4 2.154 –3.8E–7 5.68E–4 3.752

2.3.2. Разрешающее уравнение по определению жесткости опор. Преобразуем условие работоспособности (2.5) к виду:

(2.9)
$\frac{{{{l}^{2}}}}{{\mu {\kern 1pt} '}} \cdot \left( {{{\alpha }_{t}} \cdot \Delta T \cdot ES + {{P}_{F}}} \right) = {{\pi }^{2}}EJ - \frac{{4m{{l}^{4}}{{f}_{1}}^{2}}}{{\alpha {{'}^{2}}}}$
где  f1 – требуемое значение первой собственной частоты колебаний.

Для сокращения записи введем коэффициенты:

(2.10)
$a = {{l}^{2}} \cdot \left( {{{\alpha }_{t}} \cdot \Delta T \cdot ES + {{P}_{F}}} \right),\quad b = {{\pi }^{2}}EJ,\quad c = 4m{{l}^{4}}{{f}_{1}}^{2}$
и уравнение (2.9) примет вид:

(2.11)
$\frac{1}{{\mu {\kern 1pt} '\left( C \right)}} = \frac{b}{a} - \frac{1}{{\alpha {\kern 1pt} {{'}^{2}}\left( C \right) \cdot \frac{a}{c}}}$

Дальнейшее решение разрешающего уравнения (2.11) требует наличия аналитических зависимостей для функций α'2(С), µ'(С), в качестве которых выберем квадратичные функции вида (2.8). Вследствие высокой нелинейности этих функций, особенно функции α'2(С), аппроксимировать их с теми же диапазонами, что и ранее (табл. 3) затруднительно из-за недопустимого роста погрешности. Для ограничения погрешности аппроксимации диапазон жесткостей опор был разбит на четыре новые зоны: I: 0…7; II: 7…30; III: 30…300; IV: 300…∞ (рис. 4). Результаты приведены в табл. 4, погрешность аппроксимации до 3.5%.

Таблица 4.

Коэффициенты аппроксимирующих функций

Зона C Коэффициенты функции α'2(С) Коэффициенты функции µ'(С)
а1 а2 а3 b1 b2 b3
I 0…7 –0.0182 0.3694 1 –0.0212 0.371 1
II 7…30 –0.00234 0.14786 1.774 –0.002 0.11516 1.851
III 30…300 –2.6Е–5 0.01192 3.768 –1.18Е–5 0.005368 3.355
IV 300…∞ 0 0 5.134 0 0 4

Решение задачи различается в зависимости от номера зоны. Определить требуемую зону можно, рассчитав для граничных значений коэффициентов опор (табл. 4) максимальные значения первой собственной частоты колебаний (2.5), которые обеспечивает каждая зона. Если полученное максимальное значение первой собственной частоты колебаний для IV-й зоны меньше, чем требуемое значение, то это означает, что жесткость опор не сможет обеспечить требуемые условия работоспособности (1.2) и необходимо использовать другие методы: поменять базовую схему, увеличить число промежуточных опор, изменить геометрию, материал и т.д.

2.3.3. Решение разрешающего уравнения. Подставим квадратичные зависимости для α'2(С) и µ'(С) в уравнение (2.11), где искомую жесткость обозначим как х во избежание путаницы с одноименными коэффициентами:

$\frac{1}{{{{b}_{1}} \cdot {{x}^{2}} + {{b}_{2}} \cdot x + {{b}_{3}}}} = \frac{b}{a} - \frac{c}{{a \cdot ({{a}_{1}}{{x}^{2}} + {{a}_{2}}x + {{a}_{3}})}}$

Преобразуем это выражение к уравнению 4-й степени:

(2.12)
$A \cdot {{x}^{4}} + B \cdot {{x}^{3}} + C \cdot {{x}^{2}} + D \cdot x + E = 0$
где

$A = 1,\quad B = \frac{{{{b}_{2}}}}{{{{b}_{1}}}} + \frac{{{{a}_{2}}}}{{{{a}_{1}}}},\quad C = \frac{{{{b}_{3}}}}{{{{b}_{1}}}} + \frac{{{{a}_{2}}{{b}_{2}}}}{{{{a}_{1}}{{b}_{1}}}} + \frac{{{{a}_{3}}}}{{{{a}_{1}}}} - \frac{a}{{b{{b}_{1}}}} - \frac{с}{{b{{a}_{1}}}}$
$D = \frac{{{{a}_{2}}{{b}_{3}} + {{a}_{3}}{{b}_{2}}}}{{{{a}_{1}}{{b}_{1}}}} - \frac{{a{{a}_{2}} + с{{b}_{2}}}}{{b{{a}_{1}}{{b}_{1}}}},\quad E = \frac{{{{a}_{3}}\left( {b{{b}_{3}} - a} \right) - с{{b}_{3}}}}{{b{{a}_{1}}{{b}_{1}}}}$

Существуют различные подходы для аналитического решения уравнения (2.12), здесь используется подход, предложенный Ю.А. Несмеевым в работах [46, 47]. Дальнейшее решение представлено согласно его методу, с учетом значений коэффициентов (табл. 4) и того, что искомый корень будет первым положительным корнем уравнения 4-го порядка. Вначале определяются коэффициенты вспомогательного кубического уравнения:

${{a}_{B}} = 1,\quad {{b}_{B}} = - C,\quad {{c}_{B}} = BD - 4E,\quad {{d}_{B}} = - {{D}^{2}} - {{B}^{2}}E + 4CE$

Для решения кубического уравнения находим коэффициенты:

$p = \frac{{3{{a}_{B}}{{c}_{B}} - b_{B}^{2}}}{{9{{a}^{2}}}},\quad q = \frac{{{{{\left( {{{a}_{B}}{{b}_{B}}} \right)}}^{3}}}}{{27}} - \frac{{{{b}_{B}}{{c}_{B}}}}{{6a_{B}^{2}}} + \frac{{{{d}_{B}}}}{{2{{a}_{B}}}}$

Далее находим характерный угол φ:

$\varphi = {\text{arctg}}\left( {\sqrt {\frac{{{{p}^{3}}}}{{{{q}^{2}}}} - 1} } \right)$

Из трех корней кубического уравнения выбираем первое значение:

${{u}_{1}} = 2r \cdot \cos \left( {\frac{\varphi }{3}} \right) - \frac{{{{a}_{B}}{{b}_{B}}}}{3}$

Теперь расчет сводится к решению двух квадратных уравнений, из которых требуются коэффициенты первого уравнения:

(2.13)
${{k}_{1}} = 1,\quad {{k}_{2}} = \frac{B}{2} + \sqrt {\frac{{{{B}^{2}}}}{4} + {{u}_{1}} - C} ,\quad {{k}_{3}} = \frac{{{{u}_{1}}}}{2} - \sqrt {\frac{{u_{1}^{2}}}{4} - E} .$

Искомая жесткость опор будет равна первому положительному корню:

(2.14)
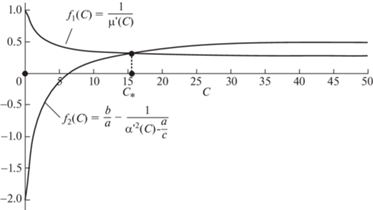
$C_{*}^{{}} = {{x}_{1}} = \frac{1}{2}\left( { - {{k}_{2}} + \sqrt {k_{2}^{2} - 4{{k}_{3}}} } \right),\quad k_{*}^{{}} = C_{*}^{{}} \cdot \frac{{EJ}}{l}$

Графически, решение уравнения (2.11) можно представить в виде двух кривых, точка пересечения которых и определяет требуемое значение жесткости опор ${{C}_{*}}$ (рис. 5).

Рис. 5.

Графическая интерпретация решения.

Кривая  f1(C) здесь фиксированная, поскольку определяется только функцией μ'(C), а кривая  f2(C) перемещается относительно нее в зависимости от исходных данных задачи (2.10) и определяет искомое решение в виде точки их пересечения с координатой ${{C}_{*}}$.

При жесткости опор С > 300 (IV-я зона) решение можно построить по изложенной выше схеме, однако увеличение жесткости опор с С = 300 до С = ∞ приведет к росту первой собственной частоты всего на 1.3%, а критическая сила возрастет на 2.4%. Данные изменения находятся в пределах погрешностей остальных зон, поэтому будем рассматривать вариант С > 300 как жесткая заделка и использовать фиксированные значения для коэффициентов опор (табл. 4).

Проверить корректность полученного значения жесткости опор ${{C}_{*}}$ для любой зоны можно, если подставить эту величину в аппроксимирующие функции α'(${{C}_{*}}$) и μ'(${{C}_{*}}$) и по формуле (2.5) определить фактическое значение первой собственной частоты  f1.

Для верификации разработанной методики и оценки точности получаемых результатов выполним сравнительные расчеты плоской протяженной балочной конструкции.

3. Примеры расчета. В качестве примера расчета рассмотрим две плоские протяженные конструкции круглого тонкостенного поперечного сечения: прямой и криволинейный трубопроводы. Исходное закрепление в обоих примерах выполнено в виде жесткой заделки на обоих краях трубопровода, промежуточных опор нет. Основные параметры трубопровода: круглое поперечное сечение наружным диаметром D = 15 мм; толщина стенки t = 1 мм; материал: сталь Е = 2 × 105 MПa, плотностью ρ = 7800 кг/м3, КТР αt = 1.2 × 10–5 1/°С.

Для обеих конструкций требуется выбрать такой способ закрепления, который обеспечит значение [f1] = 150 Гц при температуре ΔТ = 90°С. Выполним решение по разработанной методике, а полученные результаты расчетов верифицируем методом конечных элементов в программе Ansys для балочной модели с использованием конечных элементов ВЕАМ189 и COMBIN14.

3.1. Прямой трубопровод. Длина трубопровода l1 = 2.5 м. Согласно заданным условиям работоспособности, рассчитаем минимальное значение коэффициента опор по формуле (2.3), получаем: СР = 13.9 и αmin = 41.4. Из табл. 2 выбираем базовую схему 2 при N = 6 и li = 0.357 м, для которой α'(С) = 51.8 и µ'(С) = 53.83, что с запасом обеспечивает условия работоспособности (1.2). Для проверки, рассчитаем фактические значения параметров по формулам (2.5, 2.7), получим:  f1 = 227.6 Гц и ΔTcr1 = 137.8°С.

Далее выполним уточненный расчет для достижения значения первой собственной частоты f1 = 150 Гц при заданной температуре. Для этого уменьшаем число промежуточных опор (N = 5 и li = 0.417 м) и получаем значения коэффициентов опор α'(С) = = 38.76 и µ'(С) = 40.83, которые дают меньшие значения требуемых параметров: f1 = = 138.4 Гц и ΔTcr1 = 82.6°С. Проверка диапазона жесткости показывает, что решение находится в I-й зоне, которая может обеспечить f1_max = 311 Гц. Подставляя исходные данные в уравнение (2.11), получаем решение $C_{*}^{{}} = 0.58$ и k = 300 Н ⋅ м.

С целью проверки остальных зон, повысим требования к условиям работоспособности трубопровода. Пусть, например, необходимо обеспечить значение [f1] = 350 Гц при той же температуре, это соответствует II-й зоне и после решения разрешающего уравнения (2.11) получаем $C_{*}^{{}} = 12$ и ${{k}_{*}}$ = 6238 Н ⋅ м. Аналогично для III-й зоны при [f1] = 440 Гц получаем $C_{*}^{{}} = 101$, k = 52527 Н ⋅ м.

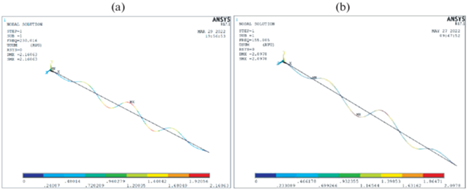
Проверка всех полученных решений выполнена в программе Ansys, на рис. 6 показаны некоторые графические результаты расчетов, а в табл. 5 приведены числовые данные.

Рис. 6.

Прямой трубопровод (a) ΔТ = 90°С, ΔС = 0 и N = 6; (b) ΔТ = 90°С, ΔС = 0.58 и N = 5.

Таблица 5.

Сравнение результатов расчета для прямого трубопровода

Параметр f1, Гц
Предлагаемая методика МКЭ Отклонение, %
ΔТ = 90°С, ${{C}_{*}}$ = 0 и N = 6 227.6 230 1
ΔТ = 90°С, ${{C}_{*}}$ = 0 и N = 5 138.4 139.6 0.87
ΔТ = 90°С, ${{C}_{*}}$ = 0.58 и N = 5 150 155.8 3.9
ΔТ = 90°С, ${{C}_{*}}$ = 12 и N = 5 350 335.4 4.2
ΔТ = 90°С, ${{C}_{*}}$ = 101 и N = 5 440 430.9 2.1

Полученные результаты свидетельствуют о хорошей сходимости результатов, максимальное отклонение составляет 4.2%.

3.2. Криволинейный трубопровод. Конструкция криволинейного трубопровода (рис. 7,а) состоит из прямых и криволинейных участков углом 90° размерами R1 = 0.29 м, R2 = 0.16 м, l2 = 2.5 м, l4 = 0.5 м. Геометрия криволинейных участков удовлетворяет условиям равножесткости, следовательно, их можно рассматривать как прямые участки такой же длины. Рассчитаем требуемое минимальное значение коэффициента опор: СР = 35.55 и αmin = 105.98. Выбираем закрепление по базовой схеме 2 , N = 10 и li = 0.364 м, для которой α'(С) = 123.98 и µ'(С) = 126.5, что с запасом обеспечивает условия работоспособности: [f1] = 202 Гц и ΔТ = 121.6°С.

Рис. 7.

Криволинейный трубопровод (a) исходная схема; (b) решение при ΔЕ = 90°C, ${{C}_{*}}$ = 146, N = 7.

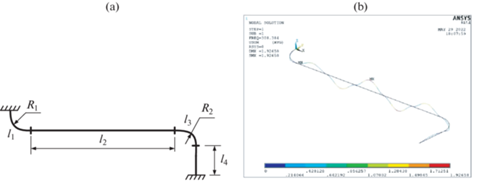
Обеспечим более точное значение первой собственной частоты колебаний трубопровода, для этого выбираем вариант N = 7, li = 0.5 м. Решение уравнения (2.11) в этом случае показывает, что условие работоспособности будет выполнено при ${{C}_{*}}$ =3.33 и k = 1444 Н ⋅ м. Также проверим остальные зоны: зададим [f1] = 250 Гц при той же температуре (II-я зона) и после расчета получаем ${{C}_{*}}$ = 19.4 и ${{k}_{*}}$ = 8401 Н ⋅ м. Задавая [f1] = = 300 Гц для III-й зоны получаем ${{C}_{*}}$ = 146, k = 63519 Н ⋅ м.

Результаты сравнительных расчетов на рис. 7 и в табл. 6 показали хорошую сходимость результатов по контролируемым параметрам.

Таблица 6.

Сравнение результатов расчета для криволинейного трубопровода

Параметр f1, Гц
Предлагаемая методика МКЭ Отклонение, %
ΔТ = 0°С и ${{C}_{*}}$ = 0, N = 7 164.8 170.7 3.58
ΔТ = 90°С и ${{C}_{*}}$ = 3.33, N = 7 150 159.89 6.7
ΔТ = 90°С и ${{C}_{*}}$ = 1444, N = 7 250 243.84 2.46
ΔТ = 90°С и ${{C}_{*}}$ = 63518, N = 7 300 308.38 2.48

Сравнение результатов расчета по предложенной методике с численными решениями по методу конечных элементов показывает максимальное различие в результатах около 6.7%.

4. Обсуждение. Задача расчета собственных частот колебаний и критических нагрузок, особенно с учетом жесткости опор, действия продольной силы и температуры даже по отдельности представляют собой сложные математические задачи, решение которых обычно требует применения численных методов. Аппроксимация зависимостей коэффициентов опор при колебаниях и потери устойчивости с помощью аналитических функций позволила получить весьма простое решение, на основе которого разработан проектный подход по выбору схемы закрепления, видов и жесткости опор, обеспечивающий заданные значения первой собственной частоты колебаний и первой критической нагрузки для плоской балочной конструкции. Предложенная здесь методика выбора закреплений основана на известных положениях теории колебаний и теории устойчивости балок с учетом действия продольных сил и поэтому полученные результаты хорошо согласуются с известными зависимостями, которые становятся частными случаями предложенного метода.

Принятые ограничения на размерность конструкции, форму и размеры поперечного сечения позволили получить весьма простую и гибкую аналитическую формулировку методики, которая может быть легко модифицирована для решения сопутствующих задач: обоснование геометрической формы и размеров сечения, материала и др. Указанные ограничения на геометрию рассчитываемой конструкции (1.1, 1.10–1.14) на практике не являются строгими границами, а только определяют области, где решение будет иметь минимальную погрешность. Например, в работе [48] по предложенной методике получено решение для протяженной конструкции волноводов, имеющей неосесимметричное тонкостенное поперечное сечение, при этом максимальное отклонение для балочной модели составило всего 2.5% и 6.39% для оболочечной модели.

Аппроксимация нелинейных зависимостей значений коэффициентов опор от жесткости в виде квадратичных функций с разделением области изменения жесткости на зоны позволило получить приемлемую погрешность аппроксимации и получить разрешающее уравнение задачи 4-й степени (2.12). Данная степень является наивысшей степенью алгебраического уравнения, для которого существует аналитическое решение, что накладывает ограничения на степени аппроксимирующих функций. Значения коэффициентов аппроксимирующих функций (табл. 4) определялись методом наименьших квадратов из условия максимально точного равенства на границах зон для их плавного сопряжения и равномерного распределения погрешностей по знакам в пределах каждой зоны. Если первое условие исключить, то это позволит снизить максимальную погрешность по зонам, однако переход между зонами будет сопровождаться некоторой разрывностью решений.

Вследствие отсутствия известных решений подобных задач аналитическими методами для сравнения использовалось численное решение методом конечных элементов, реализованным в программе Ansys, которая позволяет проводить расчеты собственных частот колебаний и критической нагрузки с учетом жесткости опор и температуры. Сравнение результатов расчета показывает хорошую сходимость результатов и различие в результатах около 3–5%, что вполне достаточно для инженерных прикладных расчетов балочных моделей конструкций.

Предложенный в работе подход позволяет проводить обоснованный выбор способа закреплений плоских балочных конструкций различного назначения для обеспечения их первой собственной частоты колебаний и первой критической нагрузки, которые имеют изгибную форму деформации. Возможными направлениями следующих исследований являются учет второй и последующих собственных частот, критических нагрузок, а также рассмотрение других видов форм колебаний и потери устойчивости: крутильные, продольные и др.

Заключение. Разработана методика управления динамическим поведением протяженных балок посредством обоснованного выбора схемы закрепления, обеспечивающая их работоспособность при заданных требованиях по частоте собственных колебаний и критической силе (или температуре). Предложенный метод имеет простую аналитическую формулировку, что позволяет инженеру-проектировщику оперативно и обоснованно проводить многофакторное исследование или проектирование любых протяженных многоопорных конструкций для обеспечения ими заданных значений первой собственной частоты колебаний и устойчивости с учетом температуры.

Методика верифицирована сравнительным расчетом прямолинейного участка трубопровода методом конечных элементов в программе Ansys для балочной и оболочечной моделей и показала хорошую сходимость по всем исследуемым параметрам.

Благодарности. Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края и Красноярского краевого фонда науки в рамках научного проекта № 20-48-242922.

Список литературы

  1. Крейн М.Г. Вибрационная теория многоопорных балок // Вестник инженеров и техников. 1933. № 4. С. 142–145.

  2. Miles L.W. Vibration of beams on many supports // ASCE J. Eng. Mech. 1956. V. 82. P. 1–9.

  3. Zhu L., Elisacoff I., Lin Y.K. Free and forced vibrations of periodic multispan beams // Shock Vibr. 1994. V. 1. № 3. P. 217–232.

  4. Бидерман В.Л. Теория механических колебаний. М.: Высшая школа, 1980. 408 с.

  5. Доев В.С. Поперечные колебания балок. М.: КНОРУС, 2016. 412 с.

  6. Banakh L.Y. Vibrations of Mechanical Systems with Regular Structure. Berlin: Springer, 2010. 262 p.

  7. Benaroya H., Nagurka M., Han S. Mechanical Vibration. Boca Raton, Florida: Taylor and Francis, 2017. 602 p.

  8. Bottega W.J. Engineering Vibrations. N. Y.: CRC Press, 2006. 750 p.

  9. Clough R.E. Dynamics of Structures. 3th ed. McGraw-Hill Education, 1995. 752 p.

  10. Geradin M., Rixen D.J. Mechanical Vibrations: Theory and Application to Structural Dynamics. 3rd Ed. L.: Wiley and Sons, 2015. 617 p.

  11. Hagedorn P., Dasgupta A. Vibrations and Waves in Continuous Mechanical Systems. John Wiley & Sons, 2007. 388 p.

  12. Hartog J.P. Mechanical Vibrations. N.Y.: Dover Publications, 1985. 449 p.

  13. Inman D.J. Engineering Vibration. Prentice Hall, 2014. 720 p.

  14. Kelly S.G. Advanced Vibration Analysis. Boca Raton: CRC Press, 2006. 650 p.

  15. Gupta S.G. Natural flexural waves and the normal modes of periodically-supported beams and plates // JSV. 1970. V. 13. № 1. P. 89–101. https://doi.org/10.1016/S0022-460X(70)80082-7

  16. Zhao Z., Wen S., Li F., Zhang C. Free vibration analysis of multi-span Timoshenko beams using the assumed mode method // Arch. Appl. Mech. 2018. V. 88. № 7. P. 1213–1228. https://doi.org/10.1007/s00419-018-1368-8

  17. Zhu L., Elishakoff, I., Lin Y.K. Free and forced vibrations of periodic multispan beams // Shock Vib. 1994. V. 1. № 3. P. 217–232. https://doi.org/10.3233/SAV-1994-1302

  18. Thomsen J.J. Vibrations and Stability: Advanced Theory, Analysis, and Tools. 2nd Ed. N.Y.: Springer, 2003. 404 p.

  19. Timoshenko S.P., Gere J.M. Theory of Elastic Stability. N. Y.: Courier Corporation, 2009. 541 p.

  20. Алфутов Н.А., Колесников К.С. Устойчивость движения и равновесия. Москва: МГТУ им. Н.Э. Баумана, 2003. 256 с.

  21. Thomsen J.J. Vibrations and Stability. Advanced Theory, Analysis, and Tools. Berlin, Heidelberg: Springer Berlin, Heidelberg, 2003. 420 p. https://doi.org/10.1007/978-3-662-10793-5

  22. Trahair N.S. Buckling analysis design of steel frames // J. Constr. Steel Res. 2009. V. 65. № 7. P. 1459–1463. https://doi.org/10.1016/j.jcsr.2009.03.012

  23. Биргер И.А., Пановко Я.Г. Прочность, устойчивость, колебания. Т. 3. М.: Машиностроение, 1988. 567 с.

  24. Уманский А.А. Справочник проектировщика. Т. 2. М.: Стройиздат, 1973. 415 с.

  25. Коренев Б.Г. Справочник по динамике сооружений. М.: Стройиздат, 1972. 511 с.

  26. Blevins R.D. Formulas for Dynamics, Acoustics and Vibration. L.: John Wiley & Sons, 2016. 464 p.

  27. Wang C.M., Wang C.Y. Exact Solutions for Buckling of Structural Members. Boca Raton: CRC Press, 2005. 224 p.

  28. Mityaev A.E., Kudryavtsev I.V., Khomutov M.P., Brungardt M.V., Kolotov A.V. Estimation of the minimum beam length for the static, dynamic, and stability problems // IOP Conf. Ser.: Mater. Sci. Eng. 2021. V. 1155. P. 012101. https://doi.org/10.1088/1757-899X/1155/1/012101

  29. Galef A.E. Bending frequencies of compressed beams // J. Acoust. Soc. Am. 1968. V. 44. № 2. P. 643. https://doi.org/10.1121/1.1911144

  30. Bokaian A. Natural frequencies of beams under compressive axial loads // JSV. 1988. V. 126. № 1. P. 49–65. https://doi.org/10.1016/0022-460X(88)90397-5

  31. Bokaian A. Natural frequencies of beams under tensile axial loads // JSV. 1990. V. 142. № 3. P. 481–498. https://doi.org/10.1016/0022-460X(90)90663-K

  32. Stephen N.G. Beam vibration under compressive axial load-upper and lower bound approximation // JSV. 1989. V. 131. № 2. P. 345–350. https://doi.org/10.1016/0022-460X(89)90498-7

  33. Грудев И.Д. Колебания криволинейных стержней. М.: МИК, 2007. 254 с.

  34. Auciello N.M., De Rosa M.A. Free vibrations of circular arches: a review // JSV. V. 176. № 4. 1994. P. 433–458. https://doi.org/10.1006/jsvi.1994.1388

  35. Chidamparam P., Leissa A. W. Vibrations of planar curved beams, rings, and arches // ASME. Appl. Mech. Rev. 1993. V. 46. № 9. P. 467–483. https://doi.org/10.1115/1.3120374

  36. Markuš Š., Tibor N. Vibration of Curved Beams // Shock Vibr. Dig. 1981. V. 13. P. 3–14.

  37. West H.H., Mafi M. Eigenvalues for beam-columns on elastic supports // J Struct Eng (US). 1984. V. 2110. № 6. P. 1305–1320. https://doi.org/10.1061/(ASCE)0733-9445(1984)110:6(1305)

  38. Lin Y.K. Free Vibration of a continuous beam on elastic supports // IJMS. 1962. V. 4. P. 409–423. https://doi.org/10.1016/S0020-7403(62)80027-7

  39. Naguleswaran S. Transverse vibration of an Euler-Bernoulli uniform beam on up to five resilient supports including ends // JSV. 2003. V. 261. № 2. P. 372–384. https://doi.org/10.1016/S0022-460X(02)01238-5

  40. Lin H., Chang S.C. Free vibration analysis of multi-span beams with intermediate flexible constraints // JSV. 2005. V. 281. № 1–2. P. 155–169. https://doi.org/10.1016/j.jsv.2004.01.010

  41. Maurizi M.J., Bambill D.V., Bellés P.M., De Rosa M.A., Grossi R.O., Marcelo A.C., Zannier L. Free vibrations of Bernoulli-Euler beams with intermediate elastic support: a concise thematic recension // JSV. 2005. V. 281. № 3–5. P. 1238–1239. https://doi.org/10.1016/j.jsv.2004.06.014

  42. Luo J., Zhu S., Zhai W. Exact closed-form solution for free vibration of Euler-Bernoulli and Timoshenko beams with intermediate elastic supports // IJMS. 2022. V. 213. P. 106842. https://doi.org/10.1016/j.ijmecsci.2021.106842

  43. Chonan S., Sasaki M. Vibration and stability of elastically supported multi-span beams under conservative and non-conservative loads // JSV. 1985. V. 99. № 4. P. 545–556. https://doi.org/10.1016/0022-460X(85)90539-5

  44. Кудрявцев И.В., Рабецкая О.И., Митяев А.Е. Аппроксимация значений коэффициентов опор балки при колебаниях и потери устойчивости // Сибирский аэрокосмический журнал. 2022. № 3. С. 461–474. https://doi.org/10.31772/2712-8970-2022-23-3-461-474

  45. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Вильямс, 2016. 912 с.

  46. Несмеев Ю.А. Об одном подходе к решению алгебраических уравнений 3-й и 4-й степеней // Вестник ТГУ. Математика и механика. 2011. № 1 (13). С. 26–30.

  47. Несмеев Ю.А. Развитие одного подхода к решению алгебраического уравнения 4-й степени // Вестник ТГУ. Математика и механика. 2013. № 4 (24). С. 29–38.

  48. Кудрявцев И.В. Обеспечение динамического состояния прямолинейных волноводных трактов при нагреве с помощью расстановки опор // Вестник МАИ. 2021. № 4 (28). С. 76–89. https://doi.org/10.34759/vst-2021-4-92-105

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал