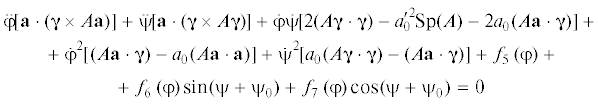Известия РАН. Механика твердого тела, 2023, № 3, стр. 123-134

1. Введение. Прецессионные движения твердого тела, имеющего неподвижную точку, в частности, регулярные прецессии, применяются в моделировании технических объектов [1]. В динамике тяжелого твердого тела и ее обобщениях на случай сложных силовых полей они изучались Д. Гриоли [2], Ф. Кляйном и А. Зоммерфельдом [3], А. Брессаном [4], автором данной статьи [5] и другими [6–8]. Прецессионные движения характеризуются свойством постоянства угла между двумя осями ${{l}_{1}},\;{{l}_{2}}$, проходящими через неподвижную точку, одна из которых (${{l}_{1}}$) связана с телом-носителем, а другая (${{l}_{2}}$) неподвижна в пространстве. В случае, когда одна из осей подвижной системы координат содержит ось ${{l}_{1}}$, то целесообразно такую систему координат называть прецессионной системой координат. Согласно [2–4], прецессионные движения подразделяются на классы: если скорости прецессии и собственного вращения постоянны, то прецессия называется регулярной; если только скорость прецессии постоянна, то прецессия называется полурегулярной прецессией первого типа; если только скорость собственного вращения постоянна, то прецессию называют полурегулярной прецессией второго типа; в других случаях прецессия называется прецессией общего типа. Наибольшее количество прецессионных движений гиростата установлено для классов регулярных и полурегулярных прецессий первого типа. Следует отметить, что уникальными случаями прецессий тяжелого твердого тела, описываемых уравнениями Эйлера–Пуассона, являются случай регулярной прецессии Д. Гриоли [2], относительно наклонной оси, случай А.И. Докшевича [9], для которого постоянно произведение скоростей прецессии и собственного вращения, прецессия А. Брессана [4] в решении В. Гесса. Полурегулярные прецессии второго типа твердого тела и гиростата относятся к меньшему числу найденных прецессий. Например, в [4] доказано, что в классической задаче полурегулярные прецессии второго типа динамически невозможны. Несмотря на это, в задаче о движении гиростата с переменным гиростатическим моментом получены некоторые решения, имеющие такое свойство [8].

Отметим, что прецессии несимметричного твердого тела с жидким заполнением изучались В.Ю. Ольшанским [10–13], а регулярные прецессии тяжелого твердого тела в жидкости – В.Н. Рубановским [14]. В задаче о движении системы связанных твердых тел также установлен нетривиальный класс прецессий [15].

Анализ литературы, посвященной изучению задачи о движении гиростата в двух однородных силовых полях, показывает, что большинство статей посвящено качественным проблемам интегрируемости уравнений движения [16–19] с использованием аналогии [20]. Однако, существуют и некоторые исследования, в которых рассматриваются регулярные прецессии гиростата [21–23] в указанной задаче.

В данной статье дана постановка задачи о прецессиях твердого тела с неподвижной точкой в трех однородных силовых полях. Записаны уравнения движения, описывающие прецессионные движения твердого тела, в качестве подвижной системы координат принята прецессионная система координат [24] (одна из осей подвижной системы координат направлена по оси ${{l}_{1}}$). Редуцированные уравнения движения получены в независимом базисе ${\mathbf{a}} \in {{l}_{1}}$, ${\mathbf{\gamma }} \in {{l}_{2}}$ и ${\mathbf{a}} \times {\mathbf{\gamma }}$. Их интегрирование рассмотрено в случае, когда совпадают скорости прецессии и собственного вращения. Данное свойство характеризует изоконическое движение твердого тела (подвижный и неподвижный годографы вектора угловой скорости симметричны друг другу относительно касательной плоскости к соответствующим аксоидам). Таким образом, по терминологии [6] в данной статье рассматриваются условия существования прецессионно-изоконических движений твердого тела в трех однородных силовых полях. Следует отметить, что аналогами этих движений являются движение гироскопа Лагранжа с равными скоростями прецессии и собственного вращения, а также движение гироскопа Гриоли. Для случая, когда эллипсоид инерции тела является сферой, в статье показано, что угол нутации равен ${\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$.

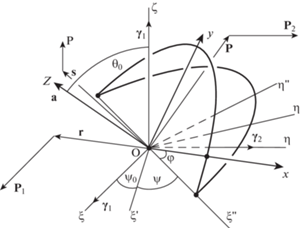
2. Постановка задачи. Рассмотрим движение твердого тела, имеющего неподвижную точку, в силовом поле, которое является суперпозицией трех однородных и постоянных силовых полей. Обозначим через ${\mathbf{\gamma }}{\text{,}}{{{\mathbf{\gamma }}}^{{(1)}}},{{{\mathbf{\gamma }}}^{{(2)}}}$ единичные векторы, характеризующие направления сил ${\mathbf{P}},{\mathbf{P}}_{1}^{{}}{\text{,}}{\mathbf{P}}_{2}^{{}}$ каждого из полей; $C,C_{1}^{{}},C_{2}^{{}}$ – центры приведения сил; ${\mathbf{s}} = P{\mathbf{OC}}$, ${\mathbf{r}} = {{{\mathbf{P}}}_{1}}{\mathbf{O}}{{{\mathbf{C}}}_{1}}$, ${\mathbf{p}} = P_{2}^{{}}{\mathbf{OC}}_{2}^{{}}$; $Oxyz$ – подвижная система координат, $O$ – неподвижная точка. Пусть тензор инерции тела в системе $Oxyz$ имеет значение $A = {\text{(}}A_{{ij}}^{{}}{\text{)}}$ $(i,j = \overline {1,3} )$. Тело вращается вокруг точки $O$ с угловой скоростью ω = (ω₁i₁ + $\omega _{2}^{{}}{\mathbf{i}}_{2}^{{}} + \omega _{3}^{{}}{\mathbf{i}}_{3}^{{}}{\text{)}}$ (${\mathbf{i}}_{1}^{{}},{\mathbf{i}}_{2}^{{}},{\mathbf{i}}_{3}^{{}}$ – единичные векторы системы $Oxyz$). Для векторов s, r, p запишем соотношения

Тогда уравнения движения тела представим в виде [21]

где точка над переменными ${\mathbf{\omega }},\;{\mathbf{\gamma }},\;{\mathbf{\gamma }}_{{}}^{{(1)}},\;{\mathbf{\gamma }}_{{}}^{{(2)}}$ обозначает дифференцирование по времени $t$. В формулах (2.2), (2.3) полагаем то есть направления силовых полей будут характеризоваться тройкой ${\mathbf{\gamma }},\;{\mathbf{\gamma }}_{{}}^{{(i)}}$ $(i = 1,2)$. Тогда очевидны равенства ${\mathbf{P}} = P\;{\mathbf{\gamma }}$, ${\mathbf{P}}_{i}^{{}} = P_{i}^{{}}{\mathbf{\gamma }}_{{}}^{{(i)}}$ $(i = 1,2)$.

Рассмотрим прецессии тела относительно вектора ${\mathbf{\gamma }}$. Они характеризуются инвариантным соотношением (ИС) [6, 7]

где $\theta _{{\text{0}}}^{{}}$ – угол между векторами ${\mathbf{a}}$ и ${\mathbf{\gamma }}$ (${\mathbf{\dot {a}}} = {\mathbf{0}}$, ${\text{|}}{\mathbf{a}}{\text{|}} = 1$). Вектор угловой скорости тела на ИС (2.5) представим так [7]:

Переменные $\varphi {\text{,}}\;{{\psi }}$ и постоянную $\theta _{{\text{0}}}^{{}}$ можно трактовать, как углы Эйлера. Используя метод [7], запишем значение вектора ${{{\mathbf{\gamma }}}^{{(1)}}}$:

где $b_{0}^{{}} = 1{\text{/}}a_{0}^{'}$ $(a_{0}^{'} = \sin \theta _{{\text{0}}}^{{}})$, $\psi _{0}^{{}}$ – постоянная.

Значение вектора ${{{\mathbf{\gamma }}}^{{(2)}}}$ найдем по второй формуле системы (2.4)

Таким образом, при получении (2.7), (2.8) полагалось, что ${\mathbf{a}} \times {\mathbf{\gamma }} \ne {\mathbf{0}}$, то есть случай равномерных вращений тела исключаем из рассмотрения. Подвижную систему координат выберем следующим образом: направим вектор i₃ по вектору a. Тогда на основании ИС (2.5), первого уравнения из (2.3) имеем [6, 7]

На основании (2.6), (2.9) запишем компоненты $\omega _{1}^{{}}{\text{,}}\;\omega _{2}^{{}},\;\omega _{3}^{{}}$ вектора ${\mathbf{\omega }}$:

На рис. 1 приведена геометрическая трактовка прецессий тела относительно вектора ${\mathbf{\gamma }}$ ($O\xi \eta \zeta $ – неподвижная система координат).

Замечание 1. При описании кинематических свойств в виде соотношений (2.5)–(2.10) использован метод [7], который отличается от методов, применяемых в [10–13, 21–23].

Замечание 2. Уравнения (2.2), (2.3) имеют интеграл энергии

где $E$ – постоянная. Как показано в [6, 7], нахождение условий существования прецессий в задачах динамики твердого тела на основании (2.11) значительно упрощается.

3. Преобразование уравнения (2.2) на ИС (2.5). Внесем в уравнение (2.2) значение ${\mathbf{\omega }}$ из (2.6) и рассмотрим полученное уравнение в базисе ${\mathbf{a}},{\mathbf{\gamma }}{\text{,}}{\mathbf{a}} \times {\mathbf{\gamma }}$ с учетом (2.7), (2.8):

где ${\text{Sp}}(A) = A_{{11}}^{{}} + A_{{22}}^{{}} + A_{{33}}^{{}}$ – след матрицы A.

По аналогии с (3.1)–(3.3) распишем интеграл (2.11) на ИС (2.5), (2.6):

Введем обозначения

Сначала запишем интеграл (3.4), в силу (3.5):

Затем обратимся к уравнениям (3.1)–(3.3). На основании (3.5) имеем

Представление соотношений (3.1)–(3.4) в виде (3.6)–(3.9) связано с решением задачи о замене одного из уравнений (3.7)–(3.9) интегралом (3.6). Вычислим производную по времени от левой части уравнения (3.6), используя соотношения

Если учесть в полученном уравнении соотношения (3.7), (3.8), то имеем тождество. То есть интеграл энергии можно рассматривать только вместо одного из уравнений (3.7), (3.8). Отметим, что данное свойство выполняется, если ни одно из уравнений (3.7), (3.8) не становится тождеством.

4. О регулярных прецессиях тела. Изучим случай регулярной прецессии тела: $\dot {\varphi } = n$, $\dot {\psi } = m$, где $\dot {\varphi } = n$ и m – постоянные. Он рассмотрен частично в [21–23], но методом, который отличается от предложенного в данной статье. Запишем уравнения (3.6), (3.8) в виде

В (4.1) не произведена замена $\psi $ на mt, поскольку данный прием может быть использован и в других случаях прецессий. Очевидно, что в силу (3.5) $f_{1}^{2}(\varphi ) + f_{2}^{2}(\varphi ) \ne 0$. Найдем из (4.1) $\sin (\psi + \psi _{0}^{{}})$, $\cos (\psi + \psi _{0}^{{}})$ и подставим их в равенство sin²(ψ + ψ₀) + + $\cos _{{}}^{2}(\psi + \psi _{0}^{{}})$ = 1. Требуя, чтобы полученное уравнение было тождеством по $\varphi $, получим

Далее будем изучать только случай m = 2n, так как другие варианты исследованы в [21, 22]. Обратимся к уравнению (3.7), полагая $\psi = 2nt$, $\varphi = nt$. Функция $(A{\mathbf{\gamma }} \cdot {\mathbf{\gamma }})$ при значении вектора ${\mathbf{\gamma }}$ из (2.7) имеет в общем случае вид

То есть функция (4.4) содержит тригонометрические функции $\cos 2\varphi $, $\sin 2\varphi $, $\cos \varphi $, $\sin \varphi $. Очевидно, что функция $f_{1}^{{}}(\varphi )\sin (2\varphi + \psi _{0}^{{}}) + f_{2}^{{}}(\varphi )\cos (2\varphi + \psi _{0}^{{}})$ не должна содержать слагаемые, содержащие $\sin 3\varphi $, $\cos 3\varphi $. Для того, чтобы указанная функция не содержала $\sin 3\varphi $, $\cos 3\varphi $, должны, в силу (3.5), выполняться условия

Запишем функции $f_{1}^{{}}(\varphi )$, $f_{2}^{{}}(\varphi )$ из (3.5) при условиях (4.5)

Подставим функции (4.4), (4.6) в уравнения (3.6) и учтем равенства $\psi = 2\varphi $, (4.6). Для того, чтобы полученное уравнение было тождеством по $\varphi $, необходимо положить

Таким образом, в силу (4.5), (4.7) для векторов ${\mathbf{p}}$ и ${\mathbf{r}}$ имеем векторные соотношения

то есть в силу (4.8) ${\mathbf{p}} \bot {\mathbf{r}}$, ${\mathbf{p}} \bot {\mathbf{a}}$, ${\mathbf{r}} \bot {\mathbf{a}}$ – ортогональные вектора p и r лежат в плоскости Oxy. Запишем дополнительные условия, при выполнении которых уравнение (3.6) становится тождеством по φ:

На основании условий (4.5)–(4.7) уравнение (3.8) будет тождеством по $t$, если имеют место равенства

Учитывая в уравнениях (4.9) равенства (4.10), получим

Рассмотрим уравнение (3.9). Потребуем, чтобы оно было тождеством по $t$ при условиях (4.5), (4.7), (4.10), (4.11). Тогда получим

Итак, условием существования регулярных прецессий ($\psi = 2nt$, $\varphi = nt$) тела относительно вектора ${\mathbf{\gamma }}$ являются равенства (4.5), (4.7), (4.10)–(4.12). Первые два условия из (4.7) означают, что вектор a перпендикулярен круговому сечению эллипсоида инерции тела. Уравнения (4.10) служат для определения постоянной $\psi _{{\text{0}}}^{{}}$:

а также постоянной $n$:

В соотношениях (4.13), (4.14) необходимо учесть значение a₀ = 1/6.

5. Прецессионно-изоконические движения. Данные движения можно описать инвариантным соотношением [6]

В силу (5.1) запишем подвижный и неподвижный годографы в виде

Из векторных равенств (5.2), (5.3) следует, что годографы (5.2), (5.3) симметричны друг другу относительно касательной плоскости к соответствующим аксоидам. То есть движение тела характеризуется не только прецессией относительно ${\mathbf{\gamma }}$, но и изоконичностью годографов.

Исследование прецессионно-изоконических движений проведен в случае, когда эллипсоид инерции является сферой:

На основании условия (5.4) систему уравнений (3.6), (3.7), (3.9) представим так

Продифференцируем левую и правую части уравнения (5.5) по $t$ и подставим в полученное уравнение $\ddot {\varphi }$ из (5.6), $f_{{\text{1}}}^{{}}(\varphi )$ и $f_{{\text{2}}}^{{}}(\varphi )$ из (3.5). Так как это уравнение должно быть тождеством по $\varphi $, то находим следующие условия на параметры задачи:

Исключим из уравнений (5.5), (5.7) величину $\dot {\varphi }_{{}}^{2}$. В результате получим уравнение, из которого следуют равенства

Если в уравнениях (5.10) положить $2a_{{\text{0}}}^{{}} - 1 \ne 0$, то получим два равенства

Приравняем величины s₁ и s₂; используя (5.8), (5.12), имеем нулевые значения для p₃, r₃, а также для s₁, s₂. На основании уравнения (5.5) и функций (4.6) находим, что $\dot {\varphi } = {\text{const}}$. Данный вариант, в силу (5.1), характеризует регулярную прецессию, что исключено из рассмотрения. Поэтому в (5.10) необходимо положить

Рассмотрим геометрическую интерпретацию условий (5.9). Введем вспомогательные векторы

Тогда из (5.9), (5.14) следует, что имеют место соотношения

Из равенств (5.8) в силу третьей формулы системы (5.9) получим

Равенства (5.16) позволяют связать параметры s₁, s₂ и $p_{3}^{{}}{\text{,}}r_{3}^{{}}$:

Преобразуем равенство (5.5) с учетом условий (5.8), (5.9), (5.16), (5.17) и значения a₀ = 1/2:

Выполним в (5.18) замену $\varphi + \beta _{{\text{0}}}^{{}} = \tilde {\varphi }$. Тогда из (5.18) имеем

Положим в (5.21) $\tilde {\varphi } = 2\varepsilon $:

или

В силу выполненных преобразований параметры задачи должны удовлетворять условию $h_{0}^{{}} > {\text{0}}$ ($h_{1}^{{}} > {\text{0}}$ для всех значений ${{r}_{3}}{\text{,}}p_{3}^{{}}$, так как $A_{1}^{{}} > {\text{0}}$), где h₀ имеет вид, указанный в (5.19). Параметр $\beta _{{\text{0}}}^{{}}$ определим из (5.20):

Из интегрального соотношения (5.22) имеем

где ${\text{am}}\tau $, ${\text{sn}}\tau $ – эллиптические функции от τ. На основании указанных выше вычислений найдем

Учтем во второй формуле из (5.25) значения (5.23), (5.24). Тогда

где в силу (5.22) $\tau = \frac{{h_{2}^{{}}}}{2}t$ $(h_{2}^{{}} = \sqrt {h_{0}^{{}} + h_{1}^{{}}} )$. Значение $\dot {\varphi }$ определим из (5.21), (5.22) а для получения cosφ(τ) необходимо использовать формулу (5.26), подставив в нее $\tau = \frac{{h_{2}^{{}}}}{2}t$. Тогда функция $\cos \varphi (t) = \sqrt {1 - \sin _{{}}^{2}\varphi (t)} $. Таким образом, решение уравнений движения сферического тела для случая прецессионно-изоконических движений построено: оно выражается формулами (2.7)–(2.10), в которых необходимо учесть условия (5.8), (5.9), (5.13), (5.27). Оно выражается через эллиптические функции ${\text{sn(}}\tau )$, ${\text{cn(}}\tau )$, ${\text{dn(}}\tau )$, где $\tau = \frac{{h_{2}^{{}}}}{2}t$. Представляет определенный интерес значение ${{\theta }_{0}} = 60^\circ $, а также условие, которое выражается ортогональностью векторов ${\mathbf{r}}{\kern 1pt} *{\text{,}}\,\,{\mathbf{p}}{\kern 1pt} *$. Отметим, что в случае регулярных прецессионных движений (см. п. 4) ${{\theta }_{0}} = \arccos \left( {{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}} \right)$.

6. Случай двух однородных силовых полей. Рассмотрим движение тела под действием двух однородных силовых полей: положим ${\mathbf{p}}{\kern 1pt} * = {\mathbf{0}}$ ($p_{{\text{i}}}^{{}} = 0$, $i = \overline {1,3} $). Тогда из условий (5.8), (5.9) найдем

Значения ${{a}_{0}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ из (5.13) не изменяется. В силу (6.1) ${\mathbf{r}} = r_{3}^{{}}{\mathbf{a}}$, то есть вектор r коллинеарен вектору a (центр приведения сил второго поля находится на оси, проходящей через a). Из последних равенств (6.1) следует, что $s_{1}^{2} + s_{2}^{2} = r_{3}^{2}$ (формулы (5.16) не имеют места, так как они получены из последней формулы системы (5.9)). Выражение для h₀ из (5.19) упрощается: $h_{0}^{{}} = - \frac{{s_{3}^{{}}}}{{9A_{1}^{{}}}}$, а значения h₁ из (5.19) и ${\text{sin}}\beta _{{\text{0}}}^{{}}$, $\cos {{\beta }_{0}}$, в силу (6.1), принимают вид

То есть и в случае (6.1), (6.2) $\varphi ({\text{t}})$, $\sin \varphi (\tau )$, $\cos \varphi (\tau )$ являются эллиптическими функциями времени. Движение тела обладает свойством периодичности (см. формулы (5.2), (5.3), (5.25), (5.26)).

Замечание 3. Из полученных выше результатов (см. пп. 4, 6) в случае, когда на тело действует сила только одного однородного поля (уравнения движения становятся уравнениями Эйлера–Пуассона), прецессионно-изоконические движения тела имеют место только в решении Лагранжа для сферического гироскопа. Данный вывод согласуется с результатами [5–7]. Отметим, что в решении Лагранжа изоконические движения (без дополнительного свойства прецессионности) возможны только в случае несферического распределения масс.

7. Прецессионно-изоконические движения динамически симметричного твердого тела. Рассмотрим случай, когда твердое тело обладает свойством динамической симметрии относительно вектора ${\mathbf{a}}$. Запишем вначале уравнения (3.6), (3.7) при $A = {\text{diag}}$(A₁, A₁, A₃):

Метод изучения уравнений (7.1), (7.2) сохраним в прежнем виде (см. п. 5). Тогда получим следующие условия на параметры задачи: равенства (5.9) не изменяются, а вместо равенств (5.8) следует рассматривать уравнения

Здесь $\mu _{{\text{0}}}^{{}} = (A_{{\text{3}}}^{{}} - h_{{\text{0}}}^{{}}){\text{/}}A_{{\text{3}}}^{{}}$, или, в силу (7.3), имеем следующее значение $\mu _{{\text{0}}}^{{}}$ через параметры задачи:

Из (7.5) следует, что $\mu _{{\text{0}}}^{{}} \ne 1$, так как в противном случае $h_{0}^{{}} = 0$, что исключаем из рассмотрения на основании значения $a_{{\text{0}}}^{{}}$: ${\text{|}}a_{{\text{0}}}^{{}}{\text{|}} > 1$, которое получаем из равенства $h_{0}^{{}}\, = \,0$.

Запишем значения $\dot {\varphi }_{{}}^{2}$ из (7.2), использовав обозначения (3.5) и условия (5.9), (7.4):

а также из уравнения (3.9) (полагаем $a_{0}^{{}}(A_{1}^{{}} - A_{3}^{{}}) - A_{1}^{{}} \ne 0$, так как в противном случае $s_{1}^{{}} = 0$, $s_{2}^{{}} = 0$):

Приравнивая $\dot {\varphi }_{{}}^{2}$ из уравнений (7.6), (7.7), найдем уравнение, которое должно быть тождеством по φ. Тогда получим

Если $A_{3}^{{}} = A_{1}^{{}}$, то из (7.8) следует ${{a}_{0}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, что соответствует уже изученному варианту. При $A_{3}^{{}} \ne A_{1}^{{}}$ параметр a₀ имеет значение

Для исследования промежутка изменения параметра a₀ целесообразно не применять формулу (7.9), а использовать графо-аналитический метод исследования функции (7.8), обозначив через $y = {{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{A}_{3}}}}} \right. \kern-0em} {{{A}_{3}}}}$, а a₀ – через x. Из неравенств треугольника на главные моменты инерции тела ${{A}_{i}}$ $(i = \overline {1,3} )$ следует, что $y > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$; из геометрического условия на параметр a₀ имеем неравенство ${\text{|}}x{\text{|}} < 1$. Таким образом, на основании (7.8) для функции $y$ получим уравнение

Нули данной функции определены равенствами $x = 1$, $x = - 2$; производная $y{\kern 1pt} ' < 0$ при $x \ne 0$, $x \ne 3$. Следовательно, функция $y > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, если $x \in (0,x_{*}^{{}})$, где

Из полученных результатов следует, что $a_{{\text{0}}}^{{}} \in (0{\text{,}}x_{*}^{{}})$.

Значение параметра E, который находится из метода рассмотрения уравнений (7.6), (7.7), зависит от параметров задачи, так как E – постоянная первого интеграла. Следовательно, дано обобщение решения п. 5 на случай динамически симметричного гироскопа, которое также описывается эллиптическими функциями.

Заключение. В статье дана постановка задачи о прецессионных движениях тела под действием трех однородных силовых полей. На основе подхода, указанного в [6, 7], получены три дифференциальных уравнения на функции $\varphi (t)$, $\psi (t)$, где $\varphi (t)$ – угол собственного вращения, $\psi (t)$ – угол прецессии тела. Изучена проблема замены одного из уравнений интегралом энергии. Рассмотрены случаи регулярных прецессий ($\dot {\varphi } = n$, $\dot {\psi } = m$, n и m – постоянные, удовлетворяющие условию $m = 2n$) и прецессионно-изоконических движений ($\dot {\varphi } = \dot {\psi }$). Показано, что в первом варианте угол нутации равен ${\text{arccos}}$(1/6), а во втором он имеет значения 60° для сферических гироскопов и $a_{{\text{0}}}^{{}}\, \in \,(0,x_{*}^{{}})$ для динамически симметричного гироскопа относительно вектора a. Рассмотрен вариант, когда движение тела происходит под действием сил двух однородных силовых полей. Получено сведение решения к эллиптическим функциям времени. В отличие от ранее использованных подходов, в данной статье применен векторный метод в описании прецессионных движений тела, что позволило установить решение уравнений движения в кратком виде. Редуцированные уравнения движения дают возможность изучить прецессии общего вида. Например, можно анонсировать результат о том, что исследование прецессионных движений тела в случае, когда скорость собственного вращения тела в два раза меньше его скорости прецессии, угол нутации равен ${\text{arccos(1/4)}}$. В связи с этим представляет интерес сравнение указанных в данной статье результатов с аналогичными результатами в классической задаче, которая описывается уравнениями Эйлера–Пуассона, и в задаче о движении гиростата под действием потенциальных и гироскопических сил, которая описывается уравнениями класса Кирхгофа–Пуассона. В первой задаче известно решение Д. Гриоли [2], характеризующееся прецессией тела относительно наклонной оси. Для него выполняются свойства $\dot {\psi } = \dot {\varphi }$, $\theta _{{\text{0}}}^{{}} = 90^\circ $. Во второй задаче имеет место решение А.В. Мазнева [25], отвечающее прецессии гиростата относительно вертикали и обладающее свойствами $\dot {\psi } = \dot {\varphi }$, $\theta _{{\text{0}}}^{{}} = 120^\circ $.