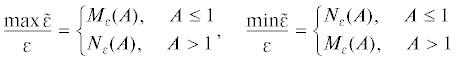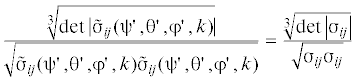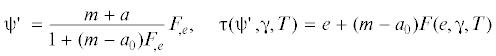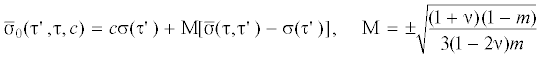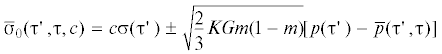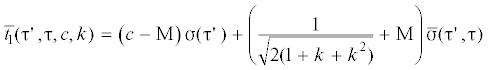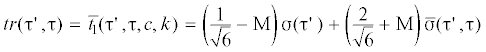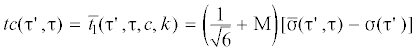Известия РАН. Механика твердого тела, 2023, № 3, стр. 73-98

Введение. Успехи, достигнутые при описании сложных явлений протекающих при деформировании микронеоднородных материалов, демонстрируют, что к наиболее плодотворным принципиальным концепциям относится идея, согласно которой представительный объем макроскопически однородного тела представляется в виде бесконечного числа связанных между собой подэлементов имеющих различные термореологические свойства. Модели предложенные различными авторами отличаются друг от друга принятыми соотношениями между локальными тензорами напряжений ${{\bar {t}}_{{ij}}}$, деформаций ${{\bar {d}}_{{ij}}}$ и макроскопическими напряжениями ${{t}_{{ij}}}$, деформациями ${{d}_{{ij}}}$. Большинство авторов ограничиваются допущением об однородном деформированном состоянии подэлементов ${{\bar {d}}_{{ij}}} = {{d}_{{ij}}}$ или об однородном напряженном состоянии ${{\bar {t}}_{{ij}}} = {{t}_{{ij}}}$. Первая многоэлементная модель среды принадлежит Мазингу [1], в которой процесс деформирования элемента тела имитируется как деформация конечного числа стержней одинаковой жесткости, обладающих свойствами идеальной пластичности с различными пределами текучести и имеющих одинаковую деформацию, что позволило довольно хорошо описать эффект Баушингера. Предполагая постоянство деформации внутри поликристаллического тела Фойгта [2] вычислил макроскопические константы упругости на основе констант упругости кристаллов. Рейсс [3] получил формулы для расчета константы упругости поликристалла, исходя из предположения о постоянстве напряжений. Распространение модели ${{\bar {d}}_{{ij}}} = {{d}_{{ij}}}$ на вязкопластические процессы деформирования первоначально изотропного материала, обнаруживающего анизотропию деформационного упрочнения, последействия и вторичную ползучесть содержится в [4]. Обычно, для этого направления исследования используется название– структурные модели [5–9]. Для анализа поведения материалов при термомеханических воздействиях используются и модели основанных на ведение внутренних переменных [10]. Исследование пластического течения поликристаллов, выведенного из поведения монокристаллов, проводили Сакс (1928) и Тейлор (1938). И те, и другие подтвердили важные прогнозы поведения поликристаллов. Но из-за очень простых базовых предположений большинство их результатов являются качественными и допускают лишь довольно слабую согласованность с экспериментальными данными.

Кренера [11] открыл новый путь с формулировкой так называемой ”самосогласованной схемы”, относящийся к проблеме включения в бесконечную матрицу. Согласно его схеме каждое зерно поликристалла последовательно рассматривается как включение в “матрицы” всех других зерен. Поведение поликристалла затем рассчитывается с помощью некоторого адекватного осреднения по всем зернам. В результате установил следующий линейный закон взаимодействия

где G – модуль сдвига, ${{\nu }} - $ коэффициент Пуассона. Модель Кренера удовлетворительно согласуется с экспериментальными данными в упругой области деформирования, однако в необратимой области приводит к завышенным внутренним напряжениям.

Для учета естественной тенденции материала к снижению флуктуаций напряжений внутри представительного объема $\Delta {{V}_{0}}$ Бервейе и Заул [12] ввели в анализ так называемую “пластическую функцию аккомодации”. Такой подход возможен только при ограничении изотропного упругопластического взаимодействия между включением и матрицей. В этой модели параметр B уменьшается с ростом пластической деформации почти на два порядка при испытании на одноосное растяжение однофазных поликристаллических материалов. Дальнейшее развитие многоэлементных моделей в рамках линейных соотношений между флуктуациями тензоров напряжений и деформаций связано с разработкой различных способов определения параметров $B$ и ${{B}_{0}}$ [12, 13 и др.]. Слабым местом исследований данного направления является несогласованность линейных уравнений связи макро- и микросостояний с первым законом термодинамики¹¹

для любых вариантов изменения параметров B и ${{B}_{0}}$, за исключением предельных: $B = {{B}_{0}} = 0$ или $B = {{B}_{0}} = \infty $. Модели, основанные на линейных уравнениях связи проблематично использовать для описания процессов разрушения или взаимодействия тепловых и механических полей в рамках связанной теории. Отсутствие взаимосвязи между девиаторными и шаровыми величинами приводит, в частности, к предсказанию о невозможности разрушения при чистом сжатии, что не согласуется с опытом. Обсуждение различных теорий, основанных на линейных уравнениях связи макро- и микросостояний, находится вне сферы этой статьи.

В условиях невозможности детального учета взаимодействий материальных частиц в представительном объеме, целесообразно построить уравнения связи макро- и микросостояний, которые бы согласовались с законами термодинамики, учитывали явление самосогласования локальных процессов необратимого деформирования и отвечали условию единственности решения задачи представления материала в модели [8]. В силу того, что линейность взаимосвязи локальных и макроскопических параметров вытекает из формулировки проблемы включения в бесконечную матрицу в [7, 8, 14, 15] был предложен иной подход к построению уравнений связи макро- и микросостояний. В качестве первичного элемента структуры выбирается подэлемент, который отождествляется со множеством материальных частиц внутри представительного объема, имеющих одинаковый тензор необратимой деформации. Частицы одного и того же подэлемента могут иметь различные ориентации и положения в пространстве конгломерата. Количество частиц в каждом подэлементе определяет их вес и не меняется в процессе деформирования. Из данного определения понятия подэлемента следуют более комплексные взаимодействия материальных частиц в представительном объеме чем взаимодействие включения с матрицей. Напряжения и обратимые деформации в подэлементе соответствуют средним значениям напряжений и деформаций возникающих во подмножестве материальных частиц с одинаковыми тензорами необратимых деформаций. В силу этого постулируется: взаимодействия между подэлементами формируются под влиянием лишь одних осредненных связей. При этом предполагается, что условие непрерывности среды обеспечивается путем действия пяти независимых систем скольжения. Экспериментально установленное небазисное скольжение позволяет описать скалярные и тензорные свойства материалов в необратимой области деформирования в обычных для Механики деформируемого твердого тела терминах. Предложенная в работах [7, 8, 14–16] модель базируется на принципах: осредненных связей, ортогональности тензоров флуктуаций напряжений и деформаций, экстремума несоответствия макроскопических мер с подходящими средними значениями микроскопических аналогов. Построенная замкнутая система уравнений удовлетворяет законам термодинамики, учитывает явление самосогласования локальных процессов необратимого деформирования и отвечает требованию единственности решения задачи представления реального материала в модели. Подробное исследование системы, содержащее и правило дискретной механической памяти материала о совокупности характерных моментов предыстории деформирования и нагрева, при циклическом пропорциональном неизотермическом деформировании нестабильных материалов проводилось в [16]. Общие закономерности поведения материалов чувствительных к скорости деформирования исследовалось в [14–16 и др.].

В перечисленных работах [7–9, 14–16] исследовались только процессы деформирования без учета процессов возникновения и накопления микротрещин, которые приводят к разрушению элемента тела. В данной работе наряду с условием текучести рассмотрим и условие разрушения подэлементов. Необратимые деформации, приводят к увеличению дефектов кристаллической решетки, росту уровня напряжений и подготавливают металл к разрушению, а нормальные напряжения растяжения приводят к разрушению. Поэтому для совместного рассмотрения процессов деформирования и разрушения необходимо исследовать закономерность изменения предельных значений трех инвариантов напряжений/деформаций во множестве подэлементов.

1. Принципы перехода от микронапряжений и деформаций к макронапряжениям и деформациям. Для описания поведения неупорядоченной среды фундаментальные понятия тензоров напряжения и деформации вводятся на двух уровнях: материальных частиц, которые обозначаются через –${{\tilde {t}}_{{ij}}},{{\tilde {d}}_{{ij}}}$ и на макроскопическом уровне –${{t}_{{ij}}},{{d}_{{ij}}}$. На основе геометрических уравнений Коши и уравнения равновесия,

а также граничных условий на поверхности $\Delta {{S}_{0}}$ элемента объема $\Delta {{V}_{0}}$

Р. Хилла [17] установил следующие уравнения связи микро- и макросостояний

где 〈·〉 – знак осреднения по объему $\Delta {{V}_{0}}$. Уравнения (1.1), (1.2) необходимы, но недостаточны для построения системы определяющих уравнений на макроскопическом уровне на основе физических соотношений на микроскопическом уровне.

Три уравнения Хилла (1.1), (1.2) можно представить в виде одного выражения [5, 7]

Из (1.3) видно, что среднее значение скалярного произведения флуктуаций тензоров напряжений и деформаций в представительном объеме аннулируется. Из опыта известно, что механизмы деформирования в поликристаллических материалах приводят к процессу самосогласования (когерентности) процессов деформирования и нагружения. Для учета явления самосогласования процессов деформирования в работах [8] предложен принцип осредненных связей: взаимодействия между подэлементами в конгломерате формируются под влиянием лишь одних осредненных связей. Исходя из этого положения в [9, 14], был принят постулат об ортогональности тензоров флуктуаций напряжений и деформаций в каждом подэлементе

Разложив в (1.4) тензоры напряжений и деформаций на девиаторные и шаровые составляющие ${{\tilde {t}}_{{ij}}} = {{{{\tilde {\sigma }}}}_{{ij}}} + {{{{\tilde {\sigma }}}}_{0}}{{{{\delta }}}_{{ij}}}$, ${{\tilde {d}}_{{ij}}} = {{{{\tilde {\varepsilon }}}}_{{ij}}} + {{{{\tilde {\varepsilon }}}}_{0}}{{{{\delta }}}_{{ij}}}$, установим первый тип уравнений связи макро- и микросостояний

Для флуктуаций девиаторных составляющих примем соотношение

где B – внутренний параметр, содержащий информацию о микроскопических характеристиках подэлементов.

Из уравнений (1.1), (1.2) видно, что усреднение по объему напряжений, деформаций и их произведений зависит единственным образом от данных на поверхности представительного объема. Однако не все микроскопические переменные обладают этим специфическим свойством. В частности, в [8] показано, что естественные макромеры энергии изменения объема и формы отличаются от усреднения по объему своих микромер. Для конкретизации параметра B в [14–16] предложен принцип экстремума несоответствия макроскопических мер с подходящими средними значениями микроскопических аналогов. В частности

Выражения (1.1), (1.5)–(1.7), представляют замкнутую систему уравнений взаимосвязи микро- и макро- термомеханических состояний. Они не содержат ссылки на свойства материалов и поэтому действительны как для обратимых, так и необратимых процессов деформирования. На их основе удается построить систему определяющих уравнений на макроскопическом уровне если известны физические соотношения на микроскопическом уровне.

2. Анализ модели в обратимой области деформирования. В уравнениях связи микро- и макросостояний (1.1), (1.5)–(1.7) фигурируют напряжения и деформации на локальном (${{\tilde {t}}_{{ij}}},{{\tilde {d}}_{{ij}}}$) и макроскопическом уровне (${{t}_{{ij}}},{{d}_{{ij}}}$). При этом, в обратимой области под ${{\tilde {t}}_{{ij}}},{{\tilde {d}}_{{ij}}}$ подразумеваются средние значения напряжений и деформаций в подмножестве частиц с одинаковой ориентацией кристаллографических осей, относительно глобальной системы координат. В рамках данной формализации на основе локального физического закона

и соотношений (1.1), (1.5)–(1.7) установим взаимосвязь ${{t}_{{ij}}}\sim {{d}_{{ij}}}$. Здесь ${{C}_{{ijnm}}}$ – тензор упругих констант в кристаллографической системе координат $x_{i}^{'}$, $\tilde {t}_{{ij}}^{'},\tilde {d}_{{ij}}^{'}$ – компоненты соответствующих тензоров в кристаллографической системе координат. Для однофазных поликристаллических материалов с кубической решеткой из (2.1) и (1.6) находим

Принимая во внимание эти значения в глобальной системе координат ${{x}_{i}}$: ${{{{\tilde {\varepsilon }}}}_{{ij}}}$ = = ${{\tilde {r}}_{{nj}}}{{\tilde {r}}_{{mj}}}{{\tilde {\varepsilon }}}_{{nm}}^{'}$ и заменив в (1.1), (1.7) интегрирование по объему интегрированием по фактору ориентации кристаллической решетки: ${{\left\langle . \right\rangle }_{V}} = {{\left\langle . \right\rangle }_{\Omega }}$ в [15] установлена следующая система:

Из (2.4) и (2.5), при условии ${{{{\sigma }}}_{{nm}}}{{{{\varepsilon }}}_{{nm}}} = {\text{const}}$, следуют формулы для $B$ и $G$ [15]:

где А – фактор анизотропии монокристалла; ${{G}_{V}}$ – модуль сдвига, полученный Войгтом в 1928 году в рамках приближения ${{\tilde {d}}_{{ij}}} = {{d}_{{ij}}}$; ${{G}_{R}}$ – модуль сдвига, полученный Рейсом в 1929 году в рамках приближения ${{\tilde {t}}_{{ij}}} = {{t}_{{ij}}}$. Таким образом, из принципа (1.7) вытекает, что макроскопический модуль сдвига G равен среднегеометрическому значению модулей сдвига, полученных в двух предельных вариантах: однородное напряженное и однородное деформированное состояние.

Важно отметить, что удивительно простая формула (2.7) хорошо согласуется с экспериментом. При использовании “самосогласованной схемы” Кренера, модуль сдвига находится из кубического уравнения [11]

В работе [9] проводилось сопоставление значений модулей сдвига, полученных в рамках модели Кренера (2.8) (${{G}_{K}}$) и Марина (2.7) (${{G}_{M}}$). В результате было установлено следующее фундаментальное неравенство

Хотя для определения параметра $B$ в модель Кренера используется решение задачи о включении, полученной Эшелби (1957), а в модели Марина – принцип экстремума несоответствия мер (1.7), тем не менее в некоторых случаях удается установить качественные соотношения. Сравнение теоретических и экспериментальных значенй ${{G}_{M}}$ и ${{G}_{K}}$ для 23 поликристаллических материалов с кубической решеткой проведенное в [9], показало, что исследуемые модели хорошо согласуются с экспериментальными данными, при этом ${{G}_{M}}$ ближе к ${{G}_{{\exp }}}$, чем ${{G}_{K}}$.

В рамках исследованной модели, удается описать явления, которые не охватываются многоэлементными моделями основанные на линейных уравнениях связи макро- и микросостояний и в обратимой области деформирования; в частности, эффекты, которые обычно объединяют общим термином “внутреннее трение”. Подобные эффекты обусловлены разнообразными процессами тепловой диссипации энергии, связанных с большими флуктуациями объемных деформаций на микроскопическом уровне.

Флуктуации объемных напряжений и деформаций, возникающих в представительном объеме поликристалла, определяются на основе (1.5), (1.6), (2.6), (2.7)

Из (2.10) следует, что флуктуации объемных напряжений в кристаллах определяются только с точностью до знака. Согласно (2.10) неоднородное поле изменения формы материальных частиц всегда порождает неоднородное поле объемных деформаций

Следует отметить, что в линейном приближении для флуктуаций шаровых величин применяется соотношение ${{{{\bar {\sigma }}}}_{0}} - {{{{\sigma }}}_{0}} = D({{{{\bar {\varepsilon }}}}_{0}} - {{\varepsilon }}{}_{0})$, которое согласуется с физическим соотношением (2.11) при условии ${{{{\bar {\sigma }}}}_{0}} = {{{{\sigma }}}_{0}}$, ${{{{\bar {\varepsilon }}}}_{0}} = {{\varepsilon }}{}_{0}$. Следовательно, линейные уравнения связи микро- и макросоостояний для шаровых величин приводят к тем же следствиям, как и предельные варианты – однородное напряженное состояние или однородное деформированное состояние.

Компоненты девиатора тензора напряжений ${{\tilde {\sigma }}}_{{ij}}^{'}$ определим на основе выражений (2.2), (2.3), (2.6) и (2.7) [18]

где ${{\psi }},{{\theta }},\varphi $ – углы Эйлера (задают ориентацию кристаллической решетки относительно глобальной системы координат), ${{{{\sigma }}}_{1}},{{{{\sigma }}}_{2}},{{{{\sigma }}}_{3}}$ – главные значения девиатора тензора макроскопических напряжений. Для упрощения анализа главные оси тензора ${{t}_{{ij}}}$ выбраны в качестве глобальной системы координат. Из (2.12), (2.13) следует, что на ${{\tilde {\sigma }}}_{{ij}}^{'}$ влияют только два фактора: коэффициент анизотропии кристалла A и ориентация кристаллической решетки – (${{\psi ,\theta ,}}\varphi $). Для изотропных кристаллов ${{M}_{\sigma }}(1) = {{N}_{\sigma }}(1) = 1$, ${{\tilde {\sigma }}}_{{ij}}^{'}({{\psi }},{{\theta }},\varphi ,1,{{{{\sigma }}}_{n}}) = {{\sigma }}_{{ij}}^{'}$.

Для компонент девиатора тензора деформации ${{\tilde {\varepsilon }}}_{{ij}}^{'}$ получаем схожие по виду соотношения [19]

На основе (2.12)–(2.15) устанавливаем закономерность изменения компонент девиаторов тензоров напряжений и деформации в зависимости от коэффициента/фактора анизотропии $A$ и ориентации кристаллографической системы кристалла ${{\Omega }} \to \varphi ,{{\theta }},{{\psi }}$. В практических и теоретических приложениях наибольший интерес представляют исследования закономерностей изменения инвариантных величин: модули девиаторов тензоров напряжений ${{\tilde {\sigma }}} = \sqrt {{{{{{\tilde {\sigma }}}}}_{{ij}}}{{{{{\tilde {\sigma }}}}}_{{ij}}}} = \sqrt {{{\tilde {\sigma }}}_{{ij}}^{'}{{\tilde {\sigma }}}_{{ij}}^{'}} $, деформации ${{\tilde {\varepsilon }}} = \sqrt {{{{{{\tilde {\varepsilon }}}}}_{{ij}}}{{{{{\tilde {\varepsilon }}}}}_{{ij}}}} = \sqrt {{{\tilde {\varepsilon }}}_{{ij}}^{'}{{\tilde {\varepsilon }}}_{{ij}}^{'}} $, объемные напряжения ${{{{\tilde {\sigma }}}}_{0}}$ и деформации ${{{{\tilde {\varepsilon }}}}_{0}}$. Из анализа выражения для модуля девиатора тензора напряжений/деформаций

с учетом равенств ${{{{\tilde {\sigma }}}}_{{33}}} = - {{{{\tilde {\sigma }}}}_{{11}}} - {{{{\tilde {\sigma }}}}_{{22}}}$ выявлены следующие свойства. Среди множества ориентаций систем координат существуют и системы, в которых

Из системы (2.17) находим направления систем координат ${{\psi }} = {{\psi }}_{{}}^{'},\;{{\theta }} = {{\theta }}_{{}}^{'},\;\varphi = \varphi _{{}}^{'}$, в которых диагональные компоненты девиатора тензора напряжений равны нулю, а из (2.18) – направления систем координат ${{\psi }} = {{\psi }}_{{}}^{{''}},\;{{\theta }} = {{\theta }}_{{}}^{{''}},\;\varphi = \varphi _{{}}^{{''}}$, в которых недиагональные компоненты девиатора тензора напряжений равны нулю. Следовательно, наряду с главной системой координат, в которой модуль девиатора тензора напряжений выражается только через диагональные компоненты, существует и система координат, в которой модуль девиатора выражается только через недиагональные компоненты.

Влияние вида девиатора тензора напряжения на решениях систем (2.17) и (2.18) можно выразить через параметр

Индексы при координатах ${{x}_{i}}$ выбираются в соответствии с неравенством (2.19). В этом случае система (2.17) принимает следующий вид

Отметим, что между введенным параметром k и параметром $\omega $ характеризующим отношение инвариантов девиатора тензора напряжений существует однозначная связь

Решения системы (2.20) получаются в виде зависимостей ${{\psi }} = {{\psi }}(k),{{\theta }} = {{\theta }}(k)$, φ = φ(k), в частности:

На основе (2.21) или (2.22) определяется положение системы координат относительно главной системы, в которой диагональные компоненты девиатора аннулируются. Недиагональные компоненты в системе координат (2.21) принимают значения

а в системе (2.22)

Таким образом, между компонентами девиатора любого симметричного тензора в системах координат с нулевыми диагональными компонентами и нулевыми недиагональными компонентами существуют простые зависимости. Отметим, что системы координат (2.21) и (2.22) эквиваленты, поэтому в исследованиях следует пользоваться только одной из них.

Учитывая в (2.21), (2.22) область изменения параметра k ($ - 0.5 \leqslant k \leqslant 0$), установим влияние вида девиатора тензора напряжений на пределы изменения ориентаций систем координат, в которых диагональные компоненты девиатора (любого симметричного тензора) равны нулю:

Факт существования не только системы координат, в которой недиагональные компоненты девиатора равны нулю, но и системы в которой диагональные компоненты аннулируются, позволяет сформулировать на основе выражений (2.12), (2.14), (2.21)–(2.24) теоремы:

Теорема 1. Крайние относительные значения модулей девиаторов тензоров напряжений 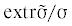и деформаци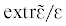й во множестве зерен, входящих в представительном объеме поликристалла с кубической решеткой, инвариантны относительно внешних условий обратимого воздействия и зависят только от фактора анизотропии кристалла A в виде зависимостей:

Теорема 2. Вид девиатора тензора напряжений/деформаций в кристаллах с экстремальными значениями модулей девиаторов тензоров напряжений/деформаций совпадает с макроскопическим видом, т.е.:

Сформулированные теоремы справедливы для любых процессов обратимого деформирования однофазных поликристаллических материалов с кубической решеткой. Отметим, что при коэффициенте анизотропии $A \geqslant 1$ в зернах, у которых кристаллографические системы координат параллельны с глобальной системой координат, модуль девиатора тензора напряжений принимает наименьшее значение, а в зернах, у которых ориентация кристаллографических осей определяется соотношением (2.21) – наибольшее значение. Таким образом, модули девиаторов тензоров напряжений и деформаций в зависимости от ориентации кристаллографической системы координат изменяются в пределах

если коэффициент анизотропии $A \leqslant 1$, и если коэффициент анизотропии A > 1.

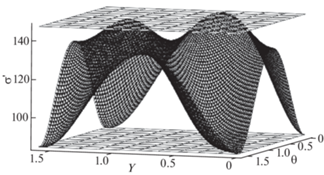
Численный анализ проведем для меди [20]: $A = 3.209$, ${{C}_{{11}}} = 16.84$ × 10⁴, ${{C}_{{12}}} = 12.14$ × × 10⁴, ${{C}_{{44}}} = 7.54$ × 10⁴ МПа. На рис. 1, для $\varphi = {{\theta }}$, представлена зависимость ${{\sigma '}}({{\theta ,\psi }}) = {{\sigma '(\theta }},{{\theta }}$, ψ, 0.5) при макроскопическом растяжении: ${{{{\sigma }}}_{1}} = 100$, ${{{{\sigma }}}_{2}} = - 50$, ${{{{\sigma }}}_{3}} = - 50$ MPa. Горизонтальные плоскости устанавливают верхний и нижний пределы изменения модуля девиатора напряжений во множестве кристаллов согласно неравенству (2.28): $0.693{{\sigma }} \leqslant {{\tilde {\sigma }}}({{\psi }},{{\theta }},\varphi ,{{{{\sigma }}}_{n}}) \leqslant 1.205{{\sigma }}$.

Закономерность изменения объемных напряжений в представительном элементе поликристалла исследовалась в [18]. Рассмотрим пределы изменения флуктуаций объемных напряжений и деформаций. На основе (2.10), (2.12) получим следующее выражение для флуктуаций величины $({{\tilde {\sigma }}}_{{ij}}^{'} - {{\sigma }}_{{ij}}^{'})$

Подставляя (2.29) в (2.10) и применяя к полученному выражению сформулированную теорему, установим пределы изменения объемных напряжений и деформаций

Основная сложность при исследовании флуктуаций объемных напряжений и деформаций связана с определением знака в полученных соотношениях. Заслуживает внимания вариант (${{M}_{{{\sigma }}}} \Rightarrow M{}_{{{\sigma }}}(A),{{N}_{{{\sigma }}}} \Rightarrow N{}_{\sigma }(A)$)

если коэффициент анизотропии $A \leqslant 1$, и если коэффициент анизотропии $A > 1$. Отметим, что выражения (2.27), (2.28), (2.33) и (2.34) справедливы для любого напряженного состояния. Переход в (2.33) и (2.34) от напряжений к деформациям можно осуществить, используя соотношения: ${{\sigma }} = 2G{{\varepsilon }},{{{{\sigma }}}_{0}} = K{{{{\varepsilon }}}_{0}}$. Для меди $A = 3.209$ из (2.33) с учетом (2.13), (2.32) установим следующие пределы изменения объемных напряжений в зернах поликристалла

Согласно (2.35), при испытании на сдвиг/кручение образцов из меди, в некоторых зернах возникают объемные напряжения, которые достигают значения ${{{{\sigma }}}_{0}} = \pm 0.67{{t}_{{12}}}$ от касательных напряжений ${{t}_{{12}}} = {{{{\sigma }}}_{{12}}}$. Этот эффект значительно меньше для материалов с небольшим коэффициентом анизотропии. В частности, для алюминия [20]: $A = 1.215$, ${{C}_{{11}}} = 10.82$ × 10⁴, ${{C}_{{12}}} = 6.13$ × 10⁴, ${{C}_{{44}}} = 2.85$ × 10⁴ MPa, на основе (2.31), (2.32) установим следующее неравенство

Сравнивая (2.35) с (2.36) обнаружим, что флуктуации объемных напряжений в поликристаллах из алюминия в 5.82 раза меньше чем в поликристаллах из меди.

3. Определяющие уравнения модели при необратимом деформировании. Большинство теорий применяемых для описания поведения поликристаллических материалов в необратимой области деформирования базируются на допущении об упругой изотропии кристаллов. Согласно принятому определению, подэлемент отождествляется не с кристаллом, а со множеством материальных частиц внутри представительного объема, имеющих одинаковый тензор необратимой деформации. В силу того, что частицы одного и того же подэлемента могут иметь различные ориентации и положения в пространстве конгломерата, возникает состояние, по характеру подобное макросостоянию в квазиизотропном теле. Акты деформации в отдельных частицах подэлемента навязаны им механическим состоянием в представительном объеме и вследствие этого происходит частичная потеря индивидуальности данной материальной частицы. Подобная схема разделения макро- и микрообластей согласуется с принципом соответствия и положения термодинамики необратимых процессов согласно которой существует локальная энтропия с такой же функциональной зависимостью от термодинамических параметров, как у глобальной энтропии. Из данного определения понятия подэлемента следуют более комплексные взаимодействия материальных частиц в представительном объеме, чем взаимодействие включения с матрицей. Допущение об упругой изотропии подэлемента не столь грубо как допущение об упругой изотропии кристалла. При нагружении в необратимой области компоненты девиаторов тензоров деформаций подэлементов ${{{{\bar {\varepsilon }}}}_{{ij}}}$ и элементa тела ${{{{\varepsilon }}}_{{ij}}}$ представляются в виде суммы обратимых ${{\bar {e}}_{{ij}}},{{e}_{{ij}}}$ и необратимых компонент – ${{\bar {p}}_{{ij}}},{{p}_{{ij}}}$

Хотя в опытах можно измерять только общую деформацию, ее разделение на две составляющие не противоречит постулату макроскопической определенности А.А. Ильюшина [21] и концепции построения теории, на величинах, поддающихся наблюдению. В работе [14] показано, что в построенной на основе модели системе макроскопических уравнений фигурирует только общая деформация. При этом, в [8–10, 14–16] устанавливается локальная связь не между напряжениями и необратимыми деформациями, а между упругими и необратимыми деформациями. Согласно закону центрального приращения предложенного в [16], предельные упругие деформации подэлементов можно представить в виде суммы двух независимых частей

Здесь ${{{{\bar {\tau }}}}_{{ij}}}$ – компоненты девиатора предельных упругих деформаций подэлементов в структурно стабильном состоянии; ${{\bar {s}}_{{ij}}}$ – приращение компонент девиатора предельных упругих деформаций подэлементов в результате изменения структуры при необратимом деформировании. Величины ${{{{\bar {\tau }}}}_{{ij}}}$ отражают термовязкопластические свойства подэлемента без учета изменения структуры материала, а ${{\bar {s}}_{{ij}}}$ – в результате ее изменения.

Переход подэлементов в отожженном состоянии материала $\left( {{{{\bar {s}}}_{{ij}}} = 0} \right)$ из обратимого состояния в необратимое, определяется критерием: ${{\bar {e}}_{{ij}}}{{\bar {e}}_{{ij}}} - {{{{\tau }}}^{2}} = 0,$ ${{{{\tau }}}^{2}} = {{{{\tau }}}_{{ij}}}{{{{\tau }}}_{{ij}}}$, откуда видно, что ${{\tau }}$ является исходным пределом упругости подэлемента, который предполагается зависящим от температуры $T$ и осредненной скорости необратимых деформаций γ

где точкой сверху обозначена производная по времени необратимой деформации, ${{\psi }}_{{}}^{'}$ – текущий вес необратимо деформируемых подэлементов. Тогда

Согласно принципам соответствия, осредненных связей и условию единственности решения задачи представления реального материала в модели, локальные пределы упругости предполагаются зависящими не от локальных значений параметров состояния, а от осредненных. Здесь в качестве параметра, определяющего принадлежность предела текучести к определенному подэлементу, выбирается вес подэлементов в момент его перехода из обратимого состояния в необратимое при первоначальном нагружении.

Упрочнение ${{\bar {s}}_{{ij}}}$ подэлемента складывается из изотропной части $\bar {s}$ и кинематического упрочнения ${{\bar {r}}_{{ij}}}$

где ${{a}_{0}}$ – коэффициент изотропного упрочнения, ${{a}_{r}}$ – кинематическое упрочнение.

Как отмечалось, подэлементы в конгломерате деформируются согласованным образом. Явление самосогласования при сложном нагружении представляется в виде двух соотношений [22]:

– условия работы подэлементов за пределами упругости (условие текучести)

– закона об общей направленности процессов необратимого течения в подэлементах:

Необходимость видоизменения условия текучести и формулировка закона об общей направленности процессов необратимого течения в подэлементах, связаны с результатами опытов на циклическое нагружение по криволинейным траекториям деформирования. В работе [23] установлено, что упрочнение при циклическом сложном нагружении больше (а не меньше, как предсказывают модели основанные на концепции поверхности текучести), чем по прямолинейным траекториям [23]. Оказалось, что для описания эффекта более интенсивного упрочнения по криволинейным траекториям деформирования, чем по прямолинейным не требуется проведения опытов при сложном нагружении, достаточно видоизменить условие текучести и учитывать эффект направленности процессов необратимого течения в подэлементах.

В рамках допущения об упругой изотропии подэлементов, уравнения связей (1.6) для однофазных поликристаллов можно представить в виде

Идентификация модели проводится на основе опытов при пропорциональном нагружении

При этом виде нагружения, уравнения связей микро- и макросостояний (3.5) приводятся к одному скалярному уравнению

На участке линейного упрочнения, для подэлементов работающих за пределами упругости ${{\tau }} \leqslant \bar {e}$ имеем

При записи (3.7) предполагалось, что в процессе необратимого деформирования имеют место два типа упрочнения подэлементов: индивидуальное – $a\bar {p}$ и скрытое – ${{a}_{0}}p$, одинаковое для всего множества подэлементов. В подэлементах с ${{\tau }} > \bar {e} - {{a}_{0}}p$, $\bar {p} = 0$ и из (3.6), (3.7) определим значение предела текучести $\tau _{{}}^{'}$ в граничащем подэлементе

На основе (3.6)–(3.8) получим следующие формулы для модулей обратимых и необратимых деформаций

Отметим, что в многоэлементных моделях осреднение производится не по объему, а по множеству реализаций, т.е. считается правомерным пользование эргодической гипотезой.

Принимая $\tau $ за единственный случайный параметр задачи, в этом случае имеем

где ${{\psi }}\left( {{\tau }} \right)$ – интегральная функция распределения начальных предельных упругих деформаций, τ_max, ${{{{\tau }}}_{0}}$ – наибольший и наименьший пределы упругости подэлементов.

Подставляя (3.9) в (3.10) и интегрируя полученное выражение по параметру разброса τ, найдем

Задача представления реального материала в модели решена в работах [14, 16]. Основные результаты (в предположении $m = {\text{const}}$) сводятся к установлению следующих зависимостей

Здесь ${{\psi }}_{{}}^{'}$ – текущий вес необратимо деформированных подэлементов; ${{{{\tau }}}_{0}}({{\gamma }},T)$ – микроскопический предел упругости (совпадает с минимальным пределом упругости в системе подэлементов). Функция $F = F({{\sigma /}}2G,{{\gamma }},T)$ определяется на основе диаграмм деформирования ${{\varepsilon }} = F({{\sigma /}}2G,{{\gamma }},T) + {{\sigma /}}2G$ материала, полученных при различных постоянных значениях параметров состояния ${{\gamma }},T$. Оказалось, что в опытах на пропорциональное нагружение трубчатых образцов растягивающей силой и внутренним давлением при различных фиксированных значениях температуры и скорости продольной деформации (перемещения захвата) ${{\dot {d}}_{{zz}}} = {\text{const}}$, осредненная скорость необратимой деформации (3.3) не меняется в процессе нагружения –${{\gamma }} = {\text{const}}$. При этом ориентация прямолинейной траектории нагружения в координатах осевого ${{t}_{{zz}}}$ и окружного ${{t}_{{\varphi \varphi }}}$ напряжений и значение параметра состояния $\gamma $ определяются выражениями:

где K – объемный модуль упругости, ${{\chi }} = a/(1 + a)$, a – коэффициент индивидуального упрочнения подэлементов (на стадии множественного скольжения $a\sim 0.002$).

Следовательно, для определения ориентации траектории нагружения в пространстве осевых и окружных напряжений и значения осредненной скорости необратимых деформаций подэлементов, достаточно знать объемный модуль упругости K, модуль сдвига G, коэффициент индивидуального упрочнения подэлементов a и параметра кинематической схемы взаимодействия между подэлементами B (соотношения (1.6), (3.5)).

Параметр $B$ определяется на основе принципа экстремума несоответствия мер (1.7), который с учетом (3.5) принимает вид

Если предположить, что в процессе необратимого деформирования параметр $m = {\text{const}}$, то из (3.16) с учетом (3.9) получим соотношение

Из условия экстремума (3.17) следует формула полученная в [8]

Согласно (2.6) и (2.7) для изотропных кристаллов ($A = 1$) в упругую область деформирования $b = B{\text{/}}2G = 1$. Так как коэффициент ${{\chi }} \leqslant 1$, то из (3.18) следует что в необратимой области деформирования параметр $b < 1$. Таким образом в предельном случае ${{\chi }} = 1$ результаты, полученные на основе формул (2.6), (2.7) и (3.18) совпадают. Хотя многие многоэлементные модели базируются на уравнении связи $b = \infty $ (однородное деформированное состояние) из приведенных результатов вытекает, что вариант b = 1 соответствует верхней оценке изменения параметра $b$ и при учете упругой анизотропии. В случае поликристаллов с кубической решеткой из (2.6), (2.7) следует $b = B{\text{/}}2G = (2A + 3){\text{/}}(3A + 2) \leqslant 1$ при любом значении коэффициента анизотропии $A \geqslant 1$.

Найденные параметры $B,m$ и функция $F(e,{{\gamma }},T)$ полностью характеризуют поведение модели на линейном участке упрочнения подэлементов. На основе (3.14) и (3.18) описываются термовязкоупругопластические процессы деформирования элемента тела если задана история изменения напряжений и температур. Перейдя в (3.14) от упругой деформации к напряжению σ, после несложных преобразований получим

Следовательно, если законы изменения модуля девиатора тензора напряжений и температуры известны, то интегрируя нелинейное дифференциальное уравнение первого порядка (3.19) при указанном начальном условии, найдем историю изменения параметра состояния ${{\gamma }} = {{\gamma }}(t)$. Затем по формуле

определим модуль девиатора тензора деформации ${{\varepsilon }} = {{\varepsilon }}(t)$, а из равенства ${{{{\varepsilon }}}_{{ij}}} = {{\sigma }}{}_{{ij}}{{\varepsilon /\sigma }}$ – его компоненты. Соотношения (3.19), (3.20) описывают процессы необратимого деформирования, когда внешнее воздействие приводит к активному нагружению во всем подмножестве необратимо деформированных подэлементов. Это условие выполняется, когда [14] если пределы упругости подэлементов растут в данном процессе, и когда уменьшаются. Когда в данном процессе влиянием реологических эффектов можно пренебречь эти неравенства определяют условия неизотермического нагружения по термомеханической поверхности – ${{\varepsilon }} = {{\sigma /}}2G + F\left( {{{\sigma /}}2G,T} \right)$, полученные при различных постоянных температурах. Определяющие уравнения для более сложных условий внешнего воздействия приводятся в [14].

В методологическом плане важно обратить внимание на следующий аспект. Из (3.19) следует, что осредненная скорость необратимой деформации (3.3) в момент наступления микротекучести пропорциональна обшей скорости деформации ${{\dot {\varepsilon }}} = \dot {e}$. Коэффициент пропорциональности $P = 1{\text{/}}(a + m)$ зависит от параметра взаимодействия между подэлементами $m$ и коэффициента упрочнения $a$. Согласно (3.6) для всех возможных схем взаимодействия между подэлементами $0 \leqslant m \leqslant 1$, поэтому коэффициент P изменяется в пределах $1{\text{/}}(a + 1) \leqslant P \leqslant 1{\text{/}}a$. Следовательно, значение P найденное на основе принципа экстремума несоответствия мер (3.18) соответствует среднему геометрическому значению предельных вариантов. Подобное следствие принципа обнаруживали и при определении макроскопических констант упругости (формула (2.7)).

Хотя соотношение (1.5) было установлено еще в работе [9] детальный анализ закономерностей изменения объемных напряжений и деформаций не проводился. Исследования ограничивались изучением определяющих уравнений без учета процессов связанных с разрушением. При переходе к вопросам связанных с разрушением постулат об ортогональности тензоров флуктуаций напряжений и деформаций играет важнейшую роль. Рассмотрим выражение (1.5) для однофазных поликристаллов

где через ${{\bar {p}}_{0}},{{p}_{0}}$ обозначены необратимые изменения объемов в подэлементах и элементе тела соответственно. В первом приближении примем что необратимое изменение объема в данном подэлементе пропорционально длине траектории необратимой деформации ${{\bar {p}}_{0}} = {{k}_{0}}{{\bar {\lambda }}},$ $d{{\bar {\lambda }}} = \sqrt {d{{{\bar {p}}}_{{ij}}}d{{{\bar {p}}}_{{ij}}}} $, k₀ – коэффициент, характеризующий влияние дефектов структуры, возникающих в процессе необратимого деформирования, на необратимое изменение объема, одинаковый для всех подэлементов [24]. При пропорциональном нагружении

Подставляя эти значения в (3.21) и учитывая в полученном равенстве соотношение (3.6), найдем

Из (3.22) следуют два допустимых с физической точки зрения решения

где ν – коэффициент Пуассона. Выбор знака в (3.24) имеет принципиальное значение. При знаке “+” подэлементы с малыми значениями пределов текучести необратимо деформируются в условиях действия высоких растягивающих объемных напряжений, а подэлементы с большими значениями пределов текучести подвергаются действиям сжимающих объемных напряжений. При отрицательном знаке в (3.24) наблюдается обратная картина.

Отметим, что постулат об ортогональности тензоров флуктуаций напряжений и деформаций (1.5) соответствует условию равенства как механической работы системы подэлементов и элемента тела

так и дополнительных работ

Согласно (3.25) макроскопическая работа деформирования представительного объема равна сумме работ деформирования подэлементов, а из (3.26) следует – макроскопическая дополнительная работа равна сумме дополнительных работ подэлементов. Если считать, что упрочнение вызывается внутренними упругими силами, сопротивляющимися необратимой деформации, тогда согласно [9], дополнительная работа представляет ту часть работы деформирования, которая не рассеивается в виде тепла. В этом случае и некомпенсированное тепло Q не зависит от характеристик уравнений связи макро- и микросостояний

Если $L,Q$ выражаются непосредственно через макроскопические тензоры напряжений и деформаций, тогда на основе первого и второго законов термодинамики

установим, что и другие термодинамические функции системы подэлементов (свободную энергию $F = U - TS$ или энтальпию $H = U - t{}_{{ij}}d{}_{{ij}}$) можно выразить через макроскопические величины: ${{t}_{{ij}}},{{d}_{{ij}}},T$. Здесь U – плотности внутренней энергии, $S$ – энтропии элемента тела, $Q_{{}}^{'}$ – внешний приток тепла, T – температура. Таким образом в рассматриваемом подходе осредненные микроскопические меры фундаментальных термодинамических величин совпадают с макроскопическими мерами. Тем самым обеспечивается выполнение постулата: энтропия S – аддитивная функция множеств.

4. Численное термодинамическое сопоставление многоэлементных моделей основанных на линейных и нелинейных уравнениях связи. Рассмотрим в качестве примера гипотетический поликристаллический материал, для которого интегральная функция распределения пределов упругости задается выражением

Подставляя (4.1) с учетом (3.9) в (3.10), получим взаимосвязь ${{\sigma }}\sim p$ в следующем параметрическом виде

Для осредненных значений энергий изменения формы и объема получены зависимости

При записи (4.6) не учитывалось неупругое изменение объема. Работу деформирования представительного объема определим на основе равенства

Учитывая, что зависимость σ ~ p задана в параметрическом виде – (4.4), (4.3), величину $dp$ на основе (4.3) выразим через $d{{\tau }}_{{}}^{'}$. В результате получим

Для $L({{\tau }}_{{}}^{'},m)$ должно выполняться следующее соотношение

Рассмотрим выполнимость условия равенства работ системы подэлементов и элемента тела (4.8), для линейных и нелинейных уравнений связи локальных и макроскопических состояний. Численные исследования проведем при чистом макроскопическом сдвиге для материала со следующими механическими характеристиками: $\Theta = 1000$, ${{{{\tau }}}_{0}} = 0.0006$, $G = 8.11$ × 10⁴, $K = {{{{\sigma }}}_{0}}{\text{/}}{{{{\varepsilon }}}_{0}} = 4.69$ × 10⁵ MPа, $a = 0.001$. Проанализируем соотношение

Величины ${{\delta }}({{\tau }}_{{}}^{'},m,c)$ для линейных уравнений связи обозначим через ${{\delta }}({{\tau }}_{{}}^{'}) = {{\delta }}({{\tau }}_{{}}^{'},0)$ и ${{\delta }}_{{}}^{'}({{\tau }}_{{}}^{'}) = {{\delta }}({{\tau }}_{{}}^{'},1)$; для нелинейных уравнений ${{\delta }}({{\tau }}_{{}}^{'},c) = 0$. Отметим, что в случае линейных уравнений связи: ${{{{\bar {\sigma }}}}_{0}} = {{{{\sigma }}}_{0}},{{{{\bar {\varepsilon }}}}_{0}} = {{{{\varepsilon }}}_{0}}$, осредненная энергия изменения объема вычисляется по формуле

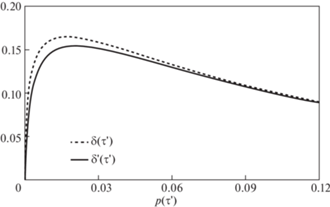
Результаты расчетов ${{\delta }}({{\tau }}_{{}}^{'})$ и ${{\delta }}_{{}}^{'}({{\tau }}_{{}}^{'})$ для двух видов напряженных состояний 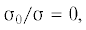1 представлены на рис. 2. Из представленных на рис. 2 диаграмм видно, что ${{\delta }}({{\tau }}_{{}}^{'},c)$, принимает наибольшее отклонение при чистом сдвиге. При этом, более детальные численные исследования показывают, что наибольшее отклонение увеличивается с уменьшением числовых значений параметров – ${{{{\tau }}}_{0}},\Theta $. Для принятых значений механических характеристик материала $\max {{\delta }}({{\tau }}_{{}}^{'},0) = 0.164$ при необратимой деформации $p({{\tau }}_{{}}^{'},m,k,a)\sim p({{\tau }}_{{}}^{'}) = 0.016$. Следовательно, для моделей, основанных на линейных уравнениях, обнаруживаются существенные отклонения от условия равенства механических работ системы подэлементов и элемента тела.

Важной энергетической характеристикой при деформации металлов является скрытая энергия, которая остается в материале после разгрузки. Скрытая энергия ${{U}_{l}}$ связана с микронапряжениями и дефектами кристаллической решетки (дислокациями, вакансиями, границами двойников и др.), возникающими в процессе необратимого деформирования. Если предполагать, что затраченная энергия на упрочнение подэлементов не рассеивается, тогда из модели следует: скрытая энергия деформирования равна дополнительной работе (3.19) с вычетом потенциальной энергии, возвращаемая при разгрузке

Учитывая (4.3), (4.4) в (4.10) при допущении об упругом изменении объема (${{p}_{0}} = 0$) получим

В рамках этого предположения рассеянная часть энергии деформирования вычисляется на основе выражения (3.20), которое при упругом изменении объема может быть представлено в виде

Формулы для расчета скрытой (4.11) и рассеянной части (4.12) энергий деформирования следует рассматривать как предельные (наибольшее и наименьшие значения соответственно), так как они базируются на допущении, что упрочнение есть эффект обратимый, т.е. дополнительная работа подэлемента $\int {\bar {p}d{{\bar {\sigma }}}} $ не рассеивается в процессе упрочнения (модель упрочнения А.Ю. Ишлинского). Вероятно, часть дополнительной работы каждого подэлемента – $(1 - r)\int {\bar {p}d{{\bar {\sigma }}}} $ $(0 \leqslant r \leqslant 1)$ рассеивается в процессе упрочнения. Исходя из подобного предположения, в выражение (4.12) следует добавить слагаемое $(1 - r)\int {\bar {p}d{{\bar {\sigma }}}} $ (в линейном приближении – $d{{\bar {\sigma }}} = ad\bar {p}$). Тогда с учетом (3.9) формулы для скрытой (4.11) и рассеянной (4.12) энергий деформирования примут вид

На рис. 3 представлены результаты численных исследований зависимости $u({{\tau }}_{{}}^{'},r)$ ~ ~ p(τ'),

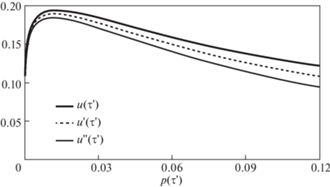
при чистом макроскопическом сдвиге. Расчеты проводились при следующих значениях механических характеристик: $\Theta = 1000$, ${{{{\tau }}}_{0}} = 0.0006$, $G = 8.11$ × 10⁴ МPа, $a = 0.001$, для трех значений коэффициента $r = 1,0.5,0$; параметр $m$ определялся по формуле (3.27). На рис. 3 приняты обозначения: $u(\tau _{{}}^{'}) = u({{\tau }}_{{}}^{'},1)$, $u_{{}}^{'}({{\tau }}_{{}}^{'}) = u({{\tau }}_{{}}^{'},0.5)$, $u_{{}}^{{''}}({{\tau '}})$ = u(τ', 0). Из представленных на рис. 3 диаграмм видно, что значение коэффициента r оказывает существенное влияние на величину скрытой энергии деформирования. С ростом необратимой деформаци разность между предельными значениями ${{\delta }}u({{\tau }}_{{}}^{'}) = u({{\tau }}_{{}}^{'},1) - u({{\tau }}_{{}}^{'},0)$ увеличивается.

5. Критерий разрушения. Из опыта известно, что способность материала к необратимой деформации существенно зависит от условий нагружения, определяемых видом напряженного состояния, температурой, скоростью деформирования и другими факторами. Наступление предельного состояния обусловлено способностью материала оказывать сопротивление касательным и нормальным напряжениям и, следовательно, определяется двумя причинами: возникновением трещин (некоторой функцией модуля девиатора тензора напряжений) и их распространением (максимальным нормальным растягивающим напряжением). Теория максимальных нормальных напряжений, ведущая свое начало от Г. Галилея, формально была обоснована в работах Г. Ламе, А. Клебша, а позднее В. Ренкина, но из-за слабой согласованности с опытом не получила широкого распространения. Однако картина существенно меняется при ее применении в рамках исследуемой модели. Из модели вытекает что в системе подэлементов, даже при чистом макроскопическом сжатии, существуют подэлементы, в которых главное нормальное напряжение ${{\bar {t}}_{1}}$ не просто положительно ${{\bar {t}}_{1}} > 0$, но по абсолютному значению больше действующего макроскопического напряжения. Более того, в части подэлементов меняется знак напряжения ${{\bar {t}}_{1}}$ в условиях монотонного внешнего воздействия, т. е. наблюдается циклическое нагружение.

Рассмотрим общее выражение для объемной деформации подэлемента. Соотношение (3.23) с учетом (3.24) и обозначения (4.6) и предположения об упругом изменении объема при пропорциональном нагружении (${{{{\sigma }}}_{0}} = c{{\sigma }}({{\tau }}_{{}}^{'})$) можно представить в виде

С учетом (3.6) флуктуации объемных напряжений можно выразить и через флуктуации необратимых деформаций

Из (5.2) следует, что объемное напряжение в упруго деформированных подэлементах линейно зависят от макроскопической необратимой деформации $p = p({{\tau }}_{{}}^{'})$. Коэффициент пропорциональности $\sqrt {2KGm(1 - m){\text{/}}3} $ аннулируется в предельных вариантах m = 1 (однородное деформированное состояние), m = 0 (однородное напряженное состояние) и принимает наибольшее значение при m = 0.5. Как следует из соотношений (2.6), (2.7) и (3.18) значение m = 0.5 соответствует чисто упругому поведению изотропного тела. Если параметр m определяется по формуле (3.18), тогда коэффициент пропорциональности в (5.2) примерно в три раза меньше, чем возможное максимальное значение.

Для упрощения записей аргументы, которые не меняются в процессе нагружения, не будут указаны. Тогда, зависимость (4.4) –${{\sigma }} = {{\sigma }}({{\tau }}_{{}}^{'},m,\Theta ,a)$ можно представить в виде функции одной переменной ${{\sigma }} = {{\sigma }}({{\tau '}})$. Модули девиаторов напряжений подэлементов определяются на основе формулы (3.9). Главные значения ${{{{\bar {\sigma }}}}_{1}}$ в подэлеметах можно выразить через модули ${{\bar {\sigma }}}$ и параметром k

Отметим, что виды девиаторов в подэлементах и элементе тела совпадают, поэтому параметр $k$ принимает одинаковые значения для всего множества подэлементов и выражается через макроскопические величины. На основе (5.1)–(5.3) составим общее выражение для максимальных нормальных напряжений ${{\bar {t}}_{1}}$ в системе подэлементов

С помощью простой формулы (5.4) удается описать сложную картину изменений главных напряжений ${{\bar {t}}_{1}}$ в системе подэлементов при произвольном напряженном состоянии (пропорциональное нагружение), характеризуемом параметрами $k = {{{{\sigma }}}_{3}}{\text{/}}{{{{\sigma }}}_{1}}$ и 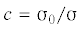. Проанализируем закономерность изменения максимального напряжения ${{\bar {t}}_{1}}$ в системе подэлементов при макроскопическом растяжении и сжатии. При растяжении $c = 1{\text{/}}\sqrt 6 $, $k = - 0.5$ формула (5.4) принимает вид

а при сжатии: $c = - 1{\text{/}}\sqrt 6 $, $k = - 2$

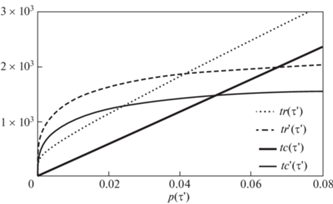
На основе (5.5), (5.6) проводились детальные численные исследования закономерностей изменения главных напряжений ${{\bar {t}}_{1}}$ вомножестве подэлементов в зависимости от величины накопленной необратимой деформации при растяжении и сжатии. Расчеты проводились для двух корней уравнения (3.22). В качестве примера на рис. 4 приведены предельные диаграммы изменения ${{\bar {t}}_{1}}$ при одноосном растяжении и сжатии. Сплошные диаграммы соответствуют опыту на растяжение, а прерывистые кривые – на сжатие. При M > 0 наибольшее значение ${{\bar {t}}_{1}}$ возникает в граничащем подэлементе ${{\tau }} = {{\tau }}_{{}}^{'}$ (разделяющий текущую зону необратимо деформированных подэлементов от обратимой зоны). Если в качестве решения уравнения (3.22) принимается отрицательный корень M < 0, тогда из анализа модели следует, что наибольшее значение ${{\bar {t}}_{1}}$ возникает в подэлементе с наименьшим пределом упругости ${{\tau }} = {{{{\tau }}}_{0}}$. Для сокращения надписей на рис. 4 приняты обозначения: 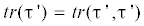, $tr'({{\tau }}') = tr'({{\tau }}'{\text{,}}{{{{\tau }}}_{0}})$, 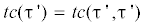, $tc'({{\tau }}') = tc'({{\tau }}'{\text{,}}{{{{\tau }}}_{0}})$. Данные свойства проявляются при любом виде напряженного состояния. Из представленных на рис. 4 диаграмм видно, что в случае когда M < 0 $\max {{\bar {t}}_{1}}$ возрастает с увеличением степени деформации вначале интенсивно, а затем замедляется, стремясь к насыщению. В подэлементах с ${{\tau }} > {{{{\tau }}}_{0}}$ напряжение ${{\bar {t}}_{1}}$ уменьшается до момента наступления текучести, а затем растет. В случае M > 0, ${{\tau }} = {{\tau }}_{{}}^{'}$ из (5.6) и (3.6) следует линейная зависимость $\max \bar {t}$ ~ p. В каждом подэлементе наибольшее нормальное напряжение возникает в момент наступления текучести, затем наблюдается уменьшение $\max {{\bar {t}}_{1}}$ с ростом необратимой деформации. Таким образом, в момент наступления текучести напряжение ${{\bar {t}}_{1}}$ в подэлементе принимает наименьшее значение если M < 0 и наибольшее при M > 0. В этом заключаются качественные различия взаимодействия между подэлементами с M < 0 от взаимодействия с M > 0. Если в качестве локального критерия прочности принимается критерий наибольшего нормального напряжения, при M > 0 опасность разрушения подэлемента минуется после его перехода из обратимого в необратимое состояние. В этом варианте разрушение в подэлементах происходит до наступления текучести. Если предполагать, что пределы прочности одинаковы для всего множества подэлементов, тогда предельное состояние достигается не в одном подэлементе, а в конечном числе подэлементов, вес которых определяется из (4.1). В этом случае, в зависимости от значения $\tau '$, при котором достигается предельное состояние, в обратимо деформированных подэлементах возможно как внезапное разрушение, так и различные варианты смешанного хрупкого и пластического разрушения. Другая картина наблюдается при ${\rm M} < 0$. Напряжение ${{\bar {t}}_{1}}$ в подэлементе увеличивается с ростом необратимой деформации. Причем наибольшее значение напряжения ${{\bar {t}}_{1}}$ всегда возникает в подэлементе с наименьшим пределом текучести. При ${\rm M} < 0$ разрушение развивается во времени как процесс последовательного разрушения подэлементов (с бесконечно малым весом), накопления веса разрушенных подэлементов (накопления микротрещин), слияния микротрещин, который завершается образованием макротрещины.

Таким образом факт существования двух физически правомерных корней решения уравнения ортогональности тензоров флуктуаций напряжений и деформаций (3.22) значительно расширяет возможности модели. При этом большое многообразие эффектов необратимого деформирования и разрушения удается с единых позиций описать даже при ограничении: предел прочности одинаков для всего множества подэлементов. Более реалистичен подход, в котором предполагается, что предельные значения ${{\bar {t}}_{1}}$ в подэлементах зависят от пределов текучести. В линейном приближении условие прочности можно представить в виде

где $c$ и $n$ константы одинаковые для всех подэлементов.

Отметим, что широкое многообразие эффектов и явлений поведения реальных материалов наблюдаемых в области необратимых деформаций и разрушения описывается с помощью минимального количества механических характеристик: коэффициента упрочнения a, микроскопического пределом текучести ${{{{\tau }}}_{0}} = {{{{\tau }}}_{0}}({{\gamma }},T)$, параметром интегральной функции распределения предела текучести $\Theta = \Theta ({{\gamma }},T)$, и двух констант c, n, фигурирующих в критерии прочности подэлементов (5.7). Все эти характеристики могут быть расшифрованы на основе диаграмм деформирования, полученных в опытах на пропорциональное нагружение трубчатых образцов растягивающей силой и внутренним давлением при различных фиксированных значениях температуры и скорости продольной деформации (перемещения захвата) ${{\dot {d}}_{{zz}}} = {\text{const}}$. В этих опытах осредненная скорость необратимой деформации (3.3) не меняется в процессе нагружения –${{\gamma }} = {\text{const}}$. При этом ориентация прямолинейной траектории нагружения в координатах осевого ${{t}_{{zz}}}$ и окружного ${{t}_{{\varphi \varphi }}}$ напряжений и значение параметр состояния ${{\gamma }}$ определяются выражениями (3.15). Если влияние реологических эффектов в исследуемом процессе можно пренебречь, тогда неизвестные параметры можно найти на основе изотермических диаграмм деформирования в опытах на растяжение или сжатие.

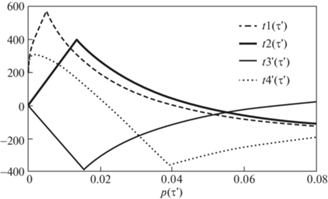
Следует обратить внимание на очень важный эффект, который не охвачен в рамках других теорий: циклическое нагружение происходящее в части подэлементов при монотонном растяжении или сжатии. Данный эффект вытекает из анализа (5.5), (5.6). На рис. 5 представлены диаграммы изменения ${{\bar {t}}_{1}}$ $\sim p$ при растяжении (прерывистые кривые) и сжатия (сплошные кривые) для четырех подэлементов. Диаграммы изменения ${{\bar {t}}_{1}}$ при растяжении обозначены через $t1({{\tau }}') = tr({{\tau }}'{\text{,}}{{{{\tau }}}_{1}})$ при ${\rm M} > 0$ и через $t4({{\tau }}') = tr'({{\tau }}'{\text{,}}{{{{\tau }}}_{4}})$ при ${\rm M} < 0$ (${{{{\tau }}}_{1}} = 2.2{{{{\tau }}}_{0}}$, ${{{{\tau }}}_{4}} = 4{{{{\tau }}}_{0}}$) а при сжатии – через $t2({{\tau }}') = tc({{\tau }}'{\text{,}}{{{{\tau }}}_{2}})$ для ${\rm M} > 0$; $t3({{\tau }}') = tc'({{\tau }}'{\text{,}}{{{{\tau }}}_{3}})$ – ${\rm M} < 0$ (${{{{\tau }}}_{2}} = 2.8{{{{\tau }}}_{0}}$, ${{{{\tau }}}_{3}} = 2.9{{{{\tau }}}_{0}}$). На основе представленных на рис. 5 диаграмм нагружения можно оценить степень сложности взаимодействий подэлементов в представительном объеме. При этом глубина проникновения в эту сложную картину взаимодействий идет рядом с простотой принципов необходимых для их описания

Согласно рис.4 на начальном этапе наступления текучести наблюдается более быстрый рост $\max {{\bar {t}}_{1}}$ при ${\rm M} < 0$ чем в случае ${\rm M} > 0$. Однако с ростом необратимой деформации наблюдается обратная картина изменения $\max {{\bar {t}}_{1}}$. Смена преобладания $\max {{\bar {t}}_{1}}$ от подэлемента ${{\tau }} = {{{{\tau }}}_{0}}$ к подэлементу ${{\tau }} = {{\tau }}_{{}}^{'}$ порождает важные следствия. На рис.6 представлены диаграммы деформирования при растяжении и сжатии для материала со следующими механическими характеристиками: $k = 1000$, ${{{{\tau }}}_{0}} = 0.001$, G = = 8.11 × 10⁴, $K = {{\sigma }_{0}}{\text{/}}{{\varepsilon }_{0}} = 4.69$ × 10⁵ MPa, $a = 0.001$. Диаграммы построены в координатах $t = {{t}_{{zz}}}$ и $d = {{d}_{{zz}}}$

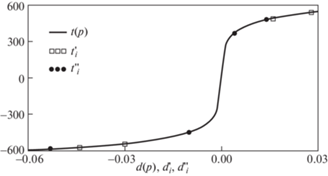
Точками на рис. 6 отмечены состояния для двух значений $\max {{\bar {t}}_{1}}$ = 1000 и 1500 МPа. Квадратиками отмечены состояния, соответствующие корню ${\rm M} > 0$ $(t_{i}^{'},d_{i}^{'})$, а кружочками – корню ${\rm M} < 0$ $(t_{i}^{{''}},d_{i}^{{''}})$, как при растяжении так и сжатии. В обоих вариантах (${\rm M} > 0$ и ${\rm M} < 0$) смещение точки определяющей состояние с заданным значением $\max {{\bar {t}}_{1}}$ (увеличивается с ростом p), от начала координат, больше при сжатии чем при растяжении. Однако наблюдаются существенные различия. В случае ${\rm M} < 0$ заданное значение $\max {{\bar {t}}_{1}}$ при растяжении достигается раньше, чем в случае ${\rm M} > 0$. Подобная закономерность отсутствует в опытах на сжатие. Из рис. 6 видно, что состояние $\max {{\bar {t}}_{1}} = 1000$ достигается раньше, как при растяжении, так и сжатии, чем в случае ${\rm M} < 0$. Другая картина наблюдается при $\max {{\bar {t}}_{1}} = 1500$. При растяжении состояние $\max {{\bar {t}}_{1}} = 1500$ достигается раньше если ${\rm M} < 0$ и позже при сжатии, чем в случае ${\rm M} > 0$. Если модуль девиатора необратимых деформаций достигает значения $p\sim 0.2$, то $\max {{\bar {t}}_{1}}\sim 6000$ МPа. Установленные закономерности показывают, что вариант ${\rm M} < 0$ характеризует вязкое разрушение, а вариант ${\rm M} > 0$ – смешаный тип разрушения. В зависимости от значений пределов упругости материальных частиц один и тот же металл может быть хрупким или пластичным. Из опыта известно, что хрупкое разрушение возникнет в случае резкого увеличения предела упругости при понижении температуры (в этом же направлении действует и увеличение скорости нагружения). При этом, для резкого изменения пластичности не требуется заметных изменений каких-либо иных физических свойств материала.

Заключение. Показано, что крайние относительные значения модулей девиаторов тензоров напряжений и деформаций во множестве зерен, входящих в представительном объеме поликристалла с кубической решеткой, инварианты относительно внешних условий обратимого воздействия и зависят только от фактора анизотропии кристалла.

Установлено: вид девиатора тензора напряженний/деформаций в кристаллах с экстремальными значениями модулей девиаторов тензоров напряжений/деформаций совпадает с макроскопическим видом девиатора напряженний/деформаций.

Исследованы закономерности изменения объемных напряжений в представительном элементе поликристалла. Установлены пределы изменения флуктуаций объемных напряжений и деформаций в поликристаллах с кубической решеткой.

Исследованы общие закономерности изменения предельных значений модулей девиаторов тензоров напряжений и объемных напряжений в системе подэлементов в необратимую область деформирования.

Получена формула для расчета наибольшего нормального напряжения возникающего в системе подэлементов при произвольном виде напряженного состояния на макроскопическом уровне. Проанализированы количественные и качественные различия закономерностей изменения наибольшего нормального напряжения для двух, физически допустимых, корней уравнения ортогональности флуктуации тензоров напряжений и деформаций.

Проведены детальные численные исследования закономерностей изменения растягивающих напряжений во множестве подэлементов в зависимости от величины накопленной необратимой деформации. Установлено, что в зависимости от знака корня возможны два варианта: наибольшее растягивающее напряжение возникает в граничащем подэлементе, разделяющем текущую зону необратимо деформированных подэлементов от обратимой зоны (${\rm M} > 0$) или в подэлементе с наименьшим пределом упругости (${\rm M} < 0$). Показано, что в случае ${\rm M} > 0$ в каждом подэлементе наибольшее нормальное напряжение возникает в момент наступления текучести, затем наблюдается уменьшение с ростом необратимой деформации. В данном варианте опасность разрушения подэлемента уменьшается после наступления текучести. В зависимости от прочностных характеристик подэлементов при ${\rm M} > 0$ возможны все варианты разрушения. Если ${\rm M} < 0$ возможно только вязкое разрушение.

Установлен эффект циклического изменения наибольшего нормального напряжения в части подэлементов при монотонном макроскопическом нагружении. При этом смена знака нормального напряжения в подэлементе в процессе монотонного внешнего воздействия обнаруживается для обоих вариантов корня уравнения ортогональности.