Известия РАН. Механика жидкости и газа, 2023, № 3, стр. 94-102
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ВЛИЯНИЯ ПОРИСТЫХ ЭЛЕМЕНТОВ КРЫЛА НА СВОЙСТВА СВЕРХЗВУКОВЫХ КОНЦЕВЫХ ВИХРЕЙ
А. Е. Луцкий a, *, А. В. Северин a, **
a Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: allutsky@yandex.ru
** E-mail: alsewerin@yandex.ru
Поступила в редакцию 20.10.2022
После доработки 27.01.2023
Принята к публикации 28.01.2023
- EDN: TMOJWC
- DOI: 10.31857/S1024708422600804
Аннотация
Исследовано влияние пористой законцовки крыла на формирование концевого вихря и его свойства при сверхзвуковом обтекании. Установлено, что пористая законцовка существенно влияет на структуру и параметры вихря, уменьшает его интенсивность.
Изучение формирования и структуры концевых вихрей является важной задачей аэродинамики. Концевые вихри образуются на внешних кромках крыльев и органов управления летательного аппарата (ЛА) благодаря перепаду давлений. Концевые вихри влияют на аэродинамические характеристики крыла, уровень шума, безопасность полета [1, 2]. Попадание ЛА или его элемента конструкции в концевой вихрь может привести к потере управления или разрушению. Для ослабления концевых вихрей используются различные конструктивные элементы типа винглетов, шарклетов и других вариантов законцовок крыла [3]. У дозвуковых ЛА законцовки существенно повышают подъемную силу и уменьшают сопротивление. В работе [4] исследуется возможность применения законцовок типа винглетов на сверхзвуковых скоростях при M = 1.62. Авторы приходят к выводу, что при данном режиме течения винглеты неэффективны с точки зрения уменьшения сопротивления крыла.
Одним из направлений совершенствования аэродинамики летательных аппаратов, интенсивно развивающихся в последнее время, является использование элементов конструкции из пористых материалов. Основой для создания пористых материалов, применяемых в летательных аппаратах, являются как различные металлы (никель, бронза и т.д.), так и материалы на основе термопрочных пористых углеродных материалов, которые обладают высокой термостойкостью (2500 К) и малым удельным весом.
Существует много работ, посвященных использованию пористых материалов для стабилизации пограничного слоя [5–8], в каналах для забора перепускаемого воздуха [9], диффузорах [10], носовых обтекателях [11–13] и других элементах конструкции летательных аппаратов.
Поэтому представляет интерес и воздействие пористых элементов конструкции и на концевые вихри. Работ на эту тему довольно мало – можно отметить, например, описание патента НАСА [14]. В этой области возможно открытие новых и полезных эффектов. Настоящая работа представляет собой исследование формирования концевых вихрей в условиях, когда все крыло или его часть изготовлены из пористого материала. В качестве примера используется прямое крыло простой геометрической формы, обтекаемое сверхзвуковым потоком.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ЧИСЛЕННЫЙ АЛГОРИТМ
Для проведения расчетов в данной работе использован пакет программ S3D [15], разработанный и программно реализованный в ИПМ им. М.В. Келдыша РАН. Данный комплекс программ предназначен для решения 3-мерных задач аэродинамики. Используется неявная разностная схема, в которой для решения системы линейных уравнений применяется метод LU SGS. Потоки на гранях ячеек вычисляются с помощью интерполяционной схемы С.К. Годунова.
Для описания течений совершенного вязкого сжимаемого газа используется система нестационарных осредненных по Рейнольдсу уравнений Навье–Стокса (URANS) с однопараметрической моделью турбулентности Спаларта–Аллмараса (SA) для сжимаемых течений. Для дискретизации уравнений используется метод конечных объемов, который, в отличие от метода конечных разностей, применим к любой геометрии, оперирует различными сетками и позволяет избежать проблем с метрическими сингулярностями обобщенных координат.
Модель течения газа в пористом материале основана на сужении модели Баера-Нунзиато [16], которая первоначально была разработана для описания процесса горения и детонации гранулированных взрывчатых веществ. Среда в этой модели рассматривается как двухфазный континуум, состоящий из твердого скелетона непрореагировавшего взрывчатого вещества (ВВ) и газовой фазы продуктов горения. Модель, которую мы используем, является редукцией модели Баера-Нунзиато, состоящей в предположении, что твердый скелетон неподвижен.
Мгновенное состояние газа определяется плотностью ρ, вектором скорости u и давлением p. Газ считается сжимаемой, вязкой и теплопроводной средой. Скелетон считается обладающим теплоемкостью и теплопроводностью, температура газа и скелетона считается одинаковой.
Предполагается, что микроструктура скелетона является изотропной и характеризуется распределением объемной доли скелетона φ = φ(x). Величина α = α(x) = 1 – φ(x) представляет собой локальное распределение пустот (пористость).
Геометрическую форму сплошного твердого тела можно задавать двумя способами: положив α = 0 и при помощи граничных условий прилипания. В данной работе поверхности сплошных тел определяются граничными условиями. Отличные от 1 значения α используются только для расчета течения в пористых частях крыла.
В результате мы приходим к следующей системе уравнений, которые в континуальном приближении описывают течение сжимаемой жидкости в стесненных условиях пористого проницаемого скелетона
(1)
$\frac{{\partial \alpha \rho }}{{\partial t}} + \frac{{\partial \alpha \rho {{u}_{k}}}}{{\partial {{x}_{k}}}} = 0$(2)
$\frac{{\partial \alpha \rho {{u}_{i}}}}{{\partial t}} + \sum\limits_{k = 1}^3 {\frac{{\partial \alpha (\rho {{u}_{i}}{{u}_{k}} + p{{\delta }_{{ik}}})}}{{\partial {{x}_{k}}}}} = p\frac{{\partial \alpha }}{{\partial {{x}_{i}}}} + \sum\limits_{k = 1}^3 {\frac{{\partial \alpha {{\tau }_{{ik}}}}}{{\partial {{x}_{k}}}}} - {{g}_{i}}$(3)
$\frac{{\partial \alpha \rho E}}{{\partial t}} + \frac{{\partial \left( {1 - \alpha } \right){{E}_{s}}}}{{\partial t}} + \sum\limits_{k = 1}^3 {\frac{{\partial \alpha \rho H{{u}_{k}}}}{{\partial {{x}_{k}}}}} = \sum\limits_{k - 1}^3 {\left( {\frac{{\partial \alpha {{\tau }_{{ik}}}{{u}_{i}}}}{{\partial {{x}_{k}}}} - \frac{{\partial {{\theta }_{k}}}}{{\partial {{x}_{k}}}}} \right)} $Здесь используются общепринятые обозначения: i, k = 1, 2, 3 – индексы; $\rho $ – плотность, ${{u}_{k}}$ – компоненты вектора скорости, p – давление, τik = 2μefeik – 2/3μefejjδik – тензор вязких напряжений, eik = 0.5(∇iuk + ∇kui) – тензор скоростей деформаций, μef = μmol + μturb – эффективная вязкость, H = E + p/ρ – полная энтальпия, E = Et + W – полная энергия газовой фазы, Et = = $p{\text{/}}[\rho \left( {\gamma - 1} \right)]$ – внутренняя энергия единицы массы (определяется уравнением состояния идеального калорически совершенного газа), W = 0.5$\Sigma _{{k = 1}}^{3}u_{k}^{2}$ – кинетическая энергия единицы массы, Es = CsT – тепловая энергия скелетона, Cs – теплоемкость единицы объема твердой фазы, ${{\theta }_{k}} = - \lambda {{\nabla }_{k}}T$ – молекулярный тепловой поток, $\lambda $ – коэффициент теплопроводности двухфазной среды, Т – температура; ${{\delta }_{{ik}}}$ – тензор Кронекера.
Коэффициент молекулярной вязкости предполагается функцией локальной температуры воздуха Т и задается полуэмпирической формулой Сазерленда. Коэффициент теплопроводности газа λg связан с коэффициентом динамической вязкости $\mu $ числом Прандтля, которое предполагается постоянным и равным $\Pr = 0.733$. Коэффициент теплопроводности твердой фазы λs считается постоянным и определяется свойствами материала. Коэффициент теплопроводности двухфазной среды λ = αλg + (1 – α)λs.
Объемная сила ${{g}_{i}}$ в уравнении (2) представляет собой вязкую силу трения, действующую со стороны скелетона на газ. Она зависит от локальной скорости и плотности газа и микроструктуры скелетона (или микроструктуры пор). В общем случае вязкая сила трения может быть записана через коэффициент вязкого сопротивления в форме Эргана [17]
Более полное описание используемых численных алгоритмов и математической модели можно найти в [18].
Параллельные алгоритмы численного решения были реализованы на многопроцессорной системе К-100 ИПМ им. М.В. Келдыша РАН [19].
ЧИСЛЕННЫЕ РАСЧЕТЫ
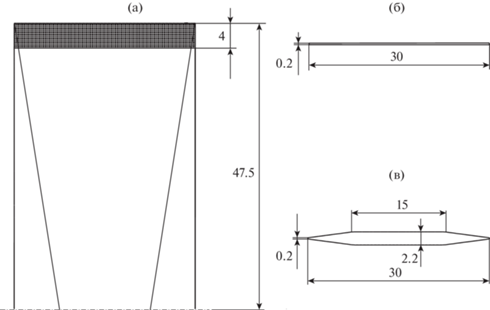
Для исследования вихревого следа в сверхзвуковом течении использовалось прямое крыло с передней и задней кромками толщиной 0.2 мм. Хорда крыла 30 мм, полуразмах 47.5 мм. Профили крыла у основания и на внешней кромке показаны на рис. 1. Форма крыла между заданными профилями такая, что все поверхности плоские – плоский четырехугольник в средней части, треугольники у передней и задней кромки. На рис. 1 показана схема крыла в плане.
Конец крыла (на рис. 1 заштрихован клетчатой штриховкой) выполнен из пористого материала с разными значениями пористости, т.е. объемной доли газовой фазы.
Пористый материал в применяемой модели считается непрерывной двухфазной средой, определяемой двумя параметрами: пористостью α, т.е. отношением объема газовой фазы к общему объему, и характерным размером пор, интерпретируемым как средний диаметр каналов в пористом материале.
Выполнены контрольный расчет для сплошного крыла и расчеты для 5 значений пористости α = 0.4, 0.6, 0.7, 0.8, 0.9.
Характерный размер пор считался равным 0.1 мм.
Все расчеты производились для одинакового набегающего потока с числом Маха M = 3, числом Рейнольдса относительно 1 м Re = 8 803 209, углом атаки α = 10°.
С целью проверки сеточной сходимости расчеты выполнялись на двух сетках.
Сетка 1: блочно-регулярная, состоящая из 5 951 600 ячеек, со сгущением к поверхности крыла, передней и задней кромке, а также к боковой кромке. Толщина ячеек у поверхности крыла 0.04 мм. Размер области за крылом – 9 хорд, с внешней стороны крыла – равно полуразмаху. На поверхности сплошной части крыла и на границе между сплошной и пористой частями установлено условие прилипания. На плоскости z = 0, на которой расположено основание крыла, установлено условие зеркальной симметрии, на передней границе области – условие сверхзвукового входа, на остальных внешних границах – условие экстраполяции.
Сетка 2: блочно-регулярная, число ячеек 7 312 800, вблизи передней и задней кромок размер ячеек в направлении x (продольном) по сравнению с сеткой 1 уменьшен в 10 раз, в направлении z (горизонтальном поперечном) вблизи боковой кромки – в 1.5 раза. В направлении y размер ячеек такой же.
Начало координат находится на плоскости симметрии у передней кромки крыла. Ось x направлена по течению газа, ось z – от плоскости симметрии к краю крыла, ось y – перпендикулярно течению вниз. Геометрические координаты выражены в метрах.
РЕЗУЛЬТАТЫ
Анализ результатов численного моделирования показал, что при всех рассмотренных значениях пористости формируется концевой вихрь, аналогичный вихрю на сплошном крыле, но не вблизи края пористой законцовки крыла, а вблизи окончания сплошного участка. Над пористой частью крыла возникает зона циркуляции, но центр вихря во всех случаях оказывается над сплошной частью.
Поскольку воздух, перетекающий с нижней стороны крыла, проходит теперь сквозь пористый материал, скорость его уменьшается, вихрь приобретает сложную несимметричную структуру и в большинстве случаев становится менее интенсивным. При больших значениях пористости интенсивность вихря может увеличиваться (рис. 7).
На рис. 2 можно видеть структуру вихрей в поперечной плоскости, проходящей через заднюю кромку крыла для различных значений пористости и контрольного расчета со сплошным крылом. Изображены векторные линии поля скоростей поперечного движения (uz, uy). Пористая часть крыла обведена пунктиром.
Рис. 2.
Векторные линии поля скоростей поперечного движения (uz, uy) в плоскости сечения x = 0.0293 (задняя кромка крыла) при разных значениях пористости α.
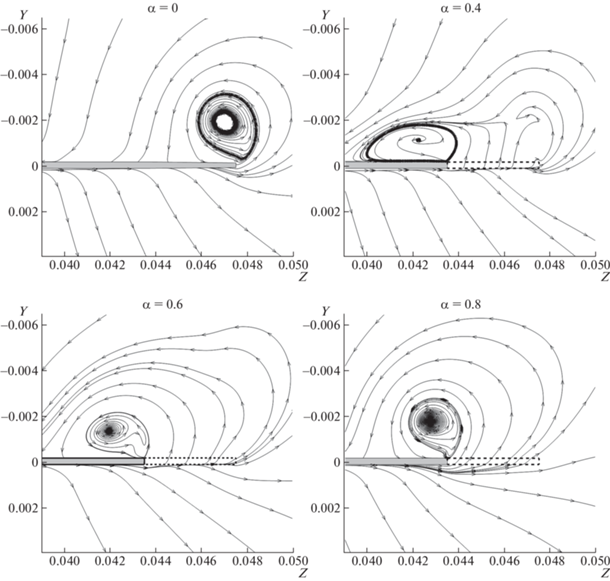
Интересно, что при α = 0.8 структура вихря качественно похожа на вихрь при сплошном крыле, вихрь только смещен на ширину пористой законцовки. Это означает, что материал с такой пористостью оказывает уже небольшое влияние на структуру течения, крыло почти эквивалентно сплошному крылу меньшего размаха. Однако наблюдаются некоторые количественные отличия.
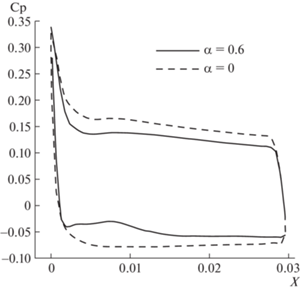
Изменение вихревой структуры приводит к изменению распределения давления. На рис. 3 показаны коэффициенты давления на поверхности крыла в сечении z = 0.042 для контрольного сплошного крыла и для α = 0.6. Видно, что уменьшается давление на нижней поверхности крыла и увеличивается на верхней.
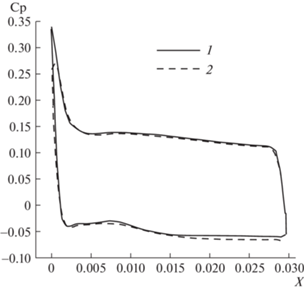
На рис. 4 показаны результаты расчетов для 2 сеток. Здесь коэффициенты давления для α = = 0.6, вычисленные с использованием сетки 2, такие же, как на рис. 3 сравниваются с расчетом на сетке 1. Видно, что есть отличие вблизи передней кромки крыла, где формируется ударная волна, но на большей части поверхности крыла расхождения невелики.
Перераспределение давления приводит к изменению лобового сопротивления крыла, подъемной силы и аэродинамического качества. В табл. 1 показаны аэродинамические коэффициенты для средней части крыла (Cxs, Cys) и для края крыла, который при α ≠ 0 является пористым. Сопротивление средней (сплошной) части крыла состоит из двух составляющих: сопротивления давления и сопротивления трения на поверхности материала. При обтекании пористого материала к ним добавляется третья: трение внутри материала. При малых значениях α воздух обтекает материал, течение внутри материала незначительно, и поэтому третья составляющая мала. При больших α значительная часть воздуха проходит сквозь материал, но сопротивление внутреннего трения мало из-за большого количества пустот в материале. Наибольшее сопротивление должно наблюдаться при средних значениях α, и мы видим, что при α = 0.6 оно действительно выше, чем при других значениях.
Таблица 1
| пористость | 0 | 0.6 | 0.8 | 0.9 |
|---|---|---|---|---|
| Cxs | 0.3 | 0.292 | 0.294 | 0.295 |
| Cxp | 0.019 | 0.068 | 0.025 | 0.009 |
| Cx | 0.319 | 0.360 | 0.319 | 0.304 |
| Cys | 1.263 | 1.22 | 1.228 | 1.229 |
| Cyp | 0.084 | 0.028 | 0.008 | 0.002 |
| Cy | 1.347 | 1.248 | 1.236 | 1.231 |
| K | 4.22 | 3.47 | 3.87 | 4.05 |
Различия в структуре и интенсивности вихря сохраняются в процессе его эволюции вниз по потоку. На рис. 5 изображены продольная завихренность Ωx = ∂uz/dy – ∂uy/dz и число Маха в центре вихря для сплошного крыла и для α = 0.6.
Рис. 5.
Продольная завихренность (Ωx, 103 с–1) и число Маха (M) в центре вихря: крыло пористое 1 и сплошное 2.
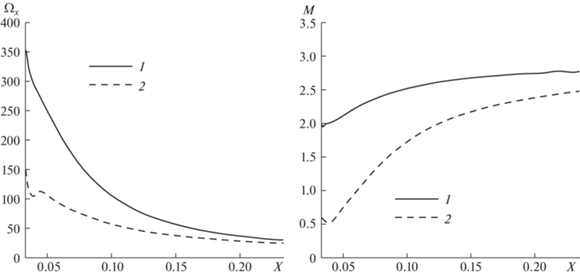
Число Маха на оси вихря в случае пористой законцовки существенно меньше. При этом скорость газа отличается незначительно, более высокими оказываются скорость звука и давление.
На рис. 6 изображены изолинии продольной завихренности для сечения x = 0.2348 (6.85 хорд от задней кромки) за сплошным крылом (сплошные линии) и крылом, оснащенным пористой законцовкой с пористостью α = 0.6 (пунктир). Для наглядности здесь же изображены контуры крыла и его задней кромки. Пористая законцовка закрашена серым. Видно, что завихренность существенно уменьшилась (максимум 23.9 вместо 29.7), а центр вихря сместился от края к границе между сплошной и пористой частями крыла.
Рис. 6.
Изолинии продольной завихренности (103 с–1) в сечениях x = 0.0293 (слева) и x = 0.2348 (справа).
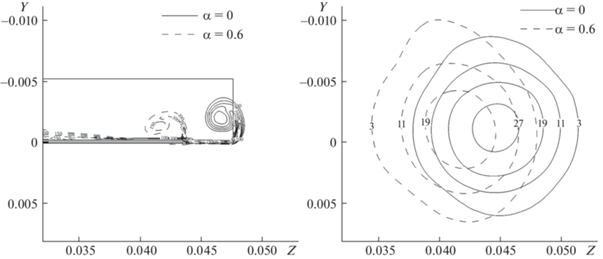
Рис. 7.
Продольная завихренность (Ωx) и тангенциальное число Маха (Myz). в сечениях x = 0.1348 и x = 0.2348.
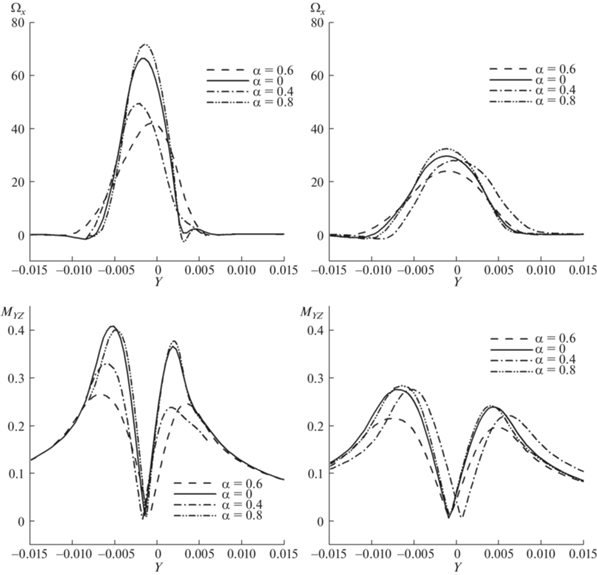
На рис. 7 показаны параметры течения – продольная завихренность (Ωx) и тангенциальное число Маха (Myz) вдоль линии, проходящей через центр вихря перпендикулярно его оси. Представлены сечения x = 0.1348 (на расстоянии 3.5 хорд за кромкой) и x = 0.2348 (6.85 хорд). Показаны графики для гладкого крыла (α = 0) и трех значений пористости α = 0.4, 0.6, 0.8.
Несмотря на то что на сплошном крыле (α = 0) и крыле с пористой законцовкой центры вихря находятся в разных местах по координате z, на рис. 7 видно, что положение центра вихря по координате y во всех случаях близко. Интересно, что структуры вихря на сплошном крыле и на крыле с α = 0.8 очень похожи, отличаются значительно меньше, чем на крыльях с другими значениями пористости. Это говорит о том, что законцовка с высокой пористостью оказывает небольшое влияние на вихрь, такое крыло почти эквивалентно гладкому крылу меньшего размаха.
ЗАКЛЮЧЕНИЕ
В работе представлены результаты численного исследования концевого вихря в сверхзвуковом потоке при числе Маха М = 3 для крыла, имеющего законцовку из пористого материала с различными значениями пористости. Для расчетов использовались математическая модель течения газа сквозь пористую среду, алгоритмы моделирования турбулентных течений и их параллельная реализация на многопроцессорных вычислительных системах.
Из полученных численных результатов видно, что у крыла с пористой законцовкой образуется концевой вихрь, аналогичный тому, что образуется на сплошном крыле. Однако параметры, структура и положение вихря существенно отличаются. Во всех рассмотренных случаях вихрь образуется у края сплошной части крыла, а не у края пористого материала.
При значениях пористости меньше 0.8 вихрь становится менее интенсивным, при пористости 0.8 и 0.9 интенсивность вихря немного увеличивается. Лобовое сопротивление и подъемная сила уменьшаются. Таким образом, появляется возможность управлять процессом генерации вихря.
Расчеты выполнены для модельного крыла простой геометрии. Это показывает принципиальную возможность управления параметрами концевого вихря при помощи пористых законцовок. При другой геометрии крыла эффекты могут быть другими. Представляет интерес и может быть предметом дальнейших исследований аналогичная задача с треугольным крылом.
Работа выполнена при финансовой поддержке Российского научного фонда, проект № 22-21-00470.
Список литературы
Гиневский А.С., Желанников А.И. Вихревые следы самолетов. М.: Физматлит, 2008. 172 с.
Вышинский В.В., Судаков Г.Г. Вихревой след самолета и вопросы безопасности полетов // Труды МФТИ. 2009. № 1 (3). С. 73–93.
Whitcomb R.T. A Design Approach and Selected Wind-Tunnel Results at High Subsonic Speeds for Wing-Tip Mounted Winglets // NASA-TN-D-8260, 1976.
Keenan J.A., Kuhlman J.M. The Effects of Winglets on Low Aspect Ratio Wings at Supersonic Mach Numbers // NASA Contractor Report 4407.
Корнилов В.И., Бойко А.В. Экспериментальное моделирование вдува воздуха в турбулентный пограничный слой при помощи внешнего напорного потока // Журнал технической физики. 2016. Т. 86. Вып. 10. С. 8–46.
Лысенко В.И., Смородский Б.В., Ермолаев Ю.Г., Гапонов С.А., Косинов А.Д., Семенов Н.В., Яцких А.А. Влияние инжекции тяжелого газа в пристеночный слой сверхзвукового пограничного слоя на его переход // Сибирский физический журнал. 2017. Т. 12. № 1. С. 50–56.
Циберкин К.Б. О структуре поля скорости стационарного течения вблизи границы раздела однородной жидкости и пористой среды Бринкмана // Журнал технической физики. 2016. Т. 8. Вып. 8.
Шиплюк А.Н., Буров Е.В., Маслов А.А., Фомин В.М. Влияние пористых покрытий на устойчивость гиперзвуковых пограничных слоев // Прикладная механика и техническая физика (ПМТФ). 2004. Т. 45. № 2. С. 169–176.
Фомин В.М., Запрягаев В.И., Локотко А.В., Волков В.Ф., Луцкий А.Е., Меньшов И.С., Максимов Ю.М., Кирдяшкин А.И. Аэродинамические характеристики тела вращения с газопроницаемыми участками поверхности // Прикладная механика и техническая физика (ПМТФ). 2010. Т. 51. № 1. С. 79–88.
Willis B.P., Davis D.O., Hingst W.R. Flowfield Measurements in a Normal-Hole-Bled Oblique Shock-Wave and Turbulent Boundary-Layer Interaction // AIAA Paper 1995–2885 (July 1995).
Poplavskaya T.V., Kirilovskiy S.V., Mironov S.G. Supersonic flow around a cylinder with front gas-permeable insert which modeled by skeleton of porous material // AIP Conference Proceedings.2016. V. 1770. 030067.
Schuelein E. Shock-wave control by permeable wake generators // 5th Flow Control Conference, Fluid Dynamics and Co-located Conferences, Chicago, Illinois, 28 June – 1 July 2010.
Фомин В.М., Миронов С.Г., Сердюк К.М. Снижение волнового сопротивления тел в сверхзвуковом потоке с помощью пористых материалов // Письма в ЖТФ. 2009. Т. 35. Вып. 3.
Winglet with injected flow. https://technology.nasa.gov/contact-us/TOP2-289
Меньшов И.С., Северин А.В. Программный комплекс S3D. https://cfd.imamod.ru/FILES/2015/2015_CFDWeekend_Abstracts.pdf
Baer M.R., Nunziato J.W. A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials // Int. J. Multiphase Flow. 1986. 12. P. 861–889.
Ergun S. Fluid flow through packed columns // Chem. Eng. Prog. 48 1952.
Северин А.В., Луцкий А.Е., Меньшов И.С. Управление высокоскоростным течением в канале при помощи пористых вставок // Матем. моделирование. 2022. V. 34. № 4. С. 100–112.
Вычислительные комплексы МВС-Экспресс, К-100 и К-60 ИПМ РАН. http://www.kiam.ru
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа