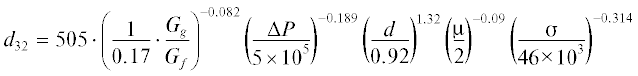Известия РАН. Механика жидкости и газа, 2023, № 3, стр. 77-82
О РЕШЕНИИ ОБРАТНОЙ ЗАДАЧИ РАСЧЕТА ФОРСУНКИ С ГАЗОЖИДКОСТНЫМ ДВУХФАЗНЫМ ПОТОКОМ
П. В. Зотикова a, *, Н. А. Кучеров a, **, И. А. Лепешинский a, ***, В. А. Решетников a, ****
a Московский авиационный институт Национальный исследовательский университет (МАИ)
Москва, Россия
* E-mail: chekmenevapolina024@gmail.com
** E-mail: n.kutcherov@bk.ru
*** E-mail: igorlepesh@yandex.ru
**** E-mail: vresh0352@mail.ru
Поступила в редакцию 31.10.2022
После доработки 16.12.2022
Принята к публикации 16.12.2022
- EDN: TMQHOO
- DOI: 10.31857/S1024708422600877
Аннотация
Рассматривается возможность решения обратной задачи расчета газожидкостной струйной форсунки с пузырьковой структурой двухфазного потока. Находятся параметры, определяющие работу форсунки (перепад давления, диаметр отверстия и концентрация воздуха), для заданного значения среднего диаметра Заутера. Для этого было проведено экспериментальное исследование работы смесителя с двухфазным рабочим телом с форсунками различного диаметра на пузырьковом режиме работы с водо-воздушным рабочим телом. В процессе эксперимента измерялись параметры подводимых к смесителю фаз (расходы, давления и температуры), а также давление перед форсунками. Дисперсные и скоростные характеристики в факеле распыла измерялись лазерным теневым методом. На основе собранной статистики была получена искомая корреляционная зависимость, позволившая решать данную задачу.
Существует множество устройств, работающих на двухфазном рабочем теле, таких как, например, распыляющие устройства форсажных и основных камер сгорания реактивных двигателей, сопла реактивного и ракетного двигателя, эжекторные устройства, установки для полива и орошения в сельском хозяйстве, установки для тушения пожара. Поэтому для повышения эффективности данных устройств и упрощения проектирования проведение исследований в этой области является актуальным. Следует отметить, что решение обратной задачи для рассматриваемых систем диспергирования в такой постановке не рассматривалось. В данной работе рассматриваются форсунки с газокапельной структурой потока, в котором объемная концентрация газа существенно ниже 0.5. Если ввести критерии подобия двухфазного потока ${{П}_{1}} = {{G}_{f}}{\text{/}}{{G}_{g}}$, П2 = = ${{w}_{f}}{\text{/}}{{w}_{g}}$, ${{П}_{5}} = {{\rho }_{f}}{\text{/}}{{\rho }_{g}}$, тогда выражение, определяющее структуру двухфазного потока, примет вид ${{\alpha }_{g}} = {{П}_{5}}{{П}_{2}}{\text{/}}({{П}_{1}} + {{П}_{5}}{{П}_{2}})$, где ${{\alpha }_{g}}$ – объемная концентрация газа. Добавляем уравнение плотности газа ${{\rho }_{g}} = p{\text{/}}RT$, при р = 10 атм. Наибольшее значение ${{\alpha }_{g}}$ в экспериментах не превышает значения 0.4, т.е. является пузырьковым режимом.
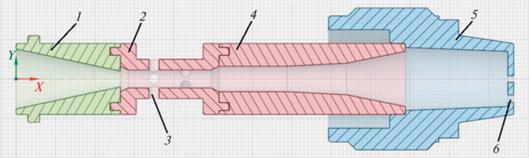
В настоящий момент процесс проектирования таких устройств (решение прямой задачи) требует проведения дополнительных экспериментальных исследований. Это обусловлено сложной физикой протекающих при данном режиме диспергирования двухфазного потока процессах. Несмотря на то что в последние годы увеличилось количество научных публикаций на эту тему, до сих пор нет работ, которые позволили бы обобщить достижения в этой области [1]. В данной работе рассматривается смеситель, формирующий двухфазный газожидкостный поток необходимой пузырьковой структуры, имеющий конструкцию, представленную на рис. 1.
Смеситель состоит из следующих элементов: входного конфузора 1, аэратора 2, диффузора 4, соединенного с испытываемой форсункой 5, снабженной необходимыми отверстиями 6 для диспергирования двухфазного потока.
Диффузор обеспечивает снижение давления воды до необходимого значения, а в случае, если давление в аэраторе меньше атмосферного, смеситель работает на режиме эжекции. Аэратор производит аэрацию воды воздухом, подаваемым или эжектируемым через отверстия 3. Диффузор увеличивает давление газожидкостной смеси до значения, необходимого на входе в форсунку, производящую распыл смеси через отверстия 6.
Исследование проводилось на установке, содержащей все необходимые устройства для формирования исходного двухфазного рабочего тела с подходящими структурой и параметрами, позволяющей их регулировать на стадиях формирования и диспергирования. Ранее на данной установке проводились аналогичные исследования [2–4].
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ
Исследование факела распыла проводилось теневым методом, входящим в программный комплекс LaVision [5]. Принцип работы данного метода следующий: поток частиц просвечивается мощным лазером. Его свет проходит через рассеиватель, приобретая равномерную структуру, и освещает частицы. Тень от частиц попадает на кросскорреляционную камеру через дистанционный микроскоп. С камеры изображение попадает в ПК, где в программном пакете DaVis происходит его анализ, идентификация капель и вычисление их размера.
Экспериментальное исследование проводилось в заданных диапазонах для определяющих параметров. Диапазоны следующие: перепад давления перед форсунками $\Delta P$ – 1–12 атм, массовая концентрация воздуха ${{G}_{g}}{\text{/}}{{G}_{f}} = 1{\text{/}}{{П}_{1}}$ – 0–0.004 (${{G}_{g}}$ – расход воздуха, ${{G}_{f}}$ – расход воды). Использовались форсунки, имеющие выходные отверстия постоянного диаметра: 2, 2.5, 3 мм, но разное число отверстий, от 6 до 9, на одну форсунку.
Исследование потока теневым методом производилось в области перехода от первичного распада к вторичному. Дробление жидкой фазы имеет две зоны формирования капельной структуры: первая зона, примыкающая к выходному сечению форсунки, формирует капли, соответствующие распылу однофазной жидкости при параметрах перед форсункой, вторая зона расположена на расстоянии от 20 до 100 калибров диаметра отверстий. Поскольку скорость газа, вытекающего из форсунки, существенно больше скорости жидкости (при одинаковом давлении перед форсункой), то реализуется вторичное дробление капель. Пример получаемого распределения приведен на рис. 2, в виде зависимости от числа капель, относящихся к данному диапазону размеров (фракции капель).
@форсунки с диаметром отверстий 2 мм, при Gf = 0.414 кг/с, Gg = 0.7 г/с, ΔP = 2 атм.
Далее для каждого распределения был найден средний диаметр Заутера и построены его зависимости от основных параметров форсунки, показанные на рис. 3, 4. Для качественной оценки и сравнения результатов работы форсунок на графиках использовалась линейная аппроксимация.
Рис. 3.
Зависимость диаметра Заутера от давления перед форсунками, диаметры отверстий которых указаны в легенде d, м.
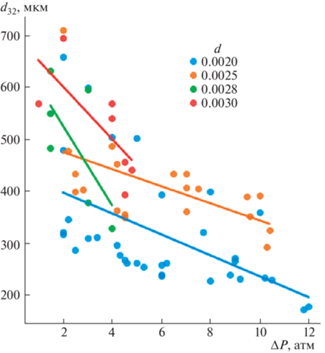
Рис. 4.
Зависимость диаметра Заутера от объемной доли воздуха перед форсунками, диаметры отверстий которых указаны в легенде d, м.

Используя полученную статистику, представим корреляционное уравнение в виде
В качестве основы корреляционного уравнения воспользуемся уравнением, полученным в работе [6], в результате 3-х мерного численного моделирования распыла двухфазного потока пузырьковой структуры
(2)
${{d}_{{32}}}_{{\left( {y \to 0} \right)}} = 0.000505{{\left( {\frac{1}{{0.12}} \cdot \frac{{Gg}}{{{{G}_{f}}}}} \right)}^{{ - 0.4686}}}{{\left( {\frac{{\Delta P}}{{5 \times {{{10}}^{6}}}}} \right)}^{{ - 0.1805}}}{{\left( {\frac{d}{{0.2}}} \right)}^{{0.6675}}}{{\left( {\frac{{{\mu }}}{{{\text{0}}{\text{.2}}}}} \right)}^{{0.1714}}}{{\left( {\frac{{{\sigma }}}{{{\text{46}}}}} \right)}^{{0.1382}}}$(3)
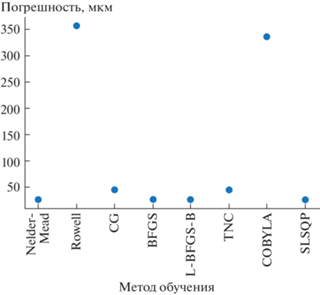
${\text{MAPE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{A}_{i}} - {{F}_{i}}}}{{{{A}_{i}}}}} \right|} $Ввиду неудовлетворительного значения MAPE “переобучим” модель на полученных экспериментальных данных. На рис. 6 представлена зависимость абсолютной погрешности модели от метода обучения. Nelder-Mead – метод деформируемого многогранника [7], Powell – метод Пауэлла или метод сопряженных направлений [8], CG – метод сопряженных градиентов (метод Флетчера–Ривcа) [9], BFGS – алгоритм Бройдена–Флетчера–Гольдфарба–Шанно [10], L-BFGS-B – модификация с ограниченным использованием памяти в многомерном кубе [11], TNC – усеченные методы Ньютона (Truncated Newton methods) [12], COBYLA – ограниченная оптимизация с линейной аппроксимацией [12], SLSQP – последовательное квадратичное программирование [13].
Как видно из рис. 6, большинство методов дало примерно одинаковый результат. Для практического использования возьмем модель, обученную методом L-BFGS-B с MAPE = 7.6%. Скорректированное уравнение имеет вид:
Благодаря наличию данного уравнения можно решить обратную задачу, т.e. найти значения параметров форсунки, обеспечивающих нужное значение d32 при заданных ограничениях. Такую задачу можно свести к задаче минимизации некоторой функции потерь, в качестве которой может выступить, например, абсолютная ошибка (разность по модулю целевого и прогнозируемого значений). Назовем такую функцию error и сформулируем задачу ее минимизации следующим образом:
где ${{\hat {d}}_{{32}}}$ и d32 – целевое и прогнозное значение диаметра Заутера.Вектор входных параметров
Дополнительно задается множество допустимых решений $X \subset {{R}^{N}}$, где N – число входных параметров, т.е. длина вектора х.
Ниже в таблице рассмотрены несколько сравнительных примеров.
Из табл. 1 видно, что предложенная корреляционная модель дает прогнозы, согласующиеся с экспериментальными данными.
ЗАКЛЮЧЕНИЕ
Получен экспериментально статистический материал, связывающий режимные параметры на входе с дисперсными характеристиками на выходе. Это было использовано вместе с математическими методами обучения и оптимизации, что позволило разработать методику решения обратной задачи определения заданных режимных и структурных параметров пузырькового двухфазного потока распыляющего струйного устройства на входе при задании параметров на выходе из него. Полученные результаты могут быть использованы при проектировании различных распыляющих устройств в камерах сгорания и в других устройствах, использующих двухфазные потоки, соплах и эжекторах, различных смесительных устройствах.
Список литературы
Czernek Krystian, Hyrycz Michał, Krupińska Andżelika, Matuszak Magdalena, Ochowiak Marek, Witczak Stanislaw, Włodarczak Sylwia. State-of-the-Art Review of Effervescent-Swirl Atomizers // Energies. 2021. V. 14. P. 2876. https://doi.org/10.3390/en14102876
Марчуков Е.Ю., Мухин А.Н., Лепешинский И.А., Решетников В.А., Кучеров Н.А. Экспериментальное исследование смесительного устройства форсажной камеры газотурбинного двигателя // Изв. РАН. МЖГ. 2022. № 4. С. 3–10.
Лепешинский И.А., Решетников В.А., Заранкевич И.А. Численное моделирование и экспериментальное исследование жидкостно-газового двухфазного эжектора со сверхзвуковым профилированным соплом// Вестник Самарского университета. Аэрокосмическая техника, технологии и машиностроение. 2017. Т. 16. № 2. С. 164–171.
Лепешинский И.А., Решетников В.А., Заранкевич И.А., Истомин Е.А., Антоновский И.В., Гузенко А.А. Экспериментальное исследование газодинамического смесителя закрытого типа // Вестник Самарского университета. Аэрокосмическая техника, технологии и машиностроение. 2016. Т. 15. № 3. С. 70–80.
Сайт фирмы Lavision [Электронный источник] URL: http://lavision.de/en/
Lin Jianzhong&Qian, Lijuan&Xiong, Hongbin. Relationship between deposition properties and operating parameters for droplet onto surface in the atomization impinging spray // Powder Technology. 2009. 191. P. 340–348. https://doi.org/10.1016/j.powtec.2008.11.009
Nelder J.A. and Mead R. // Computer Journal. 1965. V. 7. P. 308–313.
Powell M.J.D. An efficient method for finding the minimum of a function of several variables without calculating derivatives // The Computer Journal. 1964. V. 7. P. 155–162.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация / Пер. с англ. М.: Мир, 1985, 503 с.
Nocedal, Jeorge; Wright, Stephen J. Numerical Optimization / 2nd ed. N.Y.: Springer, 2006, 634 c.
Liu D.C., Nocedal J. On the Limited Memory Method for Large Scale Optimization// Mathematical Programming B.1989. V.45. № 3. P. 503–528.
Powell M.J.D. A direct search optimization method that models the objective and constraint functions by linear interpolation / Advances in Optimization and Numerical Analysis / Eds. S. Gomez and J-P Hennart. Dordrecht.: Kluwer Academic, 1994. P. 51–67.
Bonnans J.F., Gilbert J.Ch., Lemaréchal C., Sagastizabal C. Numerical Optimization // Theoretical and Practical Aspects, 2006. P. 490.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа