Известия РАН. Механика жидкости и газа, 2023, № 3, стр. 83-93
ВЛИЯНИЕ НАЧАЛЬНОЙ ФОРМЫ ПУЗЫРЬКА НА ДИНАМИКУ ВСПЛЫТИЯ В НЕПОДВИЖНОЙ ВЯЗКОЙ ЖИДКОСТИ
И. В. Моренко *
Институт механики и машиностроения ФИЦ Казанский научный центр РАН
Казань, Россия
* E-mail: morenko@imm.knc.ru
Поступила в редакцию 28.11.2022
После доработки 19.12.2022
Принята к публикации 19.12.2022
- EDN: TMUTLW
- DOI: 10.31857/S1024708422600920
Аннотация
Исследовано влияние формы одиночного пузырька в начальный момент времени на динамику всплытия в вязкой покоящейся жидкости. Рассматриваются пузырьки эллиптической формы с разным коэффициентом сжатия. Математическое моделирование процесса базируется на методе объема жидкости, который позволяет отслеживать эволюцию межфазной границы. Результаты расчета тестовых задач согласуются с данными других авторов, описанными в литературе. Получены формы межфазной поверхности, поля скорости, завихренности в процессе всплытия пузырьков в поле силы тяжести при числе Рейнольдса Re = 35, числах Бонда Bo = 10, 125. Основное внимание уделено режиму нестационарного движения. Показано, что скорость всплытия пузырька имеет один или два локальных максимума в зависимости от свойств сред. Установлено, что пузырьки, в начальный момент времени вытянутые вертикально, всплывают быстрее, чем вытянутые горизонтально.
Двухфазные пузырьковые течения широко представлены в химической промышленности, теплоэнергетике, металлургии, медицине, фармацевтике. Содержание в жидкости газовых пузырьков оказывает заметное влияние на характер и интенсивность технологических процессов. Задача о всплытии одиночного пузырька в неподвижной жидкости является классической проблемой механики жидкости и газа, имеет фундаментальное значение в теории газожидкостного потока и прикладное значение во многих приложениях.
На газовый пузырек, всплывающий в покоящейся жидкости, действуют несколько сил [1, 2]: сила Архимеда, тяжести, гидродинамического сопротивления, поверхностного натяжения, инерции, сила, связанная с присоединенной массой, “наследственная” сила Бассе. В работе [3] отмечается, что основные трудности при математическом моделировании всплывающего пузырька и теоретического анализа возникают из-за сильного нелинейного взаимного влияния действующих на пузырек сил и деформации его формы. Кроме того, трехмерность процесса привносит дополнительные сложности.
В зависимости от объема газовые пузырьки в процессе всплытия в жидкости могут иметь различные формы [4]: сферу, сплюснутого сфероида, сферического сегмента, а при определенных условиях пузырьки претерпевают нерегулярные пульсационные изменения формы, которые сопровождаются колебаниями поверхности раздела фаз. Карты режимов деформации пузырьков можно найти в [2, 5–8].
Ряд экспериментальных и численных работ [9–11] посвящен изучению траекторий всплытия одиночного пузырька и переходу от одного режима всплытия к другому. Установлено, что пузырек может всплывать прямолинейно вверх, по зигзагообразной и по спиральной траектории. Отмечено, что проблема связи динамики всплывающего пузырька и его следом мало изучена, а имеющиеся данные во многом противоречат друг другу.
Зависимость скорости подъема одиночного пузырька в жидкости от свойств сред найдена экспериментально еще в середине прошлого века [12]. Обобщенные данные о скорости всплытия одиночных пузырьков разных диаметров приводятся в [5, 13, 14]. На динамику подъема пузырька влияют наличие загрязнений, метод нагнетания газа в жидкость, взаимодействие пузырька со стенкой [15], наличие поверхностно-активных веществ [16, 17].
В промышленных установках в зависимости от конкретных условий технологического процесса генерирование пузырьков осуществляется с помощью отверстий в стенках или при диспергировании газа через пористые мембраны. Для достижения требуемых границ насыщения воды кислородом при равномерном его распределении по рабочему объему могут использоваться вихревые, ротационные воздуходувки, пластинчато-роторные сухие компрессоры.
Безусловно, экспериментальные данные являются надежным источником информации, представляют базу данных для получения эмпирических корреляций. Тем не менее не всегда на практике можно реализовать подачу пузырьков правильной сферической формы, не имеющих начальных деформаций, полностью исключить присутствие поверхностно-активных веществ. В связи с этим методы вычислительной гидродинамики являются альтернативным инструментом для получения новых данных, в том числе, информации о распределении мгновенных характеристик течения.
Анализ литературных данных показывает, что к настоящему времени опубликовано много работ, посвященных динамике пузырьков, однако не все аспекты изучены в полной мере. В данной работе проводится численное исследование влияния формы пузырька в начальный момент времени на процесс его подъема в неподвижной вязкой жидкости. Особое внимание уделяется динамике пузырька на начальном этапе его всплытия, когда его движение осуществляется в нестационарном режиме.
1. ОСНОВНЫЕ УРАВНЕНИЯ
При моделировании процесса всплытия пузырька необходимо учитывать нестационарность движения обеих сред, иметь возможность проанализировать поля скорости, давления, завихренности как внутри пузырька, так и в окружающей его жидкости. Для этого требуется решение полных уравнений гидродинамики. В настоящей работе математическое моделирование всплытия одиночного пузырька в неподвижной вязкой жидкости осуществляется с помощью метода объема жидкости (VoF) [18], который позволяет отслеживать положение межфазной границы, а также естественным образом учесть все силы, действующие на пузырек.
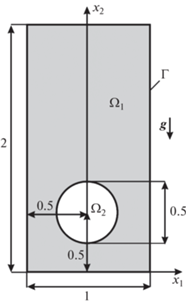
Исследование проводится в двумерной постановке, предполагается, что обе фазы являются вязкими несжимаемыми жидкостями, поверхностно-активные вещества отсутствуют. Начальное состояние системы показано на рис. 1. Прямоугольный резервуар [1 × 2] заполнен жидкостью. Начало декартовой системы координат расположено на дне резервуара по центру, а ось ординат направлена вверх. В начальный момент времени центр масс круглого пузырька ${{\Omega }_{g}}$ диаметром $d = 0.5$ находится в точке (0; 0.5). Вектор силы тяжести g направлен вертикально вниз противоположно оси ${{x}_{2}}$.
Рассматривается двухфазная среда, которая состоит из жидкой и газовой фаз. Обозначим через $\gamma $ объемную долю жидкой фазы в ячейке расчетной области. В каждой ячейке расчетной области маркерная функция $\gamma $ определяется следующим образом
Физические свойства среды рассчитываются по соответствующим значениям жидкости (индекс $l$) и газа (индекс g) с использованием маркерной функции $\gamma $: плотность $\rho = {{\rho }_{l}}\gamma + {{\rho }_{g}}\left( {1 - \gamma } \right)$, динамический коэффициент вязкости $\mu = {{\mu }_{l}}\gamma + {{\mu }_{g}}\left( {1 - \gamma } \right)$.
Математическая модель для описания нестационарного движения вязкой несжимаемой жидкости включает следующие уравнения. Уравнение сохранения массы
уравнение сохранения количества движения(1.2)
$\rho \frac{{\partial {\mathbf{u}}}}{{\partial t}} + \rho ({\mathbf{u}} \cdot \nabla ){\mathbf{u}} = - \nabla p + \nabla \cdot \left( {\mu \nabla {\mathbf{u}}} \right) + \rho {\mathbf{g}} + \sigma \kappa \nabla \gamma $(1.3)
$\frac{{\partial \gamma }}{{\partial t}} + \nabla \cdot \left( {\gamma {\mathbf{u}}} \right) + \nabla \cdot \left[ {\left( {1 - \gamma } \right)\gamma {{{\mathbf{u}}}_{r}}} \right] = 0$В начальный момент времени $t = 0$ среда находится в состоянии покоя
(1.4)
${{\Omega }_{1}} \cup {{\Omega }_{2}}:\quad {\mathbf{u}} = 0,\quad p = \rho g(2 - {{x}_{2}});\quad {{\Omega }_{1}}:\quad \gamma = 1,\quad {{\Omega }_{2}}:\quad \gamma = 0$На поверхности стенок резервуара записываются граничные условия согласно [8]
(1.5)
$\Gamma :\quad {{u}_{n}} = 0,\quad \frac{{\partial {{u}_{\tau }}}}{{\partial n}} = 0,\quad \frac{{\partial p}}{{\partial n}} = 0,\quad \frac{{\partial \gamma }}{{\partial n}} = 0$Решение поставленной задачи (1.1)–(1.5) осуществляется методом конечных объемов в свободно распространяемом программном комплексе OpenFOAM. Используется решатель interFoam. Нестационарное слагаемое дискретизируется с помощью схемы Кранка–Николсона, градиент – методом наименьших квадратов, конвективное слагаемое – схемой минимизации полной вариации с ограничителем Ван-Лира, диффузионное слагаемое – линейной схемой Гаусса с коррекцией. Используется подход с раздельным решением уравнений для скорости и давления. Решение уравнений для давления осуществляется методом сопряженных градиентов с предобусловливанием. Уравнения для скоростей и маркер-функции решаются методом Гаусса–Зейделя. Для согласования поля скорости с полем давления используется алгоритм PIMPLE, который приводит к удовлетворению уравнений неразрывности и сохранения импульса. Временной шаг в процессе счета выбирается таким образом, чтобы число Куранта Co во всех ячейках сетки не превосходило 0.05 для скорости и 0.01 для маркер-функции $\gamma $.
2. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ И ИХ ОБСУЖДЕНИЕ
Для валидации математических моделей, позволяющих отслеживать подвижную границу раздела фаз, наиболее часто используется классическая тестовая задача об обрушении столба жидкости, приведенная в [19]. Результаты тестирования применяемого алгоритма и численных методов опубликованы в [20]. Для верификации математической модели проведены также и другие методические расчеты [21, 22].
Типичный тест для двумерной задачи о всплытии одиночного пузырька приводится в работах [8, 23–26]. Задача решается в безразмерном виде, при этом характерный масштаб длины составляет d, скорости ${{u}_{g}} = \sqrt {gd} $, времени $t = {d \mathord{\left/ {\vphantom {d {{{u}_{g}}}}} \right. \kern-0em} {{{u}_{g}}}}$. В соответствии с [23] расчеты проводятся для двух наборов входных параметров – табл. 1.
Таблица 1.
Значения входных параметров для проведения тестовых расчетов
| Параметр | Тест № 1 | Тест № 2 |
|---|---|---|
| ${{\rho }_{l}}$, кг/м3 | 1000 | 1000 |
| ${{\rho }_{g}}$, кг/м3 | 100 | 1 |
| ${{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}}$ | 10 | 1000 |
| ${{{{\mu }}}_{l}}$, кг/(м ⋅ с) | 10 | 10 |
| ${{{{\mu }}}_{g}}$, кг/(м ⋅ с) | 1 | 0.1 |
| ${{{{\mu }_{l}}} \mathord{\left/ {\vphantom {{{{\mu }_{l}}} {{{\mu }_{g}}}}} \right. \kern-0em} {{{\mu }_{g}}}}$ | 10 | 100 |
| $g$, м/с2 | 0.98 | 0.98 |
| $\sigma $, Н/м | 24.5 | 1.96 |
| Re | 35 | 35 |
| Bo | 10 | 125 |
Безразмерный анализ задачи о всплытии одиночного пузырька в вязкой жидкости показал, что данная задача описывается четырьмя безразмерными параметрами, а именно отношениями плотности ${{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}}$ и вязкости ${{{{\mu }_{l}}} \mathord{\left/ {\vphantom {{{{\mu }_{l}}} {{{\mu }_{g}}}}} \right. \kern-0em} {{{\mu }_{g}}}}$ двух сред, числом Рейнольдса и числом Бонда [2]
Кроме того, в [10, 13] для анализа динамики пузырька используются числа Вебера We, Мортона Mo, Галилея Ga
Для оценки сходимости по пространству осуществляется моделирование на трех последовательно сгущающихся сетках ${{M}_{1}}$ [100 × 200], ${{M}_{2}}$ [200 × 400], ${{M}_{3}}$ [300 × 600]. В табл. 2 приводятся положения лобовой ${{P}_{1}}$ и кормовой ${{P}_{2}}$ точек полости на оси ${{x}_{2}}$ в момент времени $t = 3.0$, рассчитанные на сетках ${{M}_{1}}$, ${{M}_{2}}$ и ${{M}_{3}}$. При этом межфазная граница определяется изолинией $\gamma = 0.5$. Установлено, что для тестовой задачи № 1 расчетные данные различаются не более, чем на 1%. Тогда как для задачи № 2 положение точки ${{P}_{2}}$, полученное на сетке ${{M}_{1}}$, отличается на 2.29% от значения, полученного на сетке ${{M}_{3}}$. Для проведения дальнейших расчетов выбрана сетка ${{M}_{2}}$.
Таблица 2.
Проверка сходимости по сетке
| Тест № 1 | Тест № 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| ${{P}_{1}}$ | $\Delta $ | ${{P}_{2}}$ | $\Delta $ | ${{P}_{1}}$ | $\Delta $ | ${{P}_{2}}$ | $\Delta $ | |
| ${{M}_{1}}$ | 1.2660 | 0.34% | 0.9041 | 0.47% | 1.3553 | 0.82% | 1.0224 | 2.29% |
| ${{M}_{2}}$ | 1.2646 | 0.23% | 0.9028 | 0.32% | 1.3477 | 0.26% | 1.0065 | 0.70% |
| ${{M}_{3}}$ | 1.2617 | – | 0.8999 | – | 1.3442 | – | 0.9995 | – |
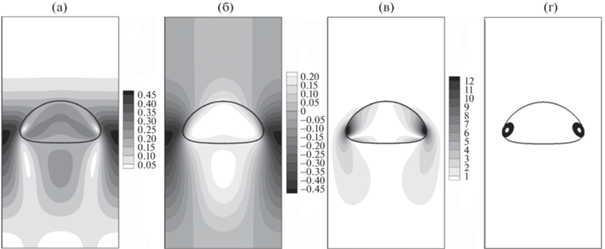
Результаты расчета тестовой задачи № 1 показаны на рис. 2. К моменту безразмерного времени $t = 3.0$ пузырек под влиянием действующих на него сил принимает форму, показанную на рис. 2. Установлено, что при дальнейшем всплытии форма пузырька не деформируется, а всплытие происходит в стационарном режиме по прямолинейной траектории. Рисунки 2a и 2б демонстрируют неравномерное распределение скорости внутри пузырька. Частицы жидкости, расположенные непосредственно за пузырьком, увлекаются вверх. Максимальные значения скорости жидкости наблюдаются между пузырьком и стенками резервуара, где жидкость перетекает вниз. Максимальные значения завихренности формируются по бокам полости, за которыми формируется пара симметричных вихревых областей (рис. 2в). Наличие циркуляции в полости демонстрирует рис. 2г.
Рис. 2.
Результаты расчета тестовой задачи № 1. Поля модуля скорости $\left| {\mathbf{u}} \right|$ (а), компоненты скорости ${{u}_{2}}$ (б), завихренности $\omega $ (в), трейсеры (г) в момент времени $t = 3.0$.
Дополнительно был проведен расчет задачи № 1 с условиями прилипания u = 0 на стенках резервуара (а не проскальзывания). Несмотря на то что взаимодействия поверхности раздела фаз со стенками резервуара не происходит, тип граничного условия на стенках влияет на результаты расчета подъема пузырька. Установлено, что при реализации условия прилипания на стенке нулевые значения вектора скорости на поверхности резервуара и силы вязкого трения способствуют более медленному всплытию пузырька в отличие от режима скольжения. Кроме того, при выполнении условия прилипания на стенке, пузырек при подъеме приобретает более узкую форму. Условия проскальзывания позволяют не учитывать влияние образующегося пограничного слоя у поверхности, снизить эффект вязких сил в пристеночной области.
Результаты расчета тестовой задачи № 2 в момент времени $t = 3.0$ показаны на рис. 3. Первоначально круглый пузырек в процессе всплытия приобретает полукруглую форму. Отметим, что коэффициент поверхностного натяжения в данном случае меньше, чем для задачи № 1. Это приводит к появлению вытянутых по бокам симметричных структур с утолщениями на концах. При этом увеличивается межфазная поверхность. В результате дальнейшей эволюции тонкие связывающие перемычки разрываются и образуются более мелкие включения, так называемые пузырьки-спутники. В области оторвавшихся мелких включений компонента скорости ${{u}_{2}}$ меняет свое направление с отрицательного около стенки до положительного за пузырьком (рис. 3б), а завихренность (рис. 3в) имеет более высокие значения по сравнению с задачей № 1 (рис. 2в), траектории трейсеров вытягиваются (рис. 3г). В пузырьке непрерывная циркуляция среды направлена вдоль его боковой поверхности вниз к кормовой части.
Рис. 3.
Результаты расчета тестовой задачи № 2. Поля модуля скорости $\left| {\mathbf{u}} \right|$ (а), компоненты скорости ${{u}_{2}}$ (б), завихренности $\omega $ (в), трейсеры (г) в момент времени $t = 3.0$.
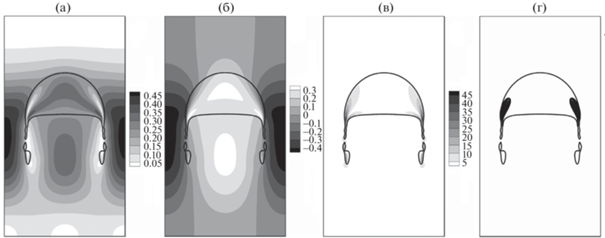
В работе [24] представлены результаты расчета тестовой задачи № 2 с помощью таких программных комплексов, как CFX, Comsol, Fluent, TP2D, FreeLIFE, MooNMD. Как правило, форма основной части пузырька хорошо согласуется для всех случаев. Однако полученные в результате расчета с использованием разных программных комплексов формы тонких вытянутых структур по бокам пузырька и оторвавшихся пузырьков-спутников отличаются. Отметим, что положение межфазной границы в момент времени $t = 3.0$ для тестовой задачи № 2 лучше согласуется с данными расчета по программе FreeLIFE [24].
В ходе проведения численных экспериментов скорость всплытия пузырька рассчитывается по формуле
На этапе нестационарного режима сравнение значений максимальной скорости всплытия пузырька $u_{{rise}}^{{\max }}$, и момента времени tmax, когда эта скорость достигается, представлено в табл. 3. Видно количественное согласие полученных расчетных данных с результатами других авторов для обеих тестовых задач.
Для анализа влияния формы пузырька в начальный момент времени на динамику его подъема в неподвижной вязкой жидкости фиксируется площадь пузырька из тестовой задачи $S = {{\pi {{d}^{2}}} \mathord{\left/ {\vphantom {{\pi {{d}^{2}}} 4}} \right. \kern-0em} 4}$, а также положение центра масс в начальный момент времени (0; 0.5). Каноническое уравнение эллипса записывается в форме ${{x_{1}^{2}} \mathord{\left/ {\vphantom {{x_{1}^{2}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}} + {{x_{2}^{2}} \mathord{\left/ {\vphantom {{x_{2}^{2}} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}} = 1$, здесь $a,\;b$ – горизонтальная и вертикальная полуоси эллипса, которые подбираются таким образом, чтобы выполнялось равенство $S = \pi ab$. Обозначим через $\eta = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$ коэффициент сжатия эллипса, характеризующий отклонение формы пузырька от круга. При проведении численных экспериментов коэффициент сжатия варьировался в диапазоне $0.309 \leqslant \eta \leqslant 3.24$. Кроме того, обозначим через TC1 набор входных параметров (${{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}} = 10$, ${{{{\mu }_{l}}} \mathord{\left/ {\vphantom {{{{\mu }_{l}}} {{{\mu }_{g}}}}} \right. \kern-0em} {{{\mu }_{g}}}} = 10$, $\operatorname{Re} = 35$, Bo = 10) для тестовой задачи № 1, и TC2 (${{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}} = 1000$, ${{{{\mu }_{l}}} \mathord{\left/ {\vphantom {{{{\mu }_{l}}} {{{\mu }_{g}}}}} \right. \kern-0em} {{{\mu }_{g}}}}$ = = 100, $\operatorname{Re} = 35$, Bo = 125) – для тестовой задачи № 2.
На рис. 4 показано, что в зависимости от начальной формы динамика пузырька имеет свои особенности. Пузырек, имеющий в начальный момент времени форму эллипса с коэффициентом сжатия $\eta = 3.24$, расположенный горизонтально, под действием силы поверхностного натяжения на начальном этапе стремится уменьшить длину межфазной поверхности и принять форму, близкую к круглой.
Рис. 4.
Эволюция формы пузырька и поля модуля скорости в процессе его всплытия для набора входных параметров TC1 при разных коэффициентах сжатия: слева – пузырек, растянутый по горизонтали ($\eta = 3.24$), по центру – круглый ($\eta = 1.00$), справа – растянутый по вертикали ($\eta = 0.309$).
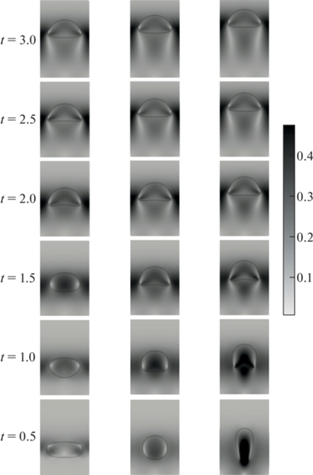
Пузырек, имеющий изначально круглую форму, при всплытии под действием массовых и поверхностных сил трансформируется. Изменение формы происходит в период нестационарного движения. Когда пузырек принимает форму полукруга, действующие на него силы Архимеда, тяжести, гидродинамического сопротивления, поверхностного натяжения уравновешиваются и дальнейшее всплытие происходит в стационарном режиме. Пузырек принимает устойчивую энергетически выгодную форму.
В случае, когда вертикальная полуось больше горизонтальной, сильно вытянутый эллипсоидальный пузырек ($\eta = 0.309$), под действием силы поверхностного натяжения, стремится к круглой форме за счет относительно высоких скоростей в нижней его части, в то время как верхняя его часть остается малоподвижной. Соответственно, наиболее активная деформация межфазной поверхности наблюдается в кормовой части пузырька. Стационарную форму такой пузырек принимает позже, чем изначально круглый.
Следует отметить, что подвижность межфазной поверхности выражается еще и в движении частиц вблизи этой поверхности в направлении от передней лобовой точки в сторону кормовой точки пузырька. При этом коэффициент сопротивления неравномерно распределяется вдоль поверхности раздела фаз. Сила сопротивления направлена против вектора скорости движения пузырька, ее величина пропорциональна поперечному сечению его формы. Следовательно, сила сопротивления частицы, ориентированной вертикально, меньше, чем ориентированной горизонтально. Это способствует более быстрому всплытию пузырька, расположенного изначально вертикально, чем вытянутого горизонтально.
Ниже представлены результаты численных экспериментов с набором входных параметров TC2. Рисунок 5 иллюстрирует деформацию поверхности и изменение поля скорости при всплытии пузырьков, имеющих разные формы в начальный момент времени. Пузырек, изначально вытянутый горизонтально ($\eta = 3.24$), в процессе всплытия постепенно деформируется в полукруг. Скорости относительно не велики. В случае, когда пузырек в начальный момент времени имеет форму вертикально вытянутого эллипса ($\eta = 0.309$), на первом этапе всплытия его кормовая часть быстро втягивается под влиянием силы поверхностного натяжения. На поверхности раздела двух сред с большой разницей плотностей (${{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}} = {{10}^{3}}$) при наличии ускорения создаются условия для развития неустойчивости Релея–Тейлора. Образуется струя жидкости, направленная внутрь пузырька. Деформация его границ увеличивает межфазную поверхность. Пузырек принимает подковообразную форму. В ходе дальнейшего подъема наблюдается трансформация к полукруглой форме с отрывом по бокам маленьких пузырьков-спутников, которые затем всплывают с меньшей скоростью, чем центральный крупный пузырек. Вертикально расположенный пузырек всплывает быстрее, его скорость больше. Нестабильность формы проявляется до некоторого момента времени, затем пузырек приобретает стабильную форму и дальнейший подъем происходит с постоянной скоростью.
Рис. 5.
Эволюция формы пузырька и поля модуля скорости в процессе его всплытия для набора входных параметров TC2 при разных коэффициентах сжатия: слева – пузырек, растянутый по горизонтали ($\eta = 3.24$), по центру – круглый ($\eta = 1.00$), справа – растянутый по вертикали ($\eta = 0.309$).

Результаты расчетов скорости всплытия для условий TC1 представлены на рис. 6a. В начальный момент времени пузырек из состояния покоя начинает движение. До некоторого момента времени tmax пузырек движется вверх с ускорением. Как отмечалось ранее, изменение скорости пузырька обусловлено деформацией его формы под влиянием действующих на него массовых и поверхностных сил. Показано, что при всплытии пузырька с параметрами TC1 скорость всплытия имеет один максимум $u_{{rise}}^{{\max }}$. Он достигается в момент времени tmax, когда нижняя часть межфазной поверхности деформируется с максимальной скоростью, а полость стремится принять форму полукруга. Установлено, что, чем меньше $\eta $, тем больше ускорение, тем выше максимальная скорость всплытия $u_{{rise}}^{{\max }}$ и раньше наступает момент tmax, когда скорость максимальна. Так, максимальная скорость всплытия достигает $u_{{rise}}^{{max}} = 0.3621$ при коэффициенте сжатия $\eta = 0.309$, $u_{{rise}}^{{max}} = 0.2377$ при $\eta = 1.00$, $u_{{rise}}^{{max}} = 0.2271$ при $\eta = 3.24$. Затем скорость пузырька монотонно снижается до постоянного значения $u_{{rise}}^{{const}} \approx 0.18$. Причем величина $u_{{rise}}^{{const}}$ не зависит от начальной формы пузырька, а только от его диаметра, физических свойств обеих фаз и ускорения свободного падения.
Рис. 6.
Изменение скорости всплытия пузырька с течением времени по результатам расчета задачи с условиями TC1 (a) и TC2 (б) при разных коэффициентах сжатия: 1–3 – $\eta = 0.309$, 1.00, 3.24.
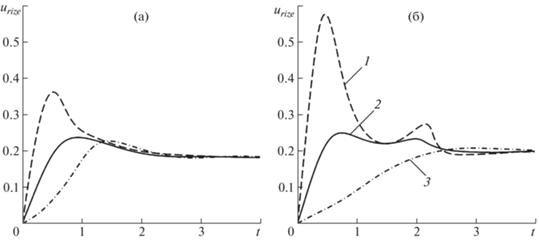
Анализ численных результатов показал (рис. 6б), что в случае условий задачи TC2 при $\eta = 0.309$ и $\eta = 1.00$, скорость всплытия пузырька ${{u}_{{rise}}}$ имеет два локальных максимума, причем второй имеет меньшую величину. Первый максимум скорости всплытия достигается в момент времени tmax, когда струя окружающей жидкости направлена по вертикали вверх на кормовую часть поверхности пузырька. В результате деформации пузырек приобретает подковообразную форму. Далее, боковые части утончаются, максимальные значения вертикальная компонента скорости принимает на боковых участках пузырька, а не в центральной ее части, как при достижении первого максимума. Затем наблюдается разрыв межфазной поверхности с образованием маленьких пузырьков-спутников. Стационарная скорость всплытия пузырька при условиях ТС2 составляет $u_{{rise}}^{{const}} \approx 0.20$.
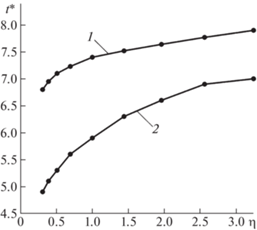
Кроме того, в ходе проведения численного эксперимента дополнительно замерялось время достижения кормовой точкой полости ${{P}_{2}}$ контрольной точки $K\left( {0.00;\;1.69} \right)$. Установлено, что время всплытия полости t* монотонно увеличивается с ростом соотношения полуосей эллипса $\eta $. На рис. 7 показано, что при фиксированном числе Рейнольдса Re = 35 полость всплывает быстрее в случае условий задачи TC2, когда больше отношение плотностей сред ${{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {{{\rho }_{g}}}}} \right. \kern-0em} {{{\rho }_{g}}}}$ и число Бонда. Так, при условиях TC1 безразмерное время всплытия до контрольной точки $K$ увеличивается на 17.6% с 6.8 при $\eta = 0.309$ до 8.0 при $\eta = 3.24$, тогда как при TC2 – увеличивается на 42.8% с 4.9 при $\eta = 0.309$ до 7.0 при $\eta = 3.24$.
ЗАКЛЮЧЕНИЕ
Исследован начальный этап всплытия пузырьков в вязкой жидкости, который происходит в нестационарном режиме. Показано, что на скорость подъема влияет исходная форма пузырьков. Пузырьки, которые в начальный момент времени имеют форму эллипса с вертикальной большой полуосью, всплывают быстрее круглых, и тем более, расположенных горизонтально. Увеличение скорости всплытия обусловлено двумя факторами: уменьшением силы сопротивления за счет сокращения поперечного сечения и формированием струи жидкости, направленной снизу на кормовую часть межфазной поверхности в результате развития неустойчивости Рэлея–Тейлора.
Список литературы
Архипов В.А., Васенин И.М., Ткаченко А.С., Усанина А.С. О нестационарном всплытии пузырька в вязкой жидкости при малых числах Рейнольдса // Изв. РАН. МЖГ. 2015. № 1. С. 88–94.
Hua J. CFD simulations of the effects of small dispersed bubbles on the rising of a single large bubble in 2D vertical channels // Chem. Eng. Sci. 2015. № 123. P. 99–115.
Козелков А.С., Куркин А.А., Курулин В.В., Лашкин С.В., Тарасова Н.В., Тятюшкина Е.С. Численное моделирование свободного всплытия пузырька воздуха // Изв. РАН. МЖГ. 2016. № 6. С. 3–14.
Лабунцов Д.А., Ягов В.В. Механика двухфазных систем: Учебное пособие для вузов. М.: Издательство МЭИ, 2000. 374 с.
Clift R., Grase J.R., Weber M.E. Bubbles, drops and particles. New York: Acad. Press, 1978. 398 p.
Архипов В.А., Васенин И.М., Усанина А.С. Анализ механизма потери устойчивости одиночного пузырька при малых значениях числа Рейнольдса // ПМТФ. 2011. Т. 52. № 3. С. 51–59.
Zahedi P., Saleh R., Moreno-Atanasio R., Yousefi K. Influence of fluid properties on bubble formation, detachment, rising and collapse. Investigation using volume of fluid method // Korean J. Chem. Eng. 2014. V. 31. № 8. P. 1349–1361.
Siriano S., Balcázar N., Tassone A., Rigola J., Caruso G. Numerical Simulation of High-Density Ratio Bubble Motion with interIsoFoam // Fluids. 2022. V. 7. № 152. P. 1–22.
Прибатурин Н.А., Меледин В.Г. Многоиформационная методика для экспериментального изучения двухфазных пузырьковых течений // Eurasian Phys. Tech. J. 2013. V. 10. № 2 (20). С. 288–292.
Cano-Lozano J.C., Martinez-Bazan C. Paths and wakes of deformable nearly spheroidal rising bubbles close to the transition to path instability // Physical review fluids. 2016. V. 1, 053604 P. 1–30.
Vries A.W.G., Biesheuvel A., Wijngaarden L. Notes on the path and wake of a gas bubble rising in pure water // Int. J. Multiph. Flow. 2002. № 28. P. 1823–1835.
Davies R.M., Taylor G.I. The mechanics of large bubbles rising through liquids in tubes // Proc. of Roy. Soc. London. 1950. V. 200. Ser. A. P. 375–390.
Козелков А.С., Ефремов В.Р., Дмитриев С.М., Куркин А.А., Пелиновский Е.Н., Тарасова Н.В., Стрелец Д.Ю. Исследование особенностей всплытия пузырьков воздуха и твердых сфер // Фундаментальная и прикладная гидрофизика. 2018. Т. 11. № 4. С. 73–80.
Baz-Rodríguez S., Aguilar-Corona A., Soria A. Rising velocity for single bubbles in pure liquids // Rev Mex Ing Quim. 2012. V. 11. № 2. P. 269–278.
Heydari N., Larachi F., Taghavi S.M., Bertrand F. Three-dimensional analysis of the rising dynamics of individual ellipsoidal bubbles in an inclined column // Chem. Eng. Sci. 2022. V. 258. 117759.
Архипов В.А., Васенин И.М., Усанина А.С. Динамика всплытия пузырька в присутствии поверхностно-активных веществ // Изв. РАН. МЖГ. 2016. № 2. С. 142–151.
Архипов В.А., Усанина А.С., Басалаев С.А., Каличкина Л.Е., Мальков В.С. Динамика всплытия кластера пузырьков в присутствии поверхностно-активного вещества // Изв. РАН. МЖГ. 2020. № 1. С. 104–112.
Hirt C.W., Nichols B.D. Volume of fluid (VOF) method for the dynamics of free boundaries // J. Computational Physics. 1981. V. 39. № 1. P. 201–225.
Martin J.C., Moyce W.J. An experimental study of the collapse of liquid columns on a rigid horizontal plane // Phil. Trans. Roy. Soc. London. 1952. V. 244. № 882. P. 312–324.
Моренко И.В. Численное моделирование обрушения столба жидкости в резервуарах разной формы // Вестник Томского государственного университета. Математика и механика. 2019. № 60. С. 119–131.
Morenko I.V. Numerical simulation of the propagation of pressure waves in water during the collapse of a spherical air cavity // Ocean Eng. 2020. V. 215. 107905. P. 1–9.
Моренко И.В. Численное моделирование имплозионного процесса в цилиндрическом резервуаре // ТВТ. 2019. Т. 57. № 5. С. 755–763.
Klostermann J., Schaake K., Schwarze R. Numerical simulation of a single rising bubble by VOF with surface compression // Int. J. Numer. Meth. Fluids. 2013. V. 71. P. 960–982.
Hysing S., Turek S., Kuzmin D., Parolini N., Burman E., Ganesan S., Tobiska L. Quantitative benchmark computations of two-dimensional bubble dynamics // Int. J. Numer. Meth. Fluids. 2009. № 60. P. 1259–1288.
Štrubelj L., Tiselj I., Mavko B. Simulations of free surface flows with implementation of surface tension and interface sharpening in the two-fluid model // Int. J. Heat Fluid Flow. 2009. № 30. P. 741–750.
Чжан И., Лян Б., Ни Ц. Численное исследование подъема пузырька в вертикальном клинообразном канале модифицированным методом функции уровня // Изв. РАН. МЖГ. 2020. № 2. С. 99–110.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа