Известия РАН. Механика жидкости и газа, 2023, № 4, стр. 146-155
ИССЛЕДОВАНИЕ РЕЖИМОВ ТЕПЛООБМЕНА В ДОЗВУКОВЫХ СТРУЯХ ДИССОЦИИРОВАННОГО АЗОТА ВЫСОКОЧАСТОТНОГО ИНДУКЦИОННОГО ПЛАЗМОТРОНА ПРИ ДОПОЛНИТЕЛЬНОМ НАГРЕВЕ ПОВЕРХНОСТИ ЛАЗЕРНЫМ ИЗЛУЧЕНИЕМ
С. А. Васильевский a, С. С. Галкин a, А. Ф. Колесников a, М. А. Котов a, И. В. Лукомский a, Н. Г. Соловьев a, Е. С. Тептеева a, А. В. Чаплыгин a, *, А. Н. Шемякин a, М. Ю. Якимов a
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: chaplygin@ipmnet.ru
Поступила в редакцию 06.01.2023
После доработки 28.02.2023
Принята к публикации 28.02.2023
- EDN: WLHQXY
- DOI: 10.31857/S1024708423600112
Аннотация
На индукционном ВЧ-плазмотроне ВГУ-4 (ИПМех РАН) проведены эксперименты по исследованию теплообмена цилиндрической водоохлаждаемой медной модели диаметром 30 мм, оснащенной калориметрическим датчиком с тепловоспринимающей поверхностью диаметром 13.8 мм из графита, при комбинированном режиме нагрева поверхности плазмой азота и лазерным излучением, а также для случаев нагрева поверхности только лазерным излучением или только струей плазмы азота. Эксперименты в струях ВЧ-плазмотрона проведены при давлении в барокамере установки p = 1 × 104 Па, массовом расходе азота G = 2.4 г/c, мощности ВЧ-генератора плазмотрона по анодному питанию Na.p. = 22 кВт. Для выбранных экспериментальных режимов установлено, что струя диссоциированного азота и высокочастотный индукционный разряд не оказывают заметного влияния на проходящий через них лазерный луч. Получены значения плотности теплового потока в зависимости от подведенной мощности лазерного излучения. Для рассмотренных условий экспериментов проведено численное моделирование дозвукового течения плазмы азота в кварцевом разрядном канале и в пространстве барокамеры установки ВГУ-4, основанное на решении полных уравнений Навье–Стокса методом Патанкара–Сполдинга.
Для атмосферного участка полета спускаемого космического аппарата в некоторых точках траектории радиационные тепловые потоки могут достигать значений, сопоставимых с конвективными тепловыми потоками [1–3]. В [4] показано, что радиационный тепловой поток со стороны излучающего газа к донной области аппарата Schiaparelli при спуске в атмосфере Марса может составлять до 70% от суммарного теплового потока. Задачи создания и исследования материалов тепловой защиты будущих межпланетных миссий потребуют глубокой модернизации существующих наземных экспериментальных установок для более достоверного моделирования условий радиационно-конвективного нагрева [5–7]. Примером такой модернизации служит создание в Центре Эймса (США) испытательного комплекса, где реализован нагрев поверхности плоских образцов потоком воздушной плазмы и лазерным излучением [8–10].
В ИПМех РАН выполнены эксперименты, демонстрирующие возможность комбинированного нагрева поверхности образца теплозащитного материала дозвуковыми струями плазмы азота индукционного ВЧ-плазмотрона ВГУ-4 и лучом иттербиевого импульсного волоконного лазера. Детальное описание экспериментов представлено в [11]. Целью данной работы являлось более подробное исследование особенностей режимов течения плазмы и теплообмена в условиях, близких к проведенным демонстрационным экспериментам.
1. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
Подробное описание 100-киловаттного ВЧ-плазмотрона ВГУ-4 (ИПМех РАН) приведено в [12]. Для реализации режимов комбинированного радиационно-конвективного нагрева установка была модернизирована: 1) в состав установки включен импульсный волоконный лазер; 2) изменена конструкция формирователя потока газа в нижнем интерфейсе разрядного канала плазмотрона (предусмотрено кварцевое окно и канал для наведения лазерного луча на поверхность образцов материалов или моделей). Схема ВЧ-плазмотрона ВГУ-4, дополнительно оснащенного источником лазерного излучения, приведена на рис. 1.
Рис. 1.
Схема ВЧ-плазмотрона ВГУ-4, дополнительно оснащенного источником лазерного излучения: 1 – импульсный волоконный лазер; 2 – линза; 3 – поворотное зеркало; 4 – кварцевое окно; 5 – дозвуковая струя плазмы азота; 6 – лазерный луч; 7 – медная водоохлаждаемая модель с калориметрическим датчиком; 8 – смотровое окно.
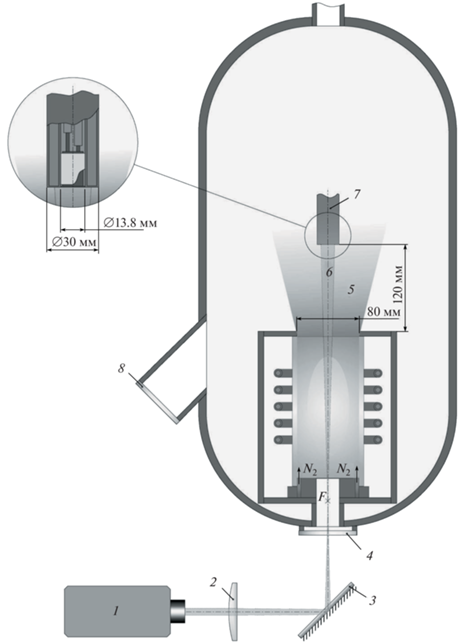
В качестве источника лазерного излучения выбран иттербиевый волоконный лазер IPG Photonics YPLN-1-100-200-R с высокой направленностью и стабильностью излучения. Коэффициент поглощения излучения на длине волны лазерного излучения 1.064 мкм составляет 0.8–0.9 для широкого спектра высокотемпературных материалов. Для транспортировки излучения от лазерной головки 1 (рис. 1) к поверхности водоохлаждаемой цилиндрической медной модели 7 вдоль оси плазменного потока индукционного плазмотрона 5 была собрана внешняя оптическая система, формирующая пятно облучения с известным распределением интенсивности. Система транспортировки излучения включала поворотное зеркало 3, предназначенное для совмещения осей лазерного луча 6 и плазменного потока. Положение зеркала и угол его наклона регулировались с помощью микрометрических винтов для точной настройки положения пятна облучения на поверхности модели. Размер пятна облучения определялся пространственными характеристиками лазерного луча и параметрами линзы 2, расположенной на оси системы транспортировки излучения. Модель помещалась в расходящуюся часть лазерного пучка за фокусом линзы F, так что размер пятна зависел от отношения фокусного расстояния линзы к расстоянию от линзы до модели вдоль оптической оси. Лазерный луч вводился в вакуумный объем испытательной камеры через прозрачное кварцевое окно 4. В экспериментах распределение облученности поверхности модели в пятне было близко к гауссовскому распределению с радиусом 10 мм. В лобовой части модели предусмотрено гнездо для установки образцов исследуемых материалов. В представленной работе вместо образца в лобовой части водоохлаждаемой цилиндрической медной модели располагался датчик теплового потока. Через смотровое окно 8 с помощью тепловизора проводились измерения температуры поверхности датчика.
2. ЭКСПЕРИМЕНТЫ
В экспериментах исследовался теплообмен лобовой части цилиндрической водоохлаждаемой медной модели диаметром dm = 30 мм с плоским торцом в режимах радиационного нагрева поверхности лазерным лучом, а также в режимах комбинированного радиационно-конвективного нагрева поверхности лазерным лучом и дозвуковым потоком плазмы азота. Расстояние от торца модели до выходного сечения разрядного канала плазмотрона составляло Z = 120 мм. Диаметр цилиндрического кварцевого разрядного канала плазмотрона D = 80 мм. Эксперименты проводились при давлении в барокамере установки p = 1 × 104 Па. Массовый расход азота во всех экспериментах составлял G = 2.4 г/c и контролировался с помощью электронного газового ротаметра Bronkhorst MV-306. Мощность ВЧ-генератора плазмотрона по анодному питанию при комбинированном нагреве поверхности поддерживалась постоянной Na.p. = 22 кВт.
Тепловые потоки определялись с помощью цилиндрического проточного стационарного калориметра [13], установленного в центре лобовой части модели. Диаметр тепловоспринимающей поверхности калориметра составлял 13.8 мм. Калориметр был теплоизолирован от модели с помощью фторопластовой втулки. Погрешность измерений для проточного калориметра не превышала 10% [14]. При измерениях тепловых потоков от радиационного нагрева или в режиме комбинированного радиационно-конвективного нагрева не представлялось возможным использовать калориметры с тепловоспринимающей поверхностью из высококаталитичной меди, которые широко распространены в исследованиях конвективного теплообмена моделей, обтекаемых струями высокоэнтальпийных химически активных газов; полированная медная поверхность отразила бы основную часть лазерного излучения, и потребовалось чернение поверхности датчика. Для решения проблемы использован калориметр с тепловоспринимающей поверхностью из графита, обладающей высокой поглощательной способностью на длине волны ~1 мкм [15]. Массовый расход охлаждающей воды в калориметре измерялся ультразвуковым жидкостным расходомером Bronkhorst ES-FLOW и составлял 2 г/c во всех экспериментах. Разность температур охлаждающей воды на выходе из калориметра и на входе в него измерялась экранированной дифференциальной термопарой типа ХА (хромель-алюмель).
В экспериментах использовался импульсно-периодический режим работы лазера с высокой частотой следования импульсов. При частоте 1 МГц импульсная мощность излучения превышала среднюю менее чем в 10 раз. Для нагрева поверхности режим работы лазера с высокой частотой повторения импульсов практически не отличается от непрерывного режима.
Потери излучения на элементах оптической системы складывались из поглощения, рассеяния и обратного отражения от прозрачных поверхностей. Пропускание кварцевой линзы и кварцевого окна (τwin = τlens = 0.935) без просветляющих покрытий составляло суммарно τwin ∙ τlens = = 0.87. Поглощение на поворотном зеркале приводило к коэффициенту пропускания τmir = 0.92. Таким образом, суммарно пропускание оптической системы составляло τs = τwin ∙ τlens ∙ τmir = 0.8, т.е. мощность лазерного излучения, подводимая к модели, Nincident была на 20% ниже выходной мощности лазера. Для проверки этого соотношения была измерена зависимость Nincident от заданной выходной мощности лазера. Nincident контролировалась с помощью предварительно откалиброванного измерителя мощности лазера OPHIR Starlite с термопарной измерительной головкой 50(150)A-BB-26. Измерительная головка располагалась в расходящемся пучке таким образом, чтобы соотношение диаметров пятна излучения и приемной площадки было таким же, как на исследуемой модели. При расчете средней интенсивности излучения на поверхности датчика Iincident мощность излучения, подводимая к поверхности датчика, рассчитывалась как интеграл от распределения интенсивности по поверхности датчика. Распределение интенсивности считалось гауссовским и нормировалось на измеренную величину Nincident.
На рис. 2 точками показана измеренная величина Nincident в зависимости от задаваемой выходной мощности лазера Nlaser. Пунктиром показана линейная интерполяция зависимости Nincident = = 0.8 ∙ Nlaser – 0.4. Сплошной линией показана рассчитанная из данных измерения зависимость средней интенсивности излучения Iincident на поверхности проточного калориметра диаметром 13.8 мм, расположенного на месте облучаемого образца, от выходной мощности излучения лазера Nlaser (ось ординат Iincident справа).
Рис. 2.
Измеренные значения мощности лазерного излучения (Nincident), подводимой к модели, и рассчитанная зависимость средней интенсивности излучения (Iincident) на поверхности проточного калориметра диаметром 13.8 мм, установленного в лобовой части модели, в зависимости от выходной мощности лазерного излучения (Nlaser).

Результаты измерений тепловых потоков стационарным проточным калориметром с тепловоспринимающей поверхностью из графита в режиме радиационного нагрева лобовой поверхности модели лучом лазера и в режиме комбинированного радиационно-конвективного нагрева поверхности лучом лазера и дозвуковым потоком плазмы азота приведены на рис. 3.
Рис. 3.
Измеренные значения плотности теплового потока в области лобовой точки цилиндрической медной модели в зависимости от подводимой мощности лазерного излучения (Nincident): 1 – радиационный нагрев лазерным излучением; 2 – комбинированный нагрев при одновременном воздействии дозвуковой струи диссоциированного азота и лазерного излучения.

В табл. 1 представлены значения измеренных калориметром плотностей тепловых потоков (qw) для режимов радиационного нагрева поверхности лучом лазера без воздействия плазмы азота и рассчитанные значения средней интенсивности излучения на поверхности калориметра (Iincident) в зависимости от подведенной мощности лазерного излучения (Nincident).
Таблица 1.
Радиационный нагрев
| Nincident (Вт) | Iincident (Вт/см2) | qw (Вт/см2) | Tw (°C) |
|---|---|---|---|
| 15 | 6.2 | 6.0 | 30 |
| 31 | 12.7 | 11.8 | 36 |
| 39 | 16.0 | 14.1 | 39 |
| 47 | 19.3 | 17.6 | 42 |
В табл. 2 представлены значения измеренных калориметром плотностей тепловых потоков (qw) для режимов комбинированного радиационно-конвективного нагрева поверхности лучом лазера и дозвуковым потоком плазмы азота (при мощности ВЧ-генератора плазмотрона Na.p. = = 22 кВт) в зависимости от подведенной мощности лазерного излучения (Nincident). Также в табл. 1, 2 приведены температуры поверхности датчика (Tw), измеренные с помощью тепловизора Testo 890.
Таблица 2.
Комбинированный радиационно-конвективный нагрев
| Nincident (Вт) | qw (Вт/см2) | Tw (°C) |
|---|---|---|
| 0 | 10.4 | 54 |
| 15 | 16.7 | 60 |
| 31 | 22.8 | 61 |
| 39 | 24.4 | 64 |
| 47 | 29.0 | 66 |
Как видно из табл. 1 и 2, несмотря на водяное охлаждение калориметра и высокую теплопроводность графита, наблюдается рост температуры нагреваемой поверхности по мере роста подводимого теплового потока, как в режимах комбинированного нагрева, так и при воздействии только лазерного луча.
Как видно из рис. 3, тепловые потоки в режиме комбинированного нагрева превышают тепловые потоки, полученные в режиме радиационного нагрева при тех же мощностях подведенного лазерного излучения, на величину вклада конвективного теплового потока от струи азотной плазмы, зарегистрированную при выключенном источнике лазерного излучения. Таким образом, струя плазмы азота и высокочастотный индукционный разряд не оказывают заметного влияния на проходящий через них лазерный луч для выбранных экспериментальных режимов. В первую очередь это связано с относительно низким давлением в барокамере установки (p = = 1 × 104 Па).
3. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Для рассмотренных условий экспериментов в ВЧ-плазмотроне ВГУ-4 проведено численное моделирование течения плазмы азота, включавшее решение двух задач:
1) численное моделирование дозвукового течения плазмы азота в цилиндрическом кварцевом разрядном канале диаметром 80 мм;
2) численное моделирование течения в струе, истекающей из разрядного канала в пространство барокамеры установки ВГУ-4 и обтекающей цилиндрическую модель диаметром 30 мм с плоским носком.
Расчет течения равновесной плазмы азота в разрядном канале проводился по программе Alpha [16] на основе уравнений Навье–Стокса. Потери энергии, связанные с излучением плазмы, принимались малыми и не учитывались. Течение в разрядном канале считалось ламинарным, стационарным и осесимметричным с азимутальной закруткой потока. Полные уравнения Навье–Стокса решались методом конечных объемов по алгоритму SIMPLE Патанкара–Сполдинга [17]. На рис. 4 показаны результаты расчета изолиний безразмерной функции тока (а) и изотерм (б).
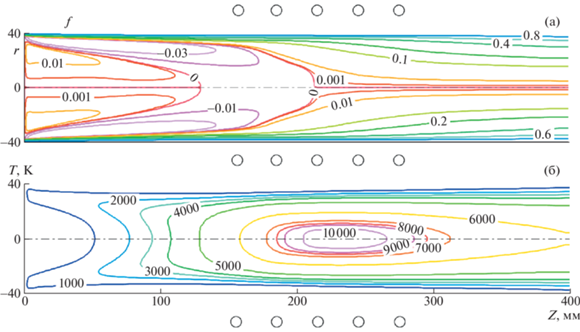
Рис. 4.
Изолинии безразмерной функции тока (а) и изотермы (б) плазмы азота в разрядном канале установки ВГУ-4 для p = 1 × 104 Па, Na.p. = 22 кВт, Npl = 12.65 кВт, G = 2.4 г/c.
Численное моделирование течения в струе, истекающей из разрядного канала и обтекающей цилиндрическую модель, проводилось по программе Beta [16]. Уравнения Навье–Стокса также решались методом Патанкара–Сполдинга. В качестве граничных условий в начале расчетной области использованы параметры газа на срезе разрядного канала, полученные в результате решения предыдущей задачи в программе Alpha. Расчет по программе Beta тоже проводится в предположении термодинамически и химически равновесного течения плазмы азота.
Результаты расчета по программе Beta показаны на рис. 5–7. На рис. 5 приведены изолинии безразмерной функции тока. На рис. 6 приведены изотермы струи диссоциированного азота. На рис. 7 представлены распределения скорости (а), энтальпии (б), динамического давления (в) и молярной концентрации атомов азота (г) на оси струи между выходным сечением разрядного канала и лобовой поверхностью цилиндрической модели в зависимости от расстояния Z до выходного сечения разрядного канала. Энтальпия на оси струи вблизи выходного сечения канала h = 20.4 МДж/кг, скорость U = 76 м/c, молярная концентрация атомов азота XN = 0.53. Из рис. 7 видно, что в рассмотренном режиме дозвуковая струя плазмы азота низконапорная (максимальное расчетное значение динамического давления на оси струи Pdyn = 12 Па), что затрудняет экспериментальные измерения динамических давлений с помощью трубки Пито и дифференциального мембранного преобразователя давления “Элемер” АИР-20/М2-ДД (максимальный верхний предел измерений 1.6 кПа, предел допускаемой основной приведенной погрешности ±0.2%).
Рис. 5.
Изолинии безразмерной функции тока дозвуковой струи диссоциированного азота, обтекающей цилиндр с плоским торцом диаметром 30 мм для p = 1 × 104 Па, Na.p. = 22 кВт, Npl = 12.65 кВт, G = 2.4 г/c, Z = 120 мм.
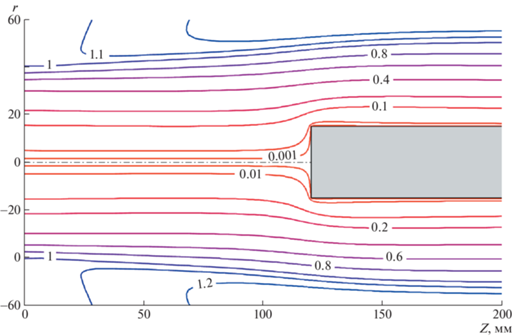
Рис. 6.
Изотермы дозвуковой струи диссоциированного азота, обтекающей цилиндр с плоским торцом диаметром 30 мм для p = 1 × 104 Па, Na.p. = 22 кВт, G = 2.4 г/c, Z = 120 мм.
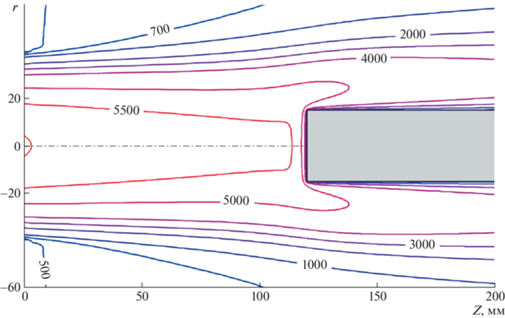
Рис. 7.
Распределение скорости (а), энтальпии (б), динамического давления (в) и молярной концентрации атомов азота (г) на оси струи между выходным сечением разрядного канала и лобовой поверхностью цилиндрической модели в зависимости от расстояния Z до выходного сечения разрядного канала для p = 1 × 104 Па, Na.p. = 22 кВт, G = 2.4 г/c.

Основные рабочие параметры ВЧ-плазмотрона ВГУ-4 (давление в барокамере установки, массовый расход азота и мощность ВЧ-генератора плазмотрона по анодному питанию), использованные при численном моделировании течения плазмы и в экспериментах по определению тепловых потоков в данной работе, соответствовали реализованным в [11] при нагреве образца низкотеплопроводного теплозащитного материала. Геометрия передней части водоохлаждаемой медной модели отличалась от геометрии образца теплозащитного материала: образец был выполнен со скругленной лобовой частью (радиусом 62.3 мм) и скругленными кромками (радиусом 4 мм), в то время как лобовая часть медной модели представляла собой плоский торец. При этом совпадали расстояния от выходного сечения разрядного канала до лобовой части образца и модели (Z), максимальный диаметр образца и диаметр цилиндрической медной модели. Таким образом, результаты численного моделирования основных параметров дозвуковой струи плазмы азота, истекающей из разрядного канала ВЧ-плазмотрона ВГУ-4, можно также распространить на соответствующие режимы течения в экспериментах [11] и использовать при анализе их результатов. Численное моделирование течения вблизи поверхности образца низкотеплопроводного теплозащитного материала потребует уточнения геометрии расчетной области и граничных условий на поверхности образца.
ЗАКЛЮЧЕНИЕ
Численно и экспериментально исследованы новые режимы радиационно-конвективного нагрева водоохлаждаемой цилиндрической медной модели, оснащенной проточным калориметром с тепловоспринимающей поверхностью из графита, в дозвуковых струях плазмы азота ВЧ-плазмотрона ВГУ-4 при одновременном воздействии лазерного излучения.
В условиях радиационного нагрева лазерным лучом (без воздействия плазмы азота) плотность теплового потока к графитовой поверхности проточного калориметра составляла от 6.0 до 17.6 Вт/см2. При комбинированном воздействии плазмы азота и лазерного излучения на графитовой поверхности проточного калориметра реализована плотность теплового потока от 16.7 до 29.0 Вт/см2. Установлено, что для выбранных режимов дозвуковая струя плазмы азота и индукционный высокочастотный разряд не оказывают заметного влияния на проходящий через них лазерный луч.
Представленные результаты будут использованы при анализе данных экспериментов по теплообмену образцов теплозащитных материалов для соответствующих режимов комбинированного радиационно-конвективного нагрева.
Работа выполнена по теме гранта РНФ 22-79-10083 (https://rscf.ru/project/22-79-10083/) с использованием ВЧ-плазмотрона ВГУ-4, который входит в состав уникальной научной установки РФ “Высокочастотные индукционные плазмотроны ВГУ-3 и ВГУ-4” (http://www.ckp-rf.ru//usu/441568).
Список литературы
Park C. Calculation of stagnation-point heating rates associated with stardust vehicle // J. Spacecr. Rockets. 2007. V. 44. № 1. P. 24–32. https://doi.org/10.2514/1.15745
Dikalyuk A., Kozlov P., Romanenko Y., Shatalov O., Surzhikov S. Nonequilibrium Spectral Radiation Behind the Shock Waves in Martian and Earth Atmospheres // 44th AIAA Thermophysics Conf. Reston, Virginia. 2013. P. 1–27. https://doi.org/10.2514/6.2013-2505
Surzhikov S.T. Radiative-Collisional Models in Non-Equilibrium Aerothermodynamics of Entry Probes // J. Heat Transfer. 2012. V. 134. № 3. P. 1–11. https://doi.org/10.1115/1.4005127
Суржиков С.Т., Яцухно Д.С. Анализ летных данных по конвективному и радиационному нагреву поверхности спускаемого марсианского космического аппарата Schiaparelli // Изв. РАН. МЖГ. 2022. № 6. С. 74–85. https://doi.org/10.31857/S0568528122600394
Venkatapathy E., Ellerby D., Gage P., Prabhu D., Gasch M., Kazemba C., Kellerman C., Langston S., Libben B., Mahzari M., Milos F., Murphy A., Nishioka O., Peterson K., Poteet C., Splinter S., Stackpoole M., Williams J., Young Z. Entry system technology readiness for ice-giant probe missions // Space Sci. Rev. 2020. V. 216. № 2. P. 1–21. https://doi.org/10.1007/s11214-020-0638-2
Laub B., Venkatapathy E. Thermal protection system technology and facility needs for demanding future planetary missions // Planetary Probe Atmospheric Entry and Descent Trajectory Analysis and Science. ESA Publications Division. 2004. V. 544. P. 239–247.
Venkatapathy E., Laub B., Hartman G.J., Arnold J.O., Wright M.J., Allen Jr G.A. Thermal protection system development, testing, and qualification for atmospheric probes and sample return missions: Examples for Saturn, Titan and Stardust-type sample return // Adv. Sp. Res. 2009. V. 44. № 1. P. 138–150. https://doi.org/10.1016/j.asr.2008.12.023
Cushman G., Alunni A., Balboni J., Zell P., Hartman J., Empey D. The Laser Enhanced Arc-Jet Facility (LEAF-Lite): Simulating Convective and Radiative Heating with Arc-jets and Multiple 50-kW CW Lasers // Joint Thermophysics and Heat Transfer Conf. 2018. P. 3273. https://doi.org/10.2514/6.2018-3273
Gokcen T., Alunni A. CFD Simulations of the IHF Arc-Jet Flow: 9-Inch Nozzle, Flow Surveys, LEAF Wedge Calibration Data // AIAA Aviation Forum. 2019. P. 3008. https://doi.org/10.2514/6.2019-3008
Alunni A.I., Gokcen T., Boghozian T. Laser-Enhanced Arc-Jet Facility Wedge Tests: Avcoat Material Performance Under Convective and Radiative Heating Environments // Joint Thermophysics and Heat Transfer Conf. 2019. № ARC-E-DAA-TN62912.
Chaplygin A., Kotov M., Yakimov M., Lukomskii I., Galkin S., Kolesnikov A., Shemyakin A., Solovyov N. Combined Surface Heating by Laser Beam and Subsonic Nitrogen Plasma Jet // Fluids. 2023. 8 (1): 11. https://doi.org/10.3390/fluids8010011
Колесников А.Ф., Гордеев А.Н. Высокочастотные индукционные плазмотроны серии ВГУ // Актуальные проблемы механики: Физико-химическая механика жидкостей и газов. М.: Наука, 2010. С. 151–177.
ASTM E422-05(2016). Standard Test Method for Measuring Heat Flux Using a Water-Cooled Calorimeter // ASTM International, West Conshohocken, PA. 2016.
Bottin B., Chazot O., Carbonaro M., Van Der Haegen V., Paris S. The VKI plasmatron characteristics and performance: tech. rep. Von Karman Institute For Fluid Dynamics. Rhode-Saint-Genese (Belgium). 2000. 27 p.
Touloukian Y.S., DeWitt D.P. Thermophysical properties of matter. Purdue Univ. 1972. V. 8. P. 1890.
Васильевский С.А., Колесников А.Ф. Численное исследование течений и теплообмена в индукционной плазме высокочастотного плазмотрона // Энциклопедия низкотемпературной плазмы. Серия Б. 2008. Т. 1, Ч. 2. С. 220–234.
Patankar S.V. Numerical Heat Transfer and Fluid Flow. CRC Press, 2018. 214 p.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


