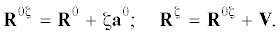Проблемы машиностроения и надежности машин, 2022, № 3, стр. 29-44

Расчет тонкой оболочки в форме эллипсоида на основе совместного треугольного элемента дискретизации с инвариантной интерполяционной процедурой

Ю. В. Клочков^1, *, Н. А. Гуреева², О. В. Вахнина¹, Т. А. Соболевская¹, М. Ю. Клочков³

¹ Волгоградский государственный аграрный университет
Волгоград, Россия

² Финансовый университет при Правительстве РФ
Москва, Россия

³ Московский государственный университет им. М.В. Ломоносова
Москва, Россия

^* E-mail: klotchkov@bk.ru

Поступила в редакцию 24.01.2021
После доработки 05.02.2022
Принята к публикации 11.02.2022

EDN: FLJVKF
DOI: 10.31857/S0235711922030075

Полный текст (PDF)

Аннотация

Разработан алгоритм получения матрицы жесткости элемента дискретизации в форме треугольного фрагмента срединной поверхности эллипсоидальной оболочки с узловыми неизвестными в его вершинах в виде компонент векторов перемещений и их частных производных первого порядка по криволинейным координатам. Для улучшения условий непрерывности на границах смежных элементов в значениях производных перемещений, перпендикулярных к срединной поверхности, вдоль касательных нормалей к граничным кривым смежных дискретных элементов использованы множители Лагранжа в серединах сторон. На примере расчета тонкой упругой оболочки со срединной поверхностью в форме эллипсоида, нагруженного внутренним давлением, показана эффективность разработанного конечного элемента.

Ключевые слова: эллипсоидальная оболочка, радиус-вектор, параметризация эллипсоида, треугольный конечный элемент, базисные векторы, скалярная интерполяция, векторная интерполяция, множители Лагранжа, условный функционал, матрица жесткости

В настоящее время область применения оболочечных конструкций все более расширяется благодаря их легкости и экономичности с точки зрения расхода материала. Причем геометрия такого рода конструкций все более усложняется [1], не ограничиваясь только цилиндрической формой. Несмотря на достаточно подробно разработанную теорию деформирования твердых тел [2–8] аналитическое решение систем дифференциальных уравнений, описывающих процесс деформирования оболочечных конструкций возможно лишь для наиболее простых случаев, в основном, для оболочек цилиндрической формы. Поэтому, в последнее время наибольшую популярность приобрели численные методы расчета оболочечных конструкций [9–16], среди которых на первый план вышел метод конечных элементов (МКЭ). Несмотря на значительное количество публикаций [17–29] актуальной задачей остается совершенствование конечно-элементных алгоритмов расчета оболочек сложной геометрии с использованием альтернативной общепринятой формой интерполяционной процедуры, основанной на интерполяции компонент вектора перемещения как составляющих векторных полей [30]. В настоящей статье излагается алгоритм расчета тонкой упругой оболочки в форме трехосного эллипсоида на основе конечного элемента треугольной формы, для улучшения совместности которого на границах смежных элементов применяются дополнительные узловые неизвестные в виде множителей Лагранжа. На основе векторной формы интерполяционной процедуры получены интерполяционные выражения для компонент вектора перемещения и их производных в глобальной криволинейной системе координат.

Геометрия эллипсоидальной оболочки. Срединная поверхность эллипсоидальной оболочки, например, эллипсоида в декартовой системе координат задается радиус-вектором

(1)

${{{\mathbf{R}}}^{{\text{0}}}} = x{\mathbf{i}} + y{\mathbf{j}} + c\sqrt {1 - {{{\left( {x{\text{/}}a} \right)}}^{{\text{2}}}} - {{{\left( {y{\text{/}}b} \right)}}^{{\text{2}}}}} {\mathbf{k}}{\text{,}}$

где a, b, c – полуоси трехосного эллипсоида.

Дифференцированием (1) по x и y можно получить тангенциальные векторы локального базиса точки срединной поверхности эллипсоида

(2)

$\begin{gathered} a_{1}^{0} = R_{{,x}}^{0} = i - \frac{{cx}}{{{{a}^{2}}\sqrt {1 - {{{\left( {x{\text{/}}a} \right)}}^{2}} - {{{\left( {y{\text{/}}b} \right)}}^{2}}} }}k; \\ a_{2}^{0} = R_{{,y}}^{0} = j - \frac{{cy}}{{{{b}^{2}}\sqrt {1 - {{{\left( {x{\text{/}}a} \right)}}^{2}} - {{{\left( {y{\text{/}}b} \right)}}^{2}}} }}k{\text{.}} \\ \end{gathered} $

Использование формул (2) не вполне удобно вследствие необходимости соблюдения условия

(3)

${\text{1}} - {{\left( {x{\text{/}}a} \right)}^{{\text{2}}}} - {{\left( {y{\text{/}}b} \right)}^{{\text{2}}}} > {\text{0}}{\text{.}}$

Поэтому наиболее приемлемым является использование параметрической формулы [31]

(4)

${{{\mathbf{R}}}^{{\text{0}}}} = x{\mathbf{i}} + {{b}_{x}}\sin t{\mathbf{j}} + {{c}_{x}}\cos t{\mathbf{k}}.$

Входящие в (4) ${{b}_{x}}$ и ${{c}_{x}}$ представляют собой полуоси эллипса, являющегося сечением эллипсоида плоскостью, перпендикулярной оси $Ox$ на расстоянии $x$ от начала координат

(5)

${{b}_{x}} = b\sqrt {{\text{1}} - {{{\left( {x{\text{/}}a} \right)}}^{{\text{2}}}}} {\text{;}}\quad {{c}_{x}} = c\sqrt {{\text{1}} - {{{\left( {x{\text{/}}a} \right)}}^{{\text{2}}}}} {\text{.}}$

Дифференцируя (4) по x и t можно получить векторы локального базиса, лежащие в соприкасающейся плоскости к срединной поверхности эллипсоида

(6)

${\mathbf{a}}_{{\text{1}}}^{{\text{0}}} = {\mathbf{i}} - \frac{{bx\sin t}}{{{{a}^{2}}\sqrt {1 - {{{\left( {x{\text{/}}a} \right)}}^{2}}} }}{\mathbf{j}} - \frac{{cx\cos t}}{{{{a}^{2}}\sqrt {1 - {{{\left( {x{\text{/}}a} \right)}}^{2}}} }}{\mathbf{k}}{\text{;}}\quad {\mathbf{a}}_{{\text{2}}}^{{\text{0}}} = {{b}_{x}}\cos t{\mathbf{j}} - {{c}_{x}}\sin t{\mathbf{k}}{\text{.}}$

Орт нормали к срединной поверхности эллипсоида определяется векторным произведением

(7)

${{a}^{0}} = \frac{{a_{1}^{0} \times a_{2}^{0}}}{{\sqrt {{{a}^{0}}} }} = \frac{{\left( {{{bcx} \mathord{\left/ {\vphantom {{bcx} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}} \right)i + \left( {{{c\sqrt {{{a}^{2}} - {{x}^{2}}} \sin t} \mathord{\left/ {\vphantom {{c\sqrt {{{a}^{2}} - {{x}^{2}}} \sin t} a}} \right. \kern-0em} a}} \right)j + \left( {{{b\sqrt {{{a}^{2}} - {{x}^{2}}} \cos t} \mathord{\left/ {\vphantom {{b\sqrt {{{a}^{2}} - {{x}^{2}}} \cos t} a}} \right. \kern-0em} a}} \right)k}}{{\sqrt {{{a}^{0}}} }},$

где ${{a}^{{\text{0}}}} = \left( {{\mathbf{a}}_{{\text{1}}}^{{\text{0}}} \cdot {\mathbf{a}}_{{\text{1}}}^{{\text{0}}}} \right)\left( {{\mathbf{a}}_{{\text{2}}}^{{\text{0}}} \cdot {\mathbf{a}}_{{\text{2}}}^{{\text{0}}}} \right) - {{\left( {{\mathbf{a}}_{{\text{1}}}^{{\text{0}}} \cdot {\mathbf{a}}_{{\text{2}}}^{{\text{0}}}} \right)}^{{\text{2}}}}$ – детерминант метрического тензора, отнесенного к точке срединной поверхности эллипсоида.

На основании (6) и (7) можно скомпоновать прямую и обратную матричные зависимости

(8)

$\mathop {\left\{ {{{{\mathbf{a}}}^{{\text{0}}}}} \right\}}\limits_{{\text{3}} \times {\text{1}}} = \mathop {\left[ {{{d}^{{\text{0}}}}} \right]}\limits_{{\text{3}} \times {\text{3}}} \mathop {\left\{ {\mathbf{i}} \right\}}\limits_{{\text{3}} \times {\text{1}}} {\text{;}}\quad \mathop {\left\{ {\mathbf{i}} \right\}}\limits_{{\text{3}} \times {\text{1}}} = {{\mathop {\left[ {{{d}^{{\text{0}}}}} \right]}\limits_{{\text{3}} \times {\text{3}}} }^{{ - {\text{1}}}}}\mathop {\left\{ {{{{\mathbf{a}}}^{{\text{0}}}}} \right\}}\limits_{{\text{3}} \times {\text{1}}} {\text{,}}$

где ${{\left\{ {{{{\mathbf{a}}}^{{\text{0}}}}} \right\}}^{T}} = \left\{ {{\mathbf{a}}_{{\text{1}}}^{{\text{0}}}{\mathbf{a}}_{{\text{2}}}^{{\text{0}}}{\mathbf{a}}_{{}}^{{\text{0}}}} \right\}$; ${{\left\{ {\mathbf{i}} \right\}}^{T}} = \left\{ {{\mathbf{ijk}}} \right\}$.

Дифференцируя первое матричное соотношение (8) по $x$ и $t$, получим производные векторов локального базиса, которые можно представить компонентами этого же базиса

(9)

$\begin{gathered} \left\{ {a_{{,x}}^{0}} \right\} = \left[ {d_{{,x}}^{0}} \right]\left\{ i \right\} = \left[ {d_{{,x}}^{0}} \right]{{\left[ {d_{{}}^{0}} \right]}^{{ - 1}}}\left\{ {a_{{}}^{0}} \right\}; \\ \left\{ {a_{{,t}}^{0}} \right\} = \left[ {d_{{,t}}^{0}} \right]\left\{ i \right\} = \left[ {d_{{,t}}^{0}} \right]{{\left[ {{{d}^{0}}} \right]}^{{--1}}}\left\{ {a_{{}}^{0}} \right\}{\text{.}} \\ \end{gathered} $

В процессе деформирования под действием заданной нагрузки точка ${{N}^{{\text{0}}}}$ срединной поверхности эллипсоида займет новое положение $N$, а точка N^0ζ, отстоящая от точки N по нормали на расстоянии ζ, переместится в точку N^ζ.

Радиус-векторы, характеризующие положения точек N^0ζ и N^ζ, определяются выражениями

(10)

Входящий в (10) вектор перемещения точки N^0ζ на основании гипотезы о прямой нормали определяется выражением

(11)

${\mathbf{V}} = {\mathbf{v}} + {{\zeta }}\left( {{\mathbf{a}} - {{{\mathbf{a}}}^{{\text{0}}}}} \right){\text{,}}$

где ${\mathbf{a}}$ – орт нормали к срединной поверхности точки $N$.

Входящий в (11) вектор перемещения точки срединной поверхности N⁰ и его производные по $x$ и $t$ можно представить компонентами, отнесенными к локальному базису этой же точки

(12)

$v = {{{v}}^{\rho }}a_{\rho }^{0} + {v}a_{{}}^{0};\quad {{v}_{{,\alpha }}} = l_{\alpha }^{\rho }a_{\rho }^{0} + l_{\alpha }^{{}}a_{{}}^{0},$

где ${{{v}}^{\rho }}$, ${v}$ – тангенциальная и нормальная компоненты вектора перемещения соответственно; $l_{\alpha }^{\rho }$, ${{l}_{\alpha }}$ – компоненты первой производной вектора перемещения. Здесь нижний индекс α принимает значения x, t, а индекс ρ последовательно принимает значения 1, 2.

Векторы базисов точек N^0ζ и N^ζ определяются дифференцированием (10) по x и t

(13)

$\begin{gathered} g_{\alpha }^{{\text{0}}} = R_{{,\alpha }}^{{0\zeta }} = {{\left( {R_{{}}^{0} + {{\zeta }}{{a}^{0}}} \right)}_{{,\alpha }}} = a_{\alpha }^{0} + {{\zeta }}a_{{,\alpha }}^{0}; \\ g_{\alpha }^{{}} = R_{{,\alpha }}^{\zeta } = g_{\alpha }^{0} + l_{\alpha }^{\rho }a_{\rho }^{{\text{0}}} + l_{\alpha }^{{}}a_{{}}^{{\text{0}}} + {{\zeta }}{{\left( {a - {{a}^{{\text{0}}}}} \right)}_{{,\alpha }}}. \\ \end{gathered} $

Ковариантные компоненты тензора деформаций определяются соотношениями механики сплошной среды [32]

(14)

$\varepsilon _{{\alpha \beta }}^{\zeta } = \left( {{{g}_{{\alpha \beta }}} - g_{{\alpha \beta }}^{0}} \right){\text{/}}2,$

где $g_{{{{\alpha \beta }}}}^{{}} = {\mathbf{g}}_{{{\alpha }}}^{{}} \cdot {\mathbf{g}}_{{{\beta }}}^{{}}$; $g_{{{{\alpha \beta }}}}^{{\text{0}}} = {\mathbf{g}}_{{{\alpha }}}^{{\text{0}}} \cdot {\mathbf{g}}_{{{\beta }}}^{{\text{0}}}$.

Конечный элемент и интерполяционная процедура. Срединная поверхность эллипсоида моделируется совокупностью треугольных конечных элементов с узлами m, n, p, расположенными в точках пересечения линий треугольной конечно-элементной сетки. Узловыми варьируемыми параметрами были выбраны компоненты вектора перемещения и их частные производные первого порядка по x и t. Треугольный фрагмент срединной поверхности эллипсоида отображается на прямоугольный треугольник с единичными катетами в локальной системе координат $0 \leqslant \xi $, $\eta \leqslant 1$, используемой для организации численного интегрирования по формуле Хаммера. Столбцы узловых неизвестных в глобальной (x, t) и локальной системах координат можно записать в виде соответствующих матриц-строк

(15)

${{\mathop {\left\{ {{{U}^{G}}} \right\}}\limits_{{\text{1}} \times {\text{27}}} }^{T}} = \left\{ {{{{\mathop {\left\{ {{{{v}}^{{{\text{1}}G}}}} \right\}}\limits_{{\text{1}} \times {\text{9}}} }}^{T}}{{{\mathop {\left\{ {{{{v}}^{{{\text{2}}G}}}} \right\}}\limits_{{\text{1}} \times {\text{9}}} }}^{T}}{{{\mathop {\left\{ {{{{v}}^{G}}} \right\}}\limits_{{\text{1}} \times {\text{9}}} }}^{T}}} \right\}{\text{;}}$

(16)

${{\mathop {\left\{ {{{U}^{L}}} \right\}}\limits_{1 \times 27} }^{T}} = \left\{ {{{{\mathop {\left\{ {{{{v}}^{{1L}}}} \right\}}\limits_{1 \times 9} }}^{T}}{{{\mathop {\left\{ {{{{v}}^{{2L}}}} \right\}}\limits_{1 \times 9} }}^{T}}{{{\mathop {\left\{ {{{{v}}^{L}}} \right\}}\limits_{1 \times 9} }}^{T}}} \right\},$

где

(17)

${{\mathop {\left\{ {{{q}^{G}}} \right\}}\limits_{1 \times 9} }^{Т}} = \left\{ {{{q}^{m}}{{q}^{n}}{{q}^{p}}q,_{x}^{m}q,_{x}^{n}q,_{x}^{p}q,_{t}^{m}q,_{t}^{n}q,_{t}^{p}} \right\};$

(18)

${{\mathop {\left\{ {{{q}^{L}}} \right\}}\limits_{1 \times 9} }^{Т}} = \left\{ {{{q}^{m}}{{q}^{n}}{{q}^{p}}q,_{\xi }^{m}q,_{\xi }^{n}q,_{\xi }^{p}q,_{\eta }^{m}q,_{\eta }^{n}q,_{\eta }^{p}} \right\}.$

Под q в (17) и (18) понимается компонента вектора перемещения ${{{v}}^{1}}$, ${{{v}}^{2}}$ или ${v}$.

Одним из важнейших аспектов в МКЭ является организация интерполяционной процедуры. Общепринятой в настоящее время в МКЭ является интерполяция отдельных компонент вектора перемещения как составляющих скалярных полей [17–23, 33]

(19)

$q = {{\mathop {\left\{ \psi \right\}}\limits_{1 \times 9} }^{T}}\mathop {\left\{ {q_{y}^{L}} \right\}}\limits_{9 \times 1} ,$

где ${{\left\{ \psi \right\}}^{Т}} = \left\{ {{{\psi }_{1}}{{\psi }_{2}} \ldots {{\psi }_{9}}} \right\}$ – матрица-строка функций формы, представленная полными полиномами третьей степени.

Из (19) следует, что каждая компонента вектора перемещения точки внутренней области конечного элемента интерполируется через узловые значения этой же компоненты и ее производные. Такой подход позволяет получать корректные результаты при использовании декартовой системы координат. При анализе НДС тел, имеющих криволинейные поверхности, в частности трехосного эллипсоида, удобнее использовать криволинейные координаты, связанные с геометрией исследуемой поверхности.

Однако использование криволинейных систем координат требует учета возможных смещений конечного элемента как жесткого целого. На данную проблему имеются указания как в ранних научных публикациях по МКЭ [34], так и в работах современного периода [35, 36]. В настоящей статье эту проблему предлагается решить за счет использования интерполяции компонент вектора перемещения как составляющих векторных полей [37, 38], согласно которой интерполяционное выражение записывается для вектора перемещения точки внутренней области конечного элемента

(20)

$v = {{\mathop {\left\{ \psi \right\}}\limits_{1 \times 9} }^{T}}\mathop {\left\{ {v_{y}^{L}} \right\}}\limits_{9 \times 1} = {{\mathop {\left\{ \psi \right\}}\limits_{1 \times 9} }^{T}}\mathop {\left[ {PR} \right]}\limits_{9 \times 9} \mathop {\left\{ {v_{y}^{G}} \right\}}\limits_{9 \times 1} ,$

где

(21)

${{\mathop {\left\{ {v_{y}^{L}} \right\}}\limits_{1 \times 9} }^{Т}} = \left\{ {{{v}^{m}}{{v}^{n}}{{v}^{p}}v,_{\xi }^{m}v,_{\xi }^{n}v,_{\xi }^{p}v,_{\eta }^{m}v,_{\eta }^{n}v,_{\eta }^{p}} \right\};$

(22)

${{\mathop {\left\{ {v_{y}^{G}} \right\}}\limits_{1 \times 9} }^{Т}} = \left\{ {{{v}^{m}}{{v}^{n}}{{v}^{p}}v,_{x}^{m}v,_{x}^{n}v,_{x}^{p}v,_{t}^{m}v,_{t}^{n}v,_{t}^{p}} \right\};$

$\left[ {PR} \right]$ – матрица перехода от столбца (21) к столбцу (22).

Столбец векторных узловых неизвестных $\left\{ {{\mathbf{v}}_{y}^{G}} \right\}$ в глобальной системе координат на основании (12) можно представить матричным произведением

(23)

$\mathop {\left\{ {{\mathbf{v}}_{y}^{G}} \right\}}\limits_{{\text{9}} \times {\text{1}}} = \mathop {\left[ {\mathbf{A}} \right]}\limits_{9 \times 27} \mathop {\left\{ {{{t}_{y}}} \right\}}\limits_{{\text{27}} \times 1} {\text{,}}$

где элементами квазидиагональной матрицы $\left[ {\mathbf{A}} \right]$ являются векторы локальных базисов узлов треугольного конечного элемента ${\mathbf{a}}_{1}^{{0s}}$, ${\mathbf{a}}_{2}^{{0s}}$, ${{{\mathbf{a}}}^{{0s}}}$ $\left( {s = m,n,p} \right)$, а столбец $\left\{ {{{t}_{y}}} \right\}$ имеет вид

(24)

$\mathop {\left\{ {{{t}_{y}}} \right\}}\limits_{1 \times 27} = \left\{ {{{{v}}^{{1m}}}{{{v}}^{{2m}}}{{{v}}^{m}}{{{v}}^{{1n}}}{{{v}}^{{2n}}}{{{v}}^{n}}{{{v}}^{{1p}}}{{{v}}^{{2p}}}{{{v}}^{p}}l_{x}^{{1m}}l_{x}^{{2m}}l_{x}^{m} \ldots l_{x}^{p} \ldots l_{t}^{{1m}}l_{t}^{{2m}}l_{t}^{m} \ldots l_{t}^{p}} \right\}.$

Интерполяционное выражение (20) с учетом (23) можно выразить как

(25)

$v = {{\mathop {\left\{ \psi \right\}}\limits_{1 \times 9} }^{T}}\mathop {\left[ {PR} \right]}\limits_{9 \times 9} \mathop {\left[ A \right]}\limits_{9 \times 27} \mathop {\left[ T \right]}\limits_{27 \times 27} \mathop {\left\{ {U_{y}^{G}} \right\}}\limits_{9 \times 1} = {{\mathop {\left\{ \varphi \right\}}\limits_{1 \times 9} }^{T}}\mathop {\left[ A \right]}\limits_{9 \times 27} \mathop {\left[ T \right]}\limits_{27 \times 27} \mathop {\left\{ {U_{y}^{G}} \right\}}\limits_{9 \times 1} ,$

где $\left[ T \right]$ – матрица перехода от столбца $\left\{ {{{t}_{y}}} \right\}$ к столбцу $\left\{ {U_{y}^{G}} \right\}$ (15).

Входящие в структуру матрицы $\left[ {\mathbf{A}} \right]$ векторы локального базиса узлов треугольного конечного элемента на основании (8) можно выразить через векторы базиса точки внутренней области конечного элемента

(26)

$\mathop {\left\{ {{{{\mathbf{a}}}^{{{\text{0}}s}}}} \right\}}\limits_{{\text{3}} \times {\text{1}}} = \mathop {\left[ {{{d}^{{{\text{0}}s}}}} \right]}\limits_{{\text{3}} \times {\text{3}}} {{\mathop {\left[ {{{d}^{{\text{0}}}}} \right]}\limits_{{\text{3}} \times {\text{3}}} }^{{ - {\text{1}}}}}\mathop {\left\{ {{{{\mathbf{a}}}^{{\text{0}}}}} \right\}}\limits_{{\text{3}} \times {\text{1}}} = \mathop {\left[ {{{b}^{{{\text{0}}s}}}} \right]}\limits_{{\text{3}} \times {\text{3}}} \mathop {\left\{ {{{{\mathbf{a}}}^{{\text{0}}}}} \right\}}\limits_{{\text{3}} \times {\text{1}}} {\text{,}}$

где ${{\mathop {\left\{ {{{{\mathbf{a}}}^{{{\text{0}}s}}}} \right\}}\limits_{{\text{3}} \times {\text{1}}} }^{T}} = \left\{ {{\mathbf{a}}_{1}^{{0s}}{\mathbf{a}}_{2}^{{0s}}{\mathbf{a}}_{{}}^{{0s}}} \right\}$.

Интерполяционную зависимость (25) с учетом (12) и (26) можно записать в виде

${{\left\{ {{{a}^{0}}} \right\}}^{T}}\left\{ \begin{gathered} {{{v}}^{1}} \\ {{{v}}^{2}} \\ {v} \\ \end{gathered} \right\} = \left\{ {\left. {{{\varphi }_{1}}a_{1}^{{0m}}} \right|\left. {{{\varphi }_{1}}a_{2}^{{0m}}} \right|\left. {{{\varphi }_{1}}a_{{}}^{{0m}}} \right|\left. {{{\varphi }_{2}}a_{1}^{{0n}}} \right|\left. {{{\varphi }_{2}}a_{2}^{{0n}}} \right|\left. {\left. {{{\varphi }_{2}}a_{{}}^{{0n}} \ldots {\kern 1pt} } \right|\left. {{{\varphi }_{9}}a_{1}^{{0p}}} \right|\left. {{{\varphi }_{9}}a_{2}^{{0p}}} \right|{{\varphi }_{9}}a_{{}}^{{0p}}} \right|} \right\}\left\{ {{{Z}_{y}}} \right\} = $

(27)

$ = \left\{ {\left. {{{\varphi }_{1}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{11}}^{{0m}} \hfill \\ b_{{12}}^{{0m}} \hfill \\ b_{{13}}^{{0m}} \hfill \\ \end{gathered} \right\}} \right|} \right.\left. {{{\varphi }_{1}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{21}}^{{0m}} \hfill \\ b_{{22}}^{{0m}} \hfill \\ b_{{23}}^{{0m}} \hfill \\ \end{gathered} \right\}} \right|\left. {{{\varphi }_{1}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{31}}^{{0m}} \hfill \\ b_{{32}}^{{0m}} \hfill \\ b_{{33}}^{{0m}} \hfill \\ \end{gathered} \right\}} \right|\left. {{{\varphi }_{2}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{11}}^{{0n}} \hfill \\ b_{{12}}^{{0n}} \hfill \\ b_{{13}}^{{0n}} \hfill \\ \end{gathered} \right\}} \right|\left. {{{\varphi }_{2}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{21}}^{{0n}} \hfill \\ b_{{22}}^{{0n}} \hfill \\ b_{{23}}^{{0n}} \hfill \\ \end{gathered} \right\}} \right| \times $

$ \times \;\left| {\left. {{{\varphi }_{2}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{31}}^{{0n}} \hfill \\ b_{{32}}^{{0n}} \hfill \\ b_{{33}}^{{0n}} \hfill \\ \end{gathered} \right\}{\kern 1pt} } \right| \ldots {\kern 1pt} } \right|\left. {{{\varphi }_{9}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{11}}^{{0p}} \hfill \\ b_{{12}}^{{0p}} \hfill \\ b_{{13}}^{{0p}} \hfill \\ \end{gathered} \right\}} \right|\left. {{{\varphi }_{9}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{21}}^{{0p}} \hfill \\ b_{{22}}^{{0p}} \hfill \\ b_{{23}}^{{0p}} \hfill \\ \end{gathered} \right\}} \right|\left. {{{\varphi }_{9}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{31}}^{{0p}} \hfill \\ b_{{32}}^{{0p}} \hfill \\ b_{{33}}^{{0p}} \hfill \\ \end{gathered} \right\}} \right\}\left\{ {{{Z}_{y}}} \right\},$

где $\left\{ {{{Z}_{y}}} \right\} = \left[ T \right]\left\{ {U_{y}^{G}} \right\}$.

Из (27) можно получить интерполяционные выражения для компонент вектора перемещения точки внутренней области треугольного конечного элемента при реализации интерполяционной процедуры компонент вектора перемещения как составляющих векторных полей

(28)

$\begin{gathered} {{{v}}^{1}} = \left\{ {\left. {{{\varphi }_{1}}b_{{11}}^{{0m}}} \right|\left. {{{\varphi }_{1}}b_{{21}}^{{0m}}} \right|\left. {{{\varphi }_{1}}b_{{31}}^{{0m}}} \right|\left. {{{\varphi }_{2}}b_{{11}}^{{0n}}} \right|\left. {{{\varphi }_{2}}b_{{21}}^{{0n}}} \right|\left. {{{\varphi }_{2}}b_{{31}}^{{0n}}} \right| \ldots \left| {{{\varphi }_{9}}b_{{11}}^{{0p}}} \right|\left. {{{\varphi }_{9}}b_{{21}}^{{0p}}} \right|{{\varphi }_{9}}b_{{31}}^{{0p}}} \right\}\left\{ {{{Z}_{y}}} \right\}; \\ {{{v}}^{2}} = \left\{ {\left. {{{\varphi }_{1}}b_{{12}}^{{0m}}} \right|\left. {{{\varphi }_{1}}b_{{22}}^{{0m}}} \right|\left. {{{\varphi }_{1}}b_{{32}}^{{0m}}} \right|\left. {{{\varphi }_{2}}b_{{12}}^{{0n}}} \right|\left. {{{\varphi }_{2}}b_{{22}}^{{0n}}} \right|\left. {{{\varphi }_{2}}b_{{32}}^{{0n}}} \right| \ldots \left| {{{\varphi }_{9}}b_{{12}}^{{0p}}} \right|\left. {{{\varphi }_{9}}b_{{22}}^{{0p}}} \right|{{\varphi }_{9}}b_{{32}}^{{0p}}} \right\}\left\{ {{{Z}_{y}}} \right\}; \\ {v} = \left\{ {\left. {{{\varphi }_{1}}b_{{13}}^{{0m}}} \right|\left. {{{\varphi }_{1}}b_{{23}}^{{0m}}} \right|\left. {{{\varphi }_{1}}b_{{33}}^{{0m}}} \right|\left. {{{\varphi }_{2}}b_{{13}}^{{0n}}} \right|\left. {{{\varphi }_{2}}b_{{23}}^{{0n}}} \right|\left. {{{\varphi }_{2}}b_{{33}}^{{0n}}} \right| \ldots \left| {{{\varphi }_{9}}b_{{13}}^{{0p}}} \right|\left. {{{\varphi }_{9}}b_{{23}}^{{0p}}} \right|{{\varphi }_{9}}b_{{33}}^{{0p}}} \right\}\left\{ {{{Z}_{y}}} \right\}. \\ \end{gathered} $

Анализируя (28), отметим их принципиальные отличия от (19), которые заключаются в том, что при реализации интерполяционной процедуры компонент вектора перемещения как составляющих векторных полей каждая компонента вектора перемещения зависит от столбца узловых неизвестных, в структуру которого входят узловые значения всех трех компонент вектора перемещения и их производные. Кроме того, в интерполяционные выражения (28) входят параметры используемой криволинейной системы координат, чего не наблюдается при использовании интерполяционной процедуры отдельных компонент вектора перемещения как скалярных величин (19).

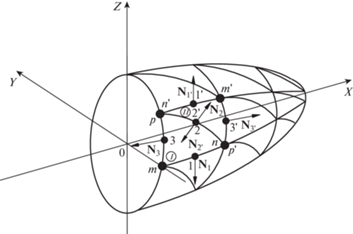
Описанный выше треугольный конечный элемент является совместным по компонентам вектора перемещения, но несовместным по их производным, что может приводить к некорректным результатам в зонах значительных градиентов деформаций. Так, например, в значениях производных нормальных компонент векторов перемещений, вычисленных в направлении нормалей к серединам сторон смежных конечных элементов I и II будет иметь место скачок (рис. 1)

(29)

$\frac{{\partial {{{v}}_{i}}}}{{\partial {{{\mathbf{N}}}_{i}}}} \ne \frac{{\partial {v}_{i}^{'}}}{{\partial {\mathbf{N}}_{i}^{'}}}{\text{,}}\quad \left( {i = {\text{1,2,3}}} \right){\text{.}}$

Рис. 1.

Дискретизация эллипсоида.

Для обеспечения равенства в значениях производных предлагается использовать в качестве дополнительных узловых неизвестных треугольного конечного элемента множители Лагранжа ${{\lambda }_{i}}$ $\left( {i = 1,2,3} \right)$. В этом случае выражение (29) можно представить в виде

(30)

${{{{\lambda }}}_{i}}\left( {\frac{{\partial {{{v}}_{i}}}}{{\partial {{{\mathbf{N}}}_{i}}}} - \frac{{\partial {v}_{i}^{'}}}{{\partial {\mathbf{N}}_{i}^{'}}}} \right) = {\text{0}}{\text{.}}$

Входящие в (30) производные нормальных компонент векторов перемещений, вычисленные вдоль нормалей к серединам сторон треугольных конечных элементов можно представить через частные производные нормальных компонент по глобальным криволинейным координатам

(31)

$\frac{{\partial {{{v}}_{i}}}}{{\partial {{{\mathbf{N}}}_{i}}}} = {{\left( {{{{v}}_{{,x}}}} \right)}_{i}}\cos {{\alpha }_{i}} + {{\left( {{{{v}}_{{,t}}}} \right)}_{i}}\cos {{\beta }_{i}},$

где ${{\alpha }_{i}}$ и ${{\beta }_{i}}$ – углы между векторами ${{{\mathbf{N}}}_{i}}$ и тангенциальными векторами локального базиса ${{\left( {{\mathbf{a}}_{1}^{0}} \right)}_{i}}$, ${{\left( {{\mathbf{a}}_{2}^{0}} \right)}_{i}}$.

Для определения входящих в (31) частных производных нормальной компоненты ${{\left( {{{{v}}_{{,x}}}} \right)}_{i}}$ и ${{\left( {{{{v}}_{{,t}}}} \right)}_{i}}$ необходимо выполнить операцию дифференцирования интерполяционного выражения (20) по x и t

(32)

$\begin{gathered} {{v}_{{,x}}} = \left( {{{{\left\{ {{{\psi }_{{,\xi }}}} \right\}}}^{T}}{{\xi }_{{,x}}} + {{{\left\{ {{{\psi }_{{,\eta }}}} \right\}}}^{T}}{{\eta }_{{,x}}}} \right)\left[ {PR} \right]\left\{ {U_{y}^{G}} \right\}; \\ {{v}_{{,t}}} = \left( {{{{\left\{ {{{\psi }_{{,\xi }}}} \right\}}}^{T}}{{\xi }_{{,t}}} + {{{\left\{ {{{\psi }_{{,\eta }}}} \right\}}}^{T}}{{\eta }_{{,t}}}} \right)\left[ {PR} \right]\left\{ {U_{y}^{G}} \right\}{\text{.}} \\ \end{gathered} $

С учетом (23)–(25) выражения (32) примут следующий вид

(33)

${{v}_{{,x}}} = {{\left\{ {{{\varphi }_{x}}} \right\}}^{T}}\left[ {\mathbf{A}} \right]\left[ T \right]\left\{ {U_{y}^{G}} \right\};\quad {{v}_{{,t}}} = {{\left\{ {{{\varphi }_{t}}} \right\}}^{T}}\left[ {\mathbf{A}} \right]\left[ T \right]\left\{ {U_{y}^{G}} \right\}{\text{.}}$

Принимая во внимание второе равенство (12) из (33) можно получить следующие матричные соотношения:

${{\left\{ {{{a}^{0}}} \right\}}^{T}}\left\{ \begin{gathered} l_{x}^{1} \\ l_{x}^{2} \\ {{l}_{x}} \\ \end{gathered} \right\} = \left\{ {\left. {{{\varphi }_{{x1}}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{11}}^{{0m}} \hfill \\ b_{{12}}^{{0m}} \hfill \\ b_{{13}}^{{0m}} \hfill \\ \end{gathered} \right\}} \right|} \right.\left. {{{\varphi }_{{x1}}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{21}}^{{0m}} \hfill \\ b_{{22}}^{{0m}} \hfill \\ b_{{23}}^{{0m}} \hfill \\ \end{gathered} \right\}} \right|\left. {{{\varphi }_{{x1}}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{31}}^{{0m}} \hfill \\ b_{{32}}^{{0m}} \hfill \\ b_{{33}}^{{0m}} \hfill \\ \end{gathered} \right\}} \right| \ldots $

(34)

$...\left. \begin{gathered} _{}^{} \hfill \\ \hfill \\ \hfill \\ \hfill \\ \end{gathered} \right|\left. {{{\varphi }_{{x9}}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{11}}^{{0p}} \hfill \\ b_{{12}}^{{0p}} \hfill \\ b_{{13}}^{{0p}} \hfill \\ \end{gathered} \right\}} \right|\left. {{{\varphi }_{{x9}}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{21}}^{{0p}} \hfill \\ b_{{22}}^{{0p}} \hfill \\ b_{{23}}^{{0p}} \hfill \\ \end{gathered} \right\}} \right|\left. {{{\varphi }_{{x9}}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{31}}^{{0p}} \hfill \\ b_{{32}}^{{0p}} \hfill \\ b_{{33}}^{{0p}} \hfill \\ \end{gathered} \right\}} \right\}\left\{ {{{Z}_{y}}} \right\};$

${{\left\{ {{{a}^{0}}} \right\}}^{T}}\left\{ \begin{gathered} l_{t}^{1} \hfill \\ l_{t}^{2} \hfill \\ {{l}_{t}} \hfill \\ \end{gathered} \right\} = \left. {\left\{ {\left. {{{\varphi }_{{t1}}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{11}}^{{0m}} \hfill \\ b_{{12}}^{{0m}} \hfill \\ b_{{13}}^{{0m}} \hfill \\ \end{gathered} \right\}} \right|} \right. \ldots {\kern 1pt} } \right|\left. {{{\varphi }_{{t9}}}{{{\left\{ {{{a}^{0}}} \right\}}}^{T}}\left\{ \begin{gathered} b_{{31}}^{{0p}} \hfill \\ b_{{32}}^{{0p}} \hfill \\ b_{{33}}^{{0p}} \hfill \\ \end{gathered} \right\}} \right\}\left\{ {{{Z}_{y}}} \right\}{\text{.}}$

Из (34) можно записать искомые интерполяционные зависимости

(35)

$\begin{gathered} {{l}_{x}} = \left\{ {\left. {{{\varphi }_{{x1}}}b_{{13}}^{{0m}}} \right|\left. {{{\varphi }_{{x1}}}b_{{23}}^{{0m}}} \right|\left. {\left. {{{\varphi }_{{x1}}}b_{{33}}^{{0m}}} \right| \ldots {\kern 1pt} } \right|\left. {{{\varphi }_{{x9}}}b_{{13}}^{{0p}}} \right|\left. {{{\varphi }_{{x9}}}b_{{23}}^{{0p}}} \right|{{\varphi }_{{x9}}}b_{{33}}^{{0p}}} \right\}\left\{ {{{Z}_{y}}} \right\}; \\ {{l}_{t}} = \left\{ {\left. {{{\varphi }_{{t1}}}b_{{13}}^{{0m}}} \right|\left. {{{\varphi }_{{t1}}}b_{{23}}^{{0m}}} \right|\left. {\left. {{{\varphi }_{{t1}}}b_{{33}}^{{0m}}} \right| \ldots {\kern 1pt} } \right|\left. {{{\varphi }_{{t9}}}b_{{13}}^{{0p}}} \right|\left. {{{\varphi }_{{t9}}}b_{{23}}^{{0p}}} \right|{{\varphi }_{{t9}}}b_{{33}}^{{0p}}} \right\}\left\{ {{{Z}_{y}}} \right\}, \\ \end{gathered} $

где ${{l}_{x}}$ и ${{l}_{t}}$ – многочлены, содержащие производные ${{{v}}_{{,x}}}$ и ${{{v}}_{{,t}}}$.

При рассмотрении каждого треугольного конечного элемента в отдельности, можно записать равенство

(36)

${{{{\lambda }}}_{1}}\frac{{\partial {{{v}}_{1}}}}{{\partial {{{\mathbf{N}}}_{1}}}} + {{{{\lambda }}}_{2}}\frac{{\partial {{{v}}_{2}}}}{{\partial {{{\mathbf{N}}}_{2}}}} + {{{{\lambda }}}_{3}}\frac{{\partial {{{v}}_{3}}}}{{\partial {{{\mathbf{N}}}_{3}}}} = 0{\text{,}}$

которое с учетом (31) и (35) представим матричным произведением

(37)

${{\mathop {\left\{ {{\lambda }} \right\}}\limits_{1 \times 3} }^{T}}\mathop {\left[ L \right]}\limits_{3 \times 27} \mathop {\left\{ {U_{y}^{G}} \right\}}\limits_{27 \times 1} = {\text{0,}}$

где ${{\left\{ {{\lambda }} \right\}}^{T}} = \left\{ {{{{{\lambda }}}_{1}}{{{{\lambda }}}_{2}}{{{{\lambda }}}_{3}}} \right\}$.

Для компоновки матрицы жесткости и столбца узловых усилий треугольного конечного элемента воспользуемся функционалом Лагранжа

(38)

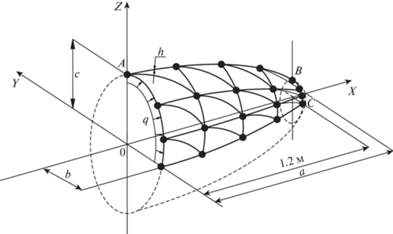
${{F}_{L}} = \int\limits_V {{{{\left\{ {\varepsilon _{{\alpha \beta }}^{\zeta }} \right\}}}^{T}}\left\{ {{{\sigma }^{{\alpha \beta }}}} \right\}dV} - \int\limits_S {{{{\left\{ U \right\}}}^{T}}\left\{ P \right\}dS} + {{\left\{ \lambda \right\}}^{Т}}\left[ L \right]\left\{ {U_{y}^{G}} \right\} = 0,$

где ${{\left\{ {\varepsilon _{{\alpha \beta }}^{\zeta }} \right\}}^{T}} = \left\{ {\varepsilon _{{xx}}^{\zeta }} \right\}\left\{ {\varepsilon _{{tt}}^{\zeta }} \right\}\left\{ {2\varepsilon _{{xt}}^{\zeta }} \right\}$, ${{\left\{ {{{\sigma }^{{\alpha \beta }}}} \right\}}^{T}} = \left\{ {{{\sigma }^{{xx}}}} \right\}\left\{ {{{\sigma }^{{tt}}}} \right\}\left\{ {{{\sigma }^{{xt}}}} \right\}$ – деформации и напряжения в точке ${{N}^{\zeta }}$; ${{\left\{ U \right\}}^{T}} = \left\{ {{{u}_{1}}{{u}_{2}}u} \right\}$ – матрица-строка компонент вектора перемещения точки ${{N}^{{\text{0}}}}$; ${{\left\{ P \right\}}^{T}} = \left\{ {{{p}^{1}}{{p}^{2}}p} \right\}$ – столбец внешней поверхностной нагрузки.

Пример расчета. В качестве примера была решена задача по определению НДС усеченного эллипсоида, нагруженного внутренним давлением интенсивности $q = 5$ МПа. Параметры эллипсоида имели следующие значения: $a = 1.3$ м; $b = 0.92$ м; $c = 0.9$ м. Осевая координата x изменялась в пределах $0 \leqslant x \leqslant 1.2$ м. Модуль упругости был равен $E = 2 \times {{10}^{5}}$ МПа, коэффициент Пуассона $\nu = 0.3$, толщина оболочки была принята равной $h = 0.02$ м.

Вследствие наличия плоскостей симметрии рассматривалась 1/8 часть эллипсоида (рис. 2). Расчеты были выполнены в трех вариантах: в первом варианте элементом дискретизации трехосного эллипсоида был выбран треугольный фрагмент без множителей Лагранжа со стандартной интерполяционной процедурой (19); во втором варианте применялся описанный в настоящей статье конечный элемент с интерполяцией компонент вектора перемещения как составляющих векторных полей (20)–(25) с применением множителей Лагранжа для улучшения совместности на границах смежных элементов дискретизации; в третьем контрольном варианте использовался четырехугольный конечный элемент с аналогичным числом неизвестных в узле [30].

Рис. 2.

Сечение эллипсоида.

Результаты повариантных расчетов представлены в табл. 1, в которой приведены значения нормальных напряжений ${{{{\sigma }}}_{{xx}}}$ и ${{{{\sigma }}}_{{tt}}}$ на внутренней ${{\sigma }^{{in}}}$ и наружной ${{\sigma }^{{out}}}$ поверхностях эллипсоида в зависимости от густоты конечно-элементной сетки.

Таблица 1.

Значения нормальных напряжений на поверхностях эллипсоида

Номер варианта	Густота сетки	Координаты точек (x, м; t, рад)
		А $\left( {0.0;0.0} \right)$		В $\left( {1.2;0.0} \right)$		С $\left( {1.2;\pi } \right)$
		Напряжения, МПа
		$\sigma _{{xx}}^{{in}}$	$\sigma _{{tt}}^{{out}}$	$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$	$\sigma _{{xx}}^{{in}}$	$\sigma _{{xx}}^{{out}}$	$\sigma _{{tt}}^{{in}}$
I	81 × 81	175.3	183.5	–636.2	611.0	–328.9	313.0	463.3
	101 × 101	175.3	183.5	–649.7	624.9	–344.7	330.8	462.6
	121 × 121	175.3	183.5	–659.8	635.7	–355.9	343.1	462.0
II	81 × 81	173.7	180.3	–235.9	214.9	26.8	–40.1	534.8
	101 × 101	174.8	179.4	–258.1	230.7	22.7	–35.5	533.6
	121 × 121	175.5	178.8	–276.7	244.8	18.6	–31.2	532.1
III	61 × 61	174.9	184.0	–200.1	277.5	2.36	–22.0	542.5
	81 × 81	174.8	184.0	–208.5	264.4	0.45	–14.5	550.6
	101 × 101	174.8	184.0	–213.2	257.0	–0.41	–10.4	555.1

Анализ данных, представленных в табл. 1, показывает, что в точке, лежащей на пересечении вертикальных плоскостей симметрии ($x = 0.0$ м; $t = 0.0$ рад) наблюдается по сути безмоментное напряженное состояние и численные значения напряжений по всем трем вариантам имеют достаточно близкие значения. В концевом сечении ($x = 1.2$ м), где имеет место моментное напряженное состояние, различие между первым и вторым вариантом расчета весьма значительно. В точке B $(1.2;0.0)$ ${{\sigma }_{{tt}}}$ в первом варианте в 2.5–3.0 раза больше, чем во втором варианте расчета, а в точке С $(1.2;\pi )$ ${{\sigma }_{{tt}}}$ в первом варианте оказались меньше на 18%, чем во втором варианте расчета. Кроме того, в концевом сечении напряжения ${{{{\sigma }}}_{{xx}}}$ должны монотонно уменьшаться, что и наблюдается во втором варианте расчета. В первом варианте ${{{{\sigma }}}_{{xx}}}$ в точке С на порядок больше, чем во втором варианте и имеют тенденцию к росту при сгущении сетки дискретизации, что является некорректным.

Сравнение между собой второго и контрольного третьего вариантов расчета показывает, что вычисленные значения напряжений достаточно близки между собой и разница между ними некритична.

Итак, можно сделать вывод, что разработанный совместный треугольный конечный элемент с множителями Лагранжа и инвариантной векторной формой интерполяционной процедуры обладает принципиальными преимуществами по сравнению с треугольным конечным элементом в традиционной формулировке и позволяет получать корректные значения прочностных параметров при расчете оболочек в форме трехосного эллипсоида.

Численные эксперименты. Численный эксперимент 1. С целью верификации в первом приближении разработанного треугольного элемента дискретизации был реализован численный эксперимент по расчету кругового цилиндра, загруженного внутренним давлением интенсивностью $q = 1$ Н/см². Радиус цилиндра $R$ был принят равным 10 см, толщина стенки $h = 0.1$ см, длина образующей $L = 1$ см, модуль упругости $E = {\text{2}}{\text{.1}} \times {\text{1}}{{{\text{0}}}^{{\text{7}}}}$ Н/см², коэффициент Пуассона $\nu = 0.3$. Расчеты, как и в примере исследования НДС трехосного эллипсоида, были выполнены в трех вариантах. Результаты численного эксперимента представлены в табл. 2, в которой приведены значения напряжений ${{{{\sigma }}}_{{tt}}}$ на наружной и внутренней поверхностях цилиндра в зависимости от сетки узлов дискретизации.

Таблица 2.

Значения нормальных напряжений ${{{{\sigma }}}_{{tt}}}$ в круговом цилиндре, загруженным внутренним давлением

Номер варианта	Густота сетки	Координаты точек (x, см; t, рад)
		А $\left( {1.0;0.0} \right)$		В $\left( {0.0;0.0} \right)$		С $\left( {1.0;\pi {\text{/}}2} \right)$		D $\left( {0.0;\pi {\text{/}}2} \right)$
		Напряжения, Н/см²
		$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$	$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$	$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$	$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$
I	21 × 2	99.69	100.23	99.21	100.85	99.21	100.85	99.69	100.23
I	31 × 2	99.48	100.44	98.97	101.11	98.97	101.11	99.48	100.44
II	21 × 2	100.5	99.5	100.5	99.5	100.5	99.5	100.5	99.5
II	31 × 2	100.5	99.5	100.5	99.5	100.5	99.5	100.5	99.5
III	21 × 2	100.5	99.5	100.5	99.5	100.5	99.5	100.5	99.5
III	31 × 2	100.5	99.5	100.5	99.5	100.5	99.5	100.5	99.5

Анализ результатов (табл. 2) показывает, что во всех трех вариантах наблюдается устойчивая сходимость вычислительного процесса. Причем, во втором и третьем вариантах сходимость – абсолютная. Численные значения напряжений соответствуют аналитическому решению, полученному из условия статического равновесия

${{\sigma }_{{tt}}} = qR{\text{/}}t = 1 \times 10{\text{/}}0.1 = 100.0\;{\text{Н/с}}{{{\text{м}}}^{{\text{2}}}}{\text{.}}$

Представленный численный эксперимент является наиболее простейшим и выполнен для верификации разработанного треугольного элемента дискретизации лишь в первом приближении. Для более полного анализа эффективности разработанного алгоритма необходимо выполнить численные эксперименты с другими видами внешней нагрузки и отличной от круговой геометрической формы.

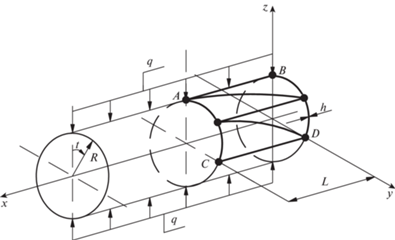
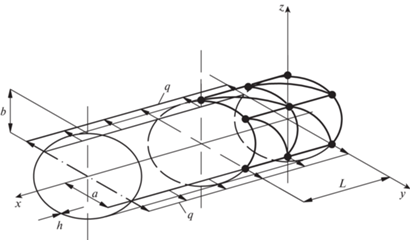
Численный эксперимент 2. С целью наиболее полной верификации разработанного треугольного элемента дискретизации был выполнен следующий численный эксперимент по определению НДС кругового цилиндра с образующей единичной длины $L = 1$ см, загруженного двумя диаметрально противоположно направленными линейно распределенными нагрузками интенсивностью $q = 0.1$ Н/см (рис. 3). Были приняты следующие исходные данные: радиус цилиндра $R = 10$ см, толщина стенки $h = 0.1$ см, модуль упругости $E = 2.1 \times {{10}^{7}}$ Н/см², коэффициент Пуассона $\nu = 0.3$. Вследствие наличия плоскостей симметрии рассчитывалась 1/4 часть цилиндра. Численный эксперимент был реализован, как и в предыдущем примере, в трех вариантах.

Рис. 3.

Расчетная схема кругового цилиндра с линейно распределенной нагрузкой q.

Результаты численного эксперимента представлены в табл. 3, в которой приведены значения нормального напряжения ${{{{\sigma }}}_{{tt}}}$ на внутренней ${{\sigma }^{{in}}}$ и на наружной ${{\sigma }^{{out}}}$ поверхностях цилиндра в точках приложения линейной нагрузки $q\left( {t = 0} \right)$ и в точках с параметром $t = \frac{\pi }{2}$ в зависимости от густоты сетки дискретизации. Анализ табличных данных показывает, что результаты первого варианта численного эксперимента нельзя признать удовлетворительными по причине отсутствия сходимости вычислительного процесса и увеличивающегося до неприемлемого уровня различия между значениями напряжений в точках A, B и C, D по мере сгущения сетки дискретизации. Исходя из расчетной схемы кругового цилиндра (рис. 3) и наличия плоской деформации напряжения в точках A, B и C, D должны быть попарно одинаковыми.

Таблица 3.

Значения напряжений ${{{{\sigma }}}_{{tt}}}$ в круговом цилиндре, загруженном линейно распределенной нагрузкой q

Номер варианта	Густота сетки	Координаты точек (x, см; t, рад)
		А $\left( {1.0;0.0} \right)$		В $\left( {0.0;0.0} \right)$		С $\left( {1.0;\pi {\text{/}}2} \right)$		D $\left( {0.0;\pi {\text{/}}2} \right)$
		Напряжения, Н/см²
		$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$	$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$	$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$	$\sigma _{{tt}}^{{in}}$	$\sigma _{{tt}}^{{out}}$
I	2 × 21	110.0	–119.9	23.6	–12.2	–8.66	0.04	–60.3	67.3
	2 × 31	77.1	–86.1	–9.28	23.8	8.90	–19.9	–42.7	48.9
	2 × 51	64.2	–75.9	–27.4	48.1	18.4	–33.8	–36.8	45.0
II	2 × 21	190.9	–191.4	191.5	–190.8	–110.3	108.3	–110.3	108.3
	2 × 31	190.7	–190.5	191.9	–190.3	–110.2	108.1	–110.2	108.1
	2 × 51	191.9	–190.1	191.9	–190.1	–110.1	108.0	–110.1	108.0
III	2 × 21	191.0	–191.2	191.0	–191.2	–110.3	108.3	–110.3	108.3
	2 × 31	191.7	–190.4	191.7	–190.4	–110.2	108.1	–110.2	108.1
	2 × 51	191.9	–190.1	191.9	–190.1	–110.1	108.0	–110.1	108.0

Во втором и третьем вариантах численного эксперимента можно констатировать быструю сходимость вычислительного процесса и равенство значений напряжений в точках A, B и C, D соответственно. Различия между вторым и третьим вариантами практически отсутствуют. Погрешность полученных в ходе численного эксперимента значений напряжений можно оценить, воспользовавшись известной формулой сопротивления материалов для задачи о сжатии кольца двумя сосредоточенными силами P [39]. В точке приложения сил момент по формуле сопротивления материалов равен ${{M}_{A}} = 0.3183$ PR = $0.3183 \times 0.1 \times 10$ = 0.3183 Н см. В точках кольца с координатой $t = \frac{\pi }{2}$ момент равен ${{M}_{C}} = 0.1817$ PR = $0.1817 \times 0.1 \times 10$ = 0.1817 Н см.

Для вычисления напряжений можно воспользоваться формулой

(39)

$\sigma = M{\text{/}}W,$

где W – момент сопротивления поперечного сечения.

Подставив в формулу (39) значения исходных данных, можно получить следующие значения напряжений: ${{\sigma }_{A}}$ = $0.3183{\text{/}}(1 \times {{0.1}^{2}}{\text{/}}6)$ = 190.98 Н/см²; ${{\sigma }_{C}}$ = $0.1817{\text{/}}(1 \times {{0.1}^{2}}{\text{/}}6)$ = = 109.02 Н/см².

Сопоставив значения ${{\sigma }_{A}}$ и ${{\sigma }_{C}}$ со значениями, полученными в ходе численного эксперимента, можно отметить, что погрешность данных (табл. 3) минимальна, и не превышает 1%.

Таким образом, можно сделать вывод, что проведенный численный эксперимент подтверждает эффективность разработанного треугольного элемента дискретизации и демонстрирует достаточную для инженерных расчетов точность вычислений, полученных при его использовании.

Численный эксперимент 3. Исследовано НДС эллиптического цилиндра с различным соотношением полуосей эллипса поперечного сечения. Эллиптический цилиндр был загружен приложенной вдоль диаметрально противоположных образующих линейно распределенной растягивающей нагрузкой интенсивностью $q = 0.1$ Н/см (рис. 4). Были использованы следующие исходные данные: длина образующей $L = 1$ см, длина большей полуоси $a = 10$ см, толщина стенки $h = 0.1$ см, модуль упругости $E = 2.1 \times {{10}^{7}}$ Н/см², коэффициент Пуассона $\nu = 0.3$. Длина малой полуоси эллипса поперечного сечения варьировалась от 10 см до 6.67 см. Численный эксперимент, как и в предыдущих расчетах, был реализован в трех вариантах.

Рис. 4.

Расчетная схема эллиптического цилиндра с линейно распределенной нагрузкой q.

Результаты численного эксперимента представлены в табл. 4, в которой приведены значения нормальных напряжений ${{{{\sigma }}}_{{tt}}}$ на внешней и внутренней поверхностях эллиптического цилиндра в зависимости от соотношения полуосей эллипса поперечного сечения $k = a{\text{/}}b$ при фиксированной сетке узлов дискретизации $31 \times 2$. Анализ данных, представленных в табл. 4, показывает, что в первом варианте численного эксперимента получены некорректные значения нормальных напряжений ${{{{\sigma }}}_{{tt}}}$. Так, например, в точке С $\sigma _{{tt}}^{{in}}$ – растягивающие, тогда как исходя из расчетной схемы (рис. 4), они должны быть сжимающими. То же самое можно сказать и о нормальных напряжениях на наружной поверхности эллиптического цилиндра в точке С $\sigma _{{tt}}^{{out}}$. Они должны быть растягивающими, а в таблице $\sigma _{{tt}}^{{out}}$ в точке С – отрицательные, т.е. сжимающие.

Таблица 4.

Значения нормальных напряжений ${{{{\sigma }}}_{{tt}}}$ в эллиптическом цилиндре, загруженном линейно распределенной нагрузкой q

Номер варианта	Координаты точек (x, см; t, рад)	Напряжение ${{{{\sigma }}}_{{tt}}}$, Н/см²	Отношение полуосей эллипса $k = a{\text{/}}b$ поперечного сечения
Номер варианта	Координаты точек (x, см; t, рад)	Напряжение ${{{{\sigma }}}_{{tt}}}$, Н/см²	1.0	1.1	1.3	1.5
I	С$\left( {1.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	9.28	9.86	8.29	5.55
	С$\left( {1.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	–23.81	–26.20	–27.62	–26.70
	D$\left( {0.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	–77.15	–66.21	–51.29	–41.72
	D$\left( {0.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	86.10	75.45	60.53	49.89
II	С$\left( {1.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	–191.85	–177.37	–154.5	–137.2
	С$\left( {1.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	190.3	175.6	152.2	134.4
	D$\left( {0.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	–191.68	–177.2	–154.4	–137.1
	D$\left( {0.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	190.48	175.7	152.3	134.5
III	С$\left( {1.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	–191.7	–177.25	–154.4	–137.1
	С$\left( {1.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	190.4	175.7	152.3	134.5
	D$\left( {0.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	–191.7	–177.25	–154.4	–137.1
	D$\left( {0.0;\pi {\text{/}}2} \right)$	$\sigma _{{tt}}^{{in}}$	190.4	175.7	152.3	134.5
Решение по формулам сопротивления материалов [39]		${{\sigma }_{{tt}}}$	190.98	177.0	153.0	136.2

Можно констатировать абсолютное несовпадение значений напряжений в точках С и D в первом варианте численного эксперимента, в то время как, исходя из расчетной схемы эллиптического цилиндра, напряжения в точках С и D должны полностью совпадать.

Во втором и третьем вариантах численного эксперимента можно констатировать обязательное, вследствие наличия плоскостей симметрии в деформированном состоянии, совпадение значений нормальных напряжений в точках С и D (процент расхождения между значениями напряжений в этих точках во втором варианте пренебрежимо мал). Можно отметить практически полное совпадение значений напряжений, полученных во втором и третьем вариантах численного эксперимента.

Для верификации выполненного численного эксперимента в нижней строке табл. 4 приведены значения напряжений, вычисленные с привлечением формул сопротивления материалов для задачи о растяжении эллиптического кольца двумя сосредоточенными силами [39], согласно которым изгибающий момент в точках приложения сил равен

(40)

$M = kPa,$

где $k = a{\text{/}}b$ – коэффициент отношения полуосей эллипса поперечного сечения.

Подставив в (40) исходные данные проводимого численного эксперимента и воспользовавшись формулой (39), получили значения нормальных напряжений (табл. 4).

Сравнительный анализ напряжений, полученных во втором и третьем вариантах численного эксперимента и значений нормальных напряжений, вычисленных по формулам сопротивления материалов показывает, что расхождения между ними минимальны и в целом не превышают 1%.

Вывод. На основании рассмотренных примеров по определению НДС трехосного эллипсоида и выполненных с целью верификации разработанного алгоритма численных экспериментов, можно сделать вывод об эффективности представленного треугольного элемента дискретизации с корректирующими множителями Лагранжа, матрица жесткости которого скомпонована на основе векторной формы интерполяционной процедуры компонент вектора перемещения и их производных.

Треугольный элемент дискретизации без корректирующих множителей Лагранжа, матрица жесткости которого формируется на основе общепринятой в МКЭ скалярной формы интерполяционной процедуры, позволяет получать удовлетворительные по точности результаты лишь в случаях простых геометрических форм оболочечных конструкций, загруженных равномерно распределенным давлением. В случае отличного от равномерного давления вида внешней нагрузки или усложнения геометрических форм оболочек, получить удовлетворительные значения напряжений не представляется возможным.

Список литературы

Krivoshapko S.N. Optimal shells of revolution and main optimizations // Structural mechanics of engineering structures and structures. 2019. V. 15. № 3. P. 201.
Новожилов В.В. Теория тонких оболочек. Санкт-Петербург: Изд-во Санкт-Петербургского ун-та, 2010. 378 с.
Галимов К.З., Паймушин В.Н., Терегулов И.Г. Основания нелинейной теории оболочек. Казань: Изд-во “Фэн”, 1996. 216 с.
Тимошенко С.П. Пластины и оболочки. М.: Физматгиз, 1963. 635 с.
Петров В.В. Нелинейная инкрементальная строительная механика. М.: Инфра-Инженерия, 2014. 480 с.
Беляев А.К. и др. Приближенная теория колебаний многослойных анизотропных пластин // Известия Саратовского университета. Новая серия. Серия: математика. Механика. Информатика. 2018. Т. 18. № 4. С. 397.
Trusov P.V., Yanz A.Y. Physical meaning of nonholonomic strain measure // Physical Mesomechanics. 2016. V. 19. № 2. P. 215.
Trusov P.V., Kondratev N.S., Shveykin A.I. About geometrically nonlinear constitutive relations for elastic material // PNRPU Mechanics Bulletin. 2015. № 3. P. 182.
Storozhuk E.A., Maksimyuk V.A., Chernyshenko I.S. Nonlinear elastic state of a composite cylindrical shell with a rectangular hole // International Applied Mechanics. 2019. V. 55. № 4. P. 504.
Storozhuk E.A., Chernyshenko I.S., Yatsura A.V. Stress-strain state near a hole in a shear-compliant composite cylindrical shell with elliptical cross-section // International Applied Mechanics. 2018. V. 54. № 5. P. 559.
Krysko V.A., Vetsel’ S.S., Dobriyan V.V., Saltykova O.A. Chaotic interaction dynamics of three structures: two cylindrical shells nested into each other and their reinforcing local rib // Journal of Applied Mechanics and Technical Physics. 2017. V. 58. № 3. P. 489.
Badriev I.B., Makarov M.V., Paimushin V.N. Contact statement of mechanical problems of reinforced on a contour sandwich plates with transversally-soft core // Russian Mathematics. 2017. V. 61. № 1. P. 69.
Storozhuk E.A., Yatsura A.V. Exact solutions of boundary-value problems for noncircular cylindrical shells // International Applied Mechanics. 2016. V. 54. № 4. P. 386.
Paimushin V.N. On the forms of loss of stability of a cylindrical shell under an external side pressure // Journal of Applied Mathematics and Mechanics. 2016. V. 80. № 1. P. 65.
Urnev A.S., Chernyatin A.S., Matvienko Y.G., Razumovskii I.A. Experimental and numerical sizing of delamination defects in layered composite materials // Inorganic Materials. 2019. V. 55. № 15. P. 1516.
Петров В.В., Кривошеин И.В. Влияние неоднородности материала на устойчивость нелинейно деформируемых пологих оболочек двоякой кривизны // Вестник Саратовского государственного технического университета. 2014. Т. 4. № 1 (77). С. 20.
Agapov V., Golovanov R. Comparative analysis of the simplest finite elements of plates in bending // Advances in Intelligent Systems and Computing. 2018. V. 692. P. 1009.
Belostotsky A.M., Akimov P.A., Afanasyeva I.N., Kaytukov T.B. Contemporary problems of numerical modelling of unique structures and buildings // International Journal for Computational Civil and Structural Engineering. 2017. V. 13. № 2. P. 9.
Игнатьев А.В., Чумаков А.В., Гилка В.В. Моделирование неполной алгебраической проблемы собственных значений и векторов методом частотно-динамической конденсации на основе МКЭ в форме классического смешанного метода // Строительная механика инженерных конструкций и сооружений. 2019. Т. 15. № 1. С. 62.
Tyukalov Yu.Ya. Finite element model of reisner’s plates in stresses // Civil Engineering Journal. 2019. V. 89. № 5. P. 61.
Лалин В.В., Денисов Г.В. Трансформация волн, распространяющихся по заглубленному трубопроводу, вследствие конструктивных включений // Строительная механика инженерных конструкций и сооружений. 2013. № 2. С. 56.
Голованов А.И., Тюленева О.Н., Шигабутдинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций. Москва: Физматлит, 2006. 392 с.
Бате К.-Ю. Методы конечных элементов. Москва: Физматлит, 2010. 1022 с.
Leonetti L., Magisano D., Madeo A., Garcea G., Kiendl J., Reali A. A simplified Kirchhoff–Love large deformation model for elastic shells and its effective isogeometric formulation // Computer Methods in Applied Mechanics and Engineering. 2019. V. 354. P. 369.
Rogovoi A.A., Stolbova O.S. Stress recovery procedure for solving boundary value problems in the mechanics of a deformable solid by the finite element method // Journal of Applied Mathematics and Mechanics. 2010. V. 74. № 3. P. 341.
Rogovoi A.A., Stolbova O.S. A Stress recovery procedure for solving geometrically non-linear problems in the mechanics of a deformable solid by the finite element method // Journal of Applied Mathematics and Mechanics. 2010. V. 74. № 6. P. 710.
Magisano D., Liang K., Garcea G., Leonetti L., Ruess M. An efficient mixed variational reduced-order model formulation for nonlinear analyses of elastic shells // International Journal for Numerical Methods in Engineering. 2018. V. 113. № 4. P. 634.
Likeb A., Gubeljak N., Matvienko Y. The determination of the stress intensity factor solutions for the new pipe-ring specimen using fea // Archive of Applied Mechanics (Ingenieur Archiv). 2019. V. 89. № 5. P. 897.
Kirichevsky R.V., Skrynnykova A.V. The effect of approximating functions in the construction of the stiffness matrix of the finite element on the convergence rate of the finite element method // Tomsk State University Journal of Mathematics and Mechanics. 2019. № 57. P. 26.
Klochkov Yu.V., Nikolaev A.P., Kiseleva T.A., Marchenko S.S. Comparative analysis of the results of finite element calculations based on an ellipsoidal shell // Journal of Machinery Manufacture and Reliability. 2016. V. 45. № 4. P. 328.
Klochkov Yu.V., Nikolaev A.P., Fomin S.D., Vakhnina O.V., Sobolevskaya T.A., Klochkov M.Yu. A finite elemental algorithm for calculating the arbitrarily loaded shell using three-dimensional finite elements // ARPN Journal of Engineering and Applied Sciences. 2020. V. 15. № 13. P. 1472.
Седов Л.И. Механика сплошной среды. Москва: Наука. 1976. Т. 1. 536 с.
Solodovnikov A.S., Sheshenin S.V. Numerical study of strength properties for a composite material with short reinforcing fibers // Moscow University Mechanics Bulletin. 2017. V. 72. № 4. P. 94.
Кантин Г., Клауф Р. Искривленный дискретный элемент цилиндрической оболочки // Ракетная техника и космонавтика. 1968. № 6. С. 82.
Sultanov L.U. Analysis of finite elasto-plastic strains. Medium kinematics and constitutive equations // Lobachevskii Journal of Mathematics. 2016. V. 37. № 6. P. 787.
Игнатьев А.В., Игнатьев В.А., Гамзатова Е.А. Расчет тонких пластин по методу конечных элементов в форме классического смешанного метода с исключением перемещений конечных элементов как жесткого целого // Известия высших учебных заведений. Строительство. 2018. № 3 (711). С. 5.
Клочков Ю.В., Николаев А.П., Соболевская Т.А., Фомин С.Д., Клочков М.Ю. Конечноэлементные модели дискретизации тонкостенных конструкций предприятий АПК // Известия Нижневолжского агроуниверситетского комплекса: Наука и высшее профессиональное образование. 2019. Т. 53. № 1. С. 255.
Dzhabrailov A.Sh., Klochkov Yu.V., Nikolaev A.P. The finite element analysis of shells of revolution with a branching meridian // Russian Aeronautics. 2009. V. 52. № 1. P. 22.
Рудицын М.Н., Артемов П.Я., Любошиц М.И. Справочное пособие по сопротивлению материалов. Минск: Вышейшая школа, 1970. 630 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал