Проблемы машиностроения и надежности машин, 2022, № 3, стр. 50-62

Статья посвящена методу расчета вторичного гидроакустического поля конечной упругой цилиндрической оболочки, погруженной в жидкость, в дальней зоне. Первичное поле это звуковое поле, излучаемое колеблющейся оболочкой под действием внутренних источников возбуждения, дискретных сил приложенных к оболочке. Вторичное поле (дифрагированное) это поле, которое возникает в результате действия на оболочку внешнего падающего звукового поля, создаваемого зондирующим источником. В результате этого возбуждаются вынужденные колебания оболочки, и возникает излученное рассеянное (дифрагированное) гидроакустическое поле. Рассеянное поле включает две составляющие: 1) поле излученное, создаваемое вынужденными колебаниями оболочки; 2) поле, отраженное от оболочки, как от абсолютно твердого тела. Процессы излучения и дифракции могут рассматриваться как в ближнем, так и в дальнем поле. Рассматривается конечная оболочка со свободными концами.

Исследованиям колебаний, излучения и дифракции цилиндрических оболочек посвящено большое количество работ [1–20]. Эти работы регулярно появляются, начиная с середины прошлого века, что свидетельствует о незавершенности и, следовательно, актуальности исследований. Импеданс излучения цилиндрической оболочки используется при расчетах вынужденных колебаний и излучения оболочек в ближнем и дальнем поле.

Проведем анализ современного состояния решения задач, связанных с импедансом, колебаниями и вторичным полем конечных упругих цилиндрических оболочек на основе наиболее известных работ.

В широко известной книге [1] приведено решение волнового уравнения для расходящейся цилиндрической волны в виде

где $H_{n}^{{(1)}}$(arg) – функция Ганкеля; k = ω/c – волновое число; ω = 2πf – частота колебаний; c – скорость звука в среде (жидкости); k_z – осевое волновое число; n – окружная гармоника по углу φ; t – время; r – радиальная координата.

Решение (1) не верное, т.к. в вместо k должно быть k_r, и частота ω

При k_z ≠ 0 определена не верно. В [1] рассматривалась только плоская задача.

В работе [2] со ссылкой на [1] приведено решение задачи излучения колеблющейся бесконечной цилиндрической оболочки, на поверхности которой задана деформация в виде

где λ – длина волны деформации; m – продольная гармоника; z – осевая координата. Формула звукового давления в ближнем поле приведена в виде где ρ – плотность среды. В формуле (3) принято k_z = 2πm/λ. Но в формуле (3) k_z должно быть осевым волновым числом звуковой волны, распространяющееся в жидкости, а не изгибной формой колебаний (деформаций) оболочки – 2πm/λ (2). Эти параметры являются разнородными по физической природе и, следовательно, не могут быть взаимозаменяемыми. Поэтому формулу (3) нельзя признать обоснованной.

Задачи дифракции звука на упругих цилиндрических оболочках в ближнем поле впервые были рассмотрены в работах [3, 4]. Работа [3] посвящена дифракции на ограниченной оболочке с граничными условиями Навье. В работе [4] рассмотрена дифракция на бесконечной оболочке. Уравнения колебаний оболочки в перемещениях взяты из [5]. Звуковое давление на поверхности оболочек, обусловленное деформацией ограниченной и бесконечной оболочек, представлено формулой, в которой осевое волновое число k_z является неизвестной переменной интегрирования в пределах (–∞, ∞). Формула звукового давления такая же, как (5), о которой сказано ниже. В работах [6, 7] рассмотрены задачи дифракции звука на бесконечном абсолютно твердом цилиндре.

В фундаментальной монографии по акустике [8] приведена формула импеданса излучения колеблющейся цилиндрической оболочки (по мнению многих авторов бесконечной оболочки)

Недостатком формулы (4) является то, что она не доведена до конца, т.к. в ней осевое волновое число k_z не определено, не указано как его определять.

О волновом числе k_z из [8] известно следующее: 1) дана ссылка на [2], где k_z = = 2πm/λ; 2) в результате некорректного определения скорости фронта бегущей волны постоянной фазы получено k_z/k_r = tg θ. На основе этого принято k_z = ksinθ, где θ угол распространения волны, который якобы зависит от частоты (от k). При высоких частотах, таких, что k² $ \gg $ $k_{z}^{2}$, излучаемые волны распространяются перпендикулярно к поверхности цилиндра, по мере уменьшения частоты (k) угол θ увеличивается и при k = k_z происходит акустическое короткое замыкание; 3) в случае k < k_z и $k_{r}^{2}$ = k² – $k_{z}^{2}$ < 0, когда величина k_r становится мнимой, рекомендуется функцию Ганкеля заменять на функцию Макдональда. Возможность превышения k_z > k допускали многие авторы [3, 4, 8, 9, 12]. В итоге, ссылаясь на значения k_z = 2πm/λ, не критикуя возможность изменения k_z – как переменной интегрирования в пределах –∞ < k_z < ∞ [3, 4] и признавая возможность k_z > k, автор [8] не смог дать формулу определения осевого волнового числа k_z.

В работе [9] для конечной упругой цилиндрической оболочки виброперемещение представлено в виде интеграла Фурье, а решение волнового уравнения принято в виде

Излучаемое ближнее поле, вызванное вибрациями конечной упругой оболочки, представлено (без суммирования гармоник) в виде

Формулы звукового давления излучаемого ближнего поля, вызванного вибрациями оболочек, в работах [3, 4, 9] (при интегрировании в пределах –∞ < k_z < ∞), совпадают, но из-за их необоснованности доверия не вызывают.

Например, в [9] при рассмотрении излучения пульсирующего цилиндра при интегрировании по k_z в пределах (–∞ < k_z < ∞) выполнялась замена переменных k_z = k sin(α₁ + iα₂) с последующим определением α₁ и α₂.

В работах [4, 9] также решалась задача дифракции звука на бесконечной импедансной оболочке в ближнем поле. Без обоснования принято k_z = k sin ψ, где ψ – угол падения звуковой волны.

В работе [10] впервые решена задача излучения колеблющейся конечной цилиндрической оболочки в дальнем поле с использованием формулы Кирхгофа. Задача вынужденных колебаний оболочки не решалась. Перемещения задавались в виде гармонической функции. В качестве импеданса использован импеданс излучения бесконечной цилиндрической оболочки (3), в котором параметр 2π/λ без обоснований заменен на ξ = –k cos θ. Замена объяснена тем, что в формулу Кирхгофа входят интегралы с экспонентами exp(ikz cos θ) (12). Эти интегралы необоснованно названы преобразованиями Фурье и их отношение гипотетически принято в качестве импеданса излучения конечной оболочки. Такой выбор импеданса нельзя признать теоретически обоснованным.

Импеданс излучения ограниченной цилиндрической оболочки приведен в [11]. Колебательная скорость оболочки задана в таком же виде, как (2) только λ = L, где L – длина оболочки. Авторы представили давление излучаемого поля в виде

где в качестве Z₁ взяли формулу для бесконечной цилиндрической оболочки (4). Импеданс излучения ограниченной оболочки в конечном виде можно представить формулой

Формула (7) точно такая же, как (3), с учетом λ = L. Отметим, что ссылка на [2] отсутствует. Замечания, высказанные по поводу (3), относятся и к данному случаю. Здесь причиной получения ошибочного результата является формула (6). В [11] ошибочно сказано, что при стремлении L → ∞ импеданс ограниченной оболочки стремится к импедансу бесконечной оболочки.

В работе [12] рассмотрена задача дифракции звука на конечном абсолютно твердом цилиндре в дальнем поле с использованием формулы Кирхгофа

где ψ – угол падения звуковой волны. В формуле Кирхгофа в качестве импеданса взят импеданс для бесконечного цилиндра. Вместо полного давления взято только давление рассеянного поля и производная полного давления, вопреки граничному условию, не приравнена к нулю. В результате формула (8) ошибочная.

Задача дифракции звука на твердом цилиндре, ограниченном по торцам полусферами, рассмотрена в [13] в дальнем поле. В ней также как в [12] в формуле Кирхгофа вместо суммарного полного поля ошибочно взятa только часть его, т.е. рассеянное поле.

В ряде работ предложены численные методы расчета [8, 14, 15], но они по сложности и трудоемкости значительно превосходят аналитические методы. Современным численным методом является метод конечных элементов (МКЭ) на базе программного комплекса ANSYS. В работе [15] проведено моделирование рассеянного поля методом МКЭ на модели цилиндрической оболочки длиной 10 м и диаметром 0.9 м. В этой же работе сказано о невозможности расчета дальнего гидроакустического поля реальных подводных объектов методом МКЭ, поскольку количество элементов расчетной модели возрастает пропорционально кубу дистанции. В принятой модели оболочка была представлена 20 000, а жидкость – 180 000 элементами.

Проведенный анализ показал, что рассматриваемая задача до сих пор полностью не решена, аналитические формулы, позволяющие рассчитать суммарное вторичное поле конечной цилиндрической оболочки в дальней зоне при произвольных углах падения и наблюдения, отсутствуют.

Сказанное является обоснованием актуальности рассматриваемой задачи.

Настоящая статья является продолжением и развитием работы [16], в которой приведено решение задачи дифракции звука на конечной абсолютно твердой цилиндрической оболочке в дальнем поле.

Целью исследований является разработка теоретических основ аналитического метода расчета полного дифрагированного поля конечной упругой цилиндрической оболочки в дальней зоне при произвольных углах наблюдения. Новизна заключается в том, что предложенный метод является полным, т.е. включает расчет вынужденных колебаний цилиндрической оболочки, возбуждаемых падающим полем, и рассеяние на оболочке как упругого, так и твердого тела. Метод предложен впервые. В расчеты вынужденных колебаний оболочки и вторичного поля входит импеданс излучения цилиндрической оболочки, который по-разному проявляется в дисперсионном уравнении и в формуле Кирхгофа. Впервые в дисперсионном уравнении и в расчете звукового давления вторичного поля использован точный импеданс излучения, в котором осевое волновое число k_z, определено на основе решения волнового уравнения.

Полезность метода заключается в том, что его можно использовать при решении различных прикладных задач гидроакустики, в том числе при акустическом проектировании оболочечных конструкций.

Рассматривается задача дифракции звука на конечной упругой цилиндрической оболочке, погруженной в жидкость, в дальнем поле. Рассеяние звуковых волн рассматривается на цилиндрической поверхности оболочки без учета концевых заглушек (сферических и др.). В ряде прикладных задач заглушки отсутствуют, и учитывать их не требуется. При необходимости рассеяние на заглушках можно рассматривать отдельно [8, 12]. Оно имеет смысл при малых углах падения (ψ ≈ 0°–5°) и учете продольных колебаний цилиндрической оболочки.

Обозначения параметров оболочки: a – радиус; L – длина; h – толщина. Источником излучения звука является монополь с объемной скоростью V, находящийся на большом расстоянии H от оболочки. Вынужденные колебания оболочки возбуждаются падающим на поверхность оболочки звуковым полем.

Звуковое давление поля, падающего на оболочку под углом ψ к оси z оболочки [16]

Излучаемое поле, определяемое решением волнового уравнения в цилиндрических координатах (без суммирования гармоник), представим в виде

где B_n – искомая функция, определяемая из граничных условий; $H_{n}^{{(2)}}$(arg) – функция Ганкеля второго рода (далее индекс (2) опускаем); k_z – искомый коэффициент. Этот коэффициент определим из решения волнового уравнения, которое можно представить в виде k²= $k_{r}^{2}$ + $k_{z}^{2}$. Математическим решением этого уравнения является k_r k sin θ, k_z = k cos θ. Физический смысл угла θ – это угол между направлением распространения излучаемой цилиндрической волны с волновым числом k и осью z в цилиндрической системе координат. Новизна этого решения заключается в определении осевого волнового числа k_z в явном виде. Полезность заключается в однозначном определении импеданса излучения цилиндрической оболочки (4), безотносительно к ее длине, т.е. конечной или бесконечной. Формула импеданса (4) с k_z = k cos θ устраняет имевшиеся разногласия и различные ее трактовки и становится основой для решения всех задач гидроакустики любых цилиндрических оболочек в жидкости.

С использованием граничных условий на поверхности цилиндрической оболочки $\left. {\frac{{\partial p}}{{\partial r}}} \right|$ = $\rho {{\omega }^{2}}w(z)\cos n\varphi $, найдем функцию B_n

Давление звукового поля, рассеянного вблизи оболочки

Рассеянное звуковое поле в дальней зоне определим с использованием формулы Кирхгофа [10]

В результате проведенных преобразований этого выражения, для краткости опущенных, формула рассеянного поля в дальней зоне имеет вид

где μ = ak sin θ. Следует отметить, что формула (12) является развитием формулы, приведенной в [10]. Отметим, что полный вывод формулы в [10] не был приведен и в окончательной формуле и в промежуточных выкладках имелись описки и ошибки, которые здесь исправлены.

Полное поле на поверхности оболочки p = p₀+ p_s. Подставим в (12) выражения p₀ (9) и p_s (11), заменим exp(iπn/2) = iⁿ и получим давление вторичного поля, рассеянного конечной цилиндрической оболочкой в дальней зоне

где $\mu {\kern 1pt} * = a\sqrt {{{k}^{2}} - k_{z}^{2}} $; $\eta = ak\sin \psi $; $E = \frac{{{{e}^{{ - ikR}}}}}{R}$; $\beta = \cos \psi + \cos \theta $.

Полное дальнее поле p_N состоит из суммы двух частей, одна из которых p_t соответствует отраженному полю как от абсолютно твердого тела, и вторая p_w – вызванная вибрациями упругой оболочки p_N = p_t + p_w.

С учетом суммирования гармоник дальнее поле, отраженное абсолютно твердой цилиндрической оболочкой имеет вид

где ${{T}_{\eta }} = \mu {\kern 1pt} *{\kern 1pt} H_{n}^{'}\left( {\mu {\kern 1pt} *} \right){{J}_{n}}\left( \eta \right) - \eta J_{n}^{'}\left( \eta \right){{H}_{n}}\left( {\mu {\kern 1pt} *} \right)$, $\beta = \cos \psi + \cos \theta $.

Рассеянное дальнее поле, вызванное вибрациями упругой цилиндрической оболочкой

Для расчета диаграммы направленности в дальнем поле в общем случае нужны обе формулы (13) и (14). Формулы можно упростить, если ограничиться определением давления только в направлениях зеркального отражения θ₁ = π – ψ и теневого луча θ₂ = π + ψ.

Для расчета по формуле (14) нужно знать деформации w(z) оболочки, которые должны определяться из расчета вынужденных колебаний оболочки в жидкости, возбуждаемых падающим полем. Считаем, что внешнее звуковое давление на оболочку, возбуждающее ее колебания, происходит в радиальном направлении по координате w [17–20].

Для каждой окружной гармоники n с учетом опущенной временной зависимости e^iωt уравнение вынужденных колебаний оболочки в жидкости можно представить в виде

Полное решение уравнения (15) можно представить в виде суммы общего решения соответствующего однородного уравнения, содержащего восемь постоянных, и частного решения вынужденных колебаний, возбуждаемых суммарным давлением p = p₀+ p_s

где n – окружные гармоники ряда Фурье, n = 0, 1, 2, 3, …, α_jn – корни дисперсионного уравнения,  j = 1–8 – порядковые номера корней; С_jn – искомые коэффициенты; $\Delta $_jn – миноры матрицы уравнения колебаний оболочки (15); ω = 2πf – угловая частота колебаний; f – частота колебаний; ξ = z/a. В решение (16) входят подлежащие определению корни дисперсионного уравнения α_jn и коэффициенты С_jn. Для получения дисперсионного уравнения решение (16) представим в виде

В результате подстановки этих решений в уравнение (15) при p₀ = 0 получим уравнение свободных колебаний оболочки

где p_s0 – звуковое давление в жидкости, вызываемое свободными колебаниями оболочки, учитывающее влияние присоединенной массы жидкости. Считая, что излучение происходит в радиальном направлении по координате w, т.е. нормально к поверхности оболочки, принимаем r = a, θ = 90° и, следовательно, в (4) получаем k_z = 0

Входящие в решение показатели экспонент α являются корнями дисперсионного уравнения свободных колебаний. После соответствующих преобразований дисперсионное уравнение колебаний цилиндрической оболочки в жидкости получим в виде [21]

Однако отличие полученного результата заключается в том, что ранее в [21] это уравнение было получено не обосновано, исходя из ошибочных предпосылок определения p_s0 [9]. Определение корней проводится так же, как в [21].

Определим частное решение уравнения (15), приняв его в виде (u_p cos nφ, ${{{v}}_{p}}$sin nφ, w_p cos nφ)e^iγξ , где γ = kα cos ψ фаза падающего поля.

При подстановке решений в уравнение (17) элементами матрицы будут

где a₁, b₁ – параметры стрингеров; а₂, b₂, z₂ – параметры шпангоутов; E₁= E₀(1 + iχ) – комплексный модуль упругости; χ – потери в материале оболочки; r = a; ν – коэффициент Пуассона; ${{\rho }_{*}}$ – плотность материала оболочки.

Обозначив матрицу в (15)

определим вектор частного решения уравнения (15)

Из (20) получим радиальное перемещение

где Δ₁ – минор и Δ₀ – определитель матрицы L_i, j, с учетом (19)

После подстановки выражений давления падающего поля p₀ и рассеянного поля p_s в формулу (21) и проведения соответствующих преобразований получим

где Z_м= Δ₀/Δ₁ – механический импеданс оболочки. Подставим w(z) = w_p из (22) в (14) и с учетом (13) и (14), определим окончательное выражение p_N.

Методика составления уравнений вынужденных колебаний для составной оболочечной конструкции, включающей набор цилиндрических оболочек, соединенных между собой кольцами, для вторичного поля аналогична методике, изложенной в [21] для первичного поля, но отличается от нее выражениями правых частей уравнений вынужденных колебаний, обусловленных падающим полем.

В результате получается система матричных уравнений вынужденных колебаний относительно перемещений колец z_k

Общее матричное уравнение для оболочечной конструкции, состоящей из набора отсеков и колец, имеет ленточную диагональную структуру расположения блок-матриц размером 4 × 4 и в сумме может иметь порядок нескольких сотен. В результате решения этой системы определяются искомые векторы перемещений колец z_q.

После определения векторов перемещений z_q на кольцах q из уравнения (23) можно построить АЧХ колебаний в заданных сечениях (кольцах) оболочечной конструкции, а также формы вынужденных колебаний для каждой оболочки и всей оболочечной конструкции в целом.

Форма колебаний для каждой оболочки определяется выражением [21]

Формулы (13), (14), (22), (23) и метод в целом по сути новые, не имеют аналогов. Метод точный, т.к. основан на точной теории. Никаких допущений, предположений и условий, ограничивающих точность решения, принято не было. Разработаны алгоритмы и компьютерные программы на Fortran. По ним проведены расчеты.

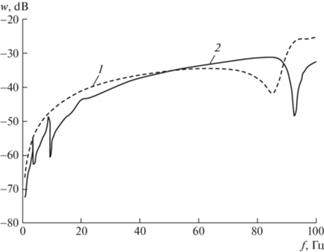
На рис. 1 в качестве примера показана АЧХ изгибных колебаний цилиндрической оболочки при двух углах падения для n = 1. Параметры оболочки: a = 4 м, L = 70 м, h = = 0.04 м. Шаг вычисления по частоте 0.25 Гц. По осям координат отложены радиальные ускорения w в dB и частота в Гц.

Сравнивая АЧХ на рис. 1 с аналогичными АЧХ, полученными при возбуждении колебаний оболочки дискретными силами [21 видим, что резонансные пики маловыразительны, и при больших углах падения ψ вовсе пропадают, т.е. вид АЧХ зависит от угла падения.

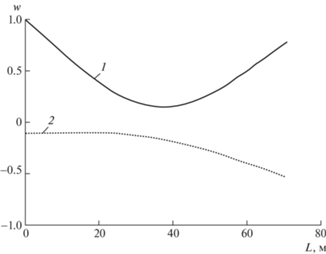
На рис. 2 показана форма изгибных колебаний оболочки в области первого резонанса изгибных колебаний f = 3.75 Гц при n = 1, ψ = 30°, сплошная линия – мнимая (Im) и пунктирная линия действительная (Re) – составляющие.

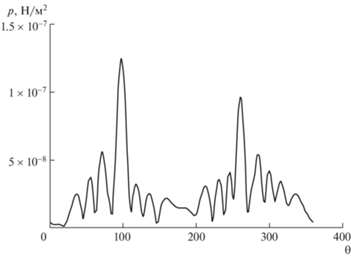
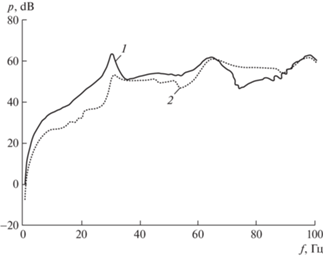
На рис. 3 показана диаграмма направленности вторичного поля при угле падения ψ = 80° на частоте f  = 100 Гц. По осям отложены приведенное звуковое давление в долях 10⁵ в размерности Н/м² и угол наблюдения ψ в градусах. На рис. 4 показано изменение максимального давления диаграммы направленности по частоте колебаний при двух углах падения по сумме восьми гармоник n = 0–7.

Таким образом, получено новое аналитическое решение задачи дифракции, позволяющее определить полное вторичное (дифрагированное) дальнее поле конечной упругой цилиндрической оболочки в жидкости.

Полученное решение является строго теоретически обоснованным (основанном на теории колебаний оболочек, волновом уравнении, формуле Кирхгофа), полученном без каких-либо допущений, ограничений и условий. Метод является теоретической основой практических расчетов при акустическом проектировании оболочечных конструкций в жидкости.

Новизна решения определяется следующим. При расчете колебаний и вторичного поля использован теоретически обоснованный точный импеданс излучения конечной цилиндрической оболочки в жидкости. Определены корни дисперсионного уравнения колебаний оболочки в жидкости. Определены АЧХ и формы вынужденных колебаний конечной упругой цилиндрической оболочки в жидкости, возбуждаемые падающим полем. Аналогов у предложенного метода нет. Экспериментальная проверка метода является самостоятельной задачей.