Проблемы машиностроения и надежности машин, 2023, № 3, стр. 17-28

Технологии почвощадящего земледелия становятся все более актуальной темой аграрного сектора. Обоснованием актуальности этих методов является не только экологическая обстановка и все большее внимание к ней со стороны регулятора [1], но и технический аспект. Современные сельскохозяйственные машины обладают большими КПД и, как следствие, массами. Для того, чтобы передвижение машин по грунтам было возможно, сельхозпроизводители все чаще прибегают к использованию движителей на гусеничных лентах. Основной задачей таких движителей является увеличение площади контакта между гусеничной лентой и поверхностью грунта для более эффективной передачи крутящего момента, а также снижения динамических нагрузок на агрегаты машины [2]. Производители таких агрегатов успешно справились с такой задачей. Однако необходимо учитывать и тот факт, что режимы работы сельскохозяйственных машин разнятся. Поэтому, такой критерий как пятно контакта гусеничной ленты может быть решающим при разработке приводов машин, работающих в условиях поля и менее значимым при разработке приводов машин, работающих в условиях передвижения по дорогам общего пользования. В этом случае, увеличенное пятно контакта снижает динамические характеристики машины и является ограничителем скорости ее передвижения [3].

Для обеспечения разнорежимной работы движителя используют различные методы. Например, производители колесных тракторов опционально оснащают свою технику механизмами автоматизированного регулирования давления в шинах. Эти механизмы позволяют увеличивать пятно контакта колеса при работе машины на слабых грунтах или с тяжелыми навесками и орудиями и уменьшать его, при передвижении средства по дорогам общего пользования. Вероятным логическим развитием гусенично-модульных устройств (ГМУ), которыми оборудуют современную технику, является осуществление возможности динамического регулирования пятна контакта между гусеничной лентой и опорной поверхностью в зависимости от режима работы средства. Попытки реализации этой концепции предпринимает немецкий производитель сельскохозяйственной техники CLAAS [4]. В кормоуборочном комбайне Claas Jaguar 960 Terra Trac компания реализовала механизм изменения положения переднего опорного катка для снижения пятна контакта гусеницы при маневрировании.

Такие системы реализуются посредством интеграции гидравлических демпферов подвески и гидравлического управления подвеской, что в большинстве случаев ведет к увеличению массы гусеничного движителя и нивелирует увеличенное пятно контакта гусеницы, усложняя процесс управления движителем. В целях исключения такого влияния, нами предлагается использовать в качестве демпфера топологически оптимизированную под проектные нагрузки раму устройства со сверхупругими упрочняющими элементами из композитного материала с термоупругими мартенситными превращениями (рис. 1). Отечественные и зарубежные исследования показывают эффективность использования функционально-организованных композитных материалов или функционально-ориентированных поверхностных композиций из материалов с термоупругими мартенситными превращениями в условиях многофакторных воздействий, в том числе с повышенными требованиями демпфирования и обратимости деформаций [5]. Для оценки влияния данного решения необходимо поэтапно синтезировать расчетную модель устройства. С этой целью разработана имитационная математическая модель с заделом на уточнение модели в части описания работы упругих структур рамы из специальных материалов. Математическая модель, синтезированная для определения особенностей и режимов работы предлагаемого устройства, должна решать следующие задачи: 1) выявить закономерности распределения динамической нагрузки на опоры гусенично-модульного устройства (ГМУ); 2) сформулировать требования и исходные данные для синтеза алгоритма определения оптимального расположения опор ГМУ относительно топологически оптимизированных структур; 3) сформулировать требования к системам подрессоривания с энергетической точки зрения.

Постановка задачи. В раннее выполненных исследованиях [6] большое внимание уделяется такой характеристике гусеничной машины, как техническая средняя скорость движения. В рамках настоящей статьи допускается проводить аналогию между машинами на гусеничном приводе и машинами на полугусеничном ходу, т.к. условия их эксплуатации и ограничения схожи. Средняя скорость движения в каждых конкретных условиях дает возможность оценить потенциальные скоростные способности машины в заданных условиях, а следовательно, и ее техническое совершенство как транспортного средства. В связи с тем, что в период уборки зерновых, машины необходимо транспортировать между угодьями на достаточно высоких скоростях, то такая характеристика как техническая средняя скорость движения играет решающую роль для потребителя. Однако, при увеличении скорости передвижения машины на полугусеничном ходу, появляются такие же возмущающие внешние частоты колебаний траков, как и при эксплуатации машины на гусеничном ходу. Этот негативный эффект может повлиять на работоспособность сельскохозяйственной машины, так как ее узлы не рассчитаны на резонансные частоты движителей.

Цель – разработать математическую модель гусенично-модульного устройства задней оси сельскохозяйственной машины для определения оптимальной схемы расположения опорных катков и демпфирующих элементов катков внутри гусеничного обвода устройства, а также провести анализ распределения усилий между опорными катками при выходе из контакта с землей задней пары катков.

Для определения оптимальной схемы расположения опорных катков воспользуемся рекомендациями, предложенными в [6], в которой авторы проводят анализ реакции системы трехосного шасси на возмущающие внешние частоты, а также влияния частот на среднюю техническую скорость и управляемость машины в резонансных частотах. Из работы [6] следует, что для колесных машин военного назначения, по критерию плавности хода, больше подходит к применению классическая схема расположения осей (две приводные в задней части машины и одна рулевая в передней). Однако, предложенная математическая модель релевантна только для машин со статическим расположением осей относительно центра масс при движении. В рамках же настоящей статьи предлагается опорные катки гусенично-модульного устройства или его оси, как в предыдущем примере, поочередно “вывешивать”, изменяя таким образом динамическую характеристику всего гусенично-модульного устройства, и косвенно влиять на динамическую характеристику машины в целом. В основе исследования также лежат методы и части математического описания процесса движения многоосной колесной машины, предложенные в работах [7, 8]. Чтобы определить оптимальное расположение опорных катков в гусенично-модульном устройстве, необходимо составить его схему, в момент, когда машина движется по полю и в контакте с землей находятся сразу все шесть опорных катков. В качестве исходного устройства будем использовать схему гусенично-модульного устройства с возможностью регулировки пятна контакта посредством упругого подрамника [9].

Исходные данные для моделирования. Основные допущения. Для возможности дальнейшего исследования модели гусенично-модульного устройства необходимо разработать его структурную схему, с возможностью дальнейшей интеграции в программный комплекс Simulink. Воспользуемся методиками, изложенными в [10], и сформулируем требования, позволяющие судить об эксплуатационных качествах модели: 1) модель должна описывать динамику ГМУ с точностью, необходимой для оценки нагруженности элементов устройства; 2) в модели должны быть ограничения на параметры профиля трасы в вертикальной плоскости, т.к. объект моделирования рассматривается вне зависимости от динамики реальной машины и имеет граничные условия рабочего хода; 3) движение ГМУ должно моделироваться без учета сцепления с грунтом, при этом симулируя инерционные свойства вращающихся объектов.

Структурно, схема представляется следующим образом. Гусенично-модульное устройство для расчетов состоит из абсолютно жесткой рамы, на которой с возможностью вращения закреплены пара приводных колес и две пары опорных катков. Третья пара опорных колес расположена в задней части устройства на рычаге, который, в свою очередь, шарнирно сочленен с задней частью абсолютно жесткой рамы. Все структурные компоненты модели выполнены из стали и сохраняют свое исходное геометрическое состояние в процессе анализа.

С целью оптимизации анализируемых параметров принимаются следующие допущения к модели: 1) моменты инерции тел учтены с условием материала и геометрии формы; 2) массы компонентов приведены к расчетным центрам масс; 3) площадь опоры определяется как абсолютно жесткая, профиль трасы соответствует отнулевому циклическому нагружению по синусоидальному закону с максимальной амплитудой, соответствующей рабочему ходу ГМУ; 4) силы сопротивления, другие внешние возмущения не учитываются.

Уравнение динамики гусенично-модульного устройства. Уравнения динамики ГМУ строятся исходя из допущения, что ГМУ перемещается в пространстве отдельно от корпуса машины как твердое тело. При этом, его движение и зависимость этого движения от профиля опорной трассы описывается дифференциальными уравнениями, сходящимися в точках соприкосновения опорных катков с трассой. Для того, чтобы линеаризовать задачу, накладывается также кинематические ограничения на фланец рамы гусеничного модуля, имитирующие его закрепление на рулевой оси машины. При этом система уравнений, описывающая движение ГМУ, содержит динамические уравнения движения на основе законов сохранения количества движения и момента количества движения и кинематические уравнения угловых и линейных скоростей с угловыми и пространственными координатами, полученные на основе уравнений связи между координатными системами устройства и отдельных его элементов.

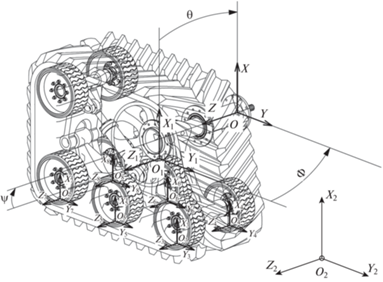
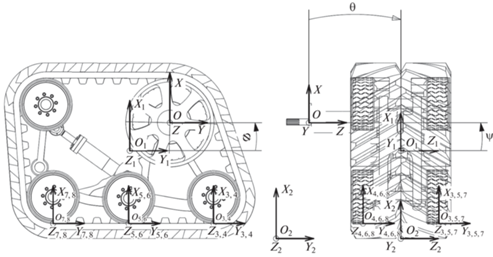
Систем же координат в модели несколько. Основная неподвижная система координат (НСК) ${{O}_{2}}{{X}_{2}}{{Y}_{2}}{{Z}_{2}}$, с помощью которой задаем исходные условия передвижения модуля по трассе, частоту и амплитуду неровностей, а также ее частотную характеристику, показана на рис. 2.

Вторая система координат, полусвязанная (ПСК) ${{O}_{1}}{{X}_{1}}{{Y}_{1}}{{Z}_{1}}$, совпадает с центром масс гусеничного модуля и перемещается вместе с ним в пространстве, при этом одноименные оси ПСК коллинеарны направлениям осей НСК. Следующая система координат – глобальная подвижная система (ГПСК) OXYZ, относительно нее прикладывается внешняя нагрузка на ГМУ и оценивается динамика перемещения всего средства. Эта система координат ограничена перемещением вдоль плоскости OXY, чтобы на данном этапе моделирования исключить из расчетов податливость всей системы и линеаризовать задачу.

В модели обозначены точки касания опорных колес с поверхностью трассы в виде локальных полусвязанных систем координат (ЛПСК) ${{O}_{{3 - 8}}}{{X}_{{3 - 8}}}{{Y}_{{3 - 8}}}{{Z}_{{3 - 8}}}$, с помощью которых в дальнейшем будет проводиться оптимизация параметра нормальной нагрузки на колесо посредством процедуры машинного обучения модели методом стохастического градиентного спуска. Эти же точки являются исходными, при имитации податливости высокопрочной упругой рамы ГМУ в дальнейших расчетах. Перечисленные системы координат также отражены на (рис. 3).

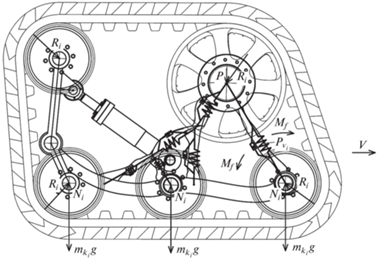
Уравнения движения ГМУ. Силы в устройстве распределены следующим образом. Нагрузка, симулирующая вес машины величиной 50 кН, прикладывается к фланцу крепления к точке O, глобальной подвижной системы OXYZ, в отрицательном направлении оси X. Силы реакций опорных колес прикладываются к точкам контакта колес с опорной поверхностью в точках ${{O}_{{3 - 8}}}$, локальных полусвязанных систем координат ${{O}_{{3 - 8}}}{{X}_{{3 - 8}}}{{Y}_{{3 - 8}}}{{Z}_{{3 - 8}}}$, в положительных направлениях осей ${{X}_{{3 - 8}}}$.

При этом, опорные колеса гусеничного модуля выполняют поступательное неравномерное движение относительно центра масс устройства, а именно относительно полусвязанной системы координат (ПСК) ${{O}_{1}}{{X}_{1}}{{Y}_{1}}{{Z}_{1}}$, тогда как сама полусвязанная система координат ${{O}_{1}}{{X}_{1}}{{Y}_{1}}{{Z}_{1}}~$будет совершать сложное движение относительно неподвижной системы координат (НСК) ${{O}_{2}}{{X}_{2}}{{Y}_{2}}{{Z}_{2}}$. Таким образом, строим систему дифференциальных уравнений движения полусвязанной системы координат ${{O}_{1}}{{X}_{1}}{{Y}_{1}}{{Z}_{1}}$, используя теорему об изменении количества движения, в проекции на оси глобальной подвижной системы (ГПСК) $OXYZ$

где $m$ – масса гусеничного модуля; $F_{k}^{X}$, $F_{k}^{Y}$, $F_{k}^{Z}$ – силы, действующие на раму устройства.

Уравнение связи вращательного движения. Чтобы полученные результаты расчета скорости и положения локальной системы координат центра масс устройства были транспарентными на полусвязную систему координат, необходимо ввести понятие угловых координат и матрицы перехода из локальной системы в полусвязную. Эта связь в механике классически определяется с помощью углов Эйлера–Крылова или уравнениями связи вращательного движения [7, 11]

В расчетах принято использовать значения скорости изменения углов ${{\varphi }}$, ${{{{\psi }}}_{i}}$, θ, которые определяются из уравнений

Преобразуем уравнения в матрицу перехода из локальной полусвязной системы координат в несвязную систему

Следующим шагом определим уравнение движения колес гусеничного модуля относительно рамы. В процессе движения гусеничного модуля его колеса совершают возвратно-поступательное движение относительно оси крепления модуля и можно было бы ограничиться уравнением движения колеса относительно вертикальной составляющей ПСК ${{O}_{1}}{{X}_{1}}$. Необходимо учесть, что в реакции также участвуют упругие сегменты топологически оптимизированной рамы, обозначенные на схеме упруго диссипативными силами ${{P}_{{{{{v}}_{i}}}}}$, учитывается также сила натяжения резиноармированной гусеницы ${{R}_{i}}$, вес самих катков ${{m}_{{{{k}_{i}}}}}g$ и их инерциальные характеристики M_f, (рис. 4). Кроме того, указанные реакции со стороны сегментов рамы, вследствие сложного пространственного расположения самих сегментов, проецируются на оси ПСК ${{O}_{1}}{{X}_{1}}{{Y}_{1}}{{Z}_{1}}$. Для корректного расчета реакций в упругих сегментах воспользуемся теоремой направляющих косинусов

где $\cos {{\alpha }_{{{{P}_{{{{{v}}_{i}}}}}}}}$, $\cos {{\beta }_{{{{P}_{{{{{v}}_{i}}}}}}}}$ и $\cos {{\gamma }_{{{{P}_{{{{{v}}_{i}}}}}}}}$ – направляющие косинусы силы ${{P}_{{{{{v}}_{i}}}}}$.

Аналогично определяются силы реакции упругого сегмента рамы ${{P}_{{{{h}_{i}}}}}$. Заранее примем ограничение о том, что опорное колесо также как и резиноармированная гусеница считается недеформируемым, что позволит пренебречь упругой и диссипативной реакцией резинового корда колеса и гусеницы. Это позволит упростить вычисления реакции площади опоры колеса на гусеницы и пятна контакта гусеницы на грунте.

Кроме того, в уравнении (1) не участвуют силы трения в паре опорное колесо–резиноармированная гусеница и резиноармированная гусеница–грунт

где $m$ – масса i-го колеса гусеничного модуля; $F_{{{{k}_{i}}}}^{X}$, $F_{{{{k}_{i}}}}^{Y}$, $F_{{{{k}_{i}}}}^{Z}$ – силы, действующие на i-е колесо устройства.

Уравнение динамики вращательного движения ПСК относительно НСК. Уравнения динамики вращательного движения корпуса вокруг центра масс устройства можно получить на основе теоремы об изменении главного момента количества движения. В векторной форме для общего случая в соответствии с формулой Бура

где ${{K}_{0}} = J\bar {\omega }$ – главный момент количества движения; $\frac{{\tilde {d}{{K}_{0}}}}{{dt}}$ – локальная производная по времени от главного момента количества движения твердого тела относительно центра C [6], $L_{0}^{{\left( e \right)}} = \sum\nolimits_{k = 1}^N {{{r}_{k}}} \times F_{k}^{{\left( e \right)}}$ – главный момент внешних сил, приложенных к твердому телу, относительно того же центра.

В данном случае главный момент можно найти с помощью третьего закона Ньютона. В проекциях на оси подвижной системы координат уравнения динамики вращательного движения корпуса вокруг ЦМ можно записать в виде системы

Раскрывая проекции векторного произведения $\left( {{{\omega }} \times {{K}_{0}}} \right)$ и подставляя компоненты из (2), рассматриваемую систему динамических уравнений можно представить в виде

В частном случае совпадения выбранных осей с осями эллипсоида инерции корпуса система уравнений (3) принимает вид динамических уравнений Эйлера и в проекции на подвижные оси системы имеет вид

где A, B, C – соответствующие осевые моменты инерции тела относительно трех ортогональных главных осей инерции.

Имитационное моделирование. После синтеза математической модели переходим к имитационному моделированию в программном комплексе MATLAB/SIMULINK и анализу нагружения гусенично-модульного устройства исходной нагрузкой. Для этого воспользуемся рекомендациями, приведенными в [12]. Положение заднего рычага управления положением третьей пары опорных колес изменяется по синусоиде в диапазоне работы гидроцилиндра. Симуляция проводилась в течение семи секунд, половину времени устройство перемещалось на всех шести катках, а вторую половину на четырех передних. До второй секунды испытаний, результаты демонстрируют установочный режим и эти данные для понимания механики модели индифферентны, они включают в себя ошибки начального положения рамы в пространстве и ими можно пренебречь. Пиковые значения усилий в точках контакта, равные значениям много выше исходной нагрузки, в рамках данного исследования будем игнорировать как ошибки решателя. Основной диапазон результатов расположен до отметки 160 кН, который будем считать репрезентативной частью.

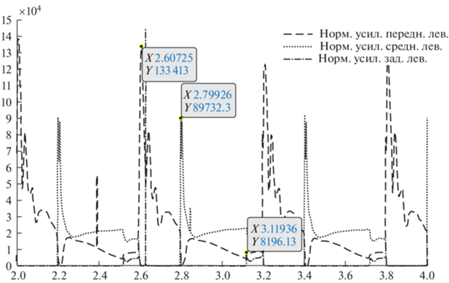
Чтобы анализировать изменение динамического нагружения на опоры введем понятие фазы нагружения, характеризующей время прохода единицы условного препятствия под всеми катками устройства, с учетом их равномерного движения. Для недеформируемой рамы рассмотрим участок времени 2.1–3.1 с (рис. 5). Здесь наблюдаем, как наибольшее значение контактного усилия (133 кН) возникает в первых (по направлению движения) катках устройства. При переходе условного препятствия ко второй паре колес контактные усилия снижаются до 90 кН, а при переходе к третьей паре колес до 8.2 кН. Это свидетельствует о том, что при гармоническом движении устройства по условным недеформируемым препятствиям наиболее нагруженными опорами являются передние по ходу движения, а недеформируемость рамы ухудшает баланс нагруженности между левыми и правыми опорными катками. Предлагаемая демпфирующая система устройства (топологически оптимизированная рама) с оптимальным расположением опорных катков должна нивелировать этот эффект.

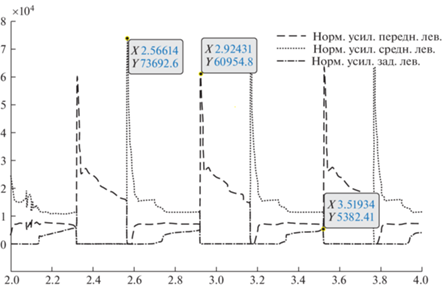
Для сравнения приведем аналогичные диаграммы для деформируемой рамы устройства, представляющей собой топологически оптимизированную раму со сверхупругими упрочняющими элементами из композитного материала с термоупругими мартенситными превращениями (рис. 6). Для деформируемой рамы наибольшее значение контактного усилия 61 кН возникает в первых (по направлению движения) катках устройства (рис. 6), затем при переходе препятствия ко второй паре колес значения увеличиваются и становятся равные 74 кН, еще ниже значения для третьей пары колес 5.4 кН.

Выводы. В результате проведенных исследований: 1) синтезирована математическая модель предложенного гусенично-модульного устройства с реализованной концепцией изменения площади пятна контакта между почвой и гусеничной лентой. По предварительной оценке, предложенная конструкция позволит изменять площадь пятна контакта в диапазоне 10–15%. Эти данные могут быть использованы при проектировании аналогичных устройств, а также для расчета момента сопротивления повороту гусенично-модульных устройств и уточнения методики расчета; 2) определены характер и величины силовых факторов, возникающих в упругих сегментах, при возникновении динамической нагрузки на устройство; 3) на основании полученных амплитудно-частотных характеристик усилий на каждом колесе устройства выявлены зависимости для требуемых жесткостных характеристик упругих сегментов, благодаря которым становится возможным решение задачи подбора формы и площади сечений упругих элементов на основе учета выполняемой ими работы.