Проблемы машиностроения и надежности машин, 2023, № 6, стр. 54-61

Одной из важных областей применения механизмов параллельной структуры является медицина, что обусловлено такими качествами подобных механизмов, как более высокая точность позиционирования и жесткость по сравнению с механизмами с последовательной структурой. Наиболее часто механизмы такого типа применяются в хирургии, в частности нейрохирургии и минимально‑инвазивной абдоминальной хирургии [1, 2]. При этом могут использоваться различные структурные схемы механизмов, однако наибольшее распространение получили устройства с удаленным центром вращения. В этих механизмах выходное звено (чаще всего – хирургический инструмент) совершает вращение вокруг постоянной точки, а промежуточные звенья всегда находятся на некотором удалении от этой точки. Такая особенность обусловлена тем, что упомянутая точка, как правило, является местом прокола или разреза, в котором инструмент вводится в тело пациента. Двумя основными типами механизмов с удаленным центром вращения являются сферические и плоские механизмы.

Сферические механизмы представляют собой устройства, обладающие, как правило, тремя степенями свободы. В подавляющем большинстве случаев такие механизмы являются пространственными, т.е. их звенья не находятся в одной плоскости. В качестве примеров медицинских сферических механизмов можно привести робот CoBRASurge [3] с классической структурой, включающей дуговые звенья, предназначенный для малоинвазивных операций, а также робот ESTELE [4] с похожей структурой, основное назначение которого – роботизированное ультразвуковое исследование абдоминальной области.

Плоские механизмы, звенья которых лежат в одной плоскости, также могут использовать дуговые элементы, как, например, это сделано в роботах SASSU [5] и Probot [6]. Однако наиболее распространенными являются механизмы с пантографами, в которых движение приводного звена (кривошипа) копируется инструментом. Примерами могут служить робот LARS [7], являющийся одним из первых представителей подобных устройств, и робот BlueDragon [8], в котором используется несколько пантографов, каждый из которых управляет отдельным инструментом. Основным недостатком таких механизмов является относительно низкая жесткость, что для медицинского оборудования является недопустимым [9]. В настоящей статье предлагается возможный вариант решения такой проблемы за счет введения дополнительной приводной избыточности в плоский механизм с пантографом.

Базовый механизм. Для начала рассмотрим базовое исполнение механизма (рис. 1).

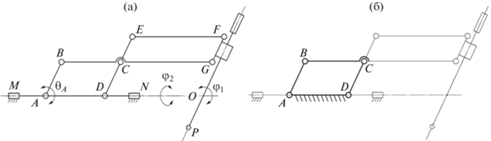
Основной частью механизма является пара плоских параллелограммов ABCD и CEFG. В каждой точке располагается вращательный шарнир. При этом звено CD первого параллелограмма и звено второго параллелограмма CE представляют собой две части физически единого звена DE. Аналогично звенья BC и CG являются частями единого звена BG. На звене FG закреплен инструмент, ось которого параллельна данному звену. Воспользовавшись известной формулой Чебышева, можно увидеть, что подвижность рассматриваемого механизма будет равна единице

где n – число подвижных звеньев механизма; p₅ – число одноподвижных кинематических пар (пар 5-го класса); p₄ – число двухподвижных кинематических пар (пар 4-го класса).

Кинематическая структура механизма обеспечивает синхронное движение звеньев AB, DE, FG и, соответственно, инструмента. Иными словами, вращение приводной кинематической пары А приводит к повороту инструмента вокруг точки O. При этом угол поворота входного звена θ_A будет равен углу поворота инструмента φ₁. В свою очередь звено AD расположено на поворотной оси MN, что дает механизму вторую степень свободы – возможность вращения вокруг оси, характеризуемого углом φ₂. Таким образом, рассматриваемый механизм имеет две вращательных степени свободы. При этом центр вращения расположен в точке O и удален от непосредственно звеньев механизма: через данную точку в процессе работы проходит только инструмент. Перемещение инструмента вдоль собственной оси, а также его вращение вокруг этой оси может осуществляться вручную, либо с помощью отдельных приводов и в рамках настоящей статьи не рассматривается.

Можно легко видеть, что в основе механизма, по сути, лежит шарнирный четырехзвенник ABCD (рис. 1б). Такой механизм является простейшим представителем класса механизмов параллельной структуры, которому присущи достоинства и недостатки подобных механизмов. Одним из главных таких недостатков является наличие так называемых особых положений (сингулярностей), при попадании в которые, механизм теряет степень свободы или управление [10, 11]. При этом шарнирный четырехзвенник, как было показано Д. Златановым [12], может попадать в особые положения, характеризующиеся вырождением связей [13].

Негативные эффекты, заключающиеся в снижении точности позиционирования, потере жесткости, увеличении нагрузки на приводы и конструктивные элементы механизма, как правило, начинают проявляться при приближении к особым положениям [14, 15], что уменьшает реальную рабочую зону механизма. Поскольку для рассматриваемого механизма в качестве основной области применения предлагается медицина, а именно манипулирование хирургическими инструментами, очевидной становится недопустимость возникновения перечисленных явлений, поскольку каждое из них может привести к травме или создать угрозу жизни пациента.

Одним из способов борьбы с особыми положениями является введение в механизм избыточности, заключающейся в использовании только дополнительных приводов (приводная избыточность), либо дополнительных приводов в паре со вспомогательной подвижностью (кинематическая избыточность). Легко видеть, что появление дополнительной подвижности в рассматриваемом механизме привело бы к изменению структуры и, соответственно, потере синхронности движения приводного звена AB и инструмента. Из этого следует, что наиболее рациональным решением в данном случае было бы использование приводной избыточности.

Модифицированный механизм с приводной избыточностью. Наиболее простым способом введения приводной избыточности является замена любой пассивной кинематической пары на приводную. В рассматриваемом механизме наиболее рациональной представляется замена кинематической пары D, поскольку эта пара расположена на основании механизма, а значит ее физический привод (электродвигатель) можно удобно расположить там же. Это позволяет не увеличивать массу подвижных частей механизма и нагрузку на них, поскольку нет необходимости перемещать привод в процессе работы. В то же время можно видеть, что геометрия рассматриваемого механизма далеко не оптимальна с точки зрения обеспечения его жесткости. Действительно, удаление центра обеспечивается “вытянутой” геометрией механизма, являющегося, по сути, консольной балкой с заделкой по звену AD. Уменьшение консоли позволило бы потенциально повысить жесткость механизма без увеличения сечения и, как следствие, массы подвижных звеньев.

Для решения обозначенной проблемы целесообразно добавить в механизм простейшую структурную группу Ассура с приводной кинематической парой. При этом место присоединения такой группы к механизму должно быть, с одной стороны, максимально близким к инструменту, а с другой – не сильно увеличивать габариты механизма, поскольку поворот вокруг оси MN, в любом случае, будет осуществляться для всей конструкции. В качестве такого решения в настоящей статье предлагается использовать дополнительную диаду RRR (R – обозначает вращательный шарнир), присоединенную к точке Е (рис. 2а).

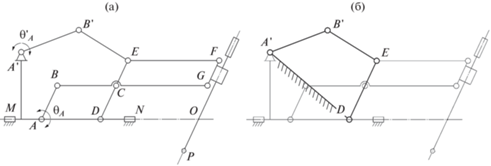
Дополнительная диада A'B'E располагается в задней части механизма и не препятствует функционированию его основной рабочей части (параллелограмму CEFG). При этом приводная пара A' расположена на основании механизма. Стоит заметить, что в точке E соединяются три звена: B'E, DE и EF, поэтому теоретически в данной точке расположены две одноподвижных пары. С учетом этого, для модифицированного механизма структурная формула Чебышева будет иметь вид

Введение дополнительной диады RRR позволило создать в структуре механизма дополнительный контур A'B'ED, представляющий собой, по сути, еще один шарнирный четырехзвенник (рис. 2б).

Поскольку звено DE движется синхронно звену АВ, в рассматриваемом четырехвезннике его можно считать приводным. Поскольку звено A'B' также является приводным, очевидна приводная избыточность механизма. При этом положение точки Е зависит от углов поворота двух приводных звеньев, а не одного, как в случае базового механизма, что потенциально делает механизм с диадой в целом более жестким.

Перейдем к решению задачи о положениях. Поскольку, отмечено что углы θ_A и φ₁ равны, задача будет заключаться в вычислении угла $\theta _{A}^{'}$ по заданному значению θ_A или φ₁. При этом расчетную схему для решения задачи можно упросить, рассматривая только шарнирный четырехзвенник A'B'ED (рис. 3).

Координаты точки E определяются длиной l_DE звена DE и углом θ_A

где x_D, y_D – известные координаты точки D.

Координаты точки В' можно аналогичным образом выразить через координаты точки A' и длину l_A'B' звена A'B', а также угол $\theta _{A}^{'}$.

Используя выражения (1) и (2), а также постоянство длины l_B'Е звена В'E можно записать уравнение связи

В неособом положении уравнение (3) будет иметь два решения, которые можно получить аналитически [16]. При этом, очевидно, более предпочтительным будет решение, при котором точка B ' расположена выше, что уменьшает риск интерференции звеньев A'B' и B'E и параллелограмма ABCD.

Расположение точки A', а также длины l_A'B' и l_B'E определяют допустимые углы поворота звена DE, и, как следствие инструмента. Для того, чтобы угол поворота был теоретически неограничен, должно выполняться следующее условие для φ₁:

На практике необходимость в неограниченном повороте инструмента может отсутствовать, т.к. имеется возможность наклона всего механизма в противоположную сторону за счет изменения угла φ₂. Поэтому условие (4) не является обязательным в реальном устройстве.

Компьютерное моделирование механизма. Одним из важных этапов разработки реального устройства является компьютерное моделирование конструкции. Помимо того, что такая модель служит отправной точкой для создания конструкторской документации, необходимой для изготовления изделия, моделирование в CAD позволяет оценить ряд важных параметров, таких как размеры рабочей зоны с учетом конструктивных ограничений, нагрузки на приводы и т.п. Для дальнейшей проработки были созданы модели базового механизма (рис. 4а) и механизма с приводной избыточностью (рис. 4б).

После первичной проработки был создан действующий прототип базового механизма для проверки основных конструктивных решений и отработки системы управления. При этом конструкция была несколько изменена и для приводов были использованы ременные передачи. Кроме того, была осуществлена балансировка механизма (рис. 5).

Для управления механизмом разработан ряд четырехкоординатных задатчиков движения. Один из них, для применения в хирургии, имитирует лапароскоп (рис. 6а). На выходе задатчика – четыре аналоговых сигнала, пропорциональных отклонению рукоятки от нейтрального положения.

Возможность освобождения рук оператора обеспечивает педальный задатчик движения (рис. 6б). Четыре педальных выключателя на платформе позволяют оператору, работать стоя, или в сидячем положении, поставив ноги на платформу, ее конструкция дает возможность стоять на платформе, не нажимая ни на одну из педалей. Управление четырьмя реверсивными приводами осуществляется за счет выбора сочетания нажатых педалей. При этом настройку указанных сочетаний можно выполнить индивидуально.

Механизм предполагается использовать в качестве альтернативы системы Soloassist, выпускаемой немецкой компанией ActorMed [17], назначение которой – управление эндоскопической камерой при малоинвазивных операциях.

Заключение. В настоящей статье рассмотрен механизм с удаленным центром вращения, основной частью которого является плоский пантограф. Показано, что такой механизм можно рассмотреть в качестве шарнирного четырехзвенника. Плоские механизмы с удаленным центром вращения, как правило, имеют относительно низкую жесткость. Для решения поставленной задачи предложено ввести в механизм приводную избыточность за счет использования дополнительной приводной диады RRR. Добавление диады формирует дополнительный контур, эквивалентный четырехзвенному механизму с двумя приводными звеньями. Для такого механизма показано решение задачи о положениях. Базовый и модифицированный механизм смоделированы в CAD. Кроме того, представлен прототип базового механизма с ременными передачами, для которого выполнена балансировка.

Финансирование. Исследование выполнено за счет гранта Российского научного фонда № 23-29-00789, https://rscf.ru/project/23-29-00789/

Конфликт интересов. Авторы заявляют, что у них нет конфликта интересов.