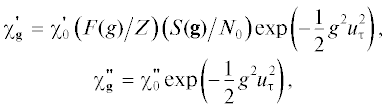Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 7, стр. 78-83
Когерентное рентгеновское излучение, возбуждаемое расходящимся пучком релятивистских электронов в монокристалле в направлении оси пучка
Д. О. Шкуропат a, С. В. Блажевич a, *, А. С. Горлов b, А. В. Носков a, b, **, А. Э. Федосеев a
a Белгородский государственный университет
308015 Белгород, Россия
b Белгородский государственный технологический университет им. В.Г. Шухова
308012 Белгород, Россия
* E-mail: blazh@bsu.edu.ru
** E-mail: noskovbupk@mail.ru
Поступила в редакцию 26.12.2020
После доработки 26.01.2021
Принята к публикации 30.01.2021
Аннотация
В геометрии рассеяния Лауэ развита теория когерентного рентгеновского излучения, возбуждаемого пучком релятивистских электронов в монокристалле в направлении, близком к оси электронного пучка. Теория учитывает асимметрию отражения электронного поля относительно поверхности кристалла и расходимость электронного пучка. Получены выражения, описывающие спектрально-угловые плотности параметрического рентгеновского излучения вблизи направления скорости электрона, переходного излучения и их интерференции. Изучено влияние расходимости электронного пучка и асимметрии отражения поля электрона относительно поверхности мишени на спектрально-угловые плотности излучений.
ВВЕДЕНИЕ
Параметрическое рентгеновское излучение (ПРИ) генерируется вблизи направления рассеяния Брэгга, вследствие рассеяния псевдо-фотонов кулоновского поля релятивистского электрона на системе параллельных атомных плоскостях кристалла [1–3]. Наряду с фотонами, генерируемыми в направлении рассеяния Брэгга, теория излучения предсказывает генерацию фотонов ПРИ вблизи направления скорости релятивистского электрона (ПРИ вперед (ПРИВ)) [4–6].
Первые сообщения об обнаружении ПРИВ релятивистских электронов в монокристалле в геометрии рассеяния Лауэ появились в работах [7, 8]. В эксперименте [8] регистрировалось рентгеновское излучение релятивистских электронов из толстой поглощающей монокристаллической мишени в условиях генерации ПРИВ, однако искомый рефлекс весьма слабо проявился на фоне излучения рождаемого электронами на элементах конструкции экспериментальной установки, а также на фоне переходного излучения и возможной интерференции ПРИВ и переходного излучения (ПИ). Больше экспериментов по исследованию свойств ПРИВ не проводилось. Таким образом, теоретическое исследование свойств ПРИ вперед и поиск оптимальных условий для более яркого экспериментального наблюдения данного динамического эффекта остается актуальным.
Детальное теоретическое описание ПРИВ в монокристалле для случая симметричного отражения в геометриях рассеяния Лауэ и Брэгга было дано в работах [9, 10]. Для случая асимметричного отражения поля электрона относительно поверхности мишени, когда отражающие плоскости монокристалла расположены под произвольным углом к поверхности мишени, теория ПРИВ была развита в [11]. Влияние расходимости электронного пучка на когерентное рентгеновское излучение в направлении Брэгга в геометрии рассеяния Лауэ было рассмотрено в работах [12]. Теория когерентного рентгеновского излучения пучка релятивистских электронов в монокристалле в направлении, близком к направлению оси пучка в геометрии рассеяния Брэгга была развита в работе [13], а в периодической слоистой среде – в работе [14].
В настоящей работе, в рамках динамической теории дифракции, получены и исследованы выражения, описывающие спектрально-угловые характеристики ПРИВ в геометрии рассеяния Лауэ, в общем случае асимметричного отражения. Показано влияние расходимости электронного пучка на угловую плотность ПРИВ. Показано влияние асимметрии отражения на спектрально-угловые характеристики когерентного рентгеновского излучения.
ГЕОМЕТРИЯ ПРОЦЕССА ИЗЛУЧЕНИЯ
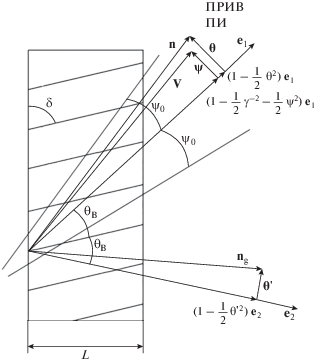
Рассмотрим излучение пучка релятивистских электронов, пересекающих монокристалл в геометрии рассеяния Лауэ (рис. 1). Пусть отражающая система параллельных атомных плоскостей монокристалла расположена под некоторым углом $\delta $ к поверхности мишени (рис. 1), что соответствует случаю асимметричного отражения поля излучения ($\delta = 0$ – частный случай симметричного отражения). Введем угловые переменные ${\mathbf{\psi }},$ ${\mathbf{\theta }}{\kern 1pt} '$ и ${\mathbf{\theta }}$ в соответствии с определениями скорости релятивистского электрона ${\mathbf{V}}$ и единичных векторов: ${\mathbf{n}}$ – в направлении импульса фотона, излученного вблизи направления вектора скорости электрона, и ${{{\mathbf{n}}}_{{\mathbf{g}}}}$ – в направлении рассеяния Брэгга:
(1)
$\begin{gathered} {\mathbf{V}} = \left( {1 - \frac{1}{2}{{\gamma }^{{ - 2}}} - \frac{1}{2}{{\psi }^{2}}} \right){{{\mathbf{e}}}_{1}} + {\mathbf{\psi }},\,\,\,\,{{{\mathbf{e}}}_{1}}{\mathbf{\psi }} = 0, \\ {\mathbf{n}} = \left( {1 - \frac{1}{2}{{\theta }^{2}}} \right){{{\mathbf{e}}}_{1}} + {\mathbf{\theta }},\,\,\,\,{{{\mathbf{e}}}_{1}}{\mathbf{\theta }} = 0,\,\,\,\,{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}} = \cos 2{{\theta }_{{\text{B}}}}, \\ {{{\mathbf{n}}}_{{\mathbf{g}}}} = \left( {1 - \frac{1}{2}{{\theta }^{{'2}}}} \right){{{\mathbf{e}}}_{2}} + {\mathbf{\theta }}{\kern 1pt} ',\,\,\,\,{{{\mathbf{e}}}_{2}}{\mathbf{\theta }} = 0, \\ \end{gathered} $СПЕКТРАЛЬНО-УГЛОВЫЕ ПЛОТНОСТИ ИЗЛУЧЕНИЙ
В рамках двух-волнового приближения динамической теории дифракции, методом аналогичным использованным в работе [11] получены выражения для спектрально-угловых плотностей ПРИВ, ПИ и их интерференции в случае тонкой непоглощающей мишени:
(2а)
$\omega \frac{{{{d}^{2}}N_{{{\text{ПРИВ}}}}^{{(s)}}}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}\frac{{{{\Omega }^{{{{{(s)}}^{2}}}}}}}{{{{{(\Delta - \chi _{0}^{'})}}^{2}}}}R_{{{\text{ПРИВ}}}}^{{(s)}},$(2б)
$\begin{gathered} R_{{{\text{ПРИВ}}}}^{{(s)}} = \frac{1}{{{{\xi }^{{(s)}}}^{2} + \varepsilon }} \times \\ \times \,\,\frac{{{{{\sin }}^{2}}\left( {\frac{{{{b}^{{(s)}}}}}{2}\left( {{{\sigma }^{{(s)}}} + \frac{{{{\xi }^{{(s)}}} - \sqrt {{{\xi }^{{(s)}}}^{2} + \varepsilon } }}{\varepsilon }} \right)} \right)}}{{{{{\left( {{{\sigma }^{{(s)}}} + \frac{{{{\xi }^{{(s)}}} - \sqrt {{{\xi }^{{(s)}}}^{2} + \varepsilon } }}{\varepsilon }} \right)}}^{2}}}}, \\ \end{gathered} $(3а)
$\omega \frac{{{{d}^{2}}N_{{{\text{ПИ}}}}^{{(s)}}}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}{{\Omega }^{{{{{(s)}}^{2}}}}}{{\left( {\frac{1}{\Delta } - \frac{1}{{\Delta - \chi _{0}^{'}}}} \right)}^{2}}R_{{{\text{ПИ}}}}^{{(s)}},$(4а)
$\omega \frac{{{{d}^{2}}N_{{{\text{ИНТ}}}}^{{(s)}}}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}{{\Omega }^{{{{{(s)}}^{2}}}}}\left( {\frac{1}{\Delta } - \frac{1}{{\Delta - \chi _{0}^{'}}}} \right)\frac{1}{{\Delta - \chi _{0}^{'}}}R_{{{\text{ИНТ}}}}^{{(s)}},$(4б)
$\begin{gathered} R_{{{\text{ИНТ}}}}^{{(s)}} = - \frac{1}{{\sqrt {{{\xi }^{{(s)}}}^{2} + \varepsilon } \left( {{{\sigma }^{{(s)}}} + \frac{{{{\xi }^{{(s)}}} - \sqrt {{{\xi }^{{(s)}}}^{2} + \varepsilon } }}{\varepsilon }} \right)}}\,\,\left[ {\left( {1 - \frac{{{{\xi }^{{(s)}}}}}{{\sqrt {{{\xi }^{{{{{(s)}}^{2}}}}} + \varepsilon } }}} \right)\left( {{{{\cos }}^{2}}\left( {\frac{{{{b}^{{(s)}}}\sqrt {{{\xi }^{{{{{(s)}}^{2}}}}} + \varepsilon } }}{\varepsilon }} \right) - } \right.} \right. \\ - \,\,\left. {\cos \left( {\frac{{{{b}^{{(s)}}}\sqrt {{{\xi }^{{(s)}}}^{2} + \varepsilon } }}{\varepsilon }} \right)\cos \left( {{{b}^{{(s)}}}\left( {{{\sigma }^{{(s)}}} + \frac{{{{\xi }^{{(s)}}}}}{\varepsilon }} \right)} \right)} \right) + \,\,2\left( {1 + \frac{{{{\xi }^{{(s)}}}}}{{\sqrt {{{\xi }^{{{{{(s)}}^{2}}}}} + \varepsilon } }}} \right)\left. {\,\,{{{\sin }}^{2}}\left( {\frac{{{{b}^{{(s)}}}}}{2}\left( {{{\sigma }^{{(s)}}} + \frac{{{{\xi }^{{(s)}}} - \sqrt {{{\xi }^{{(s)}}}^{2} + \varepsilon } }}{\varepsilon }} \right)} \right)} \right], \\ \\ \end{gathered} $(5)
$\begin{gathered} {{\Omega }^{{(1)}}} = {{\theta }_{ \bot }} - {{\psi }_{ \bot }},\,\,\,\,{{\Omega }^{{(2)}}} = {{\theta }_{\parallel }} - {{\psi }_{\parallel }}, \\ \Delta \left( {{{\theta }_{ \bot }},{{\theta }_{\parallel }},{{\psi }_{ \bot }},{{\psi }_{\parallel }},\gamma } \right) = {{\gamma }^{{ - 2}}} + {{\left( {{{\theta }_{ \bot }} - {{\psi }_{ \bot }}} \right)}^{2}} + {{\left( {{{\theta }_{\parallel }} - {{\psi }_{\parallel }}} \right)}^{2}}, \\ {{\eta }^{{(s)}}}(\omega ) = \frac{{2{{{\sin }}^{2}}{{\theta }_{{\text{B}}}}}}{{{{V}^{2}}\left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}}\left( {\frac{{\omega (1 - {{\theta }_{\parallel }}\cot {{\theta }_{{\text{B}}}})}}{{{{\omega }_{{\text{B}}}}}} - 1} \right), \\ \varepsilon = \frac{{\sin (\delta + {{\theta }_{{\text{B}}}})}}{{\sin (\delta - {{\theta }_{{\text{B}}}})}},\,\,\,\,{{b}^{{(s)}}} = \frac{1}{{2\sin \left( {\delta - {{\theta }_{{\text{B}}}}} \right)}}\frac{L}{{L_{{{\text{ext}}}}^{{(s)}}}}, \\ L_{{{\text{ext}}}}^{{(s)}} = \frac{1}{{\omega \left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}},\,\,\,\,{{\nu }^{{(s)}}} = \frac{{\chi _{{\mathbf{g}}}^{'}{{C}^{{(s)}}}}}{{\chi _{0}^{'}}},\,\,\,\,{{С}^{{(1)}}} = 1, \\ {{С}^{{(2)}}} = \cos 2{{\theta }_{{\text{B}}}}, \\ {{\sigma }^{{(s)}}} = \frac{1}{{\left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}}\left( {\Delta \left( {{{\theta }_{ \bot }},{{\theta }_{\parallel }},{{\psi }_{ \bot }},{{\psi }_{\parallel }},\gamma } \right) - \chi _{0}^{'}} \right). \\ \end{gathered} $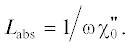 Для того, чтобы проявлялись эффекты динамической дифракции рассматривается монокристаллическая
пластина такой толщины, при которой длина пути электрона в пластинке ${{L}_{e}} \approx {{L}_{f}}$ = ${L \mathord{\left/ {\vphantom {L {\sin \left( {\delta - {{\theta }_{{\text{B}}}}} \right)}}} \right. \kern-0em} {\sin \left( {\delta - {{\theta }_{{\text{B}}}}} \right)}}$ во много раз превышает длину экстинкции рентгеновских волн в монокристалле $L_{{{\text{ext}}}}^{{(s)}} = {1 \mathord{\left/ {\vphantom {1 {\omega \left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}}} \right. \kern-0em} {\omega \left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}},$ т.е. ${{b}^{{(s)}}} \gg 1.$ Параметр $\varepsilon $ определяет асимметрию отражения поля электрона относительно поверхности мишени.
Для того, чтобы проявлялись эффекты динамической дифракции рассматривается монокристаллическая
пластина такой толщины, при которой длина пути электрона в пластинке ${{L}_{e}} \approx {{L}_{f}}$ = ${L \mathord{\left/ {\vphantom {L {\sin \left( {\delta - {{\theta }_{{\text{B}}}}} \right)}}} \right. \kern-0em} {\sin \left( {\delta - {{\theta }_{{\text{B}}}}} \right)}}$ во много раз превышает длину экстинкции рентгеновских волн в монокристалле $L_{{{\text{ext}}}}^{{(s)}} = {1 \mathord{\left/ {\vphantom {1 {\omega \left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}}} \right. \kern-0em} {\omega \left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}},$ т.е. ${{b}^{{(s)}}} \gg 1.$ Параметр $\varepsilon $ определяет асимметрию отражения поля электрона относительно поверхности мишени.
В выражениях (3) $\chi _{{\mathbf{g}}}^{'}$ и 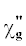 определяются следующим образом:
определяются следующим образом:
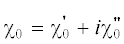 – средняя диэлектрическая восприимчивость, F(g) – форм-фактор атома, содержащего Z электронов, $S({\mathbf{g}})$ – структурный фактор элементарной ячейки, содержащей ${{N}_{0}}$ атомов, ${{u}_{{{\tau }}}}$ – среднеквадратичная амплитуда тепловых колебаний атомов кристалла. В работе рассматривается
рентгеновская область частот ($\chi _{{\mathbf{g}}}^{'} < 0,$ $\chi _{0}^{'} < 0$). Выражение (2) при значении параметра $s = 1$ описывает поля $\sigma $-поляризованные, а при $s = 2$ поля $\pi $-поляризованные.
– средняя диэлектрическая восприимчивость, F(g) – форм-фактор атома, содержащего Z электронов, $S({\mathbf{g}})$ – структурный фактор элементарной ячейки, содержащей ${{N}_{0}}$ атомов, ${{u}_{{{\tau }}}}$ – среднеквадратичная амплитуда тепловых колебаний атомов кристалла. В работе рассматривается
рентгеновская область частот ($\chi _{{\mathbf{g}}}^{'} < 0,$ $\chi _{0}^{'} < 0$). Выражение (2) при значении параметра $s = 1$ описывает поля $\sigma $-поляризованные, а при $s = 2$ поля $\pi $-поляризованные.
Отметим, что выражения (2)–(4) описывают спектрально-угловые плотности ПРИВ, ПИ и их интерференцию, генерируемые пересекающим монокристаллическую пластинку релятивистским электроном, направление скорости ${\mathbf{V}}$ которого отклонено относительно оси пучка ${{{\mathbf{e}}}_{1}}$ на угол ${\mathbf{\psi }}({{\psi }_{ \bot }},{{\psi }_{{||}}}).$
Рассмотрим спектрально-угловые плотности излучений и их интерференцию с учетом угловой расходимости электронного пучка ${{\psi }_{0}}.$ Для этого усредним выражения (2)–(4) по всем возможным прямолинейным траекториям электрона в пучке. В качестве примера проведем усреднение угловой плотности ПРИВ по функции распределения Гаусса $f({{\psi }_{ \bot }},{{\psi }_{\parallel }})$ = $\frac{1}{{\pi \psi _{0}^{2}}}{{e}^{{ - \frac{{\psi _{ \bot }^{2}\,\, + \,\,\psi _{\parallel }^{2}}}{{\psi _{0}^{2}}}}}},$ получим выражения:
(7)
$\begin{gathered} \left\langle {\omega \frac{{{{d}^{2}}N_{{{\text{ПРИВ}}}}^{{(s)}}}}{{d\omega d\Omega }}} \right\rangle = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}\frac{1}{{\pi \psi _{0}^{2}}} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\left( {{{e}^{{ - \frac{{\psi _{ \bot }^{2}\,\, + \,\,\psi _{\parallel }^{2}}}{{\psi _{0}^{2}}}}}}\frac{{{{\Omega }^{{(s)}}}^{2}}}{{{{{(\Delta - \chi _{0}^{'})}}^{2}}}}R_{{{\text{ПРИВ}}}}^{{(s)}}} \right)} } {\kern 1pt} d{{\psi }_{ \bot }}d{{\psi }_{\parallel }}, \\ \end{gathered} $(8)
$\begin{gathered} \left\langle {\omega \frac{{{{d}^{2}}N_{{{\text{ПИ}}}}^{{(s)}}}}{{d\omega d\Omega }}} \right\rangle = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}\frac{1}{{\pi \psi _{0}^{2}}} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\left( {{{e}^{{ - \frac{{\psi _{ \bot }^{2}\,\, + \,\,\psi _{\parallel }^{2}}}{{\psi _{0}^{2}}}}}}{{\Omega }^{{{{{(s)}}^{2}}}}}{{{\left( {\frac{1}{\Delta } - \frac{1}{{\Delta - \chi _{0}^{'}}}} \right)}}^{2}}R_{{{\text{ПИ}}}}^{{(s)}}} \right)} } {\kern 1pt} d{{\psi }_{ \bot }}d{{\psi }_{\parallel }}, \\ \end{gathered} $(9)
$\begin{gathered} \left\langle {\omega \frac{{{{d}^{2}}N_{{{\text{ИНТ}}}}^{{(s{\text{)}}}}}}{{d\omega d\Omega }}} \right\rangle = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}\frac{1}{{\pi \psi _{0}^{2}}} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\left( {{{e}^{{ - \frac{{\psi _{ \bot }^{2}\,\, + \,\,\psi _{\parallel }^{2}}}{{\psi _{0}^{2}}}}}}{{\Omega }^{{{{{(s)}}^{2}}}}}\left( {\frac{1}{\Delta } - \frac{1}{{\Delta - \chi _{0}^{'}}}} \right)\frac{1}{{\Delta - \chi _{0}^{'}}}R_{{{\text{ИНТ}}}}^{{(s)}}} \right)} } \times \\ \times \,\,d{{\psi }_{ \bot }}d{{\psi }_{\parallel }}. \\ \end{gathered} $Необходимо отметить, важность выражений (7)–(9) для нахождения оптимальных параметров эксперимента по исследованию пика ПРИВ с точки зрения увеличения интенсивности спектрально-угловой плотности ПРИВ, а также оптимизации фона переходного излучения и интерференции ПРИВ и ПИ. Также выражения (7)–(9) можно использовать для интерпретации результатов уже проведенного эксперимента.
Для примера проведем численные расчеты спектрально-угловых плотностей ПРИВ, ПИ и их интерференции пучка релятивистских электронов, пересекающих с энергией Е = 102.2 МэВ ($\gamma = 200$) монокристаллическую пластинку алмаза С(111). Рассмотрим угол между системой дифрагирующих атомных плоскостей монокристалла и осью падающего пучка электронов (угол Брэгга) ${{\theta }_{{\text{B}}}} = 16.2^\circ ,$ частоту Брэгга ${{\omega }_{{\text{B}}}} = 10.9\,\,{\text{кэВ}}.$ Система отражающий плоскостей (111) монокристаллической мишени расположена под углом $\delta = 151.3^\circ $ к поверхности мишени, что соответствует случаю асимметричного отражения поля электрона относительно поверхности мишени ($\varepsilon = 0.3$). В расчетах также рассматриваются значения угла $\delta = 156.4^\circ $ ($\varepsilon = 0.2$) и $\delta = 138.6^\circ $ ($\varepsilon = 0.5$). Толщина мишени $L = 17.7$ мкм. Расчеты проведены для фиксированного угла наблюдения, соответствующего максимуму угловой плотности ПРИВ ${{\theta }_{ \bot }} = \sqrt {{{\gamma }^{{ - 2}}} - \chi {{{_{0}^{'}}}_{{}}}} \approx 6\,\,{\text{мрад}},$ при этом ${{\theta }_{\parallel }} = 0.$ Расчеты будем проводить для $\sigma $-поляризации (s = 1).
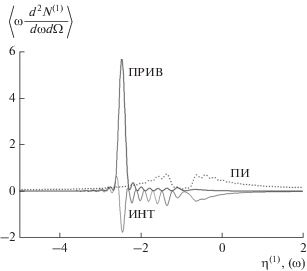
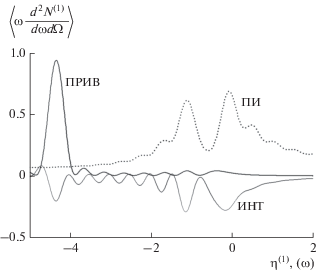
На рис. 2 представлены кривые, описывающие спектрально угловые плотности ПРИВ, ПИ и их интерференции, построенные согласно формулам (7)–(9) для фиксированного угла наблюдения в случае расходимости электронного пучка ${{\psi }_{0}} = 0.1\,\,{\text{мрад}}.$ Видно подавление частот, далеких от частоты Брэгга $\left( {\left| {{{\eta }^{{(s)}}}(\omega )} \right| \gg 0} \right),$ за счет деструктивной интерференции волн переходного излучения, испущенных из входной и выходной поверхности мишени. Это произошло из-за того, что толщина мишени была подобрана так, чтобы выполнялось резонансное условие деструктивной интерференции волн с частотами далекими от частоты Брэгга: ${{b}^{{(s)}}}{{\sigma }^{{(s)}}} = 2\pi m,$ $m$ – натуральное число, подробнее см. в работе [14]. При этом интерференция ПРИВ и ПИ на пик ПРИВ в рассматриваемом случае влияет деструктивно. Из рис. 2 следует возможность экспериментального наблюдения пика ПРИВ в резко асимметричном случае $\varepsilon = 0.3$ (симметричное отражение при $\varepsilon = 1$). Рассмотрим влияние расходимости пучка релятивистских электронов на спектрально-угловые плотности ПРИВ, ПИ и их интерференцию. На рис. 3 и 4 представлены кривые демонстрируют те же результаты, что и на рис. 2, но при ${{\psi }_{0}} = 0.5\,\,{\text{мрад}}$ и ${{\psi }_{0}} = 1\,\,{\text{мрад}}$ соответственно. Из рис. 3 и 4 следует, что при таких расходимостях электронного пучка вклад в когерентное рентгеновское излучение вдали от частот Брэгга $\left( {\left| {{{\eta }^{{(s)}}}(\omega )} \right| \gg 0} \right)$ дают волны ПИ, испущенные только из выходной поверхности мишени. При этом наблюдаются небольшие колебания в спектре ПИ в окрестности частоты Брэгга, связанные с интерференцией волн, генерируемых на входной и выходной поверхностях мишени. Таким образом, расходимость электронного пучка влияет на спектрально-угловую плотность ПИ. Также из рис. 3, 4 следует заметное влияние расходимости электронного пучка на амплитуду спектра ПРИВ. Видно, что при увеличении расходимости электронного пучка амплитуда спектра ПРИВ уменьшается.
Рис. 2.
Спектрально-угловые плотности ПРИВ, ПИ и их интерференция для фиксированного угла наблюдения. Расходимость электронного пучка ${{\psi }_{0}} = 0.1\,\,{\text{мрад}}.$ Параметр асимметрии $\varepsilon = 0.3.$
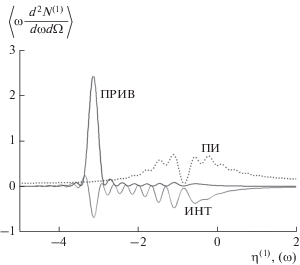
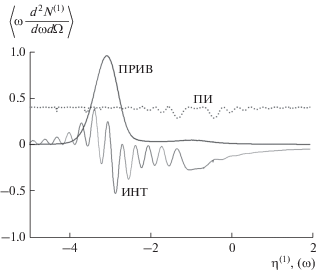
Рис. 3.
Спектрально-угловые плотности ПРИВ, ПИ и их интерференция для фиксированного угла наблюдения. Расходимость электронного пучка ${{\psi }_{0}} = 0.5\,\,{\text{мрад}}{\text{.}}$ Параметр асимметрии $\varepsilon = 0.3.$
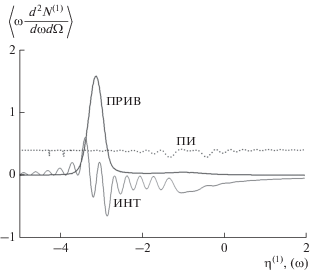
Рис. 4.
Спектрально-угловые плотности ПРИВ, ПИ и их интерференция для фиксированного угла наблюдения. Расходимость электронного пучка ${{\psi }_{0}} = 1\,\,{\text{мрад}}{\text{.}}$ Параметр асимметрии $\varepsilon = 0.3.$
Рассмотрим влияние асимметрии отражения поля электрона относительно поверхности мишени (параметр $\varepsilon $) на спектрально угловые характеристики излучений. На рис. 2 спектрально-угловые плотности излучений построены при значении угла $\delta = 151.3^\circ {\text{,}}$ что соответствует $\varepsilon = 0.3.$ На рис. 5 и 6 построены аналогичные кривые, но при $\delta = 156.4^\circ $ ($\varepsilon = 0.2$) и $\delta = 138.6^\circ $ ($\varepsilon = 0.5$) соответственно. В случае $\varepsilon = 0.2$ (рис. 5) амплитуда спектра ПРИВ более чем в 2 раза превышает амплитуду спектра ПРИВ при $\varepsilon = 0.3,$ при этом угол $\delta ,$ как мы видим, меняется незначительно. В случае же $\varepsilon = 0.5,$ наоборот, амплитуда спектра ПРИВ более чем в два раза меньше, чем при $\varepsilon = 0.3.$ При этом спектрально-угловая плотность ПИ существенно не меняется. Таким образом, спектрально-угловая плотность ПРИВ существенно зависит от асимметрии отражения. Данный факт можно использовать для постановки эксперимента по поиску и исследованию свойств ПРИВ.
ЗАКЛЮЧЕНИЕ
В геометрии рассеяния Лауэ получены выражения, описывающие спектрально-угловые плотности параметрического рентгеновского излучения вблизи направления скорости электрона, переходного излучения и их интерференции. Получены выражения, описывающие нормированные на один электрон усредненные спектрально-угловые плотности ПРИВ, ПИ и их интерференции в зависимости от угла расходимости электронного пучка ${{\psi }_{0}}$ и параметра асимметрии отражения $\varepsilon .$ Для примера проведены численные расчеты спектрально-угловых плотностей ПРИВ, ПИ и их интерференции для пучка релятивистских электронов, пересекающих монокристаллическую пластинку алмаза. Показано, что расходимость электронного пучка влияет на спектрально-угловую плотность ПИ: при увеличении расходимости электронного пучка амплитуда спектра ПРИВ уменьшается. Показанa существенная зависимость спектрально-угловой плотности ПРИВ от асимметрии отражения.
Список литературы
Тер-Микаэлян М.Л. Влияние среды на электромагнитные процессы при высоких энергиях. Ереван: АН АрмССР, 1969. 459 с.
Гарибян Г.М., Ян Ши // ЖЭТФ. 1971. Т. 61. С. 930.
Барышевский В.Г., Феранчук И.Д. // ЖЭТФ. 1971. Т. 61. С. 944.
Гарибян Г.М., Ян Ши // ЖЭТФ. 1972. Т. 63. С. 1198.
Baryshevsky V.G., Feranchuk I.D. // Phys. Lett. A. 1976. V. 57. P. 183.
Baryshevsky V.G., Feranchuk I.D. // J. Physique. 1983. V. 44. P. 913.
Kalinin B.N., Naumenko G.A., Padalko D.V. et al. // Nucl. Instr. Meth. In Phys. Res. B. 2001. V. 173. P. 253.
Алейник А.Н., Балдин А.Н., Богомазова Е.А. и др. // Письма в ЖЭТФ. 2004. Т. 80. С. 447.
Kubankin A.S., Nasonov N.N., Sergienko V.I., Vnukov I.E. // Nucl. Instrum. Methods Phys. Res. B. 2003. V. 201. P. 97.
Nasonov N., Noskov A. // Nucl. Instrum. Methods Phys. Res. B. 2003. V. 201. P. 67.
Блажевич С.В., Носков А.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2010. № 4. С. 40.
Блажевич С.В., Носков А.В. // ЖЭТФ. 2015. Т. 147. С. 875.
Блажевич С.В., Люшина К.С., Носков А.В. // ЖЭТФ. 2019. Т. 155. Вып. 2. С. 242.
Блажевич С.В., Дрыгина Ю.А., Шевчук О.Ю., Носков А.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 6. С. 43.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования