1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 8, 2022

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 8, стр. 50-55

Энергетическая и транспортная длины для описания зоны модификации резиста в ионной литографии

Я. Л. Шабельникова a, *, С. И. Зайцев a

a Институт проблем технологии микроэлектроники и особочистых материалов РАН
142432 Черноголовка, Россия

* E-mail: janeshabeln@yandex.ru

Поступила в редакцию 26.12.2021
После доработки 22.02.2022
Принята к публикации 28.02.2022

Полный текст (PDF)

Аннотация

Одним из способов использования фокусированного ионного пучка в литографических процессах для создания наноструктур является экспонирование специальных чувствительных материалов – резистов. В результате экспонирования растворимость такого материала увеличивается (“позитивный” резист) или, наоборот, уменьшается (“негативный” резист), что позволяет путем селективного облучения и последующего проявления сформировать на подложке заранее заданный рисунок. Настоящая работа направлена на развитие теоретических основ этого метода ионной литографии. Рассматривается практически важный случай торможения тяжелых ионов в органическом резисте, где средняя атомная масса много меньше, чем у налетающего иона. Получены выражения для энергетической и транспортной длин пробега ионов. Расчеты проведены в предположении степенного потенциала взаимодействия. Энергетическая длина характеризует глубину проникновения ионов в материал, а транспортная связана с расширением пучка ионов из-за рассеяния, поэтому эти длины являются основными характеристиками зоны, в которой поглощается энергия пучка ионов. Полученные выражения, предположительно, лягут в основу аналитического описания распределения поглощенной энергии, использование которого позволит до проведения эксперимента оценивать размеры зоны трансформации резиста пучком ионов.

Ключевые слова: ионная литография, резист, полиметилметакрилат, энергетическая длина, транспортная длина, степенной потенциал, сечение рассеяния, тормозная способность.

ВВЕДЕНИЕ

Ионная литография, основанная на облучении чувствительного резиста пучком частиц [1–6], имеет ряд преимуществ перед широко используемым методом электронной литографии [7–9]. Это и более высокая эффективность, поскольку большая часть энергии пучка поглощается резистом и тратится на его трансформацию, и лучшее предельное пространственное разрешение, так как траектории ионов более короткие и прямые, чем у электронов, и отсутствие паразитной засветки резиста вторичными частицами, так называемого “эффекта близости” [10, 11]. Однако несмотря на преимущества, применяется этот метод достаточно редко, хотя в последнее время можно отметить некоторое возрастание интереса к нему [12–17]. В основном для облучения резиста используют легкие ионы He [12, 14] или Ne [13].

Помочь повысить интерес к методу ионной литографии и осветить преимущества использования более тяжелых ионов (например, из ряда инертных газов) и резистов большей плотности может понимание влияния характеристик пучка ионов и резиста на конкретные размеры области модификации облучаемого материала. Для этого в предположении, что мерой модификации является плотность поглощенной энергии, нужно получить описание пространственного распределения энергии, куда в качестве параметров будут входить величины, характеризующие процессы торможения и рассеяния ионов. Кроме того, информация о размерах области резиста, поглотившей энергию, важна для планирования эксперимента по ионной литографии, возможности оценивать размер зоны модификации до проведения экспериментов, разрешение и время экспозиции. Эта информация может быть не только результатом численного моделирования, но и, что более удобно, представлена в виде аналитических выражений.

Ранее [18] на основе данных моделирования методом Монте-Карло было показано, что распределение поглощенной энергии по глубине резиста зависит от энергетической длины ионов (средней длины пробега ионов в резисте). Распределение же в плоскости резиста, согласно [19], связано со средним углом рассеяния и транспортной длиной пробега ионов. Это верно, по крайней мере, для случаев, когда энергия, переносимая каскадами смещенных атомов, составляет не более 10% всей энергии ионного пучка, и влиянием каскадов можно пренебречь. Проведенные авторами [20] оценки показали, что тяжелые ионы до 90% своей энергии могут передавать атомам резиста, смещая их, и тогда каскады приводят к существенному перераспределению энергии и увеличению как глубины, так и ширины зоны взаимодействия на десятки процентов. Однако получить описание распределения поглощенной энергии без учета каскадов смещенных атомов важно по двум причинам. Во-первых, оно может применяться в случае легких ионов (Z < 10), когда влиянием каскадов можно пренебречь. Во-вторых, на его основе в дальнейшем можно будет вывести учитывающее каскады распределение энергии как свертку функции распределения без учета каскадов и функции каскадного размытия энергии. Поэтому для полностью аналитического описания распределения поглощенной энергии важно получить выражения для энергетической и транспортной длин.

ЭНЕРГЕТИЧЕСКАЯ ДЛИНА ИОНОВ

Среднюю длину пробега ионов в резисте R можно вычислить, опираясь на величину энергии, поглощенной слоем резиста толщиной dx за счет упругих взаимодействий [21–23]:

(1)
${{\left( {\frac{{dE}}{{dx}}} \right)}_{n}} = - n{{S}_{n}}\left( E \right).$
Здесь n – концентрация атомов мишени, Sn(E) – ядерное тормозное сечение:
(2)
${{S}_{n}}\left( E \right) = \int\limits_0^{{{\Lambda }}E} {T\frac{{d{{\sigma }}}}{{d{{\Omega }}}}d{{\Omega }}} {\text{,}}$
(3)
${{\Lambda }} = \frac{{4{{M}_{1}}{{M}_{2}}}}{{{{{\left( {{{M}_{1}} + ~{{M}_{2}}} \right)}}^{2}}}} = \frac{{4{{\gamma }}}}{{{{{\left( {1~ + ~{{\gamma }}} \right)}}^{2}}}},$
$T = {{\Lambda }}E{\kern 1pt} {\text{si}}{{{\text{n}}}^{2}}\left( {{{{\alpha }} \mathord{\left/ {\vphantom {{{\alpha }} 2}} \right. \kern-0em} 2}} \right)$ – энергия, переданная при рассеянии иона массой М1 с энергией Е на атоме массой М2, α – угол рассеяния в системе центра масс иона пучка и атома мишени [24], γ = М1/М2 и dσ/dΩ – дифференциальное сечение рассеяния. Энергетическая длина, т.е. расстояние, при прохождении которого ион, первоначально имевший энергию Е0, потеряет ее всю, будет равна:

(4)
$R = \int\limits_{{{E}_{0}}}^0 {\frac{{dE}}{{{{dE} \mathord{\left/ {\vphantom {{dE} {dx}}} \right. \kern-0em} {dx}}}}} = \int\limits_0^{{{E}_{0}}} {\frac{{dE}}{{n{{S}_{n}}\left( E \right)}}} .$

Строго говоря, при торможении ион теряет энергию в ходе как упругих соударений (или ядерных, при которых происходит взаимодействие с атомом мишени как с целым), так и неупругих (или электронных, сопровождающихся выбиванием электронов из атомных оболочек). Однако с помощью моделирования распределения поглощенной энергии [18] было показано, что для тяжелых ионов с атомными номерами Z > 20 и энергией порядка нескольких десятков кэВ электронные потери составляют не более ~10%, и, следовательно, не играют ключевой роли.

Дифференциальное сечение рассеяния dσ/dΩ определяется потенциалом взаимодействия сталкивающихся частиц V(r) через прицельный параметр и интеграл столкновений [24]. Для быстрых ионов, у которых приведенная энергия

(5)
$\varepsilon = \frac{E}{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}\frac{a}{{\left( {1~\,\, + \,\,~{{\gamma }}} \right)}},$
много больше единицы (здесь Z1 и Z2 – атомные номера налетающего иона и атома мишени соответственно, $a = 0.885{{a}_{0}}{{\left( {Z_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}~\,\, + \,\,~Z_{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$ – радиус Томаса–Ферми, a0 = 0.0529 нм – радиус Бора), хорошо работает [22, 23, 25, 26] кулоновский потенциал взаимодействия
(6)
$V\left( r \right) = \frac{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{r},$
которому соответствует сечение Резерфорда

(7)
$\frac{{d\sigma }}{{d{{\Omega }}}} = {{\left( {\frac{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}\left( {1 + {{\gamma }}} \right)}}{{4E}}} \right)}^{2}}\frac{1}{{{{{\text{si}}{{{\text{n}}}^{2}}{\kern 1pt} {{\alpha }}} \mathord{\left/ {\vphantom {{{\text{si}}{{{\text{n}}}^{2}}{\kern 1pt} {{\alpha }}} 2}} \right. \kern-0em} 2}}}.$

В случае медленных частиц (ε < 1) экранирование кулоновского потенциала электронами становится существенным. Для учета экранирования в литературе были предложены различные потенциалы, большинство из них в виде [22, 27]:

(8)
$V\left( r \right) = \frac{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{r}\left[ {\sum\limits_{i\,\, = \,\,0}^n {{{c}_{i}}{\text{exp}}\left( { - {{d}_{i}}\frac{r}{a}} \right)} } \right].$

С потенциалами такого вида весьма сложно проводить аналитические вычисления. Поэтому резонно заменить реальный потенциал потенциалом, имеющим простое аналитическое выражение, но справедливым в некоторой ограниченной области значений энергии. Этому критерию удовлетворяет степенной потенциал [23, 25, 26]:

(9)
${{V}_{s}}\left( r \right) = \frac{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{{{r}^{s}}}}\frac{{{{k}_{s}}{{a}^{{s - 1}}}}}{s},$
где s = 1, 2, 3; ks = const. Высоким энергиям (ε $ \gg $ 1), как уже было отмечено, соответствует потенциал Кулона и s = 1. Для столкновений атомов не очень больших энергий хорошие результаты получаются со степенным потенциалом с s = 2, которому соответствует сечение [23]:

(10)
$\frac{{d{{\sigma }}}}{{d{{\Omega }}}} = \frac{{4.1a{{Z}_{1}}{{Z}_{2}}{{e}^{2}}\left( {1 + {{\gamma }}} \right)}}{{32{{\pi }}E}}\frac{1}{{{{{\text{si}}{{{\text{n}}}^{3}}{{\alpha }}} \mathord{\left/ {\vphantom {{{\text{si}}{{{\text{n}}}^{3}}{{\alpha }}} 2}} \right. \kern-0em} 2}}}.$

А для рассеяния медленных ионов (ε $ \ll $ 1) – s = 3 и сечение

(11)
$\frac{{d\sigma }}{{d{{\Omega }}}} = 0.179{{\left( {\frac{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}{{a}^{2}}\left( {1 + {{\gamma }}} \right)}}{E}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\frac{1}{{{{{\text{si}}{{{\text{n}}}^{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}}{{\alpha }}} \mathord{\left/ {\vphantom {{{\text{si}}{{{\text{n}}}^{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}}{{\alpha }}} 2}} \right. \kern-0em} 2}}}.$

Для вычисления энергетической длины удобно перейти к приведенной ядерной тормозной способности sn(ε), которая связана с Sn(E) как:

(12)
${{s}_{n}}\left( \varepsilon \right) = \frac{{{\varepsilon \mathord{\left/ {\vphantom {\varepsilon E}} \right. \kern-0em} E}}}{{\pi {{a}^{2}}\Lambda }}{{S}_{n}}\left( E \right).$

Тогда выражение (4) для “энергетической длины” преобразуется в

(13)
$R = \frac{{{{L}_{0}}\left( {Z_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}~ + ~Z_{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right)}}{{{\Lambda }}}\int\limits_0^{{{\varepsilon }_{0}}} {\frac{{d\varepsilon }}{{{{s}_{n}}\left( \varepsilon \right)}}} ,$
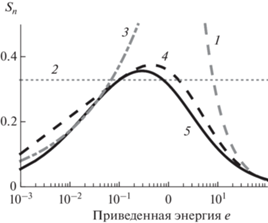
где L0 = 1/(π(0.885a0)2n). Расчет приведенной ядерной тормозной способности согласно (12) и (2), (3), (5) с сечениями (7), (10), (11) для степенного потенциала приводит к
(14)
${{s}_{n}}\left( \varepsilon \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{L}{{2\varepsilon }},}&{s = 1;} \\ {0.327,}&{s = 2;} \\ {1.07K{{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},}&{s = 3.} \end{array}} \right.$
Здесь L – кулоновский логарифм и K = 0.75 – поправочный коэффициент.

Приведенная ядерная тормозная способность для разных степеней потенциала, вычисленная согласно (14), показана на рис. 1. Там же приведена sn(ε) для потенциала Томаса–Ферми–Фирсова [28] и для приближения Мольера (потенциала для ионов с диапазонами атомных масс Kr–C) [29]. Последнее, как было отмечено, в том числе в [27], позволяет получить более точные количественные данные, чем использование статистической модели Томаса–Ферми. Поэтому, чтобы sn(ε) при s = 3 была наиболее близка к данным для Kr–C-потенциала, был введен поправочный коэффициент K.

Рис. 1.

Ядерная тормозная способность для степенного потенциала при s = 1 (1), 2 (2), 3 (3), а также потенциалов Томаса–Ферми–Фирсова (4) и “Kr–C” (5).

Графическим способом по данным рис. 1 были определены значения приведенной энергии ε12 ≈ 8 и ε23 ≈ 0.07, при которых кривые sn(ε), рассчитанные для разных степеней потенциала, пересекаются. В предположении, что при ε23 ≤ ε ≤ ε12 действует sn(ε) для s = 2, при бóльших значениях приведенной энергии – для s = 1, а при меньших – для s = 3, кусочно-непрерывная функция (14) была проинтегрирована согласно (13). В результате для энергетической длины было получено выражение:

(15)
$R = \frac{{{{L}_{0}}\left( {Z_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}~ + ~Z_{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right)}}{{{\Lambda }}}\left[ {\begin{array}{*{20}{c}} {\Theta \left( {{{\varepsilon }_{0}} - {{\varepsilon }_{{12}}}} \right)\left( {\frac{{{\text{li}}\left( {A{{\varepsilon }_{{12}}}} \right)~\,\, - \,\,~{\text{li}}\left( {A{{\varepsilon }_{0}}} \right)}}{{0.25{{A}^{2}}}} + \frac{{{{\varepsilon }_{{12~}}} - {{\varepsilon }_{0}}}}{{0.327}}} \right) + } \\ { + \,\,\left( {{{\Theta }}\left( {{{\varepsilon }_{0}} - {{\varepsilon }_{{23}}}} \right) - {{\Theta }}\left( {{{\varepsilon }_{0}} - {{\varepsilon }_{{12}}}} \right)} \right)\frac{{{{\varepsilon }_{{0~}}} - {\text{\;}}{{\varepsilon }_{{12}}}}}{{0.327}} + \frac{{1.4{\text{min}}\left( {\varepsilon _{0}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}},{\text{\;}}\varepsilon _{{23}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right)}}{K}} \end{array}} \right],$
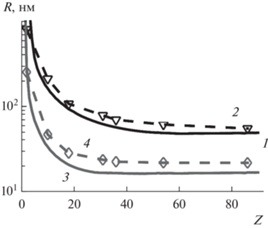
где li(Aε) – интегральный логарифм, а также
(16)
$A = \frac{{{{{\left( {Z_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}~ + ~Z_{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{8p{{Z}_{1}}{{Z}_{2}}\left( {1 + {{\gamma }}} \right)0.885}},$
p = 1836M1 – отношение массы иона к массе электрона и Θ(ε) – функция Хевисайда.

Энергетическая длина (15) была рассчитана для органического резиста – полиметилметакрилата, часто используемого в литографии, и широкого диапазона атомных масс налетающих ионов. Результат показан на рис. 2, там же для сравнения приведены значения, полученные по данным моделирования методом Монте-Карло c помощью программы SRIM [30]. Можно отметить хорошее совпадение представленных кривых. Оценочные расчеты показали, что для энергии 10–50 кэВ пучка ионов тяжелее Ne относительное среднеквадратичное отклонение рассчитанной по программе SRIM и вычисленной по формулам для степенного потенциала кривых находится в пределах 2–12%. В случае более легких ионов выражение (15) плохо описывает энергетическую длину. Но это не результат использования степенного потенциала, а следствие рассмотрения только упругих (ядерных) потерь при торможении в материале. Для ионов с Z < 10 и энергией 10–50 кэВ ε ≥ 1. В этом случае основной механизм потерь энергии – это ионизация или неупругое взаимодействие с электронами. А значит выражение (1) уже нельзя использовать для получения оценок энергетической длины.

Рис. 2.

Энергетическая длина ионов в зависимости от атомного номера для степенного потенциала (1, 3) и рассчитанная по данным SRIM (2, 4). Расчетные величины для энергии пучка ионов и 50 (1, 2) и 10 (3, 4) кэВ.

ТРАНСПОРТНАЯ ДЛИНА ИОНОВ

Отвечающая за радиальный размер зоны поглощенной энергии транспортная длина ионов

(17)
${{L}_{{{\text{tr}}}}} = \frac{1}{{n{{\sigma }_{{{\text{tr}}}}}}}$
определяется транспортным сечением
(18)
${{\sigma }_{{{\text{tr}}}}} = \int {\left( {1 - {\text{cos}}{\kern 1pt} {{\theta }}} \right)\frac{{d\sigma }}{{d{{\Omega }}}}d{{\Omega }}} $
и имеет физический смысл отрезка траектории, который необходимо пройти иону, чтобы рассеяться на значительный угол – порядка π рад [19]. В выражении (18) θ – угол рассеяния; dσ/dΩ – дифференциальное сечение рассеяния; dΩ – элемент телесного угла в лабораторной системе отсчета. Выражения (7), (10) и (11) задают сечения рассеяния в системе центра масс. Разницей между лабораторной системой и системой центра масс можно пренебречь, когда легкая частица налетает на тяжелую, но не в рассматриваемом случае рассеяния тяжелых ионов в легких резистах. В данном случае следует перейти от системы центра масс (CMS) к лабораторной системе (LS), используя соотношения [19]:

(19)
${{\left( {\frac{{d\sigma }}{{d{{\Omega }}}}} \right)}_{{{\text{CMS}}}}}d{{{{\Omega }}}_{{{\text{CMS}}}}} = {{\left( {\frac{{d\sigma }}{{d{{\Omega }}}}} \right)}_{{{\text{LS}}}}}d{{{{\Omega }}}_{{{\text{LS}}}}},$
(20)
${\text{tg}}{\kern 1pt} {{\theta }} = \frac{{{\text{sin}}{\kern 1pt} \alpha }}{{{\text{cos}}{\kern 1pt} {{\alpha }} + {{\gamma }}}}.$

Можно отметить, что при расчете энергетической длины вычисление сечения в лабораторной системе не требовалось, поскольку в (2), (3) входит правая часть (19) и α (угол рассеяния в системе центра масс). Для транспортной длины тоже можно, учитывая (19), избежать вычисления (dσ/dΩ)LS, но угол θ в таком случае необходимо выразить через α с помощью (20). Выражение (18) для транспортного сечения примет следующий вид:

(21)
${{\sigma }_{{{\text{tr}}}}} = 2\pi \int\limits_0^{{\pi }} {\left( {1 - \frac{{{\text{cos}}{\kern 1pt} {{\alpha }} + {{\gamma }}}}{{\sqrt {1{\text{\;}} + {\text{\;}}2{{\gamma }}{\kern 1pt} {\text{cos}}{\kern 1pt} {{\alpha }} + {{{{\gamma }}}^{2}}} }}} \right){{{\left( {\frac{{d\sigma }}{{d{{\Omega }}}}} \right)}}_{{{\text{CMS}}}}}{\text{sin}}{\kern 1pt} \alpha d\alpha } {\text{.}}$

В результате вычисления транспортного сечения согласно (21) с дифференциальными сечениями (7), (10), (11) для степенного потенциала получаем:

(22)
${{\sigma }_{{{\text{tr}}}}} = \left\{ {\begin{array}{*{20}{c}} {\frac{{\pi {{a}^{2}}}}{{2{{\varepsilon }^{2}}{{{\left( {1~ + ~\gamma } \right)}}^{2}}}}\left[ {{\text{ln}}\left( {\frac{{{{{\left( {1\,\,~ + \,\,~\gamma } \right)}}^{2}}}}{{\varepsilon A}}} \right) - {\text{min}}\left( {{{\gamma }^{2}},~1} \right)} \right],}&{s = 1;} \\ {\frac{{4.1{{a}^{2}}}}{{4\varepsilon }}\left[ {\frac{{{\text{arcsin}}{{\Lambda }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{\gamma }^{{1/2}}}}} - \frac{{2{\text{min}}\left( {\gamma ,1} \right)}}{{\left( {1~\,\, + \,\,~\gamma } \right)}}} \right],}&{s = 2;} \\ {\frac{{4\pi \times 1.79{{a}^{2}}}}{{{{\varepsilon }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}\left[ {\frac{{\left( {1~\,\, + ~\,\,2\gamma } \right)}}{{2\gamma }}{{\Lambda }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{B}_{\Lambda }}\left( {\frac{2}{3},~\frac{1}{2}} \right) - \frac{{6{\text{min}}\left( {\gamma ,1} \right)}}{{\left( {1\,\,~ + \,\,~\gamma } \right)}}} \right],}&{s = 3.} \end{array}} \right.$
Здесь ${{B}_{{{\Lambda }}}}\left( {\frac{2}{3},\frac{1}{2}} \right)$ = $\int_0^{{\Lambda }} {{{t}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}{{{\left( {1 - t} \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt} $ – неполная бета-функция.

В рассматриваемом случае тяжелых ионов пучка (γ $ \gg $ 1) в (22) для s = 1 вторым слагаемым в квадратных скобках можно пренебречь, а также, учитывая, что Λ $ \ll $ 1, воспользоваться приближениями arcsinΛ1/2 ≈ Λ1/2 + (Λ1/2)3/6 и для подынтегрального выражения бета-функции (1 – t)–1/2 ≈ 1 + t/2. Это позволяет получить окончательное выражение для транспортной длины в виде:

(23)
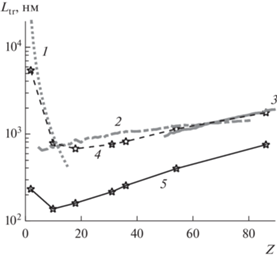
${{L}_{{{\text{tr}}}}} = \left\{ {\begin{array}{*{20}{c}} {\frac{{2{{L}_{0}}{{\varepsilon }^{2}}{{{\left( {1~\,\, + \,\,~\gamma } \right)}}^{2}}\left( {Z_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}} + \,\,~Z_{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right)}}{{{\text{ln}}\left[ {{{{{{\left( {1~\,\, + \,\,~\gamma } \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {1~\,\, + \,\,~\gamma } \right)}}^{2}}} {\left( {\varepsilon A} \right)}}} \right. \kern-0em} {\left( {\varepsilon A} \right)}}} \right]}},}&{s = 1;} \\ {\frac{{3\pi {{L}_{0}}\varepsilon {{{\left( {1~\,\, + \,\,~\gamma } \right)}}^{3}}\left( {Z_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}} + \,\,~Z_{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right)}}{{4,1{{\gamma }}}},}&{s = 2;} \\ {\frac{{5{{L}_{0}}{{\varepsilon }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{\gamma }^{3}}\left( {Z_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}} + \,\,~Z_{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right)}}{{6.45}},}&{s = 3.} \end{array}} \right.$

Транспортная длина (23) для разных степеней потенциала показана на рис. 3, там же приведены результаты расчета по данным программы SRIM. Расчет в приближении степенного потенциала практически совпадает (среднеквадратичное отклонение не более 1%) с результатами моделирования, когда транспортная длина рассчитывается с учетом только однократного рассеяния иона. В случае моделирования методом Монте-Карло с рассмотрением многократного рассеяния вдоль траектории соответствие между кривыми хуже, значения транспортной длины сильно занижены, поскольку в процессе торможения с потерей энергии растет и угол рассеяния. Однако ни (23), ни само определение транспортной длины этот факт не учитывают.

Рис. 3.

Зависимость транспортной длины ионов от атомного номера для разных степеней потенциала при s = 1 (1), 2 (2), 3 (3), а также расчет Ltr по данным программы SRIM с учетом только однократного (4) и многократного (5) рассеяния вдоль траектории; Е0 = 30 кэВ.

Можно отметить, что кривые на рис. 3 для разных степеней потенциала пересекаются при Z ≈ 10 и 60, что соответствует значениям приведенной энергии 2.5 и 0.05. Это в целом свидетельствует о приемлемости выбора значений ε12 ≈ 8 и ε23 ≈ 0.07 в качестве границ диапазонов приведенной энергии, в которых действует определенная степень потенциала s. Также можно отметить, что в случае тяжелых ионов транспортная длина медленно (не быстрее чем $ \sim {\kern 1pt} M_{1}^{{{{19} \mathord{\left/ {\vphantom {{19} 9}} \right. \kern-0em} 9}}}$ согласно оценке, полученной из (23)) возрастает с ростом атомной массы ионов. Здесь реализуется случай рассеяния тяжелых частиц на мишени из легких атомов (для полиметилметакрилата среднее значение М2 ~ 3.6), т.е. γ $ \gg $ 1, и угол рассеяния ограничен величиной М2/М1. По-видимому, из-за этого, несмотря на увеличение сечения (11), транспортное сечение (которое при малых углах рассеяния равно половине среднего квадрата угла рассеяния) убывает, что и обуславливает рост транспортной длины. На качественном уровне возрастание транспортной длины означает, что траектории ионов становятся все более прямыми, рассеяние пучка в резисте уменьшается, как и радиальный размер зоны поглощенной энергии. Это, вероятно, свидетельствует о возможности создания структур с высоким отношением размеров при использовании в литографическом процессе тяжелых ионов.

ЗАКЛЮЧЕНИЕ

Выведены выражения для энергетической и транспортной длин в приближении степенного потенциала взаимодействия бомбардирующих ионов с атомами резиста. Указаны диапазоны значений приведенной энергии, в которых следует применять формулы для той или иной степени потенциала. Рассмотрены предпосылки вхождения энергетической и транспортной длин в качестве параметров в распределение плотности поглощенной энергии. Полученные выражения позволят определить, с какой скоростью изменяются размеры области резиста, поглощающей энергию, в зависимости от массы и энергии используемых ионов. Вывод эмпирического выражения для описания плотности поглощенной энергии находится в планах дальнейшей работы авторов.

Список литературы

  1. Komuro M., Atoda N., Kawakatsu H. // J. Electrochem. Soc.: Solid State Sci. Technol. 1979. V. 126. № 3. P. 483.https://doi.org/10.1149/1.2129067

  2. Kubena R.L., Ward J.W., Stratton F.P., Joyce R.J., Atkinson G.M. // J. Vac. Sci. Technol. B. 1991. V. 9. № 6. P. 3079.https://doi.org/10.1116/1.585373

  3. Mladenov G.M., Braun M., Emmoth B., Biersack J.P. // J. Appl. Phys. 1985. V. 58. P. 2534.https://doi.org/10.1063/1.335932

  4. Winston D., Ferrera J., Battistella L., Vladár A.E., Berggren K.K. // Scanning. 2012. V. 34. № 2. P. 121.https://doi.org/10.1002/sca.20290

  5. Melngailis J. // J. Vac. Sci. Technol. B. 1998. V. 5. № 2. P. 469.https://doi.org/10.1116/1.583937

  6. Notte J., Ward B., Economou N., Hill R., Percival R., Farkas L., McVey S. // AIP Conf. Proc. 2007. V. 931. P. 489.https://doi.org/10.1063/1.2799423

  7. Broers A.N., Molzen W.W., Cuomo J.J. Wittels N.D. // Appl. Phys. Lett. 1976. V. 29. № 9. P. 596.https://doi.org/10.1063/1.89155

  8. Haller I., Hatzakis M., Srinivasan R. // IBM J. Res. Development. 1968. V. 12. № 3. P. 251.https://doi.org/10.1147/RD.123.0251

  9. Tseng A.A., Chen K., Chen C.D., Ma K.J. // IEEE Trans. Electron. Pack. Manuf. 2003. V. 26. № 2. P. 144.https://doi.org/10.1109/TEPM.2003.817714

  10. Chang T.P.H. // J. Vac. Sci. Technol. 1975. V. 12. P. 1271.https://doi.org/10.1116/1.568515

  11. Owen G., Rissman P. // J. Appl. Phys. 1983. V. 54. № 6. P. 3537.https://doi.org/10.1063/1.332426

  12. Sidorkin V., Van Veldhoven E., Van Der Drift E., Alkemade P., Salemink H., Maas D. // J. Vac. Sci. Technol. B. 2009. V. 27. № 4. P. 53.https://doi.org/10.1116/1.3182742

  13. Winston D., Manfrinato V.R., Nicaise S.M., Cheong L.L., Duan H., Ferranti D., Marshman J., McVey S., Stern L., Notte J., Berggren K.K. // Nano Lett. 2011. V. 11. № 10. P. 4343.https://doi.org/10.1021/nl202447n

  14. van Veldhoven E., Sidorkin V., Chen P., Alkemade P., van der Drift E., Salemink H., Zandbergen H., Maas D. // Microsc. Microanal. 2010. V. 16. № S2. P. 202.https://doi.org/10.1017/s1431927610063270

  15. Mladenov G.M., Vutova K.J., Koleva E.G. // Phys. Chem. Solid State. 2009. V. 10. № 3. P. 707.

  16. Cai J., Zhu Z., Alkemade P.F.A., van Veldhoven E., Wang Q., Ge H., Rodrigues S.P., Cai W., Li W.D. // Adv. Mater. Interfaces. 2018. V. 5. № 12. P. 1800203.https://doi.org/10.1002/admi.201800203

  17. Kalhor N., Mulckhuyse W., Alkemade P., Maas D. // Proc. SPIE. 2015. V. 9425. P. 942513.https://doi.org/10.1117/12.2085791

  18. Shabelnikova Ya.L., Zaitsev S.I. Ion Beam Lithography with Resist Exposure: Simulation and Fitting of the Deposited Energy Distribution // Proc. 26th Int. Symp. Phys. Technol. Minsk, 2018. P. 161.

  19. Рязанов М.И., Тилинин И.О. Исследование поверхности по обратному рассеянию частиц. М.: Энергоатомиздат, 1985. 155 с.

  20. Шабельникова Я.Л., Зайцев С.И. // Наноиндустрия. 2020. № S96-2. С. 753. https://doi.org/10.22184/1993-8578.2020.13.3s.753.755

  21. Lindhard Y.J., Scharff M., Schiøt H.E., København T. // Mat. Fys. Medd. Dan. Vid. Selsk. 1963. V. 33. № 14. P. 44.

  22. Gnaser H. Low-Energy Ion Irradiation of Solid Surfaces. Berlin: Springer, 1999. 293 p.

  23. Готт Ю.В., Явлинский Ю.Н. Взаимодействие медленных частиц с веществом и диагностика плазмы. М.: Атомиздат, 1973. 129 с.

  24. Ландау Л.Д., Лифшиц Е.М. Механика. Изд. 4-е. М.: Наука, 1988. 216 с.

  25. Sigmund P. // Rev. Roum. Phys. 1972. V. 17. P. 1079.

  26. Lindhard J., Nielsen V., Scharff M., Dan. Vidensk K. // Selsk. Mat. Fys. Medd. 1968. V. 36. P. 10.

  27. Борисов А.М., Машкова Е.С. Физические основы ионно-лучевых технологий. I. Ионно-электронная эмиссия. М.: Университетская книга, 2011. 141 с.

  28. Фирсов О.Б. // ЖЭТФ. 1957. Т. 33. № 3. С. 696.

  29. Wilson W.D., Haggmark L.G., Biersack J.P. // Phys. Rev. B. 1977. V. 15. P. 2458.

  30. J. Ziegler. SRIM – the Stopping and Range of Ions in Matter. http://www.srim.org/

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал