Акустический журнал, 2019, T. 65, № 1, стр. 42-48
Измерение импульсного отклика акустического MLS-сигнала в среде с потоком
А. А. Белоус a, *, А. И. Корольков a, А. В. Шанин a, Н. Н. Остриков b, **
a Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 Москва, ГСП-1Ленинские горы, Россия
b Центральный аэрогидродинамический ин-т им. проф. Н.Е. Жуковского, Московский комплекс (НИМК ЦАГИ)
105005 Москва, ул. Радио 17, Россия
* E-mail: artem.belous@gmail.com
** E-mail: aeroacoustics@tsagi.ru
Поступила в редакцию 04.05.2018
После доработки 28.08.2018
Принята к публикации 04.05.2018
Аннотация
Представлены результаты эксперимента по измерению импульсного отклика при прохождении сигнала через воздушную струю при помощи MLS-техники. Полученные данные сравниваются с результатами численного моделирования, проведенного путем решения уравнения для распространения звука в постоянном потоке методом конечных разностей. Показывается, что продольная компонента потока вызывает снос и фокусировку сигнала.
ВВЕДЕНИЕ
В данное время широко используемым методом измерения импульсных откликов и частотных характеристик различных акустических рассеивателей является техника измерения импульсного отклика с помощью псевдослучайной последовательности максимальной длины (MLS – Maximum Length Sequence) [1–3]. Суть техники заключается в зондировании испытуемой системы квазишумовой посылкой, автокорреляционная функция которой близка к дельта-функции, и последующей корреляционной обработке полученных данных.
Ценность дифракционного MLS-эксперимента состоит в возможности непосредственного наблюдения полей, дифрагированных на различных, в том числе и сложных объектах. В данной работе ставится практически важная задача применить технику MLS-эксперимента в случае прохождения акустического сигнала через воздушную струю.
Эксперименты по изучению воздушных струй акустическими методами уже проводились и описаны в существующих работах. В [4] изучается экранирование струей монохроматического сигнала в зависимости от взаимных ориентаций струи и источника сигнала. Аналитическая модель этого процесса предложена в [5]. Вопрос о поведении фазы акустической волны при прохождении через турбулентный поток численно рассмотрен в [6]. Экспериментальное изучение случайных характеристик струи на основе поведения монохроматической акустической волны, проходящей через струю перпендикулярно направлению потока, проведено в [7].
Имеются и работы по изучению влияния акустических волн на потоки воздуха с небольшими скоростями [8, 9]. В данной работе такое влияние не рассматривается.
Кроме того, имеется множество работ, посвященных отражению и прохождению акустических волн через тангенциальный разрыв на плоской границе двух движущихся жидкостей [10–13].
В [14] описаны эксперименты по корреляционному детектированию широкополосного сигнала, проходящего через воздушную струю. В первом из них точечный источник помещался на оси потока, рядом с ним располагался контрольный микрофон, а снаружи потока размещался измерительный микрофон. По корреляции между сигналами с микрофонов определялась задержка прохождения сигнала и, соответственно, угол рефракции на границе потока. Во втором эксперименте источник с контрольным микрофоном также находится на оси потока, а два измерительных микрофона располагаются вне потока и на оси потока ниже по течению. Рассматривая поток как отличную от воздуха среду, авторы измеряют и моделируют углы преломления и отражения на границе поток–пространство.
В данной работе с помощью монопольного источника и MLS-техники [1–3] производится экспериментальное измерение импульсного отклика при наличии потока на акустической трассе. Изучаются явления сноса сигнала потоком и фокусировки сигнала цилиндрической струей. Проводится математическое моделирование этого процесса путем решения уравнения для распространения звука в постоянном потоке [15] методом конечных разностей.
ОПИСАНИЕ ЭКСПЕРИМЕНТА
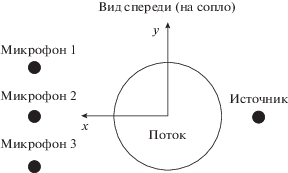
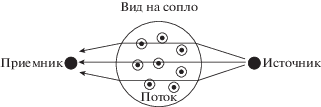
Эксперименты проводились в заглушенной камере с потоком АК-2 ЦАГИ. Схема эксперимента показана на рис. 1. На рисунке показана система координат $(x,y,z),$ используемая ниже для задания положений микрофонов и источника.
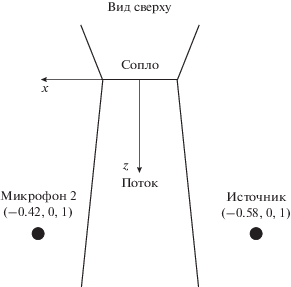
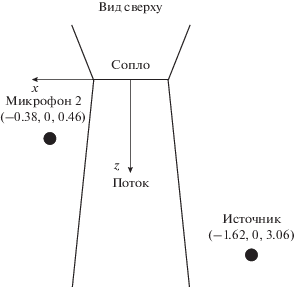
Поток воздуха со скоростями 20, 40, 60 и 80 м/с создавался соплом круглого сечения диаметром 40 см. На некотором расстоянии от сопла были расположены три микрофона и источник звука так, чтобы акустическая трасса проходила через струю (см. рис. 1). Проводилась серия экспериментов, в которых акустическая трасса была как перпендикулярна оси потока (рис. 2), так и неперпендикулярна ей (рис. 3).
Экспериментальное оборудование и алгоритм корреляционной обработки данных были аналогичны описанным в [1–3]. В качестве источника использовался всенаправленный излучатель Omnisource тип 4295 фирмы Bruel & Kjaer с датчиком объемной скорости, в качестве микрофонов применялись ¼-дюймовые микрофоны типа 4935 фирмы Bruel & Kjaer.
ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ
Полноценное описание волновых процессов в среде с потоком было дано в [15]. В данной монографии указывается, что скорость потока может быть представлена в виде средней скорости и флуктуации. Средняя скорость обуславливает снос и фокусировку звуковой волны, а переменная часть скорости ведет к рассеянию звука на флуктуациях. Для описания эффектов, связанных с переменной составляющей потока, необходимы данные о масштабах флуктуаций его скорости. Измерения этих масштабов в настоящей работе не производились. Ниже будет дано теоретическое описание эффектов, обусловленных постоянной составляющей потока.
Расчет сноса звукового поля
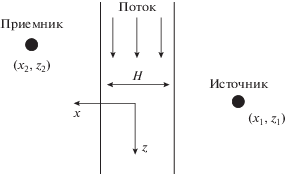
Для оценки сноса акустического сигнала будем рассматривать упрощенную двумерную (в координатах $x,z$) модель (рис. 4). Будем считать, что скорость потока постоянна внутри струи и равна нулю за ее пределами. Тогда акустический потенциал ϕ удовлетворяет уравнению [15]
(1)
$\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)\phi = {{\left( {{\text{M}}\frac{\partial }{{\partial z}} + \frac{1}{c}\frac{\partial }{{\partial t}}} \right)}^{2}}\phi ,$Используя принцип локальности [16], выпишем представление акустического потенциала звукового поля на приемнике в виде фазового интеграла, полученного в [17]:
(3)
$\begin{gathered} f(\omega ,{{k}_{z}}) = - \omega {\kern 1pt} t + {{k}_{z}}({{z}_{2}} - {{z}_{1}}) + ({{x}_{2}} - {{x}_{1}} - H) \times \\ \times \,\,\sqrt {\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}} - k_{z}^{2}} + H\sqrt {{{{\left( {\frac{\omega }{c} - {\text{M}}{{k}_{z}}} \right)}}^{2}} - k_{z}^{2}} . \\ \end{gathered} $Этот интеграл получен в результате применения преобразования Фурье к уравнению (1) по времени и по координате z, направленной вдоль потока. В функции f (3) третий член описывает распространение вдоль оси x в пространстве без потока, а четвертый – в пространстве с потоком.
В случаях, когда длины волн меньше характерных масштабов неоднородностей, для анализа фазовых интегралов обычно применяют метод стационарной фазы или метод перевала [18]. В рассматриваемом случае интеграла (2) необходимо применять метод стационарной фазы для двух комплексных переменных, для чего в комплексной плоскости переменных $(\omega ,{{k}_{z}})$ нужно отыскать стационарные точки, в которых для подынтегральной функции выполняются условия
(4)
$\frac{{\partial f}}{{\partial \omega }} = 0,\,\,\,\,\frac{{\partial f}}{{\partial {{k}_{z}}}} = 0.$В окрестностях стационарных точек осцилляции подынтегральной функции замедляются, и поэтому такие точки дают существенный вклад в интеграл, а в окрестности остальных точек подынтегральная функция быстро осциллирует, и такие окрестности не дают существенного вклада в интеграл.
Введем переменную $\gamma = {{{{k}_{z}}} \mathord{\left/ {\vphantom {{{{k}_{z}}} {({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c})}}} \right. \kern-0em} {({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c})}}$ и перепишем (3) в виде
(5)
$\begin{gathered} f(\omega ,\gamma ) = \omega \left[ { - t + \frac{{\gamma ({{z}_{2}} - {{z}_{1}})}}{c} + \frac{{{{x}_{2}} - {{x}_{1}} - H}}{c}} \right. \times \\ \times \,\,\sqrt {1 - {{\gamma }^{2}}} + \left. {\frac{H}{c}\sqrt {{{{(1 - {\text{M}}\gamma )}}^{2}} - {{\gamma }^{2}}} } \right]. \\ \end{gathered} $Условия (4) перепишутся как
(6)
$\frac{{\partial f}}{{\partial \omega }} = 0,\,\,\,\,\frac{{\partial f}}{{\partial \gamma }} = 0,$(7)
$\begin{gathered} t = \frac{{\gamma {\text{*}}({{z}_{2}} - {{z}_{1}})}}{c} + \frac{{{{x}_{2}} - {{x}_{1}} - H}}{c}\sqrt {1 - \gamma _{*}^{2}} + \\ + \,\,\frac{H}{c}\sqrt {{{{(1 - {\text{M}}\gamma *)}}^{2}} - \bar {\gamma }_{*}^{2}} , \\ \end{gathered} $(8)
$\begin{gathered} ({{z}_{2}} - {{z}_{1}}) - ({{x}_{2}} - {{x}_{1}} - H)\frac{\gamma }{{\sqrt {1 - {{\gamma }^{2}}} }} - \\ - \,\,H\frac{{\gamma + {\text{M}}(1 - {\text{M}}\gamma )}}{{\sqrt {{{{(1 - {\text{M}}\gamma )}}^{2}} - {{\gamma }^{2}}} }} = 0. \\ \end{gathered} $Решения уравнений (7) и (8) дают оценку времени прихода сигнала.
В общем случае время прихода сигнала t для случая с потоком будет отличаться от времени распространения сигнала при отсутствии потока. Причина этого физически очевидна – часть времени сигнал распространяется против потока, что уменьшает его фазовую скорость. В случае распространения звука по потоку время прохождения сигнала уменьшится. В данной работе случай ускорения звука не рассматривается, и соответствующий эксперимент проведен не был.
Расчет фокусировки звукового поля
Если проекция единичного вектора вдоль звукового луча на скорость потока отрицательна, то фазовая скорость сигнала, распространяющегося вдоль такого луча, уменьшается, и тем самым поток может рассматриваться как акустически менее плотная среда. В этом случае цилиндрический поток выступает как собирающая линза. Схема фокусировки показана на рис. 5.
Для расчета эффекта фокусировки необходимо рассматривать трехмерную модель. Таким образом, следует решать уравнение
(9)
$\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)\phi = {{\left( {{\text{M}}\frac{\partial }{{\partial z}} + \frac{1}{c}\frac{\partial }{{\partial t}}} \right)}^{2}}\phi ,$В простейшем случае можно предположить, что поток имеет цилиндрическую форму и число Маха в любой его точке постоянно. Однако такое представление не описывает реальной физической картины уже на расстояниях порядка одного калибра от сопла. Ниже предлагается более “реалистичная” форма потока.
Как известно, поток состоит из начального, переходного и основного участков [19]. Для простоты будем полагать, что длина переходного участка равна нулю. В начальном участке струя имеет потенциальное ядро течения конусовидной формы. Скорость в этом ядре постоянна. Убывание скорости вне ядра может быть описано следующим гауссовым законом [20]:
(10)
$V = \left\{ \begin{gathered} {{V}_{0}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(r < h), \hfill \\ {{V}_{0}}\exp \left\{ { - \ln 2{{{\left( {\frac{{r - h(z)}}{{b(z)}}} \right)}}^{2}}} \right\},\,\,\,\,(r \geqslant h). \hfill \\ \end{gathered} \right.$Здесь $h(z)$ – радиус ядра, $b(z)$ – полуширина слоя смешения, $r = \sqrt {{{x}^{2}} + {{y}^{2}}} ,$ ${{V}_{0}}$ – скорость потока в ядре. Аналогичным образом скорость потока может быть рассчитана и на основном участке:
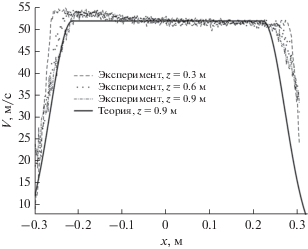
где ${{V}_{c}}$ – скорость на оси потока. Мы предполагаем, что скорость на оси потока спадает обратно пропорционально расстоянию от сопла. Здесь $b(z)$ – расстояние от оси ядра до окружности, на которой скорость ядра спадает вдвое. Параметры $h(z),b(z)$ оценивались на основе данных анемометрии для сопла диаметром 0.6 м на скоростях 50, 45 и 35 м/с. Пример экспериментальных данных для начального участка струи и расчета по формуле (10) приведен на рис. 6.Рис. 6.
Данные термоанемометрии потока для скорости 55 м/c и сравнение с теоретическим расчетом по формуле (10).
В общем случае для потенциального неоднородного потока решается уравнение Блохинцева, а для неоднородного потока с завихрениями – уравнение Блохинцева–Хоу [21, стр. 22]. В данной работе рассматриваемый поток неоднороден и завихрен в слое смешения, однако при малых числах Маха уравнение Блохинцева–Хоу переходит в уравнение (1). Поэтому для расчета амплитуды сфокусированного сигнала численно решалось уравнение (1) с помощью метода конечных разностей. Производные по пространственным координатам заменялись симметричными конечно-разностными аппроксимациями первого порядка, интегрирование по времени осуществлялось с помощью метода Рунге–Кутта 4-го порядка. Для подавления волн, отраженных от границ сетки, использовался метод полностью согласованного слоя (PML) [22]. Шаг сетки выбирался равным 2 см. Такой выбор позволил корректно описывать распространение волн в частотном диапазоне до 2 кГц.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ И МОДЕЛИРОВАНИЕ
Сигналы, полученные в эксперименте, подвергались корреляционной обработке, алгоритм которой подробно изложен в [1–3]. Коротко говоря, в обработку входит вычисление корреляции с эталонным MLS-сигналом, вычисление объемной скорости источника по методу двух микрофонов и фильтрация в частотной области. В результате получается импульсный отклик акустического тракта. Нормировка амплитуды для простоты выбирается таким образом, чтобы максимальное значение сигнала было равно единице на расстоянии 1 м от источника. Сигналы подвергаются полосовой фильтрации в диапазоне 500–4000 Гц.
Таблица 1.
Задержки сигналов, вычисленные с помощью формул (7), (8), в сравнении с результатами эксперимента
| V = 0 м/c | V = 20 м/с | V = 40 м/с | V = 60 м/с | V = 80 м/с | |
|---|---|---|---|---|---|
| Расчет | $ct = 3.280$ м | $ct = 3.310$ м | $ct = 3.339$ м | $ct = 3.366$ м | $ct = 3.394$ м |
| Эксперимент | $ct = 3.280$ м | $ct = 3.312$ м | $ct = 3.343$ м | $ct = 3.375$ м | $ct = 3.395$ м |
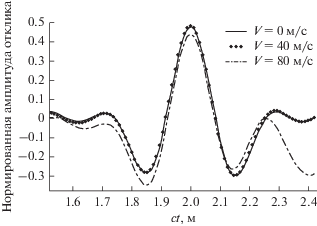
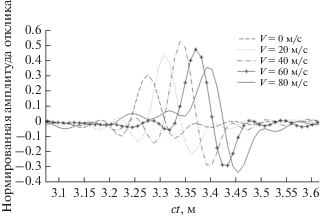
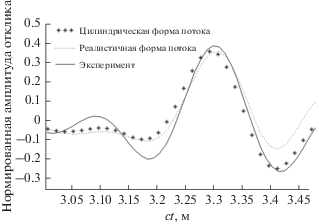
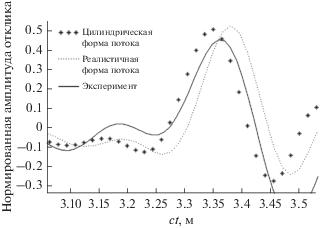
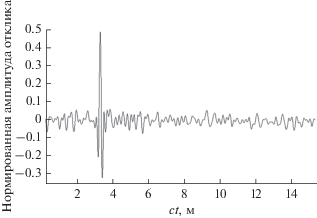
Результаты корреляционной обработки сигнала на микрофоне 2 для случая перпендикулярной и неперпендикулярной трасс распространения представлены на рис. 7 и 8 соответственно.
Из представленных результатов следует, что влияние потока в случае перпендикулярной трассы распространения незначительно. Отсутствие сноса сигнала и фокусировки объясняется тем фактом, что проекция луча на поток (z-компонента волнового вектора) в данном случае равна нулю. В случае неперпендикулярной трассы распространения увеличение средней скорости потока приводит к увеличению задержки сигнала. Кроме того, для потоков со скоростью 0, 20 и 40 м/c наблюдается рост амплитуды с ростом скорости потока. Наиболее вероятная причина этого роста – фокусировка сигнала. Также наблюдается падение амплитуды на скоростях 60 и 80 м/с.
Моделирование уравнений (7), (8) для координат микрофона 2 в случае неперпендикулярной трассы распространения дает значения времени задержки, которые приведены в таблице. Данные оценки хорошо согласуются с экспериментом.
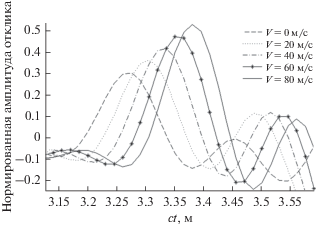
На рис. 9 приводятся результаты численного моделирования сигналов методом конечных разностей для потока, скорость струи в котором рассчитывалась с помощью формул (10) и (11). Отметим, что результаты численного моделирования фильтруются в диапазоне 500–2000 Гц в соответствии с пространственным разрешением сетки.
Для наглядности на рис. 10 и 11 совместно приведены результаты численного моделирования и эксперимента для скоростей потока 20 и 60 м/с. Кроме струи “реалистичной формы”, скорость которой рассчитывалась по формулам (10) и (11), также представлены результаты моделирования для потока цилиндрической формы с постоянной по сечению скоростью.
Как видно из графиков, теоретические результаты вполне удовлетворительно согласуются с экспериментальными данными. Также стоит отметить, что моделирование не описывает падение амплитуды сигнала на скоростях 60 и 80 м/с. Это косвенно свидетельствует о том, что падение амплитуды обусловлено флуктуациями в потоке, которые здесь не учитываются.
Сигналы на микрофонах 1 и 3 (выше и ниже микрофона 2, см. рис. 1) слабо отличаются от сигналов на микрофоне 2. На этих микрофонах снос выражен слабее, а фокусировка приводит не к усилению, а ослаблению амплитуды.
ШУМЫ И ВРЕМЯ НАКОПЛЕНИЯ
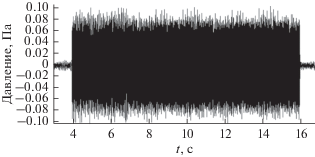
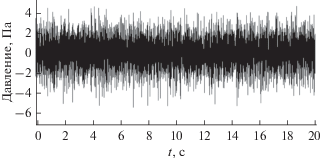
Стоит отметить, что “сырой” сигнал на приемном микрофоне сильно зашумлен, особенно при большой скорости потока. Использование MLS-техники в данном случае может рассматриваться как эффективная противошумовая мера. А именно, квазишумовые сигналы до корреляционной обработки выглядят как показано на рис. 12 и 13. Полезный сигнал составляет примерно 0.1 Па, он начинает теряться на фоне шумов уже при скорости потока 20 м/c (шум на микрофоне составляет 1 Па) и совсем теряется при скорости потока 80 м/c (шум составляет 10 Па). Корреляционная обработка позволяет выделить импульсный отклик весьма хорошо до 60 м/c (рис. 14).
Дальнейшее снижение шума возможно за счет увеличения времени накопления сигнала. Был проведен эксперимент по увеличению времени накопления в три раза. При этом средний квадрат шума также снижался в три раза, в полном соответствии с теоретическими представлениями. При работе в сильных потоках авторы предлагают увеличивать время накопления еще существеннее.
ЗАКЛЮЧЕНИЕ
В данной работе представлены результаты проведения прямого дифракционного эксперимента в присутствии воздушной струи. Проверялась возможность проведения измерений с использованием MLS-техники на фоне струи, создающей значительный шум. В рамках данного подхода удалось восстановить импульсный отклик, а также пронаблюдать основные эффекты, оказываемые потоком на звук: фокусировку и снос сигнала. Кроме того, был произведен теоретический расчет этих эффектов в предположении небольших чисел Маха и двух различных форм потока: цилиндрической и реалистичной, основанной на данных. Результаты расчета показали хорошее согласование с экспериментом.
Список литературы
Шанин А.В., Валяев В.Ю. Метод последовательностей максимальной длины в дифракционном эксперименте // Акуст. журн. 2011. Т. 57. № 3. С. 420–425.
Валяев В.Ю., Шанин А.В. Экспериментальная оценка параметров пористого дорожного покрытия акустическим методом // Акуст. журн. Т. 58. № 6. С. 776–784.
Денисов С.Л., Корольков А.И. Исследование эффективности экранирования шума с помощью метода последовательностей максимальной длины в приложении к задачам авиационной акустики // Акуст. журн. Т. 63. № 4. С. 419–435.
Candel M., Julliano M., Julienne A. Shielding and scattering by a jet flow // 3rd AIAA Aero-acoustics Conference, 1976.
Gerhold C.H. Analytical model of jet shielding // AIAA J. 1983. V. 21. № 5. P. 694−698.
Karweit M., Blanc-Benon Ph., Juve D., Comte-Bellot G. Simulation of the propagation of an acoustic wave through a turbulent velocity field: A study of phase variance // J. Acoust. Soc. Am. 1991. V. 89. № 1. P. 52–62.
Chi-Ming Ho, Kovasznay L.S.G. Propagation of a coherent acoustic wave through a turbulent shear flow // J. Acoust. Soc. Am. 1976. V. 60. № 1. P. 40–45.
Голованов А.Н. Влияние акустических возмущений на свободно-конвективное течение // Прикладная механика и техническая физика. 2006. Т. 47. № 5. С. 27–33.
Власов Е.В., Гиневский А.С. Влияние акустических возмущений на переход ламинарного пограничного слоя в турбулентный // Ученые записки ЦАГИ. 1971. Т. 2. № 2.
Friedland A.B., Pierce A.D. Reflection of acoustic pulses from stable and unstable interfaces between moving fluids // The Physics of Fluids. 1969. V. 12. № 6. P. 1148–1159.
Годин О.А. Отражение сферической волны от движущейся среды // Акуст. журн. 1988. Т. 34. № 3. С. 445–452.
Jones D.S. The reflection of acoustic pulse by a plane vortex sheet // Proc. Camb. Phil. Soc. 1973. V. 74. P. 349–364.
Gottlieb P. Sound Source near velocity discontinuity // J. Acoust. Soc. Am. 1960. V. 32. № 9. P. 1117.
Ahuja K.K., Tanna H.K., Tester B.J. An experimental study of transmission, reflection and scattering of sound in a free jet flight simulation facility and comparison with theory // J. Sound Vibr. 1981. V. 75 (1). P. 51–85.
Блохинцев Д.И. Акустика неоднородной движущейся среды. 2-е изд. М.: Наука, 1981. 210 с.
Keller J.B. Geometrical theory of diffraction // J. Opt. Soc. Am. 1962. V. 52. № 2. P. 115−130.
Миронов М.А. Воздействие гармонического источника объемной скорости на течение с плоским тангенциальным разрывом (плоская задача) // Акуст. журн. 1975. Т. 21. № 1. С. 79–85.
Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. 3-е изд. М.: Наука, 1974. 319 с.
Абрамович Г.Н. Теория турбулентных струй. М.: ЭКОЛИТ, 2011. 720 с.
Tam C.K.W., Burton D.E., Sound generated by instability waves of supersonic flows. Part 2. Axisymmetric jets // J. Fluid. Mech. 1984. V. 138. P. 273–295.
Мунин А.Г., Кузнецов В.М., Леонтьев Е.А. Аэродинамические источники шума. М.: Машиностроение, 1981. 248 с.
Grothe M.J., Sim I. Efficient PML for the wave equation // ArXiv: 1001.0319v1 (2010).
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал