Акустический журнал, 2019, T. 65, № 2, стр. 232-240
Ударное возбуждение звука при схлопывании створок полулунных клапанов сердца
В. Г. Андреев a, *, В. В. Грамович b, О. Н. Выборов b, Т. В. Мартынюк b, О. В. Родненков b, О. В. Руденко a, c, d, e
a Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 ГСП-1, Ленинские горы, Москва, Россия
b ФГБУ “НМИЦ кардиологии” Минздрава России
121552 Москва, 3-я Черепковская ул. 15а, Россия
c Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия
d Институт физики Земли им. О.Ю. Шмидта РАН
123242 Москва, Б. Грузинская ул. 10, стр. 1, Россия
e Blekinge Institute of Technology
Karlskrona, Sweden
* E-mail: andreev@acs366.phys.msu.ru
Поступила в редакцию 15.10.2018
После доработки 30.10.2018
Принята к публикации 15.10.2018
Аннотация
Предложена простая модель работы полулунного клапана с целью оценки спектра акустических колебаний, возникающих при его схлопывании. Проведен теоретический анализ схлопывания упругих створок легочного клапана под действием перепада давления крови в артерии и желудочке. Показано, что при учете вязкости крови скорость движения створок ограничена, и время схлопывания имеет конечное значение. Решена задача излучения акустических волн в жидкость колеблющимися створками при их ударном возбуждении. Проведены оценки времен схлопывания и соударения створок с учетом упругих параметров створок и вязкости крови. Рассчитана форма волны, излучаемая в кровь колеблющимися створками. Результаты могут быть использованы для разработки метода измерения давления в легочной артерии по анализу звуков второго тона сердца.
1. ВВЕДЕНИЕ
Несмотря на то, что в современной кардиологии широко распространены разнообразные высокотехнологичные методы исследования сердца, и прежде всего эхокардиография (ультразвуковое исследование сердца), тем не менее, метод аускультации (выслушивания) сердца, который используется в медицине более 200 лет со времен изобретения стетоскопа Рене Лаэннеком, сохраняет свою актуальность [1]. Например, у пациента с острым инфарктом миокарда и повышением температуры тела может выслушиваться шум трения перикарда, что свидетельствует о перикардите (воспалении сердечной сорочки), но при этом эхокардиография еще не выявляет выпота в полости перикарда, т. к. патологический процесс находится на ранней стадии своего развития. Другим примером может служить случай пациента с повышением давления в легочной артерии (легочной гипертензией), когда врач при аускультации сердца может обнаружить усиление второго тона над легочной артерией, но при этом с помощью эхокардиографии невозможно оценить давление в легочной артерии, если отсутствует недостаточность трикуспидального клапана.
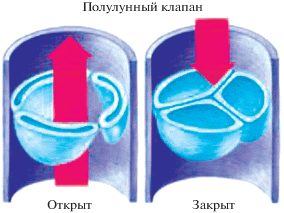
В норме у человека в большинстве случаев выслушивается два основных сердечных тона. Первый тон S1 возникает в начале систолы после захлопывания створчатых клапанов, расположенных между предсердиями и желудочками, что обеспечивает продвижение крови из желудочков в магистральные сосуды, отходящие от сердца (аорту и легочную артерию). Второй тон S2 возникает в начале диастолы после захлопывания полулунных клапанов, отделяющих аорту и легочную артерию от левого и правого желудочков сердца, что препятствует возврату крови из магистральных сосудов в желудочки сердца. Таким образом, система клапанов сердца способствует последовательному продвижению крови по сердцу от крупных вен, через правые отделы сердца, и далее в легкие, где венозная кровь обогащается кислородом, а затем через левые отделы сердца уже насыщенная кислородом кровь попадает в аорту, откуда по артериям распределяется по всему организму.
Несмотря на давнюю историю изучения сердечных тонов с помощью аускультации и фонокардиографии, до настоящего времени существуют споры относительно их происхождения и наилучшего места для выслушивания на поверхности грудной клетки [2]. В работе основное внимание уделено второму тону сердца в связи с проблемой диагностики легочной гипертензии и ряда заболеваний сердца [3]. Второй тон сердца S2 генерируется в начале диастолы при закрытии полулунных клапанов (аортального и легочного), которые отделяют желудочки сердца от крупных магистральных сосудов, отходящих от сердца (аорты и легочной артерии). При этом между левым желудочком и аортой располагается аортальный клапан, а между правым желудочком и легочной артерией – легочный. Строение аортального и легочного клапанов не имеет существенных различий, за исключением того, что легочный клапан несколько больше по размеру и его створки тоньше, чем у аортального. Вышеуказанные отличия объясняются гемодинамическими условиями функционирования клапанов, поскольку легочный клапан работает при значительно меньшем перепаде давления, чем аортальный. Полулунные клапаны в норме состоят из трех заслонок, которые во время систолы открываются под давлением крови из желудочков, при этом кровь поступает в аорту и легочную артерию. Во время диастолы заслонки закрываются под действием давления крови в аорте и легочной артерии, препятствуя обратному току крови в желудочки (рис. 1). Поскольку изгнание крови из правого желудочка в норме заканчивается немного позднее, чем из левого, то захлопывание аортального клапана предшествует легочному клапану. В связи с этим различают два компонента второго тона: A2 – аортальный и Р2 – легочный. Компонента Р2 в норме при спокойном дыхании запаздывает по отношению к А2 приблизительно на 30–40 мс [4].
История изучения тонов сердца насчитывает уже более века. Еще J. Rouanet (1832) в первой половине 19-го в. связывал возникновение второго тона сердца с закрытием аортального и легочного клапанов. Хотя это объяснение до настоящего времени является общепринятым и приводится во всех учебниках по кардиологии, тем не менее, у большинства врачей отсутствует точное представление о том, как именно происходит генерация второго тона сердца. В настоящее время существует несколько рабочих гипотез, которые пытаются описать этот феномен. D.J. Сoleman объясняет появление второго тона быстрым соударением узелков Аранци (утолщений на середине свободного края створок полулунных клапанов), которое происходит в момент полного закрытия створок, что должно вызывать вибрацию натянутых створок клапана [5]. Однако в последующих исследованиях эта теория не нашла подтверждения, поскольку было показано, что смыкание створок полулунных клапанов происходит не одновременно, а скорее асинхронно, что минимизирует энергию, которая образуется при их соударении. Эта энергия главным образом рассеивается до возникновения S2, поскольку второй тон появляется уже после полного закрытия створок клапана [6]. Наиболее убедительная теория происхождения S2 предполагает, что закрытие аортального и легочного клапанов запускает серию событий, которые приводят к формированию второго тона сердца. В соответствии с современными представлениями, главные выслушиваемые компоненты S2 возникают вследствие вибрации сердечных структур уже после закрытия полулунных клапанов. В экспериментальных исследованиях с использованием высокоточных микроманометров и эхофонокардиографии было показано, что полулунные клапаны сердца закрываются бесшумно, а коаптация (сближение) створок аортального клапана предшествует появлению S2 на несколько миллисекунд [6]. Следовательно, S2 формируется в результате последующих вибраций створок, стенок и столбов крови в аорте и легочной артерии и левом и правом желудочках. Энергия этих колебаний возникает из-за внезапного замедления тока крови в аорте и легочной артерии при достижении предела растяжимости натянутых створок полулунных клапанов. Это внезапное замедление создает вибрации во всей кардиогемической системе – сердце с кровью в его полостях и магистральных сосудах [4].
Для врача, проводящего аускультацию сердца, важно понимание того, что второй тон сердца возникает в результате вибрации закрытых створок полулунных клапанов сразу после их беззвучного сближения. Если рассматривать закрытый клапан в качестве вибрирующей натянутой мембраны, тогда становятся понятны факторы, оказывающие влияние на диастолическую вибрацию клапана и, в конечном итоге, на интенсивность (звучность) второго тона сердца. К таким факторам относятся: быстрота изменения диастолического градиента давления между магистральным сосудом и желудочком сердца; эластичность клапана, его масса и диаметр; плотность и вязкость крови; частота вибрации клапана; коэффициент поглощения звука стенками желудочка и геометрия желудочка [7]. Примечательно, что вышеперечисленные факторы являются независимыми от множества причин, влияющих на распространение звуковых волн. В статье D.L. Sikarskie [8] предложена одномерная модель клапана в виде упругой мембраны, закрывающей аорту. Она дает возможность оценить частоту акустических колебаний при правильном задании упругости мембраны и перепада давления крови по разные стороны от нее. Однако эта модель не описывает сам процесс перекрытия потока и не дает характерных времен, за которые происходит торможение крови. А именно это время определяет инерцию столба крови в аорте и дальнейшие колебания ее упругих стенок за счет давления, вызванного резким торможением потока. В данной работе рассматривается именно процесс закрытия створок клапана и оценивается как время закрытия клапана, так и длительность соударения упругих створок. На основании полученных результатов делаются оценки характерных частот колебаний створок и форма излучаемой волны.
2. МЕХАНИКА СХЛОПЫВАНИЯ СТВОРОК
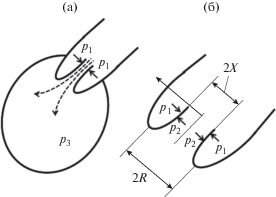
Обсудим схему, изображенную на рис. 2, с целью построения математической модели процесса схлопывания створок сердечного клапана. Рассмотрим фазу сердечного цикла, наступающую после того, как давление в камере упадет до значения ${{p}_{3}} < {{p}_{1}}$ и начнется кратковременный обратный ток крови, показанный штриховыми стрелками на рис. 2а. Вначале пренебрежем вязкостью крови. Считаем течение потенциальным и воспользуемся интегралом Бернулли, записав его для трех поперечных сечений потока: на входе клапана, внутри него и на его выходе. Соответствующие значения параметров отмечены индексами 1, 2 и 3. Имеем два соотношения:
Рис. 2.
(а) Схема, иллюстрирующая работу сердечного клапана, и (б) сам клапан в увеличенном размере с указанием его основных геометрических характеристик.
Из закона сохранения массы несжимаемой жидкости следует еще одно простое соотношение:
В соотношениях (1) и (2) буквой U обозначена скорость течения, X – это половина ширины щели между створками клапана, R – половина расстояния между створками клапана в наиболее широкой части, то есть на выходе в резервуар.
Очевидно, что расстояние между створками клапана должно изменяться со временем. Однако обратный ток крови у здоровых людей – кратковременное явление; при этом объем текущей назад крови незначителен, и до закрытия клапана перепад давления изменяется мало. Для простоты вначале считаем его постоянным. Такое приближение позволит получить наглядные аналитические решения. Учет зависимостей ${{p}_{i}}(t)\,\,(i = 1,2,3)$ может быть проведен для уточнения результатов с помощью численного анализа модели.
Уравнение движения для функции $X = X(t)$ запишется в виде
Здесь m – масса одной створки клапана, приходящаяся на единицу площади ее поверхности в направлении, ортогональном плоскости рис. 2. Нормировка на площадь необходима, поскольку рассматривается идеализированная 1одномерная задача. С помощью соотношений (1) и (2) правая часть уравнения (3) примет вид
(4)
$ - \frac{1}{2}\rho U_{2}^{2} = - \frac{1}{2}\rho U_{3}^{2}{{\left( {\frac{R}{X}} \right)}^{2}} = - \left( {{{p}_{1}} - {{p}_{3}}} \right){{\left( {\frac{R}{X}} \right)}^{2}}.$Подставляя (4) в уравнение (3), приведем его к виду
Заметим, что нелинейное уравнение (5) встречается при описании движения точечной массы (или заряда) в центрально–симметричном гравитационном (или электрическом) поле. Его удается один раз проинтегрировать:
Считаем, что в начальный момент времени раскрытие клапана равно $X(0) = {{X}_{0}},$ а скорость его движения $\dot {X}(0) = 0.$ Определяя константу $С = {{ - 2a} \mathord{\left/ {\vphantom {{ - 2a} {{{X}_{0}}}}} \right. \kern-0em} {{{X}_{0}}}}$ в уравнении (6) и интегрируя еще раз, найдем:
(7)
$\arcsin \sqrt {\frac{X}{{{{X}_{0}}}}} - \sqrt {\frac{X}{{{{X}_{0}}}}} \sqrt {1 - \frac{X}{{{{X}_{0}}}}} = \frac{\pi }{2}\left( {1 - \frac{t}{{{{t}_{0}}}}} \right).$Здесь ${{t}_{0}}$ – вторая константа интегрирования, определяющая промежуток времени, за который ширина щели уменьшится от исходного значения ${{X}_{0}}$ до нуля, то есть время схлопывания (закрытия) щели. Это время равно
При $X = 0$ возникает особенность – скорость $\dot {X}$ в момент схлопывания обращается в бесконечность. Этот факт непосредственно следует из записи уравнения (6) в следующей форме:
(9)
$\frac{{\dot {X}}}{{{{X}_{0}}}} = - \sqrt {\frac{{2a}}{{X_{0}^{3}}}} \sqrt {\frac{{{{X}_{0}}}}{X} - 1} .$Поскольку “громкость” звука, идущего от клапана, зависит от скорости удара, особенность при $X = 0$ необходимо устранить. Это можно сделать путем очевидного усложнения модели. Именно, нужно учесть вязкость крови на последней стадии захлопывания, после того как ширина щели уменьшится до размера порядка толщины пограничного слоя $X{\text{*}}.$
3. СХЛОПЫВАНИЕ СТВОРОК В ВЯЗКОЙ ЖИДКОСТИ
Простейшее предположение, позволяющее учесть вязкость, состоит в следующем. Будем считать, что в диапазоне расстояний между створками клапана ${{X}_{0}} > X > X{\text{*}}$ справедлива математическая модель (5), основанная на гидродинамике идеальной несжимаемой жидкости. На меньших расстояниях ${{X}_{ * }} > X > 0,$ перед схлопыванием створок, справедлива модель Пуазейля для течения вязкой жидкости. Как известно, средняя по сечению скорость течения Пуазейля дается формулой
Здесь η – сдвиговая вязкость крови, L – длина участка между створками, на котором реализуется пуазейлевское течение. Подставляя (10) в уравнение движения (3), приведем его к виду
(11)
$\ddot {X} + b{{X}^{4}} = 0,\,\,\,\,b = \frac{\rho }{{2m}}\frac{{{{{({{p}_{1}} - {{p}_{3}})}}^{2}}}}{{{{{\left( {3\eta L} \right)}}^{2}}}}.$Уравнение (11) один раз интегрируется, и получается такое уравнение для квадрата скорости $\dot {X} = V$ сближения створок:
Здесь ${{V}_{{{\text{FIN}}}}}$ – финальная скорость в момент удара, то есть когда створки соприкоснулись и расстояние между ними обратилось в ноль: $X = 0.$
Выпишем теперь аналогичное уравнение (6) для первой стадии схлопывания в следующем виде:
При $X = X{\text{*}}$ формулы (12) и (13) должны приводить к одинаковому результату. Для удобства запишем (12) и (13) в безразмерных переменных:
(14)
$\begin{gathered} {{{\dot {Z}}}^{2}} = \dot {Z}_{{{\text{FIN}}}}^{2} - \beta {{Z}^{5}},\,\,\,\,{{{\dot {Z}}}^{2}} = \alpha \left( {\frac{1}{Z} - 1} \right); \\ Z = \frac{X}{{{{X}_{0}}}},\,\,\,\,\beta = \frac{2}{5}bX_{0}^{3},\,\,\,\,\alpha = \frac{{2a}}{{X_{0}^{3}}}. \\ \end{gathered} $Приравнивая два выражения для скорости при значении $Z = Z*,$ найдем
(15)
$\dot {Z}_{{{\text{FIN}}}}^{2} = \beta Z_{ * }^{5} + \alpha \left( {\frac{1}{{{{Z}_{ * }}}} - 1} \right).$Поскольку $Z* < 1,$ оба слагаемых в формуле (15) положительны. Минимальное значение финальной скорости как функции от ${{Z}_{ * }}$ достигается при $Z_{ * }^{6} = {\alpha \mathord{\left/ {\vphantom {\alpha {5\beta }}} \right. \kern-0em} {5\beta }}$ и равно
(16)
${{\left( {{{{\dot {Z}}}_{{{\text{FIN}}}}}} \right)}_{{{\text{MIN}}}}} = \sqrt \alpha {{\left[ {\frac{6}{5}{{{\left( {\frac{{5\beta }}{\alpha }} \right)}}^{{\frac{1}{6}}}} - 1} \right]}^{{\frac{1}{2}}}}.$Можно предположить, что высокая громкость стука сердечного клапана нежелательна для организма, и поэтому в нормальном состоянии минимальная скорость схлопывания (16) должна быть близкой к нулю. Переходя в формуле (16) к размерным обозначениям параметров, придем к соотношению
(17)
$\frac{b}{a}X_{0}^{6} = \frac{{X_{0}^{6}}}{{18}}\frac{{\rho ({{p}_{1}} - {{p}_{3}})}}{{{{{\left( {\eta LR} \right)}}^{2}}}} = 1.$Таким образом, если вязкость крови вдруг вырастет при неизменных значениях прочих параметров в (17), должен заметно вырасти перепад давления $({{p}_{1}} - {{p}_{3}})\sim {{\eta }^{2}}$ или очень слабо – расстояние ${{X}_{0}}$ между створками клапана, поскольку $\eta \sim X_{0}^{3}.$
Для построения фазового портрета $\dot {Z}\left( Z \right)$ с учетом вязкости наложим два дополнительных условия. Первое требование – это непрерывность фазовой траектории в точке сшивания $Z = {{Z}_{ * }};$ второе – непрерывность производной ${{d\dot {Z}} \mathord{\left/ {\vphantom {{d\dot {Z}} {dZ}}} \right. \kern-0em} {dZ}}$ в этой точке. Первое условие приводит к соотношению (15), второе – к новому соотношению
Из пары формул (15), (18) следует выражение для координаты точки сшивания:
Интересно, что (19) совпадает со значением, при котором скорость (15) достигает своего минимума (16). Таким образом, при правильном выборе (19) точки сшивания внешнего (невязкого) и внутреннего (вязкого) решений скорость схлопывания створок сердечного клапана оказывается минимальной из всех возможных.
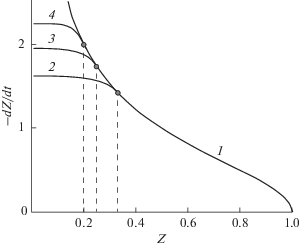
На рис. 4 изображены “сшитые” фазовые траектории, описывающие процесс схлопывания створок. Все кривые построены для значения параметра $\alpha = 1.$ Кривая 1 отвечает случаю невязкой крови. Для нее скорость схлопывания стремится к бесконечности в момент соударения сворок, как и для кривой 2 на рис. 3. Три другие кривые 2, 3, 4 отвечают значениям координаты сшивания $Z* = 0.33,\,\,0.25,\,\,0.2$ соответственно. Предельное значение скорости в момент удара дается формулой (16):
Рис. 3.
Уменьшение полуширины клапана в процессе смыкания его створок (кривая 1) и рост скорости этого смыкания (кривая 2).
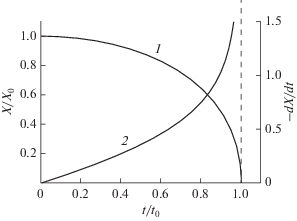
Рис. 4.
Фазовые траектории $ - \dot {Z}\left( Z \right),$ описывающие процесс схлопывания сердечного клапана. Точки сшивания двух решений без учета и с учетом вязкости, расположенные при $Z* = 0.33,\,\,\,0.25,\,\,\,0.2$ (кривые 2, 3, 4 соответственно), отмечены жирными кружками. Кривая 1 изображает фазовую траекторию без учета вязкости.
4. ПРОЦЕСС СОУДАРЕНИЯ И ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ
Соударение створок происходит не мгновенно, а занимает некоторое время, начиная от момента их соприкосновения друг с другом и заканчивая моментом полной остановки (в общем случае, когда конечная скорость удара ${{V}_{{{\text{FIN}}}}}$ отлична от нуля). Пренебрегая трением в процессе взаимного торможения створок, запишем соотношение для энергии:
В левой части (21) стоит кинетическая энергия створки в момент соприкосновения, в правой части – сумма кинетической и потенциальной энергии в текущий момент времени. Из (21) получим
(22)
$t = \int\limits_0^X {\frac{{dX{\kern 1pt} {\text{'}}}}{{\sqrt {V_{{{\text{FIN}}}}^{2} - \frac{2}{m}W\left( {X{\kern 1pt} {\text{'}}} \right)} }}} .$Для грубой оценки положим $W\left( X \right) = {{\mu {{X}^{2}}} \mathord{\left/ {\vphantom {{\mu {{X}^{2}}} 2}} \right. \kern-0em} 2},$ т.е. используем линейный закон Гука, где коэффициент упругости μ есть величина постоянная, порядка модуля сдвиговой упругости мышечной ткани. При этом интеграл (22) вычисляется и дает простую формулу для смещения створок в процессе их деформирования:
(23)
$X = {{V}_{{{\text{FIN}}}}}\sqrt {\frac{m}{\mu }} \sin \left( {t\sqrt {\frac{\mu }{m}} } \right),\,\,\,\,0 < t\sqrt {\frac{\mu }{m}} < \pi .$Сила, действующая на створку клапана при его деформировании, в рамках линейной модели равна $F = \mu X\left( t \right).$
Из формул (21), (23) находим величину максимального “сдавливания” створки клапана и полное время соударения:
(24)
${{X}_{{{\text{MAX}}}}} = {{V}_{{{\text{FIN}}}}}\sqrt {\frac{m}{\mu }} ,\,\,\,{{t}_{{{\text{MAX}}}}} = \pi \sqrt {\frac{m}{\mu }} .$Результат (24) показывает, что с ростом модуля упругости (жесткости) створки μ максимальная деформация ${{X}_{{{\text{MAX}}}}}$ и длительность соударения ${{t}_{{{\text{MAX}}}}}$ уменьшаются. Деформация и сила удара растут с увеличением скорости соударения ${{V}_{{{\text{FIN}}}}}$. Эти выводы носят качественный характер; они справедливы и при более общем (нелинейном, то есть не гуковском) законе деформирования, когда потенциальная энергия дается не квадратичной, а более сложной функцией смещения $X$.
Перейдем теперь к расчету колебаний створки клапана, считая его упругой тонкой пластинкой, расположенной параллельно оси y. Пластинка совершает изгибные колебания со смещениями вдоль оси x, которые обозначим как $\varsigma \left( {y,\,t} \right).$ Колебания возбуждаются ударной нагрузкой $F = \mu X\left( t \right)$ (23), сосредоточенной в центре пластинки y = 0. Схема возбуждения и обозначения пояснены на рис. 5.
Изгибные колебания пластинки, граничащей с жидкостью (кровью), будем описывать уравнением
(25)
$\rho h\frac{{{{\partial }^{2}}\varsigma }}{{\partial {{t}^{2}}}} + D\frac{{{{\partial }^{4}}\varsigma }}{{\partial {{y}^{4}}}} = - F\left( t \right)\delta \left( y \right) - {{\rho }_{b}}\frac{{\partial \varphi }}{{\partial t}}.$Здесь $\varsigma $ – смещение поверхности пластинки вдоль оси $x$; $\rho ,\,\,h$ – плотность пластинки и ее толщина; число $D = {{E{{h}^{3}}} \mathord{\left/ {\vphantom {{E{{h}^{3}}} {12\left( {1 - {{\sigma }^{2}}} \right)}}} \right. \kern-0em} {12\left( {1 - {{\sigma }^{2}}} \right)}},$ где $E,\,\,\sigma $ – модуль Юнга и коэффициент Пуассона. Второй член правой части (25) описывает давление, оказываемое на пластину убегающей в жидкость акустической волной с потенциалом колебательной скорости φ. Потенциал описывается волновым уравнением
(26)
$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}} - c_{b}^{2}\left( {\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{y}^{2}}}}} \right) = 0.$В формулах (25) и (26) ${{\rho }_{b}},\,\,{{с }_{b}}$ – плотность крови и скорость звука в ней. Переменные связаны соотношением
(27)
$\frac{{\partial \varsigma }}{{\partial t}} = {{V}_{x}} = {{\left. {\frac{{\partial \varphi }}{{\partial x}}} \right|}_{{x = 0}}}.$Его смысл – равенство скорости колебаний поверхности пластины и нормальной компоненты скорости крови на этой поверхности.
Ищем решение задачи методом интегрального преобразования Фурье, т.е. в виде разложений
(28)
$\begin{gathered} \varphi = \int\limits_{ - \infty }^\infty {\tilde {\varphi }\left( {\omega ,{{k}_{y}}} \right)} \times \\ \times \,\,\exp \left( { - i\omega t + ix\sqrt {\frac{{{{\omega }^{2}}}}{{с _{b}^{2}}} - k_{y}^{2}} + i{{k}_{y}}y} \right)d\omega d{{k}_{y}}, \\ \end{gathered} $(29)
$\varsigma = \int\limits_{ - \infty }^\infty {\tilde {\varsigma }\left( {\omega ,{{k}_{y}}} \right)} \exp \left( { - i\omega t + i{{k}_{y}}y} \right)d\omega d{{k}_{y}},$(30)
$F\left( t \right)\delta \left( y \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\tilde {F}\left( \omega \right)} \exp \left( { - i\omega t + i{{k}_{y}}y} \right)d\omega d{{k}_{y}}.$Здесь
При записи формулы (28) в явном виде учтен следующий из волнового уравнения (26) закон дисперсии:
Подставляя разложения (28)–(30) в уравнение (25) и граничное условие (27), получим
(32)
$\begin{gathered} \left( { - \rho h{{\omega }^{2}} + Dk_{y}^{4}} \right)\tilde {\varsigma } - {{\rho }_{b}}i\omega \tilde {\varphi } = - \frac{1}{{2\pi }}\tilde {F}\left( \omega \right), \\ \omega \tilde {\varsigma } - \tilde {\varphi }\sqrt {\frac{{{{\omega }^{2}}}}{{с _{b}^{2}}} - k_{y}^{2}} = 0. \\ \end{gathered} $Исключая из этой системы фурье-образ поля смещений пластинки, найдем
(33)
$\tilde {\varphi } = \frac{1}{{2\pi }}\frac{{\omega \tilde {F}\left( \omega \right)}}{{i{{\omega }^{2}}{{\rho }_{b}} + \left( {\rho h{{\omega }^{2}} - Dk_{y}^{4}} \right)\sqrt {\frac{{{{\omega }^{2}}}}{{с _{b}^{2}}} - k_{y}^{2}} }}.$Таким образом, для расчета пространственно-временной структуры акустического поля нужно вычислить интеграл (28) с учетом (33):
(34)
$\begin{gathered} \varphi = - \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{{\omega \tilde {F}\left( \omega \right)d\omega d{{k}_{y}}}}{{i{{\omega }^{2}}{{\rho }_{b}} + \left( {\rho h{{\omega }^{2}} - Dk_{y}^{4}} \right)\sqrt {\frac{{{{\omega }^{2}}}}{{с _{b}^{2}}} - k_{y}^{2}} }}} \times \\ \times \,\exp \,\left( { - i\omega t + ix\sqrt {\frac{{{{\omega }^{2}}}}{{с _{b}^{2}}} - k_{y}^{2}} + i{{k}_{y}}y} \right). \\ \end{gathered} $Если нас интересует не полная структура поля, а лишь форма во времени волны, бегущей от пластинки вдоль оси x, проинтегрируем решение (34) по y в бесконечных пределах. Для интегрального потенциала это дает
(35)
$\begin{gathered} \tilde {\varphi } = \int\limits_{ - \infty }^\infty {\varphi dy} = \\ = \int\limits_{ - \infty }^\infty {\frac{{\omega \tilde {F}\left( \omega \right)\delta \left( {{{k}_{y}}} \right)d\omega d{{k}_{y}}}}{{i{{\omega }^{2}}{{\rho }_{b}} + \left( {\rho h{{\omega }^{2}} - Dk_{y}^{4}} \right)\sqrt {\frac{{{{\omega }^{2}}}}{{с _{b}^{2}}} - k_{y}^{2}} }}} \times \\ \times \,\,\exp \left( { - i\omega t + ix\sqrt {\frac{{{{\omega }^{2}}}}{{с _{b}^{2}}} - k_{y}^{2}} } \right) = \\ = \int\limits_{ - \infty }^\infty {\frac{{\tilde {F}\left( \omega \right)d\omega }}{{i\omega {{\rho }_{b}} + \frac{{\rho h{{\omega }^{2}}}}{{{{c}_{b}}}}}}} \exp \left( { - i\omega \left( {t - \frac{x}{{{{c}_{b}}}}} \right)} \right). \\ \end{gathered} $Переход к интегральному полю акустического давления производится по формуле
(36)
$\begin{gathered} \hat {p} = - {{\rho }_{b}}\frac{{\partial{ \tilde {\varphi }}}}{{\partial t}} = \int\limits_{ - \infty }^\infty {\frac{{\tilde {F}\left( \omega \right)d\omega }}{{1 - \frac{\rho }{{{{\rho }_{b}}}}\frac{{h\omega }}{{{{c}_{b}}}}}}} \exp \left( { - i\omega \tau } \right), \\ \tau = t - \frac{x}{{{{c}_{b}}}}. \\ \end{gathered} $Соотношение (36) удобно записать в виде дифференциального уравнения:
(37)
$\frac{{\partial{ \hat {p}}}}{{\partial \tau }} + \chi \hat {p} = \chi F\left( \tau \right),\,\,\,\,\chi = \frac{{{{\rho }_{b}}{{c}_{b}}}}{{\rho h}}.$Решение уравнения (37) имеет простой вид:
(38)
$\hat {p} = \chi \int\limits_{ - \infty }^\tau {F\left( t \right)} \exp \left( { - \chi \tau + \chi t} \right)dt.$Задавая профиль импульсного воздействия на пластинку $F\left( t \right)$ и вычисляя интеграл (38), найдем форму волны $\hat {p}\left( \tau \right)$ акустического давления, бегущей от пластинки.
Положим для примера
(39)
$\frac{{F\left( t \right)}}{{{{F}_{0}}}} = \left( {\frac{t}{{{{t}_{1}}}}} \right)\exp \left( { - \frac{t}{{{{t}_{1}}}}} \right),\,\,\,\,t \geqslant 0.$Здесь ${{t}_{1}}\sim \sqrt {{m \mathord{\left/ {\vphantom {m \mu }} \right. \kern-0em} \mu }} ,$ согласно формуле (23). Расчет по формуле (38) дает
(40)
$\begin{gathered} \hat {p} = {{F}_{0}}\frac{{\chi {{t}_{1}}}}{{{{{\left( {\chi {{t}_{1}} - 1} \right)}}^{2}}}} \times \\ \times \,\,\left[ {\exp \left( { - \chi \tau } \right) - \exp \left( { - \frac{\tau }{{{{t}_{1}}}}} \right) + \left( {\chi {{t}_{1}} - 1} \right)\frac{\tau }{{{{t}_{1}}}}\exp \left( { - \frac{\tau }{{{{t}_{1}}}}} \right)} \right]. \\ \end{gathered} $В решении (40) при $\chi {{t}_{1}} = 1$ возникает неопределенность. Раскрывая ее, найдем простую форму одиночного акустического удара:
(41)
$\hat {p} = \frac{{{{F}_{0}}}}{2}{{\left( {\frac{\tau }{{{{t}_{1}}}}} \right)}^{2}}\exp \left( { - \frac{\tau }{{{{t}_{1}}}}} \right).$Одиночные импульсные сигналы, построенные по формулам (40), (41), изображены на рис. 6.
Рис. 6.
Форма акустического импульса для значений параметра $\chi {{t}_{1}},$ равных 0.5, 1, 2, 4, 8 (кривые 1–5 соответственно).

Заметим, что в процессе соударения створок, описываемом моделью (21), накопление упругих напряжений происходит только на первой стадии, описываемой решением (23) в промежутке времени $0 < t < {{t}_{{{\text{MAX}}}}} = \pi \sqrt {{m \mathord{\left/ {\vphantom {m \mu }} \right. \kern-0em} \mu }} .$ При больших значениях времени $t > {{t}_{{{\text{MAX}}}}}$ потенциальная энергия деформирования переходит в кинетическую – наступает разгрузка. Возникают колебания. Однако из-за вязких свойств мышечной ткани они будут не гармоническими (23), а затухающими. Поэтому положим в формуле (38) функцию $F\left( t \right)$, в отличие от (39), равной
(42)
$\frac{{F\left( t \right)}}{{{{F}_{0}}}} = \exp \left( { - \delta \frac{t}{{{{t}_{1}}}}} \right)\sin \left( {\frac{t}{{{{t}_{1}}}}} \right),\,\,\,\,t \geqslant 0.$Здесь безразмерный коэффициент δ, пропорциональный вязкости ткани, описывает затухание колебаний. Для функции (42) решение (38) примет вид
(43)
$\begin{gathered} \hat {p} = {{F}_{0}}\frac{{\chi {{t}_{1}}}}{{{{{\left( {\chi {{t}_{1}} - \delta } \right)}}^{2}} + 1}} \times \\ \times \,\,\left\{ {\left( {\chi {{t}_{1}} - \delta } \right)\exp \left( { - \delta \frac{\tau }{{{{t}_{1}}}}} \right)\sin \left( {\frac{\tau }{{{{t}_{1}}}}} \right) + } \right. \\ + \,\,\left. {\left[ {\exp \left( { - \chi {{t}_{1}}\frac{\tau }{{{{t}_{1}}}}} \right) - \exp \left( { - \delta \frac{\tau }{{{{t}_{1}}}}} \right)\cos \left( {\frac{\tau }{{{{t}_{1}}}}} \right)} \right]} \right\}. \\ \end{gathered} $Для значений параметра $\chi {{t}_{1}} \gg 1$ формула (43) упрощается. Из нее следует, что звуковой импульс представляет собой цуг затухающих гармонических колебаний:
(44)
$\hat {p} = {{F}_{0}}\exp \left( { - \delta \frac{\tau }{{{{t}_{1}}}}} \right)\sin \left( {\frac{\tau }{{{{t}_{1}}}}} \right).$Характерная частота звука, как видно из (44), равна
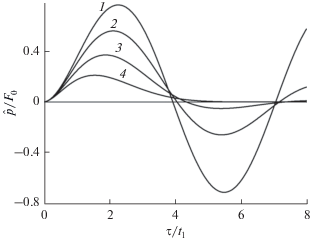
При других значениях параметров возможны формы акустических возмущений типа как одиночных импульсов, так и квазипериодических колебаний (см. рис. 7).
Рис. 7.
Форма акустических импульсных колебаний для параметра $\chi {{t}_{1}} = 1$ и значений диссипативного параметра $\delta = 0,\,\,0.2,\,\,0.5,\,\,1$ (кривые 1–4 соответственно).
Оценим характерные численные значения параметров акустических сигналов, возникающих при схлопывании пульмонального клапана сердца. Численные значения для механических свойств клапана сердца взрослого человека взяты из работ [9–11]. Начнем с частоты (45). Учтем, что
Полагая плотность ткани ρ = 1 г/см3, модуль Юнга E = 10…20 кПа, L = 1 см, h = 0.2…0.3 мм, найдем характерное значение частоты ν ~ 280…500 Гц. Характерное время закрытия (схлопывания створок) клапана согласно (8) равно
Полагая перепад давления в процессе закрытия равным 2 мм рт. ст., R = 1 см, X0 = 0.6 см, найдем t0 ~ 3 мс. Время соударения оценим по формуле (24):
Для используемых значений параметров получим tMAX ~ 1.4 мс. Несмотря на различие физических и геометрических параметров, содержащихся в формулах для ${{t}_{0}}$ и ${{t}_{{{\text{MAX}}}}}$, эти времена оказываются величинами одного порядка – несколько миллисекунд. Более громоздкие оценки показывают, что вязкость крови, в соответствии с моделью (11), немного увеличивает время закрытия ${{t}_{0}}$, и оно может достичь сотой доли секунды. Удивительно, что три различные оценки, основанные на трех независимых физических параметрах (это перепад давления, модуль Юнга ткани и вязкость крови) дают близкие численные значения.
В настоящей работе мы ограничились анализом схлопывания створок легочного клапана сердца и показали, что процесс схлопывания происходит хоть и за малое (несколько миллисекунд), но конечное время. Это означает, что торможение потока крови также происходит не мгновенно, а растянуто во времени, что снижает нагрузку на стенки артерии. На следующем этапе планируется рассмотреть колебания упругих стенок артерии при торможении потока крови и сравнить частоты возникающих колебаний с колебаниями створок клапана.
Работа выполнена при финансовой поддержке гранта РФФИ 18-02-00736.
Список литературы
Fuster V. The stethoscope’s prognosis very much alive and very necessary // J. Am. Coll. Cardiol. 2016. V. 67. P. 1118–1119.
Юзбашев З.Ю. Эволюция взглядов на происхождение звуков сердца и места их выслушивания (обзор литературы) // Верхневолжский мед. журн. 2013. Т. 11. № 4. С. 19–24.
Adolph R.J., Fowler N.O. The second heart sound: a screening test for heart disease // Mod. Conc. Cardiovasc. Dis. 1970. V. 39. P. 91–96.
Felner J.M. The Second Heart Sound / In: Clinical Methods: The History, Physical, and Laboratory Examinations. Eds Walker H.K., Hall W.D., Hurst J.W. 3rd edition. Chap. 23. Boston: Butterworths, 1990.
Coleman D.J. On the origin of the second heart sound // Am. Heart J. 1963. V. 65. P. 237−239.
Sabbah H.N., Stein P.D. Investigation of the theory and mechanism of the origin of the second heart sound // Circ. Res. 1976. V. 39. P. 874–882.
Stein P.D., Sabbah H.N. Origin of the second heart sound: clinical relevance of new observations (editorial) // Am. J. Cardiol. 1978. V. 41. P. 108–110.
Sikarskie D.L., Stein P.D., Vable M. A mathematical model of aortic valve vibration // J. Biomech. 1984. V. 17. P. 831–837.
van Geemen D., Soares A.L.F., Oomen P.J.A., Driessen-Mol A., Janssen-van den Broek M.W.J.T., van den Bogaerdt A.J., Bogers A.J.J.C., Goumans M.J.T.H., Baaijens F.P.T., Bouten C.V.C. Age-dependent changes in geometry, tissue composition and mechanical properties of fetal to adult cryopreserved human heart valves. PLoS ONE 11 (2): e0149020 (2016). doi 10.1371/journal.pone.0149020
Stradins P., Lacis R., Ozolanta I., Purina B., Ose V., Feldmane L., Kasyanov V. Comparison of biomechanical and structural properties between human aortic and pulmonary valve // Eur. J. Cardio-Thoracic Surg. 2004. V. 26. P. 634–639.
Hasen A., Ragaert K., Swieszkowski W., Selimović Š., Paul A., Camci-Unal G., Mofrad M.R., Khademhosseini A. Biomechanical properties of native and tissue engineered heart valve constructs // J. Biomech. 2014. V. 13. P. 1949–1963.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал