Акустический журнал, 2019, T. 65, № 4, стр. 540-550
Локализация источника в акустическом волноводе с неточно известными параметрами с использованием согласованной обработки в модовом пространстве
А. Г. Сазонтов a, b, *, И. П. Смирнов a
a Институт прикладной физики РАН
Нижний Новгород, Россия
b Нижегородский государственный университет им. Н.И. Лобачевского
Нижний Новгород, Россия
* E-mail: sazontov@appl.sci-nnov.ru
Поступила в редакцию 19.09.2018
После доработки 10.01.2019
Принята к публикации 20.03.2019
Аннотация
Построен адаптивный модовый алгоритм MUSIC, позволяющий локализовать акустический источник с помощью вертикальной антенной решетки, работающей в условиях неполной информации о волноводном канале распространения. Представлены результаты статистического моделирования, демонстрирующие вероятности правильной локализации источника в зависимости от входного отношения сигнал/шум и объема выборки. Приведена верификация предложенного метода с использованием экспериментальных данных, полученных в Ладожском озере. Показано, что указанный способ обеспечивает большую устойчивость процедуры оценивания к рассогласованию между истинной и ожидаемой репликой сигнала по сравнению с традиционным методом MUSIC, осуществляющим обработку в пространстве элементов антенны.
ВВЕДЕНИЕ
Локализация источника в условиях неточного знания морской среды является одной из важных прикладных задач гидроакустики [1, 2]. Однако ее решение, основанное на методе согласованного поля (предполагающего априорное знание реплики принятого сигнала), сталкивается с трудностями принципиального характера. Главной причиной, не позволяющей получить корректное решения обратной задачи, является несоответствие (рассогласование) между расчетной моделью среды распространения и реальным акустическим волноводом. Для частичной компенсации эффекта рассогласования в акустике океана предложен ряд адаптивных методов (см., например, [3–6]), применение которых позволяет несколько повысить качество восстановления источника.
В мелком море возможна ситуация, когда число распространяющихся мод сопоставимо или меньше числа элементов приемной антенной решетки (АР). В этом случае с вычислительной точки зрения пространственную обработку удобно реализовать в модовом пространстве11. Метод решения задачи локализации источника, основанный на анализе модовой структуры сигнала, был первоначально предложен Е. Шэнгом [7–9]. Результаты более поздних исследований в этой области отражены в работах [10–20]. Важно подчеркнуть, что при использовании обработки, согласованной с ожидаемым модовым составом, можно учитывать не все распространяющиеся моды, а только слабо взаимодействующие со дном. Последнее позволяет обеспечить повышенную устойчивость модовых алгоритмов локализации к эффекту рассогласования, обусловленному неточным знанием геоакустических характеристик донных осадков.
В последнее десятилетие в общей теории адаптивных АР интенсивно развивается направление, связанное с построением робастных алгоритмов, учитывающих отличие ожидаемой реплики от истинной и позволяющих повысить эффективность локализации источника в условиях неполной информации о среде распространения (см. например [21, 22]). Такой подход рассчитан на наихудший сценарий приема и предполагает ограниченность по норме соответствующего вектора рассогласования, при этом процедура адаптации заключается в нахождении робастного вектора отклика АР, обеспечивающего максимум выходной мощности процессора и удовлетворяющего наложенным на него ограничениям.
В настоящей работе в рамках наихудшего сценария построен адаптивный алгоритм NM–MUSIC (“normal mode based MUSIC”), предназначенный для локализации источника в акустическом волноводе с неточно известными параметрами, учитывающий эффекты рассогласования между принятым модовым составом и его расчетной моделью. Представлены результаты сравнительного анализа эффективности данного способа оценивания с методом максимума правдоподобия и традиционным методом MUSIC, осуществляющим обработку в пространстве элементов антенны. Приведена экспериментальная апробация предложенного алгоритма, демонстрирующая его работоспособность в мелководной акватории Ладожского озера.
ПОСТАНОВКА ЗАДАЧИ. ИСХОДНЫЕ СООТНОШЕНИЯ
Пусть в точках с координатами ${{{\mathbf{\theta }}}_{1}} = {{({{r}_{1}},{{z}_{1}})}^{{\text{T}}}},$ $ \ldots ,{{{\mathbf{\theta }}}_{J}} = {{({{r}_{J}},{{z}_{J}})}^{{\text{T}}}}$ волноводного канала находятся $J$ источников звука, излучающих частично-когерентные узкополосные сигналы с одинаковой несущей частотой. (Верхний индекс ${\text{T}}$ обозначает операцию транспонирования.) Прием осуществляется линейной вертикальной АР, состоящей из $N$ элементов, расположенных на горизонтах $\{ {{z}_{n}}\} _{{n = 1}}^{N}.$ (Начало координат по дальности выбрано в месте установки АР.)
В узкополосном приближении полное поле на входе АР характеризуется N-мерным вектором наблюдения ${{{\mathbf{x}}}_{l}}$:
(1)
${{{\mathbf{x}}}_{l}} = {\mathbf{G}}({\mathbf{\theta }}){{{\mathbf{s}}}_{l}} + {{{\mathbf{n}}}_{l}},\,\,\,\,l = 1,2, \ldots ,L.$Здесь $\;\;l$ – номер выборочного отсчета, ${\mathbf{\theta }} = {{({\mathbf{\theta }}_{1}^{{\text{T}}}, \ldots ,{\mathbf{\theta }}_{J}^{{\text{T}}})}^{{\text{T}}}}$ – искомый вектор размерности $2J{\kern 1pt} \times 1,$ определяющий положения источников, ${\mathbf{G}}({\mathbf{\theta }}) = [{\mathbf{g}}({{{\mathbf{\theta }}}_{1}}), \ldots ,{\mathbf{g}}({{{\mathbf{\theta }}}_{J}})]$ – передаточная матрица канала размерности $N \times J,$ ${\mathbf{g}}({{{\mathbf{\theta }}}_{j}})$ = = ${{[G(0,{{z}_{1}}\left| {{{{\mathbf{\theta }}}_{j}}} \right.), \ldots ,G(0,{{z}_{N}}\left| {{{{\mathbf{\theta }}}_{j}}} \right.)]}^{{\text{T}}}}$ – вектор отклика АР, компонентами которого являются функции Грина среды $\{ G(0,{{z}_{n}}\left| {{{{\mathbf{\theta }}}_{j}}} \right.)\} _{{n = 1}}^{N},$ связывающие координаты j-го источника с координатами приемных элементов, ${{{\mathbf{s}}}_{l}} = {{[{{s}_{1}}(l), \ldots ,{{s}_{J}}(l)]}^{{\text{T}}}}$ – вектор комплексных огибающих излученных сигналов размерности $J \times 1,$ ${{{\mathbf{n}}}_{l}}$ – вектор аддитивного шума размерности $N \times 1,$ а $L$ – объем входной выборки. Задача состоит в построении адаптивного алгоритма обработки, позволяющего по принятой выборке $\{ {{{\mathbf{x}}}_{l}}\} _{{l = 1}}^{L}$ оценить искомые координаты источника без знания истинных параметров акустического волновода.
Ниже, при нахождении ожидаемой реплики сигнала мы воспользуемся волновым подходом, в рамках которого функция Грина $G(0,{{z}_{n}}\left| {{{{\mathbf{\theta }}}_{j}}} \right.)$ может быть представлена в виде суперпозиции конечного числа $M$ распространяющихся нормальных мод [23]:
(2)
$\begin{gathered} G(0,{{z}_{n}}\left| {{{{\mathbf{\theta }}}_{j}}} \right.) = \sum\limits_{m\, = \,1}^M {{{a}_{m}}({\mathbf{\theta }}{}_{j}){{\varphi }_{m}}({{z}_{n}})} , \\ {{a}_{m}}({{{\mathbf{\theta }}}_{j}}) = \frac{{{{\varphi }_{m}}({{z}_{j}})}}{{\sqrt {8\pi {{\kappa }_{m}}{{r}_{j}}} }}\exp [(i{{\kappa }_{m}} - {{\alpha }_{m}}){{r}_{j}} + {{i\pi } \mathord{\left/ {\vphantom {{i\pi } 4}} \right. \kern-0em} 4}]. \\ \end{gathered} $Здесь ${{\varphi }_{m}}({{z}_{n}})$ – собственные функции волновода в месте расположения $n$-го гидрофона, ${{\kappa }_{m}}$ и ${{\alpha }_{m}}$ – постоянная распространения и коэффициент затухания в грунте m-ой моды. В свою очередь, для модели дна в виде однородного жидкого поглощающего полупространства с плотностью ${{\rho }_{b}}$ и продольной скоростью звука ${{c}_{l}} = {{c}_{b}}(1 - i\alpha )$ модовые коэффициенты ${{\alpha }_{m}}$ могут быть рассчитаны по формуле (см., например, [24]):
Здесь $H$ – глубина канала, ${{k}_{0}}$ – опорное волновое число звуковой волны, ${{\rho }_{w}}$ – плотность воды, ${{n}_{b}}$ – акустический показатель преломления в дне, а параметр α характеризует поглощающие свойства донных осадков и связан с измеряемым коэффициентом затухания $\beta $ соотношением $\beta = 40\pi \lg e\alpha $ дБ/λ.
В рамках волнового описания для вектора отклика АР ${\mathbf{g}}({\mathbf{\theta }})$ имеем
Здесь ${\mathbf{a}}({\mathbf{\theta }})$ – вектор размерности $M \times 1,$ компонентами которого являются амплитуды мод, определяемые формулой (2), а ${\mathbf{U}}$ – матрица модовой структуры размерности $N \times M$ с элементами ${{U}_{{nm}}} = {{\varphi }_{m}}({{z}_{n}}).$
При $N > {\kern 1pt} \,M$ матричное соотношение (3) представляет собой переопределенную линейную систему уравнений относительно вектора ${\mathbf{a}}({\mathbf{\theta }}).$ Решение этой системы, минимизирующее норму невязки $\left\| {{\mathbf{g}} - {\mathbf{Ua}}({\mathbf{\theta }})} \right\|,$ дается известным выражением
В общем случае случайный вектор ${{{\mathbf{n}}}_{l}},$ фигурирующий в (1), является суммой двух компонент: пространственно белого шума и распределенной помехи, представляющей собой динамические шумы морской среды, которые (также как и полезный сигнал) формируются преимущественно модами дискретного спектра. В рамках такого сценария результирующая пространственная ковариационная матрица аддитивного шума записывается в виде
Здесь $\sigma _{w}^{2}$ – дисперсия собственного шума АР, ${{{\mathbf{I}}}_{N}}$ – единичная матрица $N \times N,$ $\sigma _{m}^{2}$ и ${{K}_{m}}$ – уровень модового шума и его нормированная ковариационная матрица размерности $M \times M,$ а ${{( \cdot )}^{ + }}$ и $\left\langle \cdot \right\rangle $ означают операции эрмитового сопряжения и статистического усреднения, соответственно. Отметим, что для расчета матрицы ${{K}_{m}}$ можно воспользоваться моделью, предложенной в [25] (см. также [24], глава IX).
При выполнении неравенства $N > {\kern 1pt} \,M > J$ с вычислительной точки зрения пространственную обработку удобно реализовать в модовом пространстве, в котором вектор наблюдения ${{{\mathbf{y}}}_{l}}$ связан с исходным вектором (1) следующим образом:
(4)
${{{\mathbf{y}}}_{l}} = {{({{{\mathbf{U}}}^{T}}{\mathbf{U}})}^{{ - 1}}}{{{\mathbf{U}}}^{T}}{{{\mathbf{x}}}_{l}}.$Ковариационная матрица соответствующего M‑мерного вектора ${{{\mathbf{y}}}_{l}}$ равна
(5)
$\begin{gathered} {{{\mathbf{\Gamma }}}_{{\mathbf{y}}}} = {\kern 1pt} {\mathbf{A}}({\mathbf{\theta }}){\mathbf{S}}{{{\mathbf{A}}}^{ + }}({\mathbf{\theta }}) + {\mathbf{\Sigma }}, \\ {\mathbf{\Sigma }} = {{{\mathbf{U}}}^{{\dag }}}{{{\mathbf{\Gamma }}}_{{\mathbf{n}}}}{{({{{\mathbf{U}}}^{{\dag }}})}^{T}} \equiv \sigma _{w}^{2}{{({{{\mathbf{U}}}^{T}}{\mathbf{U}})}^{{ - 1}}} + \sigma _{m}^{2}{{{\mathbf{K}}}_{{\mathbf{m}}}}, \\ \end{gathered} $(6)
${{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{y}}}} = {{({{{\mathbf{U}}}^{T}}{\mathbf{U}})}^{{ - 1}}}{{{\mathbf{U}}}^{T}}{{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{x}}}}{\mathbf{U}}{{({{{\mathbf{U}}}^{T}}{\mathbf{U}})}^{{ - 1}}},\,\,\,\,{{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{x}}}} = \frac{1}{L}\sum\limits_{l = 1}^L {{{{\mathbf{x}}}_{l}}{\mathbf{x}}_{l}^{ + }} ,$Одним из наиболее распространенных способов локализации является метод MUSIC [26], являющийся обобщением метода Писаренко [27] на случай произвольной размерности шумового подпространства. При приеме сигнала на фоне коррелированных помех с известной ковариационной матрицей ${{{\mathbf{\Gamma }}}_{{\mathbf{n}}}}$ эта процедура основана на использовании информации, содержащейся в системе собственных векторов обобщенной задачи на собственные значения
(7)
${{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{x}}}}{{{\mathbf{\hat {\psi }}}}_{i}} = {{\lambda }_{i}}{{{\mathbf{\Gamma }}}_{{\mathbf{n}}}}{{{\mathbf{\hat {\psi }}}}_{i}},\,\,\,\,i = 1, \ldots N.$Здесь ${{\lambda }_{1}}, \ldots ,{{\lambda }_{N}}$ – положительные собственные числа, пронумерованные в порядке убывания (т.е. ${{\lambda }_{1}} \geqslant {{\lambda }_{2}} \geqslant \cdots \geqslant {{\lambda }_{N}}$), а ${{{\mathbf{\hat {\psi }}}}_{1}}, \ldots ,{{{\mathbf{\hat {\psi }}}}_{N}}$ – отвечающие им собственные векторы, причем ${\mathbf{\hat {\psi }}}_{i}^{ + }{{{\mathbf{\Gamma }}}_{{\mathbf{n}}}}{{{\mathbf{\hat {\psi }}}}_{j}} = {{\delta }_{{ij}}}.$
Если ранг сигнальной матрицы ${\mathbf{S}}$ равен $J,$ то число максимальных собственных чисел уравнения (7) совпадает с числом источников. Соответствующие им собственные векторы $\{ {\mathbf{\hat {\psi }}}\} _{{i = 1}}^{J}$ принадлежат сигнальному подпространству, а остальные $N - J$ младших собственных векторов $\{ {\mathbf{\hat {\psi }}}\} _{{i = J + 1}}^{N}$ формируют шумовое подпространство. В случае, когда матрица ${{{\mathbf{K}}}_{{\mathbf{m}}}},$ описывающая взаимные корреляции мод, возбуждаемых распределенными шумовыми источниками, имеет полный ранг, равный $M,$ на $N - M$ векторов $\{ {\mathbf{\hat {\psi }}}\} _{{i = M + 1}}^{N}$ накладываются дополнительные условия вида (см., например [28])
Для рассматриваемого способа обработки искомые координаты источников находятся из условия ортогональности ожидаемого вектора ${\mathbf{g}}({\mathbf{\theta }})$ к векторам шумового подпространства
и процедура оценивания сводится к поиску $J$ минимумов целевой функции ${{{\mathbf{g}}}^{ + }}({\mathbf{\theta }}){{{\mathbf{\hat {\Pi }}}}_{{\mathbf{n}}}}{\mathbf{g}}({\mathbf{\theta }}),$ где ${{{\mathbf{\hat {\Pi }}}}_{{\mathbf{n}}}} = {{{\mathbf{\hat {\Psi }}}}_{{\mathbf{n}}}}{\mathbf{\hat {\Psi }}}_{{\mathbf{n}}}^{ + },$ а ${{{\mathbf{\hat {\Psi }}}}_{{\mathbf{n}}}} = [{{{\mathbf{\hat {\psi }}}}_{{J + 1}}}, \cdots ,{{{\mathbf{\hat {\psi }}}}_{M}}]$ – матрица размерности $N \times \,\,(M - J).$ (При написании (9) учтено представление (3) и соотношение (8).)
Очевидно, что приведенный алгоритм (9) путем замен ${\mathbf{g}}({\mathbf{\theta }}) \to {\mathbf{a}}({\mathbf{\theta }}),$ $\;{{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{x}}}} \to {{{\mathbf{\hat {\Gamma }}}}_{y}}$ и ${{{\mathbf{\Gamma }}}_{{\mathbf{n}}}} \to {\mathbf{\Sigma }}$ может быть непосредственно перенесен в модовое пространство, в котором $M$-мерные собственные векторы $\{ {\mathbf{\hat {\varphi }}}\} _{{i = 1}}^{M}$, формирующие сигнальное и шумовое подпространства, являются решениями обобщенной задачи
(10)
${{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{y}}}}{{{\mathbf{\hat {\varphi }}}}_{i}} = {{\lambda }_{i}}{\mathbf{\Sigma }}{\kern 1pt} {{{\mathbf{\hat {\varphi }}}}_{i}},\,\,\,\,i = 1, \ldots ,M$и удовлетворяют условиям ортогональности ${\mathbf{\hat {\varphi }}}_{i}^{ + }{\mathbf{\Sigma }}{{{\mathbf{\hat {\varphi }}}}_{j}} = {{\delta }_{{ij}}}.$ Отметим, что соответствующие векторы ${{{\mathbf{\hat {\varphi }}}}_{i}}$ связаны с решениями уравнения (7) соотношениями ${{{\mathbf{\hat {\varphi }}}}_{i}} = {{{\mathbf{U}}}^{T}}{{{\mathbf{\hat {\psi }}}}_{i}},$ $(i = 1, \ldots ,M).$
Модовый критерий MUSIC непосредственно следует из условия (9) при подстановке в него (3):
где ${{{\mathbf{\hat {\Pi }}}}_{{\mathbf{n}}}} = {{{\mathbf{\hat {\Phi }}}}_{{\mathbf{n}}}}{\mathbf{\hat {\Phi }}}_{{\mathbf{n}}}^{ + },$ а ${{{\mathbf{\hat {\Phi }}}}_{{\mathbf{n}}}} = {{{\mathbf{U}}}^{T}}{{{\mathbf{\hat {\Psi }}}}_{{\mathbf{n}}}} \equiv [{{{\mathbf{\hat {\varphi }}}}_{{J + 1}}}, \cdots ,{{{\mathbf{\hat {\varphi }}}}_{M}}]$ – матрица размерности $M \times (M - J),$ составленная из собственных векторов уравнения (10), отвечающих наименьшим собственным числам.Таким образом, при выполнении (8) традиционный метод MUSIC (9) и его модовый аналог (11) являются эквивалентными способами оценивания. Однако, применение процедуры (11) допускает возможность модовой фильтрации, позволяющей в процессе локализации исключить моды, сильно взаимодействующие с дном, и тем самым повысить устойчивость решения обратной задачи к эффектам рассогласования.
Ниже мы построим адаптивный алгоритм NM–MUSIC, предназначенный для локализации источника в акустическом волноводе с неточно известными параметрами. С этой целью введем в рассмотрение $M$-мерные векторы ${{{\mathbf{\tilde {\varphi }}}}_{i}}$, связанные с ${{{\mathbf{\hat {\varphi }}}}_{i}}$ равенством ${{{\mathbf{\hat {\varphi }}}}_{i}} = {{{\mathbf{\Sigma }}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{{\mathbf{\tilde {\varphi }}}}_{i}},$ и сформируем из них матрицы ${{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{s}}}}$ и ${{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}}$ вида ${{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{s}}}} = [{{{\mathbf{\tilde {\varphi }}}}_{1}}, \ldots ,{{{\mathbf{\tilde {\varphi }}}}_{J}}]$ и ${{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}} = [{{{\mathbf{\tilde {\varphi }}}}_{{J + 1}}}, \cdots ,\,{{{\mathbf{\tilde {\varphi }}}}_{M}}].$ Отметим, что векторы ${{{\mathbf{\tilde {\varphi }}}}_{i}}$ взаимно ортогональны (${\mathbf{\tilde {\varphi }}}_{i}^{ + }{{{\mathbf{\tilde {\varphi }}}}_{j}} = {{\delta }_{{ij}}}$) и являются собственными векторами матрицы ${{{\mathbf{\tilde {\Gamma }}}}_{{\mathbf{y}}}} = {{{\mathbf{\Sigma }}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{y}}}}{{{\mathbf{\Sigma }}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$ (Последняя представляет собой выборочную матрицу модового вектора наблюдения ${{{\mathbf{\tilde {y}}}}_{l}},$ получаемого из (4) в результате операции выбеливания ${{{\mathbf{\tilde {y}}}}_{l}} = {{{\mathbf{\Sigma }}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{{\mathbf{y}}}_{l}}$.) В свою очередь, матрицы ${{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{s}}}}$ и ${{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}}$ удовлетворяют соотношениям ${\mathbf{\tilde {\Phi }}}_{{\mathbf{s}}}^{ + }{{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{s}}}} = {{{\mathbf{I}}}_{J}},$ ${\mathbf{\tilde {\Phi }}}_{{\mathbf{n}}}^{ + }{{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}} = {{{\mathbf{I}}}_{{M - J}}}$ и ${\mathbf{\tilde {\Phi }}}_{{\mathbf{s}}}^{ + }{{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}} = {\mathbf{0}},$ вытекающим из условия ортогональности векторов $\{ {\mathbf{\tilde {\varphi }}}\} _{{i = 1}}^{M}.$ Учитывая, что ${{{\mathbf{\hat {\Phi }}}}_{{\mathbf{n}}}} = {{{\mathbf{\Sigma }}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}},$ для проекционной матрицы ${{{\mathbf{\hat {\Pi }}}}_{{\mathbf{n}}}},$ фигурирующей в (11), получим ${{{\mathbf{\hat {\Pi }}}}_{{\mathbf{n}}}} = {{{\mathbf{\Sigma }}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{{\mathbf{\tilde {\Pi }}}}_{{\mathbf{n}}}}{{{\mathbf{\Sigma }}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$ где ${{{\mathbf{\tilde {\Pi }}}}_{{\mathbf{n}}}} = {{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}}{\mathbf{\tilde {\Phi }}}_{{\mathbf{n}}}^{ + }.$ В результате критерий 1(11) может быть переформулирован следующим образом:
(12)
$\begin{gathered} {\mathbf{\hat {\theta }}} = \arg \mathop {\max }\limits_{\mathbf{\theta }}^ {{P}_{{NM - MU}}}({\mathbf{\theta }}), \\ {{P}_{{NM - MU}}}({\mathbf{\theta }}) = \frac{{{{{\left\| {\tilde {a}({\mathbf{\theta }})} \right\|}}^{2}}}}{{{{{\tilde {a}}}^{ + }}({\mathbf{\theta }}){{{{\mathbf{\tilde {\Pi }}}}}_{{\mathbf{n}}}}\tilde {a}({\mathbf{\theta }})}}, \\ \end{gathered} $Приведенный способ локализации (12) предполагает априорное знание модового вектора $\tilde {a}({\mathbf{\theta }}).$ Однако на практике в качестве этого вектора (вследствие неполной информации о канале распространения) используется некоторый оценочный вектор ${{{\mathbf{\tilde {a}}}}_{0}}({\mathbf{\theta }}),$ рассчитываемый для номинальных акустических характеристик волновода. При наличии рассогласования между соответствующими векторами указанный метод оценивания нуждается в адаптации. Следует отметить, что для реального канала истинная матрица модовой структуры ${\mathbf{U}},$ фигурирующая в модовых алгоритмах локализации, точно неизвестна и при непосредственной реализации соответствующих алгоритмов заменяется оценочной матрицей ${{{\mathbf{U}}}_{0}},$ рассчитываемой (как и вектор ${{{\mathbf{\tilde {a}}}}_{0}}({\mathbf{\theta }})$) на основе имеющихся входных данных о параметрах морской среды. Обратим также внимание, что при переходе в модовое пространство для соответствующей шумовой матрицы ${\mathbf{\Sigma }}$ может быть получена лишь оценка ${\mathbf{\hat {\Sigma }}}$ в результате замены ${\mathbf{U}} \to {{{\mathbf{U}}}_{0}}$ в выражении (5).
ПОСТРОЕНИЕ АДАПТИВНОГО МОДОВОГО АЛГОРИТМА NM–MUSIC
При построении адаптивной процедуры NM–MUSIC, основанной на наихудшем сценарии приема, будем предполагать возможность контролируемого отклонения ожидаемого модового вектора ${{{\mathbf{\tilde {a}}}}_{0}}({\mathbf{\theta }})$ от истинного $\tilde {a}({\mathbf{\theta }})$: евклидова норма вектора рассогласования не должна превышать заданную величину, т.е. ${{\left\| {\tilde {a}({\mathbf{\theta }}) - {{{\tilde {a}}}_{0}}({\mathbf{\theta }})} \right\|}^{2}} \leqslant \varepsilon ,$ где $\varepsilon $ – положительный параметр регуляризации. Адаптация к неизвестным условиям приема состоит в нахождении нормированного робастного вектора $\tilde {a}({\mathbf{\theta }},\varepsilon ),$ обеспечивающего максимум выходной мощности (12) (или минимум целевой функции ${{{\mathbf{\tilde {a}}}}^{ + }}({\mathbf{\theta }}){{{\mathbf{\tilde {\Pi }}}}_{{\mathbf{n}}}}{\mathbf{\tilde {a}}}({\mathbf{\theta }})$) и удовлетворяющего указанному выше неравенству:
(13)
$\begin{gathered} \mathop {\min }\limits_{\tilde {a}}^ \{ {{{{\mathbf{\tilde {a}}}}}^{ + }}({\mathbf{\theta }}){{{{\mathbf{\tilde {\Pi }}}}}_{{\mathbf{n}}}}{\mathbf{\tilde {a}}}({\mathbf{\theta }})\} \,\,\,\,{\text{п р и }}\,\,\,\,{{\left\| {\tilde {a}({\mathbf{\theta }}) - {{{\tilde {a}}}_{0}}({\mathbf{\theta }})} \right\|}^{2}} \leqslant \varepsilon , \\ {{\left\| {\tilde {a}({\mathbf{\theta }})} \right\|}^{2}} = 1. \\ \end{gathered} $Условия нормировки ${{\left\| {{\mathbf{\tilde {a}}}({\mathbf{\theta }})} \right\|}^{2}} = {{\left\| {{{{{\mathbf{\tilde {a}}}}}_{0}}({\mathbf{\theta }})} \right\|}^{2}} = 1$ позволяют исключить тривиальное решение оптимизационной задачи и переписать (13) в виде
Здесь аргумент ${\mathbf{\theta }}$ опущен для краткости записи.
Для нахождения оптимального вектора ${\mathbf{\tilde {a}}}$ составим функцию Лагранжа
(14)
${\mathbf{\tilde {a}}} = \mu {{({{{\mathbf{\tilde {\Pi }}}}_{{\mathbf{n}}}} + \nu {{{\mathbf{I}}}_{M}})}^{{ - {\kern 1pt} 1}}}{{{\mathbf{\tilde {a}}}}_{0}}.$Для вычисления множителя Лагранжа $\mu $ воспользуемся соотношением
вытекающим из ограничения на норму вектора рассогласования, откуда
(15)
$\mu = \frac{{1 - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}}}{{{\mathbf{\tilde {a}}}_{0}^{ + }{{{({{{{\mathbf{\tilde {\Pi }}}}}_{n}} + \nu {{{\mathbf{I}}}_{M}})}}^{{ - 1}}}{{{{\mathbf{\tilde {a}}}}}_{0}}}},\,\,\,\,\varepsilon < 2.$В свою очередь, множитель $\nu $ находится из условия ${{\left\| {{\mathbf{\tilde {a}}}} \right\|}^{2}} = 1$ при подстановке в него (14) совместно с (15):
(16)
$\frac{{{\mathbf{a}}_{0}^{ + }{{{({{{{\mathbf{\tilde {\Pi }}}}}_{{\mathbf{n}}}} + \nu {{{\mathbf{I}}}_{M}})}}^{{ - 2}}}{{{{\mathbf{\tilde {a}}}}}_{0}}}}{{{{{[{\mathbf{\tilde {a}}}_{0}^{ + }{{{({{{{\mathbf{\tilde {\Pi }}}}}_{{\mathbf{n}}}} + \nu {{{\mathbf{I}}}_{M}})}}^{{ - 1}}}{{{{\mathbf{\tilde {a}}}}}_{0}}]}}^{2}}}} = \frac{1}{{{{{(1 - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2})}}^{2}}}}.$Для определения $\nu $ воспользуемся известной формулой обращения матриц, согласно которой ${{({\mathbf{A}} + {\mathbf{BC}})}^{{ - 1}}}$ = ${{{\mathbf{A}}}^{{ - 1}}} - {{{\mathbf{A}}}^{{ - 1}}}{\mathbf{B}}{{({\mathbf{I}} + {\mathbf{C}}{{{\mathbf{A}}}^{{ - 1}}}{\mathbf{B}})}^{{ - 1}}}{\mathbf{C}}{{{\mathbf{A}}}^{{ - 1}}}.$ Полагая ${\mathbf{A}} = \nu {{{\mathbf{I}}}_{M}},$ ${\mathbf{B}} = {{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}},$ ${\mathbf{C}} = {\mathbf{\tilde {\Phi }}}_{{\mathbf{n}}}^{ + }$ и учитывая, что ${\mathbf{\tilde {\Phi }}}_{{\mathbf{n}}}^{ + }{{{\mathbf{\tilde {\Phi }}}}_{{\mathbf{n}}}} = {{{\mathbf{I}}}_{{M - J}}},$ получим
(17)
$\begin{gathered} {{({{{{\mathbf{\tilde {\Phi }}}}}_{{\mathbf{n}}}}{\mathbf{\tilde {\Phi }}}_{{\mathbf{n}}}^{ + } + \nu {{{\mathbf{I}}}_{M}})}^{{ - 1}}} = \frac{1}{\nu }\left[ {{{{\mathbf{I}}}_{M}} - \frac{{{{{{\mathbf{\tilde {\Phi }}}}}_{{\mathbf{n}}}}{\mathbf{\tilde {\Phi }}}_{{\mathbf{n}}}^{ + }}}{{\nu + 1}}} \right] \equiv \\ \equiv {{\nu }^{{ - 1}}}{{(1 + \nu )}^{{ - 1}}}({{{{\mathbf{\tilde {\Pi }}}}}_{{\mathbf{s}}}} + \nu {{{\mathbf{I}}}_{M}}), \\ \end{gathered} $(18)
${{\nu }^{2}} + 2\nu {{V}_{0}} - \frac{{{{{(1 - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2})}}^{2}}{{V}_{0}} - V_{0}^{2}}}{{\varepsilon - {{{{\varepsilon }^{2}}} \mathord{\left/ {\vphantom {{{{\varepsilon }^{2}}} 4}} \right. \kern-0em} 4}}} = 0,$(19)
$\begin{gathered} \nu \equiv \nu ({\mathbf{\theta }},\varepsilon ) = {{V}_{0}}({\mathbf{\theta }}) - 1 + \frac{{\sqrt {{{V}_{0}}({\mathbf{\theta }})[1 - {{V}_{0}}({\mathbf{\theta }})]} }}{{\sqrt {{{\rho }^{2}} - 1} }}, \\ \rho = \frac{1}{{1 - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}}}. \\ \end{gathered} $Знание $\nu $ позволяет на основании (14), (15) и (17) найти робастный модовый вектор
рассчитать целевую функцию ${{V}_{{NM - MU}}}({\mathbf{\theta }},\varepsilon )$ = = ${{{\mathbf{\tilde {a}}}}^{ + }}({\mathbf{\theta }},\varepsilon ){{{\mathbf{\tilde {\Pi }}}}_{{\mathbf{n}}}}{\mathbf{\tilde {a}}}({\mathbf{\theta }},\varepsilon )$ адаптивного алгоритма NM–MUSIC и в итоге оценить искомые координаты источников путем поиска максимумов выходной мощности ${{P}_{{NM - MU}}}({\mathbf{\theta }},\varepsilon )$ = ${1 \mathord{\left/ {\vphantom {1 {{{V}_{{NM - MU}}}({\mathbf{\theta }},\varepsilon )}}} \right. \kern-0em} {{{V}_{{NM - MU}}}({\mathbf{\theta }},\varepsilon )}}$ или из эквивалентного критерия
(20)
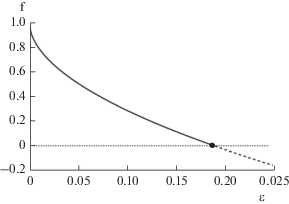
$\begin{gathered} {\mathbf{\hat {\theta }}} = \arg \mathop {\min }\limits_{\mathbf{\theta }}^ {{V}_{{NM - MU}}}({\mathbf{\theta }},\varepsilon ), \\ {{V}_{{NM - MU}}}({\mathbf{\theta }},\varepsilon ) = {{f}^{2}}({\mathbf{\theta }},\varepsilon ){{V}_{0}}({\mathbf{\theta }}), \\ \end{gathered} $Рис. 1.
Поведение функции $f{\kern 1pt} ({{V}_{0}}({\mathbf{\theta }}),\varepsilon )$ в зависимости от $\varepsilon $ при ${{V}_{0}}({\mathbf{\theta }}) = 0.18.$
Оценка ${\mathbf{\hat {\theta }}},$ при которой целевая функция в (20) достигает минимума, удовлетворяет соотношению $V_{{NM - MU}}^{'}({\mathbf{\hat {\theta }}},\varepsilon ) = 0,$ где $V_{{NM - MU}}^{'}$ означает взятие градиента ${{V}_{{NM - MU}}}$ по ${\mathbf{\hat {\theta }}}.$ Вычисление приводит к результату
Очевидно, что при выполнении неравенства
(21)
$[2{{V}_{0}}({\mathbf{\theta }})\partial {{f({\mathbf{\theta }},\varepsilon )} \mathord{\left/ {\vphantom {{f({\mathbf{\theta }},\varepsilon )} {\partial {{V}_{0}}}}} \right. \kern-0em} {\partial {{V}_{0}}}} + f({\mathbf{\theta }},\varepsilon )]f({\mathbf{\theta }},\varepsilon ) > 0$минимизация ${{V}_{{NM - NM}}}({\mathbf{\theta }},\varepsilon )$ эквивалентна минимизации ${{V}_{0}}({\mathbf{\theta }}).$ Простой анализ показывает, что неравенство (21) будет удовлетворено при любых ${\mathbf{\theta }},$ если $f{\kern 1pt} ({{V}_{0}}({\mathbf{\theta }}),\varepsilon ) > 0$ или ${{\varepsilon }^{2}} - 4\varepsilon + 4{{V}_{0}}({\mathbf{\theta }}) < 0,$ откуда
Таким образом, при соблюдении (22) адаптивный алгоритм NM–MUSIC приводит к тем же оценкам координат, что и его неадаптивная версия. Однако при конечном $\varepsilon ,$ принадлежащим интервалу (22), наличие множителя ${{f}^{2}}({\mathbf{\theta }},\varepsilon )$ в критерии (20) заметно уменьшает целевую функцию ${{V}_{{NM - NM}}}({\mathbf{\theta }},\varepsilon ),$ обеспечивая резкий максимум выходной мощности в области локализации источника. Последнее означает, что робастная процедура обладает повышенной разрешающей способностью и позволяет значительно подавить ложные пики на выходе процессора, затрудняющие получение корректного решения обратной задачи.
При $\varepsilon > 2[1 - \sqrt {1 - {{V}_{0}}({\mathbf{\theta }})} ]$ множитель Лагранжа $\nu ,$ определяемый формулой (19), становится отрицательным. В этом случае решение исходной оптимизационной задачи (13) не зависит от $\varepsilon $ и дается выражением
Это решение обращает в ноль целевую функцию в (13), удовлетворяет условию нормировки и для рассматриваемых ε автоматически гарантирует выполнение ограничения на допустимую норму рассогласования. Очевидно, что в процессе поиска координат параметр регуляризации ε должен удовлетворять неравенству (22), поскольку в противном случае $V{}_{{NM - MU}}({\mathbf{\theta }},\varepsilon ) \equiv 0.$
Для реализации предложенного адаптивного модового алгоритма используется следующая последовательность операций.
1. Для номинальных параметров акустического волновода и заданной геометрии АР строятся матрица модовой структуры ${{{\mathbf{U}}}_{0}}$ и псевдообратная к ней (с использованием при необходимости процедуры регуляризации); в области поиска рассчитываются ожидаемые модовые векторы ${{a}_{0}}({\mathbf{\theta }}).$
2. По принятой реализации входного процесса с помощью формулы (6) (в которой матрица ${\mathbf{U}}$ заменена на ${{{\mathbf{U}}}_{0}}$) вычисляется выборочная ковариационная матрица ${{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{y}}}}$ модового вектора наблюдения, и в соответствии с определением ${\mathbf{\hat {\Sigma }}} = {\mathbf{U}}_{0}^{{\dag }}{{{\mathbf{\Gamma }}}_{{\mathbf{n}}}}{{({\mathbf{U}}_{0}^{{\dag }})}^{T}}$ находится оценка шумовой матрицы в модовом представлении.
3. Формируется матрица ${{{\mathbf{\tilde {\Gamma }}}}_{{\mathbf{y}}}} = {{{\mathbf{\hat {\Sigma }}}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{y}}}}{{{\mathbf{\hat {\Sigma }}}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$ и проводится ее спектральное разложение. Найденные собственные векторы шумового подпространства используются для построения проекционной матрицы ${{{\mathbf{\tilde {\Pi }}}}_{{\mathbf{n}}}}.$
4. На основании (20) определяется адаптивная целевая функция ${{V}_{{NM - MU}}}({\mathbf{\theta }},\varepsilon )$ модового алгоритма NM–MUSIC, находятся ее минимумы, служащие оценками искомых координат.
В заключение этого раздела отметим, что при использовании адаптивного метода MUSIC, осуществляющего обработку в пространстве элементов АР, соответствующие координаты источников могут быть оценены из условия (20), в котором необходимо сделать замены
РЕЗУЛЬТАТЫ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Приведем результаты статистического моделирования, иллюстрирующие работоспособность предложенного способа оценивания (20), и сравним его эффективность с адаптивным алгоритмом MUSIC, осуществляющим обработку принятого сигнала в пространстве элементов АР, а также с модовым методом максимума правдоподобия, реализованном в [29] применительно к морским условиям. Согласно последнему методу положения источников определяются из следующего критерия:
(23)
${\mathbf{\hat {\theta }}} = \arg \mathop {\max }\limits_{\mathbf{\theta }}^ {{P}_{{{\text{ML}}}}}({\mathbf{\theta }}),\,\,\,\,{{P}_{{{\text{ML}}}}}({\mathbf{\theta }}) = Tr({{{\mathbf{\hat {\Sigma }}}}^{{ - 1}}}{{{\mathbf{P}}}_{{{\mathbf{A}}({\mathbf{\theta }})}}}{{{\mathbf{\hat {\Gamma }}}}_{y}}),$Подчеркнем, что адаптивный метод MUSIC по умолчанию учитывает все распространяющиеся моды акустического волновода, а процедура (23) опирается на априорное знание среды распространения.
Для определенности рассмотрим акваторию Баренцева моря, в которой звуковое поле создается двумя некоррелированными источниками, расположенными на глубинах 70 и 40 м и излучающими узкополосные сигналы с несущей частотой 250 Гц.
Истинный профиль скорости звука, измеренный в данном регионе, показан на рис. 2 сплошной линией (пунктиром показан профиль, используемый при расчетах). В рамках численного эксперимента глубина моря принималась равной $H = 160$ м; дно моделировалось жидким поглощающим полупространством с плотностью ${{\rho }_{b}} = 1.8$ г/см3, скоростью звука ${{c}_{b}} = 1750$ м/с и коэффициентом поглощения в грунте $\beta = 0.13$ дБ/λ, а при расчете ожидаемого модового вектора в качестве номинальных геоакустических параметров использовались значения $H = 162.5$ м, ${{\rho }_{b}} = 1.75$ г/см$^{3}$, ${{c}_{b}} = 1735$ м/с и $\beta = 0.1$ дБ/λ. Полное число мод $M$ для рассматриваемых акустических характеристик канала и несущей частоты составляло 28.
Предполагалось, что прием осуществлялся линейной вертикальной антенной (с центром на глубине 80 м), состоящей из 32 элементов, расположенных через 3 м. Дистанция между источниками и антенной составляла соответственно 15 и 10 км. При моделировании комплексные огибающие излученных сигналов и компоненты шума рассматривались как статистически независимые гауссовские случайные процессы, при этом сигнальная матрица задавалась в виде ${\mathbf{S}} = diag(\sigma _{1}^{2},\sigma _{2}^{2}),$ где $\sigma _{1}^{2}$ и $\sigma _{2}^{2}$ – уровни излучения, а для ковариационной матрицы модового шума, следуя [28, 29], использовалось представление ${{{\mathbf{K}}}_{m}} = {{{\mathbf{I}}}_{M}}.$ Для определенности считалось, что уровень динамического шума $\sigma _{m}^{2}$ в 4 раза превосходит уровень $\sigma _{w}^{2}$ пространственно белого шума. Входные отношения сигнал/шум, определяемые соотношениями
считались одинаковыми, т.е. SNR1 = SNR2 = = SNR. Поиск источников по дальности осуществлялся в диапазоне $(5 - 18)$ км с шагом 10 м, а по глубине – в интервале $(1 - 141)$ м с шагом 1 м.
Для рассматриваемого сценария на рис. 3 построен спектр собственных значений матрицы ортогональности мод $U_{0}^{T}{{{\mathbf{U}}}_{0}}.$ Из приведенного графика видно, что из 28 компонент этого спектра первые 15 практически одинаковы, а последние 9 близки к нулю. Следовательно, соответствующая матрица $U_{0}^{T}{{{\mathbf{U}}}_{0}}$ плохо обусловлена и при ее обращении необходима регуляризация. Ниже при нахождении матрицы, псевдообратной к ${{{\mathbf{U}}}_{0}}$, использовалось сингулярное разложение, учитывающее 15 наибольших собственных чисел. (В этом случае матрица $U_{0}^{T}{{{\mathbf{U}}}_{0}}$ близка к единичной, а выделяемые моды ортогональны на апертуре антенны.)
Одной из важных характеристик алгоритма является достигаемая с его помощью вероятность правильной локализации, определяемая как доля реализаций, для которых ошибки в совместном определении положений источников по дистанции и глубине не превосходят заданных значений $\delta {\kern 1pt} r$ и ${\delta }z.$ В качестве оценки соответствующей вероятности бралась величина
Для используемых методов оценивания на рис. 4a представлены результаты расчета указанной вероятности в зависимости от $SNR{\kern 1pt} ,$ при этом выборочная ковариационная матрица формировалась по $L = 100$ временным отсчетам общей длительностью 60 секунд. На рис. 4б показана зависимость ${{\hat {P}}_{{CL}}}$ от числа выборок $L$, по которым оценивается ковариационная матрица входного процесса, при $SNR = 0$ дБ. При вычислениях значения ${\delta }r$и ${\delta }z$ принимались соответственно равными 400 и 2 м. Кривая 1 на рис. 4 отвечает методу максимума правдоподобия (23), а кривые 2 и 3 – робастным алгоритмам MUSIC (при $\varepsilon = 0.3$), осуществляющим обработку в пространстве элементов АР и модовом пространстве, соответственно. Для рассматриваемого численного эксперимента, как следует из рис. 4, обычный алгоритм MUSIC незначительно уступает в эффективности модовому аналогу, однако его вычислительные затраты в разы больше, чем у MN–MUSIC. Что касается метода максимума правдоподобия, использующего неадаптивные ожидаемые модовые векторы, то он не в состоянии обеспечить гарантированной локализации источника для всех рассматриваемых значений $SNR$ и $L$.
ЭКСПЕРИМЕНТАЛЬНАЯ АПРОБАЦИЯ МЕТОДА
Для верификации предложенного метода локализации были использованы экспериментальные данные, полученные в августе 2014 года на Ладожском озере в стационарных условиях. Профиль скорости звука в месте проведения работ показан на рис. 5. На глубину 12 м был опущен источник, работавший одновременно на пяти частотах в килогерцовом диапазоне. Прием осуществлялся на вертикальную антенну (с центром на глубине 10.1 м), состоящую из 96 элементов, расположенных эквидистантно с шагом 0.2 м. Дистанция между источником и антенной была равной 150 м. Входное отношение сигнал/шум составляло порядка 15 дБ. Точные значения параметров дна в рассматриваемой акватории априори неизвестны и при моделировании ожидаемого модового вектора считалось, что осадочные породы представляли собой илы с характерными значениями плотности 1.2 г/см$^{3}$ и скорости звука 1450 м/с. Коэффициент затухания в грунте $\beta $ при вычислениях брался 0.1 дБ/λ. Выборочная ковариационная матрица оценивалась по первым 300 отсчетам, взятым из 2-х минутного фрагмента записи. При расчетах поиск источника по дальности осуществлялся в диапазоне (0–300) м с шагом 1 м, а по глубине – в интервале (0–18) м с шагом 0.5 м.
Ниже мы приведем решение задачи локализации источника, работавшего на несущей частоте 5025 Гц22, полагая что полезный сигнал регистрируется на фоне белого шума. Для данной частоты и указанных акустических характеристик водоема полное число распространяющихся мод составляло 12, профили которых в месте установки антенны представлены на рис. 6а. Поскольку в описываемом эксперименте приемная антенна перекрывала весь канал, то при выделении модового состава из исходного вектора наблюдения не требовалась процедура регуляризации. Средние интенсивности разрешаемых мод (нормированные на суммарную интенсивность), оцениваемые как диагональные элементы выборочной матрицы ${{{\mathbf{\hat {\Gamma }}}}_{{\mathbf{y}}}},$ показаны на рис. 6б. При построении ожидаемого модового вектора исключались компоненты с номерами $m > 6,$ так что в соответствующих алгоритмах локализации учитывались только наиболее энергонесущие моды, в наименьшей степени взаимодействующие со дном.
Рис. 6.
(а) Профили выделяемых мод в месте установки приемной антенны и (б) их нормированные средние интенсивности.

На рис. 7а изображена нормированная (на максимальное значение) выходная мощность ${{P}_{{{\text{ML}}}}}({\mathbf{\theta }}),$ построенная согласно (23) с использованием ожидаемого модового вектора ${{{\mathbf{a}}}_{0}}({\mathbf{\theta }}),$ рассчитанного для номинальных параметров волновода. Для сравнения на рис. 7б и 7в показано поведение нормированной выходной мощности адаптивных процессоров MUSIC, осуществляющих обработку в модовом пространстве и в пространстве элементов антенны. (При расчетах параметр регуляризации ε в рассматриваемых адаптивных алгоритмах выбран 0.15 и 0.9, соответственно.)
Рис. 7.
Нормированная мощность на выходе процессора, использующего (а) метод максимума правдоподобия, (б) адаптивную модовую и (в) стандартную версии MUSIC, в зависимости от ожидаемого положения источника.

Из приведенных графиков видно, что в первых двух случаях положение абсолютного максимума выходного эффекта наблюдается при $\hat {r} = 148$ м и $\hat {z} = 11$ м, что довольно близко к истинным значениям координат источника. Однако применение метода максимума правдоподобия приводит к существенному уширению основного пика (области локализации), а следовательно, к значительному снижению разрешающей способности АР. В то же время при использовании традиционного алгоритма MUSIC, как следует из рис. 7в, наблюдается появление дополнительного ложного пика при $\hat {r} = 118$ и $\hat {z} = 11$ м, уровень которого превышает уровень правильного. Это можно объяснить тем, что традиционный метод по умолчанию учитывает все моды волновода, включая высокие. Последнее обстоятельство не позволяет обеспечить устойчивость данного способа локализации к детерминированному рассогласованию, обусловленному неточным знанием геоакустических характеристик донных осадков. Отметим также, что адаптивная процедура MN–MUSIC без привлечения модовой фильтрации приводит к точно такому же некорректному решению, что и стандартный алгоритм MUSIC.
ЗАКЛЮЧЕНИЕ
В настоящей работе построен адаптивный модовый алгоритм NM–MUSIC, позволяющий локализовать неподвижный источник с использованием вертикальной АР, работающей в условиях неполной информации о среде распространения. Путем статистического моделирования установлено, что данный способ обладает наилучшими потенциальными возможностями и обеспечивает бóльшую вероятность правильной локализации по сравнению с методами максимума правдоподобия и MUSIC.
Приведена верификация предложенного метода с использованием экспериментальных данных, полученных в Ладожском озере. Показано, что соответствующий модовый алгоритм характеризуется достаточно высокой разрешающей способностью и гарантирует большую устойчивость процедуры оценивания к детерминированному рассогласованию, обусловленному неточным знанием геоакустических характеристик донных осадков, по сравнению с традиционным методом MUSIC, осуществляющим обработку в пространстве элементов АР.
Работа выполнена в рамках государственного заказа ИПФ РАН (тема № 0035–2014–0011).
Список литературы
Baggeroer A.B., Kuperman W.A., Mikhalevsky P.N. An overview of matched field methods in ocean acoustics // IEEE J. Oceanic Eng. 1993. V. 18. P. 401–423.
Сазонтов А.Г., Малеханов А.И. Cогласованная пространственная обработка сигналов в подводных звуковых каналах (Обзор) // Акуст. журн. 2015. Т. 61. № 2. 233–253.
Richardson M., Nolte L.W. A posteriori probability source localization in an uncertain sound speed, deep ocean environment // J. Acoust. Soc. Amer. 1991. V. 89. № 5. P. 2280.
Shorey J.A., Nolte L.W., Krolik J.L. Computationally efficient Monte Carlo estimation algorithms for matched field processing in uncertain ocean environments // J. Comp. Acoust. 1994. V. 2. № 3. P. 285–314.
Harrison B.F., Vaccaro R.J., Tufts D.W. Robust matched-field localization in uncertain ocean environments // J. Acoust. Soc. Amer. 1998. V. 103. № 6. P. 721–3724.
Tabrikian J., Krolik J.L., Messer H. Maximum–likelihood source localization in an uncertain shallow–water waveguide // J. Acoust. Soc. Amer. 1997. V. 101. № 1. P. 241–249.
Shang E.C. Source depth estimation in waveguides // J. Acoust. Soc. Amer. 1985. V. 77. № 4. P. 1413–1418.
Shang E.C., Clay C.S., Wang Y.Y. Passive harmonic ranging in waveguides by using mode filter // J. Acoust. Soc. Amer. 1986. V. 78. № 1. P. 172–175.
Shang E.C. An efficient high-resolution method of source localization processing in mode space // J. Acoust. Soc. Amer. 1989. V. 86. № 5. P. 1960–1967.
Yang T.C. A method of range and depth estimation by modal decomposition // J. Acoust. Soc. Amer. 1987. V. 82. № 5. P. 1736–1745.
Wilson G.R., Koch R.A., and Vidmar P.J. Matched mode localization // J. Acoust. Soc. Amer. 1988. V. 84. № 1. P. 310–320.
Yang T.C. Modal beamforming array gain // J. Acoust. Soc. Amer. 1989. V. 85. № 1. P. 146–151.
Hinich M.J., Sullivan E.J. Maximum-likelihood passive localization using mode filtering // J. Acoust. Soc. Amer. 1989. V. 85. №. 1. P. 214–219.
Yang T.C. Modal shading coefficients for high resolution source-depth localization // J. Acoust. Soc. Amer. 1990. V. 87. № 2. P. 668–672.
Yang T.C. Effectiveness of mode filtering: A comparison of matched-field and matched-mode processing // J. Acoust. Soc. Amer. 1990. V. 87. № 5. P. 2072–2084.
Shang E.C., Wang Y.Y. Environmental mismatching effects on source localization processing in mode space // J. Acoust. Soc. Amer. 1991. V. 89. № 5. P. 2285–2290.
Jesus S.M. Normal mode matching localization in shallow water: Environmental and system mismatch // J. Acoust. Soc. Amer. 1991. V. 90. № 4. P. 2034–2041.
Bogart C.W., Yang T.C. Comparative performance of matched-mode and matched-field localization in a range dependent environments // J. Acoust. Soc. Amer. 1992. V. 92. № 4. P. 2051–2068.
Lin Y.-T., Newhall A.E., Lynch J.F. Low-frequency broadband sound source localization using an adaptive normal mode back-propagation approach in a shallow-water ocean // J. Acoust. Soc. Amer. 2012. V. 131. № 2. P. 1798.
Yang T.C. Data-based matched-mode source localization for a moving source // J. Acoust. Soc. Amer. 2014. V. 135. № 3. P. 1218.
Robust Adaptive Beamforming / Eds. by Li J. and Stoica P. Published by John Wiley & Sons, Inc. Hoboken, New Jersey, 2006. 422 p
Vorobyov S.A. Principles of minimum variance robust adaptive beamforming design // Signal Processing. 2013. V. 93. № 12. P. 3264–3277.
Бреховских Л.М., Лысанов Ю.П. Теоретические основы акустики океана. Л.: Гидрометеоиздат. 1982. 264 с.
Katsnelson B., Petnikov V., Lynch J. Fundamentals of Shallow Water Acoustics. Springer, 2012. 540 p.
Kuperman W.A., Ingenito F. Spatial correlation of surface generated noise in a stratified ocean // J. Acoust. Soc. Amer. 1980. V. 67. № 6. P. 1988–1996.
Schmidt R.O. Multiple emitter location and signal parameter estimation // IEEE Trans. on Antennas and Propagation. 1986. V. 34. № 3. P. 276–280.
Pisarenko V.F. The retrieval of harmonics from a covariance function // Geophys. J. Roy. Astronom. Soc. 1973. V. 33. №. 3. P. 347–366.
Byrne C.L., Brent R.T., Feuillade C., and DelBalzo D.R. A stable data-adaptive method for matched field processing in acoustic waveguides // J. Acoust. Soc. Amer. 1990. V. 87. № 4. P. 2493–2502.
Mirkin A.N., Sibul L.H. Maximum likelihood estimation of the locations of multiple sources in an acoustic waveguide // J. Acoust. Soc. Amer. 1994. V. 95. № 2. P. 877–888.
Сазонтов А.Г., Смирнов И.П., Чащин А.С. Локализация когерентного источника излучения в мелководном канале с использованием частично калиброванной адаптивной антенной решетки // Известия Вузов. Радиофизика. 2016. Т. 59. № 2. С. 99–107.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал








