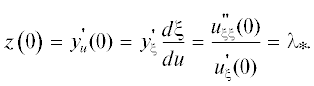Акустический журнал, 2019, T. 65, № 6, стр. 816-827

ВВЕДЕНИЕ

Атмосфера и ионосфера являются динамически взаимодействующими областями окружающей Землю среды. Возмущения на отдельном уровне этой системы переносятся на другие высотные уровни. Значительную информацию о механизмах взаимодействия в цепи ионосфера–атмосфера дают эксперименты со взрывами на различных высотных уровнях. В 1988–91-м гг. в Волгоградской области были осуществлены контролируемые опыты со взрывами и инжекциями вещества на высотах 120 < H < 150 км, проведенные с помощью геофизических ракет. Опыты осуществлялись с целью изучения процесса переноса энергии возмущений с ионосферных высот до земной поверхности [1]. Некоторые результаты обсуждаются в настоящей работе.

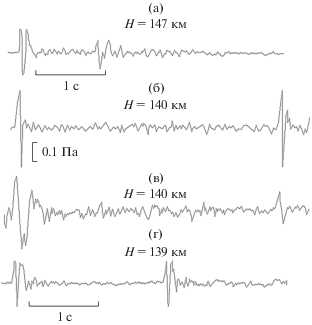
Эквивалентная энергия высотных взрывных источников составляла Q = 5–15 кг тротила (ТНТ) (1 кг ТНТ = 4.2 × 10⁶ Дж). Приемники акустических волн располагались на земной поверхности на незначительных удалениях от проекций центров взрывов на земную поверхность. Зарегистрированные акустические сигналы имели сложную структуру и представляли собой последовательность отдельных приходов, разделенных во времени на несколько секунд. Причем в каждом приходе поздние акустические импульсы обладали существенно меньшей амплитудой, чем ранние. Характерные записи сигналов от высотных взрывов, взятые из работы [1], демонстрируются на рис. 1. Проанализируем представленные в [1] экспериментальные записи акустических сигналов.

2. АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

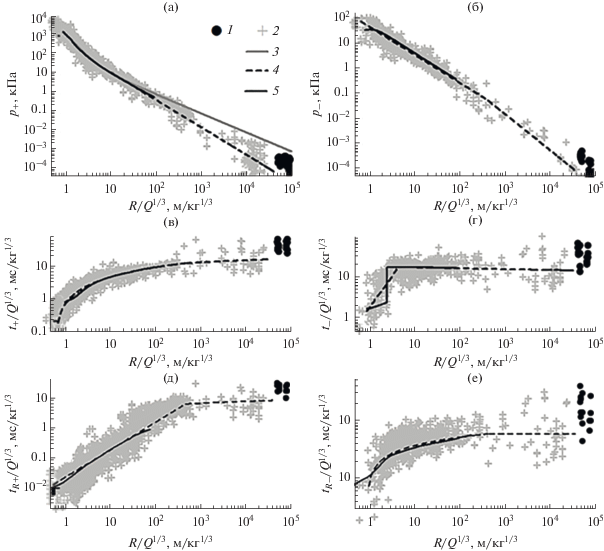
Поскольку рассматриваемые точечные импульсные источники находились в безграничном пространстве, то амплитудно-временные параметры первых двух импульсов в каждом приходе представим в приведенных к значениям энергии источника величинах типа Ф/Q^1/3 (Ф – анализируемый параметр или удаление R = H – z от центра взрыва, z – высота точки наблюдения над земной поверхностью). Обработанные таким образом значения амплитуд положительной P₊ и отрицательной P_– мод каждого импульса, длительностей t₊ и t_– этих мод, а также времен достижения t_R+ и t_R– давлением амплитудных значений P₊ и P_– в этих модах отмечены символами (1) на рис. 2.

Здесь же для сравнения символами (2) показаны значения указанных параметров, полученные в [2–4] при обработке опытных эпюр избыточного давления p(t) взрывных волн, распространяющихся вдоль земной поверхности в условиях нейтральной или неустойчивой стратификации пограничного слоя атмосферы (энергии взрывов химических ВВ составляют 10^–3 < Q < 10⁶ кг ТНТ). Линией (3) представлена известная зависимость М.А. Садовского

асимптотически (R → ∞) учитывающая только пространственное расхождение взрывных волн, но не учитывающая факта значительной диссипации энергии волн в акустической области. Наконец, линиями (4) демонстрируются аппроксимационные зависимости для экспериментальных данных (2) [2–4]:

Различие между опытными данными (1) и (2) проявляется в значениях характерных амплитуд и длительностей зарегистрированных акустических импульсов. Так, в соответствии с эмпирическими зависимостями (2)–(7), если бы акустические волны от взрывов 5–15 кг ТНТ распространялись вдоль земной поверхности, то их амплитуды P₊ и P_– должны были бы в среднем составлять 0.03…0.05 Па, а их длительности, равные сумме t₊ + t_–, – 0.05–0.07 с. В реальных же экспериментах амплитуды импульсов имели на порядок большие значения – 0.2–0.5 Па, а их длительности также были существенно больше – 0.09–0.38 с. Данное сравнение обнаруживает незначительное поглощение коротких акустических импульсов (имеющих характерные частоты процесса 2.6–11 Гц) по мере их распространения с высот ионосферы к земной поверхности, по сравнению со случаем распространения аналогичных импульсов в плотных слоях атмосферы.

Анализируя опытные данные, представленные в [1], оценим количество энергии, доставляемой волной от высотного взрыва к земной поверхности. Для количественного анализа возьмем график на рис. 1а. Здесь видно два прихода – два цуга волн – с временным интервалом между ними примерно 1 с. Длительность каждого цуга примерно 0.3–0.5 с. Найдем поток энергии, переносимой акустической волной, взяв интеграл

Здесь p – избыточное давление в акустической волне, c₀ = 340 м/с и ρ₀ = 1.29 кг/м³ – скорость звука и плотность воздуха у земной поверхности. Деление величины p на 4 учитывает двухкратное увеличение интенсивности p слабой волны при ее отражении от земной поверхности.

В результате получаем в первом приходе П_Е ≈ ≈ 5.2 × 10^–6 Дж/м², а во втором приходе П_Е = 1.8 × × 10^–6 Дж/м². Далее интегрируем поток энергии П_Е по сфере радиусом R = 1.47 × 10⁵ м, получаем энергию E = 2πR² П_Е в первом цуге волн 1.4 × 10⁶ Дж, а во втором цуге – 4.9 × 10⁵ Дж. Суммарная энергия, переносимая двумя пакетами волн на расстояние R = 147 км, составляет 1.9 × 10⁶ Дж, что эквивалентно по энергии заряду тротила массой ≈0.45 кг. Таким образом, до поверхности Земли дошло ≈9% от энергии взрыва Q = 5 кг ТНТ. От взрывов энергией Q = 15 кг ТНТ на высотах H = = 140 км, характеризуемых графиками на рис. 1б и 1в, до поверхности Земли дошло, соответственно, около 7.5 и 14.4% от выделившейся энергии Q. Наконец, от взрыва на высоте H = 139 км в соответствии с графиком на рис. 1г до поверхности Земли дошло ≈8.9% от энергии взрыва Q = 5 кг ТНТ. Данные значения переносимой энергии намного больше, чем это следует из оценок для случая распространения взрывной волны у поверхности Земли.

Чтобы в этом убедиться, воспользуемся зависимостями (2)–(5) амплитудно-временных параметров P₊ и P_–, t₊/Q^1/3 и t_–/Q^1/3 от приведенного расстояния R/Q^1/3. При определении потока энергии взрывной волны на единицу площади используем формулу

Оценки по (8) показывают, что на расстояния в R = 139–147 км должно доходить только около 0.036–0.05% от энергии взрыва Q = 5–15 кг ТНТ. Это в 250–290 раз меньше энергии, перенесенной взрывными волнами, представленными графиками p(t) на рис. 1. Другими словами, в рассматриваемых опытах значительная часть начальной энергии высотного взрыва доходит до земной поверхности, не испытывая при этом существенного поглощения. Следует заметить, что при ракетно-гранатном методе зондирования атмосферы также не наблюдается существенного поглощения звука от высотных взрывов [5].

В целях качественного объяснения рассматриваемого эффекта обратимся к результатам работ [6–8]. В них на основе линеаризованных уравнений газодинамики идеального газа исследовано вертикальное распространение акустических волн в неоднородной сжимаемой атмосфере. Показано, что для вертикальной монохроматической волны длительностью t₊ + t_– < 200 с земная атмосфера почти полностью прозрачна, т.е. такая волна практически не отражается на неоднородностях атмосферы. Поскольку авторы [6–8] рассматривают идеальный газ, то акустическая волна у них не испытывает поглощения. В результате в пределе (R → ∞) амплитуда волны должна снижаться как P₊ ∼ R^–1 (это примерно демонстрируется линией (3) на рис. 2а), плотность потока энергии волны – как

а энергия волны должна изменяться как

Другими словами, энергия в волне в пределе (R → ∞) должна переноситься по пространству не затухая, а только распределяясь по все большей сфере (с увеличением R). Исходя из этого авторы [6–8] и делают вывод, что акустические волны при своем вертикальном распространении в атмосфере способны практически без заметного затухания переносить энергию на большие высоты. В рассматриваемом нами случае акустические волны должны также без заметного затухания переносить энергию в обратном направлении – с ионосферных высот к земной поверхности.

Вместе с тем, линия (4) на рис. 2а демонстрирует, что в соответствии с формулой (2) в однородном безграничном воздухе у акустической волны амплитуда затухает как P₊ ∼ R^–1.45. О том, что формулы (2)–(7) описывают изменение параметров волны для случая ее распространения именно в безграничном однородном воздухе, свидетельствует удовлетворительное соответствие линий (4) и (5) на рис. 2. Представленные здесь линиями (5) зависимости получены посредством интегрирования уравнений нелокальной трехпотоковой (НЛТП) газодинамической модели трансформации сильной взрывной волны в безграничном однородном воздухе в акустическое возмущение: уравнений неразрывности, движения и внутренней энергии [9, 10],

Замыкает систему (10) уравнение состояния воздуха.

В основу уравнений НЛТП-модели положена гипотеза о возникновении локальных зон интенсивного развития неустойчивости Кельвина–Гельмгольца во фронтовой области волны при сильном сжатии в ней воздуха, когда градиенты избыточного давления составляют 10⁵–10⁷ Па/м [9]. В результате возникающих пульсирующих микроструй происходит нарушение лагранжевости течения газа и возникает обмен массой, импульсом и энергией на мезоуровне между соседними слоями воздуха, что и приводит к расширению фронтовой области взрывной волны. Определяющие функциональные параметры НЛТП-модели (10) f_u, α, δ и f(r' – r) представляют собой, соответственно, взаимосвязь u' = f_uu между средней скоростью пульсирующих струй u' и средней массовой скоростью потока u, относительное количество струй α, покидающих слой воздуха против и по течению потока, полуширину δ зоны локального пульсационного обмена, а также функцию плотности распределения f(r' – r) пульсационных потоков массы, импульса и энергии по соседним слоям воздуха.

Вместе с тем, в классическом случае законы сохранения массы, импульса и энергии формируются для индивидуальных лагранжевых объемов среды. Далее, с использованием эквивалентности лагранжевого и эйлерова способов описания движения получаются уравнения газовой динамики в эйлеровых координатах. В случае движения с развитой неустойчивостью, как в рассматриваемой гипотезе, или при турбулентности становится невозможным уровень описания, идентифицирующий индивидуальный лагранжевый объем сплошной среды.

Для турбулентности возникающий кризис лагранжевого описания проявляется в том, что уравнения неразрывности, движения и энергии потока в эйлеровых координатах для средних характеристик меняют вид [11]. В их правых частях появляются источниковые члены типа $\left\langle {u_{i}^{'}u_{k}^{'}} \right\rangle $ или $\left\langle {u_{k}^{'}T{\kern 1pt} '} \right\rangle ,$ определяемые корреляциями между пульсационными составляющими потока. Самый простой способ замыкания уравнений турбулентного движения, предложенный еще Т. Карманом, состоит в выражении пульсационных членов через средние характеристики потока и структурные константы (путь перемешивания молей Кармана l, (k, ε)–модель турбулентности и пр.) [11].

Уравнения (10) построены в полном соответствии с описанным выше подходом. Здесь величины ρ, u, E, p в левых частях уравнений – это средние характеристики газодинамического потока. Правые же части уравнений (10) представляют собой источниковые члены пульсационной природы. Параметры f_u, α, δ и f(r' – r) подбираются таким образом, чтобы расширение фронтовой области волны в процессе ее распространения осуществлялось по закону (6).

Рассмотрим уравнения системы (10) для случая, когда δ → 0 [12]. Обозначим ϖ(r, r', t) разность потоковых членов в подынтегральных выражениях правых частей уравнений. Например, для уравнения неразрывности эта разность имеет вид

Тогда правые части уравнений (10) будут иметь идентичный вид

Из уравнения нормировки $\int_{r - {\delta }}^{r + {\delta }} {{{f}_{ + }}\left( {r{\kern 1pt} ' - r} \right)dr{\kern 1pt} '} $ = 1 при δ → 0 следует оценка f(r' – r) ∼ 1/δ и правые части в форме (11) преобразуются к виду

Делая замену переменной интегрирования z = = r' – r, dz = dr' и разлагая подынтегральную функцию в (12) в ряд Тейлора по степеням z

преобразуем (12) к виду

В подынтегральном выражении ненулевой вклад дают только члены с четными степенями z, поскольку члены с нечетными степенями обращаются в нуль, например,

Пренебрегая членами со степенями, равными 4 и более (они дают вклад в (13) ∼О(δ²)), получим окончательно для правых частей (10) в приближении δ → 0 выражение вида

Подставляя в это соотношение соответствующие выражения для ϖ, преобразуем систему (10) к следующему виду [12]:

Отсюда следует, что правые части уравнений НЛТП-модели (10), представляющие собой источниковые члены пульсационной природы, описывают необратимым процесс перемешивания вещества (диффузию, но диффузию мезоуровня), [12]. Диффузия здесь пропорциональна характерному линейному размеру задачи δ. Это обеспечивает геометрическое, а в случае взрывов энергетическое подобие явления расширения фронтовой области волны, следующее из результатов многочисленных опытов (см. рис. 2д). При δ → 0 правые части уравнений НЛТП-модели (10) обращаются в ноль, и мы имеем классические уравнения газовой динамики для адиабатического процесса.

Результаты исследований [9, 10, 12] НЛТП-модели (10), в частности, свидетельствуют, что снижение интенсивности волны по закону (2) как P₊ ∼ R^–1.45 при одновременном расширении ее фронтовой области (области, в которой параметры течения изменяются от начального невозмущенного состояния до своего максимального значения) по закону (6) обусловлено собственными свойствами воздуха. Эти свойства приводят к необратимому перемешиванию воздуха во фронтовой области волны, к расширению фронтовой области и последующему превращению взрывной волны в акустическое возмущение.

Наконец, анализ отношений P₊/P_–, t₊/t_–, t_R+/t₊, t_R–/t_– амплитудно-временных параметров акустических волн, получаемых посредством использования экспериментальных данных (2) и аппроксимационных зависимостей (4) на рис. 2, показывает следующее. У акустических импульсов на приведенных расстояниях R/Q^1/3 = 500 м/кг^1/3 от центра взрыва длительности t_R+ и t_R– достигают практически половины от длительностей положительной t₊ и отрицательной t_– фаз, а сами длительности фаз и их амплитуды P₊ и P_– почти выравниваются (P₊/P_–, ≈ 1, t₊/t_– ≈ 1, t_R+/t₊ ≈ 0.54 и t_R–/t_– ≈ 0.45). Другими словами, на удалениях R/Q^1/3 > 500 м/кг^1/3 от центра взрыва акустический импульс практически приобретает форму монохроматической волны.

Таким образом, анализ всей совокупности экспериментальных и расчетных данных позволяет сделать следующие выводы. В виду общности как свойств самого воздуха, так и механизмов распространения в нем взрывных возмущений, акустические импульсы от высотного взрыва должны распространяться в атмосфере, изменяя свои амплитудно-временные параметры по законам (2)–(7) (с учетов влияния разреженного воздуха). Тогда уже на приведенном расстоянии R/Q^1/3 > 500 м/кг^1/3 от источника акустические импульсы должны принять форму, близкую к монохроматической волне. В соответствии с правилом Сакса [13] при таких высотных взрывах приведенная дальность R/Q^1/3 > 500 м/кг^1/3 реализуется на абсолютных высотах z = 90–96 км над земной поверхностью.

Тогда возникает закономерный вопрос. Каким образом большая доля энергии высотного взрыва переносится к земной поверхности, ведь даже в условиях безотражательного вертикального распространения акустических импульсов их интенсивность должна затухать как P₊ ∼ R^–1.45 (опять же, с учетом влияния разреженного воздуха).

Также до сих пор не получила объяснение и сложная структура акустических сигналов от высотных взрывов, состоящая из последовательности отдельных приходов, разделенных временными интервалами от 1 до 4 с (рис. 1). Причем в каждом приходе поздние акустические импульсы имеют меньшую амплитуду и приходят в точку наблюдения с задержкой примерно в 0.1–0.4 с относительно ранних и более интенсивных импульсов.

Если предположить, что все эти временные задержки вызваны отражением взрывной волны от неоднородностей атмосферы, то тогда эти неоднородности должны располагаться на удалениях порядка 34–136 м и 340–1360 м друг от друга. Вместе с тем, результаты уже упомянутых работ [6–8] демонстрируют, что наблюдаемое распределение скорости звука в земной атмосфере хорошо аппроксимируется по вертикали четырьмя безотражательными профилями. Точки сшивки указанных профилей, на которых за счет скачка градиента скорости звука или скачка второй производной возможно незначительное отражения акустических волн, находятся на высотах 30, 70 и 100 км. Другими словами, неоднородности атмосферы, на которых возможно отражение вертикальных акустических импульсов, отстранены друг от друга на 30 и 40 км, что на 1–3 порядка больше характерных размеров 0.03–1.4 км, получаемых при анализе акустических волн.

3. ОСНОВНОЕ УРАВНЕНИЕ

Попытаемся объяснить отмеченное в [1, 5] явление незначительного затухания акустических импульсов при их распространении из верхних слоев атмосферы к земной поверхности возможным распадом формирующейся при высотном взрыве одиночной взрывной волны в волновые пакеты (цуги волн). Основанием для такой гипотезы является возможность описания распространения взрывной волны уравнениями (10) НЛТП-модели и трансформации сильной взрывной волны в воздухе в непрерывное возмущение [9].

Проанализируем, как указанная модель описывает взрывное возмущение малой, но конечной амплитуды в процессе его распространения в атмосфере. Условие малости амплитуды подразумевает, что анализ импульсного возмущения будет осуществляться на значительных расстояниях от источника в акустическом приближении, а не в приближении ударной волны.

В этой связи анализ проведем при следующих допущениях:

1) движение плоское, одномерное;

2) избыточное давление р и массовая скорость и малые величины порядка ε, плотность ρ = ρ₀(1 ± ε);

3) связь между избыточным давлением р и массовой скоростью и в волне предполагается такой же, как в классической плоской акустической волне (в линейном случае) р = ρ₀си, где с – скорость звука;

4) определяющие параметры модели f_u, α и δ являются константами.

В соответствии с принятыми допущениями в уравнении движения НЛТП-модели (10) можно в интегралах сократить сомножители (r '²) и r², ответственные за сферическую расходимость. Естественно предположить, что в случае слабого возмущения дополнительные потоки массы, импульса и энергии, возникающие при развитии неустойчивости Кельвина–Гельмгольца, подчиняются закону равномерного распределения f(r' – r) = 1/(2δ). Наконец, в виду условия несжимаемости dρ/dt = 0 сокращаем обе части уравнения импульсов на плотность ρ, выносим постоянные величины за знак интеграла и приводим это уравнение к виду

Здесь изменено обозначение пространственной переменной с “r” на “х” для того, чтобы подчеркнуть, что уравнение описывает одномерное плоское движение.

Разлагая подынтегральную функцию в (14) в ряд Тейлора по степеням ($x{\text{'}} - x$), учитывая, что интегралы от нечетных членов разложения (первого и третьего) равны нулю и сохраняя в разложении члены до четвертого порядка малости включительно, получим для правой части (14):

Имеем также

Осуществляя соответствующие подстановки полученных выражений для ∂²(u²)/∂x² и ∂⁴(u²)/∂x⁴ в (15), получим

Обозначая

учитывая $\frac{{\alpha {{f}_{u}}\delta }}{3}\frac{{\partial u}}{{\partial x}}$ ~ δ² и делая замену p = ρ₀cu, получим

Пренебрегая в правой части перед конвективным членом ∂u/∂x малой величиной δ² по сравнению с u, имеем

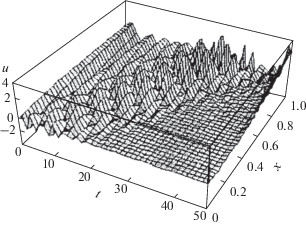
Это нелинейное эволюционное уравнение четвертого порядка является обобщением уравнения Курамото–Сивашинского, поскольку дополнительно учитывает дисперсию посредством члена с производной третьего порядка [14, 15]. Члены в правой части уравнения фактически представляют собой источниковый член пульсационной природы, свойства которого описаны выше. Численные исследования [14] таких уравнений показали, что при малой амплитуде акустического сигнала начальное возмущение распадается в пакет практически монохроматических волн, каждая из которых распространяется со своей фазовой скоростью (рис. 3).

Рассмотрим более простой вариант этого уравнения, отбросив член с производной четвертого порядка. Тогда получаем уравнение

обобщающее уравнение Кортевега–де Вриза–Бюргерса (КдВБ) на случай волнового знакопеременного движения. Отличие этого уравнения от классического уравнения КдВБ с постоянными коэффициентами μ и κ состоит в следующем.

Эффективная вязкость μ в (16) не является константой, а зависит от параметров движения газа в акустической волне. При этом для взрывных волн, когда δ ~ Q^1/3 [9], а массовая скорость u в положительной фазе зависит от приведенного расстояния R/Q^1/3, эффективная вязкость оказывается пропорциональной кубическому корню из энергии источника, μ ~ Q^1/3, что обеспечивает энергетическое подобие расширения фронтовой области акустических волн по закону (6) (при пренебрежении условиями, отклоняющими от подобия – неоднородностью свойств атмосферы, влиянием ее эффективной толщины и пр.). Вместе с тем, в отрицательной фазе волны (когда u < 0) отрицательная вязкость μ может приводить к неустойчивости. Не является константой также и эффективный коэффициент κ в (16) перед членом Кортевега–де Вриза, причем величина κ изменяет знак в процессе акустических колебаний, что приводит к изменению дисперсионных свойств, обусловленных данным членом, и быстрому “расплыванию” волны.

Следует отметить, что уравнением КдВБ описывается движение как акустических импульсов от слабых источников (Q ~ 10 кг ТНТ) при их распространении в пограничном слое атмосферы в инверсионных условиях [16], так и акустико–гравитационных волн от сверхмощных источников (Q ~ 10¹⁰ кг ТНТ) при их распространении в атмосфере на сверхдальние дистанции [17]. Описание слабого возмущения уравнением КдВБ также является общим для волновых процессов различной природы. Это может означать, что на достаточно большом удалении от источника при определенных условиях первоначально формирующийся одиночный сигнал может распадаться в волновой пакет (цуг волн) [16].

Для дальнейшего формулирования гипотезы, объясняющей незначительное затухание и сложную структуру акустических импульсов при их распространении из верхних слоев атмосферы к земной поверхности, необходимо оценить, может ли уравнение (17), в отличие от классического уравнения КдВБ с постоянными коэффициентами μ и κ, описывать волновой знакопеременный процесс. С этой целью проверим, имеет ли уравнение (17) точное решение для акустической волны, состоящей из положительной и отрицательной фаз.

4. АНАЛИЗ ОСНОВНОГО УРАВНЕНИЯ

Перейдем в систему координат ξ = x – ct, движущуюся вместе с акустической волной со скоростью звука с, ξ – бегущая переменная (волна бежит вправо, ξ ≤ 0 в области решения). Тогда (17) примет формально вид

Пренебрегая вторым членом в выражении (16) для коэффициента μ по сравнению с первым, получим

или, обозначая μ₁ = $\frac{{\alpha {{f}_{u}}\delta }}{3},$ κ₁ = $ - \frac{{\alpha {{f}_{u}}{{\delta }^{3}}}}{{15}},$

Уравнение (18) обладает следующими особенностями: оно однородно (т.е. если u – решение, то βu – тоже решение, β – const); нелинейно (т.е. сумма двух решений не является решением) и не квазилинейно. На языке теории колебаний такое уравнение можно классифицировать как амплитудно-независимое, но одновременно фазозависимое.

Для того чтобы решить уравнение (18), сведем его к системе обыкновенных дифференциальных уравнений первого порядка. Для этого обозначим $y = \frac{{du}}{{d\xi }} = u_{\xi }^{'}.$ Тогда вместо (18) имеем

Рассмотрим в качестве независимой переменной массовую скорость u. Тогда

Используя полученные соотношения, вместо (19) получим

Введем новую переменную

т.е. и вместо (20) получим откуда, разрешая это уравнение относительно производной $z_{u}^{'},$ получим

Добавляя уравнение (21), получим систему двух обыкновенных дифференциальных уравнений первого порядка относительно неизвестных функций

Начальные условия (u = 0 – точка вступления в акустической волне, u = 0 соответствует ξ = 0, рис. 4) находим из соотношения для профиля массовой скорости во фронтовой области взрывной волны

Данное соотношение получено из точного решения для структуры фронтовой области, найденного посредством интегрирования уравнений НЛТП-модели (10) в одномерном плоском случае [18]. Здесь u₊ – максимальная массовая скорость во фронтовой области взрывной волны, Δ_R+ – ширина фронтовой области волны, $\lambda {\text{*}}$ – показатель степени. Тогда для функций y = y(u) и z = z(u) начальные условия задаются так:

Из начальных условий следует, что форма профиля стационарной акустической волны согласно предлагаемой модели определяется (рис. 4):

а) скоростью нагружения во вступлении (крутизной волны) $u_{\xi }^{'}(0);$

б) кривизной профиля волны во вступлении

Получив численное решение y = f(u), далее численно интегрируя уравнение $y = \frac{{du}}{{d\xi }} = f(u),$ находим профиль u = f(ξ).

На рис. 5а черной непрерывной линией представлен результат расчета по уравнениям (21) и (22) формирующейся уединенной волны-составляющей при условии, что волновой пакет образуется из взрывного возмущения, чей экспериментальный профиль избыточного давления p(t) показан на рис. 5б серой линией. Указанная взрывная волна была зарегистрирована на расстоянии R = 250 м от места подрыва заряда взрывчатого вещества энергией Q ≈ 0.76 кг ТНТ [19]. Для задания исходных данных в расчетах использовались параметры фронтовой области этой эпюры p(t) со следующими значениями – P₊ = 100 Па, u₊ ≈ ≈ P₊/(c₀ρ₀) ≈ 0.227 м/с, Δ_R+ ≈ 0.93 м и $\lambda {\text{*}}$ = 7.29/Δ_R+. Кроме того, константы μ₁ = αf_uδ/3 = 0.031 и κ₁ = = –αf_uδ³/15 ≈ –0.0054 в уравнении (22) задавались при следующих определяющих параметрах НЛТП-модели (10) – α = 0.5, f_u = 0.2 и δ = Δ_R+.

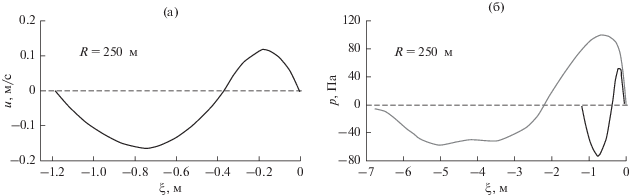
После перемножения значений u(t), демонстрируемых на рис. 5а черной линией, на плотность ρ₀ и скорость звука с₀ в невозмущенном воздухе, получаем значения избыточного давления p(t) в выделяющейся волне. Они обозначены на рис. 5б также черной линией. Сопоставление расчетной (черная линия) и экспериментальной (серая линия) эпюр p(t) на рис. 5б свидетельствует, что длительность выделяющейся волны-составляющей (соответственно, сумма длительностей t₊ и t_– ее положительной и отрицательной фаз) может быть до 6 раз короче, а интенсивность P₊ – до 2 раз ниже, чем у исходного сигнала. Причем выделяющаяся волна по форме близка к монохроматической волне.

Отличие результатов расчетов на рис. 5 от результатов работы [16] состоит в том, что в [16] автор ограничился рассмотрением распада первичной волны в волновой пакет и осциллирующий “хвост” только для условий инверсионного пограничного слоя атмосферы. В настоящей же работе уравнения (17) и (18), как и исходная НЛТП–модель (10), применимы к различным условиям устойчивости пограничного слоя атмосферы, а также к условиям безграничного однородного воздушного пространства.

Существование точного решения уравнения (18), являющегося обобщением уравнения (17) на случай стационарной акустической волны, позволяет сделать следующие выводы. Во-первых, уравнение (17) в отличие от классического уравнения КдВБ с постоянными коэффициентами μ и κ может описывать волновой знакопеременный процесс. Во-вторых, при относительно малых κ слабая взрывная волна может распадаться в волновой пакет практически монохроматических волн-составляющих. В-третьих, поскольку в (17) дисперсия отлична от нуля (κ ≠ 0), то фазовые скорости отдельных волн-составляющих будут различны, а начальная форма волнового пакета (цуга волн) будет меняться с течением времени – он будет расплываться. Отсюда и вытекает гипотеза, объясняющая формирование многомодовых акустических сигналов от высотных взрывов (рис. 1), переносящих с собой довольно заметную часть взрывной энергии.

5. ФОРМУЛИРОВКА ГИПОТЕЗЫ

В диапазоне высот от 120–150 до ≈50 км скорость звука с в целом возрастает при приближении к Земле, поэтому начальное возмущение от взрыва растягивается в пространстве, градиент массовой скорости ∂u/∂x во взрывной волне снижается. Кроме того, градиент массовой скорости ∂u/∂x снижается в результате расширения фронтовой области волны (этот процесс иллюстрируется, в частности, изменением параметра t_R+ на рис. 2д). Все это приводит к уменьшению параметра κ в уравнении (17). В результате возникают предпосылки к распаду начальной взрывной волны в волновой пакет практически монохроматических волн-составляющих. Здесь следует заметить, что не вся первоначальная энергия взрыва, а только ее часть переходит вначале в энергию взрывной волны, а затем и в энергию формирующегося волнового пакета.

Самая большая по амплитуде выделяющаяся волна-составляющая из волнового пакета должна распространяться с самой большой фазовой скоростью. Далее должна следовать волна-составляющая меньшей амплитуды и с меньшей фазовой скоростью распространения и т.д. В результате выделяющийся из начальной взрывной волны волновой пакет (цуг волн) должен постепенно растягиваться (расплываться), причем поздние в нем волны-составляющие должны иметь меньшие амплитуды, чем ранние.

К высотам ≈50 км доходят только первые 2–3 волны-составляющие с наибольшими амплитудами из сформировавшегося в начале волнового пакета. Здесь картина меняется. Теперь температура, а с ней и скорость с звука снижается при приближении к Земле, длительность волн сокращается, градиент ∂u/∂x либо возрастает, либо слабее убывает, чем это нужно для поддержания прежнего режима движения. Таким образом, вблизи высоты 50 км в уравнении (17) возрастает (или начинает слабо убывать) параметр κ в члене Кортевега–де Вриза. Это должно приводить к еще одному распаду дошедших акустических импульсов в волновые пакеты. В результате 2–3 волновых пакета (цуга колебаний) от распада на высоте в 50 км 2–3 предыдущих волн-составляющих доходят до Земли и регистрируются здесь. Этим и предлагается объяснить выявленную в [1] сложную структуру зарегистрированных акустических сигналов (рис. 1).

Главной особенностью волновых пакетов (цугов волн) является их распространение в плоском случае и в идеальной среде с сохранением формы и амплитуды, то есть P₊ ∼ R⁰ ∼ const. При распространении в диссипативной среде амплитуда волн-составляющих снижается [15]. Соответственно, для случая сферически симметричного распространения в атмосфере амплитуды выделяющихся волновых пакетов должны затухать по закону P₊ ∼ R^–n (где n несколько превышает 1), то есть приблизительно по зависимости (3) на рис. 2а. Тогда, исходя из оценок (9) и расчетов [6–8], можно предположить, что энергия в волновых пакетах, выделяющихся из первоначальной одиночной взрывной волны (даже если в волновой пакет перешла не вся первоначальная энергия взрыва, а лишь ее доля), должна переноситься вертикально по атмосфере с незначительным затуханием, распределяясь по все большей сфере (с удалением R от центра высотного взрыва). Этим и объясняется не только сложная структура зарегистрированных акустических сигналов, но и большая переносимая ими энергия. Соответственно, зарегистрированные акустические сигналы от высотного взрыва доносят информацию как об этом событии, так и о каких-то деталях вертикального распространения акустических импульсов в атмосфере и особенностях стратификации самой атмосферы.

ЗАКЛЮЧЕНИЕ

В заключение следует еще раз подчеркнуть, что суть описанного в [1] явления не в том, что высокочастотный сигнал доходит до поверхности Земли в условиях, когда он не может этого сделать и нужно искать какие-то уточнения в теории поглощения для разреженных газов, а в том, что плотность энергии в зарегистрированных колебаниях оказывается невероятно большой для высотного взрыва. Перенос этой энергии волновыми пакетами (формирующимися при последовательном распаде отдельных волн) должен осуществляться в процессе их движения сверху вниз по атмосфере, являющейся практически “прозрачной” для таких акустических возмущений.

Предложенная в настоящей работе гипотеза может расширить существующие представления об энергетическом обмене в системе ионосфера – верхняя стратосфера – тропосфера. Если она верна, то аналогичный эффект должен наблюдаться и при взрывах у поверхности Земли, когда волна движется снизу вверх [7, 20]. Справедливости ради следует отметить, что аномальные акустические возмущения наблюдались в ионосфере непосредственно над местами запусков космических кораблей и мощных взрывов [21–23]. Поэтому дальнейшее изучение рассматриваемого эффекта целесообразно направить на более подробный анализ труднообъяснимых акустических сигналов, а также на численное исследование уравнения (15) с целью математического моделирования указанного эффекта. Анализ и моделирование должны проводиться с позиции предположения о последовательном распаде взрывной волны в волновые пакеты по мере их вертикального движения в атмосфере.

Работа выполнена при частичной финансовой поддержке гранта РФФИ № 18-05-00576 и программы Президиума РАН П-22/КП19-280.