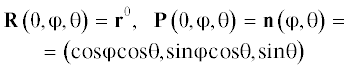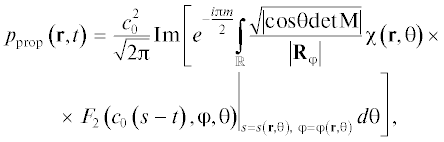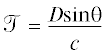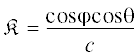Акустический журнал, 2019, T. 65, № 6, стр. 799-807
Об использовании асимптотических формул на основе модифицированного канонического оператора Маслова при моделировании распространения импульсных акустических сигналов в трехмерных волноводах мелкого моря
П. С. Петров a, *, С. А. Сергеев b, c, **, А. А. Толченников b, c, d, ***
a Федеральное государственное бюджетное учреждение науки Тихоокеанский океанологический институт
им. В.И. Ильичева ДВО РАН
690041 Владивосток, ул. Балтийская 43, Россия
b Институт проблем механики им. А.Ю. Ишлинского РАН
119526 Москва, пр-т Вернадского 101, к. 1, Россия
c Московский физико-технический институт (Государственный университет)
141701 Московская обл., Долгопрудный, Институтский пер. 9, Россия
d Московский государственный университет им. М.В. Ломоносова
119991 Москва, Россия
* E-mail: petrov@poi.dvo.ru
** E-mail: sergeevse1@yandex.ru
*** E-mail: tolchennikovaa@gmail.com
Поступила в редакцию 23.04.2019
После доработки 05.07.2019
Принята к публикации 09.07.2019
Аннотация
В работе описывается методика моделирования распространения импульсных акустических сигналов в волноводе мелкого моря с трехмерными неоднородностями рельефа дна. Описываемая методика основана на лучевой теории распространения звука и методе модифицированного канонического оператора Маслова. Представление акустического поля в терминах канонического оператора дает ряд важных преимуществ при выполнении практических расчетов. В частности, оказывается возможным вычислить временной ряд импульсного сигнала в точке приема, расположенной на каустике семейства лучей. Кроме того, значительная часть вычислений в рамках предлагаемой методики может быть выполнена аналитически, что существенно повышает общую скорость расчетов. В качестве примера мы рассматриваем распространение звука в клиновидном волноводе, который является простейшей моделью прибрежного участка акватории на шельфе. Обсуждается геометрия лучей в таком волноводе как в случае постоянной скорости звука, так и при наличии термоклина в водном слое. Для обоих случаев рассчитываются также временные ряды импульсного акустического сигнала от точечного источника для трассы, ориентированной вдоль изобаты (параллельно ребру клина).
ВВЕДЕНИЕ
Многие практические задачи подводной акустики приводят к необходимости моделировать распространение импульсных звуковых сигналов в сложных двумерных и трехмерных океанических волноводах с неоднородностями различной природы. Интенсивные исследования последних десятилетий привели к разработке нескольких групп математических моделей трехмерного распространения звука [1], среди которых можно отметить трехмерные параболические уравнения [2, 3], модовые параболические уравнения [4, 5], метод гауссовых пучков [6], трехмерную лучевую теорию [6, 7], а также различные комбинации указанных подходов [8] (например, теорию “вертикальные моды–горизонтальные лучи”). Эти методы, как правило, ориентированы на проведение расчетов в частотной области и не допускают других способов применения к нестационарным задачам, кроме проведения вычислений для большого ряда отдельных частот и последующего Фурье-синтеза сигнала в точке приема. Данный способ, однако, характеризуется высокой вычислительной сложностью [1–3] (и, соответственно, низкой скоростью вычислений) даже в случае двумерных задач и частот порядка нескольких сотен герц. Применение его для практических расчетов распространения широкополосных сигналов с центральными частотами 0.5 кГц и выше в волноводах с трехмерными неоднородностями, а также на протяженных трассах в сотни километров в настоящее время полностью исключено. Сигналы такого рода, однако, находят приложение в задачах подводной навигации и связи [9–11], которые в последнее время приобретают все большее значение в связи разработкой и активным использованием автономных подводных аппаратов.
При моделировании распространения навигационных и коммуникационных сигналов [9, 10] зачастую можно пренебречь, например, строением дна и ограничиться приближением акустически мягкой (либо жесткой) границы, поскольку звуковые поля на высоких частотах и на удалениях в десятки и сотни километров от источника так или иначе характеризуются, в основном, вертикальными углами распространения, близкими к нулю, при которых наблюдается полное внутреннее отражение от дна (мы имеем в виду угол между волновым вектором и горизонталью). При этом, однако, учет рельефа дна и гидрологических условий остается необходимым [9, 10], так как обусловленная ими вертикальная и горизонтальная рефракция звука весьма сильно сказывается на геометрии распространения, дальности приема и формировании вертикальных и горизонтальных зон акустической тени.
Единственным доступным инструментом для решения задач такого рода в настоящее время, по-видимому, является лучевая теория распространения звука [1, 6, 7]. На практике, однако, оказывается, что в реалистичных моделях (например, для гидрологии и батиметрии, взятых их натурных данных) геометрия лучей оказывается настолько сложной, что для некоторой фиксированной точки приема найдется момент времени, когда она будет находиться в малой окрестности фокальной точки приходящего в этот момент волнового фронта. В этом случае, как известно, стандартная лучевая теория неприменима ввиду расходимости [1], возникающей из-за того, что выражение для амплитуды содержит якобиан, который близок к нулю.
Данное ограничение может быть устранено путем использования метода модифицированного канонического оператора Маслова [12–14]. Как показано в данной работе, представление решения в терминах канонического оператора в вычислительном отношении лишь незначительно сложнее, чем то, что получается из стандартной лучевой теории распространения звука [1]. Мы опишем здесь универсальный алгоритм расчета временных рядов в точке приема, который применим как для регулярных, так и для фокальных точек [14]. Ранее мы уже использовали его в работе [15] для решения двумерных задач распространения звука в глубоком океане. Как показано в настоящем исследовании, этот метод может быть с успехом применен и в условиях мелкого моря с трехмерными неоднородностями дна.
ПОСТАНОВКА ЗАДАЧИ
Моделирование распространения импульсного сигнала в волноводе мелкого моря с непроницаемым дном сводится к решению задачи Коши для трехмерного волнового уравнения для акустического давления $p = p\left( {t,x,y,z} \right)$ в области $\left( {x,y} \right) \in {{\mathbb{R}}^{2}},$ $0 < z < D\left( {x,y} \right)$ (граница $z = 0$ соответствует поверхности моря, поверхность $z = D\left( {x,y} \right)$ описывает батиметрию) со скоростью $c = c\left( {x,y,z} \right){\text{:}}$
(1)
$\frac{1}{{{{c}^{2}}}}{{p}_{{tt}}} - {{{\Delta }}_{{\mathbf{r}}}}p = Q\left( {{\mathbf{r}},t} \right),\,\,\,\,~{\mathbf{r}} = \left( {x,y,z} \right).$На поверхности жидкости ставится условие Дирихле ${{\left. p \right|}_{{z = 0}}} = 0,$ а на дне ставится условие Неймана ${{\left. {{{p}_{{\mathbf{n}}}}} \right|}_{{z = D\left( {x,y} \right)}}} = 0.$
Правая часть $Q\left( {{\mathbf{r}},t} \right),$ описывающая источник, представляется в виде произведения (этот источник был введен в работах [12, 16]):
(3)
$Q\left( {{\mathbf{r}},t} \right) = {{{\lambda }}^{2}}g_{0}^{'}\left( {{\lambda }t} \right)\frac{1}{{{{{\mu }}^{3}}}}V\left( {\frac{{{\mathbf{r}} - {{{\mathbf{r}}}^{0}}}}{{\mu }}} \right).$Выбор такой правой части уравнения означает, что в точке ${{{\mathbf{r}}}^{0}}$ располагается источник звука с малым характерным размером ${\mu }$ и в начальный момент времени источник излучает импульсный сигнал длительности 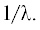 Такое представление излучаемого сигнала $f\left( t \right) = {{{\lambda }}^{2}}g_{0}^{'}\left( {{\lambda }t} \right)$ необходимо для использования асимптотик из [12, 15, 16], и, как будет видно далее, в конечные формулы для акустического давления войдет
только функция $f\left( t \right).$
Такое представление излучаемого сигнала $f\left( t \right) = {{{\lambda }}^{2}}g_{0}^{'}\left( {{\lambda }t} \right)$ необходимо для использования асимптотик из [12, 15, 16], и, как будет видно далее, в конечные формулы для акустического давления войдет
только функция $f\left( t \right).$
Вещественные функции $V\left( {\mathbf{w}} \right)~\,\left( {{\mathbf{w}} \in {{\mathbb{R}}^{3}}} \right)$ и ${{g}_{0}}\left( {\tau } \right)~\,\left( {{\tau } \in \left[ {0,\infty } \right)} \right)$ выбираются такими, что
(4)
$\begin{gathered} \left| {{{V}^{{\left( {\alpha } \right)}}}\left( {\mathbf{w}} \right)} \right| \leqslant {{C}_{{\alpha }}}{{(1 + \left| {\mathbf{w}} \right|)}^{{ - \left| {\alpha } \right| - \kappa }}},\,\,\,\,\left| {\alpha } \right| = 0,1,2, \ldots , \\ \int\limits_{{{\mathbb{R}}^{3}}} {V\left( {\mathbf{w}} \right)d{\mathbf{w}}} = 1, \\ \end{gathered} $(5)
$\begin{gathered} {{g}_{0}}\left( 0 \right) = 0,\,\,\,\,\int\limits_0^\infty {{{g}_{0}}\left( {\tau } \right)d{\tau }} = 1, \\ ~\left| {g_{0}^{{\left( k \right)}}\left( {\tau } \right)} \right| \leqslant {{C}_{k}}{{e}^{{ - {\nu }\tau }}},\,\,\,\,k = 0,1,2 \ldots \\ \end{gathered} $Нас интересует асимптотическое решение задачи (1), (2) при ${\mu } \to 0 + ,$ ${\lambda } \to \infty .$ Физически эта асимптотика описывает сигнал, излучаемый точечным источником, расположенным в точке ${\mathbf{r}} = {{{\mathbf{r}}}^{0}}.$ На основании асимптотических формул мы строим временную историю звукового сигнала в заданной точке ${\mathbf{r}}{\text{*,}}$ в которой располагается приемник сигнала.
Как показано в [12, 16], решение задачи распадается на два слагаемых: быстрозатухающую часть ${{p}_{{{\text{trans}}}}},$ локализованную в окрестности точки ${{{\mathbf{r}}}^{0}},$ и распространяющуюся часть ${{p}_{{{\text{prop}}}}}.$ Мы будем интересоваться только распространяющейся частью.
Отметим, что указанные ограничения относительно параметров ${\mu },{\lambda }$ не являются существенными и что описанные ниже асимптотические формулы применимы для решения практически любых задач вычислительной подводной акустики.
АСИМПТОТИКА РАСПРОСТРАНЯЮЩЕЙСЯ ЧАСТИ РЕШЕНИЯ В РЕГУЛЯРНОЙ ТОЧКЕ
Вывод асимптотического решения использует понятие канонического оператора Маслова и его модификации. Метод построения канонического оператора представляет собой обобщение лучевого метода и метода ВКБ. Канонический оператор позволяет строить глобальные асимптотические решения и позволяет получать асимптотику в окрестности фокальных точек и каустик, где метод ВКБ уже неприменим. Однако мы не имеем возможности в этой статье приводить определение канонического оператора и приведем только окончательные формулы для асимптотического решения.
Для начала определим поверхность ${{{\Lambda }}_{s}}$ в фазовом пространстве $\left( {{\mathbf{r}},{\mathbf{p}}} \right) \in {{\mathbb{R}}^{6}}.$ Рассмотрим гамильтониан $H\left( {{\mathbf{r}},{\mathbf{p}}} \right)$ = $c\left( {x,y,z} \right)\sqrt {{{{\left( {{{p}^{x}}} \right)}}^{2}} + {{{\left( {{{p}^{y}}} \right)}}^{2}} + {{{\left( {{{p}^{z}}} \right)}}^{2}}} $ и определим поверхность ${{{\Lambda }}_{s}}$ как объединение концов всех траекторий соответствующей системы Гамильтона, выпущенных с единичным импульсом из точки ${{{\mathbf{r}}}^{0}}$ и отражающихся по обычным правилам от поверхности и дна моря. Более точно, пусть ${\mathbf{R}}\left( {s,{\varphi },{\theta }} \right)$ = $\left( {X\left( {s,{\varphi },{\theta }} \right),Y\left( {s,{\varphi },{\theta }} \right),Z\left( {s,{\varphi },{\theta }} \right)} \right),$ ${\mathbf{P}}\left( {s,{\varphi },{\theta }} \right)$ = $\left( {{{P}^{x}}\left( {s,{\varphi },{\theta }} \right),{{P}^{y}}\left( {s,{\varphi },{\theta }} \right),{{P}^{z}}\left( {s,{\varphi },{\theta }} \right)} \right)$ есть решение гамильтоновой системы
(6)
$\frac{{d{\mathbf{R}}}}{{ds}} = {{H}_{{\mathbf{p}}}},\,\,\,\,\frac{{d{\mathbf{P}}}}{{ds}} = - {{H}_{{\mathbf{r}}}},$(8)
$\begin{gathered} {{{\Lambda }}_{s}} = \left\{ {\left( {{\mathbf{r}},{\mathbf{p}}} \right) \in \mathbb{R}_{{x,p}}^{6}:\left\{ {\begin{array}{*{20}{c}} {r = R\left( {s,{\varphi },{\theta }} \right)} \\ {p = P\left( {s,{\varphi },{\theta }} \right)} \end{array}} \right.,} \right. \\ \left. {{\varphi } \in \left( {0,{\text{\;}}2{\pi }} \right),\,\,\,\,{\theta } \in \left[ { - \frac{{\pi }}{2},\frac{{\pi }}{2}} \right]} \right\}. \\ \end{gathered} $Эта поверхность не гладкая, она терпит разрыв там, где траектории выходят на границу области.
Фронтом в конфигурационном пространстве называется множество ${{\gamma }_{s}} = \{ \left( {x,y,z} \right)$ = $R\left( {s,{\varphi },{\theta }} \right){\kern 1pt} :$ $0 \leqslant {\varphi } < 2{\pi },$ $ - {\pi /}2 < {\theta } < {\pi /}2\} ,$ являющееся проекцией в фиксированный момент времени $s$ поверхности ${{{\Lambda }}_{s}}$ на конфигурационное прострaнство. Лучом называется множество $\{ \left( {x,y,z} \right)$ = = ${\mathbf{R}}\left( {s,{{{\varphi }}_{0}},{{{\theta }}_{0}}} \right):s > 0\} .$ При $s = 0$ фронт ${{\gamma }_{0}}$ представляет собой точку ${{x}^{0}}$, при малых временах $s$ фронт ${{\gamma }_{s}}$ представляет собой просто сферу. В каждый момент времени $t$ распространяющаяся часть решения ${{p}_{{{\text{prop}}}}}$ локализована в окрестности ${{\gamma }_{t}},$ геометрия которого усложняется с увеличением t.
Зафиксируем точку ${\mathbf{r}}{\text{*}}$ (точку приема сигнала, в которой мы хотим вычислить его временной ряд), тогда на конечном отрезке $s \in \left[ {0,{{s}_{0}}} \right]$ уравнение ${\mathbf{R}}\left( {s,{\varphi },{\theta }} \right) = {\mathbf{r}}{\text{*}}$ будет иметь конечное число k решений ${\mathbf{\alpha }}_{j}^{{\text{*}}} = \left( {s_{j}^{{\text{*}}},{\varphi }_{j}^{{\text{*}}},{\theta }_{j}^{{\text{*}}}} \right),$ $j = 1, \ldots ,k.$ Пусть все точки ${\mathbf{\alpha }}_{j}^{{\text{*}}},$ $j = 1, \ldots ,k$ являются регулярными, т.е. в этих точках якобиан $\left| {\frac{{\partial {\mathbf{R}}\left( {t,{\varphi },{\theta }} \right)}}{{\partial \left( {t,{\varphi },{\theta }} \right)}}} \right|$ не равен нулю (формулы для решения в случае наличия нерегулярных точек приведены в [15]).
Построим следующие функции
(9)
$F\left( {{\eta },{\varphi },{\theta }} \right) = \int\limits_0^\infty {{\rho }{{e}^{{i{\eta \rho }}}}\overline {{{{\tilde {g}}}_{0}}} \left( {\frac{{{{c}_{0}}}}{{{\lambda \mu }}}{\rho }} \right)\tilde {V}\left( {{\rho }{\mathbf{n}}\left( {{\varphi },{\theta }} \right)} \right)d{\rho }} .$(10)
$\begin{gathered} \tilde {V}\left( {\mathbf{\xi }} \right) = \frac{1}{{{{{(2{\pi })}}^{{3{\text{/}}2}}}}}\int\limits_{{{\mathbb{R}}^{3}}} {{{e}^{{ - i\langle {\mathbf{\xi }},{\mathbf{r}}\rangle }}}V\left( {\mathbf{r}} \right)d{\mathbf{r}}} , \\ ~\overline {\tilde {g}} \left( s \right) = \frac{1}{{\sqrt {2{\pi }} }}\int\limits_0^\infty {{{e}^{{is{\tau }}}}{{g}_{0}}\left( {\tau } \right)d{\tau }} . \\ \end{gathered} $Для каждого $j = 1, \ldots ,k$ в окрестности ${\mathbf{r}}{\text{*}}$ существует решение $s = {{s}_{j}}\left( {\mathbf{r}} \right),$ ${\varphi } = {{{\varphi }}_{j}}\left( r \right),$ ${\theta } = {{{\theta }}_{j}}\left( {\mathbf{r}} \right)$ уравнения ${\mathbf{R}}\left( {s,{\varphi },{\theta }} \right) = {\mathbf{r}}$ такое, что $s_{j}^{{\text{*}}} = {{s}_{j}}\left( {{\mathbf{r}}{\text{*}}} \right),$ ${\varphi }_{j}^{{\text{*}}} = {{{\varphi }}_{j}}\left( {r{\text{*}}} \right),~$ ${\theta }_{j}^{{\text{*}}} = {{{\theta }}_{j}}\left( {r{\text{*}}} \right).$ Далее определим число ${{m}_{j}}$ = ${{m}_{j}}\left( {s_{j}^{{\text{*}}},{\varphi }_{j}^{{\text{*}}},{\theta }_{j}^{{\text{*}}}} \right)$ для траектории ${\mathbf{R}}\left( {s,{\varphi }_{j}^{{\text{*}}},{\theta }_{j}^{{\text{*}}}} \right)~~\left( {s \in \left( {0,s_{j}^{{\text{*}}}} \right]} \right),$ как число перемен знака якобиана $\left| {\frac{{\partial {\mathbf{X}}\left( {s,{\varphi },{\theta }} \right)}}{{\partial \left( {s,{\varphi },{\theta }} \right)}}} \right|$ на полуоткрытом интервале $\left( {0,t_{j}^{{\text{*}}}} \right]$ (с учетом того, что якобиан на траектории может иметь разрывы и меняет знак при отражении траектории от дна и поверхности) минус число отражений траектории от границы, на которой поставлено условие Неймана (дно), плюс число отражений от границы, на которой поставлено условие Дирихле (поверхность).
Тогда распространяющаяся часть асимптотического решения задачи имеет вид
(11)
$\begin{gathered} ~{{p}_{{{\text{prop}}}}}\left( {{\mathbf{r}},t} \right) = ~\mathop \sum \limits_{j = 1}^k \frac{1}{{{{{\mu }}^{2}}}}\sqrt {\frac{{c_{0}^{5}}}{{c\left( {\mathbf{r}} \right)}}} \sqrt {\frac{{{\text{cos}}\theta }}{{\left| {{{{\mathbf{R}}}_{{\varphi }}} \times {{{\mathbf{R}}}_{{\theta }}}} \right|}}} \times \\ {{\left. { \times \,\,~{\text{Im}}\left[ {{{e}^{{ - \frac{{i{\pi }{{m}_{j}}}}{2}}}}F\left( {\frac{{{{c}_{0}}\left( {s - t} \right)}}{{\mu }},{\varphi },{\theta }} \right)} \right]} \right|}_{{s = {{s}_{j}}\left( {\mathbf{r}} \right),\,\,{\varphi } = {{{\varphi }}_{j}}\left( {\mathbf{r}} \right),\,\,{\theta } = {{{\theta }}_{j}}\left( {\mathbf{r}} \right)}}}, \\ \end{gathered} $Отметим еще раз, что формула (11) представляет собой наиболее общий вид для асимптотики при общих предположениях. Дальнейшее упрощение этой формулы связано с конкретными предположениями о виде функций $V\left( {\mathbf{r}} \right)$ и ${{g}_{0}}\left( {\tau } \right)$ (см. [15]).
УПРОЩЕНИЯ ФОРМУЛ И ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ
В типичной постановке задач подводной акустики размеры источника звука, как правило, пренебрежимо малы по сравнению с размерами расчетной области. Рассмотрим, как упрощаются формулы для решения, если мы формально устремим размер источника к нулю. В этом случае можно считать, что $V\left( {\mathbf{r}} \right) = {\delta }\left( {\mathbf{r}} \right){\text{;}}$ таким образом, $\tilde {V}\left( {\mathbf{\xi }} \right) = {1 \mathord{\left/ {\vphantom {1 {{{{(2{\pi })}}^{{\frac{3}{2}}}}}}} \right. \kern-0em} {{{{(2{\pi })}}^{{\frac{3}{2}}}}}},$ и, используя свойства преобразования Фурье, получаем следующее выражение для функции $F\left( {{\eta },{\varphi },{\theta }} \right)$
(12)
$F\left( {{\eta },{\varphi },{\theta }} \right) = \frac{{ - i{{{\lambda }}^{2}}{{{\mu }}^{2}}}}{{{{{(2{\pi })}}^{{\frac{3}{2}}}}{{c}_{0}}^{2}}}g_{0}^{'}\left( {\frac{{{\lambda \mu \eta }}}{{{{c}_{0}}}}} \right).$Подставив данное выражение (12) в формулу (11), получим окончательную формулу для акустического давления в регулярной точке
Формула (13) соответствует стандартной лучевой теории распространения звука в океане, фактически суммирование в ней ведется по всем лучам, приходящим в данную точку.
АСИМПТОТИКА РЕШЕНИЯ ДЛЯ ФОКАЛЬНОЙ ТОЧКИ
Рассмотрим теперь случай, когда точка волнового фронта ${\mathbf{\alpha }}{\text{*}} = {\mathbf{\alpha }}_{j}^{{\text{*}}}$ является фокальной. В этом случае векторы ${{{\mathbf{R}}}_{{\varphi }}}\left( {{\mathbf{\alpha }}{\text{*}}} \right),$ ${{{\mathbf{R}}}_{{\theta }}}\left( {{\mathbf{\alpha }}{\text{*}}} \right)$ линейно зависимы, и формула (11) оказывается неприменимой по тем же причинам, что и стандартная лучевая теория распространения звука [1]. Решение волнового уравнения, описывающего распространение звука в глубоком океане для этого случая, получено в работе [15] в терминах канонического оператора Маслова, которая сводится к формуле, аналогичной (11). Ниже мы приводим лишь результат упрощения этой формулы для случая точечного источника (аналог формулы (13)), который, несмотря на некоторую громоздкость, вполне пригоден для практических вычислений. Читателя, интересующегося техникой вывода этих формул, мы приглашаем ознакомиться с ним в работах [12, 14, 16].
Обозначим $rk = {\text{rank}}\left( {{{{\mathbf{R}}}_{{\varphi }}}\left( {{\mathbf{\alpha }}{\text{*}}} \right),\,\,{{{\mathbf{R}}}_{{\theta }}}\left( {{\mathbf{\alpha }}{\text{*}}} \right)} \right)$ (rank обозначает ранг матрицы, составленной из данных векторов) в точке ${\mathbf{\alpha }}* = \left( {s*,{\varphi }*,{\theta *}} \right).$ Приведем формулы для фокальной точки, где $rk = 1$ (это устойчивая особенность). Пусть ${{{\mathbf{R}}}_{{\varphi }}}\left( {{\mathbf{\alpha }}{\text{*}}} \right) \ne 0.$ Рассмотрим систему уравнений
(14)
$\begin{gathered} \left\langle {{\mathbf{P}}\left( {s,{\varphi },{\theta }} \right),\,\,{\mathbf{r}} - {\mathbf{R}}\left( {s,{\varphi },{\theta }} \right)} \right\rangle = 0, \\ ~\left\langle {{{{\mathbf{R}}}_{{\varphi }}}\left( {s,{\varphi },{\theta }} \right),\,\,{\mathbf{r}} - {\mathbf{R}}\left( {s,{\varphi },{\theta }} \right)} \right\rangle = 0 \\ \end{gathered} $Определим теперь якобиан ${{J}^{{\varepsilon }}}\left( {s,{\varphi },{\theta }} \right)$ = = 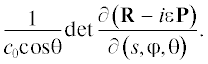 Затем определим число $m$ следующим образом (для простоты рассмотрим случай, когда соответствующая траектория
при $s \in \left( {0,s{\text{*}}} \right)$ не достигает дна и поверхности):
Затем определим число $m$ следующим образом (для простоты рассмотрим случай, когда соответствующая траектория
при $s \in \left( {0,s{\text{*}}} \right)$ не достигает дна и поверхности):
(15)
$m = \frac{1}{{\pi }}\left( {\left. {{\text{arg}}~{{J}^{\varepsilon }}\left( {{{{\alpha }}_{0}}} \right)} \right|_{{\varepsilon = 0}}^{{\varepsilon = 1}}\, + \,{\text{va}}{{{\text{r}}}_{{\gamma }}}{\text{arg}}~{{J}^{1}}\left( {\alpha } \right) - \sum\limits_{s = 1}^4 {{\text{arg\;}}{{{\lambda }}_{s}}} } \right),$(16)
$\left( {\begin{array}{*{20}{l}} {{{E}_{3}} - i~{{s}_{{rr}}}\left( {{\mathbf{r}}{\text{*}},{\theta *}} \right)}&{ - i~{{s}_{{{\mathbf{r}}{\theta }}}}\left( {{\mathbf{r}}{\text{*}},{\theta *}} \right)} \\ { - i~{{s}_{{{\theta }{\mathbf{r}}}}}\left( {{\mathbf{r}}{\text{*}},{\theta *}} \right)}&{ - i~{{s}_{{{\theta \theta }}}}\left( {{\mathbf{r}}{\text{*}},{\theta *}} \right)} \end{array}} \right),$Тогда формула для соответствующего слагаемого в асимптотическом решении имеет вид
гдеПРИМЕР: РАСПРОСТРАНЕНИЕ ЗВУКА В ПРИБРЕЖНОМ КЛИНОВИДНОМ ВОЛНОВОДЕ
В качестве простого, но весьма показательного примера рассмотрим задачу о распространении звука в прибрежном клиновидном волноводе, показанном на рис. 1 (ребро клина – береговая линия, плоскость дна образует угол ${\beta }$ с плоскостью поверхности моря). В случае, если угол наклона дна ${\beta }$ мал, геометрия лучей в клине допускает простое аналитическое описание на языке инвариантов Вестона [17], которое мы приводим здесь для полноты изложения.
Рис. 1.
Прибрежный клиновидный волновод с акустической трассой, ориентированной вдоль изобаты y = 0. Источник и приемник отмечены на схеме буквами S и R соответственно.
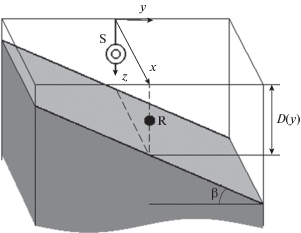
Будем описывать лучи в клине двумя углами: ${\theta }$ – угол скольжения, образуемый лучом и плоскостью $z = 0$ (измеряется в вертикальной плоскости, содержащей в себе луч), и ${\varphi }$ – угол, образуемый проекцией луча на горизонтальную плоскость и осью $x$ (ориентированной вдоль изобат и поперек градиента глубины). Заметим, что данные обозначения соответствуют тем, что использовались в предыдущих разделах, и не совпадают с обозначениями из работ Вестона (см. [17]). Напомним, что в этих работах установлены следующие факты
1. Для каждого луча величина
в однородной среде является инвариантом (инвариант Вестона). Здесь $D\left( {x,y} \right)$ – глубина моря в данной точке траектории луча, ${\theta }$ – угол скольжения луча относительно поверхности в данной точке траектории. Таким образом, если скорость звука в клине постоянна, то вертикальный угол луча не зависит от траектории его распространения, а определяется лишь глубиной $D$ в данной точке, глубиной в начальной точке ${{D}_{0}}$ и начальным вертикальным углом ${{{\theta }}_{0}}$ (в этом смысле распространение консервативно).2. Вдоль траектории луча величина
является постоянной и определяется только начальными углами запука луча ${{{\theta }}_{0}}$ и ${{{\varphi }}_{0}}$ (величину K также называют вторым инвариантом Вестона).В нашей работе горизонтальная ось x ориентирована вдоль ребра клина, а ось y – вдоль изобат (см. рис. 1). Мы будем полагать, что источник звука расположен в точке x = 0, y = 0, находящейся на расстоянии L от ребра клина. В данной работе нас будет интересовать распространение звука на трассе, ориентированной вдоль ребра. Таким образом, источник и приемник звукового сигнала находятся на одной изобате (линии y = 0).
Заметим, что инвариантность $\mathcal{T}$ и K в частности, означает, что если луч был запущен с оси $y = 0$ и после некоторого путешествия вверх по клину вернулся на эту же ось (с другой координатой $x$), то соответствующий угол ${\theta }$ будет тем же, что угол запуска луча в источнике, а соответствующий угол ${\varphi }$ будет составлять $ \pm {{{\varphi }}_{0}}.$
При ${\beta } \to 0$ проекции лучей на горизонтальную плоскость $\left( {x,y} \right)$ будут приближаться к гиперболам
(20)
$\frac{{{{{(y + L)}}^{2}}}}{{1 - {{\mathfrak{K}}^{2}}{{c}^{2}}}} - \frac{{{{{(x \pm d)}}^{2}}}}{{{{\mathfrak{K}}^{2}}{{c}^{2}}}} = \frac{{{{L}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{{\theta }}_{0}}}}{{{{{(1 - {{\mathfrak{K}}^{2}}{{c}^{2}})}}^{2}}}}~,$Интересно отметить, что проекции лучей с общим меридианальным углом выхода из источника ${{{\theta }}_{0}}$ имеют огибающую, которая также является гиперболой. Именно, рассмотрим однопараметрическое семейство гипербол, задаваемых (20) с фиксированным вертикальным углом ${{{\theta }}_{0}}.$ Огибающая этого семейства гипербол имеет вид ([18])
(21)
${{\left( {\frac{{y + L}}{{L~{\text{sin}}{{{\theta }}_{0}}}}} \right)}^{2}} - {{\left( {\frac{x}{{L~{\text{cos}}{{{\theta }}_{0}}}}} \right)}^{2}} = 1.$Из уравнения (20) легко видеть, что для одного и того же значения ${{{\theta }}_{0}}$ и фиксированных горизонтальных координат точек излучения (0, 0) и приема (xr, yr) всегда найдется две различные гиперболы с двумя различными значениями ${\varphi }{\text{.}}$
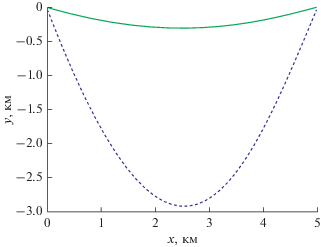
Зафиксируем параметры задачи следующим образом: пусть ${\beta } = 0.5^\circ ,$ c = 1485 м/с, глубина моря в точке излучения D0= 100 м. Рассмотрим акустическую трассу длиной 5 км, ориентированную вдоль изобаты (т.о., xr = 5 км, yr = 0). Для примера на рис. 2 показаны проекции на горизонтальную плоскость двух лучей (в дальнейшем мы называем эти кривые просто горизонтальными лучами), соединяющих источник и приемник и соответствующих значению ${{{\theta }}_{0}} = 45^\circ .$ Видно, что одна из гипербол соответствует почти прямолинейному распространению в горизонтальной плоскости, в то время как вторая соответствует сигналу с горизонтальным лучом, имеющим точку заворота вблизи ребра клина. Если зафиксировать все прочие параметры, то как при уменьшении ${{{\theta }}_{0}},$ так и при стремлении ${\beta }$ к нулю “ближняя” гипербола (сплошная линия на рис. 2) будет стремиться к прямой y = 0, а точка заворота дальней “гиперболы” (пунктирная линия на рис. 2) будет удаляться от этой прямой. Если зафиксировать ${\beta }$ и уменьшать ${{{\theta }}_{0}},$ то точка заворота будет стремиться к ребру клина.
Рис. 2.
Горизонтальные проекции трехмерных лучей с углом относительно горизонтали ${{{\theta }}_{0}} = 45^\circ $ в клине с углом наклона ${\beta } = 0.5^\circ ,$ для краткости называемые нами “ближняя” (сплошная линия) и “дальняя” (пунктирная линия) гиперболы.
Рассмотрим теперь распространение короткого импульса того же вида, что в работе [15] в описанном волноводе (сигнал, подобный по своей форме и спектру сейсморазведочному импульсу [19]).
Результаты расчета временного ряда импульсного сигнала по формуле (13), принимаемого на расстоянии xr = 5 км (трасса ориентирована вдоль изобаты), показаны на рис. 3 (пунктирная линия) для временного интервала от 3.35 до 3.5 секунд с начала отсчета времени. Для сравнения на этом же рисунке представлен временной ряд, рассчитанный по методу изображений (сплошная линия) [20]. Рисунок показывает идеальное совпадение результатов, полученных двумя методами. Заметим, что представленные на рис. 3 первые приходы импульсного сигнала в приемник соответствуют “ближним” гиперболам и малым углам ${{{\theta }}_{0}}$ (т.е. распространению почти вдоль прямой y = 0), поэтому они практически совпадают с решением на этом интервале, рассчитанным для случая, когда дно параллельно поверхности. Таким образом, наклон дна и трехмерность рассматриваемой задачи в этой части сигнала не проявляются.
Рис. 3.
Временной ряд в точке приема для случая xr = = 5 км, временной отрезок от 3.35 до 3.5 с от начала отсчета времени, рассчитанный по методу изображений (сплошная линия) и с помощью лучевой теории (пунктирная линия), т.е. по формуле (13).

Сигналы, распространяющиеся по “дальним” гиперболам, приходят в приемник существенно позднее. Соответствующий им фрагмент временного ряда в точке приема показан, например, на рис. 4 (интервал от 10.75 до 11 с от начала излучения). Показанные на рисунке сигналы соответствуют углам ${{{\theta }}_{0}},$ близким к $ \pm 45^\circ .$ Горизонтальные проекции соответствующих им лучей показаны на рис. 5, они весьма близки к “дальней” гиперболе на рис. 2. Как и в двумерном случае, приходы формируют четверки, имеющие форму “трезубцев”, показанных на рис. 4 и соответствующих группам очень близких друг к другу лучей. Три эти группы показаны сплошной, пунктирной и штрихпунктирной линией на рис. 5. Для сравнения на рис. 4 также представлен соответствующий фрагмент временного ряда решения, рассчитанный по методу изображений, идеально совпадающий с вычисленным с помощью лучевой теории.
Рис. 4.
Временной ряд в точке приема для случая xr = = 5 км, временной отрезок от 10.75 до 11 с от начала отсчета времени, рассчитанный по методу изображений (сплошная линия) и с помощью лучевой теории (пунктирная линия). Дополнительно показано решение на этом интервале в случае, если дно параллельно поверхности (штрихпунктирная линия).
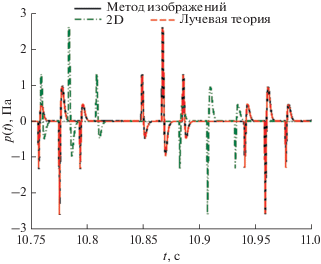
Рис. 5.
(а) – Проекции лучей на горизонтальную плоскость для приходов на рис. 4. (б) – Увеличенное изображение горизонтальных лучей поблизости от точки заворота. На рисунке выделяется три группы по 4 луча (два луча в каждой группе фактически сливаются), изображенные сплошными, штриховыми и штрихпунктирными линиями. Каждая группа лучей соответствует “трезубцу” приходов на рис. 4.
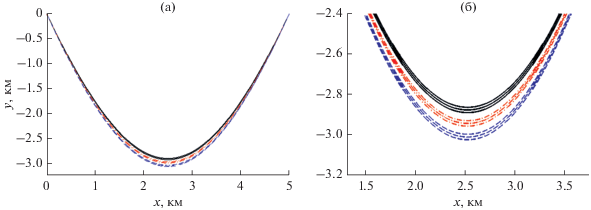
На рис. 5 также представлено решение задачи для случая, когда дно параллельно поверхности. Видно, что в отличие от интервала времени на рис. 3 в данном случае оно радикально отличается от решения в клине. Таким образом, трехмерность задачи начинает существенным образом сказываться лишь для приходов с большим запаздыванием и большими значениями ${{{\theta }}_{0}},$ которые в реальной ситуации соответствуют большим потерям, связанным с взаимодействием с дном. Для лучей с малыми углами распространения к горизонтали трехмерностью задачи обычно можно пренебречь. По этой причине горизонтальной рефракции подвержены обычно лишь компоненты сигнала, соответствующие модам наивысших номеров.
ЗАКЛЮЧЕНИЕ И ВЫВОДЫ
В работе предложены формулы, которые могут быть использованы для моделирования распространения импульсных акустических сигналов в волноводах мелкого моря с трехмерными неоднородностями дна. Наши формулы (13) и (17) по существу являются удобными для практических вычислений упрощениями формул из работ [14–16] (в них мы формально перешли к пределу, соответствующему точечному источнику). Данные формулы расширяют область применимости стандартной лучевой теории распространения звука на случай фокальных точек волновых фронтов (точек, расположенных на каустиках семейства лучей).
В качестве примера нами рассмотрена задача о распространении звука в клиновидном прибрежном волноводе мелкого моря, описана структура лучей и рассчитаны временные ряды в точке приема для трассы, ориентированной вдоль изобаты. Показано, что результаты расчетов с помощью формул (13) и (17) в точности совпадают с результатами, полученными по методу изображений [20].
Результаты нашей работы могут быть использованы, например, для анализа распространения импульсных сигналов на сложных акустических трассах большой протяженности (сотни и тысячи километров), включающих как шельфовый, так и глубоководный участки (см., например, [9]). При этом эффективность расчетов с помощью лучевых методов во временной области очень высока, в связи с чем даже для таких трасс представляется возможным учитывать эффекты, связанные с горизонтальной рефракцией звука как на неоднородностях дна, так и на гидродинамических неоднородностях различного масштаба в водном слое. Для вычислений такого масштаба в задачах подводной акустики альтернативы лучевой теории, по-видимому, в настоящее время нет. По этой причине ее дальнейшее развитие представляется весьма важной и актуальной задачей. Настоящая работа представляет собой шаг в этом направлении.
В заключение отметим, что основным препятствием для дальнейшего развития изложенного метода является то, что его затруднительно непосредственно обобщить на случай проницаемого (неидеального) дна. Действительно, в этом случае различные частотные компоненты импульсного сигнала по-разному ведут себя при отражении от дна, и проведение расчетов во временной области представляется в настоящий момент невозможным. По этой причине лучевая теорий распространения звука в волноводах с проницаемым дном обычно строится для уравнения Гельмгольца [1, 6], т.е. в частотной области. Качественный анализ сложных интерференционных и рефракционных эффектов, связанных с распространением импульсных сигналов в клиновидных прибрежных волноводах, представлен в [21].
Список литературы
Jensen F.B., Kuperman W.A., Porter M.B., Schmidt H. Computational Ocean Acoustics. N.Y.: Springer, 2012. 794 p.
Lin Y.T., Duda T.F., Newhall A.E. Three-dimensional sound propagation models using the parabolic-equation approximation and the split-step Fourier method // J. Comput. Acoust. 2013. V. 21. № 1. P. 1250018.
Sturm F. Leading-order cross term correction of three-dimensional parabolic equation models // J. Acoust. Soc. Am. 2016. V. 139. № 1. P. 263–270.
Petrov P.S., Sturm F. An explicit analytical solution for sound propagation in a three-dimensional penetrable wedge with small apex angle // J. Acoust. Soc. Am. 2016. V. 139. № 3. P. 1343–1352.
Трофимов М.Ю. Узкоугольные параболические уравнения адиабатического распространения звука одной моды в горизонтально-неоднородном мелком море// Акуст. журн. 1999. Т. 45. № 5. С. 647–652.
Rodriguez O.C., Sturm F., Petrov P., Porter M. Three-dimensional model benchmarking for cross-slope wedge propagation // Proc. Meetings on Acoustics. 2017. V. 30. № 1. P. 070 004.
de Moraes Calazan R., Rodríguez O.C. Simplex based three-dimensional eigenray search for underwater predictions // J. Acoust. Soc. Am. 2018. V. 143. № 4. P. 2059–2065.
Trofimov M.Y., Zakharenko A.D., Kozitskiy S.B. Mode Gaussian beam tracing // Computer Physics Communications. 2016. V. 207. P. 179–185.
Безответных В.В., Буренин А.В., Моргунов Ю.Н., Половинка Ю.А. Экспериментальные исследования особенностей распространения импульсных сигналов из шельфа в глубокое море // Акуст. журн. 2009. Т. 55. № 3. С. 374–380.
Моргунов Ю.Н., Безответных В.В., Буренин А.В., Войтенко Е.А. Исследование влияния гидрологических условий на распространение псевдослучайных сигналов из шельфа в глубокое море // Акуст. журн. 2016. Т. 62. № 3. С. 341–347.
Акуличев В.А., Безответных В.В., Моргунов Ю.Н., Половинка Ю.А. Применение псевдослучайных сигналов для подводной дальнометрии на шельфе // ДАН. 2010. Т. 432. № 4. С. 541–543.
Dobrokhotov S.Yu., Nazaikinskii V.E., Tirozzi B. Asymptotic solutions of 2D wave equations with variable velocity and localized right-hand side // Russian J. Math. Phys. 2010. V. 17. № 1. P. 66–76.
Маслов В.П., Федорюк М.В. Квазиклассическое приближение для уравнений квантовой механики. Москва: Наука, 1976.
Доброхотов С.Ю., Назайкинский В.Е., Шафаревич А.И. Новые интегральные представления канонического оператора Маслова в особых картах // Изв. РАН. Сер. матем. 2017. Т. 81. № 2. Т. 53–96.
Petrov P.S., Sergeev S.A., Tolchennikov A.A. Modeling of pulse signals in 3D propagation problems of deep-water acoustics based on the modified Maslov’s canonical operator // Russian J. Math. Phys. 2018. V. 25. № 1. P. 102–112.
Dobrokhotov S.Yu., Minenkov D.A., Nazaikinskii V.E., Tirozzi B. Functions of noncommuting operators in an asymptotic problem for a 2D wave equation with variable velocity and localized right-hand side // Operator Theory: Adv. and Appl. 2013. V. 228. P. 95–125.
Weston D.E. Horizontal refraction in a three-dimensional medium of variable stratification // Proc. Physical Society. 1961. V. 78. № 1. P. 46–52.
Harrison C.H. Acoustic shadow zones in the horizontal plane // J. Acoust. Soc. Am. 1979. V. 65. № 1. P. 56–61.
Рутенко А.Н., Боровой Д.И., Гриценко В.А., Петров П.С., Ущиповский В.Г., Boekholt М. Мониторинг акустического поля сейсморазведочных импульсов в прибрежной зоне // Акуст. журн. 2012. Т. 58. № 3. С. 356–369.
Tang J., Петров П.С., Piao S., Козицкий С.Б. К вопросу о методе изображений в задаче о распространении звука в клине в акустике океана: некоторые исправления и дополнения // Акуст. журн. 2018. Т. 64. № 2. С. 228–240.
Кацнельсон Б.Г., Малыхин А.Ю. Пространственно-временная интерференция звукового поля в горизонтальной плоскости в области берегового склона // Акуст. журн. 2012. Т. 58. № 3. С. 330–337.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал