Акустический журнал, 2020, T. 66, № 2, стр. 119-127

ВВЕДЕНИЕ

Анализ колебаний неоднородных полуограниченных структур может служить для идентификации их переменных упругих свойств, т.е. для решения некоторой обратной задачи. Обычно постановке обратной задачи предшествует детальный анализ решений прямой задачи, в частности анализ волновых полей на поверхности волновода в дальней зоне. Этот анализ позволяет определить, какие компоненты решений и в каких частотных диапазонах наиболее чувствительны к законам изменения упругих свойств, что позволяет в дальнейшем давать рекомендации о том, какую информацию выбирать в качестве дополнительной при решении обратных задач.

Различным аспектам решения прямых задач для неоднородных волноводов (в частности, упругой полосы) посвящены монографии [1, 2]. Обсуждены вопросы отбора единственного решения, различные аспекты строения дисперсионных множеств, способы расчета полей в дальней и ближней зонах, решен ряд контактных задач. В [3] дан анализ влияния законов изменения упругих характеристик (гладкие и кусочно-гладкие законы) на дисперсионные соотношения радиально-неоднородного цилиндрического волновода. В [4] описан подход к анализу вынужденных колебаний неоднородного волновода, причем неоднородность волновода связана как с переменностью упругих модулей, так и с наличием переменных полей предварительных напряжений различной структуры. Результаты этих работ свидетельствуют о том, что в низкочастотной области, где распространяется лишь одна мода (близкая к стержневой) волновые поля определяются лишь средними по поперечному сечению величинами упругих модулей.

В монографии [5] исследован ряд задач для нерегулярных вдоль трассы упругих волноводов, причем исследование базируется на методе однородных решений и анализе получающихся при этом бесконечных алгебраических систем.

Идентификация переменных характеристик требует решения некоторых обратных задач и обычно является нелинейной некорректной задачей. Различным аспектам решения таких задач посвящены монографии [6–8]. В монографии [6] основной анализ базируется на нестационарных задачах для полупространства и сведению обратных задач к нелинейным уравнениям типа Вольтерра, в [8] исследования проведены в случае установившихся колебаний для ограниченных структур (балки, стержни, пластины).

В работах [9, 10] приводится исследование обратных задач, основанное на минимизации функционала невязки. Описан подход к идентификации коэффициентов для эллиптических краевых задач, в частности при идентификации переменных коэффициентов Ляме, причем задача минимизации изучена в банаховом пространстве, даны некоторые оценки устойчивости. Для численного исследования использована конечно-элементная дискретизация в сочетании с регуляризирующими подходами. Продемонстрирована возможность оценить быстро меняющиеся или даже разрывные коэффициенты. Предложенный метод позволяет эффективно определять параметры Ламе в системе линейной изотропной упругости.

Путем минимизации функционала невязки решено значительное количество обратных задач, в том числе и при определении постоянных характеристик [11, 12], где упругие модули ортотропного композита определяются по информации о поле перемещений на поверхности.

Вопросы выбора параметра регуляризации, применительно к методу регуляризации Тихонова, по критерию L-кривой и решению регуляризованных систем алгебраических уравнений рассматриваются в [13].

Задача идентификации свойств поперечно-неоднородной полосы рассматривалась в ряде работ в различных постановках. В статье [14] исследуется задача об определении упругих свойств неоднородного слоя. Показано, что при задании полей смещений на всей границе волновода возможно построить решение обратной задачи в трансформантах Фурье, не прибегая к процедуре обращения. В рамках такой идеологии, используя осреднение по продольной координате волновода, авторы работ [15, 16] получили более простые коэффициентные обратные задачи, в которых осуществлено расщепление на менее сложные проблемы, аналогичные задачам для стержней. Представлены итерационные процессы, требующие решения прямой задачи и решения интегрального уравнения Фредгольма первого рода с гладким ядром, представлены вычислительные эксперименты. Подробно эти подходы и реализации отражены в [8].

Исследование подобных задач при задании полей смещений в ограниченной области на поверхности волновода требует процедуры обращения по Фурье построенных операторных уравнений. Так, в работе [17] рассмотрены прямая и обратная задачи об антиплоских колебаниях поперечно-неоднородного упругого слоя, причем плотность и модуль сдвига считаются функциями поперечной координаты. Предложена схема решения прямой задачи, основанная на использовании интегрального преобразования Фурье и решении краевой задачи методом пристрелки. Построен итерационный процесс, сформулированы интегральные уравнения Фредгольма первого рода в оригиналах, приведены результаты численных экспериментов.

1. ПОСТАНОВКА ПРЯМОЙ ЗАДАЧИ ДЛЯ НЕОДНОРОДНОГО ВОЛНОВОДА

Рассмотрим волны в неоднородном по радиальной координате изотропном цилиндрическом волноводе с кольцевым поперечным сечением, занимающем область $\left( {a \leqslant r \leqslant b,\,\, - \infty < z < \infty } \right).$ Осесимметричная форма уравнений при установившемся режиме продольно-радиальных колебаний в цилиндрической системе координат имеет вид [18]:

а определяющие соотношения представимы в форме

Здесь ${{u}_{r}}$, ${{u}_{z}}$ – компоненты вектора перемещений, ${{{\sigma }}_{r}}$, ${{{\sigma }}_{{rz}}}$ – компоненты тензора напряжений Коши, ${\lambda } = {\lambda }\left( r \right),$ ${\mu } = {\mu }\left( r \right)$ – параметры Ламе, функции, зависящие от радиальной координаты. Колебания осуществляются под действием нагрузки ${{\left. {{{{\sigma }}_{r}}\left( {r,z} \right)} \right|}_{{r = b}}} = {{{\mu }}_{0}}{\delta }\left( z \right),$ сосредоточенной на окружности на внешней границе волновода. Остальная часть границы волновода свободна от напряжений.

Введем следующие безразмерные параметры и переменные: $x = \frac{r}{b},$ ${{\xi }_{0}} = \frac{a}{b},$ $y = \frac{z}{b},$ ${{u}_{r}} = b{{X}_{1}},$ ${{u}_{z}} = ib{{X}_{2}},$ ${{\sigma }_{r}} = {{\mu }_{0}}{{X}_{3}},$ ${{\sigma }_{{rz}}} = i{{\mu }_{0}}{{X}_{4}},$ ${{\kappa }^{2}} = {{\rho {{\omega }^{2}}{{b}^{2}}} \mathord{\left/ {\vphantom {{\rho {{\omega }^{2}}{{b}^{2}}} {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}},$ ${\lambda } = 2{\nu }{{{\mu }}_{0}}G{{\left( {1 - 2{\nu }} \right)}^{{ - 1}}},$ ${\mu } = {{{\mu }}_{0}}G,$ где ${{{\mu }}_{0}}$ – характерное значение модуля сдвига, $\rho $ – плотность, $\nu $ – коэффициент Пуассона.

Для решения задачи выполним интегральное преобразование Фурье вдоль продольной координаты, вводя трансформанты

Тогда относительно трансформант можно сформировать операторный пучок в виде векторного дифференциального уравнения первого порядка с двумя ($\kappa ,\alpha $) спектральными параметрами следующего вида

причем ненулевые компоненты матриц пучка представлены ниже:

Граничные условия примут вид

Для решения задачи (3)–(4) используем метод пристрелки. Для этого построим решения двух вспомогательных задач, для которых сформулируем следующие данные Коши

Решения сформулированных задач Коши могут быть построены численно с помощью метода Рунге–Кутты.

Пусть ${{{\mathbf{\tilde {X}}}}^{{\left( 1 \right)}}}$ есть решение (3), (5), ${{{\mathbf{\tilde {X}}}}^{{\left( 2 \right)}}}$ есть решение (3), (6), тогда их линейная комбинация ${\mathbf{\tilde {X}}} = {{c}_{1}}{{{\mathbf{\tilde {X}}}}^{{\left( 1 \right)}}} + {{c}_{2}}{{{\mathbf{\tilde {X}}}}^{{\left( 2 \right)}}}$ удовлетворяет уравнениям и граничным условиям на внутренней границе. Удовлетворяя граничным условиям на внешней границе, найдем ${{c}_{1}},{{c}_{2}}$. Таким образом, задача в пространстве трансформант может быть решена численно для любой пары ($\kappa ,\alpha $) спектральных параметров за исключением тех точек, в которых определитель пристрелочной системы равен нулю. Эти точки образуют дисперсионное множество задачи – множество полюсов вектор-функции ${\mathbf{\tilde {X}}}$.

Основные свойства ветвей дисперсионного множества описаны в работе [18]. Ключевым свойством функций, описывающих ветви дисперсионного множества, является их аналитичность [1], что позволяет строить их методом продолжения по параметру.

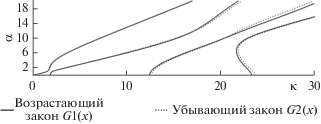
В качестве примера на рис. 1 приведены первые 4 ветви вещественной части дисперсионного множества для двух законов неоднородности с одинаковыми средними $\int_{{{\xi }_{0}}}^1 {G1(x)dx} = \int_{{{\xi }_{0}}}^1 {G2(x)dx} .$ На рис. 1 ветви, отвечающие функции $G1(x) = 1$ + $ + \,\,0.2{\text{th}}\left( {20\left( {x - 0.5({{\xi }_{0}} + 1)} \right)} \right)$, обозначены сплошной линией, а ветви, отвечающие функции $G2(x) = 1.2$ – $ - \,\,0.6{{(x - {{\xi }_{0}})}^{2}}{{(1 - {{\xi }_{0}})}^{{ - 2}}}$, точками; ${{\xi }_{0}} = 0.75.$ Вычислительные эксперименты для функций с одинаковыми средними показали, что в низкочастотной области первые две ветви практически совпадают. Различие для дисперсионных кривых становится более выраженным для частот, расположенных выше второго радиального резонанса.

Помимо вещественных дисперсионных кривых существуют комплексные и чисто мнимые ветви. Дисперсионное множество для неоднородного волновода обладает свойством симметрии, поскольку точки $({{\kappa }_{0}},{{\alpha }_{0}}),$ $\left( {{{\kappa }_{0}}, - {{\alpha }_{0}}} \right),$ $\left( {{{\kappa }_{0}},\overline {{{\alpha }_{0}}} } \right),$ $\left( {{{\kappa }_{0}}, - \overline {{{\alpha }_{0}}} } \right)$ принадлежат дисперсионному множеству одновременно.

Для нахождения оригиналов смещений требуется выполнить обратное интегральное преобразование. При этом для построения решения в дальней зоне удобно воспользоваться теоремой о вычетах и представить решение в виде суперпозиции распространяющихся мод. Техника построения полей перемещений на внешней границе волновода подробно изложена в работе [4]. На основе анализа полей в дальней зоне, которые определяются скоростями и комплексными амплитудами, обычно формируются обратные задачи, позволяющие с различной степенью точности определять законы радиальной неоднородности. Воспользуемся следующей формулой при построении полей перемещений

При вычислении интеграла в равенстве (7) по теории вычетов контур Г выбирается в соответствии с принципом предельного поглощения [1] и огибает положительные полюса снизу, а отрицательные сверху, разделяя комплексную плоскость на верхнюю и нижнюю части; через ${{{\alpha }}_{n}}$ обозначены полюса подынтегральной функции, расположенные в нижней части. В дальнейших построениях рассмотрен случай $y > 0$. Заметим, что такое расположение контура справедливо в области нормальной дисперсии, в случае аномальной дисперсии наименьший по модулю вещественный полюс контур Г в соответствии с принципом предельного поглощения обходит противоположным образом.

2. ПОСТАНОВКА ОБРАТНОЙ ЗАДАЧИ

Пусть обратная задача будет заключаться в нахождении полного вектора неизвестных $\left( {{{X}_{1}},{{X}_{2}},{{X}_{3}},{{X}_{4}}} \right),$ трансформанты которого удовлетворяют краевой задаче (3)–(4), и функции $G(x)$ в предположении постоянства коэффициента Пуассона (т.е. ${\nu } = {\text{const}}$) по информации о поле радиальных перемещений на внешней границе волновода в ограниченной области $y \in \left[ {{{y}_{1}},{{y}_{2}}} \right]$, удаленной от источника колебаний

В такой постановке задача существенно нелинейна и требуется формирование некоторого итерационного процесса типа метода Ньютона, который ранее был достаточно успешно реализован в задачах для стержней и балок [8]. При этом весьма важным является вопрос выбора начального приближения, которое обычно строится путем минимизации функционала невязки в достаточно простом классе функций (линейные, дробно-рациональные), и составление операторного уравнения, позволяющего находить уточняющую поправку. Представим способ построения такого операторного соотношения на основе метода линеаризации в окрестности некоторого решения ${{{\mathbf{\tilde {X}}}}_{0}},$ ${{G}_{0}}\left( x \right).$

Введем в рассмотрение формальный малый параметр ${\varepsilon }$ и представления G(x) = G₀(x) + $ + \,\,\varepsilon {{G}_{1}}\left( x \right) + ...,$ ${\mathbf{\tilde {X}}} = {{{\mathbf{\tilde {X}}}}_{0}} + \varepsilon {{{\mathbf{\tilde {X}}}}_{1}} + ....$ Пусть B = $ = {{{\mathbf{A}}}_{0}} - {{\kappa }^{2}}{{{\mathbf{A}}}_{{01}}}$ + $\alpha {{{\mathbf{A}}}_{1}} + {{\alpha }^{2}}{{{\mathbf{A}}}_{2}},$ тогда ${\mathbf{B}}(G(x))$ можно представить в виде разложения в ряд Тейлора: ${\mathbf{B}}(\varepsilon ) = {{{\mathbf{B}}}_{0}}({{G}_{0}})$ + $\varepsilon {{G}_{1}}(x){{{\mathbf{B}}}_{1}}({{G}_{0}}) + ....$ Таким образом, собирая коэффициенты при одинаковых степенях формального параметра ${\varepsilon }$, можно сформировать две краевые задачи.

Задача 1 при ${{{\varepsilon }}^{0}}$:

Задача 2 при ${{{\varepsilon }}^{1}}$:

Будем считать, что начальное приближение ${{G}_{0}}(x)$ известно (или найдено путем минимизации функционала невязки в некотором простом классе функций), а поправку ${{G}_{1}}(x)$ требуется найти, исходя из краевой задачи (11)–(12) и дополнительного условия (8). Отметим, что задача 1 (9)–(10), как описано выше, решается методом пристрелки, а задача 2 (11)–(12) не может решаться таким же образом, поскольку содержит неизвестную функцию ${{G}_{1}}\left( x \right)$ в правой части операторного уравнения. Вместе с тем, главные операторы в задачах 1 и 2 совпадают, что позволяет сформировать операторное уравнение, минуя прямое решение задачи 2. Такое построение опирается на использование условия разрешимости уравнения (11) [19].

Далее введем скалярное произведение комплекснозначных вектор-функций $\left( {{\mathbf{s}}(x),{\mathbf{t}}(x)} \right)$ = $\int_{{{\xi }_{0}}}^1 {\left( {\sum\limits_{i = 1}^4 {{{s}_{i}}\left( x \right){{{\bar {t}}}_{i}}\left( x \right)} } \right)xdx} $, где ${{\bar {t}}_{i}}$ – компоненты комплексно-сопряженного к ${\mathbf{t}}$ вектора.

Имеет место следующее свойство. Пусть ${{{\mathbf{\tilde {X}}}}_{0}}$ – нетривиальное решение краевой задачи для векторного дифференциального уравнения (9) с граничными условиями (10). Тогда соответствующая краевая задача для уравнения (11) с граничными условиями (12) разрешима, если выполнено условие разрешимости

где ${\mathbf{\tilde {Y}}}$ – решение следующей сопряженной задачи: где ${\mathbf{B}}_{0}^{T}$ – транспонированная матрица. Граничные условия (15) выбраны таким образом, чтобы выполнить условие $\left. {\left( {{{{{\mathbf{\tilde {X}}}}}_{1}}{\mathbf{\tilde {Y}}}} \right)x} \right|_{{{{\xi }_{0}}}}^{1} = - {{\tilde {X}}_{{11}}}\left( 1 \right),$ где $\left( {{{{{\mathbf{\tilde {X}}}}}_{1}}{\mathbf{\tilde {Y}}}} \right) = \sum\nolimits_{i = 1}^4 {{{{\tilde {X}}}_{{i1}}}{{{\tilde {Y}}}_{i}}} $ – обыкновенное скалярное произведение комплекснозначных векторов.

Для доказательства приведенного свойства умножим векторное уравнение (11) на некоторую вектор-функцию ${\mathbf{\tilde {Y}}}$ справа, в левой части равенства осуществим интегрирование по частям, а затем воспользуемся свойством скалярного произведения в правой части уравнения

Потребуем, чтобы вектор-функция ${\mathbf{\tilde {Y}}}$ являлась решением сопряженного уравнения (14) с граничными условиями (15), удовлетворяющими соотношению $\left. {\left( {{{{{\mathbf{\tilde {X}}}}}_{1}}{\mathbf{\tilde {Y}}}} \right)x} \right|_{{{{\xi }_{0}}}}^{1} = - {{\tilde {X}}_{{11}}}(1)$. Таким образом, из полученного выше соотношения получаем искомое условие (13). Нетрудно показать, что ${\mathbf{\tilde {Y}}}\left( {x,{\alpha }} \right)$ выражается через компоненты ${{{\mathbf{\tilde {X}}}}_{0}}\left( {x,{\alpha }} \right)$ следующим образом: ${\mathbf{\tilde {Y}}} = \left( {{{{\tilde {X}}}_{{30}}},{{{\tilde {X}}}_{{40}}}, - {{{\tilde {X}}}_{{10}}}, - {{{\tilde {X}}}_{{20}}}} \right).$

В развернутом виде формула (13) приводит к соотношению

которое можно трактовать как интегральное уравнение Фредгольма первого рода с мероморфным ядром в пространстве трансформант. Для его практического использования надо знать трансформанту поля смещений на всей внешней границе волновода. В случае, когда информация о поле смещений известна лишь на части границы, необходимо для получения операторного уравнения, связывающего известные и неизвестные функции, осуществить обратное преобразование Фурье в (17).

Найдем обратное интегральное преобразование Фурье для функций, фигурирующих в (17): $\tilde {X}_{{40}}^{2}\left( {x,\alpha ,\kappa } \right),$ $\tilde {X}_{{30}}^{2}\left( {x,\alpha ,\kappa } \right),$ ${{\alpha }^{2}}\tilde {X}_{{20}}^{2}\left( {x,\alpha ,\kappa } \right),$ $\alpha {{\tilde {X}}_{{20}}}\left( {x,\alpha ,\kappa } \right){{\tilde {X}}_{{10}}}\left( {x,\alpha ,\kappa } \right),$ $\tilde {X}_{{10}}^{2}\left( {x,\alpha ,\kappa } \right),$ ${{\tilde {X}}_{{10}}}\left( {x,\alpha ,\kappa } \right).$ Будем считать, что ${{\tilde {X}}_{{11}}}\left( {1,\alpha ,\kappa } \right)$ ≈ ${{\tilde {X}}_{1}}\left( {1,\alpha ,\kappa } \right)$ – $ - \,\,{{\tilde {X}}_{{10}}}\left( {1,\alpha ,\kappa } \right).$

Для нахождения обратного преобразования (оригинала) воспользуемся представлением оригинала в виде суммы вычетов (7). Затрудняет нахождение вычетов то обстоятельство, что все фигурирующие в ядре и правой части (17) функции находятся численно при конкретном значении параметра преобразования. Отметим, что функции ${{\tilde {X}}_{j}},\,j = 1,2,3,4$ имеют полюса первого порядка, а ${{\tilde {X}}_{i}}{{\tilde {X}}_{j}},$ $i = 1,2,3,4,$ $j = 1,2,3,4$ имеют те же полюса, но второго порядка. Найдем вычеты в полюсах ${{{\alpha }}_{n}}$, используя следующую схему. Пусть ${{{\mathbf{\tilde {X}}}}^{{\left( 1 \right)}}},\,{{{\mathbf{\tilde {X}}}}^{{\left( 2 \right)}}}$ – решения задач (3), (5) (3), (6). Разыскивая решение задачи в виде ${\mathbf{\tilde {X}}} = {{с}_{1}}{{{\mathbf{\tilde {X}}}}^{{\left( 1 \right)}}} + {{с}_{2}}{{{\mathbf{\tilde {X}}}}^{{\left( 2 \right)}}}$ и удовлетворяя граничным условиям при $x = 1$, получим

где ${\mathbf{B}}\left( {1,\alpha } \right) = \left( {\begin{array}{*{20}{c}} {\tilde {X}_{3}^{{(1)}}\left( {1,\alpha } \right)}&{\tilde {X}_{3}^{{(2)}}\left( {1,\alpha } \right)} \\ {\tilde {X}_{4}^{{(1)}}\left( {1,\alpha } \right)}&{\tilde {X}_{4}^{{(2)}}\left( {1,\alpha } \right)} \end{array}} \right),$ ${\mathbf{C}}\left( \alpha \right) = \left( {\begin{array}{*{20}{c}} {{{c}_{1}}\left( \alpha \right)} \\ {{{c}_{2}}\left( \alpha \right)} \end{array}} \right),$ ${\mathbf{F}} = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right).$

Осуществим разложение вектор-функции ${\mathbf{С}}\left( {\alpha } \right)$ в ряд Лорана в окрестности простого полюса ${{{\alpha }}_{n}}$

и регулярное разложение

Подставляя (19) в (18) и группируя слагаемые при одинаковых степенях, получим последовательность уравнений, решая которые найдем коэффициенты в разложении вектор-функции ${\mathbf{С}}(\alpha ).$ В результате вычет в полюсе первого порядка находится по формуле

а вычет в полюсе второго порядка по формуле

На основе предыдущих построений сформируем уравнение Фредгольма первого рода для отыскания поправки

Ядро уравнения и правая часть должны быть вычислены аналогично формуле (7), однако при численной реализации для построения поля перемещений в дальней зоне достаточно учесть вычеты в вещественных и комплексных полюсах с достаточно малой мнимой частью:

Итерационный алгоритм решения обратной задачи основан на многократном решении интегрального уравнения типа (20) методом регуляризации Тихонова. Чтобы начать итерационный процесс, найдем нулевое приближение. Для этого выберем ${{G}_{0}}\left( x \right)$ в классе постоянных или линейных функций, находя минимум функционала невязки $J = \mathop {\max }\limits_{y \in \left[ {{{y}_{1}},{{y}_{2}}} \right]} \left| {F\left( {y,\kappa } \right)} \right|$ на компактном множестве. Далее найдем ${{G}_{1}}\left( x \right)$, решая (20). Для перехода к следующей итерации формируем новое начальное приближение, новые ядра интегрального уравнения (20) и его правую часть. Выход из итерационного процесса происходит при достижении правой частью некоторого порогового значения.

3. ЧИСЛЕННОЕ РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ ПО ВОССТАНОВЛЕНИЮ ФУНКЦИИ $G1\left( x \right)$

Пусть известна радиальная компонента смещений в области, задаваемой границами ${{y}_{1}} = 0.1,\,\,{{y}_{2}} = 1,$ для параметра $\kappa = 13,$ для которого имеется три бегущие волны. На отрезке $\left[ {{{y}_{1}},{{y}_{2}}} \right]$ выберем 40 точек, а на отрезке $\left[ {{{\xi }_{0}},1} \right]$ 25 точек с равномерным шагом. В расчетах принято ${\nu } = 0.3$. Пусть начальное приближение ${{G}_{0}}\left( x \right) = 1.$

Формируя итерационный процесс по восстановлению $G1\left( x \right)$, как описано выше, получим результаты, представленные на рис. 2. На этом рисунке проиллюстрировано движение полюсов на итерациях к полюсам задачи для искомой функции ${{{\alpha }}_{1}} = - 2.00509,$ ${{{\alpha }}_{2}} = - 8.03158,$ ${{{\alpha }}_{3}} = - 15.7825$ в зависимости от номера итерации. На рис. 3 показан процесс движения вычетов в полюсах для $N = 2...30$. Отметим стабилизацию расчетов, начиная со значения $N = 3$. На рис. 4 приведен результат работы итерационного процесса. Сплошной линией обозначена искомая функция $G\left( x \right),$ точками обозначен результат восстановления на последней итерации $N = 30.$ Погрешность восстановления в этом случае в равномерной метрике не превысила 3%.

Осуществим аналогичный вычислительный эксперимент для функции $G2\left( x \right)$ при неизменных значениях остальных параметров. Начальное приближение найдено в классе линейных функций ${{G}_{0}}\left( x \right) = 2.8619 - 2.128x.$ Функции $G2\left( x \right)$ соответствуют следующие значения первых трех вещественных полюсов ${{{\alpha }}_{1}} = - 1.54232,$ ${{{\alpha }}_{2}} = - 8.16044,$ ${{{\alpha }}_{3}} = - 15.795.$

Построенные графики движения полюсов соответствуют $N = 1 \ldots 16$. Результаты, приведенные на рис. 5, свидетельствуют, что стабилизация итерационного процесса для полюсов начинается при большем числе итераций ($N = 10$), чем в первом случае. Для вычетов в полюсах наблюдается аналогичная картина стабилизации. На рис. 6 приведены результаты восстановления функции (сохранены обозначения рис. 4). Максимальная погрешность восстановления функции достигается на правом краю и составляет 8%.

Отметим, что при попытке реализации итерационного процесса для этих же функций в частотной области, расположенной до первого радиального резонанса ($\kappa < 1.927$ для функции $G1\left( x \right)$), когда имеется лишь одна распространяющаяся мода, сходимости в итерационном процессе достичь не удалось.

В частотной области, содержащей две распространяющиеся волны ($1.928 < \kappa < 12.477$ для функции $G1\left( x \right)$), для достаточно хорошего восстановления искомой функции требуется обеспечить хорошее начальное приближение, при этом удается достичь погрешности восстановления порядка 10%. Как и в той частотной области, в которой имеется одна распространяющаяся волна, в этой частотной области небольшая эффективность процедуры реконструкции связана со слабой зависимостью (малой чувствительностью) точек дисперсионного множества к закону изменения $G\left( x \right)$, отмеченной выше.

Замечание. Задача об отыскании двух функций $G\left( x \right)$ и $\nu (x)$ также может быть сформулирована, однако она требует знания дополнительной информации, например, в виде двух компонент вектора перемещений на внешней границе, либо информации о частотно-пространственных зависимостях.

ЗАКЛЮЧЕНИЕ

Разработан метод определения переменного модуля сдвига при анализе колебаний цилиндрического волновода при задании дополнительной информации в некоторой ограниченной части поверхности на фиксированной частоте колебаний. Реализован итерационный процесс построения решения, построено операторное уравнение Фредгольма первого рода с гладким ядром для отыскания поправки, которое решено на основе метода регуляризации А.Н. Тихонова. Представлены результаты вычислительных экспериментов по восстановлению возрастающей и убывающей функции на частоте, для которой существует три распространяющихся моды. Приведены графики, отражающие некоторые аспекты сходимости итерационного процесса.

Часть исследования, выполненная В.О. Юровым, поддержана Российским Научным Фондом (проект № 18-71-10045).