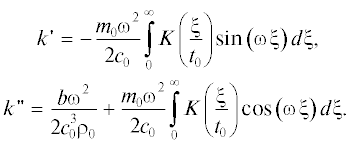Акустический журнал, 2021, T. 67, № 1, стр. 3-30
Звуковой удар: от физики нелинейных волн до акустической экологии (обзор)
О. В. Руденко a, b, c, *, Ю. Н. Маков a, b
a Московский государственный университет имени М.В. Ломоносова, физический факультет
119991 Москва, Ленинские горы, ГСП-1, Россия
b Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ГСП-1, ул. Вавилова 38, Россия
c Институт физики Земли им. О.Ю. Шмидта Российской академии наук
123995 Москва, ул. Большая Грузинская 10, стр. 1, Россия
* E-mail: rudenko@acs366.phys.msu.ru
Поступила в редакцию 28.08.2020
После доработки 28.08.2020
Принята к публикации 08.09.2020
Аннотация
Изложена история вопроса. Вначале дана информация о развитии сверхзвуковой авиации. Затем кратко описана история изучения явления звукового удара, генерируемого при полете пуль и снарядов. Приведены результаты классиков аэроакустики – К. Доплера, Э. Маха и малоизвестные исторические факты, обнаруженные в старых зарубежных источниках. Указано на необходимость правильного использования термина “звуковой удар”, который не ограничен задачами авиационной акустики и присущ многим природным и техногенным явлениям. Отмечен 100-летний приоритет акустического эффекта перед более слабым оптическим аналогом – излучением Вавилова–Черенкова. Описаны проблемы, связанные с расчетом генерации возмущений при взаимодействии трансзвуковых и сверхзвуковых течений с реальными телами: необходимость учета деталей формы аэродинамического профиля, особенности поведения пограничного слоя, формирование ударных волн, турбулизация потока, кинетика (релаксация и диссоциация) атмосферных газов. Обсуждается явление волнового резонанса, ответственного за формирование удара при переходе через звуковой барьер. Описаны нелинейные процессы формирования N-волны при распространении сигнала сложной формы. Описано влияние основных эффектов, искажающих N-образный профиль: дифракции, фокусировки, множественных релаксационных явлений, уширяющих ударный фронт. Изложена теория N-волн в неоднородной среде. Построены примеры картины лучей в стандартной атмосфере и в области за турбулентным пограничным слоем. Изложены методы расчета, основанные на приближениях нелинейной геометрической акустики и нелинейной квазиоптики. Указаны проблемы, связанные с последствиями ударов и вредным их воздействием на окружающую среду, сооружения и живые организмы. Приведена обширная библиография и перечень основных обзоров в отечественной и зарубежной литературе.
ВВЕДЕНИЕ
В этом обзоре, рассчитанном на физиков-акустиков, предпринята попытка рассмотреть звуковой удар (ЗУ) как нелинейное волновое явление, сопровождающее протекание многих природных и техногенных процессов. Однако сам термин “ЗУ” принято связывать с движением в атмосфере тел со скоростями, превышающими скорость звука, чаще всего – со сверхзвуковой авиацией. Именно поэтому при изложении конкретных моделей, методов и результатов будет сделан акцент в основном на их традиционные приложения к нелинейной авиационной акустике.
История развития авиации насчитывает примерно 120 лет. Достижения в этой области являются одновременно как индикатором, так и следствием научно-технического прогресса. Принципиально важным можно считать начало формирования “сверхзвуковой эры” в первой половине 50-х годов прошлого столетия. Эти годы примечательны созданием и становлением сверхзвуковой (СЗ) военной истребительной авиации, происходившим благодаря усилиям лидирующих в авиастроении стран (США, СССР, Англия, Франции). Именно тогда налаживалось производство, заводские испытания и последующая летная эксплуатация первых серийных моделей СЗ истребителей [1, 2] в этих странах (данные приведены в табл. 1).
Таблица 1.
Первые серийные сверхзвуковые истребители
| № | Страна | Обозначение серийного истребителя |
Начало выпуска, год | Максимальные скорость, км/ч и число Маха, М |
|---|---|---|---|---|
| 1 | США | F-100 Super Sabre | 1953 | 1390 (М = 1.3) |
| 2 | СССР | МиГ-19 | 1954 | 1450 (М = 1.4) |
| 3 | Англия | Hunter F.Mk.3 | 1953 | 1164 (М = 1.1) |
| 4 | Франция | Супер Мистэ́р (фр. Dassault Super Mystère) | 1955 | 1250 (М = 1.2) |
Уже первые СЗ полеты и быстрое увеличение их интенсивности способствовали формированию повышенного внимания (чаще всего, с негативным отношением) к сопутствующему эффекту в виде внезапного импульсного аудио-воздействия (“хлопка”). После ряда вариаций его названия в разных публикациях (см. [3, 4]) данный эффект к концу первого десятилетия приобрел устойчивое современное наименование “звуковой удар” (ЗУ) с англоязычным эквивалентом “sonic boom”.
Вскоре после наблюдения ЗУ при первых СЗ полетах были начаты теоретические и экспериментальные (натурные) исследования, непосредственно касающиеся фактора ЗУ. Это, в свою очередь, “запустило” публикационный процесс по данной тематике. Если в США, где уже в 1947 году на экспериментальном самолете X-1 была преодолена скорость звука, вся эта деятельность (исследования ЗУ и публикация первых статей) стартовала в начале последующего десятилетия [3, 4], то отечественные летно-испытательные центры вплотную занялись этой проблемой примерно на пять лет позже [5]. Работа [6] является, по-видимому, первой отечественной научной публикацией по проблеме ЗУ. Далее, с каждым годом показатели по объему экспериментально-исследовательской работы и по числу публикаций неуклонно росли (частично, за счет подключения к этому процессу специалистов из других стран). При этом тенденция монотонного роста нарушена двумя “пиками активности” в изучении ЗУ. Первый пик, приходящийся на 1960-е годы, связан с разработкой и подготовкой к эксплуатации двух сверхзвуковых пассажирских самолетов (СПС) первого поколения: Ту-144 (СССР) [5, 7, 8] и “Конкорд” (Франция–Великобритания) [9]. Новый подъем активности связан с проблемой создания СПС следующего поколения [10, 11]; он занимает временной интервал с начала нашего тысячелетия вплоть до настоящего времени.
При существующем огромном потоке информации (в виде журнальных статей, отчетов, патентов) необходимую функцию “ориентиров” традиционно выполняют обзорные материалы, список которых дан в Приложении. Представленные там работы расположены в хронологическом порядке и охватывают весь 70-летний период реализации СЗ полетов, а сопровождающий эффект ЗУ является для них основным объектом исследования. Актуальность этих работ обусловлена тем, что проявления ЗУ в виде слышимых импульсных звуков (а в некоторых случаях, дополнительного акусто-механического воздействия) становятся реально ощутимыми и, чаще всего, раздражающими факторами для отдельных индивидуумов или целых сообществ людей на подстилающей поверхности под трассой СЗ полета.
Собранные в Приложении обзорные работы позволяют говорить о некоторых стереотипах и ограничениях в трактовке термина “ЗУ”. Например, вряд ли оправдана сложившаяся практика пояснять суть фактора ЗУ исключительно через его связь со СЗ самолетами, поскольку имеется ряд природных явлений, порождающих ЗУ (гром, метеоры), а также техногенных причин (движение снарядов, спускаемых космических аппаратов и др.). С другой стороны, вряд ли стоит слишком широко толковать понятие “звуковой удар”, ассоциируя с ним и аэродинамику сверхзвукового движения, и процесс образования первичной ударной волны, и распространение этой волны (с ее превращением в слабую ударную волну) от движущегося объекта к месту нахождения объектов воздействия. Кстати, часто эксперты в области механики и аэродинамики не используют упрощенные и универсальные модели для описания слабой ударной волны, то есть аппарат нелинейной акустики. Отметим также, что большое число обзоров по ЗУ и их 70-летняя эволюция не привели к появлению общепринятого понимания термина “звуковой удар”. Добавим сюда наблюдаемую и вполне объяснимую неполноту изложения исторических фактов, относящихся к обнаружению, наблюдению и оптимизации проявлений эффекта ЗУ.
Уточним, что эти соображения не относятся к специализированным и профильным изданиям, где возможность ограничиться рамками обсуждения только авиационных проблем (в том числе, относительно ЗУ) вполне оправдана. Напротив, появляющиеся в общефизических журналах работы с, казалось бы, широким названием “Звуковой удар (Sonic Boom)" оказываются по содержанию целиком ориентированными на авиационную интерпретацию эффекта, что не способствует пониманию ЗУ как физического явления, присущего многим природным и антропогенным процессам.
На наш взгляд, среди акустиков в меньшей степени принято проводить сравнение с аналогичными явлениями в других областях физики. Гораздо чаще это делают специалисты, работающие в иных направлениях (например, электродинамики, теории плазмы, вулканологии, метеоритики).
Приведем пример такой ситуации. В октябре 1958 года лауреатами Нобелевской премии по физике стали три советских ученых: Игорь Евгеньевич Тамм, Илья Михайлович Франк, Павел Алексеевич Черенков “За открытие и интерпретацию эффекта Черенкова” (формулировка Нобелевского комитета). Напомним, что экспериментально этот эффект был открыт в 1934 году С.И. Вавиловым и П.А. Черенковым [12, 13] (С.Н. Вавилов ушел из жизни в 1951 году, до присуждения премии, что автоматически исключило его из числа лауреатов), а теоретически объяснен И.Е. Таммом и И.М. Франком в 1937 году [14]. В заключающих акт вручения премии Нобелевских лекциях (см. [15–17]) двое из трех награжденных (Тамм и Черенков) проводили аналогию между излучением движущегося в среде “сверхсветового” электрона с акустическим излучением движущегося со сверхзвуковой скоростью твердого тела в атмосфере, признавая при этом исторический приоритет именно второго (акустического) явления. Однако нужно уточнить: И.Е. Тамм в статье [18] (1939), являющейся развитием основополагающей работы [14] по теории эффекта Черенкова, вместе с подробным изложением той же самой аналогии упомянул и о различии двух эффектов. По его мнению, генерация акустического (маховского) излучения сверхзвуковой частицей является явлением “более сложным … из-за нелинейности гидродинамических уравнений”. Причину этого высказывания легко понять. Дело в том, что в 30-е годы прошлого века отсутствовали необходимые знания для учета физической нелинейности в оптике (нелинейности материальных уравнений сред). При линейном виде уравнений Максвелла (т.е. в отсутствие геометрической нелинейности) теория эффекта Вавилова–Черенкова в работах [14, 18] была разработана в безальтернативной линейной форме без каких-либо приближений относительно линеаризации. Линейная теория оказалась достаточной, чтобы объяснить экспериментальные результаты (касающиеся интенсивности излучения, его углового распределения, поляризации), полученные ранее [13] Черенковым.
В начале 1960-х годов, когда нелинейные свойства сред оказались в центре внимания многих разделов науки, появились первые исследования характеристик черенковского излучения с учетом нелинейных оптических свойств сред. Впервые на такое обобщение эффекта Вавилова–Черенкова обратил внимание Г.А. Аскарьян в статье [19]. С тех пор работы по этой тематике образуют непрерывающийся поток вплоть до настоящего времени (см. библиографию в источнике [20]).
Обращаясь ко второй “стороне” упоминаемой аналогии – к описанию акустического (маховского) излучения твердой частицы, движущейся со сверхзвуковой скоростью в газовой (жидкой) среде, – следует напомнить, что часто для этого используется линеаризованный вариант известного нелинейного уравнения для потенциала генерируемого возмущения скорости, что дает обычное волновое уравнение в акустическом приближении. Вся специфика задачи состоит в наличии нестационарного (за счет движения частицы) дельтообразного источника в волновом уравнении [21]. Решение этого линеаризованного уравнения дает и коническую область (конус Маха), в которой “содержатся” распространяющиеся акустические волны от сверхзвукового точеного источника, и саму структуру волнового поля в этом конусе Маха. Следует отметить, что в работе [22], а затем в своей же книге [23] Дж. Майлс (John W. Miles) уточнил (усложнил) математическую постановку задачи об излучении сверхзвукового точеного источника, частично сохранив в уравнении для потенциала возмущений нелинейные слагаемые, содержащие исходную невозмущенную скорость. Однако, применение преобразования Лоренца позволило автору полученное нелинейное уравнение для потенциала преобразовать в классическое волновое уравнение и найти аналитическое решение в трансформированном координатно-временном пространстве.
Этот интересный факт дает повод для следующего заключения. По аналогии с имевшими место в истории Нобелевских премий случаями с “параллельными” авторами – неудачниками тех же (или аналогичных) отмеченных премией открытий, но в силу каких-то обстоятельств не получивших такой премии, можно рассуждать об исторической “неудаче” целого научного направления – аэроакустики. Эта область в отношении своего “родного” эффекта – излучения сверхзвуковыми объектами (этот эффект даже не удостоился специального названия) – оказалась обделенной “лаврами”, в отличие от более позднего аналога – излучения Вавилова–Черенкова. Отмеченную историческую несправедливость усугубляет та тенденция, о которой говорилось выше – сужение рамок обсуждения значимости явления излучения при сверхзвуковом движении до единственного приложения к сверхзвуковой авиации.
1. РАЗВИТИЕ ПРОБЛЕМЫ ЗВУКОВОГО УДАРА. РАБОТЫ ДОПЛЕРА И МАХА
Как отмечалось выше, регулярная фиксация “слышимого” ЗУ при полетах первых СЗ самолетов и привлечение массового внимания к этому звуковому воздействию связаны с негативными реакциями населения в районах испытательных полетов, которые пришлись на первую половину 1950-х годов. Эти факты, обусловленные прогрессом в авиации, привели к тому, что весь комплекс физических, психоакустических, медицинских и социально-юридических проблем, связанных с эффектом ЗУ, становится популярным объектом исследований и публикаций в те же 1950-е годы. Интерес к ЗУ наблюдался и все последующие годы вплоть до настоящего времени. Изучались генерация возмущений поля давления вокруг СЗ самолета и их трансформация в результирующий импульс ЗУ, распространение импульса в реальной атмосфере, механизмы и результаты воздействия импульса ЗУ на население и техногенные объекты, юридические и страховые последствия воздействий ЗУ. Отметим существенный итог всех этих процессов: благодаря тому, что именно полеты СЗ самолетов сделали известным ЗУ не только для специалистов, связанных с практической авиацией, но и для значительной части населения, находящегося в “зонах воздействия” ЗУ, образовалась неразрывная смысловая связка между самим явлением и его конкретным источником. Иными словами, говоря о ЗУ, люди непременно имеют в виду ЗУ от СЗ самолета. Существование такой связки обнаруживается явно или неявно в большинстве обзорных работ по ЗУ (см. Приложение). Однако в очевидном противоречии с этим ограничением находятся, во-первых, факты из малоизвестной истории ЗУ в период дозвуковой авиации (и даже в “доавиационную” эпоху). Во-вторых – наблюдения и исследования в других областях науки и техники с иными, нежели СЗ самолеты, источниками ЗУ.
В данном разделе собраны малоизвестные факты, относящиеся к эпохе дозвуковой авиации и связанные с предсказаниями и наблюдениями физиками звуковых ударов именно через их слышимое акустическое проявление.
Начало “научной истории” почти каждой проблемы, связанной со структурой и образованием ударных волн при обтекании тел (это относится и к эффекту ЗУ) традиционно связывают c впечатляющими экспериментальными работами австрийского физика (и не менее известного философа) Эрнста Маха (1838–1916). Это работы по визуализации ударных волн (они же – баллистические волны) на основе фотографирования с использованием шлирен-метода. Такие волны генерировались при сверхзвуковом движении пуль или небольших снарядов в воздушной среде.
На рис. 1 приведена одна из самых выразительных фотографий (датирована 01.08.1893, шифр единицы хранения CD 52281), найденная нами в открытом архиве Э. Маха, находящемся в Deutsches Museum von Meisterwerken der Naturwissenschaft und Technik (Музей “шедевров” науки и техники, Германия, Мюнхен) [24]. Обращаем внимание на красоту полученных Э. Махом фотографий. Их высокое качество способствовало еще одному достижению – расшифровке и объяснению структуры (картины) ударных волн, возникающих при сверхзвуковом движении объекта, с последующим “закреплением” в физическом обиходе базовых понятий сверхзвуковой аэродинамики: головная, тыльная, боковые волны, конусная поверхность ударного фронта волны11. Эти основополагающие результаты вместе с описанием технического оснащения и методики проведения экспериментов по визуализации структуры ударных волн при СЗ обтекании пуль и снарядов изложены в двух основных по данному вопросу работах [25, 26] Э. Маха и его соавтора Питера Салчера. Обращаем внимание на приведенные здесь точные ссылки на эти две работы, поскольку их библиографические данные почти всегда даются в неполном или искаженном виде.
Представленный на рис. 1 результат Э. Маха по визуализации ударных волн относится к периоду 1886–1893 годов. В это время была выполнена большая серия экспериментов с ударными волнами, которые также играют определяющую роль в образовании акустического фактора ЗУ при полетах сверхзвуковых самолетов. Однако, несмотря на признанный статус Э. Маха как зачинателя сверхзвуковой аэродинамики с его пионерскими работами и наглядными результатами, имеются веские основания для сдвига “момента рождения” сверхзвуковой аэродинамики на 40 лет назад, до периода экспериментальной деятельности Э. Маха. Такая передвижка обусловлена тем, что зарождение сверхзвуковой аэродинамики, видимо, более справедливо связывать с теоретическими исследованиями австрийского физика Кристиана Доплера (1803–1853), хорошо всем известного по одноименному эффекту.
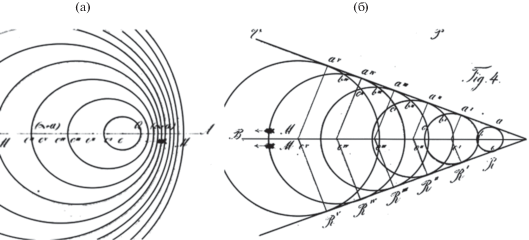
Для подтверждения этого обратимся к не самой известной, но важной для наших целей работе К. Доплера “Über den Einfluß der Bewegung des Fortpflanzungsmittels auf die Erscheinungen der Äther-, Luft- und Wasserwellen” (О влиянии движения порождающего излучение элемента на особенности волн в эфире, в воздухе и в жидкости – перевод наш), опубликованной автором в 1847 году в виде отдельной брошюры и найденной нами в оригинальном виде по электронному адресу, указанному в ссылке [28]. В этой работе К. Доплер переходит от рассмотренной ранее (в 1842 году для вывода известного одноименного эффекта) трансформации исходно сферических волновых фронтов, генерируемых движущемся с дозвуковой скоростью точечным источником возмущений среды, к случаю движения источника со звуковой, а затем и сверхзвуковой скоростью (см. рис. 2). В случае сверхзвукового движения источника Доплер на основе использования принципа Гюйгенса и геометрических построений получает результирующий волновой фронт в виде конусной поверхности, которая много позднее будет названа “конусом Маха”. Для описанного им конусного волнового фронта К. Доплер в этой работе теоретически определил величину угла раскрыва конуса, введя в рассмотрение знаменитое отношение скоростей движущегося источника волн и скорости самих волн в среде. Это отношение позже (82 года спустя) назовут “числом Маха”. В добавление к основным перечисленным результатам К. Доплер теоретически рассмотрел несколько важных частных случаев движения источника возмущения (движение с ускорением, по криволинейным траекториям и т.п.). Всю работу [28] отличает ее теоретический характер, а также постановка и анализ новых на тот момент задач. На рис. 2а, 2б приведены две иллюстрации самого К. Доплера из аннотируемой работы [28], показывающие способность автора в “предвидении” значимости рассматриваемых им задач для будущего.
Теперь сопоставим с работой К. Доплера, которую можно рассматривать как первую (речь идет о 1847 годе), имеющую прямое отношение к сверхзвуковой аэродинамике, с работой [25] Э. Маха и П. Салчера (это уже 1887 год – на 40 лет позднее), сыгравшей также ключевую роль для этой области. Содержание последней работы демонстрирует сильную экспериментальную сторону авторов (техника визуализации и описание структуры ударных волн при сверхзвуковых полетах пуль и снарядов). Однако теоретическая составляющая в этой работе, используемая для пояснения причин возникновения и структуры ударных волн при полете снаряда/пули, занимает более “скромное” по своему значению положение – все ограничивается демонстрацией трех простейших схематических рисунков волновых фронтов с интерпретацией их вида на основе принципа Гюйгенса. Эти рисунки практически идентичны представленным в работе К. Доплера (рис. 2), однако ни работа К. Доплера, ни его авторство рисунков с интерпретацией формы ударных фронтов Махом не упоминаются.
Таким образом, работа [28] и представленные в ней результаты дают основание считать К. Доплера “прародителем” (по крайней мере, в части теории) сверхзвуковой аэродинамики. Через 40 лет Э. Мах продолжил эту деятельность как уникальный экспериментатор и впервые дал возможность увидеть объекты исследования – структуру ударных волн при сверхзвуковом обтекании тел.
Теперь обратим внимание на имевшиеся в эпоху дозвуковой авиации представления об акустическом (звуковом) факторе ЗУ, который является основным и привычным проявлением и воздействием ЗУ от СЗ самолетов. Прежде всего, отметим, что в отсутствие таких эффективных и регулярных источников ЗУ, каковыми сегодня являются СЗ самолеты, фиксация звуковых сигналов, генерируемых какими-то другими сверхзвуковыми объектами, являлась довольно “экзотическим” событием. Поэтому правильное понимание и объяснение этого процесса в физической литературе встречалось нечасто.
При описании таких примеров следует опять начать с Э. Маха, который во время фотографической визуализации структуры ударных волн при полете пуль и снарядов фиксировал возникающие попутно акустические факторы, что соответствует сложившемуся через полвека термину “звуковой удар”; но у Маха они были значительно меньшей интенсивности. В своей небольшой книге, изданной в 1909 году и написанной на основе прочитанных в 1897 году лекций (эта книга в переводе на русский язык издана в 2001 году [29]), в главе 9 “О явлениях полета пуль” Э. Мах пишет: “Таким образом, когда часть головной волны достигнет уха, последнее должно расслышать треск. Похоже на то, будто пуля движется с треском. Кроме этого треска, движущегося со скоростью полета пули, большей обыкновенно, чем скорость распространения звука, должен быть еще слышен треск пороховых газов, распространяющийся с обыкновенной скоростью звука. Слышны, следовательно, два различных по времени взрыва. Этот факт долгое время оставался совсем неизвестным людям практики…”. Приведенное описание с учетом масштабирования соответствует восприятию ЗУ от СЗ самолетов.
В свете демонстрации фактов об имевшихся представлениях относительно звуковых “проявлений” сверхзвуковой аэродинамики важно упомянуть еще одну приоритетную работу Э. Маха, опубликованную им с соавтором в 1893 году [30]. Она посвящена объяснению (с тех же позиций, что и для СЗ пуль) фиксируемых “при случае” звуковых явлений (ЗУ в современном представлении) при падениях метеоритов в земной атмосфере.
Следующее по хронологии описание “из прошлого” акустического эффекта от сверхзвукового обтекания примечательно своей “неожиданностью” и авторитетностью. В 1920 году нобелевский лауреат по физике 1915 года “За заслуги в исследовании структуры кристаллов с помощью рентгеновских лучей” Уильям Генри Брэгг написал и издал книгу “The World of Sound (Six Lectures)", которая вместе с "парной” книгой про свет переведена на русский язык и издана в 1967 году в издательстве “Наука”. Интересно, что У.Г. Брэгг получил Нобелевскую премию вместе с сыном Уильямом Лоренсом Брэггом, причем сын был и остается самым молодым (25 лет) лауреатом.
В 6-ой лекции книги про звук автор подробно описывает акустические эффекты при сверхзвуковом движении. Приведем показательную выдержку из текста: “Когда таким образом образующаяся, благодаря очень большой скорости гранаты, V-образная волна проходит мимо наблюдателя, то он слышит шум, похожий на выстрел орудия; это происходит потому, что эта волна содержит сильно сжатый воздух. Обычное воздушное давление, которое окружает голову наблюдателя, переходит в давление волны, находящейся позади снаряда, и это изменение, происходя очень внезапно, производит сильное действие на наши уши. Волна, происходящая при взрыве – onde du choc, т.е. ударная волна, как ее называют французы, происходит всякий раз, когда некоторое тело движется быстрее, чем звук (выделено нами)".
Последний пример акустического эффекта при сверхзвуковом движении приведен в известной книге Л. Прандтля “Гидродинамика” (1942 год, перевод на русский язык в 2000 году [32]), где читаем: “Волны уплотнения, образующиеся при движении тела со сверхзвуковой скоростью и располагающиеся в виде конуса, распространяются в направлении, перпендикулярном к поверхности конуса, и воспринимаются наблюдателем как резкий короткий звук, напоминающий щелканье бича. В связи с этим заметим, что щелканье бича имеет такое же происхождение; оно возникает в тех случаях, когда самый внешний кончик бича движется в воздухе со сверхзвуковой скоростью”.
Приведенная здесь “мини-коллекция” представлений об акустических явлениях от сверхзвуковых движений различных объектов (пули, метеориты, конец хлыста) являются, по сути дела, правильными описаниями звуковых ударов для данных СЗ объектов, составленных в эпоху дозвуковой авиации, т.е. без представления о “ярко выраженных” ЗУ от СЗ самолетов. Это демонстрирует общность и единый физический механизм в формировании и структуре генерируемого акустического импульсного шума, обозначаемого как “звуковой удар” и сопровождающего движущиеся со сверхзвуковой скоростью объекты.
2. ГЕНЕРАЦИЯ ВОЛН ИСТОЧНИКАМИ, ДВИЖУЩИМИСЯ С ОКОЛОЗВУКОВЫМИ СКОРОСТЯМИ. ФОРМИРОВАНИЕ N-ВОЛН
Расчет генерации возмущений при взаимодействии трансзвуковых и сверхзвуковых течений с реальными телами – весьма сложная задача газовой динамики. Необходимо учитывать детали формы аэродинамического профиля, особенности поведения пограничного слоя, формирование ударных волн и турбулизацию потока. Кроме того, происходит множество явлений, часто требующих перехода от модели сплошной среды к кинетическому описанию. Среди них – возбуждение внутренних степеней свободы молекул при нагревании газа вблизи обтекаемой поверхности, их диссоциация. Ясно, что для получения результатов, имеющих прикладное значение, требуется привлечение специальных численных методов с использованием современных суперкомпьютеров. Существуют тысячи работ на эту тему, систематизация которых невозможна в рамках данного обзора, ориентированного на задачи нелинейной акустики.
2.1. О волновом резонансе
Опишем кратко явление волнового резонанса, лежащее в основе генерации возмущений телами, движущимися в среде с околозвуковыми скоростями [33].
Как известно, обычный колебательный резонанс в простейшей системе с одной степенью свободы возникает при совпадении частоты колебаний “вынуждающей внешней силы” с собственной частотой системы. Уравнение и его нужное частное решение имеют вид [34]:
(1)
$\begin{gathered} \frac{{{{d}^{2}}X}}{{d{{t}^{2}}}} + {\omega }_{0}^{2}X = A\cos \left( {{\omega }t} \right), \\ X = \frac{A}{{{\omega }_{0}^{2} - {{{\omega }}^{2}}}}\left[ {\cos \left( {{\omega }t} \right) - \cos \left( {{{{\omega }}_{0}}t} \right)} \right]. \\ \end{gathered} $Решение (1) содержит неопределенность типа 0/0 при $\omega \to {{\omega }_{0}}$. Раскрывая эту неопределенность, получим:
Амплитуда вынужденных колебаний, согласно (2), при резонансе линейно нарастает со временем. Рост может быть ограничен затуханием, а в случае слабого затухания – нелинейными эффектами, которые становятся существенными при больших амплитудах.
Волновой резонанс во многом аналогичен колебательному. Он возникает при совпадении скорости $c$ перемещения в пространстве “внешних источников” со скоростью ${{c}_{0}}$ собственной волновой моды среды. В данном случае эта мода – акустическая, а ${{c}_{0}}$ – скорость звука. Аналогом уравнения (1) для распределенной системы будет неоднородное волновое уравнение:
(3)
$\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} - c_{0}^{2}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}f\left( {t - \frac{x}{c}} \right).$Здесь функция $f$ описывает распределение источников. Нужное частное решение уравнения (3)
(4)
$u = \frac{{f\left( {t - \frac{x}{c}} \right) - f\left( {t - \frac{x}{{{{c}_{0}}}}} \right)}}{{1 - \frac{{c_{0}^{2}}}{{{{c}^{2}}}}}}$(5)
$u = \frac{x}{{2{{c}_{0}}}}\frac{\partial }{{\partial t}}f\left( {t - \frac{x}{{{{c}_{0}}}}} \right).$Как и в решении (2), при волновом резонансе “вынужденная волна” линейно нарастает, но только не со временем, а с увеличением пройденного волной расстояния $x$. Такой рост наблюдается при любой форме “внешних источников”, не обязательно гармонической. Обратим внимание, что резонансной может быть только одна из двух собственных волн $u\left( {t \pm {x \mathord{\left/ {\vphantom {x {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}} \right)$, а именно та, которая бежит в ту же сторону, что и “внешние источники”. Этот факт позволяет от уравнения второго порядка (3) перейти к уравнению первого порядка [35]:
(6)
$\frac{{\partial u}}{{\partial x}} + \frac{1}{{{{c}_{0}}}}\frac{{\partial u}}{{\partial t}} = \frac{1}{{2{{c}_{0}}}}\frac{\partial }{{\partial t}}f\left( {t - \frac{x}{c}} \right).$Более простое уравнение (6) позволяет включить в рассмотрение нелинейный и диссипативный члены, содержащие коэффициенты нелинейности $\varepsilon $ и диссипации $b$:
(7)
$\frac{{\partial u}}{{\partial x}} + \frac{1}{{{{c}_{0}}}}\frac{{\partial u}}{{\partial t}} - \frac{\varepsilon }{{c_{0}^{2}}}u\frac{{\partial u}}{{\partial t}} - \frac{b}{{2c_{0}^{3}{{\rho }_{0}}}}\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} = \frac{1}{{2{{c}_{0}}}}\frac{\partial }{{\partial t}}f\left( {t - \frac{x}{c}} \right),$Полезной будет безразмерная форма уравнения (7), содержащая малое число коэффициентов. Как принято в нелинейной акустике, перейдем к нормированным обозначениям:
(8)
$\begin{gathered} z = \frac{x}{{{{x}_{{NL}}}}} = \frac{\varepsilon }{{c_{0}^{2}}}{{\omega }_{0}}{{u}_{0}}x, \\ \theta = {{\omega }_{0}}\left( {t - \frac{x}{{{{c}_{0}}}}} \right),\,\,\,\,V = \frac{u}{{{{u}_{0}}}}. \\ \end{gathered} $Здесь константы ${{\omega }_{0}},\,{{u}_{0}}$ имеют смысл характерной частоты и амплитуды волны колебательной скорости $u$, ${{x}_{{NL}}}$ – характерная нелинейная длина. Уравнение (7) примет вид:
(9)
$\frac{{\partial V}}{{\partial z}} - V\frac{{\partial V}}{{\partial \theta }} - \Gamma \frac{{{{\partial }^{2}}V}}{{\partial {{\theta }^{2}}}} = \frac{\partial }{{\partial \theta }}F\left( {\theta + z\Delta } \right).$(10)
$\Gamma = \frac{{b{{\omega }_{0}}}}{{2\varepsilon {{c}_{0}}{{\rho }_{0}}{{u}_{0}}}},\,\,\,\,F = \frac{{{{c}_{0}}}}{{2\varepsilon u_{0}^{2}}}f,\,\,\,\,\Delta = \frac{{c - {{c}_{0}}}}{{{{c}_{0}}c}}{{\omega }_{0}}{{x}_{{NL}}}.$Число $\Gamma $, равное отношению нелинейной и диссипативной длин, называют обратным акустическим числом Рейнольдса (Гольдберга), $F$ – нормированная функция, описывающая внешние источники, $\Delta $ – безразмерная расстройка скоростей, пропорциональная разности скорости движения источников и скорости звука.
Пренебрегая в уравнении (9) нелинейным и диссипативным членами, найдем решение:
(11)
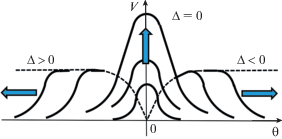
$V = \frac{{F\left( {\theta + \Delta z} \right) - F\left( \theta \right)}}{\Delta },\,\,\,\,\,{{\left. V \right|}_{{\Delta \to 0}}} = z\frac{d}{{d\theta }}F\left( \theta \right).$Решение (11) удовлетворяет условию на границе $V\left( {z = 0,\,\theta } \right) = 0$ и с точностью до обозначений совпадает с (5). Это решение для колоколообразного распределения источников изображено на рис. 3 [39].
При точном выполнении условия волнового резонанса ($\Delta = 0$) происходит неограниченный рост волны с увеличением пройденного ею расстояния $z$. Возбуждаемая волна повторяет форму производной от функции $F\left( \theta \right)$. Если же имеется расстройка от резонанса ($\Delta \ne 0$), энергия вносится источниками в область, где производная $F{\kern 1pt} '\left( \theta \right) \ne 0$, а затем “вытекает” из этой области вправо ($\Delta < 0$) или влево ($\Delta > 0$), поскольку собственная волна бежит по среде с другой (по сравнению с источниками) скоростью. Максимальное значение возмущения при этом оказывается конечным.
Например, для источников в виде “лоренцевского колокола” $F{\kern 1pt} '\left( \theta \right) = {A \mathord{\left/ {\vphantom {A {\left( {1 + {{\beta }^{2}}{{\theta }^{2}}} \right)}}} \right. \kern-0em} {\left( {1 + {{\beta }^{2}}{{\theta }^{2}}} \right)}}$ резонансная кривая будет такой:
(12)
${{\left| {{{V}_{{{\text{MAX}}}}}\left( \Delta \right)} \right|}_{{z \to \infty }}} = \frac{{\pi A}}{{2\left| {\Delta \beta } \right|}}\sim \frac{1}{{\left| {c - {{c}_{0}}} \right|}}.$При резонансе $\Delta \to 0$ стационарного значения не существует и $\left| {{{V}_{{{\text{MAX}}}}}\left( \Delta \right)} \right| \to \infty $. Этот режим соответствует неограниченному резонансному росту волны, показанному на рис. 3.
С учетом диссипативного члена в уравнении (9) решение, удовлетворяющее условию $V\left( {z = 0,\,\theta } \right) = 0$, имеет вид:
(13)
$\begin{gathered} V = \int\limits_{ - \infty }^\infty {\frac{{G\left( \omega \right)}}{{\Delta + i\omega \Gamma }}} \times \\ \times \,\,\left[ {\exp \left( { - i\omega \Delta z} \right) - \exp \left( { - \Gamma {{\omega }^{2}}z} \right)} \right]\exp \left( { - i\omega \theta } \right)d\omega . \\ \end{gathered} $Здесь
(14)
$G\left( \omega \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {F\left( \theta \right)} d\theta $(15)
$\left| V \right| = \frac{{\left| {G\left( {{{\omega }_{0}}} \right)} \right|}}{{\sqrt {{{\Delta }^{2}} + \omega _{0}^{2}\Gamma } }}.$Видно, что поглощение устраняет резонансную особенность при $\Delta \to 0$. То же происходит и для других форм $F{\kern 1pt} '\left( \theta \right)$.
В общем случае неоднородное уравнение Бюргерса можно линеаризовать. Замена переменной и соответствующее линейное уравнение имеют вид:
(16)
$V = 2\Gamma \frac{\partial }{{\partial \theta }}\ln U,\,\,\,\,\frac{{\partial U}}{{\partial z}} - \Gamma \frac{{{{\partial }^{2}}U}}{{\partial {{\theta }^{2}}}} = \frac{U}{{2\Gamma }}F\left( {\theta + z\Delta } \right).$Резонансные кривые для возбуждаемой волны в модели (16) удается построить аналитически [41]. Результат таков: максимум имеет конечную величину и сдвинут в сверхзвуковую область. Расчетные формулы из-за их громоздкости здесь не приводятся.
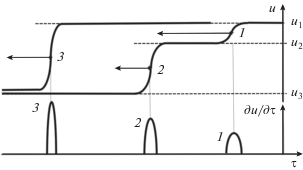
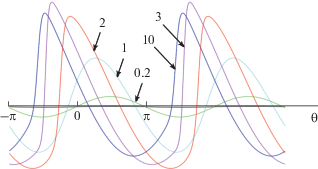
Процесс возбуждения волны движущимися источниками, имеющими гармоническую во времени форму $F{\kern 1pt} '\left( \theta \right) = A\sin \theta $, показан на рис. 4 [39]. На малых расстояниях $z$ волновой профиль повторяет форму гармонической внешней силы. С увеличением $z$ амплитуда волны растет и профиль волны искажается. В случае ненулевой расстройки рост профиля и увеличение крутизны переднего фронта сопровождаются сдвигом профиля, поскольку при $\Delta \ne 0$ источник и свободно бегущая волна движутся с разными скоростями.
Рис. 4.
Профили периодической волны, возбуждаемой синусоидальным бегущим внешним источником в нелинейной диссипативной среде для значений параметров $\Gamma = 0.1,\,\,A = 1$ и Δ = 0.1. Расстояние $z$, прошедшее волной, указано при каждой кривой.
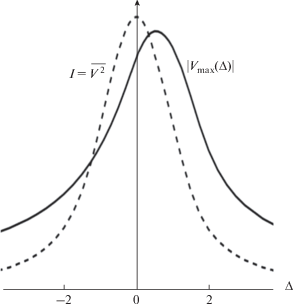
Резонансная кривая $\,\left| {{{V}_{{{\text{MAX}}}}}\left( \Delta \right)} \right|$ показана сплошной линией на рис. 5 [39]. Видно, что максимум достигается не при выполнении “линейного” резонансного условия $\Delta = 0$, а при некотором положительном значении $\Delta $. Заметим, что в предшествующих работах [41, 42] аналогичные кривые в отсутствие диссипации рассчитаны аналитически.
Рис. 5.
Нелинейные резонансные кривые – зависимости максимального значения амплитуды волны (сплошная кривая) и ее интенсивности (штриховая кривая) от расстройки Δ для значений $\Gamma = 0.1$ и A = 1.
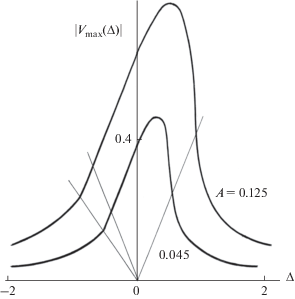
На рис. 6 изображены кривые, построенные по формулам работы [41] в отсутствие диссипации для двух различных значений амплитуды $А$ “синусного” источника. Прямые линии – сепаратрисы, разделяющие области, в которых наблюдаются гладкие волновые профили и профили с разрывами.
Рис. 6.
Нелинейные резонансные кривые для значения $\Gamma = 0$ и двух значений $А = 0.125$ и $А = 0.045$.
Одномерная задача о возбуждении нелинейной волны движущимся источником, наиболее просто иллюстрирующая явление волнового резонанса, является сильной идеализацией для генерации волн телами, обтекаемыми потоком газа. Однако она вполне адекватна задаче о возбуждении волн “тепловой стенкой”, которая создается в слабо поглощающей жидкости сканирующим вдоль ее поверхности щелевым лазерным лучом (см. рис. 8.2 из учебника [33], а также статью [36]).
2.2. Генерация волны при обтекании тонкого профиля
Рассмотрим в упрощенной постановке задачу обтекания тонкого тела трансзвуковым потоком газа. В качестве модели возьмем уравнение типа Хохлова–Заболотской [43]:
(17)
$\frac{\partial }{{\partial x}}\left[ {\frac{{\partial u{\kern 1pt} '}}{{\partial t}} + \left( {{{V}_{0}} - {{c}_{0}}} \right)\frac{{\partial u{\kern 1pt} '}}{{\partial x}} + \varepsilon u{\kern 1pt} '\frac{{\partial u{\kern 1pt} '}}{{\partial x}} + Q} \right] = \frac{{{{c}_{0}}}}{2}{{\Delta }_{ \bot }}u{\kern 1pt} '.$Здесь ${{V}_{0}}$ – невозмущенная скорость однородного потока, направленного вдоль оси $x$, $u{\kern 1pt} {\kern 1pt} '$ – проекция возмущения скорости потока на эту ось, ${{\Delta }_{ \bot }}$ – лапласиан по поперечным координатам $y,\,z$; пространственное распределение источников массы и тепла обозначено как $Q$.
Упрощенной моделью может служить также уравнение Линя–Рейсснера–Цзяна [44], похожее по структуре на уравнение (17):
(18)
$\frac{\partial }{{\partial x}}\left[ {\frac{{\partial \varphi }}{{\partial t}} + \varepsilon \frac{{{{c}_{0}}}}{2}{{{\left( {\frac{{\partial \varphi }}{{\partial x}}} \right)}}^{2}}} \right] = \frac{{{{c}_{0}}}}{2}\frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}},\,\,\,\,{\mathbf{u}}{\kern 1pt} ' = {{c}_{0}}\nabla \varphi .$Здесь $\varphi $ – потенциал возмущения ${\mathbf{u}}{\kern 1pt} '$ скорости потока. Сравнительное обсуждение (17) и (18) приведено в обзоре [45].
Чтобы связать (17), (18) с моделями, использованными при описании волнового резонанса, положим в (17) $\varepsilon = 0,\,\,Q = {{ - dF} \mathord{\left/ {\vphantom {{ - dF} {dx}}} \right. \kern-0em} {dx}}$. Решением, как нетрудно проверить, будет функция
(19)
$\begin{gathered} u{\kern 1pt} ' = \frac{1}{{{{V}_{0}} - {{c}_{0}}}}\left[ {F\left( x \right) - F\left( {x - \left( {{{V}_{0}} - {{c}_{0}}} \right)t} \right)} \right], \\ {{\lim }_{{{{V}_{0}} \to {{c}_{0}}}}}u{\kern 1pt} ' = t\frac{{dF\left( x \right)}}{{dx}}. \\ \end{gathered} $Следовательно, в пренебрежении зависимостью от поперечной координаты $z$ уравнение (17) также описывает волновой резонанс – неограниченный рост возмущения во времени.
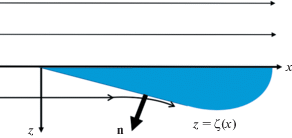
Если распределенные источники отсутствуют и $Q = 0$ в уравнении (17), возбуждать волну будет обтекаемый аэродинамический профиль. Граничное условие на его поверхности – равенство нулю нормальной компоненты возмущения скорости, то есть ${\mathbf{un}} = 0$. Если профиль тонкий, то ${{\left. {{\mathbf{un}}} \right|}_{{z = 0}}} = 0$.
Рассмотрим двумерную задачу обтекания тонкого профиля, верхняя грань которого параллельна набегающему потоку газа (рис. 7). Для этой геометрии очевидно, что подъемная сила будет создаваться за счет “отдачи” от волны, идущей от профиля в область $z > 0$. Если нет волны, не будет и подъемной силы.
В случае сверхзвукового набегающего потока $\left( {{{V}_{0}} - {{c}_{0}}} \right) > 0$ наиболее просто рассчитывается установившийся (стационарный) режим течения, структура которого не зависит от времени. При этом уравнение (17) примет вид:
(20)
$\frac{{{{\partial }^{2}}w}}{{\partial {{z}^{2}}}} = \frac{\varepsilon }{{{{c}_{0}}}}\frac{{{{\partial }^{2}}{{w}^{2}}}}{{\partial {{x}^{2}}}},\,\,\,\,\,w = u{\kern 1pt} '\,\, + \frac{{\left( {{{V}_{0}} - {{c}_{0}}} \right)}}{\varepsilon }.$Нелинейное уравнение (20) обладает рядом замечательных свойств [46]. Оно линеаризуется с помощью преобразования годографа. Частные решения можно найти методом разделения переменных, а также воспользоваться симметриями этого уравнения. Приведем здесь лишь уравнение первого порядка, которое следует из (20) и позволяет рассчитать волну в области $z > 0$:
(21)
$\frac{{\partial w}}{{\partial z}} = \sqrt {\frac{{2\varepsilon }}{{{{c}_{0}}}}} \sqrt w \frac{{\partial w}}{{\partial x}}.$Решение (21), отвечающее условию ${{\left. w \right|}_{{z = 0}}} = \Phi \left( x \right)$, имеет вид:
Форма волны находится из граничного условия
(23)
${{\left. {\frac{{\partial u{\kern 1pt} '}}{{\partial z}}} \right|}_{{z = 0}}} = {{\left. {\frac{{\partial w}}{{\partial z}}} \right|}_{{z = 0}}} = {{V}_{0}}\frac{{{{d}^{2}}\varsigma \left( x \right)}}{{d{{x}^{2}}}}.$Здесь $z = \varsigma \left( x \right)$ – форма поверхности (см. рис. 7). Подставляя решение (22) в условие (23), найдем форму волны вблизи обтекаемого профиля:
(24)
${{\Phi }^{{3/2}}}\left( x \right) = \sqrt {\frac{{9{{c}_{0}}}}{{8\varepsilon }}} {{V}_{0}}\frac{d}{{dx}}\varsigma \left( x \right).$Видим, что изломы аэродинамического профиля (скачки производной функции $\varsigma \left( x \right)$) приводят к появлению разрывов в профиле волны. Дополнительно, разрывы образуются из-за нелинейного искажения формы волны при ее распространении (увеличения крутизны передних фронтов с ростом расстояния $z$). Разрывы взаимодействуют друг с другом, приводя к формированию N-образного профиля. Эти процессы обсуждаются в следующем разделе.
2.3. Формирование N-волны при распространении в нелинейной среде импульсного сигнала сложной формы
Покажем вначале, что ограниченные в пространстве акустические волны должны быть такими, чтобы интеграл по времени от формы импульса на оси пучка равнялся нулю. Воспользуемся уравнением Хохлова–Заболотской (ХЗ), записанным для акустического давления $p$ [47]:
(25)
$\frac{\partial }{{\partial \tau }}\left[ {\frac{{\partial p}}{{\partial x}} - \frac{\varepsilon }{{c_{0}^{2}{{\rho }_{0}}}}p\frac{{\partial p}}{{\partial \tau }}} \right] = \frac{{{{c}_{0}}}}{2}{{\Delta }_{ \bot }}p.$Здесь $x$ – координата вдоль оси, $\tau = t - x/{{c}_{0}}$ – время в системе координат, движущейся вместе с волной со скоростью звука. Для круглых в поперечном сечении пучков гауссовой формы решение линеаризованного ($\varepsilon = 0$) уравнения (25) имеет наиболее простой вид:
(26)
$\begin{gathered} p = \int\limits_{ - \infty }^\infty {\frac{{S\left( \omega \right)}}{g}} \exp \left( { - i\omega \tau - \frac{{{{r}^{2}}}}{{{{a}^{2}}g}}} \right)d\omega , \\ g\left( {\omega ,x} \right) = \left( {1 + i\frac{{2{{c}_{0}}x}}{{\omega {{a}^{2}}}}} \right). \\ \end{gathered} $Оно удовлетворяет граничному условию на поверхности излучающей системы:
(27)
${{\left. p \right|}_{{x = 0}}} = \exp \left( { - \frac{{{{r}^{2}}}}{{{{a}^{2}}}}} \right)\int\limits_{ - \infty }^\infty {S\left( \omega \right)} \exp \left( { - i\omega \tau } \right)d\omega .$На оси пучка ($r = 0$) и на больших расстояниях ($x \gg {{\omega {{a}^{2}}} \mathord{\left/ {\vphantom {{\omega {{a}^{2}}} 2}} \right. \kern-0em} 2}{{c}_{0}}$) решение (26) упрощается [47]:
(28)
$\begin{gathered} p = \frac{{{{a}^{2}}}}{{2{{c}_{0}}x}}\int\limits_{ - \infty }^\infty {( - i\omega )S\left( \omega \right)} \exp \left( { - i\omega \tau } \right)d\omega = \\ = \frac{{{{a}^{2}}}}{{2{{c}_{0}}x}}\frac{\partial }{{\partial \tau }}p\left( {x = 0,\,\,r = 0,\,\tau } \right). \\ \end{gathered} $Нетрудно видеть, что в дальней зоне волна становится сферически расходящейся, а ее исходная форма дифференцируется. Иными словами, форма импульсного сигнала в дальней зоне есть производная по времени от его исходной формы. Из выражения (28) следует, что
(29)
$\int\limits_{ - \infty }^\infty {p\,d\tau = } \frac{{{{a}^{2}}}}{{2{{c}_{0}}x}}\left. {p\left( {x = 0,\,r = 0,\,\tau } \right)} \right|_{{ - \infty }}^{\infty } = 0,$Покажем теперь, что ограничение (29) приводит к следующему условию: нелинейный импульс должен содержать две равные по площади, но разные по полярности области – сжатия и разрежения. Это проще всего продемонстрировать для плоских волн, описываемых уравнением Бюргерса, поскольку оно имеет точное аналитическое решение.
Решение однородного уравнения, следующего из (9) при $F \equiv 0$, имеет вид:
(30)
$V = 2\Gamma \frac{\partial }{{\partial \theta }}\ln \int\limits_{ - \infty }^\infty {\exp \left\{ {\frac{1}{{2\Gamma }}\left[ {{{{\tilde {V}}}_{0}}\left( {\theta {\kern 1pt} '} \right) - \frac{{{{{\left( {\theta - \theta {\kern 1pt} '} \right)}}^{2}}}}{{2z}}} \right]} \right\}} d\theta {\kern 1pt} '.$Здесь ${{\tilde {V}}_{0}}\left( \theta \right)$ – первообразная функции ${{V}_{0}}\left( \theta \right) = V\left( {z = 0,\,\theta } \right)$. Как следует из (29), она должна обращаться в ноль на концах интервала, внутри которого существует волновой импульс (см. рис. 8). Для маловязкой среды (при $\Gamma \to 0$) интеграл в формуле (30) оценивается методом перевала. Результат приведен в работе [48] и в задаче 3.10 [49]:
(31)
$V\left( {z,\,\theta } \right) = \frac{1}{z}\left[ {\theta {\text{*}}\left( {z,\,\theta } \right) - \theta } \right].$Здесь $\theta {\text{*}}\left( {z,\,\theta } \right)$ – точка абсолютного максимума функции, стоящей в квадратных скобках в формуле (30).
Эта точка находится с помощью наглядного построения, показанного на рис. 8. Оно известно под названием “метод опускания параболы” [48]. Координата абсолютного максимума $\theta {\text{*}}\left( {z,\,\theta } \right)$ есть координата первой точки касания параболы ${{{{{\left( {\theta - \theta {\kern 1pt} '{\kern 1pt} } \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\theta - \theta {\kern 1pt} '{\kern 1pt} } \right)}}^{2}}} {2z}}} \right. \kern-0em} {2z}} + h$ с кривой ${{\tilde {V}}_{0}}\left( {\theta {\kern 1pt} '} \right)$ (интегралом от исходной формы волны) при уменьшении константы $h$ от $ + \infty $ до значения в “момент” касания. После этого, чтобы построить форму волны при всех $\theta $, нужно смещать центр параболы вдоль оси абсцисс.
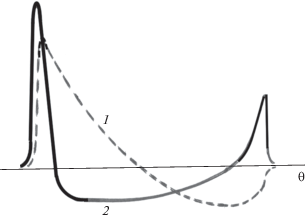
Видим, что если абсолютный максимум достигается внутри интервала, на котором первообразная ${{\tilde {V}}_{0}}\left( {\theta {\kern 1pt} '} \right)$ отлична от нуля, то волна на больших расстояниях трансформируется в симметричную $N$-волну, состоящую из двух одинаковых областей треугольной формы с разными полярностями. На переднем и заднем фронтах формируются две слабые ударные волны, соединенные прямолинейным участком профиля. Положение этих фронтов определяется формулами:
Из построения на рис. 8 видно, что на промежуточных расстояниях, когда ширина “опускаемой” параболы меньше, чем у парабол, показанных на рис. 8, форма волны оказывается более сложной; она содержит более двух ударных фронтов. Эти фронты при распространении сталкиваются и сливаются, образуя универсальную $N$-образную форму.
Чтобы описать динамику формирования $N$-волны, воспользуемся кинетическим подходом. Вначале рассмотрим акт парного соударения ударных фронтов. Покажем, что две следующие друг за другом слабые ударные волны (1 и 2 на рис. 9) сталкиваются по закону абсолютно неупругого удара двух частиц и образуют новую частицу 3 (см. задачу 2.20 [49]).
Решение уравнения Бюргерса для одиночной ударной волны (например, волны 2) с конечной шириной фронта имеет вид:
(32)
$\begin{gathered} u = \frac{1}{2}\left( {{{u}_{2}} + {{u}_{3}}} \right) + \frac{1}{2}\left( {{{u}_{2}} - {{u}_{3}}} \right)\tanh \Psi , \\ \Psi = \frac{{\varepsilon {{c}_{0}}{{\rho }_{0}}}}{b}\frac{{\left( {{{u}_{2}} - {{u}_{3}}} \right)}}{2}\left( {\tau + \frac{\varepsilon }{{c_{0}^{2}}}\frac{{\left( {{{u}_{2}} + {{u}_{3}}} \right)}}{2}x} \right). \\ \end{gathered} $Аналогия с частицей будет более наглядной, если вместо волны скорости (32) рассмотреть волну ускорения, которая пропорциональна ${{\cosh }^{{ - 2}}}\Psi $ и похожа на солитон (нижняя часть рис. 9).
Сопоставим волне (32) со “скачком” на фронте $\left( {{{u}_{2}} - {{u}_{3}}} \right)$ частицу массой ${{m}_{2}}$. Движение фронта в сопровождающей системе координат согласно (32) происходит со скоростью
(33)
${{v}_{2}} = \frac{{d{{\tau }_{2}}}}{{dx}} = - \frac{\varepsilon }{{c_{0}^{2}}}\frac{{\left( {{{u}_{2}} + {{u}_{3}}} \right)}}{2}.$Сохранение массы и линейного момента проверяется тривиально. Для соударения на рис. 9 должно быть ${{m}_{3}} = {{m}_{1}} + {{m}_{2}}$ и ${{m}_{3}}{{v}_{3}} = {{m}_{1}}{{v}_{1}} + {{m}_{2}}{{v}_{2}}$. Так и есть:
(34)
$\begin{gathered} \left( {{{u}_{1}} - {{u}_{3}}} \right) = \left( {{{u}_{1}} - {{u}_{2}}} \right) + \left( {{{u}_{2}} - {{u}_{3}}} \right), \\ \left( {{{u}_{1}} - {{u}_{3}}} \right)\left( {{{u}_{1}} + {{u}_{3}}} \right) = \\ = \left( {{{u}_{1}} - {{u}_{2}}} \right)\left( {{{u}_{1}} + {{u}_{2}}} \right) + \left( {{{u}_{2}} - {{u}_{3}}} \right)\left( {{{u}_{2}} + {{u}_{3}}} \right). \\ \end{gathered} $Однако более реальной является не последовательность ступенек, а последовательность треугольных импульсов, формирующих пилообразную волну (рис. 10). В отличие от ступенек, в промежутках между столкновениями фронтов происходит уменьшение пиковых значений “зубцов”, вызванное нелинейными потерями энергии на разрывах. Это уменьшение можно трактовать как “испарение” частиц.
Рис. 10.
Трансформация последовательности “треугольных зубцов” пилообразной волны и превращение ее в двуполярный $N$-импульс.
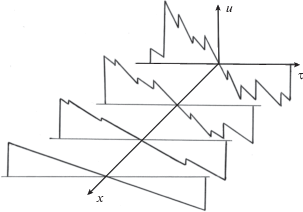
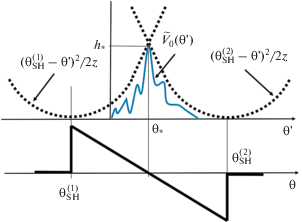
Как показано на рис. 10, в результате многократных столкновений фронтов и нелинейного затухания мелкие детали профиля исчезают, и на некотором большом расстоянии $z = {{z}_{*}} \gg 1$ формируется универсальный $N$-образный импульсный сигнал. При дальнейшем его распространении изменение параметров импульса описывается парой уравнений (см. [49], задачи 2.18, 2.19):
(35)
$\frac{{d\theta _{{{\text{SH}}}}^{{(1,2)}}}}{{dz}} = - \frac{1}{2}V_{{{\text{SH}}}}^{{(1,2)}},\,\,\,\theta _{{{\text{SH}}}}^{{(1,2)}} = - \left( {1 + z} \right)V_{{{\text{SH}}}}^{{(1.2)}}.$Отсюда следует:
(36)
$\begin{gathered} V_{{{\text{SH}}}}^{{(1,2)}}\left( z \right) = \frac{{V_{{{\text{SH}}}}^{{(1,2)}}\left( {z = {{z}_{*}}} \right)}}{{\sqrt {1 + \left( {z - {{z}_{*}}} \right)} }}, \\ \theta _{{{\text{SH}}}}^{{(1,2)}}\left( z \right) = \theta _{{{\text{SH}}}}^{{(1,2)}}\left( {z = {{z}_{*}}} \right)\sqrt {1 + \left( {z - {{z}_{*}}} \right)} . \\ \end{gathered} $Видим, что уменьшение пиковых значений на ударных фронтах (“испарение”) и увеличение длительности определяются зависимостью $\sqrt {1 + \left( {z - {{z}_{*}}} \right)} \,$.
В тех случаях, когда сигнал имеет сложную форму и содержит большое количество ударных фронтов (см. рис. 10), для его описания можно использовать статистический подход. Для этого нужно ввести функцию плотности вероятности и сконструировать соответствующее кинетическое уравнение. Пусть вероятность появления $i$-го фронта “массой” $m$ зависит только от промежутка времени $\Delta \theta $, прошедшего с момента возникновения предыдущего фронта, а интервалы $\Delta {{\theta }_{i}}$ независимы. Рассмотрим длинный интервал $\theta $, содержащий $N \gg 1$ фронтов. Плотность вероятности $g\left( {z;\,\Delta \theta ,\,m} \right)$ есть отношение числа треугольных импульсов с параметрами $\left( {\Delta \theta ,\,m} \right)$ к общему их числу $N\left( z \right)$, то есть $g = {{n\left( {z;\,\Delta \theta ,\,m} \right)} \mathord{\left/ {\vphantom {{n\left( {z;\,\Delta \theta ,\,m} \right)} {N\left( z \right)}}} \right. \kern-0em} {N\left( z \right)}}$. Ясно, что трансформация функции распределения по параметру $m$ будет происходить за счет “испарения” частиц и их столкновений – образования частиц большей массы. Изменение статистики интервалов $\Delta \theta $ происходит за счет движения – сближения и удаления фронтов друг от друга.
Уравнение, вывод которого приведен в работах [50, 51], имеет вид:
(37)
$\begin{gathered} \frac{{\partial g}}{{\partial z}} - \left[ {\frac{1}{2}\left( {m + \left\langle m \right\rangle } \right) - \frac{{\Delta \theta }}{{1 + z}}} \right]\frac{{\partial g}}{{\partial \Delta \theta }} - \frac{m}{{1 + z}}\frac{{\partial g}}{{\partial m}} = \\ = \frac{1}{2}\left\{ {m\int\limits_0^m {g\left( {z;\Delta \theta ,m{\kern 1pt} '} \right)g\left( {z;0,m - m{\kern 1pt} '} \right)} } \right.dm{\kern 1pt} ' - \\ \left. { - \left( {m - \left\langle m \right\rangle } \right)g\int\limits_0^\infty {g\left( {z;\,0,\,m{\kern 1pt} '} \right)dm{\kern 1pt} '} } \right\}. \\ \end{gathered} $Здесь $\left\langle m \right\rangle = \int_0^\infty {\int_0^\infty {mg\,dmd\Delta \theta } } $. Левая часть (37) описывает перенос вероятности. Правая часть содержит квадратичную нелинейность по функции $g$. Это – интеграл парных столкновений. В соответствии с (37) происходит увеличение вероятности больших и малых значений $m$ и уменьшение вероятности в средней части распределения. Рост вероятности малых $m$ обусловлен нелинейным затуханием. Основной вклад здесь вносят отрезки реализации, на которых поле в среднем уменьшается и столкновения происходят редко (рис. 11а).
Рис. 11.
Фрагменты реализации, приводящие к увеличению (а) вероятности малых значений $m$ и увеличению (б) вероятности больших $m$.
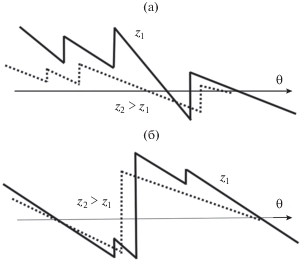
Увеличение вероятности больших значений $m$ обусловлено слиянием разрывов и образованием фронтов суммарной амплитуды; это заметно на участках реализации, где фронты догоняют друг друга и столкновения происходят чаще (рис. 11б). При наличии диссипации фронты малой амплитуды исчезают, и вероятность “перекачивается” в область больших $m$. Очевидно, что на расстояниях $z \gg 1$ “выживают” лишь две “крупные частицы”, формирующие передний и задний фронты $N$-волны (рис. 10).
В этом разделе для наглядности в основном использовалась модель плоских волн. В реальных ситуациях, когда нужно иметь количественные результаты, могут быть полезными аналогичные модели для цилиндрических, сферических волн и волн более сложной симметрии. В этих случаях нужно использовать обобщенные одномерные модели [52, 53] или модели для нелинейных пучков в неоднородной среде, которые обсуждаются в следующих разделах.
3. ОСНОВНЫЕ ПРОЦЕССЫ, ВЛИЯЮЩИЕ НА ФОРМУ N-ВОЛНЫ
Уравнения, описывающие нелинейные волны, довольно трудно решать даже в простых случаях, когда задача сильно идеализирована. В реальных условиях модель усложняется: волна не может быть плоской, а среда – однородной и стационарной. Здесь требуется анализировать сложные модели и есть риск перегрузить изложение математикой либо частными данными численного эксперимента. Поэтому мы постараемся максимально упрощать сложные модели, но так, чтобы не “выплеснуть” интересующий нас эффект. Хотелось бы “нацелить” решения на объяснение конкретных физических особенностей наблюдаемых явлений.
3.1. Влияние дифракции
Одним из основных процессов, сопровождающих распространение волны, является дифракция. Волна всегда ограничена в пространстве, чаще всего – в виде волнового пучка. В зависимости от формы исходного фронта пучок может быть квазиплоским и дифрагирующим (расходящимся), а также сфокусированным или де-фокусированным. Дифракция нелинейного пучка наиболее просто описывается уравнением с одной пространственной переменной:
(38)
$\frac{\partial }{{\partial \theta }}\left( {\frac{{\partial V}}{{\partial z}} - V\frac{{\partial V}}{{\partial \theta }}} \right) = - {{\gamma }^{2}}V.$Уравнение (38) есть “проекция” уравнения Хохлова–Заболотской (25) на ось пучка $r \to 0$ [54] . Нужное нам решение уравнения (38) имеет вид:
Первое слагаемое (линейное по переменной $\theta $) описывает гладкий профиль обычной $N$-волны, второй (квадратичный) член связан с дифракцией. Ударные фронты в профиле должны проводиться так, чтобы площади фаз сжатия и разрежения были одинаковы и не изменялись с ростом пройденного расстояния. Эти профили изображены на рис. 12. Они построены на расстояниях $z = 0$ и $z = 1$ для значения параметра ${{\gamma }^{2}} = 1.5$.
Рис. 12.
Профили волны звукового удара, искажающиеся из-за нелинейности и дифракции. Сплошные кривые построены для дифрагирующих пучков, штриховые – для плоских волн.
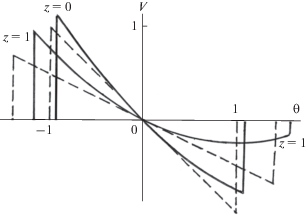
Несимметричность искажения областей сжатия и разрежения возникает из-за квадратичного по $\theta $ члена в решении (39), то есть из-за дифракции [46]. Область сжатия оказывается меньшей по длительности, но с большим “пиковым” значением возмущения. Область разрешения, напротив, сглаживается и “растягивается”. Такое поведение волн в пучках, ограниченных в поперечном сечении, довольно типично. Оно связано с появлением низкочастотной дисперсии и расфазировкой гармоник, формирующих сигнал [33] . Аналогичные явления возникают и при самолокализации пучков [55, 56].
Заметим, что одномерное уравнение (38) использовано здесь для простоты, как модель трехмерного уравнения ХЗ. Тем не менее, эта модель приводит к результатам, неплохо согласующимся с данными эксперимента и численного интегрирования [54].
3.2. Влияние фокусировки
В реальной среде встречаются локальные неоднородности, приводящие к искривлению волнового фронта. Иногда фронт становится вогнутым, а волна – сходящейся, то есть происходит фокусировка. Как при этом изменяется профиль волны?
Считаем, что продольный размер фокусирующей неоднородности невелик. По этой причине нелинейность может “накопиться” вдоль протяженной трассы еще до того, как волна достигла неоднородности, но на этапе фокусировки она практически не действует.
Процесс фокусировки по аналогии с (26) опишем решением линеаризованного уравнения ХЗ. Однако, в отличие от формулы (26), воспользуемся другим решением, учитывающим искривление исходного фронта (см. [47], формула (4.28)):
(40)
$\begin{gathered} p = \int\limits_{ - \infty }^\infty {\frac{{S\left( \omega \right)}}{{g\left( {\omega ,\,x} \right)}}} \times \\ \times \,\,\exp \left[ { - i\omega \tau - \frac{{{{r}^{2}}}}{{{{a}^{2}}g\left( {\omega ,\,x} \right)}}\left( {1 + i\frac{{{{x}_{{{\text{DIF}}}}}}}{R}} \right)} \right]\,d\omega . \\ \end{gathered} $Здесь $R$ – радиус кривизны фронта, ${{x}_{{{\text{DIF}}}}}$ – дифракционная длина,
(41)
$g\left( {\omega ,\,x} \right) = 1 - \frac{x}{R} + i\frac{x}{{{{x}_{{{\text{DIF}}}}}}},\,\,\,\,{{x}_{{{\text{DIF}}}}} = \frac{{\omega {{a}^{2}}}}{{2{{c}_{0}}}}.$Видим, что на оси пучка $(r = 0)$ и в точке геометрического фокуса $(x = R)$ решение (40) принимает вид:
(42)
$\begin{gathered} p\left( {x = R,\,r = 0,\,\tau } \right) = \frac{{ - i}}{R}\int\limits_{ - \infty }^\infty {\frac{{S\left( \omega \right)}}{{{{x}_{{{\text{DIF}}}}}}}} \times \\ \times \,\,\exp \left( { - i\omega \tau } \right)\,d\omega = \frac{{{{a}^{2}}}}{{2{{c}_{0}}R}}\frac{\partial }{{\partial \tau }}p\left( {x = 0,\,r = 0,\,\tau } \right). \\ \end{gathered} $Этот результат аналогичен следующему из формулы (28). Ясно, что форма волны, заданная на входе в неоднородность, в точке фокуса дифференцируется.
На рис. 13 изображен профиль исходной волны (штриховая кривая 1) и профиль в фокусе (сплошная кривая 2). Кривая 1 взята такой же, как сплошная кривая $z = 1$ на рис. 12. Видим, что в результате дифференцирования в области переднего и заднего фронтов $N$-волны рождаются пики, “высота” которых определяется диссипативной шириной ударных волн. Импульс приобретает форму, иногда называемую $U$-образной. Она наблюдается при распространении $N$-волны в неоднородной атмосфере [57, 58].
3.3. Релаксационные потери в атмосферных газах
Акустическая волна вызывает колебания параметров среды – давления и температуры, нарушая тем самым термодинамическое равновесие. Молекулы кислорода, азота и других атмосферных газов релаксируют к новому равновесному состоянию с собственными характерными временами, не зависящими от частоты волны. Энергия возбуждения молекул газов возвращается волне с задержкой по фазе, что приводит к ее частотно-зависимому затуханию и дисперсии – зависимости скорости распространения гармоник сигнала от частоты.
В слабо нелинейной релаксирующей среде отклонение плотности $\rho $ от равновесного значения ${{\rho }_{0}}$, вызванное акустической волной, связано с акустическим давлением $p$ интегральным соотношением [49, 59, 60]
(43)
$с_{0}^{2}\rho = p - \frac{{\varepsilon - 1}}{{с_{0}^{2}{{\rho }_{0}}}}{{p}^{2}} - m\int\limits_{ - \infty }^t {\exp \left( { - \frac{{t - t{\kern 1pt} '}}{{{{t}_{{{\text{rel}}}}}}}} \right)} \frac{{dp}}{{dt{\kern 1pt} '}}dt{\kern 1pt} '.$Видно, что плотность в данный момент времени зависит не только от давления, измеренного в тот же момент $t$, но и от предыстории, то есть от поведения давления в прошлом (от $t = - \infty $ до текущего момента $t$). Подынтегральная функция описывает “память” среды, убывающую экспоненциально с характерным временем релаксации ${{t}_{{{\text{rel}}}}}$. Здесь $m$ – безразмерное число, характеризующее “силу” релаксации.
Если в среде есть несколько релаксационных процессов, характеризуемых парами чисел $({{m}_{i}},\,\,{{t}_{{{\text{rel}},\,i}}})$, ядро может быть суммой нескольких экспонент или иметь вид более сложной убывающей функции $K\left( t \right)$ (в случае непрерывного спектра времен релаксации):
(44)
$\begin{gathered} \sum\limits_i {{{m}_{i}}} \exp \left( { - \frac{t}{{\,{{t}_{{{\text{rel}},\,i}}}}}} \right) \Rightarrow \frac{1}{{{{t}_{0}}}}\int\limits_0^\infty {m\left( {{{t}_{{{\text{rel}},\,i}}}} \right)} \times \\ \times \,\,\exp \left( { - \frac{t}{{{{t}_{{{\text{rel}},\,i}}}}}} \right)d{{t}_{{{\text{rel}},\,i}}} \equiv {{m}_{0}}K\left( {\frac{t}{{{{t}_{0}}}}} \right). \\ \end{gathered} $Уравнения механики сплошной среды с учетом определяющего соотношения (43), (44) сводятся к интегро-дифференциальному уравнению [60]:
(45)
$\begin{gathered} \frac{{\partial p}}{{\partial x}} - \frac{{\varepsilon \,}}{{c_{0}^{3}{{\rho }_{0}}}}p\frac{{\partial p}}{{\partial \tau }} - \frac{{b\,}}{{2c_{0}^{3}{{\rho }_{0}}}}\frac{{{{\partial }^{2}}p}}{{\partial {{\tau }^{2}}}} = \\ = \frac{{{{m}_{0}}}}{{2{{c}_{0}}}}\frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}\int\limits_0^\infty {K\left( {\frac{\xi }{{{{t}_{0}}}}} \right)} p\left( {\tau - \xi } \right)d\xi . \\ \end{gathered} $Для слабых волн, полагая в (45)
можно найти комплексную добавку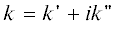 к волновому числу ${\omega \mathord{\left/ {\vphantom {\omega {{{с}_{0}}}}} \right. \kern-0em} {{{с}_{0}}}}$. Действительная и мнимая части добавки для волны, бегущей в положительном направлении$x$, равны
к волновому числу ${\omega \mathord{\left/ {\vphantom {\omega {{{с}_{0}}}}} \right. \kern-0em} {{{с}_{0}}}}$. Действительная и мнимая части добавки для волны, бегущей в положительном направлении$x$, равны
Первое выражение (47) описывает дисперсию, второе – затухание волны.
Запишем уравнение (45) в безразмерном виде, чтобы упростить последующие формулы:
(48)
$\begin{gathered} \frac{{\partial V}}{{\partial z}} - V\frac{{\partial V}}{{\partial \theta }} - \Gamma \frac{{{{\partial }^{2}}V}}{{\partial {{\theta }^{2}}}} = \\ = D\frac{{{{\partial }^{2}}}}{{\partial {{\theta }^{2}}}}\int\limits_0^\infty {K\left( s \right)\,} V\left( {\theta - s} \right)\,ds. \\ \end{gathered} $Здесь
(49)
$\begin{gathered} z = \frac{{\varepsilon {{P}_{0}}x}}{{c_{0}^{3}{{\rho }_{0}}{{t}_{0}}}},\,\,\,\,\theta = \frac{\tau }{{{{t}_{0}}}},\,\,\,\,V = \frac{p}{{{{P}_{0}}}}, \\ D = \frac{{{{m}_{0}}c_{0}^{2}{{\rho }_{0}}}}{{2\varepsilon {{P}_{0}}}},\,\,\,\,\Gamma = \frac{b}{{2\varepsilon {{t}_{0}}{{P}_{0}}}}. \\ \end{gathered} $Уравнение (48) в отсутствие вязкостной диссипации ($\Gamma = 0$) имеет точное решение для экспоненциальной формы ядра [59]:
(50)
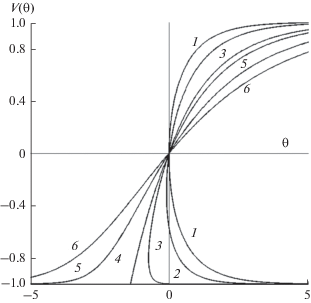
$\theta + C = \ln \frac{{{{{\left( {1 + V} \right)}}^{{D - 1}}}}}{{{{{\left( {1 - V} \right)}}^{{D + 1}}}}},\,\,\,\,\frac{{dV}}{{d\theta }} = \frac{1}{2}\frac{{\left( {1 - {{V}^{2}}} \right)}}{{\left( {D + V} \right)}}.$Это решение описывает слабую ударную волну – переход от значения $V = - 1$ (при $\theta \to - \infty $) до $V = + 1$ (при $\theta \to + \infty $). Решение однозначно при значениях параметра $D \geqslant 1$. Фронт несимметричен: в области $\theta < 0$ он более крутой, чем при положительных значениях $\theta $. Кривая $D = 1$ является граничной. Она разделяет области однозначных и неоднозначных решений. При значениях $D < 1$ в профиле появляется разрыв – скачок величиной $\left| {M + 1} \right|$. За скачком фронт описывается функцией, плавно возрастающей от значения $V = M$ до значения $V = 1$. Разрыв сглаживается, если учесть диссипативный член в (48) ($\Gamma \ne 0$).
Для импульса типа $N$-волны эти явления ведут к потерям энергии (дополнительным к нелинейному поглощению), а также к “уширению” фронтов. Особенно важно, что уменьшается крутизна ударных фронтов, то есть градиенты давления, ответственные за вредное воздействие ударов на объекты и живые организмы.
Пример эволюции такого импульса показан на рис. 15 [63]. На границе $z = 0$ исходный профиль дается функцией $V\left( {z = 0,\,\theta } \right) = \sin \theta $, отличной от нуля в области $ - 2\pi < \theta < 2\pi $. Иными словами, импульс представляет собой отрезок синусоиды, содержащий два ее периода. Наблюдается формирование ударных фронтов сжатия. Положительные и отрицательные области искажаются неодинаково, как и должно быть в среде с релаксацией. В целом импульс уширяется из-за “разбегания” ударных фронтов, занимавших исходное положение в точках $\theta = \pm 2\pi $. Этот процесс приводит на больших расстояниях к превращению исходного сигнала в двуполярный импульс типа $N$-волны.
Численный расчет проводился на основе интегро-дифференциального уравнения (48) для значений параметров $D = 0.1,\,\,\,{{\theta }_{{{\text{rel}}}}} = 1$ и ядра в виде функции Хевисайда (единичного скачка) $K = H\left( {1 - s} \right)$.
Приведем формулу, описывающую потери энергии $E = \overline {{{p}^{2}}} $ в процессе распространения нелинейной волны в среде с вязкостью и релаксацией. Из уравнения (45) следует [61]
(51)
$\begin{gathered} \frac{{\partial \,E}}{{\partial x}} = - \frac{{b\,}}{{c_{0}^{3}{{\rho }_{0}}}}\overline {{{{\left( {\frac{{\partial p}}{{\partial \tau }}} \right)}}^{2}}} + \\ + \,\,\frac{{{{m}_{0}}}}{{{{c}_{0}}}}\int\limits_0^\infty {K\left( {\frac{\xi }{{{{t}_{0}}}}} \right)} \frac{{{{\partial }^{2}}}}{{\partial {{\xi }^{2}}}}\overline {p\left( \tau \right)p\left( {\tau - \xi } \right)} d\xi . \\ \end{gathered} $Здесь черта сверху означает усреднение по $\tau $ для периодического сигнала или интеграл по всей области $\tau $, занимаемой волной. Интегральное соотношение (51) удается записать в виде разложения в ряд по средним значениям квадратов производных [61, 62]:
(52)
$\begin{gathered} \frac{{\partial E}}{{\partial z}} = - \left[ {\frac{b}{{c_{0}^{3}{{\rho }_{0}}}} + \frac{{{{m}_{0}}}}{{{{c}_{0}}}}\int\limits_0^\infty {K\left( {\frac{\xi }{{{{t}_{0}}}}} \right)} d\xi } \right]\overline {{{{\left( {\frac{{\partial p}}{{\partial \tau }}} \right)}}^{2}}} + \\ + \,\,\frac{{{{m}_{0}}}}{{{{c}_{0}}}}\left[ {\frac{1}{2}\int\limits_0^\infty {{{\xi }^{2}}K\left( {\frac{\xi }{{{{t}_{0}}}}} \right)} d\xi } \right]\overline {{{{\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{\tau }^{2}}}}} \right)}}^{2}}} - \\ - \,\,\frac{{{{m}_{0}}}}{{{{c}_{0}}}}\left[ {\frac{1}{{24}}\int\limits_0^\infty {{{\xi }^{4}}K\left( {\frac{\xi }{{{{t}_{0}}}}} \right)} d\xi } \right]\overline {{{{\left( {\frac{{{{\partial }^{3}}p}}{{\partial {{\tau }^{3}}}}} \right)}}^{2}}} + ... \\ \end{gathered} $.Отсюда видно, что затухание волны тем сильнее, чем больше крутизна ударных фронтов, на которую существенно влияют релаксационные процессы (см. рис. 14).
Рис. 14.
Форма ударного фронта в релаксирующей среде для значений $D = 0.01;0.3;0.8;1;1.5;2$ (кривые 1–6, соответственно) [62].
4. ВОЛНА В НЕОДНОРОДНОЙ СРЕДЕ
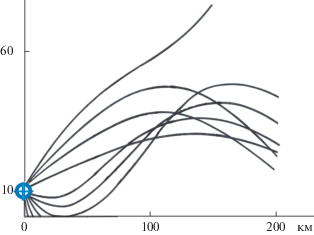
Атмосфера, как и другие природные среды, неоднородна для акустических волн. Эти неоднородности проявляются при распространении сигналов на большие расстояния [64, 65]. “Стандартная атмосфера” [66] имеет регулярную стратификацию по высоте. Ход лучей для такой стратификации в случае источника, расположенного на высоте 10 км, изображен на рис. 16. Видно, что лучи, выходящие вверх под малыми углами к вертикали, уходят в верхние слои атмосферы. Лучи под несколько большими углами идут вверх, а затем поворачивают к поверхности земли. В результате на расстояниях примерно 50–250 км образуется зона акустической тени, а далее – зона конвергенции, где происходит концентрация лучей и уровень сигнала вновь возрастает. Прямой приход волны к земле наблюдается вдоль лучей, идущих под малыми углами к вертикали вниз. Основная зона слышимости простирается до расстояний порядка 30 км.
Рис. 15.
Трансформация нелинейного импульса в релаксирующей среде. Исходный профиль $V\left( {z = 0,\,\theta } \right) = \sin \theta $ (кривая 1) отличен от нуля в области $ - 2\pi < \theta < 2\pi $. Параметры $D = 0.1,\,\,{{\theta }_{{{\text{rel}}}}} = 1$. Кривые 1–5 построены для расстояний $z = 0,2.5,5,10,15$.
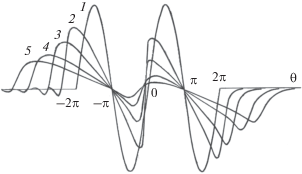
Рис. 16.
Ход лучей в стандартной атмосфере; источник расположен на высоте 10 км над поверхностью земли.
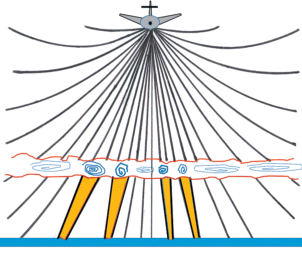
Помимо регулярной неоднородной структуры [67], влияющей на распространение звука, существуют изменяющиеся во времени неоднородности, например, ветер [68]. Важную роль играют и случайные неоднородности. На высоте порядка сотен метров часто образуется турбулентный пограничный слой, приводящий к случайной фокусировке или дефокусировке лучей [57, 69].
Сходящиеся (суживающиеся) лучевые трубки (на рис. 17 они затенены) приводят к фокусировке ударных волн и появлению “сверхударов”, вредных для наземных объектов.
Рис. 17.
Ход лучей, преломленных пограничным турбулентным слоем атмосферы; образование фокусирующих и дефокусирующих лучевых трубок.
4.1. Нелинейная геометрическая акустика, квазиоптика и лучи в неоднородной среде
Для описания разрывных волн нужно рассчитать положение и форму ударного фронта, а также скачки параметров на фронте. Однако этого недостаточно. Волна – сигнал сложного спектрального состава. В атмосфере она взаимодействует с неоднородностями, которые рассеивают и отражают ее, служат естественными волноводами, линзами, фильтрами и имеют выраженные частотно-избирательные свойства. Поэтому нужно проводить расчеты нелинейного искажения не только формы профиля, но и спектров, комбинируя два способа описания: пространственно-временное и спектральное. Эта сложная задача эффективно решается лишь в приближении нелинейной акустики с помощью методов линейной теории волн в неоднородных средах [70] и теории нелинейных волн в средах со слабой дисперсией [33].
Применительно к плавно-неоднородным средам развиты приближенные подходы (см., например, [71–74]) на основе нелинейной геометрической акустики (НГА). В работах [75–77] получены эволюционные уравнения типа ХЗ для неоднородных сред, позволившие учесть дифракцию пучков.
Имеет смысл выделить два способа упрощения исходных уравнений, облегчающих решение нелинейных задач. Первый подход основан на приближении НГА и применяется для пучков с большой расходимостью лучей. Однако он не справедлив в аберрационной области, где лучи пересекаются. Второй подход, основанный на квазиоптическом приближении, рассчитан только на пучки с узким угловым спектром, зато позволяет описать поля в окрестности фокусов и каустик.
Начнем с НГА. Исходим из волнового уравнения для неоднородной среды [75]:
(53)
$\Delta p - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}} - \frac{1}{\rho }\nabla \rho \nabla p = - \frac{\varepsilon }{{{{c}^{4}}\rho }}\frac{{{{\partial }^{2}}{{p}^{2}}}}{{\partial {{t}^{2}}}}.$Уравнение (53) без нелинейного члена приведено, например, в книге [78]. Здесь скорость звука, плотность и нелинейность среды считаются зависящими от координат. Решение (53) ищется в виде
(54)
$p = p\left( {T = t - \frac{1}{{{{c}_{0}}}}\Psi \left( {\mathbf{r}} \right),{\mathbf{r}}} \right).$В приближении НГА малой величиной считается акустическое число Маха ${p \mathord{\left/ {\vphantom {p {{{c}^{2}}\rho }}} \right. \kern-0em} {{{c}^{2}}\rho }}\sim \mu \ll 1$. Частоты считаются высокими, то есть дифференцирование ${\partial \mathord{\left/ {\vphantom {\partial {\partial T}}} \right. \kern-0em} {\partial T}}$ соответствует умножению на большой параметр ${{\mu }^{{ - 1}}}$. При этих допущениях (54) сведется к паре уравнений – эйконала $\Psi \left( {\mathbf{r}} \right)$ и переноса:
(56)
$\nabla p\nabla \Psi + \frac{p}{2}\Delta \Psi - \frac{p}{2}\nabla (\ln \rho )\nabla \Psi - \frac{{\varepsilon n}}{{{{c}^{3}}\rho }}p\frac{{\partial p}}{{\partial T}} = 0.$Уравнение эйконала (55) имеет такой же вид, как в линейной акустике. Справедливость этого очевидна для сигналов, спектр которых не содержит очень низких частот. Действительно, если приближение геометрической акустики выполнено для основной частоты, то оно тем более выполняется для высших гармоник.
Система (55), (56) замечательна тем, что ее удается проинтегрировать вдоль произвольного луча. Как показано в работе [75], эта система сводится к одному уравнению (см. также [79]):
(57)
$\frac{{\partial p}}{{\partial s}} + \frac{p}{2}\frac{d}{{ds}}\ln \left( {\frac{D}{{c\rho }}} \right) - \frac{\varepsilon }{{{{c}^{3}}\rho }}p\frac{{\partial p}}{{\partial T}} = 0.$Здесь $D$ – якобиан перехода от декартовых $x,\,y,\,z$ к криволинейным лучевым $\alpha ,\,\beta ,\,s$ координатам. Параметры $\alpha ,\,\beta $ описывают положение точки выхода луча ${{M}_{0}}\left( {\alpha ,\,\beta } \right)$ с исходной поверхности, а $s$ – расстояние, отсчитываемое вдоль луча (длина дуги ${{M}_{0}}M$ на рис. 18).
Рис. 18.
Ход луча из точки ${{M}_{0}}$ на заданной поверхности. Показаны декартовы $x,\,y,\,z$ и криволинейные лучевые координаты $\alpha ,\,\beta ,\,s$.
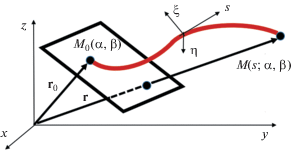
Профиль исходной (в точке ${{M}_{0}}$) волны давления $p = \Phi \left( {T;\,\alpha ,\,\beta } \right)$, где $\Phi $ – произвольная функция, искажается в соответствии с выражением
(58)
$p = \sqrt {\frac{{\rho c{{D}_{0}}}}{{{{\rho }_{0}}{{c}_{0}}D}}} \Phi \left[ {T + p\sqrt {\frac{D}{{\rho c}}} \int\limits_0^s {\frac{\varepsilon }{{{{c}^{3}}\rho }}\sqrt {\frac{{\rho c}}{D}} } ds;\alpha ,\beta } \right].$Для $N$-волны c исходной длительностью $2{{T}_{0}}$ и пиковым давлением ${{P}_{0}}$ решение (58) примет вид:
(59)
$\begin{gathered} \frac{p}{{{{P}_{0}}}} = \left\{ \begin{gathered} - \frac{T}{{{{T}_{0}}\left( {1 + Z\left( s \right)} \right)}}\sqrt {\frac{{\rho c{{D}_{0}}}}{{{{\rho }_{0}}{{c}_{0}}D}}} ,\,\,\,\frac{{\left| T \right|}}{{{{T}_{0}}}} < \sqrt {1 + Z\left( s \right)} , \hfill \\ 0,\,\,\,\,\frac{{\left| T \right|}}{{{{T}_{0}}}} > \sqrt {1 + Z\left( s \right)} , \hfill \\ \end{gathered} \right. \\ Z\left( s \right) = \frac{{{{P}_{0}}}}{{{{T}_{0}}}}\sqrt {\frac{{{{D}_{0}}}}{{{{\rho }_{0}}{{c}_{0}}}}} \int\limits_0^s {\frac{\varepsilon }{{{{c}^{3}}\rho }}\sqrt {\frac{{\rho c}}{D}} } ds. \\ \end{gathered} $Решение (58), (59) для волновых профилей, состоящих из гладких участков, соединенных ударными фронтами, проанализировано в работах [76, 77] (см. также обзор [80]). В частности, рассчитаны формы лучей и параметры нелинейных пилообразных волн и волн звукового удара в стратифицированной атмосфере.
Перейдем к описанию второго подхода, который позволяет устранить сингулярности в области пересечения лучей.
В работе [75] с использованием квазиоптического приближения теории дифракции получено уравнение, обобщающее ХЗ:
(60)
$\begin{gathered} \frac{\partial }{{\partial T}}\left[ {\frac{{\partial p}}{{\partial s}} - \frac{p}{2}\frac{d}{{ds}}\ln \left( {c\rho } \right) - \frac{\varepsilon }{{{{c}^{3}}\rho }}p\frac{{\partial p}}{{\partial T}}} \right] - \\ - \,\,\frac{1}{{2{{с}^{2}}}}{{\left[ {{{{\left( {\vec {\xi }{{\nabla }_{ \bot }}} \right)}}^{2}}с} \right]}_{{\vec {\xi } = 0}}}\frac{{{{\partial }^{2}}p}}{{\partial {{T}^{2}}}} = \frac{\rho }{2}{{\nabla }_{ \bot }}\left( {\frac{с}{\rho }{{\nabla }_{ \bot }}p} \right). \\ \end{gathered} $Идеи вывода уравнений типа (60) для линейных задач изложены в монографии [81]. Для описания поля акустического давления р в окрестности произвольно выбранного луча использованы криволинейные координаты. Расстояние s отсчитывается вдоль луча от некоторой фиксированной точки, а координаты ${\mathbf{\xi }} = \left( {\xi ,\,\eta } \right)$ (см. рис. 18) вводятся в поперечном сечении лучевой трубки специальным образом: базис этой системы повернут относительно трехгранника Френе на угол, определяемый криволинейным интегралом от кручения луча [75]. Заметим, что, используя этот подход, можно обобщить (60) на диссипативные, релаксирующие и другие среды с произвольными частотными зависимостями их линейных свойств (так, как это сделано в работе [82] для однородной среды).
4.2. Прохождение нелинейной волны через случайный фазовый экран
При распространении акустического сигнала через случайно неоднородную среду, в частности, при проникновении волны звукового удара через пограничный турбулентный слой атмосферы, возникают флуктуации параметров волны. Как известно, наиболее сильные атмосферные флуктуации наблюдаются в приземном пограничном слое на высотах порядка сотен метров. Эти расстояния обычно малы по сравнению с высотами движения больших тел на сверхзвуке. Расчет должен дать информацию о средних значениях характеристик волны и оценку вероятности появления выбросов.
Если продольный размер слоя неоднородной среды невелик, удобно использовать модель случайного фазового экрана. Слой считается плоским и бесконечно тонким. До и после него среда является однородной. При падении волны на плоскость лучи преломляются, формируя сходящиеся и расходящиеся лучевые трубки (рис. 17).
Модель неоднородности в виде одномерного фазового экрана использовалась в задачах о звуковом ударе [58, 69, 83] и в медицинских приложениях при анализе проникновения ультразвука в мозг через кости черепа [84].
Двумерный экран рассмотрен в работе [85]. Решалась система из трех нелинейных уравнений:
(61)
$\begin{gathered} \frac{{\partial X}}{{\partial z}} + X\frac{{\partial X}}{{\partial x}} + Y\frac{{\partial X}}{{\partial y}} = 0,\,\,\,\,X = \frac{{\partial \Psi }}{{\partial x}}, \\ \frac{{\partial Y}}{{\partial z}} + X\frac{{\partial Y}}{{\partial x}} + Y\frac{{\partial Y}}{{\partial y}} = 0,\,\,\,\,Y = \frac{{\partial \Psi }}{{\partial у}}, \\ \frac{{\partial p}}{{\partial z}} - \frac{\varepsilon }{{{{\rho }_{0}}c_{0}^{3}}}p\frac{{\partial p}}{{\partial T}} + X\frac{{\partial p}}{{\partial x}} + Y\frac{{\partial p}}{{\partial y}} + \frac{1}{2}p\left( {\frac{{\partial X}}{{\partial x}} + \frac{{\partial Y}}{{\partial y}}} \right) = 0. \\ \end{gathered} $Здесь $x,\,y$ – декартовы координаты в плоскости экрана, ось $z$ направлена по нормали к нему. Переменные $\left( {X,\,Y} \right) = \nabla \Psi $ определяют “наклоны” (косинусы углов наклона) лучей к осям $x,\,y$ соответственно. Они связаны двумя первыми уравнениями (61) и входят в уравнение переноса (третье уравнение системы (61)).
Система (61) замечательна тем, что имеет точное аналитическое решение. Поэтому она позволяет изучить широкий круг динамических и статистических задач. Решение для наклонов дается неявными выражениями:
(62)
$\begin{gathered} X\left( {x,y,z} \right) = {{X}_{0}}\left( {x - Xz,y - Yz} \right), \\ Y\left( {x,y,z} \right) = {{Y}_{0}}\left( {x - Xz,y - Yz} \right). \\ \end{gathered} $Здесь функции ${{X}_{0}}\left( {x,y} \right) = X\left( {x,y,z = 0} \right),$ ${{Y}_{0}}\left( {x,y} \right) = $ $ = Y\left( {x,y,z = 0} \right)$ задают углы наклона лучей на экране $z = 0$.
Далее удобно перейти к лагранжевым пространственным переменным $\alpha ,\,\beta $ (рис. 18) – координатам выхода луча из плоскости $z = 0$ и решать третье уравнение (61) (уравнение переноса) на фиксированном луче. Благодаря замене переменных $\left( {x,y,z} \right)$ на $\left( {\alpha ,\,\beta ,\,\,z} \right)$ уравнение переноса примет вид
(63)
$\frac{{\partial p}}{{\partial z}} - \frac{\varepsilon }{{{{\rho }_{0}}c_{0}^{3}}}p\frac{{\partial p}}{{\partial T}} + \frac{p}{2}\frac{d}{{dz}}\ln S = 0.$В уравнении (63) переменные $\alpha $ и $\beta $ играют роль параметров, поэтому (63) легко интегрируется. Функция $S$ – это якобиан преобразования от физических координат $\left( {x,y} \right)$ к лагранжевым $\left( {\alpha ,\,\beta } \right)$. Одновременно якобиан $S$ имеет смысл площади поперечного сечения лучевой трубки на расстоянии $z$ от экрана, сформированной близкими лучами, вышедшими из окрестности точки $\left( {\alpha ,\,\beta ,z = 0} \right)$.
На рис. 19 для примера изображено пространственное распределение максимумов акустического давления $N$-волны на поверхности земли после прохождения волной экрана с периодическими неоднородностями. Видно, что из-за схождения лучей возникают области фокусировок, создающие острые пики давления.
Рис. 19.
Распределение максимумов давления [85] за фазовым экраном с периодически расположенными неоднородностями.
Используя аналитическое решение системы (61), можно рассчитать характеристическую функцию и плотность вероятности распределения площади сечения лучевой трубки. Характеристическая функция имеет вид [85]:
(64)
$\begin{gathered} \Theta \left( \varsigma \right) = \left\langle {\exp \left( {i\varsigma S} \right)} \right\rangle = \\ = \frac{{16}}{{\sqrt {4 - i\varsigma {{l}^{2}}} \left( {8 + i\varsigma {{l}^{2}}} \right)}}\exp \left( {i\varsigma - \frac{{{{\varsigma }^{2}}{{l}^{2}}}}{{4 - i\varsigma \,{{l}^{2}}}}} \right). \\ \end{gathered} $Здесь $l = \left( {{{8{{\sigma }_{0}}} \mathord{\left/ {\vphantom {{8{{\sigma }_{0}}} {r_{0}^{2}}}} \right. \kern-0em} {r_{0}^{2}}}} \right)z$. Параметры ${{\sigma }_{0}}$ и ${{r}_{0}}$ определяются видом корреляционной функции пространственного распределения фазы волны на плоскости экрана:
(65)
$\begin{gathered} \left\langle {{{\psi }_{1}}\left( {{{x}_{1}},{{y}_{1}}} \right){{\psi }_{2}}\left( {{{x}_{2}},{{y}_{2}}} \right)} \right\rangle = \\ = \sigma _{0}^{2}\exp \left( { - \frac{{{{{\left( {{{x}_{1}} - {{x}_{2}}} \right)}}^{2}} + {{{\left( {{{y}_{1}} - {{y}_{2}}} \right)}}^{2}}}}{{r_{0}^{2}}}} \right). \\ \end{gathered} $Дифференцированием функции (64) по параметру $\varsigma $ получаются выражения для среднего значения площади лучевой трубки и ее старших моментов. В частности, средние значения равны
(66)
$\left\langle S \right\rangle = 1$, $\left\langle {{{S}^{2}}} \right\rangle = 1 + 8\nu {{z}^{2}} + 12{{\nu }^{4}}{{z}^{4}}.$Здесь $\nu = {{4\sigma _{0}^{2}} \mathord{\left/ {\vphantom {{4\sigma _{0}^{2}} {r_{0}^{4}}}} \right. \kern-0em} {r_{0}^{4}}}$. Таким образом, площадь лучевой трубки в среднем при распространении не изменяется, в тоже время дисперсия с ростом расстояния возрастает, что говорит о повышении вероятности пересечения лучевых трубок и появления каустик.
Плотность вероятности находится как Фурье-преобразование характеристической функции (64). Рассчитанная для нескольких значений параметра $l = 0,4;\,\,0,7;\,\,\,1;\,\,\,2$ (кривые 1–4) плотность вероятности представлена на рис. 20. При малых значениях параметра $l$, то есть небольших расстояниях от экрана, плотность вероятности стремится к дельта-функции $\delta \left( {S - 1} \right)$. При больших значениях $l$ максимум сдвигается влево и появляются “нефизичные хвосты” в области отрицательных значений $S$, что указывает на значительную вероятность пересечения лучей. Рост вероятности малых значений $S$ ведет к выбросам – появлению импульсов звукового удара с большими пиковыми значениями акустического давления на фронте ударной волны.
Рис. 20.
Вероятностное распределение площади сечения лучевых трубок на различных расстояниях от экрана [85].
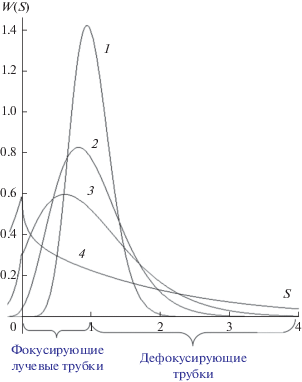
Наглядная картина роста вероятности появления “сверхударов” при удалении от экрана с одномерным распределением неоднородностей показана на рис. 21 [69]. Исходное распределение, представляющее собой дельта-функцию, расширяется как в сторону больших, так и меньших значений пикового давления $N$-волны. Появление “правого крыла” соответствует росту вероятности выбросов с большими амплитудами. Штриховая кривая для нормированного расстояния 1 на рис. 21 построена по линейной теории. Таким образом, учет нелинейности среды после прохождения экрана несколько уменьшает давление из-за потерь энергии на ударном фронте.
5. О ХАРАКТЕРИСТИКАХ И ОЦЕНКАХ СУБЪЕКТИВНОГО ВОСПРИЯТИЯ ЗВУКОВЫХ УДАРОВ, СВЯЗАННЫХ С АКУСТИЧЕСКОЙ ЭКОЛОГИЕЙ
Отмечая факт заметного влияния ЗУ от сверхзвуковых самолетов на окружающую среду (прежде всего, на население в зоне “ощутимого” выброса давления у земной поверхности), полезно обсудить развитие работ по изучению субъективного восприятия [86, 87] данного импульсного шума для исследования поведенческих и психоакустических реакций [88, 89]. Важно также иметь возможность прогноза “отдаленных” последствий воздействия ЗУ на социо- и экосистему с целью их минимизации.
Обратим внимание на общность следующего ряда исследований. После появления нового источника шума (это были первые коммерческие самолеты 1920–30-х годов) проводилось физико-техническое изучение механизмов генерации шума, а также исследование его влияния на живые субъекты (на людей, и позднее – на различных представителей фауны). Ко второму направлению относится фиксация жалоб и отрицательных реакций граждан на действие шума. Со значительным сдвигом во времени формулируются ограничительные нормативные требования к шуму. Первые итоги исследований конца 1920-х годов относительно генерируемых самолетами звуков (шумов) изложены в работе 1930 года [90].
В эти же годы появляются данные о поданных в суд жалобах на отрицательные эффекты, вызванные промышленным шумом и шумом, создаваемым пролетами первых “медленных” самолетов, имеющих маломощные двигатели [91, 92]. Затем усилились тенденции роста числа самолетов, увеличения мощности их двигателей и, соответственно, шумности (особенно на этапе взлета). В начале 1950-х годов появились более шумные реактивные самолеты, что привело к растущему потоку жалоб и обращений в суд по поводу негативного воздействия шума на жителей и домашних животных. Однако это не слишком ускорило введение нормативных ограничений на авиационный шум (до конца 1970-х годов – дозвуковых коммерческих самолетов). Только в 1972 году Международная организация гражданской авиации (ИКАО) ввела в действие стандарты по шуму, создаваемому дозвуковыми самолетами на местности. Эти стандарты основаны на положениях документа, известного как Приложение 16 (Об охране окружающей среды, том 1, раздел “Авиационный шум”) к Конвенции о международной гражданской авиации 1944 года.
Переходя к рассмотрению ЗУ, который также относят к авиационным шумам, необходимо обратить внимание на аналогии в развитии интереса к новому феномену (появившемуся на рубеже 1940-х и 50-х годов) с тем, что сообщено относительно шума от дозвуковых самолетов. Таким же образом, одна часть научно-инженерных усилий была направлена на изучение физических аспектов (генерация в режиме сверхзвукового обтекания самолета с вариациями условий и параметров обтекания, прохождение волны ЗУ через атмосферу), а другая часть – на изучение последствий ЗУ. Последняя, как и ранее, стимулировалась негативной реакцией населения, испытавшего на себе неприятные слуховые, психо-физиологические и другие воздействия. В работе [5] представлены свидетельства участников этого второго направления, стимулированного “давлением” со стороны обычных граждан, даже не знакомых с явлением ЗУ. На стр. 68 этой книги можно прочитать: “В 1956 году, по установившимся в то время в нашей стране демократическим правилам, граждане нескольких селений Горьковской области написали жалобу в ЦК КПСС, связав часто повторяющийся “гром” с полетами самолетов авиационного завода. Жалоба была направлена для рассмотрения в Министерство авиационной промышленности, а оттуда последовало указание начальнику Летно-исследовательского института Н.С. Строеву: “Разобраться и доложить”. Возглавил изучение проблемы и обоснование ответа заместитель начальника ЛИИ профессор И.В. Остославский. Первые же сведения подтвердили, что жалобы связаны с испытательными полетами самолетов МИГ-19, которые Горьковский авиазавод начал в то время строить и испытывать. Анализ показал, что жалобы вызываются только полетами с достижением сверхзвуковых скоростей (самолеты превышали скорость звука на высотах более 1500 м)…” Удивительным в этом отрывке является то, что даже высококлассные специалисты в 1956 году четко не связывали “слышимый громоподобный” эффект со сверхзвуковым полетом самолета.
Однако, в дальнейшем следует обратить внимание на развитие такого “инструментария” как критерии, метрики для количественного показателя объективного воздействия ЗУ (в общем случае, с разнообразной формой импульса ЗУ), психо-эмоциональные оценки (раздражение, страх, испуг и т.п.) субъективного восприятия импульсов ЗУ и, как интегральный результат применения этого “инструментария”, – формирование необходимого представления об ограничительных нормативах на воздействие ЗУ. Весь этот исследовательский процесс отражен в собранных в Приложении обзорных работах. Вместе с тем, вызывает удивление то, что все полученные сведения о ЗУ и эффектах его воздействия до сих пор никак не используются в официальных документах, ограничивающих шумовое воздействие СЗ самолетов гражданской авиации. В уже упоминавшемся выше Своде стандартов и сертификационных требований ИКАО по авиационному шуму (Приложение 16 ..., последнее издание 2014 г.), представляющем собой целый том в две с половиной сотни страниц, интересующая нас “Глава 12. Сверхзвуковые самолеты” состоит из нескольких строчек, занимающих менее половины страницы, которые фиксируют: “Стандарты и рекомендуемая практика для этих самолетов не разработана. Однако, в качестве инструктивных указаний могут быть использованы максимальные уровни шума настоящей части (данная глава 12 входит в Часть II “Сертификация воздушных судов по шуму” – пояснение наше), которые применяются к дозвуковым реактивным самолетам. Приемлемые уровни звукового удара не установлены и соблюдение стандартов по шуму для дозвуковых полетов нельзя рассматривать как разрешение производить сверхзвуковые полеты”. Таким образом, для шумового фактора в виде ЗУ официально зафиксировано, что до настоящего времени “приемлемые уровни звукового удара не установлены”, а значит, подтверждается отсутствие каких-либо критериев и нормативов на характерные параметры ЗУ (сами эти параметры тоже официально не утверждены). Отсюда следует, что даже при наличии спроектированного, изготовленного и прошедшего летные испытания СЗ самолета с заведомо приемлемым ЗУ воздействием на эко- и социосистемы его сертификация по шумовым характеристикам будет невозможна, что ведет к запрету его эксплуатации на трансконтинентальных маршрутах. Представленная “парадоксальная” ситуация с официальным документом ИКАО естественно порождает чувство неопределенности относительно обеспечения нужных требований для ЗУ. Несмотря на это, изучение ЗУ идет с неснижаемой интенсивностью, концентрируясь в двух основных направлениях: а) определение компоновки корпуса (планера) самолета как решение обратной задачи обеспечения заданного значения определенной метрики (например, громкости) ЗУ с целевой установкой на минимизацию эффекта воздействия/восприятия импульса ЗУ, б) определение/выявление количественных показателей (метрик), наиболее адекватно характеризующих степень (величину) воздействия и конечный результат воздействия ЗУ на отдельного индивидуума или на определенное сообщество людей (например, жителей какого-либо поселения) с учетом не только реакции слуховой системы, но также других систем организма.
Хотелось бы обратить внимание на то, что критерии типа “уровня шума в дБ”, принятые для обычных шумов, вряд ли могут дать адекватную оценку воздействиям ЗУ. Конечно, при разработке объективных критериев необходимо учитывать пиковые давления в импульсе ЗУ и крутизну (характерную длительность) фронта ударной волны, создающие разрушительные градиенты давления и огромные ускорения (инерционные нагрузки).
После появления сверхзвуковых пассажирских самолетов первого поколения (Ту-144 и “Конкорд”) некоторые страны (в т.ч., США в 1973 г.) ввели запрет на сверхзвуковые полеты над населенными территориями. Поэтому “Конкорды” прокладывали сверхзвуковые маршруты над океаном. Только военной авиации было разрешено летать по специальным “коридорам”.
Пока писался этот обзор, появилось сообщение о создании в России Научного центра мирового уровня “Сверхзвук”. В консорциум участников, реализуемого в рамках нацпроекта “Наука”, вошли такие организации, как ЦАГИ, ЦИАМ им. П.И. Баранова, ИПМ им. М.В. Келдыша, МГУ им. М.В. Ломоносова, ЛИИ им. М.М. Громова и другие.
За рубежом в США, Японии и ряде других стран ведутся работы по созданию пассажирских самолетов нового поколения, аэродинамическая форма которых позволяет несколько уменьшить интенсивность волн ЗУ.
По аналогичному пути предполагают идти Российские инженеры. Сообщается, что специалистам ЦАГИ удалось найти решение, сочетающее высокие летные качества и приемлемый уровень акустического ЗУ [93]. Решение связано с компромиссом между аэродинамическими характеристиками планера, конфигурацией и расположением двигателей. Характеристики летательного аппарата должны быть приемлемыми на всех режимах его полета. Рынок, по-видимому, примет новые бизнес-самолеты малой вместимости, поскольку спрос на дорогие полеты будет небольшим.
В конце этого раздела еще раз подчеркнем, что проблемам акустической экологии, связанным с краткосрочными и удаленными последствиями воздействия ЗУ на живые организмы, уделяется огромное внимание, особенно в зарубежной литературе, начиная с конца 1960-х годов (см., например, [94]). Довольно неожиданным оказалось явление “резонансного” проникновения ЗУ в водную среду [95], что, как показали наблюдения, оказывает сильное отрицательное влияние на поведение морских млекопитающих. Иллюстрацией к воздействию ЗУ служит рис. 22.
Ясно, что снижение уровня ЗУ при его воздействии на густонаселенные территории и водную среду может, в принципе, быть достигнуто двумя способами: (а) целевым изменением аэродинамики самолета; (б) созданием экспертной системы выбора оптимальных режимов и трасс полета. Заметим, что по первому направлению предлагались нетривиальные способы “удлинения” фюзеляжа за счет направленного вперед лазерного луча или плазменной струи [96].
ЗАКЛЮЧЕНИЕ
Следует указать, что точка зрения, изложенная в разделах 2, 3 и 4, сформировалась благодаря комплексным исследованиям, выполненным в России в 1991‑96 годах под руководством одного из авторов (О.В. Руденко). В них принимали участие физики, математики, механики и биологи А.П. и А.К. Сухоруковы, В.П. Коробейников, Н.С. Бахвалов, В.Б. Кудрявцев, А.В. Чечкин, Е.И. Маевский и другие известные специалисты. Работы были поддержаны Секцией прикладных проблем РАН и иными источниками финансирования. Итогом стало: (а) привнесение в проблематику звукового удара методов и результатов нелинейной акустики, где советские ученые были признанными лидерами; (б) разработка интеллектуального комплекса для выбора оптимальных режимов и трасс полета; (в) создание установок для лабораторного моделирования импульсов звукового удара. В частности, были разработаны эффективные численные методы для расчета параметров удара в неоднородной атмосфере, основанные на моделях нелинейной геометрической акустики и нелинейной квазиоптики. Был разработан комплекс компьютерных программ “SBOOM” в дополнение к пакету “NACSI” (Е.А. Лапшин, О.А. Васильева, Ю.Р. Лапидус [45, 80]). Результаты обсуждались со специалистами из Университета штата Техас в Остине (Блэксток, Гамильтон, Липкенс, Спарроу) и частично демонстрировались сотрудникам фирмы “Боинг”. В частности, была продемонстрирована на персональном компьютере работа одного из черновых вариантов экспертной системы, созданной группой из МГУ.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-12-50277.
Список литературы
Соболев Д.А. История самолетов мира. М.: Русавиа, 2001. 680 с.
Цихош Э. Сверхзвуковые самолеты. М.: Мир, 1983. 424 с.
Gold T. The “Double Bang” of Supersonic Aircraft // Nature. 1952. V.170. P. 808.
Warren C. Noise from Aircraft at Supersonic Speeds // Nature. 1953. V. 171. P. 214–215.
Близнюк В., Васильев Л., Вуль В. и др. Правда о сверхзвуковых пассажирских самолетах. // М.: Моск. раб., 2000. 335 с.
Остославский И.В., Миронов А.Д., Кириллов Е.А. О влиянии самолета, летящего со сверхзвуковой скоростью, на окружающее пространство // Техника воздушного флота. 1956. № 5.
Жилин Ю.Л. Влияние компоновки самолета, режима его полета и состояния атмосферы на интенсивность звукового удара // Труды ЦАГИ. 1967. Вып. 1094. С. 14–22.
Жилин Ю.Л. О звуковом ударе // Ученые записки ЦАГИ. 1971. Т. II. № 3. С. 1–11.
Parker M.A. The Sonic Boom Problem: An examination of the overpressures on the ground caused by supersonic aircraft with particular application to Concorde // Aircraft Engineering and Aerospace Technology. 1968. V. 40. № 8. P. 30–38.
Aronstein D.C., Schueler K.L. Two supersonic business aircraft conceptual designs, with and without sonic boom constraint // J. Aircraft. 2005. V. 42. № 3. P. 775–786.
Maglieri D.J. Compilation and review of supersonic business jet studies from 1963 through 1995. Report NASA/CR–2011-217144. May, 2011.
Вавилов С.И. О возможных причинах синего γ-свечения жидкостей // ДАН СССР. 1934. Т. 2. № 8. С. 457–459.
Черенков П.А. Видимое свечение чистых жидкостей под действием γ-радиации // ДАН СССР. 1934. Т. 2. № 8. С. 451–456.
Тамм И.Е., Франк И.М. Когерентное излучение быстрого электрона в среде // ДАН СССР. 1937. Т. 14. № 3. С. 107–112.
Черенков П.А. Излучение частиц сверхсветовой скорости и некоторые применения этого излучения в экспериментальной физике // УФН. 1959. Т. 68. № 3. С. 377–386.
Тамм И.Е. Общие свойства излучения, испускаемого системами, движущимися со сверхзвуковыми скоростями, и некоторые приложения к физике плазмы // УФН. 1959. Т. 68. № 3. С. 387–396.
Франк И.М. Оптика источников света, движущихся в преломляющих средах // УФН. 1959. Т. 68. № 3. С. 397–415.
Tamm I.E. Radiation Emitted by Uniformly Moving Electrons // J. Phys. USSR. 1939. V. 1. № 5–6. P. 439–461. (см. также: Тамм И.Е. Излучение, вызываемое равномерно движущимися электронами // Собрание научных трудов. Т. 1. С. 77–99. М.: Наука, 1975.)
Аскарьян Г.А. Черенковское и переходное излучение от электромагнитных волн // ЖЭТФ. 1962. Т. 42. № 5. С. 1360–1364.
Roppo V., Kalinowski K., Sheng Y. et al. Unified approach to Cerenkov second harmonic generation // Opt. Express. 2013. V. 21. № 22. P. 25715–25726.
Голдстейн М.Е. Аэроакустика (пер. с англ., ред. Мунин А.Г.). М.: Машиностроение, 1981. 294 с.
Miles J.W. Acoustical methods in supersonic aerodynamics // J. Acoust. Soc. Am. 1948. V. 20. № 3. P. 314–323.
Miles J.W. The potential theory of unsteady supersonic flow. Cambridge University Press, 1959. (перевод: Майлс Дж.У. Потенциальная теория неустановившихся сверхзвуковых течений. М.: ГИФМЛ, 1963.)
http://www.deutsches-museum.de/archiv/archiv-online/ernst-mach (дата обращения 08.09.2020 г.).
Mach E., Salcher P. Photographische Fixirung der durch Projectile in der Luft eingeleiteten Vorgange // Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften (Vienna), Mathematisch-Naturwissenschaftliche Klasse. 1887. V. 95 (2). P. 764–781.
Mach E., Salcher P. Über die in Pola und Meppen angestellten ballistisch-photographischen Versuche // Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften (Vienna), Mathematisch-Naturwissenschaftliche Klasse. 1889. V. 98 (2a). P. 41–50.
Rott N. Jakob Ackeret and the history of the Mach number // Ann. Rev. Fluid Mech. 1985. V. 17. P. 1–9.
Doppler Ch. Über den Einfluß der Bewegung des Fortpflanzungs mittels auf die Erscheinungen der Äther-, Luft- und Wasserwellen. Commission bei Borrosch & Andre, Prag. 1847. https://books.google.ru/books?id=aKteAAAAcAAJ&pg =PA13&lpg=PA13&dq=%C3%9Cber+den+Einflu%C3% 9F+der+Bewegung+des+Fortpflanzungs+mittels+auf +die+Erscheinungen&source=bl&ots=9EWZZCvmIK&sig=ACfU3U15e0oe3xFoninthnjzLdhAOaKX3A&hl=ru&sa=X&ved=2ahUKEwiQzI_7zanrAhX7isMKHXajAg4Q6AEwAnoECAEQAQ#v=onepage&q=%C3%9Cber%20den%20Einflu%C3%9F%20der%20Bewegung%20des%20Fortpflanzungs%20mittels%20auf%20die%20 Erscheinungen&f=false (дата обращения 08.09.2020 г.)
Мах Эрнст. Популярные лекции по физике (пер. с нем.). Москва–Ижевск, “R&C Dynamics”, 2001. 128 с.
Mach E., Doss B. Bemerkungen zu den Theorien der Schallphänomene bei Meteoritenfällen (Комментарии к теории звуковых явлений в случае метеорита – перевод наш) // Sitzungsber. Akad. Wiss. Wien. 1893. V. 102 (Abth. IIa). P. 248–252.
Брэгг Уильям. Мир света. Мир звука. (Пер. с англ. под ред. академика Обреимова И.В.) М.: Наука, 1967. 336 с.
Прандтль Л. Гидроаэромеханика. (Пер. со 2-го нем. изд.) Ижевск, НИЦ “Регулярная и хаотическая динамика”, 2000. 576 с.
Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн (3-е изд.) // М.: Ленанд, 2015. 448 с.
Ландау Л.Д., Лифшиц Е.М. Механика. М.: Физматлит, 2007. 216 с.
Гурбатов С.Н., Руденко О.В., Саичев А.И. Волны и структуры в нелинейных средах без дисперсии. М.: Физматлит, 2008. 496 с.
Карабутов А.А., Руденко О.В. Нелинейные плоские волны, возбуждаемые объемными источниками в движущейся с трансзвуковой скоростью среде // Акуст. журн. 1979. Т. 25. № 4. С. 536–542.
Гурбатов С.Н., Саичев А.И., Якушкин И.Г. Нелинейные волны и одномерная турбулентность в средах без дисперсии // Успехи физ. наук. 1983. Т. 141. № 2. С. 221–225.
Руденко О.В. Взаимодействия интенсивных шумовых волн // Успехи физ. наук. 1986. Т. 149. № 3. С. 413–447.
Rudenko O.V., Hedberg C.M. Wave resonance in media with modular, quadratic and quadratically-cubic nonlinearities described by inhomogeneous burgers-type equations // Acoust. Phys. 2018. V. 64. № 4. P. 422–431.
Руденко О.В. “Экзотические” модели физики интенсивных волн: линеаризуемые уравнения, точно решаемые задачи и неаналитические нелинейности // Прикл. нел. динамика. 2018. Т. 26. № 3. С. 7–34.
Enflo B.O., Hedberg C.M., Rudenko O.V. Resonant properties of a nonlinear dissipative layer excited by a vibrating boundary: Q-factor and frequency response // J. Acoust. Soc. Am. 2005. V. 117. № 2. P. 601–612.
Rudenko O.V., Hedberg C.M. Nonlinear dynamics of grains in a liquid-saturated soil // Nonl. Dynamics. 2004. V. 35. P. 187–200.
Карабутов А.А., Руденко О.В. Модифицированный метод Хохлова для исследования нестационарных трансзвуковых течений сжимаемого газа // ДАН СССР. 1979. Т. 248. № 5. С. 1082–1085.
Lin C., Reissner E., Tsien H.S. On two-dimensional non-steady motion of a slender body in a compressible fluid // J. Mathematics and Physics. 1948. V. 27. № 3. P. 220–231.
Руденко О.В. К 40-летию уравнения Хохлова-Заболотской // Акуст. журн. 2010. Т. 56. № 4. С. 452–462.
Ибрагимов Н.Х., Руденко О.В. Принцип априорного использования симметрий в теории нелинейных волн // Акуст. журн. 2004. Т. 50. № 4. С. 481–495.
Новиков Б.К., Руденко О.В., Тимошенко В.И. Нелинейная гидроакустика // Ленинград: Судостроение, 1981. 264 с.
Гурбатов С.Н., Демин И.Ю. О трансформации интенсивных шумов акустических импульсов // Акуст. журн. 1982. Т. 28. № 5. С. 634–640.
Руденко О.В., Гурбатов С.Н., Хедберг К.М. Нелинейная акустика в задачах и примерах // М.: Физматлит, 2007. 176 с.
Руденко О.В., Хохлова В.А. Кинетика одномерных пилообразных волн // Акуст. журн. 1991. Т. 37. № 1. С. 182–188.
Руденко О.В., Хохлова В.А. Кинетический подход к описанию одномерной акустической турбулентности // Акуст. журн. 1988. Т. 34. № 3. С. 500–506.
Enflo B.O., Rudenko O.V. To the Theory of Generalized Burgers’ equations // Acustica – Acta Acustica. 2002. V. 88. P. 155–162.
Руденко О.В., Гурбатов С.Н. Статистические задачи для обобщенного уравнения Бюргерса: интенсивный шум в волноведущих системах // Докл. Акад. наук. 2018. Т. 478. № 1. С. 25–28.
Руденко О.В., Хедберг К.М. Дифракция интенсивного поля в фокальной области как динамика нелинейной системы с низкочастотной дисперсией // Акуст. журн. 2015. Т.61. № 1. С. 30–39.
Маков Ю.Н. Волноводное распространение звуковых пучков в нелинейной среде // Акуст. журн. 2000. Т. 46. № 5. С. 680–684.
Маков Ю.Н. Локализованные волновые структуры, определяемые точными решениями уравнения Хохлова–Заболотской // Акуст. журн. 2019. Т. 65. № 3. С. 291–297.
Lipkens B., Blackstock D.T. Model experiment to study sonic boom propagation through turbulence. Pt. 1. General results // J. Acoust. Soc. Am. 1998. V. 103. № 1. P. 148–158. Pt. 2. J. Acoust. Soc. Am. 1998. V. 104. № 3. P. 1302–1309.
Pierce A.D. Spikes on sonic boom pressure wave forms // J. Acoust. Soc. Am. 1968. V. 44. P. 1052–1061.
Солуян С.И., Хохлов Р.В. Акустические волны конечной амплитуды в среде с релаксацией // Акуст. журн. 1962. Т. 8. № 2. С. 220–227.
Руденко О.В., Солуян С.И. К вопросу о рассеянии звука на звуке // Акуст. журн. 1972. Т. 18. № 3. С. 421–425.
Руденко О.В. Нелинейные интегро-дифференциальные модели для интенсивных волн в средах типа биотканей и геоструктур со сложной внутренней динамикой релаксационного типа // Акуст. журн. 2014. Т. 60. № 4. С. 368–375.
Руденко О.В., Гурбатов С.Н., Демин И.Ю. Поглощение интенсивных регулярных и шумовых волн в релаксирующих средах // Акуст. журн. 2014. Т. 60. № 5. С. 459–465.
Васильева О.А., Лапшин Е.А., Руденко О.В. Интенсивные импульсы в релаксирующих средах с ограниченным “временем памяти”, степенными и неаналитическими нелинейностями // Акуст. журн. 2019. Т. 65. № 1. С. 3–9.
Kulichkov S.N. Long-range sound propagation in the atmosphere (Review) // Rus. Acad. Sci. Bulletin. Physics of atmosphere and ocean. 1992. V. 28. P. 339–360.
Лернер А.М., Осташев В.Е., Фридман В.Е. К объяснению аномального распространения звука в атмосфере // Акуст. журн. 1990 Т. 36. № 2. С. 313–318.
Атмосфера стандартная: параметры. М.: Изд-во стандартов, 1981. 197 с.
Фридман В.Е. Нелинейная рефракция акустических импульсов в изотермической атмосфере // Акуст. журн. 1985. Т. 31. № 4. С. 571–572.
Чунчузов И.П. О поле точечного низкочастотного источника звука в атмосфере с неоднородным по высоте ветром // Акуст. журн. 1984. Т. 30. № 4. С. 546–552.
Rudenko O.V., Enflo B.O. Nonlinear N-wave propagation through a one-dimensional phase screen // Acustica – Acta acustica. 2000. V. 86. P. 229–238.
Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных сред. М.: Наука, 1980.
Губкин К.Е. Распространение разрывов в звуковых волнах // Прикл. Мат. Мех. 1958. Т. 22. № 4. С. 561–564.
Рыжов О.С. Затухание ударных волн в неоднородных средах // Прикл. Мех. Техн. Физ. 1961. Т. 2. № 2. С. 15–25.
Коротков П.Ф. О нелинейной геометрической акустике. Слабые ударные волны // Прикл. Мех. Техн. Физ. 1964. Т. 5. № 5. С. 30–37.
Жилин Ю.Л. Некоторые особенности распространения звукового удара в неоднородной атмосфере // Тр. ЦАГИ. 1975. Т. 6. № 4. С. 21–30.
Руденко О.В., Сухорукова А.К., Сухоруков А.П. Уравнения высокочастотной нелинейной акустики неоднородных сред // Акуст. журн. 1994. Т. 40. № 2. С. 290–294.
Руденко О.В., Сухорукова А.К., Сухоруков А.П. Двумерные нелинейные волны с разрывами в стратифицированных средах // Акуст. журн. 1995. Т. 41. № 2. С. 291‑295.
Руденко О.В., Сухорукова А.К., Сухоруков А.П. Полные решения уравнения геометрической акустики в движущихся стратифицированных средах // Акуст. журн. 1997. Т. 43. № 3. С. 396–401.
Бреховских Л.М. Волны в слоистых средах // М.: Наука, 1973. 344 с.
Руденко О.В., Шварцбург А.Б. О нелинейных и линейных волновых явлениях в узких трубках // Акуст. журн. 2019. Т. 65. № 3. С. 305–310.
Руденко О.В. Нелинейные пилообразные волны // Успехи физ. наук. 1995. Т. 165. № 9. С. 1011–1036.
Бабич В.М., Булдырев В.С. Асимптотические методы в задачах дифракции коротких волн. М.: Наука, 1972.
Руденко О.В., Солуян С.И., Хохлов Р.В. Проблемы теории нелинейной акустики // Акуст. журн. 1974. Т. 20. № 3. С. 449‑457.
Дубровский А.Н., Руденко О.В., Хохлова В.А. Флуктуационные характеристики волны звукового удара после прохождения случайно-неоднородного слоя // Акуст. журн. 1996. Т. 42. № 5. С. 623‑628.
Thomas J.L., Fink M.A. Ultrasonic beam focusing through tissue inhomogeneities with a time reversal mirror: application through transscull therapy // IEEE Trans. Ultrasonics Ferroelectr. Freq. Control. 1996. V. 43. № 6. P. 1122–1129.
Гусев В.А., Руденко О.В. Статистические характеристики интенсивной волны за двумерным фазовым экраном // Акуст. журн. 2006. Т. 52. № 1. С. 30–42.
Kjellberg A. Subjective, behavioral and psychophysiological effects of noise // Scand. J. Work Environ. Health. 1990. V. 16 (suppl. 1). P. 29–38.
Leatherwood J.D., Shepherd K.P., Sullivan B.M. A new simulator for assessing subjective effects of sonic booms // NASA Technical Memorandum 104150. Langly research Center. 1991.
Park S.H., Lee P.J., Jeong H.J. Effects of noise sensitivity on psychophysiological responses to building noise // Building and Environment. 2018. V. 136. P. 302–311.
Fastl H., Zwicker E. Psychoacoustics. Facts and Models. Springer-Verlag Berlin Heidelberg, 2007. 460 p.
Obata J. The analysis of the sounds emitted by aircraft // J. Phys. Soc. Jap. 1930. V. 12. № 4. P. 80–92.
Logan G.B. Recent Developments in aeronautical law // J. Air Law and Commerce. 1934. V. 5. Issue 4. Article 7. P. 548–563.
Domestic Air News (from the Aeronautics Branch), Tuesday, January 31, 1928.
Савинов С. Приручить ударную волну. Деловой квадрат. Ижевск 2020. http://www.d-kvadrat.ru/tekhnologii/3631 (дата обращения 08.09.2020 г.)
Manci K.M, Gladwin D.N, Villella R., Cavendish M.G. Effects of aircraft noise and sonic booms on domestic animals and wildlife: a literature synthesis // OSTI.GOV. Technical Report. Publication Date: 1988-06-01 https://www.fs.fed.us/eng/techdev/IM/sound_measure/ Manci_et_al_1988.pdf (дата обращения 08.09.2020 г.)
Маков Ю.Н. Возможно ли проникновение импульса звукового удара от современного истребителя в водную среду с его дальнейшим волновым распространением в этой среде? // NOISE. Theory and Practice.2018. V. 4. № 1. P. 18–29.
Белоконь В.А., Руденко О.В., Хохлов Р.В. Аэродинамические явления при сверхзвуковом обтекании лазерного луча // Акуст. журн. 1977. Т. 23. № 4. С. 632–634.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал