Акустический журнал, 2021, T. 67, № 2, стр. 185-202
Фазовый анализ активности голосового источника
В. Н. Сорокин a, *, А. С. Леонов b
a Институт проблем передачи информации, Российская академия наук
127051 Москва, Большой Каретный пер. 19, стр. 1, Россия
b Национальный исследовательский ядерный университет “МИФИ”
115409 Москва, Каширское ш. 31, Россия
* E-mail: vns@iitp.ru
Поступила в редакцию 02.05.2020
После доработки 14.12.2020
Принята к публикации 22.12.2020
Аннотация
Предложены математические модели, позволяющие связать параметры голосового источника с параметрами фазово-частотных характеристик (ФЧХ) сегментов речевого сигнала. В частности, установлено, что длительность работы источника можно найти по средней длине интервалов между нулями и точками разрыва этих ФЧХ. Для синтетических и реальных речевых сигналов на основе установленных свойств ФЧХ и предложенных эвристических методов их анализа проведена численная оценка периодов основного тона, длительностей работы голосового источника внутри этих периодов, а также моментов начала ${{T}_{{op}}}$ и конца ${{T}_{{cl}}}$ действия голосового источника. Экспериментально установлено существование верхней границы диапазона частот основного тона ${{F}_{0}}$, внутри которого ошибка оценки ${{F}_{0}}$ не превышает 5%. Средняя ошибка оценки длительности голосового источника по предлагаемой методике для сегментов речи из базы данных Arctic оказалась менее 0.3% для двух дикторов, а для третьего диктора равна 6.2%. Показано, что ошибка определения величин ${{T}_{{op}}}$ и ${{T}_{{cl}}}$ зависит от свойств голосового источника и значительно возрастает для ${{F}_{0}} > 220$ Гц. Наиболее вероятная ошибка оценки величин ${{T}_{{op}}}$ для трех дикторов из базы данных Arctic оценивается как 1.5, 10.2 и 13.5%, а для ${{T}_{{cl}}}$ она составляет –9.7, –20.2 и –13.9%.
1. ВВЕДЕНИЕ
Характеристики голосового источника играют заметную роль при идентификации диктора, в распознавании речи и при анализе патологии голоса. Важнейшие из этих характеристик – моменты начала и конца активности голосового источника, которые коррелированны с моментами открытия ${{T}_{{op}}}$ и закрытия ${{T}_{{cl}}}$ голосовой щели, а также частота основного тона ${{F}_{0}}$. Именно эти параметры необходимо в первую очередь определить при анализе сегмента речи с помощью математического моделирования. Они в значительной мере определяют функциональную форму голосового источника при его описании по известным математическим моделям (см., например, [1] и формулу (7) ниже).
Перед закрытием голосовой щели в речевом сигнале возникает всплеск энергии, который вызывается отрицательным пиком производной от объемной скорости потока через голосовую щель. Связанные с этим пиком явления содержат информацию о моменте закрытия голосовой щели ${{T}_{{cl}}}$. Для определения величины ${{T}_{{cl}}}$ во временной области часто применяется анализ сигнала-остатка после выполнения анализа методом линейного предсказания (см., например, [1]).
В спектрально-временной области для этих целей используются экстремумы логарифмической производной средней энергии спектра речевого сигнала в области частот второй и третьей форманты [2]. Обширный обзор других методов определения момента закрытия голосовой щели в фазово-частотной области представлен в [3]. Все эти методы позволяют достаточно точно найти моменты закрытия голосовой щели. В то же время, имеющиеся методы определения момента открытия голосовой щели дают значительную погрешность.
В задачах определения формы импульса голосового источника необходимо знать оба этих момента, и погрешность определения моментов открытия и закрытия голосовой щели существенно влияет на точность восстановления формы импульса. Это продемонстрировано, например, в работе [4], где форма импульсов голосового источника вычисляется путем обратного преобразования Фурье отношения спектров речевого сигнала на интервалах открытой и закрытой голосовой щели.
В исследованиях характеристик голосового источника основное внимание уделяется анализу амплитудно-частотных параметров речевого сигнала, тогда как фазовые характеристики мало исследованы. Это связано с двумя факторами. Во-первых, существовало мнение, что фазовые характеристики не играют существенной роли в восприятии речи. Однако постепенно было установлено, что по фазовым параметрам можно восстановить речевой сигнал [5], а фазы существенно влияют на восприятие речи [6–9]. Роль фазовых характеристик в обработке речи описывается в [10] и обзоре [11]. Второй фактор, препятствовавший использованию фазовых характеристик, заключается в том, что фазово-частотная характеристика (ФЧХ) речевого сигнала представляет собой разрывную функцию, с областью значения [–π, π]. Поэтому, в отличие от динамического амплитудного спектра, динамический фазовый спектр не позволяет визуально соотнести его признаки с параметрами речевого сигнала. Позднее выяснилось, что эти трудности анализа фаз можно частично обойти путем введения групповой задержки и мгновенной частоты. Групповая задержка была определена в работе [12] как отрицательное значение производной фазы по частоте в каждый момент времени. На этом понятии основаны методы нахождения моментов начала и конца активности голосового источника из работ [13, 14]. Мгновенная частота определяется как мнимая часть отношения аналитического сигнала к самому сигналу, что эквивалентно производной от фазы по времени [15]. Мгновенная частота также используется для определения моментов начала и конца активности голосового источника [16].
Экспериментальные исследования показали, что влияние фаз на восприятие речи сложным образом зависит от частоты основного тона, интенсивности сигнала и полосы частот [8, 17]. Оказывается, что влияние фаз тем больше, чем ниже частота основного тона, и это связано с ограниченной длительностью импульсов (0.5–2 мс) в нервных каналах слуховой системы. Существует также некая предельная частота, выше которой экспериментальная оценка фаз становится недостоверной [18].
Оценка фаз обычно осуществляется на основе вычисления кратковременного спектра речевого сигнала, и здесь необходимо подбирать форму и длительность взвешивающего окна в кратковременном преобразовании Фурье (КПФ). Считалось, что эта длительность при нахождении ФЧХ должна быть значительно больше, чем при вычислении амплитудного спектра. Например, в [5] предполагается, что она должна быть больше 1 с. Этот фактор будет обсужден ниже более детально (см. разд. 2).
Цель данной работы – проанализировать связь фазовых характеристик речевого сигнала с параметрами ${{T}_{{op}}}$, ${{T}_{{cl}}}$ и ${{F}_{0}}$ голосового источника и предложить практические алгоритмы нахождения этих параметров из сегментов реальной речи.
Известные нам приложения фазового анализа к задачам речевых технологий носят, в значительной степени, формальный характер. В частности, мгновенная частота и групповая задержка не специфичны для анализа речи, хотя они и являются универсальными характеристиками любых сигналов. Именно поэтому в нашей статье предложены математические модели, позволяющие связать параметры голосового источника с параметрами фазово-частотных характеристик сегментов речевого сигнала (см. разд. 2). Эта связь оказывается достаточно сложной даже для простейших форм источника голосового возбуждения, и ее полный математический анализ затруднителен. Тем не менее, применение в этих моделях асимптотических методов дает возможность связать характеристики ФЧХ речевых сегментов с такими параметрами речевого источника, как его длительность, моменты начала и конца его работы (открытия и закрытия голосовой щели). Этот асимптотический анализ (разд. 2, Приложения 1 и 2) и численный анализ связи ФЧХ с параметрами источника (разд. 4) проведен в нашей работе для значительного числа синтетических и реальных речевых фрагментов, описанных в разд. 3. В результате выработаны алгоритмы, позволяющие вычислить параметры источника путем анализа ФЧХ, и эти параметры могут быть использованы в различных речевых приложениях. Рекомендации по применению алгоритмов и пределы их применимости обсуждаются в разд. 5.
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ, СВЯЗЫВАЮЩИЕ ФЧХ РЕЧЕВОГО СИГНАЛА И ГОЛОСОВОЙ ИСТОЧНИК
Рассмотрим простейшие математические модели, связывающие характеристики голосового источника с речевым сегментом и, далее, с фазово-частотной характеристикой этого сегмента. Для этого используется модель речеобразования, предложенная в работах [19, 20] и основанная на известном уравнении Вебстера. Она связывает функцию голосового источника $q(t)$ – производную объемной скорости $v(t)$ воздушного потока в голосовой щели (ГЩ) – и генерируемый при $t \geqslant 0$ речевой сигнал $s(t)$ следующим образом:
Здесь
2.1. Оценки длительности голосового источника
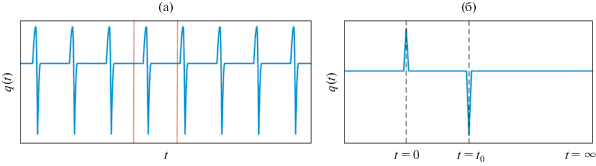
Примерный вид импульсов источника $q(t)$ голосового возбуждения приведен на рис. 1а. Каждый импульс (см., например, выделенный вертикальными линиями) характеризуется двумя пиками. Пик с положительной амплитудой находится вблизи момента открытия голосовой щели, а пик с отрицательной амплитудой – вблизи момента ее закрытия. Существует довольно много математических моделей, хорошо описывающих реальные голосовые источники. Однако, ни одна из них не позволяет выполнить хотя бы качественный анализ ФЧХ генерируемого сигнала. Чтобы сделать это, мы приняли идеализированную модель источника $q(t)$ в виде последовательности двух $\delta $-образных импульсов с положительной и отрицательной амплитудами:
(см. рис. 1б). Здесь ${{t}_{0}}$ – время действия источника, соответствующее длине интервала открытой голосовой щели. Такая форма источника пригодна для анализа небольших по сравнению с периодом основного тона величин ${{t}_{0}}$. В этой форме неявно предполагается, что к моменту $t = 0$ произошло затухание формантных колебаний, вызванных предыдущим импульсом.Рис. 1.
(а) – Импульсы голосового источника. (б) – Выделенная вертикальными линиями часть импульсов, используемая в модели вычисления ФЧХ.
Сигнал, который генерируется источником (2) по формуле (1), имеет вид
Здесь
Фазово-частотная характеристика $\varphi (\omega )$ сигнала находится из равенства
(3)
$\begin{gathered} \varphi (\omega ) = {{\left[ {\operatorname{Arg} {{S}_{1}}(\omega ) + \operatorname{Arg} {{S}_{2}}(\omega )} \right]}_{\pi }} = \\ = \left[ {\operatorname{Arg} \left( {B{{e}^{{ - i\omega {{t}_{0}}}}} - A} \right)} \right. + \\ {{\left. { + \,\,\operatorname{Arg} \sum\limits_{n = 1}^{{{N}_{0}}} {\frac{{{{\alpha }_{n}}{{\omega }_{n}}}}{{(\omega + {{\omega }_{n}} + i{{\delta }_{n}})(\omega - {{\omega }_{n}} + i{{\delta }_{n}})}}} } \right]}_{\pi }}. \\ \end{gathered} $Здесь символы $\operatorname{Arg} {{S}_{{1,2}}}(\omega )$ обозначают аргументы комплексных функций ${{S}_{{1,2}}}(\omega )$, а функция $\,{{\left[ {\operatorname{Arg} \,z} \right]}_{\pi }} = \arg z$ вычисляет для комплексного числа $z$ по величинам $\operatorname{Arg} \,z$ главное значение аргумента, лежащее в пределах от $ - \pi $ до $\pi $. Отметим, что эта функция не обладает свойством аддитивности: вообще говоря,
Проведем более детальный анализ. Установим связь параметра источника ${{t}_{0}}$ со свойствами ФЧХ. Сначала формально рассмотрим случай ${{\delta }_{n}} = 0$ (отсутствие потерь в речевом тракте). Тогда величина
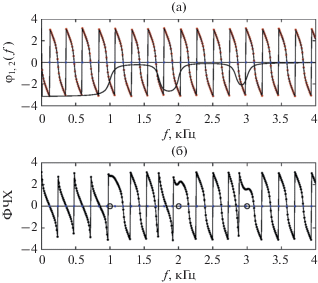
Типичный вид функции $\varphi (\omega ) = {{\varphi }_{1}}(\omega )$ показан на рис. 2 сверху линией с точками. Функция $\varphi (\omega )$ равна нулю или имеет точку разрыва при тех $\omega $, для которых мнимая часть числа $B{{e}^{{ - i\omega {{t}_{0}}}}} - A$ обращается в нуль, т.е. при $\sin \omega {{t}_{0}} = 0$. Все такие точки имеют вид: $\omega = {{\Omega }_{m}} = \frac{{\pi m}}{{{{t}_{0}}}},$ $\,m = 0, \pm 1, \pm 2,...$, и соответствующие частоты выражаются как ${{f}_{m}} = \frac{m}{{2{{t}_{0}}}}$. Расстояния между этими характерными точками, т.е. числа $\Delta {{f}_{m}} = {{f}_{{m + 1}}} - {{f}_{m}} = \frac{1}{{2{{t}_{0}}}}\,$, определяют период ФЧХ. Поэтому в идеализированном варианте, найдя нули и точки разрыва ФЧХ, мы можем вычислить параметр источника как ${{t}_{0}} = \frac{1}{{2\Delta {{f}_{m}}}}$.
Рис. 2.
(а) – Компоненты ФЧХ: периодическая часть ${{\varphi }_{1}}(\omega )$ – линия с точками, определяемая формантами; часть ${{\varphi }_{2}}(\omega )$ – непрерывная линия. (б) – ФЧХ $\varphi (\omega )$. Значения резонансных частот отмечены маркерами ○.
В случае малых потерь в речевом тракте можно провести похожий анализ. Он дан в Приложении 1. В этом случае величины $\Delta {{f}_{m}} = {{f}_{{m + 1}}} - {{f}_{m}}\,$ будут уже зависеть от $m$. Однако, формула для ${{t}_{0}}$ остается верной в виде ${{t}_{0}} = \frac{1}{{2\overline {\Delta {{f}_{m}}} }}$, где $\overline {\Delta {{f}_{m}}} = {{\lim }_{{N \to \infty }}}\frac{1}{N}\sum\nolimits_{m = 1}^N {\Delta {{f}_{m}}} $ – среднее значение величин $\Delta {{f}_{m}}$. Таким образом, вычислив приближенно это среднее значение из ФЧХ для частот, больших первой форманты, мы можем оценить параметр источника ${{t}_{0}}$ по той же формуле, что и в случае отсутствия потерь, в котором $\,\overline {\Delta {{f}_{m}}} = \Delta {{f}_{m}}$.
На рис. 2 показан пример ФЧХ, а также связанные с ней функции ${{\varphi }_{1}}(\omega ) = {{\left[ {\operatorname{Arg} {{S}_{1}}(\omega )} \right]}_{\pi }}$, $\,{{\varphi }_{2}}(\omega ) = \,\,{{\left[ {\operatorname{Arg} {{S}_{2}}(\omega )} \right]}_{\pi }}$ (рис. 2а). ФЧХ (рис. 2б) вычислена по формуле (3) с $A = 1,\,\,B = 1.5$ для резонансных частот ${{F}_{{1 - 3}}} = [1,2,3]$ кГц и величин ${{\delta }_{n}} = 2\pi {\text{[0}}{\text{.05, 0}}{\text{.04, 0}}{\text{.05]}}$, ${{\alpha }_{n}}\,\,{\text{ = }}\,\,{\text{[1, 0}}{\text{.5, 0}}{\text{.25]}}$ при ${{t}_{0}} = {\text{4}}{\text{.18}}$ мс. Численно найдя величину $\overline {\Delta {{f}_{m}}} $ для этой ФЧХ в частотном диапазоне $f \in (1,4)$ кГц, получим оценку параметра источника: ${{t}_{0}} \approx 4.17$ мс.
Численные эксперименты по верификации равенства ${{t}_{0}} = 0.5{{\left( {\overline {\Delta {{f}_{m}}} } \right)}^{{ - 1}}}$ для реальных речевых сигналов представлены ниже в разд. 4.1.
2.2. Вычисление ФЧХ для конечного периода основного тона
Откажемся от сделанного в разд. 2.1 предположения о том, что период основного тона ${{T}_{0}}$ много больше длительности ${{t}_{0}}$ открытой ГЩ. Тогда для источника с $M$ одинаковыми периодами основного тона можно принять модель
Согласно (1), модельный сигнал приобретет вид
Можно видеть, что даже при таких упрощениях аналитическое исследование поведения ФЧХ сигнала, т.е. функции
(4)
$\begin{gathered} \varphi (\omega ) = Im\left\{ {\ln \Phi (\omega )} \right\} = \\ = \operatorname{Im} \left\{ {\ln (A - B{{e}^{{ - i\omega {{t}_{0}}}}}) + \ln (1 + {{e}^{{ - i\omega {{T}_{0}}}}})} \right\} \\ \end{gathered} $Из рис. 3 и формулы (4) видно, что фазовая функция определяется двумя колебаниями. Одно с периодом ${{t}_{0}}$ связано с длительностью источника возбуждения, другое происходит с периодом основного тона ${{T}_{0}}$. Последнее свойство будет использоваться ниже (см. разд. 4) в экспериментах по определению частоты основного тона синтетических и реальных речевых сигналов. В Приложении 2 рассмотрен вопрос о нулях ФЧХ в рассматриваемом случае конечного периода основного тона. Показано, что одна из возможных серий нулей имеет вид ${{\omega }_{k}} = 2\pi {{f}_{k}} = \pi (1 + 2k){{T}_{0}}^{{ - 1}}$, и она порождает серию величин $\Delta {{f}_{k}} = {{f}_{{k + 1}}} - {{f}_{k}} = {{T}_{0}}^{{ - 1}}$.
Рис. 3.
(а) – ФЧХ для трех формант, положение которых отмечено кружками. (б) – 1 – ФЧХ для одной форманты с частотой 1 кГц; 2 – гармоника, определяемая частотой основного тона ${{F}_{0}} = {1 \mathord{\left/ {\vphantom {1 {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$; 3 – гармоника, определяемая частотой источника ${{f}_{0}} = {1 \mathord{\left/ {\vphantom {1 {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}$.

2.3. Оценка параметров голосового источника
При обработке реальных дискретных речевых сигналов вместо стандартного преобразования Фурье часто используется кратковременное преобразование Фурье (КПФ)
(5)
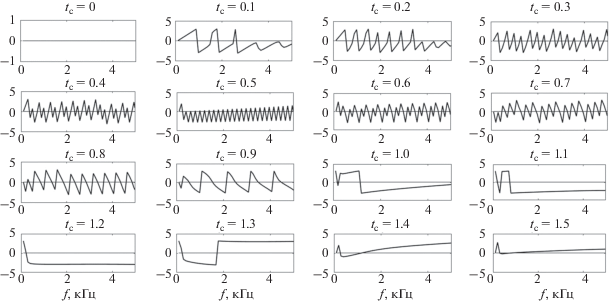
$\Phi (f,{{t}_{c}}) = \int\limits_0^{ + \infty } {{{e}^{{ - i2\pi ft}}}w(t - {{t}_{c}})s(t)dt} .$Здесь $w(t - {{t}_{c}})$ – задаваемое пользователем окно преобразования с центром ${{t}_{c}}$. В этом случае для нахождения ФЧХ используется формула $\varphi (f,{{t}_{c}}) = \operatorname{Im} \left\{ {\ln \Phi (f,{{t}_{c}})} \right\}$, и вместо одной фазовой функции получается их семейство, зависящее от ${{t}_{c}}$. Оказывается, что, анализируя изменения этих ФЧХ в зависимости от положения центра окна по отношению к сигналу, можно оценить моменты включения и выключения голосового источника. Рассмотрим эти изменения на примере сигнала
Сопоставим ФЧХ, показанные на рис. 4, с соответствующими положениями сигнала в окне, т.е. с видом функций времени $\zeta (t,{{t}_{c}}) = w(t - {{t}_{c}})s(t)$ для различных ${{t}_{c}}$ (см. рис. 5).
Рис. 5.
Сигнал в окне с центром ${{t}_{c}}$: $\zeta (t,{{t}_{c}}) = w(t - {{t}_{c}})s(t)$. Непрерывная линия – функция $\zeta (t,{{t}_{c}})$; пунктир – окно; вертикальная линия – центр окна ${{t}_{c}}$.

Модельный сигнал отличен от нуля при $t > {{T}_{{op}}} = 0.5$ мс. Поэтому первоначально (при ${{t}_{c}} = 0$) момент ${{T}_{{op}}}$ не попадает в окно полуширины 0.5 мс, и поэтому ФЧХ обращается в нуль. При ${{t}_{c}} > 0$ момент ${{T}_{{op}}}$ входит в окно, и ФЧХ приобретает колебательный характер (${{t}_{c}} = 0.1{\kern 1pt} - {\kern 1pt} 0.9$ мс). Частота ее колебаний увеличивается, пока центр окна ${{t}_{c}}$ не совпадет с ${{T}_{{op}}}$(${{t}_{c}} = {{T}_{{op}}} = 0.5$ мс). Затем эта частота уменьшается, пока при ${{t}_{c}} > 1$ мс точка ${{T}_{{op}}}$ не выходит из окна, и колебания ФЧХ практически пропадают. Квазипериодический характер по $f$ каждой из этих ФЧХ можно охарактеризовать частотой появления их нулей ${{f}_{m}}$, т.е. величиной
В дальнейшем мы будем называть функцию ${{Q}_{1}}({{t}_{c}})$ кривой квазипериодов первого типа для ФЧХ. Можно также охарактеризовать квазипериодичность фазово-частотной характеристики $\varphi (f,{{t}_{c}})$ с помощью функции $\,{{Q}_{2}}({{t}_{c}}) = \mathop {\max }\limits_m \left\{ {\Delta {{f}_{m}}} \right\}$ – кривой квазипериодов второго типа. Кривые квазипериодов ${{Q}_{1}}({{t}_{c}})$, рассчитанные для сигналов $s(t) = Ah(t - {{T}_{{op}}}){{e}^{{ - \delta (t - {{T}_{{op}}})}}}\sin 2\pi f(t - {{T}_{{op}}})$ с различными частотами: $f = [1.2,\,\,2.2,\,\,3.2]$ кГц, показаны на рис. 6а. На рис. 6б изображены кривые ${{Q}_{2}}({{t}_{c}})$, вычисленные аналогичным образом.
Рис. 6.
(а) – Кривые квазипериодов ${{Q}_{1}}({{t}_{c}})$ при положении окна КПФ вблизи момента открытия ГЩ; непрерывная линия – сигнал с $f = 1.2$кГц, пунктир – с $f = 2.2$ кГц, точки – с $f = 3.2$кГц. (б) – Аналогичные кривые квазипериодов ${{Q}_{2}}({{t}_{c}})$.
Видно, что обе кривые, ${{Q}_{1}}({{t}_{c}})$ и ${{Q}_{2}}({{t}_{c}})$, имеют выраженный локальный минимум при ${{t}_{c}} = {{T}_{{op}}}$, т.е. при совпадении центра окна КПФ с моментом открытия ГЩ. Аналогичный вид имеют зависимости ${{Q}_{1}}({{t}_{c}})$, ${{Q}_{2}}({{t}_{c}})$ вблизи момента ${{T}_{{cl}}}$ закрытия ГЩ.
Приведенные примеры не учитывают дискретизацию сигнала, характерную для реально регистрируемой речи. На рис. 7 показано, как выглядят типичные кривые квазипериодов при дискретизации с частотой 16 кГц.
Рис. 7.
Кривые квазипериодов (тонкая линия) для дискретного сигнала вблизи моментов открытия и закрытия ГЩ (вертикальные линии): (а) – ${{Q}_{1}}({{t}_{c}})$; (б) – ${{Q}_{2}}({{t}_{c}})$. Жирной линией показаны те же кривые после фильтрации (усреднения с помощью скользящего среднего).

Влияние дискретизации выражается в появлении высокочастотных осцилляций кривых. После фильтрации этих осцилляций кривые квазипериодов приобретают формы, схожие с представленными на рис. 6.
Вид кривых квазипериодов наводит на мысль о том, что их минимумы можно использовать для определения моментов открытия и закрытия ГЩ при разметке реального речевого сигнала.
Сделаем некоторые выводы из рассмотрения предложенных моделей ФЧХ.
1. Существуют две колебательные компоненты ФЧХ, период одной из которых связан с длительностью источника возбуждения, а период другой – с периодом основного тона (рис. 3).
2. Частоты, на которых наблюдается нарушение периодичности фазово-частотной функции, связаны с резонансными частотами мод (рис. 2б). Нарушение периодичности может возникнуть и для тех ФЧХ, у которых сигнал в окне КПФ не содержит момент включения источника (рис. 4, 5).
3. Моменты начала и конца активности источника возбуждения находятся вблизи минимумов кривых квазипериодов (рис. 6, 7).
На основе этих выводов было выполнено исследование свойств ФЧХ синтетических и реальных речевых сигналов. Реальный голосовой источник существенно отличается от использованных нами в модели. Часто это выражалось в том, что для сегментов речи минимумы кривых квазипериодов оказывались плохо обусловленными, и соответствующие оценки моментов ${{T}_{{cl}}}$ и ${{T}_{{op}}}$ становились ненадежными. Поэтому методы оценки параметров голосового источника пришлось несколько скорректировать в процессе численных экспериментов. В частности, наименьшая погрешность оценки искомых параметров была получена для эвристического алгоритма, состоящего в поиске экстремумов функции
вместо функций квазипериодов. Здесь $\Delta {{f}_{{\max }}}$ – максимальный интервал между нулями фазовой функции $\varphi (f,{{t}_{c}})$, аВ численных экспериментах было найдено, что функция $\theta ({{t}_{c}})$ имеет минимум вблизи момента ${{T}_{{cl}}}$, как и для описанных выше кривых квазипериода. Однако, вблизи момента ${{T}_{{op}}}$ эта функция имеет максимум. Результаты соответствующих численных экспериментов по определению частоты основного тона и моментов начала и конца активности голосового источника приведены в разд. 4.2 и 4.3. В них функция $\theta ({{t}_{c}})$ обозначается как $\theta (t)$.
3. БАЗЫ РЕЧЕВЫХ ДАННЫХ
Оценка эффективности метода определения параметров голосового источника требует знания истинных значений этих параметров. Наиболее распространенный подход для такой оценки состоит в анализе сигналов, синтезированных с заданным голосовым источником. Другой подход использует косвенные оценки параметров голосового источника путем измерения каких-либо физических характеристик, связанных с активностью голосового источника на реальных речевых сегментах. Здесь, в частности, можно использовать так называемые глоттограммы, т.е. измерения напряжения между поверхностными электродами, наложенными симметрично по обе стороны щитовидного хряща. В наших численных экспериментах использовались данные обоих типов. Им соответствовали базы данных, содержащие сигналы трех видов.
База 1. Сигналы, синтезированные по параметрам 6 русских гласных /а, э, и, ы, о, у/ в диапазоне частот основного тона от 80 до 380 Гц. Один из параметров, характеризующих импульс источника голосового возбуждения, определяет отношение длительности импульса к периоду основного тона ${{T}_{0}}$, $OQ = {{({{T}_{{cl}}} - {{T}_{{op}}})} \mathord{\left/ {\vphantom {{({{T}_{{cl}}} - {{T}_{{op}}})} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$. Ранее в [2] на материале базы Arctic [21] было установлено, что распределение величин OQ находится в диапазоне 0.25–0.8. С целью проверки влияния этого фактора на ошибки оценок моментов начала и конца импульса источника синтезировались сигналы с OQ от 0.2 до 0.8 с шагом 0.2. Формантные частоты F и ширина полосы каждого резонанса ΔF представлены в Табл. 1.
Таблица 1.
Параметры гласных звуков, Гц
| а | F | 600 | 1200 | 2300 | 3500 | 3806 | 4742 |
| ΔF | 80 | 50 | 80 | 100 | 150 | 220 | |
| о | F | 500 | 910 | 2320 | 2630 | 4030 | 4730 |
| ΔF | 100 | 50 | 70 | 90 | 140 | 190 | |
| у | F | 408 | 860 | 2040 | 2760 | 3610 | 4430 |
| ΔF | 150 | 40 | 50 | 70 | 90 | 120 | |
| и | F | 290 | 2272 | 3100 | 4000 | 5050 | 6110 |
| ΔF | 150 | 40 | 50 | 70 | 90 | 120 | |
| ы | F | 286 | 1874 | 2570 | 3730 | 4420 | 5050 |
| ΔF | 150 | 42 | 54 | 71 | 92 | 120 | |
| э | F | 490 | 1350 | 2230 | 2770 | 3670 | 4230 |
| ΔF | 70 | 40 | 60 | 80 | 110 | 140 |
Для синтеза речевых сигналов использовался источник возбуждения с пятью параметрами, описанный в [20]:
(7)
$q(t) = \left\{ \begin{gathered} \sin \frac{{\pi t}}{{2{{T}_{1}}}},\,\,\,0 \leqslant t \leqslant {{T}_{1}};\,\,\,\,({{A}_{0}} + 1)\cos \frac{{\pi \left( {t - {{T}_{1}}} \right)}}{{2({{T}_{2}} - {{T}_{1}})}} - {{A}_{0}},\,\,\,{{T}_{1}} \leqslant t \leqslant {{T}_{2}}; \hfill \\ - {{A}_{0}}\frac{{{{{\left( {{{T}_{3}} - t} \right)}}^{{2\gamma }}}}}{{{{{\left( {{{T}_{3}} - {{T}_{2}}} \right)}}^{{2\gamma }}}}},\,\,\,{{T}_{2}} \leqslant t \leqslant {{T}_{3}};\,\,\,0,\,\,\,{{T}_{{cl}}} \leqslant t \leqslant {{T}_{0}}. \hfill \\ \end{gathered} \right.$Здесь ${{T}_{0}}$ – период основного тона, ${{T}_{1}}$ и ${{T}_{2}}$ – моменты максимального и минимального значения источника возбуждения, ${{T}_{3}} = {{T}_{{cl}}}$ – момент окончания действия источника, параметр $\gamma $ определяет скорость закрытия голосовой щели. Величина${{A}_{0}}$ определяется из равенства нулю объемной скорости воздушного потока через голосовую щель в момент ее закрытия: $\int_{{{T}_{{op}}}}^{{{T}_{{cl}}}} {q(t)dt = 0} $ и вычисляется как ${{A}_{0}} = 2{{T}_{2}}(({{T}_{2}} - {{T}_{1}})(\pi - 2)$ + $\pi (2\gamma + 1)({{T}_{3}} - {{T}_{2}}){{)}^{{ - 1}}}$. Для этой модели $OQ = {{({{T}_{3}} - {{T}_{{op}}})} \mathord{\left/ {\vphantom {{({{T}_{3}} - {{T}_{{op}}})} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$.
Отметим, что в базе 1 точно известны моменты начала и конца действия источника возбуждения. Речевой сигнал синтезировался фильтром, сконструированным по методу линейного предсказания.
База 2. Сигналы из Repository3, представленные по ссылке из статьи [22]. Акустические сигналы были получены с использованием трехмерной физической модели речевого тракта для мужского и женского голосов и гласных /a, e, i, u/. Эта модель возбуждалась параметрическим голосовым источником LF ${\text{c}}$ четырьмя параметрами [23] с частотами основного тона от 100 до 380 Гц с OQ ≈ 0.36. Наряду с синтезированными сигналами, в Repository3 имеются и сигналы, соответствующие импульсам источника возбуждения. В экспериментах с этими сигналами моменты начала и конца импульса определялись численно как моменты его обращения в нуль.
База 3. В этой базе представлены сигналы из базы Arctic [21]. Имеются записи голосов трех дикторов – двух мужчин, обозначенных как BDL и JMK, и одной женщины (SLT), произносивших около 1100 фраз. Записи сигналов производились в заглушенной камере с одновременной регистрацией глоттограмм. В экспериментах с этой базой моменты начала и конца импульса источника возбуждения определялись соответственно по максимумам и минимумам производной глоттограммы. Эти параметры также использовались для оценки частоты основного тона.
Сигналы в базе 1 русских гласных синтезировались с частотой отсчетов 16 кГц, а сигналы из баз 2 и 3 были пересчитаны на эту частоту. В экспериментах использовалось кратковременное преобразование Фурье с окном Гаусса $w(t) = exp({{ - {{t}^{2}}} \mathord{\left/ {\vphantom {{ - {{t}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}})$ c параметром a = 2.5 при анализе частоты основного тона, и a = 1 при оценке моментов начала и конца импульса источника возбуждения. При оценке периода основного тона длительность окна составляла 16 мс, а при оценке моментов ${{T}_{{op}}}$ и ${{T}_{{cl}}}$ – 2.5 мс. Эти величины были найдены экспериментально. Они существенно расходятся с общепринятыми рекомендациями о необходимости использования большой длительности окна, как это упоминается во Введении.
4. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ
4.1. Оценка длительности открытой голосовой щели
В этой серии вычислительных экспериментов изучалось, насколько точно реальная длительность открытой голосовой щели может быть оценена по полученной в разд. 2.1 простой формуле ${{t}_{0}} = 0.5{{\left( {\overline {\Delta {{f}_{m}}} } \right)}^{{ - 1}}}$. В экспериментах использовалась база 3, содержащая реальные речевые сигналы. В каждом речевом сегменте этой базы начало и конец импульсов голосового источника определялись по параметрам глоттограмм. Поэтому можно сравнить экспериментальные длительности открытой ГЩ ${{t}_{{0\,\,\exp }}}$ и теоретические величины ${{t}_{0}}$, найденные из ФЧХ для каждого периода основного тона. Именно это было сделано для всех речевых сегментов трех дикторов из базы 3. Полученные эмпирические распределения относительных ошибок $\delta {{t}_{0}} = {{\left( {{{t}_{0}} - {{t}_{{0\,\,\exp }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{t}_{0}} - {{t}_{{0\,\,\exp }}}} \right)} {{{t}_{{0\,\,\exp }}}}}} \right. \kern-0em} {{{t}_{{0\,\,\exp }}}}}$ оценки ${{t}_{0}}$ для экспериментальных величин ${{t}_{{0\,\,\exp }}}$ представлены на рис. 8.
Рис. 8.
Эмпирические распределения относительных ошибок $\delta {{t}_{0}} = {{\left( {{{t}_{0}} - {{t}_{{0\,\exp }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{t}_{0}} - {{t}_{{0\,\exp }}}} \right)} {{{t}_{{0\,\exp }}}}}} \right. \kern-0em} {{{t}_{{0\,\exp }}}}}$ оценки величин ${{t}_{{0\,\exp }}}$ реальных длительностей работы ГИ для трех дикторов из базы 3.

Вычисленные распределения характеризуются величинами, приведенными в табл. 2. В ней ${{N}_{{fp}}}$ – количество периодов основного тона, использованных для фазового анализа, $\overline {\delta {{t}_{0}}} $ – средние значения ошибки $\delta {{t}_{0}}$, $\sigma (\delta {{t}_{0}})$ – среднеквадратичные уклонения ошибки.
Таблица 2.
Характеристики распределений ошибки $\delta {{t}_{0}}$ определения параметра ${{t}_{0}}$
| Диктор | ${{N}_{{fp}}}$ | $\overline {\delta {{t}_{0}}} $ | $\sigma (\delta {{t}_{0}})$ |
|---|---|---|---|
| BDL | 48 706 | –0.25 | 13.4 |
| JMK | 43 828 | 6.22 | 13.5 |
| STL | 57 139 | 0.27 | 14.6 |
Из таблицы видно, что в среднем теоретическая величина ${{t}_{0}}$ удовлетворительно описывает экспериментальные данные ${{t}_{{0\,\exp }}}$: средняя ошибка – около 1–7% со среднеквадратичным уклонением около 14%.
В расчетах величин ${{t}_{0}}$ с использованием ФЧХ (см. разд. 2.1) применялось дискретное преобразование Фурье на каждом периоде основного тона. Поэтому такой подход в вычислении ${{t}_{0}}$ по сигналу с частотой отсчетов 16 кГц пригоден в основном для периодов сравнительно большой длительности (5–10 мс), т.е. для относительно малых частот основного тона (0.1–0.2 кГц). Такое условие, однако, выполнено для значительной части речевых сегментов дикторов из базы Arctic. Убедиться в этом можно по графикам распределения частот основного тона для каждого диктора (см. ниже рис. 10). По этой причине ошибки нахождения величин ${{t}_{0}}$, приведенные в табл. 2, и оказались относительно малыми.
4.2. Оценка частоты основного тона
Оценка периода основного тона определяется по введенной выше функции $\theta (t)$ как среднее расстояние между точками локальных максимумов функции $\theta (t)$ на всем сегменте гласного. На рис. 9 представлены средние по всем гласным относительные ошибки оценки частоты основного тона для различных речевых сигналов: из базы 1 с источником вида (7), из базы 2 с LF-источником и для сигналов из базы 3. Выяснилось, что ошибки в экспериментах с базой 1 мало зависят от отношения OQ, и поэтому было выполнено усреднение по всем OQ.
Рис. 9.
Ошибки оценки частоты основного тона синтезированных русских гласных (---), сигналов из базы 2 (─) и сигналов из базы 3 (○○○).
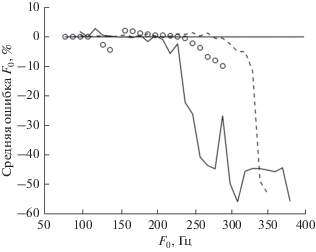
Видно, что существует некоторая критическая частота основного тона, выше которой ошибки резко возрастают. Если положить порог ошибки равным –5%, то эта частота для данных базы 2 близка к 230 Гц, несколько выше (около 260 Гц) для базы 3, а для русских гласных из базы 1 – около 320 Гц. В диапазоне частот ниже 200 Гц ошибка оказалась порядка 0.1%. Это значительно ниже по сравнению с наиболее успешным, по нашему мнению, алгоритмом [24], где ошибка достигала ±8% на этих же данных.
Ограниченная представительность частот основного тона в базе 3 определяется распределением оценок по параметрам глоттограмм (рис. 10). Наиболее вероятные значения частоты основного тона мужских голосов (дикторы BDL и JMK) оказались близки к 116 и 111 Гц, а у женского голоса (диктор SLT) к 171 Гц.
4.3. Оценки моментов начала и конца импульса голосового источника
Выше отмечалось, что при поиске моментов начала и конца импульса голосового источника ${{T}_{{op}}}$ и ${{T}_{{cl}}}$ весьма важна “настройка” параметров КПФ. В нашем случае, наиболее подходящим для спектрального анализа оказалось окно Гаусса длиной 2.5 мс с параметром $a = 1$. В экспериментах было установлено, что максимумы функции $\theta (t)$ находятся вблизи моментов ${{T}_{{op}}}$, а ее минимумы – вблизи величин ${{T}_{{cl}}}$, как для синтезированных сигналов, так и для сигналов, сгенерированных физической моделью речевого тракта. Для иллюстрации представим рис. 11. На нем вверху показана последовательность импульсов “объемной скорости” голосового источника, следующих с частотой ${{F}_{0}}$ = 100 Гц на интервале времени в 0.1 с для данных из базы 2. Внизу дан для сравнения график соответствующей функции $\theta (t)$.
Рис. 11.
(а) – Нормированная объемная скорость голосового источника. (б) – Функция $\theta (t)$. Оценка моментов начала (○) и конца источника (х). Сплошная вертикальная линия обозначает истинные моменты начала источника, а пунктирная – конца источника.

Расхождение между оценками и истинными значениями моментов ${{T}_{{op}}}$ и ${{T}_{{cl}}}$ будем характеризовать средней ошибкой по отношению к периоду основного тона ${{T}_{0}}$ на всей длительности сегмента речи. Средняя ошибка для базы 2 по всем гласным для мужского и женского голосов в зависимости от частоты основного тона оказалась удовлетворительной: относительная погрешность в большинстве случаев не превышает 5%, и всегда ниже 10% (рис. 12). Однако разброс ошибок по импульсам внутри сегмента гласного может быть весьма велик, достигая 20% и более для некоторых значений частоты основного тона.
Рис. 12.
Средние относительные ошибки для данных базы 2. Пунктиром показаны значения ошибок $ \pm $5 и $ \pm $10%.

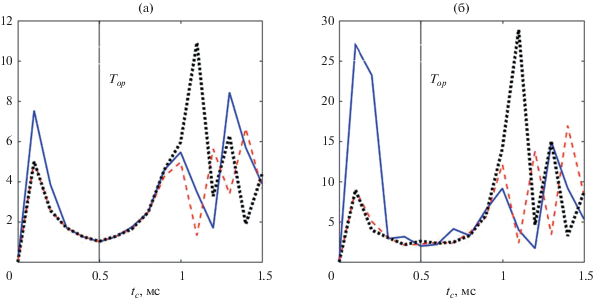
Сигналы в базе 2 были сгенерированы практически с фиксированным значением параметра OQ, тогда как прямые измерения воздушного потока через голосовую щель указывают на определенное разнообразие этого параметра. В отличие от оценок частоты основного тона, эксперименты по определению величин ${{T}_{{op}}}$и ${{T}_{{cl}}}$ с сигналами из базы 1 выявили сильную зависимость их оценок и от ${{F}_{0}}$, и от параметра OQ. Зависимости средних относительных ошибок этих оценок от ${{F}_{0}}$ приведены на рис. 13а, 13б для различных OQ.
Рис. 13.
Средние относительные ошибки оценки моментов (а) – ${{T}_{{op}}}$ и (б) – ${{T}_{{cl}}}$. Значения параметра OQ – 0.2 (─); 0.4 (–о–); 0.6 (–*–); 0.8 (---). Пунктиром размечены значения ошибок $ \pm $5 и $ \pm $10%.

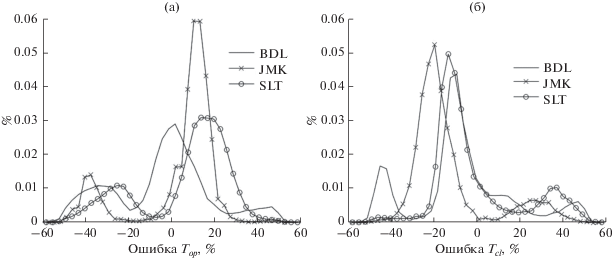
Сигналы в базе 3 позволяют оценить разброс ошибок определения моментов начала и конца работы голосового источника для разных дикторов. На рис. 14 показаны распределения этих ошибок, усредненные по всем произнесениям для каждого диктора из базы 3. На этих распределениях видно, что существует заметная доля ошибок с положительным или отрицательным знаком относительно наиболее вероятного значения.
Распределения на графиках не являются унимодальными. Для таких распределений наиболее вероятная ошибка более адекватно оценивает свойства распределения по сравнению со средней ошибкой, которая может оказаться близкой к нулю. Это наблюдалось и для распределений ошибок по всем частотам основного тона, где всплески положительных и отрицательных ошибок при оценке среднего значения компенсируют друг друга.
В табл. 3 представлены наиболее вероятные относительные ошибки ${{\delta }_{{\max }}}({{T}_{{op}}})$ и ${{\delta }_{{\max }}}({{T}_{{cl}}})$ оценок моментов открытия и закрытия голосовой щели вместе со среднеквадратическими отклонениями $\sigma ({{T}_{{op}}})$ и $\sigma ({{T}_{{cl}}})$ этих оценок. В численных экспериментах было обнаружено, что наиболее вероятная ошибка зависит от частоты основного тона, причем существует критическая частота основного тона, примерно равная 220 Гц, выше которой ошибка быстро возрастает. Отметим также, что зависимости ошибок от частоты основного тона отличаются для разных дикторов (см. рис. 15а, 15б).
Таблица 3.
Наиболее вероятная ошибка определения моментов открытия и закрытия голосовой щели, %. База 3
| Диктор | ${{\delta }_{{\max }}}({{T}_{{op}}})$ | ${{\delta }_{{\max }}}({{T}_{{cl}}})$ | $\sigma ({{T}_{{op}}})$ | $\sigma ({{T}_{{cl}}})$ |
|---|---|---|---|---|
| BDL | 1.5 | –9.9 | 0.02 | 0.04 |
| JMK | 10.2 | –20.2 | 0.04 | 0.04 |
| SLT | 13.5 | –13.9 | 0.03 | 0.03 |
Рис. 15.
Ошибки оценок моментов (а) – ${{T}_{{op}}}$ и (б) – ${{T}_{{cl}}}$. Диктор BDL представлен маркерами (х), диктор JMK – маркерами (*), а диктор SLT – маркерами (○).

Моменты открытия и закрытия голосовой щели могут быть определены не только по максимальным и минимальным значениям функции $\theta (t)$. Информация об этих моментах также содержится и в значениях частоты $\phi (t)$, с которой начинается наиболее длительный интервал между нулями дискретной фазовой функции. Максимальное и минимальное значение этой частоты сложным образом зависит от резонансных частот речевого тракта.
На рис. 16 представлен речевой сигнал и различные функции, используемые при оценке моментов открытия и закрытия голосовой щели для пятой гласной в первой фразе “Author of the danger trail …”, произнесенной диктором BDL из базы 3. Здесь средняя ошибка определения момента ${{T}_{{op}}}$ по функции $\theta (t)$ составляет –7.4, и –8.2% для момента ${{T}_{{cl}}}$. На рис. 16б показана функция, экстремумы которой используются для определения периода основного тона.
Рис. 16.
(a) – Осциллограмма звукового давления, (б) – функция $\theta (t)$с окном 16 мс, (в) – функция $\theta (t)$ с окном, равным $0.5{{T}_{0}}$, (г) – функция $\phi (t)$.
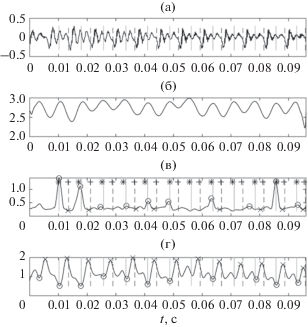
На рис. 16в маркеры (о) и (х) отмечают моменты времени открытия и закрытия голосовой щели, полученные с помощью функции $\theta (t)$. На этом же рисунке маркеры (*) и (+) отмечают моменты открытия и закрытия голосовой щели, найденные по алгоритму временного анализа [2]. Сплошные вертикальные линии обозначают моменты открытия голосовой щели как моменты максимальной производной глоттограммы, а пунктиром показаны моменты закрытия голосовой щели как моменты минимальной производной глоттограммы. На рис. 16г видно, что экстремумы $\phi (t)$ также находятся в окрестности моментов ${{T}_{{op}}}$ и ${{T}_{{cl}}}$. Здесь маркеры (о) и (х) отмечают минимум и максимум функции $\phi (t)$. Минимальное значение функции $\phi (t)$ равно 511 Гц, а максимальное – 2000 Гц, что близко к ожидаемым значениям формантных частот этой гласной.
5. ОБСУЖДЕНИЕ
Основной результат данной работы состоит в том, что параметры голосового источника связаны с величинами $\Delta {{f}_{m}}$ – расстояниями между последовательными нулями и точками разрыва ФЧХ, а также с экстремумами кривых квазипериода
Эксперименты с синтетическими сигналами для различных типов голосового источника и с реальными речевыми сигналами, записанными от разных дикторов, указывают, что ошибки определения параметров голосового источника зависят от формы импульса голосового источника. Эти формы в целом сильно отличаются от использованной в разд. 2 δ-образной формы, и поэтому не удивительно, что предлагаемые методы дают в определенных случаях значительные ошибки. Тем не менее, в среднем методы оказываются удовлетворительными.
Другой источник ошибок связан с особенностями стандартного кратковременного преобразования Фурье: при изменении длительности окна $w(t - {{t}_{c}})$ в КПФ получаемые оценки меняются. В частности, при ее увеличении оценки становятся более устойчивыми, но увеличивается их погрешность. В численных экспериментах, предшествующих реальному анализу речи, необходимо выбирать оптимальную длительность окна КПФ.
Следующий источник ошибок обусловлен дискретизацией речевого сигнала с фиксированной частотой отсчетов. Это приводит к большой погрешности вычисления кратковременного преобразования Фурье для сигналов с большой частотой основного тона, поскольку на каждый период основного тона приходится мало отсчетов. Ошибки такого рода объясняют существование критической частоты ${{F}_{0}}$ основного тона, выше которой оценки параметров становятся ненадежными.
Наконец, ошибки возникают и из-за неточностей сопоставления глоттограмм в базе данных 3 с речевыми сигналами. Они связаны с различным расстоянием каждого диктора от микрофона. И хотя в базе 3 была выполнена некоторая средняя корректировка задержки речевого сигнала в измерениях глоттограмм, их ошибки все же присутствуют. К тому же сам принцип определения моментов открытия и закрытия голосовой щели по экстремумам глоттограмм содержит погрешности, не поддающиеся оценке [2].
Заметим, что полученные в данной работе результаты относятся к синтетическим сигналам или записям речи в заглушенной камере. Поэтому мы не учитываем в алгоритмах эффекты, связанные с шумами, реверберацией и др.
Важным результатом этой работы является исследование адекватности связи оценки ${{t}_{0}} = 0.5{{\left( {\overline {\Delta {{f}_{m}}} } \right)}^{{ - 1}}}$ длительности открытой голосовой щели и экспериментальных данных. Оказалось, что погрешность оценки и ее дисперсия весьма малы (см. раздел 4.1). Длительность ${{t}_{0}}$ сама по себе представляет собой новый параметр, который, наряду с периодом основного тона, можно использовать, например, в задачах распознавания диктора. С помощью этой величины и параметра ${{T}_{{cl}}}$, для нахождения которого имеется ряд апробированных методов, можно найти параметр ${{T}_{{op}}}$ по формуле ${{T}_{{op}}} = {{T}_{{cl}}} - {{t}_{0}}$. Однако для определения величины ${{t}_{0}}$ с помощью ФЧХ необходимо знать текущий период основного тона ${{T}_{0}}$.
Его можно найти по методике из разд. 4.2. Однако и здесь возникают некоторые проблемы. На рис. 7 видно, что выше некоторой критической частоты основного тона погрешность оценки ${{F}_{0}}$ становится отрицательной. Причина этого состоит в пропуске плохо обусловленных максимумов функции $\theta (t)$ при их поиске. В результате для высокой частоты ${{F}_{0}}$ могут быть получены ложные (заниженные) оценки, если априорно неизвестно примерное значение ${{F}_{0}}$. Однако, как упоминалось в разд. 4.2, фазовый анализ обеспечивает значительно меньшую ошибку нахождения параметров источника в диапазоне частот ${{F}_{0}}$ до 200–220 Гц по сравнению с алгоритмом [24], хотя в этом алгоритме ошибка находится в диапазоне ±10% и для частот выше 220 Гц. Сопоставление оценок для ${{F}_{0}}$, полученных двумя этими алгоритмами, позволяет повысить их надежность в диапазоне низких частот ${{F}_{0}}$, а также избежать ложных оценок в диапазоне высоких частот ${{F}_{0}}$.
Обращает на себя внимание значительное отличие в оценках частоты основного тона между сигналами из базы 1, синтезированными методом линейного предсказания, и сигналами из баз 2 и 3, в которых речевой сигнал генерировался искусственной физической моделью речевого тракта и собственно речевым трактом. Отличие возникает из-за использования различных источников голосового возбуждения, а также из-за того, что в синтезе методом линейного предсказания отсутствуют возмущающие факторы, которые присущи реальным речевым сигналам. Это заставляет с осторожностью относиться к выводам, полученным исключительно на базе синтезированных речевых сигналов.
Значительный разброс ошибок определения моментов ${{T}_{{op}}}$ и ${{T}_{{cl}}}$ на рис. 15 свидетельствует о необходимости обнаружения недостоверных оценок этих параметров. В работе [2] обнаружение подобных ошибок выполнялось путем анализа последовательности оценок ${{T}_{{op}}}$ и ${{T}_{{cl}}}$ на сегменте гласного. В нашей работе к рассмотрению принимались только такие оценки ${{T}_{{op}}}$ и ${{T}_{{cl}}}$, которые не противоречат текущему значению периода основного тона. Тем не менее, и в таком подходе иногда наблюдаются недопустимо большие ошибки. Некоторая доля подобных ошибок может быть обнаружена или даже компенсирована в рамках фазового анализа с использованием информации о динамике функции $\phi (t)$ (см. рис. 16г). Экстремумы этой функции иногда оказываются лучше обусловленными, чем у функции $\theta (t)$. Это видно на нижнем графике в окрестности отсчетов времени 0.029, 0.056 и 0.074 с.
Ни один из известных алгоритмов анализа параметров речевого сигнала не обладает универсальностью, обеспечивающей малую погрешность независимо от вариаций речевого сигнала. Это относится и к оценке резонансных частот, и к оценке частоты основного тона, и к оценке моментов начала и конца действия голосового источника. Поэтому для каждого типа параметров необходимо совместно использовать методы, основанные на различных свойствах речевого сигнала. Рассмотрение рис. 16в еще раз подтверждает это. Для разметки речевого сегмента (нахождения параметров ${{T}_{{op}}}$ и ${{T}_{{cl}}}$) имеет смысл использовать фазовый анализ совместно с другими алгоритмами, основанными на использовании других, не фазовых, свойств речевого сигнала. Из рисунка видно, что оценки фазового алгоритма и алгоритма временного анализа по [2] совпадают лишь частично, что позволяет обнаружить или исправить ошибки каждого из этих алгоритмов. Например, на интервале 0.05–0.06 с моменты закрытия голосовой щели определяются точнее, и доступны на тех сегментах, где фазовый анализ отказывает. В экспериментах с синтетическими сигналами было обнаружено, что из-за влияния начальных условий для некоторых периодов основного тона происходит такое изменение фазовых характеристик, что оценки моментов ${{T}_{{op}}}$и ${{T}_{{cl}}}$ меняются местами. Это приводит к грубым ошибкам. Временной анализ нечувствителен к такому эффекту. В результате совместного анализа сегментов речи можно ожидать улучшения точности определения моментов открытия и закрытия голосового щели.
6. ЗАКЛЮЧЕНИЕ
Фазово-частотные характеристики предоставляют новую информацию о параметрах речевого сигнала, дополняющую обычный амплитудно-частотный анализ. Впервые выполнен математический анализ фазовых свойств голосового источника, на основе которого проведено обстоятельное компьютерное моделирование алгоритмов определения длительности периода основного тона, длительности действия и моментов начала и конца импульсов голосового источника. Установлен диапазон значений частоты основного тона, в котором фазовый анализ обеспечивает приемлемую погрешность оценки этих параметров в задаче идентификации диктора. Совместный анализ речевого сигнала в фазово-частотной и амплитудно-частотной областях улучшает устойчивость и точность оценок параметров голосового источника.
При выполнении работы второй автор пользовался поддержкой Программы повышения конкурентоспособности Национального исследовательского ядерного университета МИФИ (Московского инженерно-физического института), проект № 02.a03.21.0005 от 27.08.2013.
Список литературы
Ananthapadmanabha T., Yegnanarayana B. Epoch extraction from linear prediction residual for identification of closed glottis interval // IEEE Transactions on Acoustics, Speech and Signal Processing. 1979. V. 27. № 4. P. 309–319.
Сорокин В.Н. Сегментация периода основного тона голосового источника // Акуст. журн. 2016. Т. 62. № 2. С. 247–258.
Drugman T., Thomas M., Gudnason J., Naylor P., Dutoit T. Detection of glottal closure instants from speech signals: A quantitative review // IEEE Transactions on Audio, Speech, and Language Processing. 2012. V. 20. № 3. P. 994–1006.
Sorokin V.N., Leonov A.S. Determination of a vocal source by the spectral ratio method // Pattern Recognition and Image Analysis. 2017. V. 27. № 1. P. 139–151.
Oppenheim A.V., Lim J.S. The importance of phase in signals // Proc. IEEE. 1981. V. 69. № 5. P. 529–541.
Liu L., He J., Palm G. Effects of phase on the perception of inter-vocalic stop consonants // Speech Commun. 1997. V. 22. № 4. P. 403–417.
Paliwal K.K., Alsteris L.D. Usefulness of phase spectrum in human speech perception // Proceedings of the Eurospeech. 2003. P. 2117–2120.
Laitinen M.-V., Disch S., Pulkki V. Sensitivity of human hearing to changes in phase spectrum // J. Audio Eng. Soc. 2013. V. 61. № 11. P. 860–877.
Raitio T., Juvela L., Suni A., Vainio M., Alku P. Phase perception of the glottal excitation and its relevance in statistical parametric speech synthesis // Speech Communication. 2016. V. 81. P. 104–119
Aarabi P., Shi G., Shanechi M., Rabi S.A. Phase-Based Speech Processing. World Scientific Publishing. 2006.
Mowlaee P., Saeidi R., Stylianou Y. Advances in phase-aware signal processing in speech communication // Speech Communication. 2016. V. 81. P. 1–29.
Yegnanarayana B., Sreekanth J., Rangarajan A. Waveform estimation using group delay processing // IEEE Transactions on Audio, Speech, and Language Processing. 1985. V. 33. № 4. P. 832–836.
Smits R., Yegnanarayana B. Determination of instants of significant excitation in speech using group delay function // IEEE Transactions on Audio, Speech, and Language Processing. 1995. V. 3. № 5. P. 325–333.
Brookes M., Naylor P.A., Gudnason J. A quantitative assessment of group delay methods for identifying glottal closures in voiced speech // IEEE Trans. on Speech & Audio Processing. 2006. V. 14. № 2. P. 456–466.
Cohen L. Time-frequency distributions – a review // Proc. IEEE. 1989. V. 77. № 7. P. 941–981.
Vijayan K., Kumar V., Murty K.S.R. Feature extraction from analytic phase of speech signals for speaker verification // Speaker Odyssey. 2014. P. 1658–1662.
Patterson R.D. A pulse ribbon model of monaural phase perception // J. Acoust. Soc. Am. 1987. V. 82. № 5. P. 1560–1586.
Kim D.-S. On the perceptually irrelevant phase information in sinusoidal representation of speech // IEEE Trans. Speech Audio Process. 2001. V. 9. № 8. P. 900–905.
Леонов А.С., Сорокин В.Н. Об однозначности определения голосового источника по речевому сигналу и формантным частотам // Докл. Акад. наук. 2012. Т. 444. № 5. С. 492–495.
Леонов А.С., Сорокин В.Н. Верхняя граница ошибок решения обратной задачи определения голосового источника // Акуст. журн. 2017. Т. 63. № 5. С. 532–545.
CMU ARCTIC speech synthesis databases. http://festvox.org/cmu arctic
Alku P., Murtola T., Malinen J., Kuortti J., Story B., Airaksinen M., Salmi M., Vilkman E., Geneid A. OPENGLOT – An open environment for the evaluation of glottal inverse filtering // Speech Communication. 2019. V. 107. P. 38–47. https://doi.org/10.1016/j.specom.2019.01.005
Fant G., Liljencrants J., Lin Q.A. A four parameter model of glottal flow // STL–QPSR. 1985. V. 4. P. 1–13.
Tsyplikhin A.I. Analysis of vocal pulses in a speech signal // Acoust. Phys. 2007. V. 53. № 1. P. 105–118.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал