Акустический журнал, 2021, T. 67, № 3, стр. 265-269

Возможность пространственного усиления звука при его распространении представляет определенный интерес в прикладных задачах акустоэлектроники, прежде всего – при создании интегральных акустоэлектронных схем генерации, усиления и обработки сигналов. Давно показано, теоретически и экспериментально (см., напр., [1, 2]), что усиление звука в пьезоэлектрическом твердом теле при его взаимодействии с электрическим током возможно, если скорость дрейфа электрических зарядов превосходит скорость распространения звука. Работы, в которых разработаны теоретические и экспериментальные основы этого эффекта, перечислены в обзоре [3]. Практически, для реальных полупроводниковых пьезоэлектриков, это условие может выполняться при приложении только весьма высоких напряженностей электрических полей ~10⁵ В/м [1]. Именно наличие таких высоких порогов и является основным препятствием для использования этого эффекта в практических приложениях. Способ преодоления этой трудности состоит в использовании слоистых структур пьезоэлектрик–полупроводник и поверхностных акустических волн [4]. Здесь движение электрических зарядов и механические напряжения пространственно разделены – ток проходит по полупроводнику с относительно небольшим электрическим сопротивлением, а пьезоэлектрическое взаимодействие обеспечивается пьезослоем. Требуемое напряжение для создания сверхзвукового движения зарядов уменьшается.

В настоящей работе теоретически рассмотрена возможность усиления звука электрическим током в пьезополупроводниках при дозвуковой скорости движения носителей тока, соответственно – при малых напряженностях электрического поля. Качественно эффект описывается следующим образом. Пусть скорость дрейфа носителей тока меньше скорости звука. В пьезоэлектрик добавляется пространственно периодическое, стационарное во времени возмущение с волновым вектором $q$, для определенности – это изменение коэффициента жесткости среды. Распространяющаяся первичная звуковая волна $\exp ( - i{{\omega }}t + ikx)$ с частотой ω и волновым вектором $k$ рассеивается на этих неоднородностях. Создается рассеянное поле в виде пары волн с волновыми векторами, равными сумме и разности волнового вектора звуковой волны $k$ и волнового вектора неоднородности $q$: $\exp ( - i{{\omega }}t + (k \pm q)x)$. Далее предполагается, что векторы скорости дрейфа зарядов, волновой вектор звуковой волны и волновой вектор неоднородностей коллинеарны. Тогда последующее рассмотрение соответствует одномерной задаче. Волна с суммарным волновым вектором распространяется в ту же сторону, что и звуковая волна, но ее фазовая скорость меньше фазовой скорости звуковой волны. При достаточно большом волновом векторе неоднородности $q$ фазовую скорость рассеянной волны ${{c}_{ + }} = {\omega \mathord{\left/ {\vphantom {\omega {(k + q)}}} \right. \kern-0em} {(k + q)}}$ можно сделать меньше скорости дрейфа носителей заряда. Тогда эта рассеянная волна будет отбирать энергию у движущихся зарядов. Поскольку рассеянное поле жестко связано с основным акустическим полем, то эта энергия будет поступать в акустическую волну. При этом первичная звуковая волна будет отдавать энергию движущимся зарядам, так как скорость их движения меньше скорости распространения звуковой волны. Можно надеяться, что, при подходящем выборе параметров, приток энергии через канал рассеянного поля превзойдет отток энергии через канал акустической волны, так что суммарно поток энергии будет направлен от движущихся зарядов к звуковой волне. Звук будет усиливаться электрическими зарядами, движущимися с дозвуковой скоростью. В современной терминологии, неоднородные среды с периодами неоднородностей много меньшими длины звуковой волны называются метасредами, или мезосредами.

Изложенная выше качественная картина механизма усиления должна быть подтверждена количественными оценками, поскольку заранее неочевидно, сможет ли рассеянная волна достаточно эффективно взаимодействовать с зарядами. Ниже приведены расчеты и результаты для простейшей модели, подтвердившие принципиальную возможность эффекта.

Следует отметить, что близкие задачи с временными и пространственными неоднородностями в пьезополупроводниковых средах рассматривались в ряде работ. Например, в [5] рассмотрено влияние временной модуляции светового потока, облучающего фотопроводящий пьезопроводник, на распространение звука в этом кристалле с постоянным электрическим полем. Показано, что модуляция подсветки повышает поглощение при дозвуковых скоростях дрейфа и усиление при сверхзвуковых скоростях дрейфа носителей. В работах [6–10] исследовалась генерация звука в различных пьезоэлектрических и непьезоэлектрических кристаллах и слоистых структурах под действием коротких лазерных импульсов с пространственно периодическим распределением интенсивности. Эти импульсы приводят к возникновению в кристалле периодического распределения свободных электронов. Во внешнем электрическом поле решетка свободных электронов, смещаясь, создает внутреннее периодическое электрическое поле, которое возбуждает акустическую волну. Усиление звука стационарным однородным электрическим полем в этих работах не рассматривалось. Настоящая работа посвящена исследованию периодически неоднородной стационарной пьезоэлектрической среды, в стационарном однородном электрическом поле.

Рассматривается одномерная задача распространения плоских волн в пьезоэлектрической периодически неоднородной твердой среде с однородным электрическим полем, ориентированным по направлению распространения волн. Рис. 1 поясняет постановку задачи. Чередующиеся полосы на рисунке изображают неоднородность среды, электрическое поле направлено перпендикулярно слоям. Исходная система уравнений, необходимая для дальнейшего рассмотрения, имеет вид (см., напр., [1, 2]):

Здесь использованы следующие обозначения: u – смещение в звуковой волне; Е – напряженность электрического поля, коллинеарная u; n – полная концентрация электронов; ${{n}_{0}}$ – концентрация электронов в отсутствие звуковой волны; ρ – плотность среды, G – осевая упругость среды ($\sqrt {{G \mathord{\left/ {\vphantom {G \rho }} \right. \kern-0em} \rho }} $ – скорость продольной волны в отсутствие акустоэлектрического взаимодействия); β – пьезоэлектрический модуль; ε – диэлектрическая проницаемость; μ – подвижность электронов; D – коэффициент диффузии электронов; τ – время жизни свободных электронов, e – заряд электрона; x – пространственная координата, вдоль которой распространяются рассматриваемые волны, t – время. Ниже в расчетных формулах предполагается для упрощения выкладок $D = 0,\,\,\tau = \infty $.

Уравнение (1) – это волновое уравнение для продольных упругих волн, в правую часть которого добавлено слагаемое, описывающее силу, действующую со стороны электрического поля. Уравнение (2) описывает связь электрического поля с механической деформацией и с пространственным зарядом. Наконец, уравнение (3) описывает изменение концентрации заряда под действием электрического поля, диффузии и релаксации. Подробный вывод этой системы уравнений можно найти, например, в [1].

Далее считаем, что осевая упругость среды гармонически зависит от пространственной координаты $x$:

Разумеется, это чисто модельная постановка, выбранная для максимально возможного упрощения аналитических выкладок. Более эффективным может быть пространственная модуляция каких-то других коэффициентов системы уравнений (1)–(3), или же переход к слоистым структурам [4, 11, 12].

Поля $u,E,n$ представляем в виде суммы постоянной компоненты f₀ и переменной в пространстве и времени компоненты f_a. Переменная компонента, в свою очередь, представляется в виде звуковой волны с частотой ω и волновым числом ${{k}_{a}}$

и рассеянного на неоднородностях среды поля с комбинационными волновыми числами ${{k}_{ \pm }} = {{k}_{a}} \pm q$:

Подставляя (4)–(7) в (1)–(3) и группируя слагаемые с одинаковыми пространственно-временными зависимостями, получим систему линейных алгебраических уравнений для амплитуд всех волн. После преобразований их можно свести к трем уравнениям для амплитуд волн смещений:

Коэффициенты ${{L}_{a}},{{L}_{ \pm }}$ из-за их громоздкости не приводятся. Уравнения (9) и (10) выражают амплитуды рассеянных волн u_± через амплитуду акустической волны u_a, а выражение (8) описывает обратное влияние рассеянных волн на амплитуду акустической волны. Если теперь подставить амплитуды рассеянных волн в формулу (8), то получится самосогласованное выражение для амплитуды акустической волны:

Приравнивая нулю выражение в квадратных скобках, получим дисперсионное уравнение, связывающее частоту $\omega $ и волновое число ${{k}_{a}}$ акустической волны. Это уравнение учитывает как акустоэлектронное взаимодействие, так и рассеяние на периодических неоднородностях, в данном случае – на неоднородности упругости среды. Введем стандартные обозначения: $\chi = \frac{{4\pi {{\beta }^{2}}}}{{{{\rho }_{0}}\varepsilon {{c}_{0}}^{2}}}$ – константа электромеханической связи; ${{\omega }_{c}} = \frac{{4\pi \mu {{n}_{0}}e}}{\varepsilon }$ – частота диэлектрической релаксации; $\Omega = {\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}$, ${{k}_{0}} = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$; ${{c}_{0}} = \sqrt {{G \mathord{\left/ {\vphantom {G {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}} $ – скорость звука в отсутствие электрического поля; $V = \mu E$ – скорость дрейфа носителей заряда в электрическом поле; M = V/c₀ – число Маха движущихся носителей зарядов; ${{K}_{a}} = {{{{k}_{a}}} \mathord{\left/ {\vphantom {{{{k}_{a}}} {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}}$; ${{K}_{ \pm }} = {{({{k}_{a}} \pm q)} \mathord{\left/ {\vphantom {{({{k}_{a}} \pm q)} {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}}$. Дисперсионное уравнение в этих обозначениях записывается в виде:

В правой части (12) находятся функции, зависящие от ${{K}_{a}}$, так что формула (12) описывает дисперсионную зависимость неявным образом. Так как обе константы – $\chi $ и ${r \mathord{\left/ {\vphantom {r 2}} \right. \kern-0em} 2}$ – предполагаются малыми, уравнение (12) можно решать методом итераций, подставляя в правую часть в качестве начального приближения ${{K}_{a}} = 1$. При $r = 0$ второе слагаемое в фигурных скобках правой части (12) обращается в 0. Формула дает известный результат: при M < 1 мнимая часть волнового числа имеет положительный знак – $\operatorname{Im} {{k}_{a}} > 0$ – звуковая волна затухает. При превышении скорости дрейфа скорости звука M > 1 мнимая часть волнового числа становится отрицательной – звуковая волна нарастает.

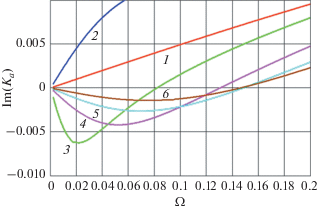
В общем случае $r > 0$ дисперсионное уравнение удобно анализировать, строя графики по формуле (12). Ниже в графическом виде приведены зависимости мнимой части волнового числа звуковой волны от частоты, вычисленные по формуле (12) при $r > 0$ и $V < {{c}_{a}}$. Коэффициент $\chi $, для определенности, принят равным 0.1.

На рис. 2 представлена зависимость мнимой части волнового числа звуковой волны $\operatorname{Im} ({{K}_{a}})$ от частоты $\Omega $ при относительно малых числах Маха, не превышающих $0.1$, на низких частотах $\Omega < 0.2$. Кривая 1 соответствует однородной среде ($r = 0$) и отсутствию движения зарядов (M = 0). Мнимая часть волнового числа звука положительна, звук затухает. Кривая 2 соответствует неоднородной среде ($r = 0.5$, $Q = 20$ – волновое число неоднородностей в 20 раз больше волнового числа звуковой волны) и числу Маха M = 0.04. Затухание оказывается даже большим, чем в однородной среде, поскольку фазовая скорость рассеянной вперед волны с волновым вектором ${{k}_{a}} + q$ больше скорости движения зарядов – MK₊ < 1. При превышении значения произведения MK₊ единицы (кривые 3–6) мнимая часть становится отрицательной в определенном диапазоне частот. Здесь накачка энергии в звук через рассеянное поле превышает потери энергии непосредственно звуковой волной. Увеличение M приводит к расширению полосы частот, в которой $\operatorname{Im} ({{K}_{a}}) < 0$, но при этом максимальное значение усиления уменьшается.

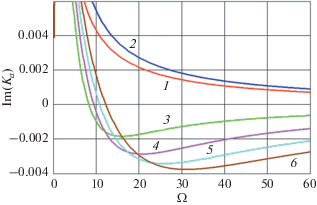
На рис. 3 приведены зависимости $\operatorname{Im} ({{K}_{a}})$ от частоты при большем значении $Q = 200$ и больших скоростях движения зарядов M = 0.1…0.25. Показана область частот $\Omega \gg 1$. Зависимости 1 (однородная среда) и 2 (неоднородная среда) получены для M = 0. В отсутствие движения зарядов рассеянные поля увеличивают поглощение звука. При увеличении скорости движения зарядов (кривые 3–6) частотная граница усиления звука ($\operatorname{Im} ({{K}_{a}}) < 0$) сдвигается в сторону высоких частот, а максимум усиления увеличивается.

Приведенные результаты расчетов показывают, что, по крайней мере, в рассмотренной модельной постановке рассеянное поле в состоянии достаточно эффективно отбирать энергию у движущихся зарядов и восполнять потери энергии основной акустической волны. Разумеется, при уменьшении амплитуды модуляции упругости $r$ вклад неоднородного поля будет убывать и усиление будет невозможно.

Для экспериментального исследования рассмотренного эффекта необходима более сложная структура. Необходимо устранить или, по крайней мере, ослабить собственные потери звукового поля, оставив механизм усиления в рассеянном поле. Этого можно добиться, используя поверхностные волны, распространяющиеся по многослойной среде, в которой пьезоактивными свойствами обладает только тонкий поверхностный слой с толщиной много меньшей глубины проникновения поверхностной волны (см., напр. [4, 11, 12]). Неоднородности должны располагаться в тонком пьезоактивном слое. В такой структуре пьезоактивный слой занимает малую часть пространства, в котором распространяется звук, но при этом рассеянное поле может быть почти полностью погружено в него. Периодическая неоднородность может создаваться не за счет изменения упругости среды, а, например, используя эффекты фотопроводимости [5, 7, 9, 10, 13] Общая схема теоретических оценок для подобных структур останется аналогичной используемой в данной работе.