1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 97, № 1, 2020

Астрономический журнал, 2020, T. 97, № 1, стр. 3-17

Эволюция вязкого протопланетного диска при образовании конвективно-неустойчивых областей

Я. Н. Павлюченков 1, *, А. В. Тутуков 1, Л. А. Максимова 1, Э. И. Воробьев 2, 3

1 Институт астрономии РАН
Москва, Россия

2 Южный федеральный университет, НИИ физики
Ростов-на-Дону, Россия

3 Институт астрофизики, Венский университет
Вена, Австрия

* E-mail: pavyar@inasan.ru

Поступила в редакцию 23.05.2019
После доработки 06.09.2019
Принята к публикации 06.09.2019

Полный текст (PDF)

Аннотация

В данной работе исследуется роль конвекции в аккреционном газопылевом диске у молодой звезды. Эволюция кеплеровского диска моделируется с помощью уравнения Прингла, описывающего изменение поверхностной плотности со временем под действием турбулентной вязкости. Одновременно с этим рассчитываются распределения плотности и температуры в полярном направлении в приближении гидростатически-равновесного диска. При расчете вертикальной структуры диска учитывается его нагрев излучением звезды, межзвездным излучением, а также вязкий нагрев. Основным фактором, управляющим эволюцией диска в рамках данной модели, является зависимость коэффициента вязкости диска от его радиуса. При расчете данного коэффициента учитывается фоновая вязкость, обеспечивающая непрерывную аккрецию газа, и конвективная вязкость, значение которой зависит от параметров конвекции на данном радиусе. Представлены результаты расчета глобальной эволюции и морфологии диска в рамках данного подхода. Показано, что в принятой модели устанавливается вспышечный характер аккреции: внутренняя область диска ($R < 3$ а.е.) заполняется веществом, после чего происходит относительно быстрый его сброс из внутренней области на звезду и процесс повторяется. Полученные результаты могут быть полезными для объяснения активности молодых объектов типа FU Ориона и EX Волка. Общий вывод работы состоит в том, что конвеция может быть одним из механизмов, ответственных за нестационарную картину аккреции в протозвездных дисках.

1. ВВЕДЕНИЕ

Изучение протопланетных дисков вокруг молодых звезд представляет огромный интерес. Действительно, молодая звезда большую часть массы накапливает в результате аккреции газа из околозвездного диска, т.е. формирование звезды неразрывно связано с эволюцией диска. В свою очередь естественным результатом поздних стадий эволюции околозвездного диска является планетная система. Исследованию физики и эволюции протозвездных дисков посвящено огромное число работ, см., напр., монографию [1]. Несмотря на большие наблюдательные и теоретические достижения в изучении протопланетных дисков, многие вопросы физики аккреционных дисков окончательно не решены. В частности, актуальным является вопрос о механизме переноса массы и момента импульса, обеспечивающим аккрецию газа. Основным подходом для описания дисковой аккреции, наряду с гравитационной неустойчивостью, является формализм турбулентной вязкости, однако механизм турбулизации течения до сих пор является дискуссионным. Одним из механизмов возникновения турбулентности может быть конвекция аккрецируемого газа в полярных направлениях.

Идея о том, что конвекция в протопланетных дисках может быть ответственна не только за перенос тепла, но и обеспечивать вязкость и таким образом влиять на эволюцию диска, была сформулирована в 80-х годах прошлого века в работах [2] и [3]. Эта идея вызвала большой энтузиазм, однако по прошествии нескольких десятков лет роль конвекции в переносе момента импульса до сих пор является дискуссионной (см. подробный исторический обзор в [4]). Первые численные модели, учитывающие конвекцию в диске [5, 6], свидетельствовали о том, что соответствующий ей коэффициент вязкости весьма мал, а сам газовый диск имеет тенденцию разбиваться на кольца. В рамках более поздних численных моделей [7, 8] конвекция обеспечивала более высокие коэффициенты вязкости (в терминах параметра Шакуры и Сюняева $\alpha = {{10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 2}}}$), однако для этого требовался дополнительный механизм нагрева газа в экваториальной плоскости аккреционного диска. Идея о дополнительной вязкости в околозвездных дисках, связанной с конвекцией, обсуждалась также в работах [9–11]. C получением высококачественных изображений протопланетных дисков и наблюдением кольцеобразных структур в них интерес к гидродинамическим моделям и конвекции в них снова возрос. В частности, в работе [12] представлены результаты трехмерного моделирования конвекции в диске, где проиллюстрировано возникновение конвективных ячеек, вихрей и других когерентных структур при инициировании конвекции. При этом авторы данной работы отмечают, что им не удается получить самоподдерживающийся режим конвекции в диске. В то же время в работах [13–15] представлен теоретический анализ конвективной неустойчивости аккреционного диска, где авторы находят условия неустойчивости и отмечают необходимость более детальных моделей. В данной работе изучаются условия возникновения конвекции и крупномасштабная эволюция конвективного протозвездного кеплеровского диска на базе модели, особенностью которой является детальный расчет вертикальной структуры диска и учет постоянной аккреции газа на диск из околозвездной оболочки. Основное внимание уделяется анализу полученного рекуррентного характера аккреционной активности протозвездного диска.

2. МОДЕЛЬ ДИСКА

Расчет эволюции околозвездного диска производится с помощью численной модели, в рамках которой последовательно рассчитывается эволюция радиальной и вертикальной структуры диска. При этом каждый временной шаг разделен на два этапа: 1) расчет эволюции поверхностной плотности газа; 2) восстановление распределений плотности и температуры в вертикальном направлении. На первом этапе вычисляется также темп нагрева среды, связанный с аккрецией вещества и необходимый для расчета тепловой структуры. В свою очередь при восстановлении вертикальной структуры диска происходит отождествление конвективно-неустойчивых областей и формирование распределения коэффициента вязкости, необходимого для расчета эволюции поверхностной плотности. Далее более подробно описаны детали обоих этапов расчета.

2.1. Расчет эволюции поверхностной плотности

Для описания эволюции поверхностной плотности диска мы используем формализм вязкого аккреционного диска. В рамках данного подхода считается, что механизмом переноса массы и момента импульса является некий физический процесс (турбулентность, магнитное поле или конвекция), математически описываемый аналогично молекулярной вязкости, т.е. в основе модели лежат уравнения Навье$ - $Стокса. В приближении аксиально-симметричного, геометрически-тонкого, кеплеровского диска и в пренебрежении градиентами давления газа в радиальном направлении, эволюция поверхностной плотности описывается уравнением Прингла [16]:

(1)
$\frac{{\partial \Sigma }}{{\partial t}} = \frac{3}{R}\frac{\partial }{{\partial R}}\left[ {\sqrt R \frac{\partial }{{\partial R}}\left( {\nu \sqrt R \Sigma } \right)} \right] + W(R,t),$
где $\Sigma $ – поверхностная плотность, $R$ – расстояние до звезды, $t$ – время, $\nu $ – коэффициент кинематической вязкости, $W(R,t)$ – темп притока вещества из оболочки. Уравнение Прингла широко используется для описания долговременной эволюции околозвездных дисков (см., напр., обзор [17]). Специфика его использования зависит от способа определения функции $\nu (R)$. В нашем случае $\nu (R)$ задается феноменологически и дополнительно определяется условиями возникновения конвективной неустойчивости.

В результате эволюции вязкого диска выделяется тепловая энергия. В конечном итоге выделяемая тепловая энергия черпается из гравитационной энергии вещества, т.е. вязкость можно рассматривать как механизм преобразования гравитационной энергии аккрецирующего газа в тепло. Темп энерговыделения тепла на единицу площади равен [16]:

(2)
${{\Gamma }_{{{\text{vis}}}}} = \frac{9}{4}\frac{{G{{M}_{ \odot }}}}{{{{R}^{3}}}}\nu \Sigma ,$
где ${{M}_{ \odot }}$ – масса центральной звезды. Этот нагрев учитывается при расчете вертикальной структуры диска. В конечном счете в рамках нашей модели именно он ответственен за возникновение конвекции.

2.1.1. Коэффициент вязкости в конвективно-устойчивых областях. В конвективно-устойчивых областях диска мы полагаем наличие некоторого фонового механизма переноса момента импульса и задаем вязкость в виде:

(3)
${{\nu }_{{{\text{bg}}}}} = {{\nu }_{0}}\mathop {\left( {\frac{R}{{{{R}_{{{\text{AU}}}}}}}} \right)}\nolimits^\beta ,$
где $\beta = 1$ и ${{\nu }_{0}} = {{10}^{{15}}}$ см2 с. При таком выборе β распределение поверхностной плотности для стационарного решения уравнения Прингла при $R \gg {{R}_{ \odot }}$,
(4)
$\dot {M} = 3\pi \Sigma \cdot {{\nu }_{{{\text{bg}}}}},$
будет обратно пропорционально расстоянию до звезды, т.е. $\Sigma \propto {{R}^{{ - 1}}}$, что хорошо согласуется с распределениями плотности в наблюдаемых протопланетных дисках [18]. При принятом значении ${{\nu }_{0}}$ и темпе аккреции $\dot {M} = {{10}^{{ - 7}}}{{M}_{ \odot }}{\text{/год}}$ масса диска между 0.1 и 100 а.е. составит ${{M}_{{{\text{disk}}}}} = {{10}^{{ - 1}}}{{M}_{ \odot }}$. Эти значения также укладываются в диапазон темпов аккреции и масс наблюдаемых протопланетных дисков [19].

Покажем, что значения $\beta = 1$ и ${{\nu }_{0}} = {{10}^{{15}}}$ см2 c согласуются с широко используемой $\alpha $-параметризацией турбулентной вязкости. В рамках параметризации Шакуры и Сюняева [20] $\nu = \alpha {{с}_{s}}H$, где ${{c}_{s}}$ – скорость звука, $H$ – высота диска. Пусть тепловая структура диска целиком определяется нагревом центральной звезды, тогда

(5)
$\varepsilon \frac{{{{L}_{ \odot }}}}{{4\pi {{R}^{2}}}} = \sigma {{T}^{4}},$
где ${{L}_{ \odot }}$ – светимость звезды, $\varepsilon $ – косинус угла между нормалью к поверхности диска и направлением на звезду, $\sigma $ – постоянная Стефана–Больцмана, $T$ – эффективная температура. Условие гидростатического равновесия диска в вертикальном направлении можно приближенно записать в виде:
(6)
$\frac{H}{R} \approx \frac{{{{c}_{s}}}}{{{{V}_{k}}}},$
где ${{V}_{k}}$ – кеплеровская скорость на радиусе $R$. Комбинируя эти два уравнения и используя связь $c_{s}^{2} = {{k}_{{\text{B}}}}T{\text{/}}{{\mu }_{{\text{g}}}}{{m}_{{\text{H}}}}$, где ${{k}_{{\text{B}}}}$ – постоянная Больцмана, ${{\mu }_{{\text{g}}}}$ – средняя молекулярная масса вещества, ${{m}_{{\text{H}}}}$ – масса атома водорода, получим:
(7)
$\begin{gathered} {{\nu }_{{{\text{bg}}}}} = \alpha {{\nu }_{\alpha }}\left( {\frac{R}{{{{R}_{{{\text{AU}}}}}}}} \right), \\ {\text{где}}\quad {{\nu }_{\alpha }} = \frac{{{{k}_{{\text{B}}}}{{R}_{{{\text{AU}}}}}}}{{{{\mu }_{{\text{g}}}}{{m}_{{\text{H}}}}{{{(G{{M}_{ \odot }})}}^{{1/2}}}}}\mathop {\left( {\frac{{\varepsilon {{L}_{ \odot }}}}{{4\pi \sigma }}} \right)}\nolimits^{1/4} . \\ \end{gathered} $
Принимая $\varepsilon = 0.1$ и подставляя значения констант, получаем ${{\nu }_{\alpha }} = {{10}^{{16}}}$ см2 c. Таким образом, используемая нами параметризация (3) для конвективно-устойчивых областей соответствует модели вязкого диска с $\alpha $-параметром $\alpha = 0.1$. Такое высокое значение $\alpha $ соответствует наиболее ранним (до 1 млн. лет) этапам эволюции протопланетных дисков, когда основной вклад в вязкость вносят, вероятно, эффекты самогравитации диска [21].

2.1.2. Коэффициент вязкости в конвективно-неустойчивых областях. Опишем алгоритм задания вязкости в конвективно-неустойчивых областях. После расчета вертикальной структуры диска с помощью метода, описанного в разделе 2.2, идентифицируются области диска, в которых выполняется условие конвективной неустойчивости. Конвективно-неустойчивыми считаются области, в которых выполнено условие [22]

(8)
$\frac{{dT}}{{dz}} < - \frac{{g(z)}}{{{{c}_{P}}}},$
где $g(z) = \tfrac{{G{{M}_{ \odot }}}}{{{{R}^{3}}}}z + 4\pi G\sigma (z)$ – вертикальная компонента гравитационного ускорения на радиальном расстоянии $R$ и высоте $z$, $\sigma (z) = \int_0^z {\rho (z{\kern 1pt} ')dz{\kern 1pt} '} $ – поверхностная плотность, отсчитываемая от экватора, ${{c}_{P}} = \tfrac{7}{2}\tfrac{{{{k}_{{\text{B}}}}}}{{{{\mu }_{g}}{{m}_{{\text{H}}}}}}$ – теплоемкость газа при постоянном давлении, соответствующая двухатомному газу, ${{\mu }_{{\text{g}}}} = 2.4$ – средняя молекулярная масса. Отметим, что критерий (8) соответствует ограничениям, лежащим в основе модели восстановления вертикальной структуры. В частности, он не учитывает процессы ионизации и диссоциации газа. Далее, для каждого вертикального столбца, определяемого радиальной координатой $R$, рассчитывается массовая доля вещества $\gamma $ в конвективно-неустойчивых областях в данном столбце к общей поверхностной плотности газа в нем. Коэффициент вязкости, определяемый конвекцией, задается в виде
(9)
${{\nu }_{{\text{c}}}} = \gamma H{{V}_{{\text{c}}}},$
где $H$ – локальная шкала высоты диска, для определения которой используется уравнение (6), ${{V}_{{\text{c}}}}$ – характерная скорость конвекции. Скорость ${{V}_{{\text{c}}}}$ определяется в приближении, что вся выделившаяся в результате аккреции газа энергия переходит в кинетическую энергию его конвективного движения, т.е. темп вязкой диссипации равен потоку кинетической энергии газа:
(10)
${{\Gamma }_{{{\text{vis}}}}} = \frac{{{{\rho }_{0}}V_{{\text{c}}}^{2}}}{2}{{V}_{{\text{c}}}},$
где ${{\rho }_{0}}$ – экваториальная плотность. Полученное таким образом распределение ${{\nu }_{{\text{c}}}}$ дополнительно сглаживается по радиусу с помощью гауссовой функции шириной $H$:
(11)
${{\tilde {\nu }}_{c}}(R) = \frac{{\int\limits_{{{R}_{{{\text{in}}}}}}^{{{R}_{{{\text{out}}}}}} \,{{\nu }_{{\text{c}}}}(r){{{\text{e}}}^{{ - \tfrac{{{{{(R - r)}}^{2}}}}{{2{{H}^{2}}}}}}}dr}}{{\int\limits_{{{R}_{{{\text{in}}}}}}^{{{R}_{{{\text{out}}}}}} \,{{{\text{e}}}^{{ - \tfrac{{{{{(R - r)}}^{2}}}}{{2{{H}^{2}}}}}}}dr}},$
где ${{R}_{{{\text{in}}}}}$ и ${{R}_{{{\text{out}}}}}$ – внутренняя и внешняя границы диска. Сглаживание по радиусу проводится в связи с тем, что конвективная область должна иметь размер в радиальном направлении не меньше, чем высота диска. Локальная высота диска является естественным выбором для радиуса сглаживания, так как именно $H$ принята за характерную длину конвекции при определении вязкости в выражении (9).

Итоговый коэффициент вязкости задается как сумма фоновой и конвективной вязкости:

(12)
$\nu = {{\nu }_{{{\text{bg}}}}} + {{\tilde {\nu }}_{c}}.$
Несмотря на то что такой подход, по-видимому, переоценивает значение конвективной вязкости, мы считаем его приемлемым начальным приближением. В дальнейшем планируется использовать элементы теории длины пути перемешивания для более корректного вычисления $\nu $ в конвективно-неустойчивых областях.

2.1.3. Граничные, начальные условия и модель аккреции из оболочки. В модели мы используем фиксированные значения поверхностной плотности на внутренней ($R = 0.1$ а.е.) и внешней ($R = 100$ а.е.) границах диска, $\Sigma = {{10}^{{ - 2}}}$ г/см2 и $\Sigma = {{10}^{{ - 5}}}$ г/см2 соответственно. Эти граничные значения поверхностной плотности на 3–4 порядка величины меньше, чем значения плотности в окрестности границ после прихода диска к квазиравновесному состоянию. Можно считать, что данные граничные условия реализуют свободное вытекание вещества, т.е. предполагается, что есть некие эффективные механизмы отбора массы на границах диска. Такие условия безусловно сильно влияют на поведение решения вблизи границы (что следует из больших градиентов поверхностной плотности вблизи границ), а также определяют характер накопления газа в диске. Введение более сложных граничных условий требует отдельного исследования, которое планируется нами в будущем.

Эволюция аккреционного диска в существенной мере определяется аккрецией вещества из околозвездной оболочки. Простые оценки показывают, что большую часть вещества звезда получает из диска, в то время как сам диск получает его из оболочки – остатка молекулярного облака. Область аккреции вещества из оболочки на диск зависит от начального углового момента облака. Для оценки “центробежного” радиуса ${{R}_{{{\text{acc}}}}}$, на который аккрецирует вещество из оболочки, воспользуемся формулой из работы [23],

(13)
${{R}_{{{\text{acc}}}}} = \frac{{{{\Omega }^{2}}R_{{{\text{core}}}}^{4}}}{{G{{M}_{{{\text{core}}}}}}},$
где $\Omega $ – угловая скорость облака, ${{R}_{{{\text{core}}}}}$ – начальное положение аккрецирующего элемента в облаке, ${{M}_{{{\text{core}}}}}$ – масса внутренней части облака (масса звезды). Данная формула получена из условия сохранения момента импульса аккрецирующего вещества. Распределение плотности в наблюдаемых протозвездных облаках принято описывать выражением
(14)
$n = \frac{{{{n}_{0}}}}{{1 + \mathop {\left( {\tfrac{r}{{{{r}_{0}}}}} \right)}\nolimits^2 }},$
где ${{n}_{0}}$ – центральная концентрация водорода, ${{r}_{0}}$ – радиус внутренней области с почти постоянной плотностью. Примером хорошо изученного протозведного облака является дозвездное ядро L1544, для которого ${{r}_{0}} = 3 \times {{10}^{3}}$ а.е., ${{n}_{0}} = 1.6 \times {{10}^{6}}$ см–3 [24]. Если аккрецируемый элемент взять на границе плато (${{R}_{{{\text{core}}}}} = {{r}_{0}}$), содержащего для данного ядра значительную часть массы облака (${{M}_{{{\text{core}}}}} = 1.2{{M}_{ \odot }}$), и использовать соответствующее L1544 значение угловой скорости $8.23 \times {{10}^{{14}}}$ с–1 [25], то центробежный радиус ${{R}_{{{\text{acc}}}}}$ получится равным 11.3 а.е. Очевидно, что более удаленные элементы облака должны аккрецировать на большие центробежные радиусы. В нашей модели аккреционный поток из оболочки на диск $W(R,t)$ задается приближенно, а именно, мы предполагаем постоянный приток вещества в кольцо между 10 и 20 а.е. с темпом ${{10}^{{ - 7}}}{{M}_{ \odot }}{\text{/год}}$. Такой постоянный во времени темп выбран в связи с тем, что мы рассматриваем только начальные фазы эволюции диска.

В начальный момент времени мы задаем диск с распределением поверхностной плотности $\Sigma (R) \propto {{R}^{{ - 1}}}$ и массой ${{10}^{{ - 7}}}{{M}_{ \odot }}$ вокруг звезды солнечной массы. Такой начальный диск носит лишь номинальный, формальный характер, поскольку масса диска после прихода к квазиравновесному состоянию существенно превысит это значение. Фактически протопланетный диск в нашей постановке полностью формируется за счет аккреции газа из оболочки.

2.1.4. Метод решения уравнения Прингла. Для решения уравнения Прингла мы используем конечно-разностный метод. Расчетная область делится на ячейки, уравнение (1) аппроксимируется в полностью неявном виде:

(15)
$\begin{gathered} \frac{{\Sigma _{i}^{{(n + 1)}} - \Sigma _{i}^{n}}}{{\Delta t}} = \\ = \;\frac{{3r_{{i + 1}}^{{1/2}}}}{{{{R}_{i}}\Delta {{r}_{i}}\Delta {{R}_{{i + 1}}}}}\left( {{{\nu }_{{i + 1}}}R_{{i + 1}}^{{1/2}}\Sigma _{{i + 1}}^{{(n + 1)}} - {{\nu }_{i}}R_{i}^{{1/2}}\Sigma _{i}^{{(n + 1)}}} \right) - \\ - \;\frac{{3r_{i}^{{1/2}}}}{{{{R}_{i}}\Delta {{r}_{i}}\Delta {{R}_{i}}}}\left( {{{\nu }_{i}}R_{i}^{{1/2}}\Sigma _{i}^{{(n + 1)}} - {{\nu }_{{i - 1}}}R_{{i - 1}}^{{1/2}}\Sigma _{{i - 1}}^{{(n + 1)}}} \right), \\ \end{gathered} $
где $\Sigma _{i}^{{(n)}}$ – значение поверхностной плотности в $i$‑й ячейке для $n$-го временного шага, $\Delta t$ – шаг по времени, ${{r}_{i}}$ – левая граница $i$-й ячейки, ${{R}_{i}}$ – центр $i$-й ячейки, $\Delta {{r}_{i}}$ – линейный масштаб $i$-й ячейки, $\Delta {{R}_{i}}$ – расстояние между центрами $i$-й и ($i - 1$)-й ячейками:
$\begin{gathered} {{R}_{i}} = \frac{1}{2}({{r}_{i}} + {{r}_{{i + 1}}}),\quad \Delta {{r}_{i}} = ({{r}_{{i + 1}}} - {{r}_{i}}), \\ \Delta {{R}_{i}} = ({{R}_{i}} - {{R}_{{i - 1}}}). \\ \end{gathered} $
Уравнения (15) представляют собой систему линейных алгебраических уравнений (относительно неизвестных $\Sigma _{i}^{{(n + 1)}}$) следующего вида:
(16)
${{A}_{i}}\Sigma _{{i - 1}}^{{(n + 1)}} + {{B}_{i}}\Sigma _{i}^{{(n + 1)}} + {{C}_{i}}\Sigma _{{i + 1}}^{{(n + 1)}} = {{D}_{i}}.$
Совместно с уравнениями, реализующими граничные условия, эти уравнения формируют систему линейных алгебраических уравнений с трехдиагональной матрицей. Решение данной системы находится с помощью метода прогонки. Применение неявной схемы при аппроксимации исходного уравнения позволяет рационально выбирать шаг по времени, исходя из принятой точности, поскольку такой метод является абсолютно устойчивым. В наших расчетах шаг по времени выбирался исходя из скорости изменения поверхностной плотности. В частности, при идентификации конвективно-неустойчивых областей шаг по времени уменьшался.

2.2. Расчет вертикальной структуры

Для расчета вертикальной структуры диска мы используем тепловую модель из работы [26]. В принятой модели решается одномерная задача о переносе излучения в вертикальном (полярном) направлении, при этом учитывается нагрев внутренними источниками, внешним излучением и перенос теплового излучения в самом диске. В модели предполагается, что единственным источником непрозрачности является пыль, причем температуры газа и пыли равны. Отношение массы пыли к массе газе предполагается постоянным по всему диску и равным ${{10}^{{ - 2}}}$. Для решения этой задачи излучение разделяется на ультрафиолетовое (звездное и межзвездное) и инфракрасное (тепловое) излучение самого диска. Интенсивность ультрафиолетового излучения находится путем прямого интегрирования уравнения переноса излучения. Так, нагрев диска ультрафиолетовым излучением звезды находится по формуле:

(17)
${{S}_{{{\text{star}}}}} = \frac{{\kappa _{{\text{P}}}^{{{\text{uv}}}}L}}{{4\pi {{R}^{2}}}}exp( - {{\tau }_{{{\text{uv}}}}}{\text{/}}cos\theta ),$
где $\kappa _{{\text{P}}}^{{{\text{uv}}}}$ – усредненный по Планку коэффициент поглощения для температуры звезды, $L$ – светимость звезды, ${{\tau }_{{{\text{uv}}}}}$ – оптическая толщина в УФ-излучении в вертикальном направлении от заданного положения до верхней границы диска, $cos\theta $ – косинус угла между нормалью к диску и направлением на звезду. Светимость звезды принята равной сумме фотосферной и аккреционной светимости. Фотосферная светимость предполагается равной солнечной, аккреционная светимость вычисляется из темпа аккреции вещества из диска на звезду. При вычислении $\kappa _{{\text{P}}}^{{{\text{uv}}}}$ и ${{\tau }_{{{\text{uv}}}}}$ использовалась температура излучения звезды ${{T}_{{{\text{star}}}}} = 6000$ K. В наших расчетах $cos\theta $ задавался постоянным по диску и равным 0.05. Это приближение существенно упрощает расчет внешнего нагрева, однако оно не описывает эффекты самозатенения, которые могут возникать при немонотонном распределении плотности. Нагрев межзвездным УФ-излучением рассчитывался по формуле:
(18)
${{S}_{{{\text{bg}}}}} = D\kappa _{{\text{P}}}^{{{\text{uv}}}}\sigma T_{{{\text{bg}}}}^{4}exp( - 2{{\tau }_{{{\text{uv}}}}}),$
где ${{T}_{{{\text{bg}}}}} = {{10}^{4}}$ K, $D = {{10}^{{ - 14}}}$ – температура и дилюция межзвездного излучения, $\sigma $ – постоянная Стефана–Больцмана. Отметим, однако, что нагрев межзвездным излучением для рассматриваемых областей вносит незначительный вклад по сравнению с нагревом от центральной звезды и потому им можно пренебречь.

Для моделирования переноса теплового излучения решается система моментных уравнений в эддингтоновском приближении и с использованием усредненных по частоте коэффициентов поглощения:

(19)
${{c}_{{\text{V}}}}\frac{{\partial T}}{{\partial t}} = c{{\kappa }_{{\text{P}}}}(E - a{{T}^{4}}) + S,$
(20)
$\frac{{\partial E}}{{\partial t}} - \frac{\partial }{{\partial z}}\left( {\frac{c}{{3\rho {{\kappa }_{{\text{R}}}}}}\frac{{\partial E}}{{\partial z}}} \right) = - \rho c{{\kappa }_{{\text{P}}}}(E - a{{T}^{4}}),$
где $T$ – температура среды, $E$ – плотность лучистой энергии, $z$ – вертикальная координата, $\rho $ – объемная плотность, ${{c}_{V}}$ – теплоемкость среды, $c$ – скорость света, $a$ – постоянная Стефана, $\sigma $ – поверхностная плотность, измеряемая от экватора, ${{\kappa }_{{\text{P}}}}$ – коэффициент поглощения, усредненный по Планку, ${{\kappa }_{{\text{R}}}}$ – коэффициент поглощения, усредненный по Росселанду. $S$ – функция нагрева (на единицу массы) звездным, межзвездным излучением, а также вязким трением:

(21)
$S = {{S}_{{{\text{star}}}}} + {{S}_{{{\text{bg}}}}} + \frac{{{{\Gamma }_{{{\text{vis}}}}}}}{\Sigma }.$

Несмотря на то что исходная тепловая модель является нестационарной, решение системы (19)–(20) находится в стационарном приближении. Другими словами, предполагается, что время достижения теплового равновесия в вертикальном направлении существенно меньше характерного времени вязкой эволюции на данном радиусе. Наши тестовые расчеты и оценки, аналогичные тем, что приведены в работе [27], показывают, что это приближение хорошо работает для принятой модели. Однако, для других параметров модели условие стационарности может нарушаться в конвективно-неустойчивых областях, где характерные времена прихода к тепловому равновесию и времена вязкой эволюции могут быть сопоставимы. Поэтому в общем случае следует использовать нестационарную модель. Однако использование нестационарной тепловой модели потребует также расчета конвективного переноса тепла в радиальном направлении, что находится за рамками используемого 1 + 1D подхода.

Важной особенностью тепловой модели является использование усредненных по Планку и Росселанду непрозрачностей, зависящих от температуры. Эти коэффициенты рассчитывались по частотно-зависимым коэффициентам поглощения и рассеяния для смеси графитовых и силикатных пылинок. Сами спектральные коэффициенты поглощения и рассеяния рассчитаны с помощью теории Ми, при этом распределение пылинок по размерам бралось степенным, $n(a) \propto {{a}^{{ - 3.5}}}$, c минимальным и максимальным радиусами пылинок ${{a}_{{min}}} = 5 \times {{10}^{{ - 7}}}$ см и ${{a}_{{max}}} = {{10}^{{ - 4}}}$ см. Зависящие от длины волны и соответствующие им усредненные по Планку, Росселанду и по внешнему потоку коэффициенты поглощения приведены на рис. 1. Важной особенностью усредненных коэффициентов поглощения является их рост с температурой при $T > 500$ K. Как показывают наши расчеты, эта особенность является одним из условий возникновения конвективно-неустойчивых областей.

Рис. 1.

Зависимости коэффициентов поглощения и рассеяния от длины волны для смеси силикатных и графитовых пылинок (слева) и соответствующие коэффициенты поглощения (справа), усредненные по Планку ${{\kappa }_{{\text{P}}}}$, по Росселанду ${{\kappa }_{{\text{R}}}}$ и по потоку ${{\kappa }_{{\text{F}}}}$.

Отметим, что в модели не учитывается испарение пыли при температурах $T \gtrsim 1500$ K, при которых должно происходить резкое уменьшение непрозрачности. При таких высоких температурах основной вклад в непрозрачность среды начинает вносить газ. Кроме того, при температурах $T \gtrsim 2000$ K существенными становятся процессы диссоциации и ионизации водорода, однако это также не учитывается в модели. На рис. 1 интервал температур, где используемые нами непрозрачности, строго говоря, некорректны, отмечен желтым цветом. В наших моделях температура среды, как правило, ниже этого критического диапазона, но в максимуме может приближаться к нему, что приводит к необходимости модификации модели. Однако соответствующая модификация существенно усложнит тепловую модель, но мы планируем провести такую модификацию в будущем.

Решение системы уравнений (19)–(20) определяется с использованием полностью неявной схемы, что делает метод абсолютно устойчивым и снимает ограничения на временной шаг. Данный метод позволяет корректно рассчитывать тепловую эволюцию во всех участках диска, включая оптически-толстые области, в которых характерные времена процессов нагрева и охлаждения сопоставимы с динамическими временами. Метод моделирования тепловой структуры в данной модели тесно связан с методом восстановления вертикальной структуры диска в предположении локального гидростатического равновесия, которое находится из следующего уравнения:

(22)
$\frac{{{{k}_{{\text{B}}}}}}{{{{\mu }_{{\text{g}}}}{{m}_{{\text{H}}}}}}\frac{{d(\rho T)}}{{\rho dz}} = - \frac{{G{{M}_{*}}}}{{{{r}^{3}}}}z - 4\pi G\sigma ,$
где ${{M}_{*}}$ – масса звезды. Первое слагаемое в правой части уравнения (22) учитывает вертикальную компоненту гравитационного поля звезды, второе слагаемое учитывает самогравитацию диска. Отметим, что при использованных параметрах модели самогравитацией диска можно пренебречь. Расчет вертикальной структуры диска позволяет получить полную информацию о распределении плотности и температуры в диске. Для решения уравнения гидростатического равновесия также используется устойчивый неявный метод.

Принципиальным условием эффективности работы этих методов является оптимальный выбор пространственной сетки в $z$-направлении. Пространственная сетка должна отслеживать все заранее неизвестные особенности решения (градиенты плотности и температуры) с учетом существенного ограничения на количество ячеек (не более 100) и больших интервалов плотности газа (до 10 порядков). Мы разработали алгоритм построения и адаптивной модификации такой сетки, основанный на приближенном быстром решении уравнения гидростатического равновесия. Данный метод восстановления вертикальной структуры диска с расчетом переноса излучения был тщательно протестирован и сопоставлен с другими методами. В стационарном режиме распределения температуры хорошо согласуются с результатами моделирования структуры диска, полученными другими авторами. В нестационарном режиме характерные времена достижения теплового равновесия соответствуют аналитическим оценкам. Более подробное описание данного метода можно найти в статье [26].

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Рассмотрим результаты моделирования на момент времени 35 тыс. лет с начала эволюции принятой модели диска. С этого момента времени устанавливается периодический, вспышечный характер аккреции: внутренняя область диска ($R < 3$ а.е.) постепенно заполняется веществом, после чего происходит обусловленный конвекцией относительно быстрый сброс вещества из внутренней области на звезду и процесс повторяется. Этот момент времени далее условно будем считать нулевым. На рис. 2 показана эволюция распределений поверхностной плотности газа, темпа вязкого нагрева, оптической толщины в ИК-излучении и температуры в ходе рядового цикла вспышечного режима аккреции.

Рис. 2.

Радиальные распределения поверхностной плотности (верхняя левая панель), темпа вязкого нагрева (верхняя правая панель), оптической толщины к ИК-излучению (нижняя левая панель) и экваториальной температуры (нижняя правая панель) для нескольких моментов времени, иллюстрирующих развитие вспышки аккреции. Время отсчитывается от конца предыдущей аккреционной вспышки. Вертикальной полосой показана область аккреции газа из оболочки.

На начальный момент времени поверхностная плотность во внутренней области диска $R < 3$ а.е. растет в радиальном направлении от звезды, что является последствием сброса вещества после предыдущего цикла. Экваториальная температура диска монотонно падает от внутреннего края диска до расстояния $R \approx 60$ а.е., а затем испытывает скачок. Этот скачок на внешней границе связан с тем, что поверхностная плотность оказывается настолько малой, что диск становится прозрачным к УФ-излучению звезды в вертикальном направлении, т.е. экваториальные области в рамках используемого одномерного приближения нагреваются непосредственно звездным излучением.

Внутренняя область $R < 3$ а.е. заполняется со временем аккрецируемым веществом. На момент $t = 3694$ года распределение плотности во внутренней области становится более монотонным. Температура во внутренней области повышается, что связано с увеличением поверхностной плотности и аккреционного потока в ней. Оптическая толщина в ИК-излучении достигает величины ${{\tau }_{{{\text{IR}}}}} \approx 400$ на радиусе $R = 0.2$ а.е.

По достижении этого момента внутренняя область становится конвективно-неустойчивой. При этом область конвективной неустойчивости распространяется наружу, а на ее фронте формируется максимум плотности. На момент времени $t = 3889$ лет этот фронт достигает радиуса 0.5 а.е.. Энерговыделение $Q$ внутри 0.5 а.е. на момент $t = 3889$ лет примерно на два порядка величины выше, чем до возникновения конвективно-неустойчивой зоны (рис. 2). Температура внутри конвективной зоны на этот момент существенно возрастает, достигая значений 1000 K на радиусе 0.2 а.е. За границей конвективной области температура также растет по сравнению с температурой, характерной для предыдущих моментов времени. Это является следствием того, что к фотосферной светимости звезды добавляется значительный нагрев, связанный с усиленной аккрецией вещества диска звездой.

На момент времени $t = 4042$ года конвективный фронт, расширяясь, достигает радиуса $R = 3$ а.е. Поверхностная плотность внутри этого радиуса значительно падает по сравнению с моментом перед вспышкой, а само распределение плотности становится близким к исходному для нулевого момента времени, с тем отличием, что на нем видны слабые осцилляции, которые в дальнейшем разглаживаются. Как видно из рис. 2, для $t = 4042$ года другие распределения также близки к распределениям для начального момента времени. С этого момента внутренняя область становится конвективно устойчивой и диск вступает в новую фазу накопления вещества.

На рис. 3 показаны распределения плотности и температуры в полярном сечении диска для трех моментов времени, иллюстрирующих развитие вспышки аккреции. В верхнем ряду рис. 3 показаны распределения для нулевого момента времени (начала цикла). Плотность газа во всем диске монотонно падает от экватора к верхней границе диска. Вблизи внутренней границы диска контраст плотности в полярном направлении диска достигает ~11 порядков величин, падая от ${{10}^{{14}}}$ на экваторе до ${{10}^{3}}$ см–3 на верхней границе. В то же время характер распределения температуры определяется расстоянием от звезды. При $R \gtrsim 1$ а.е. температура монотонно растет от экватора к атмосфере диска, тогда как при $R \lesssim 1$ а.е. температура сначала падает, а затем растет с увеличением $z$. Это связано с тем, что во внутренней области диска вязкая диссипация начинает вносить существенный вклад в нагрев диска, в то время как при $R \gtrsim 1$ а.е преимущественным источником нагрева является УФ-излучение центральной звезды.

Рис. 3.

Распределения концентрации газа (слева) и температуры газа (справа) в RZ-сечении диска для трех моментов времени, иллюстрирующих развитие вспышки аккреции. Время отсчитывается от конца предыдущей аккреционной вспышки и указано в верхнем левом углу каждой панели. По оси ординат отложено отношение высоты над экватором к радиальному расстоянию до звезды. Конвективно-неустойчивые области выделены штриховкой.

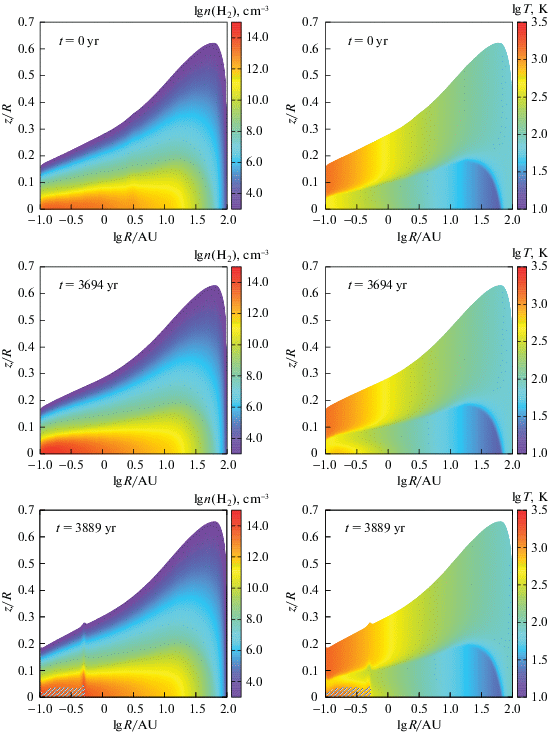
В центре рис. 3 показаны распределения плотности и температуры для времени $t = 3694$ года, соответствующего моменту непосредственно перед усилением аккреции, вызванным конвекцией. Сравнивая эти распределения с верхними панелями для нулевого момента, можно отметить, что во внутренней области диска, $R < 3$ а.е, существенно возросла концентрация (до ${{10}^{{15}}}$ см–3) и температура (до ${{10}^{3}}$ K) газа на экваторе, что связано с накоплением вещества в этой области в результате аккреции из внешних областей диска. Распределения плотности и температуры стали более монотонными в окрестности $lgR\,({\text{a}}.{\text{e}}.) = 0.5$ по сравнению с этими распределениями для нулевого момента.

Распределения на нижней панели рис. 3 относятся к моменту времени $t = 3889$ лет и соответствуют фазе развитой конвекции и сброса вещества из внутренней области. На распределении плотности в окрестности $lgR = - 0.3$ видна область повышенной плотности, соответствующая фронту распространения конвекции. Толщина диска внутри этой области несколько выше, чем на стадии накопления вещества, что связано с повышенной температурой в зоне конвекции. На всех распределениях штриховкой показаны области, удовлетворяющие критерию конвективной неустойчивости. Видно, что область конвективной неустойчивости располагается вблизи экватора и простирается до высоты $z{\text{/}}R \approx 0.03$.

На рис. 4 приведены распределения величины отношения градиента температуры $dT{\text{/}}dz$ к модулю адиабатического градиента $g(z){\text{/}}{{C}_{p}}$ вдоль $z$-направления для двух радиальных положений в диске на фазе аккреционной вспышки $(t = 3889$ лет).

Рис. 4.

Отношение градиента температуры к адиабатическому градиенту как функция $z$-координаты для $R = 0.2$ а.е. (слева) и $R = 1$ а.е. (справа) для момента 3889 лет, соответствующего фазе аккреционной вспышки. Горизонтальной оранжевой полосой отмечена область неустойчивости.

В распределении для $R \approx 0.2$ а.е. (левая панель рис. 4) видна область, где это отношение опускается ниже значения $ - 1$, при котором выполняется условие конвективной неустойчивости. Для $R = 1$ а.е. (правая панель рис. 4) также имеет место отрицательный градиент температуры вблизи экватора, но он по модулю величины не превосходит адиабатический. Поэтому эта область на данный момент остается конвективно-устойчивой.

На рис. 5 приведены зависимости аккреционного потока от радиуса для момента непосредственно после предыдущей вспышки ($t = 0$ лет), для момента перед аккреционной вспышкой (3694 года) и для самой фазы сброса вещества (3889 лет).

Рис. 5.

Радиальные распределения аккреционного потока для нулевого момента времени (верхняя панель) непосредственно перед вспышой (средняя панель) и во время вспышки (нижняя панель). Положительное значение потока (верхняя часть каждого распределения) соответствует течению от звезды, отрицательное значение (нижняя часть распределения) – к звезде. Время отсчитывается от конца предыдущей аккреционной вспышки и указано в верхней части каждой панели. Горизонтальные линии соответствуют потокам ±0.5 × 10–7${{M}_{ \odot }}{\text{/год}}$. Вертикальной полосой показана область аккреции газа из оболочки.

В фазе накопления вещества ($0 < t < 3694$ го-да) диск можно условно разделить на две части – аккреционную и декреционную, пользуясь терминологией из работы [28]. В аккреционной части, $R < 15$ а.е., вещество движется по направлению к звезде, в то время как в декреционной части, $R > 15$ а.е., газ движется наружу. Положение границы между этими областями в нашей модели определяется постоянным притоком вещества из оболочки в кольцо $10{\kern 1pt} - {\kern 1pt} 20$ а.е. Значения потоков по абсолютной величине по обе стороны от этой границы близки к $0.5 \times {{10}^{{ - 7}}}{{M}_{ \odot }}{\text{/год}}$, т.е. к половинной величине темпа аккреции из оболочки. Таким образом, около половины массы аккрецирующей оболочки поступает во внутреннюю часть диска, другая половина – во внешнюю. Отметим, однако, что аккрецируемое из оболочки вещество в рамках приведенной модели подается в диск с кеплеровской скоростью, при других предположениях картина будет другой. В общем случае эта граница может сдвигаться по мере эволюции диска. На момент времени 3694 года поток вещества в аккреционной части уменьшается по направлению к звезде, принимая минимальное значение на внутренней границе диска, что свидетельствует о процессе накопления вещества в этой области.

В фазе аккреционной вспышки (нижняя панель рис. 5) на распределении потоков видна характерная особенность – пик положительного потока с амплитудой $5 \times {{10}^{{ - 7}}}{{M}_{ \odot }}{\text{/год}}$ в окрестности $0.5$ а.е., являющийся фронтом распространения области, охваченной конвекцией. Как уже было отмечено ранее, этот фронт распространяется наружу. Внутри области $0.5$ а.е. аккреционный поток более чем на порядок превышает значения, характерные для фазы накопления. В то же время распределение потока перед конвективным фронтом, т.е. при $R > 0.5$ а.е. осталось прежним.

На рис. 6 приведены темп аккреции на звезду (верхняя панель), аккреционная светимость (средняя панель) для временного интервала 12 000 лет после установления вспышечного режима аккреции, а также темп аккреции на звезду во время фазы вспышки (нижняя панель). Аккреционная светимость всего диска (красная линия на рис. 6) вычислялась интегрированием выражения (2) от внутренней до внешней границы диска. Аккреционная светимость, связанная с аккрецией газа с внутренней границы диска на звезду, вычислялась по формуле

(23)
${{L}_{*}} = \frac{1}{2}\frac{{G{{M}_{ \odot }}\dot {M}}}{{{{R}_{ \odot }}}},$
где ${{M}_{ \odot }}$ и ${{R}_{ \odot }}$ – масса и радиус звезды (приняты солнечными). Из приведенных зависимостей видно, что интервал между вспышками составляет около $4000$ лет, а сама конвективная фаза длится порядка 200 лет. Темп аккреции на звезду во время конвективной фазы примерно на два порядка величины превышает темп аккреции в спокойный период. Общий темп энерговыделения в самом диске и на поверхности звезды во время активной фазы составляет примерно $6{{L}_{ \odot }}$, что в 50–100 раз превосходит значения, характерные для фазы накопления газа в нем.

Рис. 6.

Зависимость темпа аккреции газа диска звездой (верхняя панель) и аккреционной светимости (центральная панель) от времени для интервала 12 000 лет после установления вспышечного режима аккреции. Внизу показан темп аккреции на звезду во время фазы вспышки. Красной линией на средней панели показана аккреционная светимость всего диска, синей линией – светимость, связанная с аккрецией газа с внутренней границы диска на звезду. Вертикальные цветные (оранжевые) линии на правой панели соответствуют временам 3694, 3889 и 4042 года.

4. ОБСУЖДЕНИЕ

Сравнивая модельные темпы аккреции и светимости с молодыми вспышечными объектами типа FU Ориона (фуоры) и EX Волка (экзоры) [29], можно заключить, что представленная модель достаточно хорошо воспроизводит характерную продолжительность вспышек фуоров (от нескольких десятков до сотен лет). Продолжительность спокойной фазы между вспышками фуоров сложно получить из наблюдений, она варьируется от нескольких тысяч лет [30] до нескольких десятков тысяч лет [31]. В предложенной модели она находится вблизи нижнего предела наблюдательных оценок. С другой стороны, максимальное значение темпа аккреции в течение вспышки расположено около нижнего предела наблюдательных оценок и согласуется разве что с NGC 722 [29]. По максимальным значениям темпа аккреции и светимости наша модель больше согласуется со вспышками типа EX Волка, однако данные объекты отличаются значительно более короткими и частыми вспышками с длительностью от нескольких месяцев до нескольких лет [29]. Следует заметить, что мы пока не изучили весь спектр возможных параметров модели. В частности, мы не исследовали вид зависимости эволюции диска от закона аккреции газа из оболочки на диск. Тестовые расчеты показывают, что при увеличении темпа аккреции из оболочки время между вспышками уменьшается, однако продолжительность и интенсивность вспышек сохраняются. Необходимо дальнейшее исследование вспышечной моды аккреции, вызванной конвективной неустойчивостью, для более детального сравнения с наблюдениями.

Отметим, что представленная модель во многом носит иллюстративный характер в связи с обилием ряда физических приближений. Основная ее цель – описать картину эволюции диска и показать возможную роль конвекции в обеспечении вспышечного режима аккреции. Схематически эта картина представлена на рис. 7.

Рис. 7.

Схема, иллюстрирующая вспышечный характер аккреции в протопланетных дисках. Слева показана фаза накопления вещества, справа – конвективная фаза.

Перечислим ряд принципиальных моментов, лежащих в основе модели и требующих особого внимания при ее дальнейшем развитии. Мы предположили, что в диске наряду с конвекцией есть некоторый другой механизм, обеспечивающий “фоновою” вязкость. Именно благодаря этому механизму реализуется процесс переноса массы и углового момента в спокойной фазе эволюции диска. Благодаря фоновой вязкости происходит накопление вещества во внутренней области диска. Конвекция в нашей модели является триггером, обеспечивающим сброс вещества из внутренней области диска.

Принципиальным условием возникновения конвективно-неустойчивых областей в нашей модели является рост непрозрачности среды с увеличением температуры (см. рис. 1). Этот рост обеспечивается использованными в модели оптическими свойствами пыли, а именно, увеличением спектральных коэфициентов поглощения и рассеяния с частотой. Наши тестовые расчеты показывают, что при использовании искусственно заданных непрозрачностей, не зависящих от температуры, образующийся градиент температуры оказывается не достаточно сильным для обеспечения условия (8). Сильное влияние закона непрозрачности среды на возникновение конвективно-неустойчивых зон было отмечено в работах [32, 33], в которых авторы рассчитали и проанализировали структуру протопланетных дисков с различными параметрами. Они показали, в частности, что испарение пыли во внутренних областях диска уменьшает непрозрачность среды, что исключает возникновение конвективно-неустойчивых областей. В нашей модели испарение пыли не учитывается, но температура в максимуме может приближаться к характерным температурам испарения пыли, поэтому мы планируем включить этот процесс в будущем.

Рост непрозрачности с увеличением температуры в нашей модели приводит также к тому, что развитие конвекции во внутренней области диска является процессом с положительной обратной связью: увеличение темпа аккреции приводит к повышенному выделению энергии, росту температуры и, как следствие, – к усилению условий конвективной неустойчивости. Однако конвективно-неустойчивая область сравнительно быстро (за время порядка ста лет) истощается. Сильное уменьшение плотности ведет к падению темпов аккреции и энерговыделения, что в конечном итоге приводит к восстановлению конвективной устойчивости внутренней области. Таким образом, в данной модели конвекция является самоподдерживающейся только в короткие промежутки времени во внутренних областях диска, при этом важна роль фоновой вязкости для обеспечения ее запуска.

Условием квазипериодического (вспышечного) режима аккреции в рамках представленной модели является задание стационарного притока вещества в диск из оболочки. В текущей реализации модели аккреция газа из оболочки задавалась постоянной, область аккреции представляет собой кольцо между 10 и 20 а.е. В действительности темп аккреции и положение области аккреции вещества из оболочки зависят от времени, что необходимо учитывать при построении моделей, нацеленных на более корректное сопоставление модели с наблюдениями. При уменьшении темпа аккреции из оболочки и истощении диска внутренние области становятся более прозрачными к собственному тепловому излучению, а темп вязкого нагрева падает. Все это приводит к тому, что условия конвективной неустойчивости перестают достигаться.

Важным элементом модели является также метод расчета коэффициента вязкости в конвективно-неустойчивой области. Для этого мы использовали приближение, в котором скорость конвективных элементов вычисляется из условия, что вся выделившаяся в результате вязкости тепловая энергия переносится конвективным потоком. При таком подходе мы не учитываем, что часть энергии может переноситься излучением, т.е. скорость конвективных элементов несколько завышается. В то же время при восстановлении структуры диска в полярном направлении мы не учитываем конвективный перенос энергии и лучистый перенос энергии в радиальном направлении, т.е. распределение температуры находится только с учетом переноса излучения в вертикальном направлении, причем в стационарном приближении. Для того, чтобы устранить эти несогласованности, мы планируем в дальнейшем использовать теорию длины пути перемешивания, которая с успехом применяется для учета конвекции при расчете структуры звезд (см., напр., [34]).

Представленная картина является только одним из возможных сценариев вспышечного характера аккреции около молодых звезд. На данный момент уже предложены самые разнообразные модели для объяснений фуоров и экзоров. Например, в работе [35] представлена двумерная гидродинамическая модель, в которой вспышечный характер аккреции обеспечивается магнито-вращательной неустойчивостью, в то время как гравитационная неустойчивость ответственна за приток вещества во внутренние области диска из его внешней части. В работе [36] вспышки фуоров объясняются падением гравитационно-связанных фрагментов, формирующихся в аккреционном диске и мигрирующих к звезде. Отметим также, что для объяснения наблюдательных проявлений фуоров и динамики околозвездного газа необходимо наличие интенсивного ветра, генерируемого внутренними областями турбулизованного аккреционного диска [37]. В целом рекурентная аккреционная активность является распространенным явлением в мире аккрецирующих объектов [38].

В заключение отметим необходимость воспроизведения полученного вспышечного характера аккреции в рамках гидродинамической модели. В гидродинамической модели развитие конвективных зон можно наблюдать непосредственно, т.е. отпадает необходимость феноменологического введения коэффициента вязкости в конвективной области. В гидродинамической модели, однако, необходимо уделить повышенное внимание расчету тепловой структуры диска и выбору подходящей пространственной сетки в связи с тем, что градиенты плотности от экватора к атмосфере диска достигают многих порядков величин.

ФИНАНСИРОВАНИЕ

Я. Н. П., Л. А. М., Э. И. В. благодарят за финансовую поддержку Российский фонд фундаментальных исследований (проект 17-02-00644).

БЛАГОДАРНОСТИ

Авторы выражают благодарность рецензенту за ценные замечания и конструктивные предложения по улучшению статьи, а также А. Б. Макалкину за полезные обсуждения.

Список литературы

  1. P. J. Armitage, Astrophysics of Planet Formation (Cambridge, UK: Cambridge University Press, 2013).

  2. A. G. W. Cameron, Moon and Planets 18, 5 (1978).

  3. D. N. C. Lin and J. Papaloizou, Monthly Not. Roy. Astron. Soc. 191, 37 (1980).

  4. H. Klahr, in Convection in Astrophysics, edited by F. Kupka, I. Roxburgh, and K. L. Chan, Proc. IAU Symp. 239, 405 (2006).

  5. W. Cabot, V. M. Canuto, O. Hubickyj, and J. B. Pollack, Icarus 69, 423 (1987).

  6. W. Cabot, V. M. Canuto, O. Hubickyj, and J. B. Pollack, Icarus 69, 387 (1987).

  7. H. H. Klahr, T. Henning, and W. Kley, Astrophys. J. 514, 325 (1999).

  8. H. H. Klahr and P. Bodenheimer, Astrophys. J. 582, 869 (2003) [arXiv:astro-ph/0211629].

  9. Г. М. Липунова, Н. И. Шакура, Изв. РАН. Сер. физ. 67, 322 (2003).

  10. S. Hirose, O. Blaes, J. H. Krolik, M. S. B. Coleman, and T. Sano, Astrophys. J. 787, 1 (2014) [arXiv:1403.3096].

  11. M. S. B. Coleman, I. Kotko, O. Blaes, J. P. Lasota, and S. Hirose, Monthly Not. Roy. Astron. Soc. 462, 3710 (2016) [arXiv:1608.01321].

  12. L. E. Held and H. N. Latter, Monthly Not. Roy. Astron. Soc. 480, 4797 (2018) [arXiv:1808.00267].

  13. N. Shakura and K. Postnov, Monthly Not. Roy. Astron. Soc. 448, 3707 (2015) [arXiv:1502.01888].

  14. N. Shakura and K. Postnov, Monthly Not. Roy. Astron. Soc. 451, 3995 (2015) [arXiv:1506.00526].

  15. K. L. Malanchev, K. A. Postnov, and N. I. Shakura, Monthly Not. Roy. Astron. Soc. 464, 410 (2017) [-arXiv:1609.03799].

  16. J. E. Pringle, Ann. Rev. Astron. Astrophys. 19, 137 (1981).

  17. P. J. Armitage, Ann. Rev. Astron. Astrophys. 49, 195 (2011) [arXiv:1011.1496].

  18. J. P. Williams and L. A. Cieza, Ann. Rev. Astron. Astrophys. 49, 67 (2011) [arXiv:1103.0556].

  19. L. Hartmann, N. Calvet, E. Gullbring, and P. D’Alessio, Astrophys. J. 495, 385 (1998).

  20. N. I. Shakura and R. A. Sunyaev, Astron. and Astrophys. 24, 337 (1973).

  21. P. Cossins, G. Lodato, and C. J. Clarke, Monthly Not. Roy. Astron. Soc. 393, 1157 (2009) [arXiv:0811.3629].

  22. L. D. Landau and E. M. Lifshitz, Fluid mechanics (Pergamon Press, 1959).

  23. C. P. Dullemond, A. Natta, and L. Testi, Astrophys. J. 645, L69 (2006) [arXiv:astro-ph/0605336].

  24. A. Chacón-Tanarro, J. E. Pineda, P. Caselli, L. Bizzocchi, et al., Astron. and Astrophys. 623, id. A118 (2019) [arXiv:1901.02476].

  25. J. Klapp, L. D. G. Sigalotti, M. Zavala, F. Pe na-Polo, and J. Troconis, Astrophys. J. 780, 188 (2014).

  26. E. I. Vorobyov and Y. N. Pavlyuchenkov, Astron. and Astrophys. 606, id. A5 (2017) [arXiv:1706.00401].

  27. E. I. Vorobyov, Y. N. Pavlyuchenkov, and P. Trinkl, Astron. Rep. 58, 522 (2014).

  28. A. V. Tutukov and Y. N. Pavlyuchenkov, Astron. Rep. 48, 800 (2004).

  29. M. Audard, P. Ábrahám, M. M. Dunham, J. D. Green, in Protostars and Planets VI, edited by H. Beuther, R. S. Klessen, C. P. Dullemond, and T. K. Henning (University of Arizona Press, 2014), p. 387 [arXiv:1401.3368].

  30. E. I. Vorobyov, V. G. Elbakyan, A. L. Plunkett, M. M. Dunham, M. Audard, M. Guedel, and O. Dionatos, Astron. and Astrophys. 613, id. A18 (2018) -[arXiv:1801.06707].

  31. A. Scholz, D. Froebrich, and K. Wood, Monthly Not. Roy. Astron. Soc. 430, 2910 (2013) [arXiv:1301.3152].

  32. A. B. Makalkin and V. A. Dorofeeva, Solar System Research 29, 85 (1995).

  33. A. B. Makalkin and V. A. Dorofeeva, Solar System Research 30, 440 (1996).

  34. C. J. Hansen, S. D. Kawaler, and V. Trimble, Stellar interiors: physical principles, structure, and evolution (New York: Springer-Verlag, 2004).

  35. Z. Zhu, L. Hartmann, C. Gammie, and J. C. McKinney, Astrophys. J. 701, 620 (2009) [arXiv:0906.1595].

  36. E. I. Vorobyov and S. Basu, Astrophys. J. 650, 956 (2006) [arXiv:astro-ph/0607118].

  37. K. Milliner, J. H. Matthews, K. S. Long, and L. Hartmann, Monthly Not. Roy. Astron. Soc. 483, 1663 (2019) [arXiv:1811.12453].

  38. A. V. Tutukov and Y. N. Pavlyuchenkov, Astron. Rep. (in press).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал