Астрономический журнал, 2020, T. 97, № 2, стр. 91-110
Расчет динамики газопылевых околозвездных дисков: выход за пределы режима Эпштейна
О. П. Стояновская 1, 2, 3, *, Ф. А. Окладников 1, 3, **, Э. И. Воробьев 4, 5, ***, Я. Н. Павлюченков 6, ****, В. В. Акимкин 6, *****
1 Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия
2 Институт вычислительных технологий СО РАН
Новосибирск, Россия
3 Новосибирский государственный университет
Новосибирск, Россия
4 Южный федеральный университет, НИИ физики
Ростов-на-Дону, Россия
5 Институт астрофизики, Венской университет
Вена, Австрия
6 Институт астрономии РАН
Москва, Россия
* E-mail: o.p.sklyar@gmail.com
** E-mail: f.okladnikov@g.nsu.ru
*** E-mail: eduard.vorobiev@univie.ac.at
**** E-mail: pavyar@inasan.ru
***** E-mail: akimkin@inasan.ru
Поступила в редакцию 17.07.2019
После доработки 06.09.2019
Принята к публикации 06.09.2019
Аннотация
В околозвездных дисках размер пылевых частиц варьируется от долей микрона до нескольких сантиметров, планетезимали имеют размер сотни километров. Поэтому в дисках реализуются различные режимы трения твердых тел о газ в зависимости от их размеров и скоростей: Эпштейна, Стокса и Ньютона, а также переходные между ними. Это означает, что для расчета динамики газопылевых дисков требуется использование коэффициента трения, применимого в широком диапазоне размеров и скоростей тел. Кроме того, необходимость одинаковым образом рассчитывать динамику тел разного размера налагает высокие требования на численный метод решения такой задачи. Так, в режимах Эпштейна и Стокса сила трения линейно зависит от относительной скорости между газом и телами, а в переходных режимах и режиме Ньютона – нелинейно. С другой стороны, для мелких тел, движущихся в режиме Эпштейна, время установления относительной скорости между газом и телами может быть много меньше динамического времени задачи – времени оборота диска вокруг центрального тела. Кроме того, в отдельных областях диска пыль может концентрироваться, поэтому необходимо учитывать взаимный обмен импульсом между пылью и газом. В работе показано, что для системы уравнений движения газа и монодисперсной пыли полунеявная схема первого порядка аппроксимации по времени, в которой межфазное взаимодействие рассчитывается неявно, а другие силы, такие как градиент давления, гравитация – явно, применима для жестких задач с интенсивным межфазным взаимодействием и для расчета трения в нелинейном режиме. Показано, что распространенный в астрофизических расчетах кусочно-заданный коэффициент трения испытывает разрыв при некоторых значениях чисел Маха и Кнудсена, которые реализуются в околозвездном диске. Приведен непрерывный коэффициент трения, который соответствует экспериментальным зависимостям, полученным для разных режимов трения.
1. ВВЕДЕНИЕ
Моделирование динамики газопылевых околозвездных дисков необходимо для понимания механизмов формирования планет и выполняется многими авторами, например, [1–9]. К настоящему моменту развиты модели динамики газопылевых дисков, в которых газ считается несущей фазой, а твердые частицы – дисперсной. В этом случае динамика пылевого облака может быть описана как динамика сплошной среды (обоснование применимости такого приближения приведено в Приложении А). Если предположить, что твердая фаза в каждой точке пространства представлена частицами одного размера, то уравнения неразрывности и движения газа и пыли в диске будут иметь вид:
(1)
$\begin{gathered} \frac{{\partial {{\rho }_{{\text{g}}}}}}{{\partial t}} + \nabla ({{\rho }_{{\text{g}}}}v) = {{S}_{{\text{g}}}}, \\ {{\rho }_{{\text{g}}}}\left[ {\frac{{\partial v}}{{\partial t}} + (v \cdot \nabla )v} \right] = - \nabla p + {{\rho }_{{\text{g}}}}g - {{f}_{{\text{D}}}} + {{f}_{{\text{g}}}}, \\ \end{gathered} $(2)
$\begin{gathered} \frac{{\partial {{\rho }_{{\text{d}}}}}}{{\partial t}} + \nabla ({{\rho }_{{\text{d}}}}u) = {{S}_{{\text{d}}}}, \\ {{\rho }_{{\text{d}}}}\left[ {\frac{{\partial u}}{{\partial t}} + (u \cdot \nabla )u} \right] = {{\rho }_{{\text{d}}}}g + {{f}_{{\text{D}}}} + {{f}_{{\text{d}}}}, \\ \end{gathered} $(4)
${{F}_{{\text{D}}}} = \frac{1}{2}{{C}_{{\text{D}}}}s{{\rho }_{{\text{g}}}}\left\| {v - u} \right\|(v - u),$Пыль и твердые тела в околозвездном диске представлены объектами разного размера от субмикронных пылевых частиц до планетеземалей с размером в сотни километров. Крупные и мелкие тела по-разному взаимодействуют с газом. Мелкие пылевые частицы интенсивно обмениваются импульсом с газом, их стационарная или терминальная скорость движения относительно газа мала. Крупные тела могут иметь скорость, существенно отличающуюся от скорости газа. Это означает, что ${\text{Ma}}$ и ${\text{Kn}}$, а также $\left\| {{{f}_{{\text{D}}}}} \right\|$ в диске меняются на порядки величины. Следовательно, для численного моделирования динамики двухфазной среды в диске необходимо использовать коэффициент трения, который применим в широком диапазоне размеров ${\text{Ma}}$ и ${\text{Kn}}$. Поэтому в разделе 2 приведен анализ разных форм коэффициентов трения и показаны их принципиальные различия и преимущества для применения в моделях диска. Кроме того, $\left\| {{{f}_{{\text{D}}}}} \right\|$ в уравнениях (1) и (2) существенно превосходит сумму других сил для мелких тел, но сопоставима с ними для крупных. В общем случае ${{f}_{{\text{D}}}}$ нелинейно зависит от относительной скорости между газом и телами. Эти факторы налагают высокие требования на численный метод, применяемый для решения уравнений движения в (1) и (2). В подразделе 3.1 приведен обзор проблемной ситуации и опубликованных результатов работ по методам расчета динамики газопылевых сред с интенсивным межфазным взаимодействием. В подразделе 3.2 приведена полунеявная схема первого порядка по времени, а в подразделе 3.3 показано, что эта схема удовлетворяет необходимым требованиям для применения ее в расчетах околозвездного диска. Выводы представлены в разделе 4. В Приложе-нии А обоснована применимость модели сплошной среды для описания динамики пыли в диске, а также приведены альтернативные подходы. В Приложении B описана простая одномерная модель околозвездного диска, которая использовалась для проведения тестовых расчетов.
2. КОЭФФИЦИЕНТЫ ТРЕНИЯ
Для сжимаемого газа коэффициент трения ${{C}_{{\text{D}}}}$ в (4) является функцией двух независимых переменных ${\text{Ma}}$ и ${\text{Kn}}$. Характерный вид ${{C}_{{\text{D}}}}$ приведен на рис. 1. В режиме обтекания тела газом как сплошной средой коэффициент трения определяется числом Рейнольдса ${\text{Re}}$ (см., например, [10]), которое является производной величиной от ${\text{Ma}}$ и ${\text{Kn}}$:
Частицы, радиус которых меньше $2.25\lambda $, взаимодействуют с газом в режиме свободно-молекулярного обтекания или Эпштейна [11]. Для таких тел коэффициент трения не зависит от ${\text{Re}}$, но зависит ${\text{Ma}}$. Эту зависимость передает стандартный астрофизический коэффициент трения, предложенный в [12]:(8)
${{C}_{{\text{D}}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{8}{3}\mathop {{\text{Ma}}}\nolimits^{ - 1} ,\quad {\text{K}}{{{\text{n}}}^{{ - 1}}} < \frac{9}{4}\;\;({\text{режим}}\;{\text{Эпштейна}};\;{\text{I}}),} \\ {24\mathop {{\text{Re}}}\nolimits^{ - 1} ,\quad {\text{Re}} < 1\;\;({\text{режим}}\;{\text{Стокса}};\;{\text{II}}),} \\ {24\mathop {{\text{Re}}}\nolimits^{ - 0.6} ,\quad 1 < {\text{Re}} < 800\;\;({\text{переходный}}\;{\text{режим}}\;{\text{или}}\;{\text{нелинейный}}\;{\text{режим}}\;{\text{Стокса}};\;{\text{III}}),} \\ {0.44,\quad {\text{Re}} > 800\;\;({\text{режим}}\;{\text{Ньютона}};\;{\text{IV}}).} \end{array}} \right.$Рис. 1.
Коэффициент трения как функция числа Рейнольдса и Маха для режимов свободно-молекулярного обтекания (режим Эпштейна) и обтекания тела как сплошной средой (режим Стокса, переходный режим и режим Ньютона). Граница между свободно-молекулярным обтеканием и обтеканием сплошной средой определяется числом Кнудсена, границы режимов обтекания сплошной средой определяются числом Рейнольдса. Для режимов обтекания сплошной средой показаны линии тока вокруг сферических частиц. Для всех режимов приведена функциональная зависимость силы трения ${{F}_{{\text{D}}}}$ от радиуса частицы $a$ и скорости частицы относительно газа $\Delta V = \left\| {v - u} \right\|$.

Аппроксимация для режимов Стокса, переходного режима (также известен как нелинейный режим Стокса) и режима Ньютона в (8) была предложена в [13], а применительно к аэродинамике твердых тел в диске использовалась в [14]. В работе [12] эта аппроксимация была расширена путем добавления режима Эпштейна. В современных моделях околозвездных дисков коэффициент (8) используется в работах [4, 15] и других.
На рис. 2 приведены области I–IV, в которых коэффициент трения ${{C}_{{\text{D}}}}$ (как функция двух переменных ${\text{K}}{{{\text{n}}}^{{ - 1}}}$ и ${\text{Ma}}$) является непрерывно-дифференцируемой. На стыках областей I–II, II–III и III–IV ${{C}_{{\text{D}}}}$ непрерывен, а на границах I–III и I–IV – разрывен. Наличие разрыва является серьезным недостатком для моделирования, так как может привести к появлению искусственных особенностей решения.
Рис. 2.
Области определения кусочной функции ${{C}_{{\text{D}}}}$ (8), соответствующие разным режимам обтекания. I – режим Эпштейна, II – режим Стокса, III – переходный режим (нелинейный режим Стокса), IV – режим Ньютона. Зелеными стрелками отмечены границы, на которых функция непрерывна, красными крестиками – границы, на которых функция разрывна.
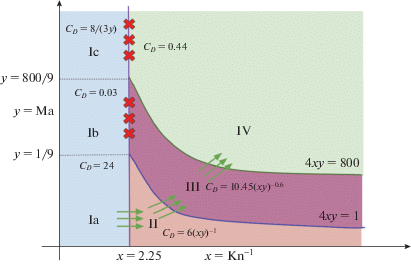
Мы убедились, что при моделировании динамики диска действительно реализуются условия, в которых частица переходит из режима Эпштейна I в переходный режим (нелинейный режим Стокса) III, что сопровождается разрывом коэффициента трения (8). Этот вывод был сделан на основании расчетов динамики вязкого самогравитирующего газового диска с пылевым компонентом по модели FEOSAD, детально описанной в [7]. Использованная модель диска отличается от базовой модели, представленной в [7], дополнительным рассмотрением влияния динамики пыли на динамику газа, а также отсутствием ограничения на размер пыли $a < 2.25\lambda $, искусственно удерживающий частицу в режиме Эпштейна. Для расчета использовались коэффициент трения (8) и численная схема из подраздела 3.2. Мы использовали постоянные по всему диску значение вязкости Шакуры–Сюняева $\alpha = {{10}^{{ - 4}}}$ и фрагментационной скорости ${{v}_{{{\text{frag}}}}} = 30$ м сек–1. Такая величина вязкости Шакуры–Сюняева соответствует диску с подавленной магниторотационной неустойчивостью, в котором перенос массы и углового момента происходит в основном за счет гравитационных моментов сил неосесимметричного диска. Фрагментационная скорость ${{v}_{{{\text{frag}}}}}$ определяет максимальный размер частицы. Выбранному значению фрагментационной скорости отвечает повышенная вероятность слипания, которая реализуется при покрытии частиц толстым слоем льда.
На протяжении 1 млн. лет эволюции диска мы вычисляли величины ${\text{Kn}}$, ${\text{Ma}}$ и ${\text{Re}}$ в каждой расчетной ячейке. Для двух моментов времени 141 тыс. лет и 707 тыс. лет мы представили все множество значений этих величин в диске на плоскостях ${\text{Ma}}$, ${\text{Re}}$ (левые панели рис. 3) и ${\text{K}}{{{\text{n}}}^{{ - 1}}}$, ${\text{Ma}}$ (центральные панели рис. 3). Из центральных панелей видно, что в значительной части диска пыль и газ взаимодействуют в режиме свободно-молекулярного обтекания Эпштейна, однако в диске реализуются все 4 режима трения из (8). При этом в диске в момент времени 707 тыс. лет (центральная панель второго ряда) присутствуют частицы на границе областей I–III, где коэффициент трения (8) претерпевает разрыв. Из правой нижней панели рис. 3, где разными цветами выделены области диска, в которых реализуются разные режимы трения, видно, что этот разрыв происходит на расстоянии 6 a.е. от звезды. Распределения физических величин, определяющих режим трения в центральной области околозвездного диска для тех же самых моментов времени, приведены на рис. 4. Черная контурная линия на верхних панелях, где приведены числа Кнудсена и Маха, показывает границу, при которой $a = 4\lambda {\text{/}}9$. Видно, что для диска возраста 141 тысяча лет эта линия проходит через область ${\text{Ma}} \approx 0.01$, обеспечивая непрерывный коэффициент трения, для диска возраста 707 тысяч лет – через область ${\text{Ma}} \approx 1{\text{/}}9$, приводя к разрыву в коэффициенте трения.
Рис. 3.
Значения Ma и Re (левый столбец) и Ma и ${\text{K}}{{{\text{n}}}^{{ - 1}}}$ (центральный столбец) для пылинок во всех ячейках околозвездного диска возраста 141 (верхний ряд) и 707 тысяч лет (нижний ряд). Разные режимы обтекания из (8) показаны на центральных панелях римскими цифрами, на правых панелях – цветом. I – режим Эпштейна (белый), II – режим Стокса (синий), III – переходный режим или нелинейный режим Стокса (зеленый), IV – режим Ньютона (красный). Черным цветом показана поглощающая ячейка в диске. На границе между белой и зеленой областью стандартный астрофизический коэффициент трения (8) разрывен.
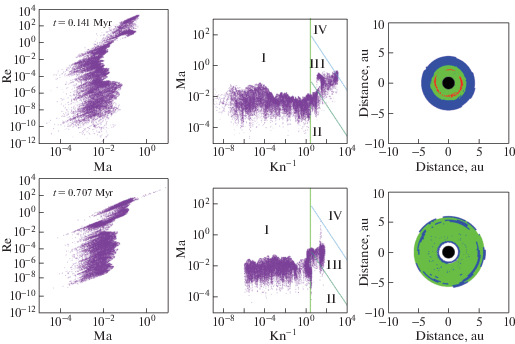
Рис. 4.
Распределения физических величин, определяющих режим трения в центральной области околозвездного диска возраста 141 тыс. лет (левые 6 панелей) и 707 тыс. лет (правые шесть панелей). На верхних панелях приведены числа Кнудсена и Маха, на нижних панелях – поверхностные плотности газа и выросшей пыли в г см–2, на центральных панелях – максимальный размер пылинки $a$ в см и относительная скорость между газом и телами $\Delta V$ в км сек–1. Черная контурная линия на верхних панелях показывает границу, при которой $a = 4\lambda {\text{/}}9$. Для диска возраста 141 тыс. лет эта линия проходит через область ${\text{Ma}} \approx 0.01$, обеспечивая непрерывный коэффициент трения, для диска возраста 707 тыс. лет – через область ${\text{Ma}} \approx 1{\text{/}}9$, приводя к разрыву в коэффициенте трения.

Поэтому мы исследовали альтернативный коэффициент трения для случая, когда обтекающая среда является сжимаемой – коэффициент трения Хендерсона [16]. Аппроксимация Хендерсона хорошо приближает известные экспериментальные зависимости (детали могут быть найдены в [16] и ссылках там) для диапазона ${\text{Re}} < 3 \times {{10}^{5}}$ и ${\text{Ma}} < 6$. Она учитывает также различия между температурой газа и температурой частиц. Для дозвуковых режимов обтекания (${\text{Ma}} \leqslant 1$)
(9)
$\begin{gathered} {{C}_{{\text{D}}}} = \frac{{24}}{{{\text{Re}} + S\left( {4.33 + \frac{{3.65 - 1.53{{T}_{{\text{d}}}}{\text{/}}{{T}_{{\text{g}}}}}}{{1 + 0.353{{T}_{{\text{d}}}}{\text{/}}{{T}_{{\text{g}}}}}}exp( - 0.247\frac{{{\text{Re}}}}{S})} \right)}} + 0.6S\left( {1 - exp\left( { - \frac{{{\text{Ma}}}}{{{\text{Re}}}}} \right)} \right) + \\ \; + exp\left( { - 0.5\frac{{{\text{Ma}}}}{{\sqrt {{\text{Re}}} }}} \right)\left( {\frac{{4.5 + 0.38\left( {0.03{\text{Re}} + 0.48\sqrt {{\text{Re}}} } \right)}}{{1 + 0.03{\text{Re}} + 0.48\sqrt {{\text{Re}}} }} + 0.1{\text{M}}{{{\text{a}}}^{2}} + 0.2{\text{M}}{{{\text{a}}}^{8}}} \right) \\ \end{gathered} $(10)
${{C}_{{\text{D}}}} = \frac{{0.9 + \frac{{0.34}}{{\mathop {{\text{Ma}}}\nolimits^2 }} + 1.86\sqrt {\frac{{{\text{Ma}}}}{{{\text{Re}}}}} \left( {2 + \frac{2}{{{{S}^{2}}}} + \frac{{1.058}}{S}\sqrt {\frac{{{{T}_{{\text{d}}}}}}{{{{T}_{{\text{g}}}}}}} - \frac{1}{{{{S}^{4}}}}} \right)}}{{1 + 1.86\sqrt {\frac{{{\text{Ma}}}}{{{\text{Re}}}}} }},$(12)
$\begin{gathered} {{C}_{{\text{D}}}} = {{C}_{{\text{D}}}}({\text{Ma}} = 1) + \frac{4}{3}({\text{Ma}} - 1)\; \times \\ \times \;({{C}_{{\text{D}}}}({\text{Ma}} = 1.75) - {{C}_{{\text{D}}}}({\text{Ma}} = 1)), \\ \end{gathered} $Значения стандартного астрофизического коэффициента трения (8) и коэффициента Хендерсона (9)–(12) для диапазона параметров околозвездного диска ${{10}^{{ - 4}}} \leqslant {\text{Ma}} \leqslant 100$, ${{10}^{{ - 12}}} \leqslant {\text{Re}} \leqslant {{10}^{3}}$ приведены на рис. 5 и рис. 6. Из панелей верхнего ряда рис. 5 следует, что при ${\text{Ma}} \leqslant 0.01$ для любого ${\text{Re}}$ оба коэффициента трения близки. Это подтверждают верхние панели рис. 6. Для $0.1 \leqslant {\text{Ma}} \leqslant 1$ значения коэффициентов трения различаются количественно, а при ${\text{Ma}} \geqslant 1$ – качественно. Во-первых, на центральной и правой панелях нижнего ряда рис. 5 заметен разрыв первого рода у стандартного астрофизического коэффициента. Кроме того, из правой нижней панели видно, что эталонный коэффициент Хендерсона убывает с ростом ${\text{Re}}$, тогда как стандартный астрофизический возрастает. Во-вторых, на центральной и правой панели нижнего ряда рис. 6 видно, что эталонный коэффициент Хендерсона имеет особенность (известный в аэромеханике горб в окрестности ${\text{Ma}} = 1$), которая отсутствует в упрощенной аппроксимации коэффициента трения.
Рис. 5.
Коэффициенты трения Хендерсона (9)–(12) и стандартный астрофизический (8) при разных ${\text{Ma}}$ как функции ${\text{Re}}$.

Рис. 6.
Коэффициенты трения Хендерсона (9)–(12) и стандартный астрофизический (8) при разных ${\text{Re}}$ как функции ${\text{Ma}}$.

Таким образом, при расчете динамики газопылевой среды с ${\text{Ma}} > 1{\text{/}}9$ можно рекомендовать к использованию только коэффициент Хендерсона, однако если ограничивать ${\text{Ma}} \leqslant 1{\text{/}}9$, стандартный астрофизический коэффициент экономичнее и удобнее для программирования.
3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ ГАЗОПЫЛЕВОЙ СРЕДЫ С ИНТЕНСИВНЫМ МЕЖФАЗНЫМ ВЗАИМОДЕЙСТВИЕМ
3.1. Обзор предыдущих работ
Определим время релаксации скорости сферически-симметричной частицы к скорости газа следующим образом:
(13)
$\begin{gathered} {{t}_{{{\text{stop}}}}} = \frac{{{{m}_{{\text{p}}}}\left\| {v - u} \right\|}}{{\left\| {{{F}_{{\text{D}}}}} \right\|}} = \frac{{\tfrac{4}{3}\pi {{a}^{3}}{{\rho }_{{\text{s}}}}\left\| {v - u} \right\|}}{{\tfrac{1}{2}{{C}_{{\text{D}}}}\pi {{a}^{2}}{{\rho }_{{\text{g}}}}{{{\left\| {v - u} \right\|}}^{2}}}} = \\ \, = \frac{8}{3}\frac{{a{{\rho }_{{\text{s}}}}}}{{{{C}_{{\text{D}}}}{{\rho }_{{\text{g}}}}\left\| {v - u} \right\|}}, \\ \end{gathered} $Для пылевых частиц с размером около 1 мкм на орбитальном радиусе 100 а.е. характерное время релаксации скорости ${{t}_{{{\text{stop}}}}}$ в диске составляет порядка 100 сек (cм., например, [17, 18]), тогда как динамику диска требуется моделировать на протяжении ${{10}^{4}}$ лет $ \approx {\kern 1pt} {{10}^{{11}}}$ сек и более. Это означает, что уравнения движения газа и пыли имеют жесткие релаксационные слагаемые, связанные с интенсивным межфазным взаимодействием. Поэтому моделирование динамики газопылевых дисков является сложной задачей современной вычислительной астрофизики (см., например, [19]).
Задачи с жестким релаксационным слагаемым активно исследуются в прикладной математике [20]. Кроме динамики многофазных сред, такие задачи встречаются в физике плазмы, моделях эластичности с памятью, кинетической теории и др. При использовании явных методов для получения устойчивых численных решений необходим временной шаг $\tau \leqslant {{t}_{{{\text{stop}}}}}$, неприемлемый для расчетов сложных систем уравнений в двумерном и трехмерном случае даже на современных суперкомпьютерах.
В частности, при моделировании динамики газового самогравитирующего диска (например, [21, 22]), временной шаг, определяемый условием Куранта, составляет несколько земных суток. При необходимости измельчить его до 100 сек, фактическое время получения решений вырастет в 100–1000 раз, что сделает невозможным проведение серийных вычислительных экспериментов.
При использовании неявных методов отсутствует ограничение на временной шаг со стороны устойчивости, однако оно может возникнуть со стороны точности [23]. Например, в одной из ранних работ авторы [24] показали, что в общем случае сеточные методы высокого порядка при наличии жестких релаксационных слагаемых воспроизводят асимптотическое поведение решения, только если используется очень мелкий шаг по пространству. Примеры проявления этих эффектов при моделировании динамики околозвездных дисков можно найти в [7, 15, 17]. В частности, авторы [15, 25] исследовали диффузионное расплывание решений, которые получаются при моделировании динамики газопылевой среды, используя гидродинамику сглаженных частиц (Smoothed Particle Hydrodynamics, SPH) с расчетом межфазного взаимодействия по классическому подходу [26]. Они получили эмпирический критерий, согласно которому расплывание решений имеет приемлемый уровень, если используется радиус сглаживания $h < {{c}_{{\text{s}}}}{{t}_{{{\text{stop}}}}}$. Согласно этому критерию, расчет динамики микронных частиц в околозвездном диске потребует пространственного разрешения $h \approx 10$ км, тогда как радиус диска составляет порядка ${{10}^{{10}}}$ км. Ясно, что такое пространственное разрешение находится за пределами возможностей современной вычислительной техники.
В ряде случаев от поиска численного решения исходной задачи можно отказаться и заменить его на решение упрощенной задачи, полученной из исходной путем разложения по малому параметру (общая идея представлена в [20], применительно к расчетам газопылевых сред в околозвездном диске, например, в [27–29]). Упрощенная задача становится нежесткой, однако такой переход обоснован только для случая, когда время релаксации много меньше времени движения несущей фазы и не позволяет моделировать переходный режим со временем релаксации, близким к динамическому времени. Кроме того, такой переход может сопровождаться сменой типа уравнений (например, переходом от гиперболического к параболическому).
Поэтому альтернативой переходу к упрощенной задаче является разработка неявных и полунеявных численных методов, которые точно воспроизводят равновесные значения даже при грубом пространственном разрешении. В настоящее время предпринимаются попытки найти общий подход к конструированию методов высокого порядка для задач с релаксационными слагаемыми, см., например, [30]. Однако в большинстве работ по численному решению таких систем методы конструируются с учетом специфики решаемой задачи и конкретного вида “жесткого релаксационного слагаемого”. В частности, при моделировании динамики газопылевых сред система имеет не одно, а два жестких релаксационных слагаемых – в уравнениях движения для газа и пыли [25, 31–33]). В среднем по диску порядок величины $\varepsilon = \frac{{{{\rho }_{{\text{d}}}}}}{{{{\rho }_{{\text{g}}}}}}$ равен 0.01, поэтому влиянием пыли на динамику газа часто можно пренебречь. С другой стороны, результаты моделирования показывают, что пылевые частицы могут концентрироваться в отдельных областях диска (в спиральных рукавах [4], во внутренней части диска [7], в самогравитирующих газовых сгустках [3]), повышая тем самым отношение плотностей до значения $\varepsilon \approx 1$ и более.
В настоящее время несколько групп исследователей работают над созданием численных моделей динамики газопылевых сред с высокой концентрацией дисперсной фазы и интенсивным межфазным взаимодействием на основе сеточных методов и SPH.
Авторы работы [34] представили безытерационный неявный сеточный метод и набор тестовых задач для среды газ-полидисперсная пыль в околозвездных дисках. В их модели каждая фракция полидисперсной пыли обменивается импульсом с газом и косвенно с другими фракциями, но теплообмен между газом и пылью отсутствует. Авторами показано, что предложенный ими метод устойчив, имеет низкие диссипативные свойства и сохраняет асимптотику решения при любых временных шагах.
Авторами [35, 36] предложена конечно-разностная схема с настраиваемыми диссипативными свойствами (сustomizible dissipative properties) для моделирования динамики среды газ-монодисперсная пыль.
В работах [15, 37, 38] авторы представили безытерационный неявный метод на основе гидродинамики сглаженных частиц для монодисперсной и полидисперсной пыли. Их модель динамики газопылевой среды основана на одножидкостном подходе (решаются уравнения для свойств газопылевой среды в целом, при этом для концентрации твердой фазы решается диффузионное уравнение). В этом подходе каждая SPH-частица является носителем характеристик как газа, так и пыли. Такой подход экономичен и лишен численной диссипации, возникающей при реализации лагранжевых методов в двухжидкостном подходе. С другой стороны, в одножидкостном подходе не гарантируется выполнение закона сохранения массы для дисперсной фазы. Кроме того, есть более жесткое ограничение сверху на размер моделируемых тел по сравнению с двухжидкостным подходом.
Авторы [31, 39] разработали двухжидкостный подход на основе гидродинамики сглаженных частиц для сред газ-монодисперсная пыль. Эти авторы обнаружили, что в полученных ими решениях диффузионное расплывание в газопылевой среде меньше,чем в классическом для SPH подходе [26]. Однако это расплывание больше диффузионного расплывания в газе за счет искусственной вязкости.
Авторами [40] предложен новый метод решения уравнений сплошной среды газ-монодисперсная пыль с интенсивным межфазным взаимодействием на основе SPH. Предложенный метод расчета межфазного взаимодействия является безытерационным и имеет низкие диссипативные свойства. Эти особенности метода определяются неявной линейной аппроксимацией силы трения и локальным выполнением закона сохранения импульса при расчете трения между газом и пылью.
Все представленные разработки были сделаны для самого распространенного в околозвездном диске режима взаимодействия твердых частиц с газом – режима Эпштейна. В этом режиме реализуется интенсивное межфазное взаимодействие, но сила трения линейно зависит от относительной скорости между газом и телами. Однако результаты моделирования указывают, что в отдельных областях диска выросшие частицы будут взаимодействовать с газом в переходном режиме и режиме Ньютона, когда межфазное взаимодействие является умеренным, а сила трения нелинейно зависит от относительной скорости между газом и телами. Поэтому в данной статье мы предлагаем схему дискретизации по времени уравнений движения газа и пыли, которая охватывает оба случая и совместима с любым способом расчета пространственных производных, если скорость газа и скорость пыли определены в одних и тех же точках пространства. Рассматриваемый метод расчета динамики среды газ-монодисперсная пыль для силы трения, линейно зависящей от относительной скорости между газом и телами, является частным случаем подхода [34], который хорошо обоснован авторами в линейном случае. Таким образом, настоящая работа может рассматриваться как обоснование подхода к расчету полидисперсной пыли [34] с переходом от линейного к нелинейному трению.
3.2. Схема дискретизации по времени уравнений движения газа и пыли, сохраняющая асимптотику
Для аппроксимации силы межфазного взаимодействия в уравнениях движения из (1), (2) мы предлагаем линеаризовать силу трения по относительной скорости между газом и телами, при этом время остановки ${{t}_{{{\text{stop}}}}}({{\rho }_{{\text{g}}}},u - v)$ рассчитывать по известным величинами с предыдущего шага, а относительную скорость между газом и телами – со следующего. Упрощенная запись такого подхода примет вид:
(14)
$\begin{gathered} \frac{{{{v}^{{n + 1}}} - {{v}^{n}}}}{\tau } + ({{v}^{n}} \cdot \nabla ){{v}^{n}} = \\ = \; - {\kern 1pt} \frac{{\nabla {{p}^{n}}}}{{\rho _{{\text{g}}}^{n}}} + {{g}^{n}} - \frac{{\rho _{{\text{d}}}^{n}}}{{\rho _{{\text{g}}}^{n}}}\frac{{{{v}^{{n + 1}}} - {{u}^{{n + 1}}}}}{{t_{{{\text{stop}}}}^{n}}} + \frac{{f_{{\text{g}}}^{n}}}{{\rho _{{\text{g}}}^{n}}}, \\ \end{gathered} $(15)
$\frac{{{{u}^{{n + 1}}} - {{u}^{n}}}}{\tau } + ({{u}^{n}} \cdot \nabla ){{u}^{n}} = {{g}^{n}} + \frac{{{{v}^{{n + 1}}} - {{u}^{{n + 1}}}}}{{t_{{{\text{stop}}}}^{n}}} + \frac{{f_{{\text{d}}}^{n}}}{{\rho _{{\text{d}}}^{n}}}.$В настоящей статье мы решали всю систему (1–2) по двухэтапной схеме, основанной на методе расщепления по физическим процессам (как и в наших предыдущих работах [17, 41]). Для решения уравнений неразрывности и движения мы использовали метод конечных разностей, подробное описание которого для чистого газа представлено Стоуном и Норманом [42]. Первый этап схемы расщепления представляет собой вычисление адвективных слагаемых и расчет переноса массы и импульса
(16)
$\frac{{\partial {{\rho }_{{\text{g}}}}}}{{\partial t}} + \nabla ({{\rho }_{{\text{g}}}}v) = 0,\quad {{\rho }_{{\text{g}}}}\left[ {\frac{{\partial v}}{{\partial t}} + (v \cdot \nabla )v} \right] = 0,$(17)
$\frac{{\partial {{\rho }_{{\text{d}}}}}}{{\partial t}} + \nabla ({{\rho }_{{\text{d}}}}u) = 0,\quad {{\rho }_{{\text{d}}}}\left[ {\frac{{\partial u}}{{\partial t}} + (u \cdot \nabla )u} \right] = 0.$На следующем этапе выполнялся расчет влияния сил давления, трения, гравитации и других, используя обновленные плотности и скорости газа с первого этапа:
(18)
$\begin{gathered} \frac{{{{v}^{{n + 1}}} - {{v}^{{n + 1/2}}}}}{\tau } = - \frac{{\nabla {{p}^{{n + 1/2}}}}}{{\rho _{{\text{g}}}^{{n + 1/2}}}} + {{g}^{{n + 1/2}}} - \\ - \;\frac{{\rho _{{\text{d}}}^{{n + 1/2}}}}{{\rho _{{\text{g}}}^{{n + 1/2}}}}\frac{{{{v}^{{n + 1}}} - {{u}^{{n + 1}}}}}{{t_{{{\text{stop}}}}^{{n + 1/2}}}} + \frac{{f_{{\text{g}}}^{{n + 1/2}}}}{{\rho _{{\text{g}}}^{{n + 1/2}}}}, \\ \end{gathered} $(19)
$\frac{{{{u}^{{n + 1}}} - {{u}^{{n + 1/2}}}}}{\tau } = {{g}^{{n + 1/2}}} + \frac{{{{v}^{{n + 1}}} - {{u}^{{n + 1}}}}}{{t_{{{\text{stop}}}}^{{n + 1/2}}}} + \frac{{f_{{\text{d}}}^{{n + 1/2}}}}{{\rho _{{\text{d}}}^{{n + 1/2}}}}.$В силу того, что из (14)–(15) явно выражаются ${{v}^{{n + 1}}}$ и ${{u}^{{n + 1}}}$, вычислительные затраты на полунеявную аппроксимацию трения близки к затратам на явную аппроксимацию.
3.3. Тестирование схемы
В пункте 3.3.1 мы исследуем уровень диффузионного расплывания схемы (14)–(15) при расчете интенсивного межфазного взаимодействия с временным шагом $\tau $, который определяется условием Куранта, а не ${{t}_{{{\text{stop}}}}}$. В пункте 3.3.2 мы сравним точность решений, полученных схемой первого порядка (14)–(15) и схемой четвертого порядка, при моделировании движения пыли в газовом диске, скорость вращения которого чуть меньше кеплеровой.
3.3.1. Тест 1. Распад разрыва в газопылевой среде. Для одномерных уравнений (1), (2) положим $g = 0$, ${{S}_{{\text{g}}}} = {{S}_{{\text{d}}}} = 0$, ${{f}_{{\text{g}}}} = {{f}_{{\text{d}}}} = 0$, ${{f}_{{\text{D}}}} = \frac{{{{\rho }_{{\text{d}}}}(v - u)}}{{{{t}_{{{\text{stop}}}}}}}$ и запишем уравнение энергии:
(20)
${{\rho }_{{\text{g}}}}\left( {\frac{{\partial e}}{{\partial t}} + v\frac{{\partial e}}{{\partial x}}} \right) = - p\frac{{\partial v}}{{\partial x}},$Для получившейся системы (1), (2), (20), (21) на границах интервала зададим условия непротекания. В начальный момент времени зададим нулевые начальные скорости пыли и газа, скачок давления газа, скачок плотности газа и пыли:
Зададим $\lambda = 5 \times {{10}^{{ - 6}}}{{l}_{*}}\frac{{{{\rho }_{*}}}}{{{{\rho }_{{\text{g}}}}}}$, ${{\rho }_{{\text{s}}}} = 2.3{{\rho }_{*}}$ и будем рассматривать 2 размера частиц: мелкая пыль $a = 5 \times {{10}^{{ - 6}}}{{l}_{*}}$ и крупные тела $a = {{10}^{{ - 2}}}{{l}_{*}}$.
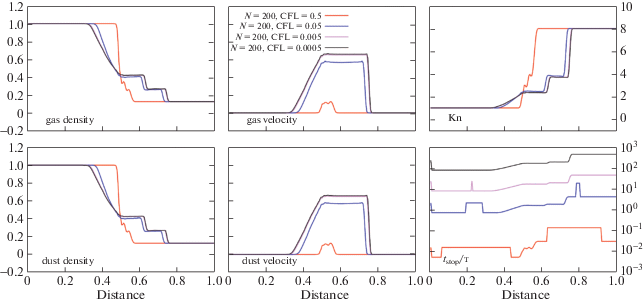
В работе [17] было показано, что полунеявная схема расщепления первого порядка (14), (15) сохраняет асимптотику решения при расчете интенсивного межфазного взаимодействия с постоянным коэффициентом трения. Из рис. 7 следует этот же вывод для случая, когда ${{C}_{{\text{D}}}}$ меняется по пространству и по времени, а ${{t}_{{{\text{stop}}}}} = {{t}_{{{\text{stop}}}}}\left( {\left\| {u - v} \right\|} \right)$.
Рис. 7.
Решение задачи ударная труба Сода по схеме (14)–(15) , сохраняющей асимптотику, для ${\text{Kn}} \geqslant 1$ (мелкая пыль $a = 5 \times {{10}^{{ - 6}}}{{l}_{*}}$, режим Эпштейна, коэффициент трения рассчитан по формуле Хендерсона (9)–(12)).

На рис. 7 приведен расчет с коэффициентом трения Хендерсона (9)–(12) и размером пылевых частиц $a = 5 \times {{10}^{{ - 6}}}{{l}_{*}}$. Будем считать эталонным результат расчета с детальным пространственным разрешением $N = 400$ ячеек на единичный отрезок и временным шагом, при котором параметр Куранта ${\text{CFL}} = 0.005$. Видно, что расчет скоростей и плотностей газа и пыли c $N = 200$, ${\text{CFL}} = 0.5$ незначительно отличается от эталонного. Кроме расчета с ${{\rho }_{{\text{d}}}}{\text{/}}{{\rho }_{{\text{g}}}} = 1$, мы провели расчеты этой же задачи с повышенным в 10 и в 1000 раз содержанием пыли относительно газа. Мы убедились, что и в этих случаях в расчетах по схеме, сохраняющей ассимптотику, уровень расплывания решения сохраняется незначительным.
Примером полунеявной аппроксимации трения, которая не сохраняет асимптотику, является
(22)
$\begin{gathered} \frac{{{{v}^{{n + 1}}} - {{v}^{n}}}}{\tau } + ({{v}^{n}} \cdot \nabla ){{v}^{n}} = \\ = \; - {\kern 1pt} \frac{{\nabla {{p}^{n}}}}{{\rho _{{\text{g}}}^{n}}} + {{g}^{n}} - \frac{{\rho _{{\text{d}}}^{n}}}{{\rho _{{\text{g}}}^{n}}}\frac{{{{v}^{{n + 1}}} - {{u}^{n}}}}{{t_{{{\text{stop}}}}^{n}}} + \frac{{f_{{\text{g}}}^{n}}}{{\rho _{{\text{g}}}^{n}}}, \\ \end{gathered} $(23)
$\frac{{{{u}^{{n + 1}}} - {{u}^{n}}}}{\tau } + ({{u}^{n}} \cdot \nabla ){{u}^{n}} = {{g}^{n}} + \frac{{{{v}^{{n + 1}}} - {{u}^{{n + 1}}}}}{{t_{{{\text{stop}}}}^{n}}} + \frac{{f_{{\text{d}}}^{n}}}{{\rho _{{\text{d}}}^{n}}}.$Решение этой же задачи с использованием схемы (22), (23) приведено на рис. 8. Из этого рисунка видно, что с изменением $CFL$ от 0.5 до 0.00005 рассчитанные скорости распространения волн изменяются в разы, при этом только при $\tau < 0.1{{t}_{{{\text{stop}}}}}$ точность получаемого решения становится удовлетворительной.
Рис. 8.
Решение задачи ударная труба Сода по схеме (22)–(23) , не сохраняющей асимптотику, с разными шагами по времени для ${\text{Kn}} \geqslant 1$ (мелкая пыль $a = 5 \times {{10}^{{ - 6}}}{{l}_{*}}$, режим Эпштейна, коэффициент трения рассчитан по формуле Хендерсона (9)–(12)).
Из правой верхней панели рис. 7 следует, что число Кнудсена для мелкой пыли превосходит 1. Это означает, что согласно классификации режимов из (8) взаимодействие газа и пыли происходит в режиме свободно-молекулярного обтекания Эпштейна. При этом расчет $t_{{{\text{stop}}}}^{n}$ производится по общей формуле (13) для линейного и нелинейного трения. Отметим, что влияние численного разрешения на результат видно только на правой нижней панели рис. 7, где представлена величина ${\text{Re}}$, линейно зависящая от $\left\| {u - v} \right\|$. Однако известно (смотри, например, [18]), что в случае ${{t}_{{{\text{stop}}}}}max(u,v) \ll {{l}_{*}}$ относительной скоростью между газом и пылью можно пренебречь и получить решение задачи для газопылевой среды из решения для газа, заменив ${{c}_{{\text{s}}}}$ на
(24)
$c_{s}^{*} = {{c}_{s}}\mathop {\left( {1 + \frac{{{{\rho }_{{\text{d}}}}}}{{{{\rho }_{{\text{g}}}}}}} \right)}\nolimits^{ - 1/2} .$Рис. 9.
Решение задачи ударная труба Сода по схеме (14)–(15) , сохраняющей асимптотику, с разными шагами по пространству и по времени для ${\text{Kn}} \ll 1$ (крупные тела, режимы Стокса, переходный и Ньютона, нелинейное трение), коэффициент трения рассчитан по формуле Хендерсона (9)–(12)).
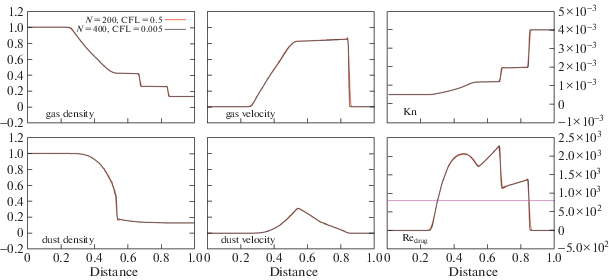
Рис. 10.
Решение задачи ударная труба Сода для крупных тел (левые панели) и мелкой пыли (правые панели) c коэффициентами трения Хендерсона (9)–(12) и стандартным астрофизическим (8).

Уровень диффузионного расплывания решения по схеме (14), (15) для задачи с умеренным межфазным взаимодействием виден из рис. 9, где показаны те же расчеты, что и на рис. 7, но размер частиц увеличен до $a = {{10}^{{ - 2}}}{{l}_{*}}$. Из правых панелей рис. 9 следует, что при заданном размере частицы обтекаются газом, как сплошной средой (${\text{Kn}} \ll 1$), при этом реализуются режим Стокса, переходный режим и режим Ньютона. Результаты расчета с $N = 200$, ${\text{CFL}} = 0.5$ незначительно отличаются от эталонного. При этом в отличие от режима интенсивного межфазного взаимодействия, скорость и распределение плотности пыли существенно отличаются от скорости газа. Отметим, что из левых панелей рис. 10, где показаны скорость газа и скорость пыли, видна более выраженная зависимость решения от коэффициента трения для крупных тел, чем для мелкой пыли.
В целом представленные результаты показывают, что схема (14), (15) сохраняет асимптотику решения при моделировании как интенсивного, так и умеренного межфазного взаимодействия.
3.3.2. Тест 2. Расчет траектории частицы в стационарном околозвездном диске. Уравнения движения частицы в поле массивного центрального тела в полярных координатах приведены, например, в [44]. Если кроме гравитационной и центробежной силы на частицу действует трение о газ, то согласно (4) уравнения примут вид:
(25)
$\left\{ \begin{gathered} \frac{{dr}}{{dt}} = {{v}_{r}}, \hfill \\ \frac{{d{{v}_{r}}}}{{dt}} = \frac{{v_{\varphi }^{2}}}{r} - \frac{{GM}}{{{{r}^{2}}}} - \frac{3}{8}\frac{{{{C}_{{\text{D}}}}{{\rho }_{{\text{g}}}}({{u}_{r}} - {{v}_{r}})\left\| {u - v} \right\|}}{{a{{\rho }_{s}}}}, \hfill \\ \frac{{d{{v}_{\varphi }}}}{{dt}} = - \frac{{{{v}_{r}}{{v}_{\varphi }}}}{r} - \frac{3}{8}\frac{{{{C}_{{\text{D}}}}{{\rho }_{{\text{g}}}}({{u}_{\varphi }} - {{v}_{\varphi }})\left\| {u - v} \right\|}}{{a{{\rho }_{{\text{s}}}}}}, \hfill \\ \end{gathered} \right.$В начальный момент времени расположим частицу на орбитальном радиусе ${{r}_{0}} = 10$ а.е. и зададим ей скорость, ${{v}_{{\varphi 0}}} = 0.25{{V}_{{\text{K}}}}({{r}_{0}})$, где ${{V}_{{\text{K}}}}(r) = \sqrt {\frac{{GM}}{r}} $, ${{v}_{{r0}}} = - {{10}^{{ - 4}}}$ а.е. ⋅ $\Omega $ ($r = 1$ а.е.), где $\Omega (r) = \frac{{{{V}_{{\text{K}}}}(r)}}{r}$. Будем считать, что размер частицы, которая дрейфует в диске, растет по закону $a = {{a}_{0}}\mathop {\left( {\frac{r}{{{{r}_{0}}}}} \right)}\nolimits^{ - 3} $, при этом на расстоянии ${{r}_{0}}$ от центрального тела частица имеет размер ${{a}_{0}} = 134.64$ см (Toymodel 1) или ${{a}_{0}} = 13.464$ см (Toymodel 2). Будем моделировать движение частицы к центральному телу до тех пор, пока ее орбитальный радиус не достигнет 1 а.е. Будем использовать полунеявную схему первого порядка
(26)
$\left\{ {\begin{array}{*{20}{l}} {\frac{{{{r}^{{n + 1}}} - {{r}^{n}}}}{\tau } = v_{r}^{n},} \\ {\frac{{v_{r}^{{n + 1}} - v_{r}^{n}}}{\tau } = \frac{{{{{(v_{\varphi }^{n})}}^{2}}}}{{{{r}^{n}}}} - \frac{{GM}}{{{{{({{r}^{n}})}}^{2}}}} - \frac{3}{8}\frac{{C_{{\text{D}}}^{n}\rho _{{\text{g}}}^{n}(u_{r}^{{n + 1}} - v_{r}^{{n + 1}})\left\| {{{u}^{n}} - {{v}^{n}}} \right\|}}{{{{a}^{n}}{{\rho }_{s}}}},} \\ {\frac{{v_{\varphi }^{{n + 1}} - v_{\varphi }^{n}}}{\tau } = - \frac{{v_{r}^{n}v_{\varphi }^{n}}}{{{{r}^{n}}}} - \frac{3}{8}\frac{{C_{{\text{D}}}^{n}\rho _{{\text{g}}}^{n}(u_{\varphi }^{{n + 1}} - v_{\varphi }^{{n + 1}})\left\| {{{u}^{n}} - {{v}^{n}}} \right\|}}{{{{a}^{n}}{{\rho }_{{\text{s}}}}}},} \end{array}} \right.$Изменение коэффициента трения ${{C}_{{\text{D}}}}$, числа Стокса $St = {{t}_{{{\text{stop}}}}}\Omega $ и радиального компонента скорости частицы ${{v}_{r}}$, отнесенного к кеплеровой скорости на соответствующем радиусе, для Toymodel 1 и 2 приведено на рис. 11. Красной линией показаны результаты, полученные с коэффициентом трения Хендерсона, многоцветной линией – со стандартным астрофизическим коэффициентом. Из верхних панелей рис. 11 видно, что в Toymodel 1 стандартный астрофизический коэффициент в первые 10 лет терпит разрыв первого рода. Точка разрыва совпадает с экстремумом модуля радиальной скорости. При этом в Toymodel 1 с непрерывным коэффициентом Хендерсона радиальная скорость также меняется с возрастающей на убывающую в первые 10 лет движения частицы. Кроме того, отметим, что в Toymodel 1 и 2 точки разрыва, экстремума или перегиба ${{C}_{{\text{D}}}}$ являются точками экстремума или перегиба ${{v}_{r}}$.
Рис. 11.
Расчет траектории растущей пылевой частицы в стационарном газовом диске массы 0.4${{M}_{ \odot }}$ вокруг центрального тела массы 0.5${{M}_{ \odot }}$ с разными коэффициентами трения. Красная линия – коэффициент трения Хендерсона (9)–(12), многоцветная линия – стандартный астрофизический коэффициент (8) с выделенными режимами I–IV.
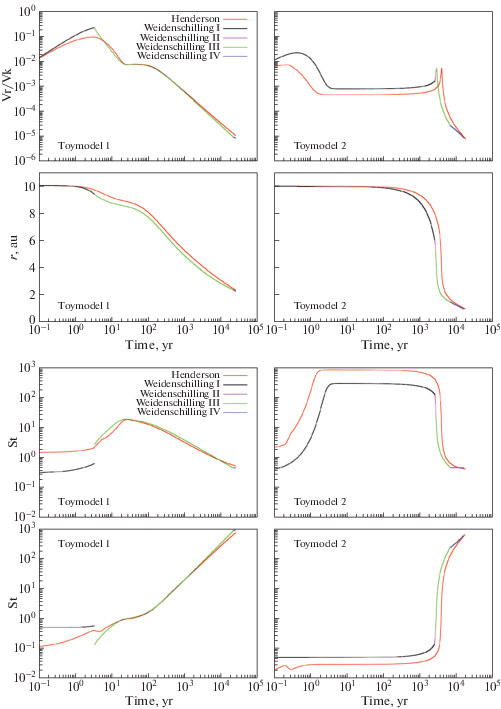
В целом за исключением точки разрыва ${{C}_{{\text{D}}}}$ расчеты Toymodel 1 с разными коэффициентами трения можно считать качественно и количественно близкими: время, за которое частица сдрейфовала с 10 а.е. до 1 а.е., оказалось порядка $3 \times {{10}^{4}}$ лет, при этом на радиусе 1 а.е. число Стокса достигло значения ${\text{St}} = {{10}^{3}}$. Видно, что за время своего движения в диске частица взаимодействовала с газом в режимах Эпштейна I, переходном III и Ньютона IV из (8), минуя режим Стокса II.
Из нижних панелей рис. 11 видно, что при уменьшении размера частицы в Toymodel 2 коэффициент трения в начальные моменты времени не изменился (в силу (8) в режиме Эпштейна он определяется ${\text{Ma}}$), но число Стокса изменилось на порядок по сравнению с Toymodel 1. В результате сократилось время дрейфа частицы с радиуса 10 а.е. до 1 а.е., при этом частица последовательно прошла I, II, III и IV режимы взаимодействия с газом. Видно, что результаты расчета Toymodel 2 со стандартным астрофизическим коэффициентом трения и коэффициентом Хендерсона качественно и количественно близки.
Как и в Toymodel 1 максимальные отличия скорости радиального движения при использовании разных коэффициентов трения имеют место в режиме Эпштейна. Это отличается от задачи распада разрыва, где чувствительность решения к смене коэффициента трения была более выражена для крупных тел в режимах Стокса, переходном и Ньютона. Чувствительность системы (25) к смене коэффициента трения в режиме Эпштейна определяется тем, что стационарное значение радиальной скорости частицы зависит от ${{t}_{{{\text{stop}}}}}$ [45] как
где $\eta $ определяется из $u_{\varphi }^{2} = (1 - \eta )V_{{\text{K}}}^{2}$ и удовлетворяет $0 < \eta \ll 1$. Из верхних панелей рис. 5 видно, что в режиме Эпштейна значение коэффициента Хендерсона примерно в три раза отличается от стандартного астрофизического, что в силу (27) приводит к выраженному отличию в радиальной скорости частицы.Во втором уравнении системы (26) присутствуют две величины ($v_{\varphi }^{2}{\text{/}}r$ и ${\text{GM/}}{{r}^{2}}$), разность которых на много порядков меньше их модуля. Поэтому для расчета траекторий частиц, динамика которых определяется равнодействующей центробежной и центростремительной силы, методы высокого порядка потребуют меньших вычислительных затрат, чем методы первого порядка (здесь мы говорим о методах решения произвольной системы обыкновенных дифференциальных уравнений, а не о специальных симплекс-методах, адаптированных под особенности задачи). Исследуем, как меняются требования к численному методу при расчете траекторий частиц, на которые действуют дополнительные силы.
Для этого мы рассчитали Toymodel 1 и Toymodel 2 с помощью явного метода Рунге-Кутты четвертого порядка с тем же шагом $\tau = 0.01{{\Omega }^{{ - 1}}}$ (r = 1 а.е.). В момент времени, когда частица пересекала $r = 1$ а.е. мы фиксировали значения $r$, ${{v}_{r}}$, ${{v}_{\varphi }}$, после этого сравнивали эти значения с величинами, рассчитанными по полунеявной схеме первого порядка. Результаты сравнения приведены в табл. 1. Видно, что в обеих моделях с обоими коэффициентами трения точность расчета по схеме первого порядка отличается от схемы четвертого порядка менее, чем на 1% при том, что число Стокса для выросших частиц в обеих моделях превосходит ${{10}^{2}}$. Среди трех переменных системы максимальную относительную погрешность имеет ${{v}_{r}}$. Расчеты Toymodel 2 разными методами и с разными коэффициентами трения отличаются незначительно. Но в Toymodel 1, где стандартный астрофизический коэффициент терпит разрыв, можно видеть, что использование коэффициента Хендерсона позволяет получать более близкие решения методом первого и четвертого порядка.
Таблица 1.
Разность значений переменных системы (25), найденных двумя методами (явным методом Рунге-Кутты четвертого порядка и полунеявным методом первого порядка), отнесенная к абсолютному значению величины, вычисленной методом Рунге-Кутты
| Модель – Коэффициент трения | Weidenschilling (1977) | Henderson (1976) |
|---|---|---|
| Toymodel 1 | $\Delta r{\text{/}}r = 1.3453 \times {{10}^{{ - 5}}}$ | $\Delta r{\text{/}}r = 7.837 \times {{10}^{{ - 6}}}$ |
| $\Delta {{v}_{r}}{\text{/}}{{v}_{r}} = 1.3718 \times {{10}^{{ - 3}}}$ | $\Delta {{v}_{r}}{\text{/}}{{v}_{r}} = 8.3969 \times {{10}^{{ - 4}}}$ | |
| $\Delta {{v}_{\varphi }}{\text{/}}{{v}_{\varphi }} = 4.297 \times {{10}^{{ - 6}}}$ | $\Delta {{v}_{\varphi }}{\text{/}}{{v}_{\varphi }} = 3.358 \times {{10}^{{ - 6}}}$ | |
| Toymodel 2 | $\Delta r{\text{/}}r = 4.1573 \times {{10}^{{ - 5}}}$ | $\Delta r{\text{/}}r = 1.0109 \times {{10}^{{ - 5}}}$ |
| $\Delta {{v}_{r}}{\text{/}}{{v}_{r}} = 9.4828 \times {{10}^{{ - 4}}}$ | $\Delta {{v}_{r}}{\text{/}}{{v}_{r}} = 4.1845 \times {{10}^{{ - 4}}}$ | |
| $\Delta {{v}_{\varphi }}{\text{/}}{{v}_{\varphi }} = 1.4979 \times {{10}^{{ - 5}}}$ | $\Delta {{v}_{\varphi }}{\text{/}}{{v}_{\varphi }} = 1.8898 \times {{10}^{{ - 5}}}$ |
Чтобы детальнее разобраться с отличиями в точности решений, которые получаются методом первого и четвертого порядка, сравним сначала решения системы (25) с нулевой силой трения. Такая система из трех уравнений имеет два первых интеграла, которые выражают законы сохранения момента импульса и энергии:
В начальный момент мы располагали частицу на радиусе ${{r}_{0}} = 10$ а.е. и задавали ей радиальную скорость, близкую к 0, а угловую скорость – кеплерову. Мы рассчитывали траекторию частицы на протяжении $t = 40 \times 2\pi {{\Omega }^{{ - 1}}}({{r}_{0}})$ (40 оборотов вокруг центрального тела) явным методом Эйлера (в который вырождается полунеявная схема первого порядка с нулевым трением) и явным методом Рунге-Кутты. В конечный момент времени мы вычисляли значения ${{C}_{1}}$ и ${{C}_{2}}$ и сравнивали их с начальными значениями этих же интегралов. Зависимость относительной погрешности ${{C}_{1}}$ и ${{C}_{2}}$ от величины временного шага $\tau $ представлена на левой панели рис. 12. Видно, что обе схемы дают заявленный порядок аппроксимации решения, при этом точность вычисления углового момента по схеме первого порядка почти в 100 раз хуже, чем точность вычисления энергии. Так, для вычисления ${{C}_{1}}$ с точностью до 1 процента схеме первого порядка необходимо более 1000 шагов на оборот вокруг центрального тела, тогда как методу Рунге-Кутты достаточно 10 шагов на оборот.
Рис. 12.
Левая панель – относительная погрешность решения системы без трения после 40 орбитальных периодов (интегралов (28)–(29)), полученных методами первого и четвертого порядка от шага по времени, центральная и правая панели – погрешность ${{v}_{r}}$ решения системы с трением полунеявным методом первого порядка для разных чисел Стокса. Время интегрирования для центральной панели – 2 орбитальных периода, для правой панели – 40 орбитальных периодов.

Исследуем, какое количество шагов на оборот потребуется схеме первого порядка для получения точности в 1 процент при добавлении в систему (26) трения. Для этого будем решать систему (26), в которой компоненты силы трения имеют вид $\left( {\frac{{({{v}_{r}} - {{u}_{r}})\Omega (r)}}{{{\text{St}}}},\;\frac{{({{v}_{\varphi }} - {{u}_{\varphi }})\Omega (r)}}{{{\text{St}}}}} \right)$ c фиксированным значением ${\text{St}}$. Для ${\text{St}} = {{10}^{{ - 6}}},\;{{10}^{{ - 5}}},\;{{10}^{{ - 4}}}$ будем проводить интегрирование на протяжении $t = $ $ = 40 \times 2\pi {{\Omega }^{{ - 1}}}({{r}_{0}})$, а для ${\text{St}} = {{10}^{{ - 2}}},\;{{10}^{{ - 1}}},\;1,\;10,\;100$ на протяжении более короткого периода $t = 2\; \times $ $ \times \;2\pi {{\Omega }^{{ - 1}}}({{r}_{0}})$. В качестве эталонного значения решения использовалось решение этой же задачи, полученное методом четвертого порядка с временным разрешением ${{10}^{7}}$ на оборот $t = 2\pi {{\Omega }^{{ - 1}}}({{r}_{0}})$. Относительные погрешности ${{v}_{r}}$, вычисленные по полунеявной схеме первого порядка, представлены на центральной и правой панели рис. 12. Видно, что для всех значений ${\text{St}}$ полунеявная схема демонстрирует первый порядок аппроксимации, однако фактическая точность решения зависит от величины ${\text{St}}$. В расчетах, представленных на правой панели, ${\text{St}} \ll 1$, поэтому динамику частицы определяет трение о газ, а не равнодействующая между центробежной и центростремительной силой. В этих расчетах чем меньше значение ${\text{St}}$, тем выше точность численного решения. В расчетах cо ${\text{St}} \geqslant 1$, представленных на центральной панели, динамика частицы определяется равнодействующей между центробежной и центростремительной силами, поэтому фактическая точность ${{v}_{r}}$ не зависит от ${\text{St}}$ и близка к точности, с которой при тех же временных шагах вычисляется ${{C}_{1}}$ в расчетах без трения.
В целом данные, представленные на рис. 12 и в табл. 1, показывают целесообразность применения схем первого порядка при моделировании динамики частиц в диске на орбитальном радиусе больше 1 а.е.
4. ЗАКЛЮЧЕНИЕ
В околозвездных и протопланетных дисках размер пылевых частиц варьируется от субмикрона до нескольких сантиметров, планетезимали имеют размер сотни километров. Поэтому обмен импульсом твердых тел с газом в дисках происходит в разных режимах, которые определяются размером и скоростями твердых тел: Эпштейна, Стокса и Ньютона. В статье приведено сравнение коэффициентов трения, охватывающих одновременно эти режимы. Показано, что для чисел Маха, определяемых по скорости движения пылинки относительно газа, ${\text{Ma}} > 1{\text{/}}9$ стандартный астрофизический коэффициент (8) представляет собой разрывную функцию, но при ${\text{Ma}} < 1{\text{/}}9$ является непрерывным. Применение стандартного астрофизического коэффициента в моделировании околозвездных дисков при ${\text{Ma}} < 1{\text{/}}9$ оправдано скоростью вычисления. При ${\text{Ma}} > 1{\text{/}}9$ рекомендуется использовать коэффициент трения Хендерсона (9–12), который валидирован и непрерывен при ${\text{Ma}} < 6$, ${\text{Re}} < 3 \times {{10}^{5}}$. При этом каждое вычисление коэффициента Хендерсона требует порядка 100 арифметических операций.
Кроме того, необходимость одинаковым образом рассчитывать динамику тел разного размера налагает высокие требования на численный метод решения такой задачи. Нами показано, что полунеявная схема первого порядка аппроксимации по времени, в которой межфазное взаимодействие линеаризуется и относительная скорость рассчитывается неявно, а время остановки и другие силы, такие как градиент давления и гравитация – явно, сохраняет асимптотику решения для задач с интенсивным межфазным взаимодействием. Это означает, что такая схема подходит для расчета динамики как малых тел, сильно связанных с газом, так и крупных, для которых сила трения нелинейно зависит от относительной скорости между газом и телами, включая влияние дисперсной фазы на динамику газа.
Список литературы
X.-N. Bai and J. M. Stone, ApJSS 190, 297 (2010), 1005.4980.
Z. Zhu, R. P. Nelson, R. Dong, C. Espaillat, and L. Hartmann, ApJ 755, 6 (2012), 1205.5042.
S.-H. Cha and S. Nayakshin, MNRAS 415, 3319 (2011), 1010.1489.
W. K. M. Rice, G. Lodato, J. E. Pringle, P. J. Armitage, and I. A. Bonnell, MNRAS 355, 543 (2004), astro-ph/0408390.
L. Barrière-Fouchet, J.-F. Gonzalez, J. R. Murray, R. J. Humble, and S. T. Maddison, AAp 443, 185 (2005), astro-ph/0508452.
N. Cuello, J.-F. Gonzalez, and F. C. Pignatale, MNRAS 458, 2140 (2016), 1601.03662.
E. I. Vorobyov, V. Akimkin, O. Stoyanovskaya, Y. Pavlyuchenkov, and H. B. Liu, Astronomy and Astrophysics 614, eidA98 (2018), 1801.06898.
V. N. Snytnikov and O. P. Stoyanovskaya, MNRAS 428, 2 (2013), 1210.0971.
T. V. Demidova and V. P. Grinin, Astronomy Letters 43, 106 (2017).
G. Bagheri and C. Bonadonna, Powder Technology 301, 526–544 (2016).
P. S. Epstein, Physical Review 23, 710 (1924).
S. J. Weidenschilling, MNRAS 180, 57 (1977).
R. F. Probstein and F. Fassio, AIAA 8, 772 (1970).
F. L. Whipple, in From Plasma to Planet, edited by A. Elvius (1972), p. 211.
G. Laibe and D. J. Price, MNRAS 420, 2365 (2012a), 1111.3089.
C. B. Henderson, AIAA 14, 707 (1976).
O. P. Stoyanovskaya, V. N. Snytnikov, and E. I. Vorobyov, Astron. Rep. 94, 1033 (2017a).
G. Laibe and D. J. Price, MNRAS 420, 2345 (2012b), 1111.3090.
T. J. Haworth, J. D. Ilee, D. H. Forgan, S. Facchini, D. J. Price, D. M. Boneberg, R. A. Booth, C. J. Clarke, J.‑F. Gonzalez, M. A. Hutchison, et al., PASA 33, 053 (2016), 1608.01315.
G.-Q. Chen, C. D. Livermore, and T.-P. Liu, Communications in Pure and Applied Mathematics 47, 787 (1994).
E. I. Vorobyov, ApJ 723, 1294 (2010), 1009.2073.
O. P. Stoyanovskaya, N. V. Snytnikov, and V. N. Snytnikov, Astronomy and Computing 21, 1 (2017b), 1809.01310.
R. Pember, SIAM Journal on Applied Mathematics 53, 1293–1330 (1993).
S. Jin and C. D. Livermore, Journal of Computational Physics 126, 449 (1996).
G. Laibe and D. J. Price, MNRAS 444, 1940 (2014a), 1407.3569.
J. J. Monaghan and A. Kocharyan, Computer Physics Communications 87, 225 (1995).
A. Johansen and H. Klahr, ApJ 634, 1353 (2005), astro-ph/0501641.
V. V. Akimkin, M. S. Kirsanova, Y. N. Pavlyuchenkov, and D. S. Wiebe, MNRAS 449, 440 (2015), 1502.06865.
V. V. Akimkin, M. S. Kirsanova, Y. N. Pavlyuchenkov, and D. S. Wiebe, MNRAS 469, 630 (2017), 1705.00269.
G. Albi, G. Dimarco, and L. Pareschi, arXiv e-prints arXiv:1904.03865 (2019), 1904.03865.
P. Lorén-Aguilar and M. R. Bate, MNRAS 443, 927 (2014), 1406.3250.
S. Ishiki, T. Okamoto, and A. K. Inoue, MNRAS 474, 1935–1943 (2018), 1708.07137.
C.-C. Yang and A. Johansen, ApJS 224, 39 (2016), 1603.08523.
P. Benítez-Llambay, L. Krapp, and M. E. Pessah, ApJSS 241, 25 (2019), 1811.07925.
D. V. Sadin, Computational Mathematics and Mathematical Physics 56, 2068 (2016).
D. Sadin and S. Odoev, Scientific and Technical Journal of Information Technologies, Mechanics and Optics pp. 719–724 (2017).
G. Laibe and D. J. Price, MNRAS 440, 2136 (2014b), 1402.5248.
M. Hutchison, D. J. Price, and G. Laibe, MNRAS 476, 2186 (2018), 1802.03213.
P. Lorén-Aguilar and M. R. Bate, MNRAS 454, 4114 (2015), 1509.08374.
O. P. Stoyanovskaya, T. A. Glushko, N. V. Snytnikov, and V. N. Snytnikov, Astronomy and Computing 25, 25 (2018a), 1811.06506.
O. P. Stoyanovskaya, V. V. Akimkin, E. I. Vorobyov, T. A. Glushko, Y. N. Pavlyuchenkov, V. N. Snytnikov, and N. V. Snytnikov, in Journal of Physics Conference Series (2018b), vol. 1103 of series of Physics Conference Series, p. 012008, 1811.06522.
J. M. Stone and M. L. Norman, ApJSS 80, 753 (1992).
P. Colella and P. R. Woodward, Journal of Computational Physics 54, 174 (1984).
L. Landau and E. Lifshitz, titleFluid Mechanics. Vol. 6 (2nd ed.). (Butterworth-Heinemann, 1987).
Y. Nakagawa, M. Sekiya, and C. Hayashi, Icarus 67, 375 (1986).
E. I. Vorobyov and C. Theis, MNRAS 373, 197 (2006), astro-ph/0609250.
Z. Zhu and J. M. Stone, ApJ 795, 53 (2014), 1405.2790.
E. I. Vorobyov and C. Theis, MNRAS 383, 817 (2008), 0709.2768.
R. A. Booth and C. J. Clarke, MNRAS 458, 2676 (2016), 1603.00029.
T. Birnstiel, M. Fang, and A. Johansen, Space Science Reviews 205, 41 (2016), 1604.02952.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


