1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 97, № 4, 2020

Астрономический журнал, 2020, T. 97, № 4, стр. 301-311

Новая оценка скорости расширения ассоциации Скорпиона–Центавра по звездам типа Т Тельца из каталога GAIA DR2

В. В. Бобылев 1, *, А. Т. Байкова 1

1 Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия

* E-mail: vbobylev@gaoran.ru

Поступила в редакцию 03.11.2019
После доработки 16.12.2019
Принята к публикации 20.12.2019

Полный текст (PDF)

Аннотация

Кинематические свойства ассоциации Скорпиона–Центавра изучены с использованием пространственных скоростей около 700 молодых звезд типа Т Тельца. Их собственные движения и тригонометрические параллаксы были отобраны Зари и др. из каталога Gaia DR2, а значения лучевых скоростей были взяты из различных источников. Новая оценка коэффициента линейного расширения ассоциации $K = 39 \pm 2$ км/с/кпк получена с учетом влияния галактической спиральной волны плотности с амплитудой радиальных возмущений ${{f}_{R}} = 5$ км/с и фазой Солнца в волне $ - 120^\circ $. Показано, что собственное вращение ассоциации мало. Эллипсоид остаточных скоростей этих звезд имеет главные полуоси ${{\sigma }_{{1,2,3}}} = (7.72,1.87,1.74) \pm (0.56,0.37,0.22)$ км/с и расположен под углом $12 \pm 2^\circ $ к галактической плоскости.

1. ВВЕДЕНИЕ

Звездная ассоциация Скорпиона–Центавра (Sco OB2) является типичной, не самой молодой OB-ассоциацией. Она расположена в непосредственной близости от Солнца, поэтому изучена детальнее других подобных структур. Например, по данным современного каталога Gaia DR2 [1, 2] к ассоциации Скорпиона–Центавра относят около 3000 вероятных членов-звезд главной последовательности и более 11 000 звезд типа Т Тельца [3]. В ассоциации выделяют три группы: US (Upper Scorpius), UCL (Upper Centaurus–Lupus) и LCC (Lower Centaurus–Crux) со средними расстояниями 145, 140 и 118 пк соответственно [4, 5].

По сравнению с рассеянными скоплениями звездные ассоциации имеют значительно меньшую плотность. Уже Амбарцумяном [6] была высказана гипотеза об их гравитационной неустойчивости и постепенном рассеивании. Одним из первых эффект расширения звездной ассоциации промоделировал [7] и оценил Блаау [8]. В частности, по данным о молодых массивных звездах спектрального класса B он нашел коэффициент линейного расширения ассоциации Скорпиона–Центавра $K = 50$ км/с/кпк, что позволило оценить время расширения 20 млн лет. Эта кинематическая оценка находится в неплохом согласии с современными оценками возраста главных членов ассоциации: US (менее 10 млн лет), UCL (16–20 млн лет) и LCC (16–20 млн лет), которые получены путем подгонки эволюционных треков звезд к изохронам на диаграмме Герцшпрунга-Рассела и другими методами [9–11].

Анализ современных кинематических данных позволил обнаружить эффекты собственного вращения и расширения у других известных OB-ассоциаций [12, 13]. Например, расширение ассоциаций Per OB1 и Car OB1 происходит со скоростью около 6 км/с [14, 15].

Сартори и др. [10] показали отсутствие различий в распределении и кинематике между массивными и маломассивными (типа Т Тельца) звездами сопоставимого возраста на примере ассоциации Скорпиона–Центавра. Ими предложена модель формирования этой ассоциации в результате воздействия галактической спиральной волны плотности на газо-пылевое протооблако. В работе [16] детально разработана модель последовательного звездообразования в приложении к ассоциации Скорпиона–Центавра.

Бобылев и Байкова [18] получили оценку коэффициента линейного расширения ассоциации Скорпиона–Центавра $K = 46 \pm 8$ км/с/кпк по выборке молодых массивных звезд из каталога HIPPARCOS [17]. В работе Торреса и др. [19] показано, что эффекту расширения приблизительно с такой скоростью подвержено значительное количество молодых звездных группировок из широкой окрестности ассоциации Скорпиона–Центавра. При анализе кинематики OB-звезд авторы [20] высказали предположение о том, что галактическая спиральная волна плотности может оказывать заметное влияние на определение K‑эффекта в поясе Гулда и в ассоциации Скорпиона–Центавра.

Целью настоящей работы являются определение пространственных и кинематических характеристик системы молодых звезд, принадлежащих ассоциации Скорпиона–Центавра, уточнение по ним известного эффекта расширения этой ассоциации, оценка собственного вращения системы, а также анализ остаточных скоростей звезд, вычисленных с учетом галактической спиральной волны плотности.

2. ДАННЫЕ

В работе Зари и др. [21] создан компилятивный каталог звезд типа Т Тельца. Эти звезды были отобраны ими из каталога Gaia DR2 по кинематическим и фотометрическим характеристикам. Все они расположены не далее 500 пк от Солнца, так как использовалось ограничение на радиус выборки $\pi < 2$ миллисекунд дуги (мсд). Подавляющее их большинство принадлежит поясу Гулда. Отбор осуществлялся по собственным движениям путем анализа сглаженного распределения точек на плоскости ${{\mu }_{\alpha }}cos\delta {{\mu }_{\delta }}$ с использованием ограничения на тангенциальную скорость звезды $\sqrt {{{{({{\mu }_{\alpha }}cos\delta )}}^{2}} + \mu _{\delta }^{2}} < 40$ км/с. Значения лучевых скоростей в каталоге [21] были взяты из различных источников, в частности, и из каталога Gaia DR2. Однако звезд с лучевыми скоростями существенно меньше, чем звезд с собственными движениями.

В настоящей работе мы используем звезды типа Т Тельца из выборки, которая наиболее тесно связана с поясом Гулда. Она имеет обозначение pmsvt3 в каталоге [21] и содержит 23 686 звезд с собственными движениями и параллаксами, а звезд с лучевыми скоростями – около 2000.

Из выборки pmsvt3 были отобраны звезды с относительными ошибками параллакса менее 15%, принадлежащие ассоциации Скорпиона–Центавра. В эту выборку вошли около 5300 звезд-вероятных членов ассоциации с собственными движениями и параллаксами. Из них примерно 700 звезд имеют измеренные лучевые скорости. При отборе были взяты звезды с широтами $b$ от $ - 15^\circ $ до $35^\circ $, согласно карте ассоциации, например, из работы [5]. Кроме того, использовались следующие ограничения: гелиоцентрическое расстояние $r < 220$ пк, координата $x$ в интервале от ‒50 пк до 250 пк, а координата $y$ от –200 пк до 50 пк.

3. МЕТОДЫ

Мы используем прямоугольную систему координат с центром в Солнце, где ось $x$ направлена в сторону галактического центра, ось $y$ – в сторону галактического вращения и ось $z$ – в северный полюс Галактики. Тогда $x = rcoslcosb$, $y = rsinlcosb$ и $z = rsinb$.

Из наблюдений нам известны три составляющие скорости звезды: лучевая скорость ${{V}_{r}}$ и две проекции тангенциальной скорости ${{V}_{l}} = 4.74r{{\mu }_{l}}cosb$ и ${{V}_{b}} = 4.74r{{\mu }_{b}}$, направленные вдоль галактической долготы $l$ и широты $b$, соответственно, выраженные в км/с. Здесь коэффициент 4.74 является отношением числа километров в астрономической единице к числу секунд в тропическом году, а $r = 1{\text{/}}\pi $ – гелиоцентрическое расстояние звезды в кпк, которое мы вычисляем через параллакс звезды $\pi $ в мсд. Компоненты собственного движения ${{\mu }_{l}}cosb$ и ${{\mu }_{b}}$ выражены в мсд/год.

Через компоненты ${{V}_{r}}$, ${{V}_{l}}$ и ${{V}_{b}}$ вычисляются пространственные скорости $U$, $V$, $W$, где скорость $U$ направлена от Солнца к центру Галактики, $V$ в направлении вращения Галактики и $W$ на северный галактический полюс:

(1)
$\begin{array}{*{20}{c}} {U = {{V}_{r}}coslcosb - {{V}_{l}}sinl - {{V}_{b}}coslsinb,} \\ {V = {{V}_{r}}sinlcosb + {{V}_{l}}cosl - {{V}_{b}}sinlsinb,} \\ {W = {{V}_{r}}sinb + {{V}_{b}}cosb.} \end{array}$
Очевидно, что для вычисления пространственных скоростей необходимо использовать звезды, для которых имеется полная информация, то есть, известны параллакс, лучевая скорость и компоненты собственного движения.

На рис. 1 дано распределение отобранных звезд с известными лучевыми скоростями в проекции на галактическую плоскость $xy$ и их пространственные скорости. На рисунке также отмечены 33 звезды со скоростями $V > 10$ км/с, которые не были использованы при решении основных кинематических уравнений. Как можно видеть из рисунка, отобранные звезды образуют очень компактное сгущение на плоскости $UV$‑скоростей (рис. 1б), и представляют большой интерес для кинематического анализа.

Рис. 1.

Распределение отобранных нами вероятных членов ассоциации Скорпиона–Центавра на галактической плоскости $xy$ (а), пространственные $UV$-скорости этих звезд (б), скорости даны относительно местного стандарта покоя, светлыми точками отмечены звезды со скоростями $V > 10$ км/с.

3.1. Остаточные скорости

При формировании остаточных скоростей мы в первую очередь учитываем пекулярную скорость Солнца относительно местного стандарта покоя (МСП), ${{U}_{ \odot }},$ ${{V}_{ \odot }}$ и ${{W}_{ \odot }}$. Протяженность рассматриваемой нами области в радиальном (вдоль $R$) направлении составляет менее 200 пк, поэтому нет особой необходимости в учете дифференциального вращения Галактики, тем более, что кривая галактического вращения близка к плоской. Но интересно учесть влияние галактической спиральной волны плотности. Выражения для учета двух указанных эффектов имеют следующий вид:

(2)
$\begin{array}{*{20}{c}} {{{V}_{r}} = V_{r}^{ * } - [ - {{U}_{ \odot }}cosbcosl - {{V}_{ \odot }}cosbsinl - } \\ { - \;{{W}_{ \odot }}sinb + {{{{\tilde {v}}}}_{\theta }}sin(l + \theta )cosb - } \\ { - \;{{{{\tilde {v}}}}_{R}}cos(l + \theta )cosb],} \end{array}$
(3)
$\begin{array}{*{20}{c}} {{{V}_{l}} = V_{l}^{ * } - [{{U}_{ \odot }}sinl - {{V}_{ \odot }}cosl - r{{\Omega }_{0}}cosb + } \\ { + \;{{{{\tilde {v}}}}_{\theta }}cos(l + \theta ) + {{{{\tilde {v}}}}_{R}}sin(l + \theta )],} \end{array}$
(4)
$\begin{array}{*{20}{c}} {{{V}_{b}} = V_{b}^{ * } - [{{U}_{ \odot }}coslsinb + {{V}_{ \odot }}sinlsinb - } \\ { - \;{{W}_{ \odot }}cosb - {{{{\tilde {v}}}}_{\theta }}sin(l + \theta )sinb + } \\ { + \;{{{{\tilde {v}}}}_{R}}cos(l + \theta )sinb],} \end{array}$
где стоящие в правых частях уравнений $V_{r}^{ * }$, $V_{l}^{ * }$, $V_{b}^{ * }$ – исходные, не исправленные скорости, а в левых частях ${{V}_{r}}$, ${{V}_{l}}$, ${{V}_{b}}$ – исправленные скорости, с которыми можем вычислить остаточные скорости $U$, $V$, $W$ на основе соотношений (1), $R$ – расстояние от звезды до оси вращения Галактики, ${{R}^{2}} = {{r}^{2}}co{{s}^{2}}b - 2{{R}_{0}}rcosbcosl + R_{0}^{2}$. Расстояние ${{R}_{0}}$ принимаем равным $8.0 \pm 0.15$ кпк [22]. Конкретные значения пекулярной скорости Солнца относительно МСП, $({{U}_{ \odot }},{{V}_{ \odot }},{{W}_{ \odot }}) = (11.1,12.2,7.3)$ км/с, берем согласно определению [23].

Интерес представляют еще две скорости: радиальная ${{V}_{R}}$, направленная от галактического центра вдоль радиуса и ортогональная ей скорость ${{V}_{\theta }}$, направленная вдоль вращения Галактики. Эти скорости вычисляются на основе следующих соотношений:

(5)
$\begin{gathered} {{V}_{\theta }} = Usin\theta + ({{V}_{0}} + V)cos\theta , \\ {{V}_{R}} = - Ucos\theta + ({{V}_{0}} + V)sin\theta , \\ \end{gathered} $
где позиционный угол $\theta $ удовлетворяет соотношению $tan\theta = y{\text{/}}({{R}_{0}} - x)$, $x$, $y$, $z$ – прямоугольные гелиоцентрические координаты звезды, ${{V}_{0}}$ – линейная скорость вращения Галактики на околосолнечном расстоянии ${{R}_{0}}$.

Для учета влияния спиральной волны плотности использована модель, основанная на линейной теории волн плотности Лина и Шу [24], в которой возмущение потенциала имеет вид бегущей волны, тогда

(6)
$\begin{gathered} {{{{\tilde {v}}}}_{R}} = {{f}_{R}}cos\chi , \\ {{{{\tilde {v}}}}_{\theta }} = {{f}_{\theta }}sin\chi , \\ \chi = m[cot(i)ln(R{\text{/}}{{R}_{0}}) - \theta ] + {{\chi }_{ \odot }}, \\ \end{gathered} $
где ${{f}_{R}}$ и ${{f}_{\theta }}$ – амплитуды возмущений радиальной и азимутальной скоростей; $i$ – угол закрутки спиралей ($i < 0$ для закручивающихся спиралей); $m$ – число рукавов; ${{\chi }_{ \odot }}$ – фазовый угол Солнца, в настоящей работе мы его отсчитываем от центра спирального рукава Киля–Стрельца, $\lambda $ – расстояние (по галактоцентрическому радиальному направлению) между соседними отрезками спиральных рукавов в околосолнечной окрестности (длина спиральной волны) вычисляется из соотношения
(7)
$tan(i) = \lambda m{\text{/}}(2\pi {{R}_{0}}).$
Изложенный метод учета влияния спиральной волны плотности применялся, например, в работе [25] или [26].

В настоящее время нет определенности в вопросе количества спиральных рукавов $m$ в нашей Галактике. Однако в нашем случае рассматриваемая окрестность мала, позиционный угол $\theta \to 0^\circ $ в формуле (6). Легко показать, что при таком условии учет спиральной волны не зависит от $m$. Действительно, согласно соотношению (7) имеем $cot(i) = 2\pi {{R}_{0}}{\text{/}}\lambda m.$ После подстановки $cot(i)$ в (6) $m$ сокращается. Таким образом, для учета влияния спиральной волны плотности необходимо иметь значения четырех параметров: $\lambda $, ${{f}_{R}}$, ${{f}_{\theta }}$ и ${{\chi }_{ \odot }}.$

Эффективность учета зависит как от амплитуды возмущения спиральной волны, так и от значения фазы Солнца в волне. То есть при определенном значении фазы даже при большой амплитуде можно получить нулевой эффект. С другой стороны, при определенной амплитуде радиальных возмущений, на такую же величину уменьшается значение определяемого коэффициента линейного расширения звездной системы $K$. Такой опыт был получен нами при анализе кинематики пояса Гулда [27].

В настоящей работе мы согласно анализу различных звездных выборок [28–31] принимаем следующие параметры спиральной волны плотности: $\lambda = 2.2$ кпк, ${{f}_{R}} = 5$ км/с, ${{f}_{\theta }} = 0$ км/с и ${{\chi }_{ \odot }} = - 120^\circ $. Так как рассматриваются очень молодые звезды, то мы ориентируемся на значения параметров спиральной волны плотности, которые получены различными авторами по наиболее молодым объектам. Например, из анализа мазерных источников с измеренными тригонометрическими параллаксами было найдено значение фазы Солнца в волне плотности ${{\chi }_{ \odot }} = - 125 \pm 10^\circ $ [29], по выборке молодых рассеянных звездных скоплений ${{\chi }_{ \odot }} = - 120 \pm 10^\circ $ [30], а по цефеидам ${{\chi }_{ \odot }} = - 121 \pm 3^\circ $ [28]. Амплитуды скоростей радиальных возмущений ${{f}_{R}}$, как правило, значимо отличаются от нуля, а тангенциальных ${{f}_{\theta }}$ нет [29, 30]. Сводка современных определений ${{f}_{R}}$ и ${{f}_{\theta }}$ дана в работе Локтина, Поповой (табл. 2 в работе [31]). На основе данных о рассеянных звездных скоплениях из текущей версии “Однородного каталога параметров рассеянных звездных скоплений” и данных каталога Gaia DR2 эти авторы нашли ${{f}_{R}} = 4.6 \pm 0.7$ км/с и ${{f}_{\theta }} = 1.1 \pm 0.4$ км/с [31]. Значение длины волны возмущений в окрестности Солнца $\lambda $ заключено в интервале 2.0–2.5 кпк [29–31], хорошо определяется как по положениям звезд, так и по их кинематике. Например, значения ${{\lambda }_{\theta }} = 2.3 \pm 0.5$ кпк и ${{\lambda }_{R}} = 2.2 \pm 0.5$ кпк были найдены как из анализа тангенциальных, так и радиальных скоростей молодых рассеянных звездных скоплений из каталога Gaia DR2 [30].

3.2. Эллипсоид остаточных скоростей

Для определения параметров эллипсоида остаточных скоростей звезд мы используем следующий известный метод [32]. В классическом варианте рассматриваются шесть моментов второго порядка $a$, $b$, $c$, $f$, $e$, $d$:

$\begin{gathered} a = \left\langle {{{U}^{2}}} \right\rangle - \left\langle {U_{ \odot }^{2}} \right\rangle , \\ b = \left\langle {{{V}^{2}}} \right\rangle - \left\langle {V_{ \odot }^{2}} \right\rangle , \\ \end{gathered} $
(8)
$\begin{gathered} c = \left\langle {{{W}^{2}}} \right\rangle - \left\langle {W_{ \odot }^{2}} \right\rangle , \\ f = \left\langle {VW} \right\rangle - \left\langle {{{V}_{ \odot }}{{W}_{ \odot }}} \right\rangle , \\ \end{gathered} $
$\begin{gathered} e = \left\langle {WU} \right\rangle - \left\langle {{{W}_{ \odot }}{{U}_{ \odot }}} \right\rangle , \\ d = \left\langle {UV} \right\rangle - \left\langle {{{U}_{ \odot }}{{V}_{ \odot }}} \right\rangle . \\ \end{gathered} $
Как было отмечено выше, при необходимости можно освобождать наблюдаемые скорости не только от пекулярного движения Солнца, но и от дифференциального вращения Галактики или от влияния спиральной волны плотности. Моменты $a$, $b$, $c$, $f$, $e$, $d$ являются коэффициентами уравнения поверхности
(9)
$a{{x}^{2}} + b{{y}^{2}} + c{{z}^{2}} + 2fyz + 2ezx + 2dxy = 1,$
а также компонентами симметричного тензора моментов остаточных скоростей
(10)
$\left( {\begin{array}{*{20}{c}} a&d&e \\ d&b&f \\ e&f&c \end{array}} \right).$
Значения всех элементов этого тензора могут быть определены из решения следующей системы условных уравнений:
(11)
$\begin{array}{*{20}{c}} {V_{l}^{2} = asi{{n}^{2}}l + bco{{s}^{2}}lsi{{n}^{2}}l - } \\ { - \;2dsinlcosl,} \end{array}$
(12)
$\begin{gathered} V_{b}^{2} = asi{{n}^{2}}bco{{s}^{2}}l + bsi{{n}^{2}}bsi{{n}^{2}}l + \\ + \;cco{{s}^{2}}b - 2fcosbsinbsinl - \\ - \;2ecosbsinbcosl + 2dsinlcoslsi{{n}^{2}}b, \\ \end{gathered} $
(13)
$\begin{gathered} {{V}_{l}}{{V}_{b}} = asinlcoslsinb + bsinlcoslsinb + \\ + \;fcoslcosb - esinlcosb + \\ + \;d(si{{n}^{2}}lsinb - co{{s}^{2}}sinb), \\ \end{gathered} $
(14)
$\begin{gathered} {{V}_{b}}{{V}_{r}} = - aco{{s}^{2}}lcosbsinb - bsi{{n}^{2}}lsinbcosb + \\ + \;csinbcosb + f(co{{s}^{2}}bsinl - sinlsi{{n}^{2}}b) + \\ + \;e(co{{s}^{2}}bcosl - coslsi{{n}^{2}}b) - \\ - \;d(coslsinlsinbcosb + sinlcoslcosbsinb), \\ \end{gathered} $
(15)
$\begin{gathered} {{V}_{l}}{{V}_{r}} = - acosbcoslsinl + bcosbcoslsinl + \\ + \;fsinbcosl - esinbsinl + \\ + \;d(cosbco{{s}^{2}}l - cosbsi{{n}^{2}}l). \\ \end{gathered} $
Решение ищется методом наименьших квадратов (МНК) относительно шести неизвестных $a$, $b$, $c$, $f$, $e$, $d$. Затем находятся собственные значения тензора (10) ${{\lambda }_{{1,2,3}}}$ из решения векового уравнения
(16)
$\left| {\begin{array}{*{20}{c}} {a - \lambda }&d&e \\ d&{b - \lambda }&f \\ e&f&{e - \lambda } \end{array}} \right| = 0.$
Собственные значения данного уравнения равны обратным значениям квадратов полуосей эллипсоида моментов скоростей и, в то же время, квадратам полуосей эллипсоида остаточных скоростей:
(17)
$\begin{array}{*{20}{c}} {{{\lambda }_{1}} = \sigma _{1}^{2},\quad {{\lambda }_{2}} = \sigma _{2}^{2},\quad {{\lambda }_{3}} = \sigma _{3}^{2},} \\ {{{\lambda }_{1}} > {{\lambda }_{2}} > {{\lambda }_{3}}.} \end{array}$
Направления главных осей тензора (16) ${{L}_{{1,2,3}}}$ и ${{B}_{{1,2,3}}}$ находятся из соотношений
(18)
$\operatorname{tg} {{L}_{{1,2,3}}} = \frac{{ef - (c - \lambda )d}}{{(b - \lambda )(c - \lambda ) - {{f}^{2}}}},$
(19)
$\operatorname{tg} {{B}_{{1,2,3}}} = \frac{{(b - \lambda )e - df}}{{{{f}^{2}} - (b - \lambda )(c - \lambda )}}cos{{L}_{{1,2,3}}}.$
Ошибки определения ${{L}_{{1,2,3}}}$ и ${{B}_{{1,2,3}}}$ оцениваются согласно следующей схеме:
$\varepsilon ({{L}_{2}}) = \varepsilon ({{L}_{3}}) = \frac{{\varepsilon (\overline {UV} )}}{{a - b}},$
$\varepsilon ({{B}_{2}}) = \varepsilon (\varphi ) = \frac{{\varepsilon (\overline {UW} )}}{{a - c}},$
(20)
$\varepsilon ({{B}_{3}}) = \varepsilon (\psi ) = \frac{{\varepsilon (\overline {VW} )}}{{b - c}},$
${{\varepsilon }^{2}}({{L}_{1}}) = \frac{{{{\varphi }^{2}}{{\varepsilon }^{2}}(\psi ) + {{\psi }^{2}}{{\varepsilon }^{2}}(\varphi )}}{{{{{({{\varphi }^{2}} + {{\psi }^{2}})}}^{2}}}},$
${{\varepsilon }^{2}}({{B}_{1}}) = \frac{{si{{n}^{2}}{{L}_{1}}{{\varepsilon }^{2}}(\psi ) + co{{s}^{2}}{{L}_{1}}{{\varepsilon }^{2}}({{L}_{1}})}}{{{{{(si{{n}^{2}}{{L}_{1}} + {{\psi }^{2}})}}^{2}}}},$
где $\varphi = cot{{B}_{1}}cos{{L}_{1}}$ и $\psi = cot{{B}_{1}}sin{{L}_{1}}$. При этом необходимо заранее вычислить три величины $\overline {{{U}^{2}}{{V}^{2}}} $, $\overline {{{U}^{2}}{{W}^{2}}} $ и $\overline {{{V}^{2}}{{W}^{2}}} ,$ тогда
(21)
$\begin{gathered} {{\varepsilon }^{2}}(\overline {UV} ) = (\overline {{{U}^{2}}{{V}^{2}}} - {{d}^{2}}){\text{/}}n, \\ {{\varepsilon }^{2}}(\overline {UW} ) = (\overline {{{U}^{2}}{{W}^{2}}} - {{e}^{2}}){\text{/}}n, \\ {{\varepsilon }^{2}}(\overline {VW} ) = (\overline {{{V}^{2}}{{W}^{2}}} - {{f}^{2}}){\text{/}}n, \\ \end{gathered} $
где $n$ – количество звезд. Здесь ошибки каждой оси оцениваются независимым способом за исключением ${{L}_{2}}$ и ${{L}_{3}}$, ошибки которых вычисляются по одной формуле.

3.3. Кинематическая модель

Из анализа остаточных скоростей ${{V}_{r}}$, ${{V}_{l}}$, ${{V}_{b}}$ можем определить среднюю групповую скорость ${{(U,V,W)}_{\diamondsuit }}$, а также четыре аналога постоянных Оорта ${{(A,B,C,K)}_{\diamondsuit }}$, которые в нашем случае характеризуют эффекты собственного вращения (${{A}_{\diamondsuit }}$ и ${{B}_{\diamondsuit }}$) и расширения/сжатия (${{C}_{\diamondsuit }}$ и ${{K}_{\diamondsuit }}$) выборки маломассивных звезд. Для этого применяется простая кинематическая модель, аналог модели Оорта-Линдблада [32]:

(22)
$\begin{gathered} {{V}_{r}} = {{U}_{\diamondsuit }}cosbcosl{{V}_{\diamondsuit }}cosbsinl + {{W}_{\diamondsuit }}sinb + \\ + \;r{{A}_{\diamondsuit }}co{{s}^{2}}{\kern 1pt} bsin2l + r{{C}_{\diamondsuit }}{\kern 1pt} co{{s}^{2}}bcos2l + r{{K}_{\diamondsuit }}co{{s}^{2}}b, \\ \end{gathered} $
(23)
$\begin{gathered} {{V}_{l}} = - {{U}_{\diamondsuit }}sinl{{V}_{\diamondsuit }}cosl + r{{A}_{\diamondsuit }}cosbcos2l - \\ - \;r{{C}_{\diamondsuit }}cosbsin2l + r{{B}_{\diamondsuit }}cosb, \\ \end{gathered} $
(24)
$\begin{gathered} {{V}_{b}} = - {{U}_{\diamondsuit }}coslsinb - {{V}_{\diamondsuit }}sinlsinb + \\ + \;{{W}_{\diamondsuit }}cosb - r{{A}_{\diamondsuit }}sinbcosbsin2l - \\ - \;r{{C}_{\diamondsuit }}cosbsinbcos2l - r{{K}_{\diamondsuit }}cosbsinb. \\ \end{gathered} $
Неизвестные ${{(U,V,W)}_{\diamondsuit }}$ и ${{(A,B,C,K)}_{\diamondsuit }}$ находим в результате совместного МНК-решения системы условных уравнений (22)–(24). Используем систему весов вида ${{w}_{r}} = {{S}_{0}}{\text{/}}\sqrt {S_{0}^{2} + \sigma _{{{{V}_{r}}}}^{2}} ,$ ${{w}_{l}} = {{S}_{0}}{\text{/}}\sqrt {S_{0}^{2} + \sigma _{{{{V}_{l}}}}^{2}} $ и ${{w}_{b}} = {{S}_{0}}{\text{/}}\sqrt {S_{0}^{2} + \sigma _{{{{V}_{b}}}}^{2}} ,$ где ${{S}_{0}}$ – “космическая” дисперсия, ${{\sigma }_{{{{V}_{r}}}}}$, ${{\sigma }_{{{{V}_{l}}}}}$, ${{\sigma }_{{{{V}_{b}}}}}$ – дисперсии ошибок соответствующих наблюдаемых скоростей. Значение ${{S}_{0}}$ сопоставимо со среднеквадратической невязкой ${{\sigma }_{0}}$ (ошибка единицы веса) при решении условных уравнений вида (22)–(24). В настоящей работе при анализе остаточных скоростей звезд ${{S}_{0}}$ принято равным 3 км/с. Применяется также критерий 3$\sigma $ для отбрасывания невязок.

С использованием найденных значений параметров ${{A}_{\diamondsuit }}$ и ${{C}_{\diamondsuit }}$ вычисляем значение угла ${{l}_{{xy}}}$ (отклонение вертекса) согласно соотношению, предложенному Паренаго [33]:

(25)
$tan(2{{l}_{{xy}}}) = \frac{{{{{(AK - BC)}}_{\diamondsuit }}}}{{{{{(AB + KC)}}_{\diamondsuit }}}},$
которое при отсутствии расширения/сжатия (при  $K = 0$) принимает более привычную (как при анализе галактического вращения) форму $tan(2{{l}_{{xy}}}) = - {{C}_{\diamondsuit }}{\text{/}}{{A}_{\diamondsuit }}$. В случае чистого вращения угол ${{l}_{{xy}}}$ показывает точно на кинематический центр.

Отметим несколько важных соотношений в нашей кинематической модели [32]:

(26)
${{({{\Omega }_{0}})}_{\diamondsuit }} = {{(B - A)}_{\diamondsuit }},\quad {{(V_{0}^{'})}_{\diamondsuit }} = {{(B + A)}_{\diamondsuit }},$
где ${{({{\Omega }_{0}})}_{\diamondsuit }}$ – угловая скорость вращения, и ${{(V_{0}^{'})}_{\diamondsuit }} = $ $ = {{(\partial {{V}_{\theta }}{\text{/}}\partial R)}_{\diamondsuit }}$ – первая производная линейной скорости вращения ${{({{V}_{\theta }})}_{\diamondsuit }}$ в точке $R = {{R}_{0}}$.

Для угловой скорости расширения/сжатия ${{({{k}_{0}})}_{\diamondsuit }}$ и первой производной линейной радиальной скорости (направленной по радиусу от кинематического центра системы) расширения/сжатия ${{V}_{R}}$ в точке $R = {{R}_{0}}$ имеем [32]:

(27)
${{({{k}_{0}})}_{\diamondsuit }} = {{(K - C)}_{\diamondsuit }},\quad {{(V_{R}^{'})}_{\diamondsuit }} = {{(K + C)}_{\diamondsuit }}.$

4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В табл. 1 даны результаты, полученные при совместном МНК-решении условных уравнений вида (22)–(24). В первой колонке перечислены искомые параметры и сопутствующие им величины, во второй колонке даны результаты, полученные по звездам, которые были исправлены за пекулярное движение Солнца относительно МСП, в третьей колонке даны результаты, полученные по тем же звездам, в собственных движениях и лучевых скоростях которых дополнительно были введены поправки за влияние спиральной волны плотности с амплитудой ${{f}_{R}} = 5$ км/с и значением фазы Солнца в волне ${{\chi }_{ \odot }} = - 120^\circ $, в четвертой колонке даны результаты, полученные по звездам, описанным на предыдущем шаге, но здесь все долготы были исправлены поправкой $l = l - {{l}_{{xy}}}$, то есть приведены к новому кинематическому центру системы. В этой новой системе координат значения параметров ${{(U,V,W)}_{\diamondsuit }}$ и ${{({v},l,b)}_{\diamondsuit }}$ не представляют большого интереса, поэтому они не даны.

Таблица 1.  

Параметры кинематической модели Оорта-Линдблада (верхняя часть) и параметры эллипсоида остаточных скоростей (нижняя часть)

Параметры до учета после учета ${{l}_{{new}}} = l - {{l}_{{xy}}}$
$\bar {U}$, км/с –10.67 ± 0.40    
$\bar {V}$, км/с –16.14 ± 0.39    
$\bar {W}$, км/с –6.19 ± 0.08    
${{N}_{ \star }}$ 697 697 697
${{\sigma }_{0}},$ км/с 2.2 2.2 2.2
${{U}_{\diamondsuit }}$, км/с 0.43 ± 0.40 2.55 ± 0.41  
${{V}_{\diamondsuit }}$, км/с –3.94 ± 0.39 –3.43 ± 0.40  
${{W}_{\diamondsuit }}$, км/с 1.11 ± 0.08 1.11 ± 0.08  
${{{v}}_{\diamondsuit }}$, км/с 4.12 ± 0.38 4.42 ± 0.39  
${{l}_{\diamondsuit }}$, град 276 ± 6 307 ± 5  
${{b}_{\diamondsuit }}$, град 16 ± 2 15 ± 2  
${{A}_{\diamondsuit }}$, км/с/кпк 2.5 ± 2.0 2.0 ± 2.0 –0.1 ± 2.0
${{B}_{\diamondsuit }}$, км/с/кпк –2.0 ± 1.8 0.8 ± 1.9 0.8 ± 1.9
${{C}_{\diamondsuit }}$, км/с/кпк 3.9 ± 1.9 –4.3 ± 1.9 –4.8 ± 2.0
${{K}_{\diamondsuit }}$, км/с/кпк 41.1 ± 2.1 36.8 ± 2.1 36.8 ± 2.1
${{l}_{{xy}}}$, град 18 ± 12 –13 ± 12 0
${{\sigma }_{1}}$, км/с 7.71 ± 0.62 8.23 ± 0.58  
${{\sigma }_{2}}$, км/с 2.40 ± 0.38 2.18 ± 0.41  
${{\sigma }_{3}}$, км/с 1.86 ± 0.24 1.58 ± 0.28  
${{L}_{1}}$, ${{B}_{1}}$, град 323 ± 7, 3 ± 1 324 ± 5, 2 ± 1  
${{L}_{3}}$, ${{B}_{3}}$, град 56 ± 9, 39 ± 3 60 ± 7, 68 ± 3  
${{L}_{2}}$, ${{B}_{2}}$, град 230 ± 9, 51 ± 2 233 ± 7, 22 ± 2  
Таблица 2.  

Параметры кинематической модели Оорта-Линдблада, найденные по выборкам в трех долготных интервалах

Параметры $l < 300^\circ $ $l:300{\kern 1pt} - {\kern 1pt} 330^\circ $ $l > 330^\circ $
${{N}_{ \star }}$ 116 213 367
${{\sigma }_{0}}$, км/с 3.5 1.4 2.1
${{U}_{\diamondsuit }}$, км/с 4.5 ± 1.1 3.9 ± 0.6 4.0 ± 0.7
${{V}_{\diamondsuit }}$, км/с −3.1 ± 1.1 −5.1 ± 0.6 −1.8 ± 0.6
${{W}_{\diamondsuit }}$, км/с 0.4 ± 0.3 1.3 ± 0.1 1.2 ± 0.1
${{{v}}_{\diamondsuit }}$, км/с 5.5 ± 1.1 6.5 ± 0.6 4.6 ± 0.6
${{l}_{\diamondsuit }}$, град. 326 ± 12 307 ± 5 335 ± 8
${{b}_{\diamondsuit }}$, град. 4 ± 4 12 ± 2 15 ± 5
${{A}_{\diamondsuit }}$, км/с/кпк 3.1 ± 6.1 15.2 ± 3.6 −11.7 ± 4.1
${{B}_{\diamondsuit }}$, км/с/кпк −11.3 ± 5.9 −11.7 ± 3.6 10.2 ± 4.1
${{C}_{\diamondsuit }}$, км/с/кпк −20.9 ± 6.3 12.1 ± 3.8 −25.9 ± 3.9
${{K}_{\diamondsuit }}$, км/с/кпк 13.6 ± 6.6 37.6 ± 3.9 41.4 ± 4.0
${{l}_{{xy}}}$, град. 16 ± 8 34 ± 5 5 ± 4

В нижней части таблицы даны параметры эллипсоида остаточных скоростей звезд, найденные в результате МНК-решения системы условных уравнений вида (11)–(15). Из анализа данных каталога Gaia в работе Райта, Мамаека (2018) были определены следующие средние значения дисперсий скоростей для трех основных группировок в ассоциации Скорпиона–Центавра: $3.20_{{ - 0.20}}^{{ + 0.22}}$ км/с (US), $2.45_{{ - 0.20}}^{{ + 0.20}}$ км/с (UCL) и $2.15_{{ - 0.24}}^{{ + 0.47}}$ км/с (LCC). Мы можем видеть из табл. 1, что значения ошибок единицы веса ${{\sigma }_{0}}$ (по смыслу она как раз является усредненной ошибкой по трем координатным осям), а также значения дисперсий эллипсоидов остаточных скоростей находятся в хорошем согласии с указанными оценками.

Во второй колонке табл. 1 даны компоненты вектора групповой скорости выборки относительно Солнца $(\overline U ,\overline V ,\overline W ) = ( - 10.7, - 16.1, - 6.2) \pm $ $ \pm \;(0.4,0.4,0.1)$ км/с. Вычислены они были как простое среднее из скоростей звезд, которые не исправлялись никакими поправками.

В работе [18] из анализа 134 ярких членов ассоциации Скорпиона–Центавра из каталога H-IPPARCOS [17] было найдено $(\bar {U},\bar {V},\bar {W}) = ( - 11.8,$ $ - 18.2, - 6.1) \pm (0.8,0.8,0.3)$ км/с. По 487 звездам подгруппы C из LCC со средним возрастом 10 млн лет Голдман и др. [35] определили $(\bar {U},\bar {V},\bar {W}) = $ $ = \;( - 8.2, - 20.9, - 6.1) \pm (1.1,1.5,0.6)$ км/с. Райт, Мамаек [5] из анализа около 250 ярких членов ассоциации Скорпиона–Центавра из каталога Gaia DR1 нашли $(\bar {U},\bar {V},\bar {W}) = ( - 7.2, - 19.6, - 6.1) \pm (0.2,$ $0.2,0.1)$ км/с.

Благодаря тому, что были отброшены 33 звезды со скоростями $V > 10$ км/с (рис. 1), была получена очень однородная в кинематическом отношении выборка. Ранее по выборке из примерно 200 массивных OB-звезд из каталога HIPPARCOS была получена оценка коэффициента линейного расширения $K = 46 \pm 8$ км/с/кпк [18]. Теперь же получаем существенно меньшую ошибку определения этого коэффициента, ±2 км/с/кпк. Значение $K = 41 \pm 2$ км/с/кпк из второй колонки табл. 1 находится в хорошем согласии с анализом массивных звезд, которые также были получены в работе [18] без учета спиральной волны плотности.

Значение ${{l}_{{xy}}} = - 13 \pm 12^\circ $ (третья колонка табл. 1) указывает на то, что кинематический центр системы этих звезд находится в четвертом галактическом квадранте. Однако велика ошибка определения этой величины. С другой стороны, направление первой оси эллипсоида остаточных скоростей звезд ${{L}_{1}} = 324 \pm 5^\circ $ (нижняя часть табл. 1) определяется с меньшей ошибкой. Оба направления, ${{l}_{{xy}}}$ и ${{L}_{1}}$ отсчитываются от направления на галактический центр $l = 0^\circ $, но в разные стороны. Для их корректного сравнения проведем отсчет от направления $l = 0^\circ $ однообразно. Например, для ${{L}_{1}}\, = \,324\, \pm \,5^\circ $ можем записать $324^\circ \, - \,360^\circ \, = \, - {\kern 1pt} 36^\circ $. Таким образом, направление $ - 36 \pm 5^\circ $ можно считать направлением на кинематический центр ассоциации Скорпиона–Центавра.

Отметим, что в системе координат с новым центром (четвертая колонка табл. 1) значения постоянных ${{A}_{\diamondsuit }}$ и ${{C}_{\diamondsuit }}$ не отличаются значимо от нуля.

На рис. 2 даны для иллюстрации скорости звезд ${{V}_{R}}$ в зависимости от расстояния $R$. Скорости исправлены за движение Солнца относительно МСП. На рис. 2a дана волна

$ - 5cos\left[ { - \frac{{2\pi {{R}_{0}}}}{{2.2}}ln\left( {\frac{R}{{{{R}_{0}}}}} \right) - 120^\circ } \right],$
записанная согласно соотношениям (6) и (7), с амплитудой возмущения ${{f}_{R}} = 5$ км/с, длиной волны $\lambda = 2.2$ кпк и фазой Солнца в волне ${{\chi }_{ \odot }} = - 120^\circ $, здесь знак минус перед формулой означает, что в центре спирального рукава (например, при $R \approx 7.2$ кпк) возмущение направлено к центру Галактики.

Рис. 2.

Галактоцентрические радиальные скорости звезд ${{V}_{R}}$ в зависимости от расстояния $R,$ исправленные за движение Солнца относительно МСП, зеленая линия показывает влияние спиральной волны плотности (а), исправленные за движение Солнца относительно МСП, учтено влияние спиральной волны плотности, оранжевая линия соответствует найденному по этим звездам $K$-эффекту (б).

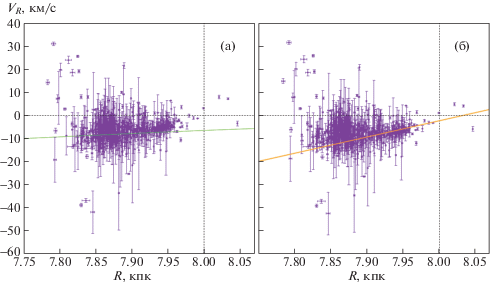
По определению $2K = {{V}_{R}}{\text{/}}R + \partial {{V}_{R}}{\text{/}}\partial R$ при независимости вращательной скорости ${{V}_{\theta }}$ от угла ${{V}_{\theta }},$ $\partial {{V}_{\theta }}{\text{/}}\partial \theta = 0$ [32]. При постоянстве угловой скорости, то есть при $\partial {{V}_{R}}{\text{/}}\partial R = 0$, $\partial {{V}_{R}}{\text{/}}\partial R = 0$ и $2K = {{V}_{R}}{\text{/}}R$. На рис. 2б дана зависимость ${{V}_{R}}{\text{/}}R = 2K$ со значением $K = 37$ км/с/кпк.

На основе решения из четвертой колонки табл. 1 с использованием соотношения (27) находим $K - C = 41.6 \pm 2.8$ км/с/кпк и $K + C = 32.0 \pm $ $ \pm \;2.8$ км/с/кпк. Эти значения показывают, что в точке, где расположен наблюдатель, имеются большая угловая скорость расширения и большая положительная производная линейной скорости расширения.

Интересно определить кинематические параметры для US, UCL и LCC в отдельности. Для этого вся выборка была разбита на три тридцатиградусные сектора по галактической долготе $l$. Результаты решения уравнений вида (22)–(24), полученные с учетом влияния спиральной волны для трех выборок, даны в табл. 2.

Как можно видеть в табл. 2, значение определяемого по звездам выборки с долготами $l < 300^\circ $ коэффициента линейного расширения $K = 13.6 \pm $ ± 6.6 км/с/кпк сильно отличается от других результатов. Эти звезды обладают также наибольшим значением ошибки единицы веса ${{\sigma }_{0}}$. Оказалось, что здесь сильное влияние оказывают звезды из первого галактического квадранта, которые, скорее всего являются фоновыми. Поэтому дальнейший анализ проведен без этих звезд.

В итоге было получено МНК-решение условных уравнений вида (22)–(24) при условии $l > 300^\circ $ с использованием 574 звезд, где вектор среднего движения равен ${{(U,V,W)}_{\diamondsuit }} = (2.96, - 2.84,$ $1.24) \pm (0.45,0.44,0.08)$ км/с (этому вектору соответствует полная скорость ${{{v}}_{\diamondsuit }} = 4.28 \pm 0.43$ км/с, с направлением ${{l}_{\diamondsuit }} = 316 \pm 6^\circ $ и ${{b}_{\diamondsuit }} = 17 \pm 3^\circ $), а также следующие значения остальных параметров:

(28)
$\begin{gathered} {{A}_{\diamondsuit }} = - 0.1 \pm 2.1\;{\text{км/с/кпк}}, \\ {{B}_{\diamondsuit }} = 1.5 \pm 2.0\;{\text{км/с/кпк}}, \\ {{C}_{\diamondsuit }} = - 9.5 \pm 2.1\;{\text{км/с/кпк}}, \\ {{K}_{\diamondsuit }} = 39.1 \pm 2.3\;{\text{км/с/кпк}}, \\ {{l}_{{xy}}} = - 1 \pm 6^\circ , \\ \end{gathered} $
где ошибка единицы веса ${{\sigma }_{0}}$ составила 1.9 км/с. На основе полученного значения коэффициента линейного расширения $K = 39 \pm 2$ км/с/кпк можем оценить характерное время расширения комплекса по известной формуле $T = 977.5{\text{/}}K$, что составляет $T = 25 \pm 2$ млн лет.

Для определения параметров вращения не обязательно иметь лучевые скорости звезд, достаточно двух уравнений (23)–(24) или даже одного (23). Таким образом, для изучения собственного вращения ассоциации Скорпиона–Центавра лучше будет использовать каталог с огромным количеством звезд из работы Дамиани и др. [3], когда этот каталог появится в Страсбургской базе данных.

Как было отмечено в разделе Данные, в нашей выборке имеются около 5300 вероятных членов ассоциации Скорпиона–Центавра с собственными движениями и параллаксами. Лучевые скорости известны для малой части звезд этой выборки. В таком случае МНК-решение системы из трех уравнений (22)–(24) ищется следующим образом: звезда с собственными движениями дает два уравнения (23) и (24), а при наличии лучевой скорости звезда дает все три уравнения. При таком подходе главным образом обращаем внимание на параметры вращения, считая, что параметр расширения уже определен надежно.

В итоге было получено следующее решение: ${{(U,V,W)}_{\diamondsuit }}\, = \,(3.11, - 1.88,1.10) \pm (0.17,0.13,0.02)$ км/с (${{{v}}_{\diamondsuit }} = 3.80 \pm 0.15$ км/с, с направлением ${{l}_{\diamondsuit }} = 329 \pm 2^\circ $ и ${{b}_{\diamondsuit }} = 17 \pm 1^\circ $), а также:

(29)
$\begin{gathered} {{A}_{\diamondsuit }} = 1.8 \pm 0.8\;{\text{км/с/кпк}}, \\ {{B}_{\diamondsuit }} = - 7.5 \pm 0.6\;{\text{км/с/кпк}}, \\ {{C}_{\diamondsuit }} = - 9.6 \pm 0.6\;{\text{км/с/кпк}}, \\ {{K}_{\diamondsuit }} = 33.1 \pm 0.9\;{\text{км/с/кпк}}, \\ {{l}_{{xy}}} = 1 \pm 2^\circ , \\ \end{gathered} $
где ${{\sigma }_{0}}$ составила 1.3 км/с. В отличие от решения (28) здесь заметно точнее определяются величины всех четырех постоянных. Значение ${{l}_{{xy}}}$ близко к нулю, поэтому переходить к новой системе координат нет необходимости.

Из решения (29) с доминирующим расширением находим с использованием соотношения (26) следующие параметры вращения: ${{({{\Omega }_{0}})}_{\diamondsuit }} = - 9.3 \pm $ $ \pm \;1.0$ км/с/кпк и ${{(V_{0}^{'})}_{\diamondsuit }} = - 5.7 \pm 1.0$ км/с/кпк. Знак этой угловой скорости говорит о том, что оно по направлению совпадает с галактическим вращением. В точке, где расположен наблюдатель, модуль этой скорости возрастает.

Для расширения с использованием соотношения (27) находим следующие параметры: ${{({{k}_{0}})}_{\diamondsuit }} = $ $ = \,42.7\, \pm \,1.1$ км/с/кпк и ${{(V_{R}^{'})}_{\diamondsuit }} = 24.5 \pm 1.1$ км/с/кпк. Таким образом, в точке, где расположен наблюдатель, модуль этой скорости также возрастает.

Применяя аналогичный подход к решению (28), а также к решению в последней колонке табл. 1, находим похожие значения для параметров расширения, и отсутствие собственного вращения. Можем заключить, что параметры расширения определяются надежно, а параметры собственного вращения сильно зависят от принятых ограничений. Но в целом собственное вращение ассоциации Скорпиона–Центавра малó.

В работе Фернандеса и др. [34] была прослежена кинематическая эволюция ассоциации Скорпиона–Центавра путем анализа галактических орбит в прошлом различных частей ассоциации. Орбиты строились в осесимметричном потенциале с дополнительным учетом спиральной волны плотности. Было подтверждено наличие расширения ассоциации. Параллельно изучалась и эволюция Местного Пузыря.

Интересно также отметить работу Райта, Мамаека [5], которые протестировали кинематику ассоциации Скорпиона–Центавра несколькими методами. В частности, рассмотрели метод поиска коэффициента линейного расширения по лучевым скоростям звезд, а также строили назад орбиты звезд с целью найти момент наименьшей области их пространственной концентрации. Эти авторы заключили, что нет доказательств того, что рассмотренные подгруппы имели более компактную конфигурацию в прошлом. Другими словами, не нашли признаков расширения ассоциации. Наоборот, в работе Голдмана и др. [35] показано наличие расширения подсистемы звезд в ассоциации и LCC с коэффициентом линейного расширения $K \sim 35$ км/с/кпк.

По звездам с лучевыми скоростями, которые были использованы при поиске решения (28), найдены следующие параметры эллипсоида остаточных скоростей:

(30)
$\begin{gathered} {{\sigma }_{1}} = 7.72 \pm 0.56\;{\text{км/с}}, \\ {{\sigma }_{2}} = 1.87 \pm 0.37\;{\text{км/с}}, \\ {{\sigma }_{3}} = 1.74 \pm 0.22\;{\text{км/с}} \\ \end{gathered} $
и параметры ориентации этого эллипсоида
(31)
$\begin{gathered} {{L}_{1}} = 323 \pm 7^\circ ,\quad {{B}_{1}} = 3 \pm 1^\circ , \\ {{L}_{2}} = 54 \pm 6^\circ ,\quad {{B}_{2}} = 12 \pm 2^\circ , \\ {{L}_{3}} = 305 \pm 6^\circ ,\quad {{B}_{3}} = 78 \pm 2^\circ . \\ \end{gathered} $
Направление ${{L}_{1}} = 323^\circ ( - 37^\circ )$, во-первых, находится в хорошем согласии с направлением на геометрический центр ассоциации Скорпиона–Центавра (рис. 1), а во-вторых, в хорошем согласии со значением ${{l}_{{xy}}} = - 44^\circ $, найденного на основе модели Оорта–Линдблада (решение (28)). Интересно отметить, что в отличие от эллипсоидов табл. 1, ориентация этого эллипсоида отлично согласуется с ориентацией пояса Гулда [36]. Например, на основе аналогичного подхода в работе Бобылева [27] показано, что эллипсоид остаточных скоростей звезд пояса Гулда имеет главные полуоси ${{\sigma }_{{1,2,3}}} = (8.9,5.6,3.0) \pm (0.1,0.2,0.1)$ км/с, и он расположен под углом $22 \pm 1^\circ $ к галактической плоскости.

5. ЗАКЛЮЧЕНИЕ

Изучена кинематика молодых звезд типа Т Тельца, принадлежащих ассоциации Скорпиона–Центавра. Для этого был использован каталог звезд этого типа с собственными движениями и параллаксами из каталога Gaia DR2 из работы Зари и др. [21]. Причем каталог [21] содержит более 23 000 и посвящен отбору звезд, принадлежащим поясу Гулда.

В настоящей работе большое место уделено поиску звезд, тесно связанных с ассоциацией Скорпиона–Центавра. Для этого были использованы ограничения как на координаты звезд, так и на их пространственные скорости. В качестве основной модели использована кинематическая модель Оорта-Линдблада, на основе которой мы определяем вектор средней групповой скорости выборки относительно местного стандарта покоя ${{(U,V,W)}_{\diamondsuit }}$, а также четыре аналога постоянных Оорта ${{(A,B,C,K)}_{\diamondsuit }}$.

Важной особенностью настоящей работы является учет влияния спиральной волны плотности. Эффективность учета зависит как от амплитуды возмущения спиральной волны, так и от значения фазы Солнца в волне. То есть при определенном значении фазы даже при большой амплитуде можно получить нулевой эффект. С другой стороны, при определенной амплитуде радиальных возмущений на такую же величину уменьшается значение определяемого коэффициента линейного расширения звездной системы ${{K}_{\diamondsuit }}$. Нами были выбраны относительно небольшое значение амплитуды радиальных возмущений и нулевое значение амплитуды тангенциальных возмущений, найденное ранее по мазерам, OB-звездам и молодым цефеидам.

Вначале был выполнен кинематический анализ около 700 звезд ассоциации Скорпиона–Центавра, для которых измерены собственные движения, параллаксы и лучевые скорости. Новая оценка коэффициента линейного расширения ${{K}_{\diamondsuit }} = 39 \pm 2$ км/с/кпк получена с учетом пекулярной скорости Солнца относительно МСП и влияния галактической спиральной волны плотности с амплитудой радиальных возмущений ${{f}_{R}} = 5$ км/с и фазой Солнца в волне –120°. По сравнению с расширением собственное вращение ассоциации Скорпиона–Центавра мало, оно плохо определяется так как параметры этого вращения сильно зависят от принятых ограничений.

Эллипсоид остаточных скоростей звезд этой выборки имеет главные полуоси ${{\sigma }_{{1,2,3}}} = (7.72,1.87,$ $1.74) \pm (0.56,0.37,0.22)$ км/с и расположен он под углом $12 \pm 2^\circ $ к галактической плоскости. Ориентация этого эллипсоида показывает, что он лежит близко к плоскости Гулда, а первая его ось лежит в направлении 143°–323°.

С использованием примерно 5300 звезд с собственными движениями и параллаксами показано, что относительно местного стандарта покоя ассоциация Скорпиона-Центавра движется со скоростью ${{{v}}_{\diamondsuit }} = 3.80 \pm 0.15$ км/с в направлении ${{l}_{\diamondsuit }} = 329 \pm 2^\circ $ и ${{b}_{\diamondsuit }} = 17 \pm 1^\circ $.

Авторы благодарны рецензенту за полезные замечания, которые способствовали улучшению статьи.

Список литературы

  1. Gaia Collaboration, A. G. A. Brown, A. Vallenari, T. Prus-ti, de Bruijne, C. Babusiaux, C. A. L. Bailer-Jones, M. Biermann, D. W. Evans, et al., Astron. and Astrophys. 616, 1 (2018).

  2. Gaia Collaboration, L. Lindegren, J. Hernandez, A. Bom-brun, S. Klioner, U. Bastian, M. Ramos-Lerate, A. de Tor-res, H. Steidelmuller, et al., Astron. and Astrophys. 616, 2 (2018).

  3. F. Damiani, L. Prisinzano, I. Pillitteri, G. Micela, and S. Sciortino, Astron. and Astrophys. 623, 112 (2019).

  4. P. T. de Zeeuw, R. Hoogerwerf, J. H. J. de Bruijne, A. G. A. Brown, and A. Blaauw, Astron. J. 117, 354 (1999).

  5. N. J. Wright and E. E. Mamajek, Monthly Not. Roy. Astron. Soc. 476, 381 (2018).

  6. V. A. Ambartsumian, Астрон. журн. 26, 3, (1949).

  7. A. Blaauw, Bull. Astron. Inst. Netherland 11, 414 (1952).

  8. A. Blaauw, Ann. Rev. Astron. and Astrophys. 2, 213 (1964).

  9. E. E. Mamajek, M. Meyer and J. Liebert, Astron. J. 124, 1670 (2002).

  10. M. J. Sartori, J. R. D. Lepine, and W. S. Dias, Astron. and Astrophys. 404, 913 (2003).

  11. T. Preibisch and E. Mamajek, Handbook of Star Forming Regions, Vol. II (The Southern Sky ASP Monograph Publications, Vol. 5, Bo Reipurth, ed., 2008).

  12. T. Cantat-Gaudin, C. Jordi, N. J. Wright, J. J. Armstrong, A. Vallenari, L. Balaguer-Nunez, P. Ramos, D. Bossini, et al., Astron. and Astrophys. 626, 17 (2019).

  13. A. Rao, P. Gandhi, C. Knigge, J. A. Paice, N. W. C. Leigh, and D. Boubert, preprint 1908.00810 (2019).

  14. A. M. Mel’nik and A. K. Dambis, Monthly Not. Roy. A-stron. Soc. 472, 3887 (2017).

  15. A. M. Mel’nik and A. K. Dambis, Astronomy Reports 62, 998 (2018).

  16. T. Preibisch and H. Zinnecker, Astron. J. 117, 2381 (1999).

  17. The HIPPARCOS and Tycho Catalogues, ESA SP–1200 (1997).

  18. V. V. Bobylev and A. T. Bajkova, Astronomy Letters 33, 571 (2007).

  19. C. A. O. Torres, R. Quast, C. H. F. Melo, and M. F. Sterzik, Handbook of Star Forming Regions Vol. II (The Southern Sky ASP Monograph Publications, Vol. 5, Bo Reipurth, ed., 2008).

  20. V. V. Bobylev and A. T. Bajkova, Astronomy Letters 39, 532 (2013).

  21. E. Zari, H. Hashemi, A. G. A. Brown, K. Jardine, and P. T. de Zeeuw, Astron. and Astrophys. 620, 172 (2018).

  22. T. Camarillo, M. Varun, M. Tyler, and R. Bharat, PASP, 130, 4101 (2018).

  23. R. Schönrich, J. Binney, and W. Dehnen, Monthly Not. Roy. Astron. Soc. 403, 1829 (2010).

  24. C. C. Lin and F. H. Shu, Astrophys. J. 140, 646 (1964).

  25. Yu. N. Mishurov and I. A. Zenina, Astron. and Astrophys. 341, 81 (1999).

  26. D. Fernández, F. Figueras, and J. Torra, Astron. and A-strophys. 372, 833 (2001).

  27. V. V. Bobylev, Astronomy Letters 46, in press, (2020).

  28. A. K. Dambis, L. N. Berdnikov, Yu. N. Efremov, et al., Astronomy Letters 41, 489 (2015).

  29. A. S. Rastorguev, M. V. Zabolotskikh, A. K. Dambis, et al., Astrophys. Bulletin, 72, 122 (2017).

  30. V. V. Bobylev and A. T. Bajkova, Astronomy Letters 45, 151 (2019).

  31. A. V. Loktin and M. E. Popova, Astrophys. Bulletin, 74, 270 (2019)].

  32. K. F. Ogorodnikov, Dynamics of stellar systems (Oxford: Pergamon, ed. Beer, A. 1965).

  33. P. P. Parenago, Course of Stellar Astronomy (Gosizdat, Moscow, in russian, 1954).

  34. D. Fernández, F. Figueras, and J. Torra, Astron. and Astrophys. 480, 735 (2008).

  35. B. Goldman, S. Roser, E. Schilbach, A. C. Moor, and T. Henning, Astrophys. J. 868, 32 (2018).

  36. V. V. Bobylev, Astrophysics, 57, 583 (2014).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал