1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 98, № 10, 2021

Астрономический журнал, 2021, T. 98, № 10, стр. 795-803

Батарейный механизм Бирмана и структура начального магнитного поля в галактиках

Е. А. Михайлов 1, 3, 4, *, Р. Р. Андреасян 2

1 Московский государственный университет им. М.В. Ломоносова, Физический факультет
Москва, Россия

2 Бюраканская астрофизическая обсерватория им. В.А. Амбарцумяна НАН РА
Бюракан, Армения

3 Физический институт им. П.Н.Лебедева РАН
Москва, Россия

4 Московский Центр фундаментальной и прикладной математики
Москва, Россия

* E-mail: ea.mikhajlov@physics.msu.ru

Поступила в редакцию 22.03.2021
После доработки 17.04.2021
Принята к публикации 30.04.2021

Полный текст (PDF)

Аннотация

В достаточно большом количестве галактик присутствуют регулярные магнитные поля с индукцией в несколько микрогаусс. Процесс их генерации объясняется за счет динамо, связанного со структурой движений межзвездной среды в соответствующих объектах. Рост магнитного поля происходит по экспоненциальному закону и стабилизируется при значениях, соответствующих равнораспределению по энергии между магнитным полем и турбулентными движениями. Вместе с тем для начала действия данного механизма необходимо наличие некоторых начальных “затравочных” полей, которые не объясняются в рамках самой теории динамо. Одним из подходов, позволяющих объяснить наличие магнитных полей в галактиках, является так называемый батарейный механизм Бирмана. Он связан с потоками протонов и электронов из центральной части объекта, которые подхватываются вращательными движениями среды. Это приводит к возникновению круговых токов, которые ввиду отличающейся массы будут различаться для разных видов частиц. Суммарный ток оказывается ненулевым, порождая магнитное поле. Ранее делались простые оценки величины данного поля. В настоящей работе построена самосогласованная модель и приведено интегральное уравнение, позволяющее не только определить порядок величины начального магнитного поля, но и детально исследовать его пространственную структуру.

Ключевые слова: механизм Бирмана, магнитное поле, Галактика

1. ВВЕДЕНИЕ

В настоящий момент твердо установлено, что как в Млечном Пути, так и в десятках других галактических объектах присутствуют крупномасштабные магнитные поля. Их индукция может разниться в зависимости от конкретных условий, но в целом, как правило, имеет величину порядка 1 мкГс [1]. Первые предположения о существовании галактических магнитных полей были сделаны в работах, посвященных изучению космических лучей. Их пространственное распределение и характерные значения интенсивности потока было затруднительно объяснить в случае отсутствия магнитного поля в Млечном Пути [2]. Другим свидетельством наличия галактического магнетизма является форма спектра синхротронного излучения.

Одна из первых оценок величины магнитного поля была предложена Ферми еще в середине прошлого века, и его результаты оказались достаточно близки к современным представлениям [3]. Вместе с тем в настоящее время магнитные поля галактик в основном изучаются путем измерений фарадеевского вращения у радиоволн [4]. Как известно, при прохождении поляризованной волны через среду с магнитным полем данная плоскость поворачивается на угол, пропорциональный квадрату длины волны и составляющей поля, направленной вдоль луча зрения [5]. В случае, если мы имеем возможность измерить поляризацию для различных длин волн (желательно, чтобы их было достаточно много и они не были кратны друг другу: последнее, впрочем, не всегда выполняется ввиду технических характеристик радиотелескопов), то это позволяет восстановить данные о структуре магнитных полей [6]. В случае Млечного Пути подобные исследования проводятся на протяжении нескольких десятилетий, и основную роль играют пульсары, служащие своеобразными “зондами”, пронизывающими межзвездную среду.

Первые работы были связаны с изучением поляризации радиоволн всего лишь от нескольких десятков объектов [7], тем не менее, они позволили в целом правильно оценить как величину, так и пространственную структуру крупномасштабных полей, присутствующих в межзвездной среде [8]. Постепенно количество изученных объектов росло, что позволяло уточнять данные о структуре магнитных полей [9, 10]. В настоящий момент существует информация о более чем 1000 объектов [11], что дает возможность исследовать магнитное поле с достаточно высокой точностью [12]. Также немаловажную роль играют внегалактические источники поляризованного радиоизлучения [13, 14]. Они позволяют как исследовать поля в других галактиках [15, 16], так и уточнить оценки, сделанные для Млечного Пути [17].

В работах теоретического характера процесс возникновения регулярных магнитных полей, как правило, связывают с работой крупномасштабного динамо [18]. Оно функционирует за счет одновременного присутствия дифференциального вращения (характеризующего нетвердотельную природу вращения объекта), и альфа-эффекта (который характеризует закрученность турбулентных движений в галактическом диске). Это приводит к экспоненциальному росту магнитного поля, который замедляется по мере приближения его величины к уровню равнораспределения, соответствующего равенству плотностей энергий магнитного поля и движений межзвездной среды, обусловленных турбулентностью [1, 15]. Теория динамо позволяет описать возникновение структур, которые соответствуют наблюдательным данным [19]. Так, можно отметить результаты, связанные с генерацией инверсий магнитного поля, характеризующих резкую смену его направления на границе между различными областями галактик [12].

Вместе с тем одной из очевидных проблем является то, что для возбуждения роста магнитного поля с помощью механизма динамо средних полей требуется наличие некоторых “затравочных” полей [20]. Достаточно разумно считать, что для крупномасштабного магнитного поля они могут быть сгенерированы с помощью мелкомасштабного динамо. Оно связано с движениями среды, сосредоточенными в турбулентных ячейках, и описывает возникновение достаточно интенсивных, хотя и локальных магнитных полей. При этом их направление меняется от ячейки к ячейке и является случайным. Поскольку характерный размер турбулентной ячейки на 2–3 порядка меньше диаметра галактики, оказывается, что среднее поле является отличным от нуля [1, 21 ]. Это вполне может служить затравкой для генерации крупномасштабного магнитного поля. Тем не менее мелкомасштабное динамо также требует своих начальных полей, и проблема, по сути, переносится на предыдущую стадию.

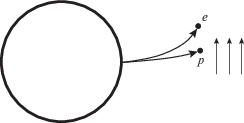
Возможный выход из данной ситуации был предложен Бирманом [22] и в дальнейшем развит Гаррисоном [23], Мишустиным и Рузмайкиным [24]. Так, в случае наличия потоков частиц (протонов и электронов) из центральных областей галактики они будут увлекаться вращательными движениями среды (рис. 1). При этом важно учитывать, что абсолютная величина их заряда одинакова, а массы и сечения взаимодействия со средой существенно отличаются. Это будет приводить к различной скорости движения, а значит и к возникновению ненулевых круговых токов. Они порождают магнитное поле, которое и может возбуждать действие динамо [21]. Один из вариантов описания данного процесса был предложен Лешем и др. [25] (отметим, что там также был изучен процесс формирования магнитного поля для галактики M 82).

Рис. 1.

Распространение частиц и их взаимодействие с вращающейся средой.

Ранее был исследован характер движения частиц и структуры магнитного поля, которое соответствует их движению [26]. Сделаны оценки типичных магнитных полей и времени их роста. Вместе с тем, есть необходимость учесть своеобразное “насыщение” данного процесса. По мере того, как круговые токи начинают создавать магнитное поле, оно начинает влиять на характер движения частиц и заметно менять его структуру. Оценка влияния уже существующего магнитного поля на круговые токи была также сделана в одной из предшествующих работ [27]. Вместе с тем необходимо построить самосогласованную модель, дающую детальную структуру поля, сгенерированного в рамках бирмановского батарейного механизма.

Одна из подобных попыток была предпринята Дэвисом и Видроу [28], которые решали уравнения гидродинамики, предполагая, что величина магнитного поля пропорциональна завихренности движений. Вместе с тем мы предлагаем несколько иной подход, не требующий данного предположения. Мы вычислили величину магнитного поля, созданного круговыми токами, и построили интегральное уравнение, описывающее его влияние на движение остальных частиц. Решение подобного уравнения дает возможность определить структуру магнитного поля, порожденного с помощью батареи Бирмана. Мы представляем характерные решения данной задачи при типичных значениях параметров, соответствующих различным астрофизическим объектам.

2. МОДЕЛЬ ДВИЖЕНИЯ ЧАСТИЦ

Рассмотрим движение частицы, имеющей массу $m$ и заряд $q$. Ее движение описывается с помощью следующего уравнения [27]:

(1)
$m{\mathbf{\ddot {r}}} = {\mathbf{F}} + {\mathbf{f}} + \frac{q}{c}[{\mathbf{\dot {r}}} \times {\mathbf{B}}],$
где ${\mathbf{F}}$ – сила, связанная с притяжением к центру и давлением излучения, ${\mathbf{f}}$ – сила сопротивления среды, ${\mathbf{B}}$ – индукция магнитного поля.

Сила ${\mathbf{F}}$ имеет радиальное направление, а для сопротивления ${\mathbf{f}}$ мы можем записать в цилиндрической системе координат ($r;\varphi ; - z$) следующее равенство (предполагая, что среда вращается с угловой скоростью $\Omega $):

${\mathbf{f}} = - \frac{m}{\tau }({\mathbf{\dot {r}}} - r\Omega {{{\mathbf{e}}}_{\varphi }}),$
где $\tau $ – характерное время взаимодействия.

Если мы введем обозначение $V = \dot {r},$ то в проекции на направление $\varphi $ уравнение (1) можно будет записать в форме:

(2)
$r\ddot {\varphi } + 2V\dot {\varphi } + \frac{r}{\tau }(\dot {\varphi } - \Omega ) + \frac{{qVB}}{{mc}} = 0.$

Оценим характерные времена происходящих процессов. Так, для времени столкновений можно использовать следующее приближенное соотношение [29]:

(3)
$\tau = \frac{{{{m}^{2}}{{V}^{3}}}}{{16\pi {{q}^{4}}Nln\Lambda }},$
где $N$ – плотность числа частиц, $ln{{\lambda }_{C}}$ – кулоновский логарифм. Плотность частиц может достаточно существенно меняться, но по порядку величины для горячего газа в центральной области возможно считать, что $N = {{10}^{3}}$ см–3, а для кулоновского логарифма $ln\Lambda \approx 20.$ Характерную величину скорости будем оценивать как $V = 3 \times {{10}^{8}}$ см/с. Для протонов, имеющих массу $m = 1.7 \times {{10}^{{ - 24}}}$ г и заряд $q = 4.8 \times {{10}^{{ - 10}}}$ ед. СГСЭ, время составляет величину $\tau = 1.4 \times {{10}^{9}}$ с. Оно составляет несколько десятков лет и является крайне малым по галактическим масштабам [15]; отметим также, что для электронов данное время имеет величину на несколько порядков меньше.

Предполагая, что $r \sim {{10}^{{21}}}$ см, мы можем заключить, что характерное время изменения расстояния до центра $r{\text{/}}v \sim {{10}^{{13}}}$ с, и оно существенно превышает время взаимодействия частиц со средой. Это означает, что вполне возможно считать, что $r$ меняется достаточно медленно, поэтому его можно заменить постоянным значением $r = R$. Тогда для угловой скорости частицы $\omega = \dot {\varphi }$ можно переписать уравнение (2) в форме:

(4)
$\dot {\omega } + \frac{1}{\tau }\left( {1 + 2\frac{{V\tau }}{R}} \right)\omega = \frac{\Omega }{\tau } - \frac{{qVB}}{{mcR}}.$

Решение (4) записывается так [30]:

$\omega = {{\omega }_{q}}\left\{ {1 - exp\left( { - \frac{t}{\tau }\left( {1 + 2\frac{{V\tau }}{R}} \right)} \right)} \right\},$
где

${{\omega }_{q}} = \Omega \left( {1 - \frac{{q\tau VB}}{{mcR\Omega }}} \right)\mathop {\left( {1 + 2\frac{{V\tau }}{R}} \right)}\nolimits^{ - 1} .$

Можно отметить, что $\tfrac{{V\tau }}{R} \ll 1,$ поэтому угловая скорость выходит на “устойчивое” значение за время порядка $\tau $. Поэтому будем полагать, что она имеет значение, которое приближенно представимо в виде:

$\omega \cong {{\omega }_{q}} \cong \Omega - \frac{{V\tau }}{R}\left( {2\Omega + \frac{{qB}}{{mc}}} \right).$
Данному движению соответствует круговой ток силой:
${{I}_{q}} = \frac{{q{{\omega }_{q}}}}{{2\pi }}.$
Отметим, что для пары “протон-электрон” ток представляется в виде:
$I = {{I}_{e}} + {{I}_{p}},$
где ${{I}_{e}}$ – ток, соответствующий электрону, ${{I}_{p}}$ – протону. Суммарная сила тока записывается в форме
$\begin{gathered} I = - \frac{e}{{2\pi }}\left\{ {\Omega - \frac{{V{{\tau }_{e}}}}{R}\left( {2\Omega - \frac{{eB}}{{{{m}_{e}}c}}} \right)} \right\} + \\ \, + \frac{e}{{2\pi }}\left\{ {\Omega - \frac{{V{{\tau }_{p}}}}{R}\left( {2\Omega + \frac{{eB}}{{{{m}_{p}}c}}} \right)} \right\}, \\ \end{gathered} $
где $e$ – элементарный заряд, ${{\tau }_{e}}$ и ${{\tau }_{p}}$ – время столкновений для электронов и протонов соответственно, а ${{m}_{e}}$ и ${{m}_{p}}$ – их массы. Учитывая, что ${{\tau }_{e}} \ll {{\tau }_{p}}$, для кругового тока мы можем получить, что [27]

(5)
$I \cong - \frac{{eV{{\tau }_{p}}}}{{\pi R}}\left( {\Omega + \frac{1}{2}\frac{{eB}}{{{{m}_{p}}c}}} \right).$

3. ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ДЛЯ МАГНИТНОГО ПОЛЯ

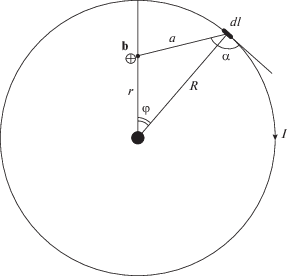
Рассмотрим ток, соответствующий паре “протон-электрон” на расстоянии $R$. Определим, какое магнитное поле создает круговой ток силы $I$ на расстоянии $r$ от центра. Для начала определим по закону Био-Савара-Лапласа [31] индукцию, связанную с элементом тока длины $dl$ (см. рис. 2):

$db = \frac{I}{c}\frac{{dlsin\alpha }}{{{{a}^{2}}}},$
где
$a = \sqrt {{{r}^{2}} + {{R}^{2}} - 2rRcos\varphi } $
– расстояние от исследуемой точки до места локализации тока. Для синуса, стоящего в числителе, выполняется соотношение:
$sin\alpha = \frac{R}{a}\left( {1 - \frac{r}{R}cos\varphi } \right).$
Учитывая, что $dl = Rd\varphi ,$ выражение для дифференциально малого магнитного поля приводится к виду
$db = \frac{I}{c}\frac{{{{R}^{2}}\left( {1 - \tfrac{r}{R}cos\varphi } \right)d\varphi }}{{{{{({{r}^{2}} + {{R}^{2}} - 2rRcos\varphi )}}^{{3/2}}}}}.$
Тогда магнитное поле можно получить с помощью интеграла
$b = \frac{{2I}}{c}\int\limits_0^\pi \frac{{{{R}^{2}}\left( {1 - \tfrac{r}{R}cos\varphi } \right)d\varphi }}{{{{{({{r}^{2}} + {{R}^{2}} - 2rRcos\varphi )}}^{{3/2}}}}}.$
Введем вспомогательную функцию:

$\Phi (\beta ) = 2\int\limits_0^\pi \frac{{(1 - \beta cos\varphi )d\varphi }}{{{{{(1 + {{\beta }^{2}} - 2\beta cos\varphi )}}^{{3/2}}}}}.$
Рис. 2.

Магнитное поле, создаваемое круговым током.

Данный интеграл не вычисляется в элементарных функциях. Вместе с тем, табличные значения данной функции могут быть вычислены численно.

Тогда магнитное поле представляется в форме:

$b = \frac{I}{{cR}}\Phi \left( {\frac{r}{R}} \right).$

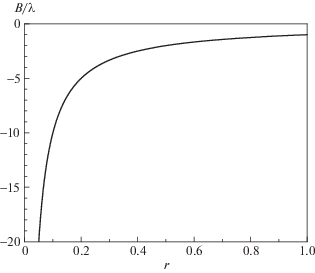
Важно отметить, что при $r = 0$ данная формула должна переходить в хорошо известную формулу для поля в центре витка с током $b = \tfrac{{2\pi I}}{{cR}}$, т.е. при $\beta = 0$ мы должны получать $\Phi = 2\pi $. В свою очередь, при больших значениях $r$ мы должны получить формулу для поля магнитного диполя $b = \tfrac{{\pi I{{R}^{2}}}}{{c{{r}^{3}}}}$, т.е. $\Phi (\beta ) = - \tfrac{\pi }{{{{\beta }^{3}}}}$. Результат численного вычисления данной функции представлен на рис. 3, демонстрирующего, что как при малых, так и при больших значениях аргумента функция соответствует ожиданиям.

Рис. 3.

Характерный вид функции $\Phi $. Сплошная линия показывает функцию Ф, пунктирная – формулу для поля магнитного диполя.

Рассмотрим теперь большое количество пар “протон-электрон”, связанных с инжекцией частиц со стороны центрального объекта и имеющих плотность $n$ (в простейших случаях можно считать ее постоянной, но в целом модель допускает и произвольный закон распределения). Предполагая, что диск имеет достаточно небольшую полутолщину $h$, кольцо частиц, расположенное в пределах от $R$ до $R + dR,$ создает на расстоянии $r$ от центра магнитное поле:

(6)
$dB(r) = \frac{{4\pi Inh}}{c}\Phi \left( {\frac{r}{R}} \right)dR.$
Для плотности частиц истекающей плазмы можно воспользоваться приближенным законом [26]
$n(R) = {{n}_{0}}\frac{{R_{{min}}^{2}}}{{{{R}^{2}}}},$
где ${{n}_{0}}$ связана со скоростью истечения плазмы из центра.

Учитывая (3) и предполагая, что плотность вращающейся среды меняется по закону $N(R) = N({{R}_{{min}}})\tfrac{{{{R}_{{min}}}}}{R}$, мы можем также представить зависимость времени столкновений от расстояния:

${{\tau }_{p}}(R) = {{\tau }_{p}}({{R}_{{min}}})\frac{R}{{{{R}_{{min}}}}}.$
Тогда уравнение (6) преобразуется к виду:
(7)
$\begin{gathered} dB(r) = - \frac{{4nheV{{\tau }_{p}}\Omega }}{{cR}}\Phi \left( {\frac{r}{R}} \right)dR - \\ \, - \frac{{2nh{{e}^{2}}V{{\tau }_{p}}}}{{{{m}_{p}}{{c}^{2}}R}}\Phi \left( {\frac{r}{R}} \right)B(R)dR. \\ \end{gathered} $
Проинтегрируем обе части данного равенства по диапазону ${{R}_{{min}}} < R < {{R}_{{max}}}$. Тогда

$\begin{gathered} B(r) = - \frac{{4{{n}_{0}}{{R}_{{min}}}heV{{\tau }_{p}}({{R}_{{min}}})\Omega }}{c}\int\limits_{{{R}_{{min}}}}^{{{R}_{{max}}}} \,\Phi \left( {\frac{r}{R}} \right)\frac{{dR}}{{{{R}^{2}}}} - \\ \, - \frac{{2{{n}_{0}}h{{e}^{2}}V{{\tau }_{p}}({{R}_{{min}}}){{R}_{{min}}}}}{{{{m}_{p}}{{c}^{2}}{{R}_{{max}}}}}\int\limits_{{{R}_{{min}}}}^{{{R}_{{max}}}} \,\Phi \left( {\frac{r}{R}} \right)B(R)\frac{{dR}}{{{{R}^{2}}}}. \\ \end{gathered} $

Достаточно удобно измерять расстояния в единицах ${{R}_{{max}}},$ а магнитные поля – в единицах $\tfrac{{4{{n}_{0}}{{R}_{{min}}}heV{{\tau }_{p}}({{R}_{{min}}})\Omega }}{{c{{R}_{{max}}}}}$. Тогда данное уравнение можно переписать в форме:

$B(r) = - \int\limits_{{{R}_{{min}}}}^1 \,\Phi \left( {\frac{r}{R}} \right)\frac{{dR}}{{{{R}^{2}}}} - \mu \int\limits_{{{R}_{{min}}}}^1 \,\Phi \left( {\frac{r}{R}} \right)B(R)\frac{{dR}}{{{{R}^{2}}}},$
где $\mu = \tfrac{{2{{n}_{0}}h{{e}^{2}}V{{\tau }_{p}}({{R}_{{min}}}){{R}_{{min}}}}}{{{{m}_{p}}{{c}^{2}}{{R}_{{max}}}}}$.

Для удобства введем функции

$F(r) = - \int\limits_{{{R}_{{min}}}}^1 \,\Phi \left( {\frac{r}{R}} \right)\frac{{dR}}{{{{R}^{2}}}},$
$Q(r,R) = - \frac{1}{{{{R}^{2}}}}\Phi \left( {\frac{r}{R}} \right).$
Тогда мы получим интегральное уравнение:
(8)
$B(r) = \mu \int\limits_{{{R}_{{min}}}}^1 \,Q(r,R)B(R)dR + F(r),$
которое будет описывать распределение магнитного поля в результате действия бирманновского механизма.

4. АНАЛИЗ РЕШЕНИЯ УРАВНЕНИЙ

Уравнение (8) относится к уравнениям Фредгольма второго рода [32, 33]. В случае достаточно малых $\mu $ оно может решаться с помощью стандартных методов, таких как метод простых итераций, разложение ядра и т.д. Однако надо учитывать, что в случае реальных объектов параметр $\mu $ обычно оказывается достаточно большим. Это значит, что интеграл в правой части заметно превышает то, что будет находиться в левой. Таким образом, по сути свойства уравнения скорее соответствуют уравнению Фредгольма первого рода (включая все присущие ему трудности решения), которое можно получить с помощью следующей замены:

$L(r,R) = \frac{1}{{\mu (1 - {{R}_{{min}}})}} - Q(r,R).$

В таком случае оно приводится к виду:

$\int\limits_{{{R}_{{min}}}}^1 \,L(r,R)B(R)dR = \frac{1}{\mu }F(r).$

Данное уравнение представляет собой типичный пример некорректно поставленной задачи. Для ее решения можно воспользоваться методом регуляризации Тихонова. С этой целью рассмотрим минимизацию тихоновского функционала [34], который для нашей задачи выглядит так:

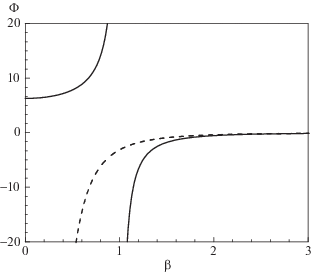
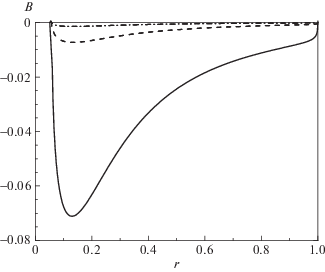
$\begin{gathered} M[B] = \int\limits_{{{R}_{{min}}}}^1 \,\mathop {\left( {\int\limits_{{{R}_{{min}}}}^1 \,L(r,R)B(R)dR - \frac{1}{\mu }F(R)} \right)}\nolimits^2 dr + \\ \, + \alpha \left( {\int\limits_{{{R}_{{min}}}}^1 \,{{B}^{2}}(R)dR + \int\limits_{{{R}_{{min}}}}^1 \,\mathop {B{\kern 1pt} '}\nolimits^2 (R)dR} \right), \\ \end{gathered} $
где $\alpha $ – так называемый параметр регуляризации. Можно показать [34], что его экстремаль достаточно хорошо приближает необходимую нам функцию $B(R)$.

Решение данной задачи при различных значениях параметров представлено на рис. 4. В данном случае мы использовали значение ${{R}_{{min}}} = 0.05$. Можно видеть, что с ростом $\mu $ решение уменьшается. Исходя из того, как вводилось выражение для $\mu $, это означает, что магнитное поле тем меньше, чем выше концентрация частиц в галактике, что можно объяснить большим сопротивлением движению частиц, инжектируемых со стороны центрального объекта и обусловливающих действие механизма Бирмана.

Рис. 4.

Зависимость магнитного поля от расстояния до центра при разных значениях параметра $\mu $: $\mu = 10$ (cплошная линия), 100 (штриховая), 500 (штрих-пунктирная).

Оценим магнитное поле, которое генерируется в случае типичной галактики. Ранее было показано, что концентрация числа протонов и электронов в истекающем веществе в единице объема пропорциональна темпу истечения. Для нее можно взять приближенное значение ${{n}_{0}} = {{10}^{2}}$ см–3. Для полутолщины диска можно взять h = $ = 500\;{\text{пк}} = 1.5 \times {{10}^{{21}}}$ см. Радиус центрального объекта примем равным ${{R}_{{min}}} = 10\;{\text{пк}} = 3 \times {{10}^{{19}}}$ см, а полный радиус галактики – ${{R}_{{max}}} = 10\;{\text{кпк}} = $ $ = 3 \times {{10}^{{22}}}$ см. Угловую скорость будем считать равной $\Omega = 5 \times {{10}^{{ - 15}}}$ с–1, а для времени столкновений около центрального объекта можно получить ${{\tau }_{p}}({{R}_{{min}}}) = 1.4 \times {{10}^{9}}$ с. Тогда для “единицы измерения” магнитного поля мы получим значение ${{B}_{0}} = 2 \times {{10}^{4}}$ Гс.

Определим теперь значение $\mu $, которое соответствует задаче. Предполагая, что ${{N}_{0}} = {{10}^{3}}$ см–3 [26], мы можем получить значение $\mu = 1.99 \times {{10}^{{23}}}$. Данное значение является исключительно большим и заметно затрудняет процесс точных вычислений. Вместе с тем можно заметить, что в таком случае для ядра интегрального оператора с исключительно высокой точностью выполнено соотношение:

$L(r,R) = - Q(r,R) = - \frac{1}{R}\Phi \left( {\frac{r}{R}} \right).$
Тогда уравнение сводится к виду:
$ - \mu \int\limits_{{{R}_{{min}}}}^1 \, - \frac{1}{R}\Phi \left( {\frac{r}{R}} \right)B(R)dR = \int\limits_{{{R}_{{min}}}}^1 \, - \frac{1}{{{{R}^{2}}}}\Phi \left( {\frac{r}{R}} \right)dR.$
Магнитное поле в таком случае можно приближенно оценить с помощью выражения:
$B = \frac{{{{B}_{0}}}}{\mu }.$
Тогда получаем $B = 1.0 \times {{10}^{{ - 19}}}$ Гс.

5. УЧЕТ ИОНИЗАЦИИ ВРАЩАЮЩЕЙСЯ СРЕДЫ

В случае высокой степени ионизации вращающейся среды (когда для плотности частиц данной среды имеем выражение $\kappa \gg n$) может быть необходимым учет влияния возникающего за счет батареи Бирмана магнитного поля на движение протонов и электронов, входящих в ее состав.

Отметим, что в таком случае протоны будут приобретать дополнительную отрицательную угловую скорость $ - \tfrac{{eB}}{{2{{m}_{p}}c}}$, а электроны – дополнительную положительную угловую скорость $\tfrac{{eB}}{{2{{m}_{e}}c}}$. Каждая из пар будет связана с током:

$I{\kern 1pt} ' = - \frac{{{{e}^{2}}B}}{{4\pi {{m}_{p}}c}} - \frac{{{{e}^{2}}B}}{{2\pi {{m}_{e}}c}} = - \frac{{{{e}^{2}}B}}{{4\pi {{m}_{e}}c}}\left( {1 + \frac{{{{m}_{e}}}}{{{{m}_{p}}}}} \right).$

С учетом того, что ${{m}_{e}} \ll {{m}_{p}},$ приближенно можно записать, что

$I{\kern 1pt} ' = - \frac{{{{e}^{2}}B}}{{4\pi {{m}_{e}}c}}.$

Подобные токи в дифференциально тонком кольце радиуса $R$ создают на расстоянии $r$ от центра магнитное поле:

$d{{B}_{{ion}}}(r) = \frac{{4\pi I'\kappa h}}{c}\Phi \left( {\frac{r}{R}} \right)dR = - \frac{{\kappa h{{e}^{2}}}}{{{{m}_{e}}{{c}^{2}}}}\Phi \left( {\frac{r}{R}} \right)B(R)dR.$

Совокупный эффект будет даваться с помощью суммы

$dB(r) = d{{B}_{{inj}}}(r) + d{{B}_{{ion}}}(r),$
где $d{{B}_{{inj}}}$ определяется формулой (7). Это означает, что
$\begin{gathered} dB(r) = - \frac{{4nheV{{\tau }_{p}}\Omega }}{{cR}}\Phi \left( {\frac{r}{R}} \right)dR - \\ \, - \frac{{2nh{{e}^{2}}V{{\tau }_{p}}}}{{{{m}_{p}}{{c}^{2}}R}}\Phi \left( {\frac{r}{R}} \right)B(R)dR - \frac{{\kappa h{{e}^{2}}}}{{{{m}_{e}}{{c}^{2}}}}\Phi \left( {\frac{r}{R}} \right)B(R)dR. \\ \end{gathered} $
Отметим, что учитывая тот факт, что $\kappa \gg n$, с большой точностью можно считать, что
(9)
$\begin{gathered} dB(r) \cong - \frac{{4nheV{{\tau }_{p}}\Omega }}{{cR}}\Phi \left( {\frac{r}{R}} \right)dR - \\ \, - \frac{{\kappa h{{e}^{2}}}}{{{{m}_{e}}{{c}^{2}}}}\Phi \left( {\frac{r}{R}} \right)B(R)dR. \\ \end{gathered} $
Поскольку количество ионов во вращающейся среде пропорционально числу частиц, мы можем считать, что оно обратно пропорционально расстоянию до центра [35, 36]:
$\kappa (R) = {{\kappa }_{0}}\frac{{{{R}_{{min}}}}}{R}.$
Тогда можно переписать (9) в форме:
(10)
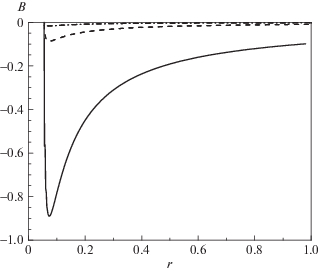
$\begin{gathered} dB(r) \cong - \frac{{4{{n}_{0}}{{R}_{{min}}}heV{{\tau }_{p}}({{R}_{{min}}})\Omega }}{{c{{R}^{2}}}}\Phi \left( {\frac{r}{R}} \right)dR - \\ \, - \frac{{\kappa {{N}_{0}}{{R}_{{min}}}h{{e}^{2}}}}{{{{m}_{e}}{{c}^{2}}R}}\Phi \left( {\frac{r}{R}} \right)B(R)dR. \\ \end{gathered} $
Данное равенство можно также привести к интегральному уравнению:
$\begin{gathered} B(r) = - \frac{{4{{n}_{0}}{{R}_{{min}}}heV{{\tau }_{p}}({{R}_{{min}}})\Omega }}{c}\int\limits_{{{R}_{{min}}}}^{{{R}_{{max}}}} \,\Phi \left( {\frac{r}{R}} \right)\frac{{dR}}{{{{R}^{2}}}} - \\ \, - \frac{{k{{N}_{0}}{{R}_{{min}}}h{{e}^{2}}}}{{{{m}_{e}}{{c}^{2}}}}\int\limits_{{{R}_{{min}}}}^{{{R}_{{max}}}} \,\Phi \left( {\frac{r}{R}} \right)B(R)\frac{{dR}}{R}. \\ \end{gathered} $
Используя те же безразмерные единицы, мы перепишем уравнение в таком виде:
(11)
$B(r) = \lambda \int\limits_{{{R}_{{min}}}}^1 \,K(r,R)B(R)dR + F(R),$
где

$K(r,R) = - \frac{1}{R}\Phi \left( {\frac{r}{R}} \right),$
$\lambda = \frac{{{{\kappa }_{0}}h{{e}^{2}}{{R}_{{min}}}}}{{{{m}_{e}}{{c}^{2}}}}.$

Используя те же подходы, мы можем получить решения для различных $\lambda $, представленные на рис. 5.

Рис. 5.

Зависимость магнитного поля от расстояния до центра в модели с учетом ионизации среды при разных значениях параметра $\lambda $: $\lambda = 10$ (cплошная линия), 100 (штриховая), 500 (штрихпунктирная).

Предполагая, что ${{\kappa }_{0}} = {{10}^{3}}$ см–3, мы получим $\lambda = 1.31 \times {{10}^{{31}}}$. В таком случае ядро интегрального оператора сводится к виду:

$L(r,R) = - K(r,R) = - \frac{1}{R}\Phi \left( {\frac{r}{R}} \right),$
а уравнение запишется так:
$ - \lambda \int\limits_{{{R}_{{min}}}}^1 \,\frac{1}{R}\Phi \left( {\frac{r}{R}} \right)B(R)dR = \int\limits_{{{R}_{{min}}}}^1 \, - \frac{1}{{{{R}^{2}}}}\Phi \left( {\frac{r}{R}} \right)dR.$
Данному уравнению очевидно удовлетворяет в безразмерных переменных решение $B(R) = - \tfrac{1}{{\lambda R}}$. В свою очередь, при переходе к стандартным единицам измерения решение для магнитного поля представляется в форме (рис. 6):
$B(r) = \frac{{{{B}_{0}}{{R}_{{max}}}}}{{\lambda r}}.$
Наибольшее значение магнитного поля будет соответствовать минимальному расстоянию до центра $r = {{R}_{{min}}}$, т.е. поле будет достигать значений порядка $B = 1.5 \times {{10}^{{ - 27}}}$ Гс.

Рис. 6.

Поведение магнитного поля при больших $\lambda $ в модели с учетом ионизации среды.

6. ЗАКЛЮЧЕНИЕ

В настоящей работе была получена модель для магнитных полей галактик на начальном этапе их эволюции. Генерация данного магнитного поля обусловлена так называемой батареей Бирмана. Показано, что заряженные частицы (протоны и электроны) достаточно быстро приобретают скорость, которая связана только с расстоянием до оси вращения объекта, что обусловливает наличие круговых токов. Они приводят к возникновению магнитного поля, которое будет слабо зависеть от времени. Его пространственную структуру можно определить, сформулировав и решив соответствующее интегральное уравнение. В зависимости от того, какова степень ионизации среды и насколько возникает необходимость учета влияния сгенерированного магнитного поля на движение частиц, величина поля может варьироваться в пределах от ${{10}^{{ - 27}}}$ Гс до ${{10}^{{ - 19}}}$ Гс.

Отметим, что в предшествующих работах были сделаны оценки, близкие к данному диапазону. Так, в классической работе Мишустина и Рузмайкина [24] для поля в протогалактике получено значение порядка ${{10}^{{ - 18..17}}}$ Гс. Гаррисоном было установлено, что магнитное поле, связанное с механизмом Бирмана, в зависимости от конкретного примера может составлять величину от ${{10}^{{ - 28}}}$ Гс до ${{10}^{{ - 26}}}$ Гс [23]. Пудритц и Силк [37] предсказывают, что магнитные поля, обусловленные батарейными эффектами, могут достигать значений порядка ${{10}^{{ - 19}}}$ Гс. Дэвис и Видроу [28] предполагают поля величиной около ${{10}^{{ - 17}}}$ Гс. Ксу и соавт. [38] получили оценки магнитных полей с использованием космологических МГД-симуляций, которые предсказывают величины полей около ${{10}^{{ - 18}}}$ Гс для раннего этапа эволюции галактики.

Отметим, что хотя разброс данных величин достаточно велик, полученное поле в любом случае будет достаточно малым. Тем не менее оно может являться источником начальных магнитных полей для механизма динамо [37]. Можно предполагать, что первоначально данное значение усиливается с помощью мелкомасштабного динамо [1]. Оценим темп роста магнитного поля за счет данного эффекта. Показатель экспоненциального роста имеет порядок величины $\gamma \sim \tfrac{l}{{v}}$, где $l$ – масштаб турбулентности, $v$ – типичная скорость ту-рбулентных движений. Предполагая, что $v \sim $ ~ 10 км/с, мы получим типичное значение γ ~ $ \sim 10$ млн. лет. Это означает, что за время около 300 млн. лет магнитное поле величины ${{10}^{{ - 19}}}$ Гс достигнет уровня равнораспределения, составляющего ${{10}^{{ - 6}}}$ Гс. В случае, если рост поля начинается с величины ${{10}^{{ - 27}}}$ Гс, то для достижения данного значения потребуется время порядка 500 млн. лет. Таким образом, к эпохе $Z \approx 3$, когда в галактиках уже генерируется крупномасштабное магнитное поле, в них уже будет присутствовать достаточно сильный мелкомасштабный компонент, который может послужить начальным условием для работы крупномасштабного динамо [1, 39]. В свою очередь, среднее магнитное поле, связанное с мелкомасштабным динамо, может являться источником генерации магнитных полей в рамках крупномасштабного динамо. Вместе с тем нельзя исключать, что в возникновении начальных полей наравне с батареей Бирмана играют роль такие механизмы, как вайбелевская неустойчивость [40] или космологические возмущения [41].

Также можно предполагать, что подобный механизм может объяснять генерацию магнитных полей в других небесных объектах, обладающих схожей геометрией. Так, ранее было показано, что характер эволюции полей в аккреционных дисках в целом схож с тем, что имеет место в галактиках [42, 43]. Поэтому вполне возможно предположить, что использованные подходы будут также актуальны и для подобных объектов.

Авторы выражают благодарность анонимному рецензенту за внимательное ознакомление с работой и высказанные замечания, которые дали возможность внести в нее ряд улучшений. Работа выполнена при частичной поддержке Министерства науки и высшего образования России (соглашение 075-15-2019-1621).

Список литературы

  1. T. Arshakian, R. Beck, M. Krause, and D. Sokoloff, Astron. and Astrophys. 494, 21 (2009).

  2. Н. Г. Бочкарев, Магнитные поля в космосе (М.: Наука, 2011).

  3. E. Fermi, Phys. Rev. 75, 1169 (1949).

  4. В. Л. Гинзбург. Распространение электромагнитных волн в плазме (М.: Наука, 1960).

  5. Я. Б. Зельдович, А. А. Рузмайкин, Д. Д. Соколов. Магнитные поля в астрофизике (Москва-Ижевск: “Регулярная и хаотическая динамика”, 2006).

  6. P. Frick, D. Sokoloff, R. Stepanov, and R. Beck, Monthly Not. Roy. Astron. Soc. 414, 2540 (2011).

  7. R. N. Manchester, Astrophys. J. 172, 43 (1973).

  8. Р. Р. Андреасян, А. Н. Макаров, Астрофизика 28, 419 (1988).

  9. J. L. Han and G. J. Qiao, Astron. and Astrophys. 288, 759 (1994).

  10. P. P. Kronberg, Nature 370, 179 (1994).

  11. А. Р. Андреасян, Р. Р. Андреасян, Г. М. Паронян, Астрофизика 59, 65 (2016).

  12. Р. Р. Андреасян, Е. А. Михайлов, А. Р. Андреасян, Астрон. журн. 97, 179 (2020).

  13. N. Oppermann, H. Junklewitz, and G. Robbers, Astron. and Astrophys. 542, 93 (2011).

  14. M. Hansen, W. Zhao, A. M. Frejsel, P. D. Naselsky, J. Kim, and O. V. Verkhodanov, Monthly Not. Roy. Astron. Soc. 426, 57 (2012).

  15. R. Beck, A. Brandenburg, D. Moss, A. Shukurov, and D. Sokoloff, Ann. Rev. Astron. Astrophys. 34, 155 (1996).

  16. M. L. Bernet, F. L. Miniati, S. J. Lilly, P. P. Kronberg, and M. Dessauges-Zavadsky, Nature 454, 302 (2008).

  17. N. Oppermann, H. Junklewitz, G. Robbers, and T. A. Ensslin, Astron. and Astrophys. 530, id. A89 (2012).

  18. Д. Д. Соколов, Успехи физ. наук 185, 643 (2015).

  19. D. Moss, Monthly Not. Roy. Astron. Soc. 275, 191 (1995).

  20. D. Moss and D. Sokoloff, Astron. Astrophys. Trans. 27, 139 (2012).

  21. А. А. Рузмайкин, Д. Д. Соколов, А. М. Шукуров, Магнитные поля галактик (М.: Наука, 1988).

  22. L. Biermann and A. Schluter, Phys. Rev. 82, 863 (1951).

  23. E. R. Harrison, Monthly Not. Roy. Astron. Soc. 147, 279 (1970).

  24. I. N. Mishustin and A. A. Ruzmaikin, Sov. J. Experim. Theoret. Phys. 34, 233 (1972).

  25. H. Lesch, A. Crusius, R. Schlickeiser, and R. Wielebinski, Astron. and Astrophys. 217, 99 (1989).

  26. Р. Р. Андреасян, Астрофизика 39, 111 (1996).

  27. E. A. Mikhailov and R. R. Andreasyan, Comm. Byurakan Astrophys. Observ. 67, 281 (2020).

  28. G. Davies and L. M. Widrow, Astrophys. J. 540, 755 (2000).

  29. Г. Альвен, К.-Г. Фельтхаммар, Космическая электродинамика (М.: Наука, 1967).

  30. Л. Э. Эльсгольц, Дифференциальные уравнения (М.: Наука, 2008).

  31. И. Е. Тамм, Основы теории электричества (М.: Физматлит, 2003).

  32. А. Б. Васильева, А. Н. Тихонов, Интегральные уравнения (М.: “Лань”, 2004).

  33. В. Т. Волков, А. Г. Ягола, Интегральные уравнения. Вариационное исчисление (М.: МГУ, 2008).

  34. А. Н. Тихонов, А. В. Гончарский, В. В. Степанов, А. Г. Ягола, Численные методы решения некорректных задач (М.: Наука, 1990).

  35. G. J. Ferland and H. Netzer, Astrophys. J. 264, 105 (1983).

  36. W. Forman, C. Jones, and W. Tucker, Astrophys. J. 293, 102 (1985).

  37. R. E. Pudritz and J. Silk, Astrophys. J. 342, 650 (1989).

  38. H. Xu, B. W. O’Shea, D. C. Collins, M. L. Norman, H. Li, and S. Li, Astrophys. J. 688, L57 (2008).

  39. L. F. S. Rodrigues, L. Chamandy, A. Shukurov, C. M. Baugh, and A. R. Taylor, Monthly Not. Roy. Astron. Soc. 483, 2424 (2019).

  40. M. V. Medvedev, L. O. Silva, M. Fiore, R. A. Fonseca, and W. B. Mori, J. Korean Astron. Soc. 37, 533 (2004).

  41. K. Takahashi, K. Ichiki, H. Ohno, H. Hanayama, and N. Sugiyama, Astron. Nachricht. 327, 410 (2006).

  42. D. Moss, D. Sokoloff, and V. Suleimanov, Astron. and Astrophys. 588, id. A18 (2016).

  43. D. Boneva, E. Mikhailov, and M. Pashentseva, in Fifteenth Intern. Conf. “Space, Ecology, Safety” (SES-2019), held 6–8 November 2019 (Sofia, Bulgaria: Space Research and Technology Institute Bulgarian Academy of Sciences, 2019), p. 57 (2019).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал