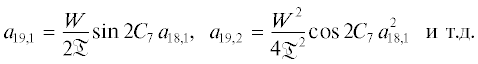1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 98, № 12, 2021

Астрономический журнал, 2021, T. 98, № 12, стр. 1030-1042

Движение в центральном поле при возмущающем ускорении, изменяющемся по закону обратных квадратов, в системе отсчета, связанной с вектором скорости

Т. Н. Санникова 1, *

1 Крымская астрофизическая обсерватория РАН
Научный, Россия

* E-mail: tnsannikova@craocrimea.ru

Поступила в редакцию 25.06.2021
После доработки 13.08.2021
Принята к публикации 31.08.2021

Полный текст (PDF)

Аннотация

Рассмотрена задача, в которой точка нулевой массы двигается под действием притяжения к центральному телу $\mathcal{S}$ и возмущающего ускорения ${\mathbf{P}}{\kern 1pt} '$, обратно пропорционального квадрату расстояния до $\mathcal{S}$, так что ${\mathbf{P}}{\kern 1pt} ' = {\mathbf{P}}{\text{/}}{{r}^{2}}$, модуль ${\mathbf{P}}{\kern 1pt} '$ мал по сравнению с основным ускорением, вызванным притяжением центрального тела, а компоненты вектора ${\mathbf{P}}(\mathfrak{T},\mathfrak{N},W)$ – постоянны в системе отсчета с началом в $\mathcal{S}$ и осями, направленными по вектору скорости, нормали к нему в плоскости оскулирующей орбиты и бинормали. Для этой задачи ранее нами получены уравнения движения в средних элементах в первом приближении по малому параметру, роль которого играет отношение возмущающего ускорения к основному. Предложено решение осредненных по средней аномалии уравнений. Система решена для круговой орбиты и в случаях, когда хотя бы один из компонентов вектора возмущающего ускорения равен нулю. Для круговой орбиты и при $\mathfrak{T} = 0$ решение представлено в виде зависимостей элементов орбиты от времени и содержит элементарные функции либо полные эллиптические интегралы. Если тангенциальный компонент возмущающего ускорения не равен нулю, время и элементы орбиты представлены функциями эксцентриситета. В этих случаях система проинтегрирована в квадратурах, приводящих к неэлементарным функциям, однако все они выражены рядами по степеням эксцентриситета $e$, сходящимися при $e < 1$. Таким образом, при $\mathfrak{T} \ne 0$ получено решение в виде рядов.

Ключевые слова: орбитальная система отсчета, вектор скорости, уравнения движения типа Эйлера, осредненные уравнения движения, аналитическое решение, полные эллиптические интегралы, разложение в ряд, тангенциальное ускорение, эффект Ярковского

1. ВВЕДЕНИЕ

Рассмотрим движение точки нулевой массы $\mathcal{A}$ (например, астероида) под действием притяжения к центральному телу $\mathcal{S}$ (например, к Солнцу) и возмущающего ускорения ${\mathbf{P}}{\kern 1pt} '$, обратно пропорционального квадрату расстояния до $\mathcal{S}$, т.е. ${\mathbf{P}}{\kern 1pt} ' = {\mathbf{P}}{\text{/}}{{r}^{2}}$. Пусть возмущающее ускорение ${\mathbf{P}}{\kern 1pt} '$ малó по сравнению с основным ускорением ${{\varkappa }^{2}}{\text{/}}{{r}^{2}}$, вызванным притяжением центрального тела:

(1)
$max\frac{{{\text{|}}{\mathbf{P}}{\kern 1pt} '{\text{|}}}}{{{{\varkappa }^{2}}{{r}^{{ - 2}}}}} = max\frac{{{\text{|}}{\mathbf{P}}{\kern 1pt} {\text{|}}}}{{{{\varkappa }^{2}}}} = \mu \ll 1.$
Здесь ${\mathbf{r}} = \mathcal{S}\mathcal{A}$, $r = {\text{|}}{\mathbf{r}}{\kern 1pt} {\text{|}}$, ${{\varkappa }^{2}}$ – произведение постоянной тяготения на массу $\mathcal{S}$, $\mu $ – малый параметр.

Рассматриваемая модель может найти применение при исследовании движения небесного тела с учетом эффекта Ярковского [1], так как в данном случае возмущающее ускорение обратно пропорционально квадрату расстояния от Солнца, а также является малым. Так, при $r = 1$ а. е. типичное значение трансверсальной составляющей ускорения, обязанного эффекту Ярковского, для астероидов, сближающихся с Землей, диаметром менее 1 км есть ${{10}^{{ - 15}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 13}}}\;{\text{а}}{\text{.е}}{\text{./су}}{{{\text{т}}}^{2}}$ [2]. Таким образом, согласно (1) величина $\mu < {{10}^{{ - 9}}} \ll 1$, следовательно, ускорение Ярковского отвечает нашему требованию. Также этой модельной задаче может удовлетворять движение космического аппарата или фрагмента космического мусора под влиянием светового давления, если выполняется условие (1). Разумеется, определение компонентов вектора ${\mathbf{P}}$ требует знания параметров вращения и теплофизических характеристик тела в первом случае, ориентации космического аппарата относительно Солнца, а также формы и свойств его поверхности во втором.

2. УРАВНЕНИЯ ДВИЖЕНИЯ

Введем координатную систему $\mathcal{O}$ с началом в $\mathcal{S}$ и осями, направленными по вектору скорости, главной нормали к оскулирующей орбите и бинормали. Предположим, что компоненты $\mathfrak{T},\;\mathfrak{N},\;W$ вектора ${\mathbf{P}}$ в системе $\mathcal{O}$ являются постоянными и малыми величинами.

В качестве переменных выберем оскулирующие элементы $n,\;e,\;i,\;\Omega ,\;\omega ,\;M$ – среднее движение, эксцентриситет, наклон, долготу восходящего узла, аргумент перицентра, среднюю аномалию. Первые пять из них образуют вектор медленных переменных ${\mathbf{x}} = ({{x}_{1}}, \ldots ,{{x}_{5}})$, а последняя – быструю переменную $y$. Уравнения движения типа Эйлера [3] имеют форму

(2)
$\begin{array}{*{20}{c}} {{\mathbf{\dot {x}}} = \mu {\mathbf{f}}({\mathbf{x}},y),} \\ {\dot {y} = {{x}_{1}} + \mu g({\mathbf{x}},y),} \end{array}$
с малыми (порядка $\mu $) правыми частями, различаясь лишь видом функций ${\mathbf{f}} = ({{f}_{1}}, \ldots ,{{f}_{5}})$ и $g$. В выбранной системе отсчета [4]
$\begin{gathered} {{f}_{1}} = - \frac{{3{{n}^{2}}}}{\eta }\frac{{{{a}^{2}}\vartheta }}{{{{r}^{2}}}}\frac{\mathfrak{T}}{{{{\varkappa }^{2}}}}, \\ {{f}_{2}} = 2n\eta \frac{{{{a}^{2}}(e + cos\theta )}}{{{{r}^{2}}\vartheta }}\frac{\mathfrak{T}}{{{{\varkappa }^{2}}}} - \eta n\frac{{asin\theta }}{{r\vartheta }}\frac{\mathfrak{N}}{{{{\varkappa }^{2}}}}, \\ \end{gathered} $
(3)
$\begin{gathered} {{f}_{3}} = \frac{n}{\eta }\frac{{acosw}}{r}\frac{W}{{{{\varkappa }^{2}}}}, \\ {{f}_{4}} = \frac{n}{{\eta sini}}\frac{{asinw}}{r}\frac{W}{{{{\varkappa }^{2}}}}, \\ {{f}_{5}} = \frac{{2n\eta }}{e}\frac{{{{a}^{2}}sin\theta }}{{{{r}^{2}}\vartheta }}\frac{\mathfrak{T}}{{{{\varkappa }^{2}}}} + \\ + \;\frac{n}{{e\eta }}\frac{{a[2e + (1 + {{e}^{2}})cos\theta ]}}{{r\vartheta }}\frac{\mathfrak{N}}{{{{\varkappa }^{2}}}} - cosi{{f}_{4}}, \\ \end{gathered} $
$\begin{gathered} g = - \frac{n}{e}\frac{{a[2sin\theta (1 + {{e}^{2}} + ecos\theta )]}}{{r\vartheta }}\frac{\mathfrak{T}}{{{{\varkappa }^{2}}}} - \\ - \;\frac{{n{{\eta }^{2}}}}{e}\frac{{acos\theta }}{{r\vartheta }}\frac{\mathfrak{N}}{{{{\varkappa }^{2}}}}. \\ \end{gathered} $
Здесь и ниже $\vartheta (\theta ,e) = \sqrt {1 + {{e}^{2}} + 2ecos\theta } $, $a = $ $ = {{\varkappa }^{{2/3}}}{{n}^{{ - 2/3}}}$ – большая полуось, $\eta = \sqrt {1 - {{e}^{2}}} $, $r = $ $ = a{{\eta }^{2}}{\text{/}}(1 + ecos\theta )$, $\theta $ – истинная аномалия, $w = $ $ = \omega + \theta $ – аргумент широты. Безразмерные постоянные $\mathfrak{T}{\text{/}}{{\varkappa }^{2}}$, $\mathfrak{N}{\text{/}}{{\varkappa }^{2}}$, $W{\text{/}}{{\varkappa }^{2}}$ в правых частях (3) приняты в качестве малого параметра $\mu $ согласно (1).

После близкой к тождественной замены оскулирующих элементов (${\mathbf{x}},y$) средними (${\mathbf{X}},Y$):

$\begin{gathered} {\mathbf{x}} = {\mathbf{X}} + \mu {\mathbf{u}}({\mathbf{X}},Y), \\ y = Y + \mu {v}({\mathbf{X}},Y), \\ \end{gathered} $
в первом порядке по $\mu $ система (2) примет вид [5]:
$\begin{gathered} {\mathbf{\dot {X}}} = \mu {\mathbf{F}}({\mathbf{X}}), \\ \dot {Y} = {{X}_{1}} + \mu G({\mathbf{X}}), \\ \end{gathered} $
где согласно методу осреднения [5] за ${\mathbf{F}},\;G$ следует взять средние значения функций ${\mathbf{f}},g$ по быстрой угловой переменной:
(4)
$\begin{gathered} {\mathbf{F}}({\mathbf{X}})\;\mathop = \limits^{{\text{def}}} \;\frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi \,{\mathbf{f}}({\mathbf{X}},Y)dY, \\ G({\mathbf{X}})\;\mathop = \limits^{{\text{def}}} \;\frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi \,g({\mathbf{X}},Y)dY, \\ \end{gathered} $
что устранит из уравнений движения в средних элементах зависимость от $Y$. Функции ${\mathbf{f}},g$ в (3) выражены явно через истинную аномалию $\theta $. При необходимости их легко выразить через эксцентрическую аномалию $E$. Поэтому интегралы (4) вычисляются переходом к $\theta $ или $E$:
$dY = dM = \frac{{{{r}^{2}}}}{{{{a}^{2}}\eta }}d\theta = \frac{r}{a}dE,$
при этом пределы интегрирования ($ - \pi ,\pi $) не меняются. Подробнее о процедуре осреднения см. в [4].

Функции замены переменных ${\mathbf{u}} = ({{u}_{1}}, \ldots ,{{u}_{5}}),{v}$ периодичны по $Y$ и обладают нулевым средним, их выражения приведены в [4], там же получены уравнения движения в средних элементах в первом порядке малости:

$\begin{gathered} \dot {n} = - \frac{{6{{n}^{2}}}}{{\pi {{\varkappa }^{2}}{{\eta }^{2}}}}[2{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]\mathfrak{T}, \\ \dot {e} = \frac{{4n}}{{\pi {{\varkappa }^{2}}e}}[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]\mathfrak{T}, \\ \end{gathered} $
(5)
$\begin{gathered} \mathop \imath \limits^ \bullet \; = - \frac{{necos\omega }}{{{{\varkappa }^{2}}\eta (1 + \eta )}}W, \\ \dot {\Omega } = - \frac{{nesin\omega }}{{{{\varkappa }^{2}}\eta (1 + \eta )sini}}W, \\ \end{gathered} $
$\begin{gathered} \dot {\omega } = \frac{{2n}}{{\pi {{\varkappa }^{2}}}}{\mathbf{K}}(e)\mathfrak{N} + \frac{{nesin\omega \operatorname{ctg} i}}{{{{\varkappa }^{2}}\eta (1 + \eta )}}W, \\ \dot {M} = n + \frac{{2n\eta }}{{\pi {{\varkappa }^{2}}}}{\mathbf{K}}(e)\mathfrak{N}. \\ \end{gathered} $
Здесь мы использовали те же обозначения для средних элементов, что и ранее для оскулирующих, точкой (для $i$ – жирной точкой) обозначили производную по времени $t$, а также применили стандартные обозначения для полных эллиптических интегралов в нормальной тригонометрической форме [6], см. Приложение. Там же выведены степенные ряды:
$\dot {n} = - \frac{{3{{n}^{2}}}}{{{{\varkappa }^{2}}}}\mathfrak{T}\left( {1 + \sum {{{a}_{{10,k}}}{{e}^{{2k}}}} } \right),$
$\dot {e}\;\mathop = \limits^{\text{*}} \;\frac{n}{{{{\varkappa }^{2}}}}\mathfrak{T}\left( {e + \sum {{{a}_{{6k}}}{{e}^{{2k + 1}}}} } \right),$
$\mathop \imath \limits^ \bullet \; = - \frac{{ncos\omega }}{{{{\varkappa }^{2}}}}W\left( {\frac{e}{2} + \sum {{{a}_{{5k}}}{{e}^{{2k + 1}}}} } \right),$
(6)
$\dot {\Omega } = - \frac{{nsin\omega }}{{{{\varkappa }^{2}}sini}}W\left( {\frac{e}{2} + \sum {{{a}_{{5k}}}{{e}^{{2k + 1}}}} } \right),$
$\dot {\omega } = \frac{n}{{{{\varkappa }^{2}}}}\mathfrak{N}\left( {1 + \sum {{a}_{{3k}}}{{e}^{{2k}}}} \right) + $
$ + \;\frac{{nsin\omega \operatorname{ctg} i}}{{{{\varkappa }^{2}}}}W\left( {\frac{e}{2} + \sum {{{a}_{{5k}}}{{e}^{{2k + 1}}}} } \right),$
$\dot {M}\;\mathop = \limits^{\text{*}} \;n + \frac{n}{{{{\varkappa }^{2}}}}\mathfrak{N}\left( {1 - \sum {{{a}_{{9,k}}}{{e}^{{2k}}}} } \right).$
Если у знака суммы не указаны индекс и границы, то осуществляется суммирование по $k$ от 1 до $\infty $. Все используемые нами ряды по степеням эксцентриситета имеют радиус сходимости, равный единице. Случаи сходимости ряда при $e = 1$ отмечены звездочкой над знаком равенства.

Перейдем к решению уравнений (5). Алгоритм их решения аналогичен построенному нами ранее в [7] для задачи, в которой постоянными являются компоненты вектора ${\mathbf{P}}{\kern 1pt} '$ в системе $\mathcal{O}$. Искомыми величинами являются зависимости элементов орбиты от времени. Далее рассмотрены различные частные случаи системы (5) и получено их приближенное решение в средних элементах, позволяющее выявить вековые эффекты возмущенного движения и исследовать долгосрочную эволюцию орбиты объекта. В некоторых частных случаях мы ограничились ссылками на [8, 9], так как системы уравнений оказались подобными рассмотренным в этих статьях. Как и в [7], система решена во всех случаях, когда хотя бы один из компонентов вектора возмущающего ускорения равен нулю. Поскольку иногда решение содержит особенности при нулевом эксцентриситете, отдельно исследована эволюция круговой орбиты. Для круговой орбиты и в случаях $\mathfrak{T} = 0$, решение представлено в виде зависимостей элементов орбиты от времени и содержит либо элементарные функции, либо полные эллиптические интегралы. Задача более сложна, если тангенциальный компонент возмущающего ускорения не равен нулю. В этих случаях совершен переход к дифференцированию по эксцентриситету, как новой независимой переменной, поэтому в решении время и остальные элементы орбиты представлены функциями эксцентриситета. Кроме того, решение содержит интегралы от специальных функций, однако все они выражены рядами по степеням эксцентриситета $e$, сходящимися при $e < 1$. Таким образом, при $\mathfrak{T} \ne 0$ приведены как замкнутые выражения, так и их разложения в ряд. Также с помощью рядов установлены важные свойства исследуемых функций.

Направление ускорения Ярковского зависит от скорости вращения астероида, ориентации оси его вращения относительно орбитальной плоскости и теплофизических свойств поверхности [10], а направление возмущающего ускорения, возникающего в результате воздействия светового давления на космический аппарат, зависит от материала и ориентации относительно Солнца светоотражающей поверхности. Таким образом, поскольку в реальных задачах направление возмущающего ускорения может быть произвольным, все частные решения представляют практический интерес. К сожалению, в общем случае нам не удалось получить полное решение, но и здесь рассмотренные частные случаи помогут исследовать поведение отдельных элементов, а нерешенная часть задачи сведена к системе двух дифференциальных уравнений первого порядка, и указаны методы их решения.

Значения переменных в начальную эпоху $t = 0$ отмечены индексом $0$.

3. ЭВОЛЮЦИЯ КРУГОВЫХ ОРБИТ

Пусть ${{e}_{0}} = 0$. Для круговой орбиты средняя аномалия и аргумент перицентра теряют смысл. Угловое положение определяется единственной переменной – средней долготой $\lambda = \Omega + \omega + M$. При $e = 0$ с учетом

${\mathbf{K}}(0) = \pi {\text{/}}2,\quad {\mathbf{E}}(0) = \pi {\text{/}}2,$
правая часть уравнения для эксцентриситета в (5) содержит неопределенность вида $0:0$, поэтому обратимся ко второму уравнению (6), из которого получим $\dot {e} = 0$.

Остальные уравнения (5) значительно упростятся:

(7)
$\dot {n} = - \frac{{3{{n}^{2}}}}{{{{\varkappa }^{2}}}}\mathfrak{T},\quad \mathop \imath \limits^ \bullet \; = 0,\quad \dot {\Omega } = 0,\quad \dot {\lambda } = n + \frac{{2n}}{{{{\varkappa }^{2}}}}\mathfrak{N}.$
Отсюда
$e = 0,\quad i = {{i}_{0}},\quad \Omega = {{\Omega }_{0}}.$
Если $\mathfrak{T} = 0$, то $n,a = {\text{const}}$,
$\lambda = {{\lambda }_{0}} + \left( {1 + \frac{{2\mathfrak{N}}}{{{{\varkappa }^{2}}}}} \right){{n}_{0}}t.$
Область определения решения – вся временная ось ($ - \infty < t < \infty $).

Пусть $\mathfrak{T} \ne 0$. В первом уравнении (7) переменные разделятся:

$\frac{{dn}}{{{{n}^{2}}}} = - \frac{{3\mathfrak{T}}}{{{{\varkappa }^{2}}}}dt.$
Интегрируя, получим
$\frac{1}{n} - \frac{1}{{{{n}_{0}}}} = \frac{{3\mathfrak{T}}}{{{{\varkappa }^{2}}}}t,$
так что
(8)
$n = {{n}_{0}}\mathop {\left( {1 + \frac{t}{{{{t}_{1}}}}} \right)}\nolimits^{ - 1} ,\quad a = {{a}_{0}}\mathop {\left( {1 + \frac{t}{{{{t}_{1}}}}} \right)}\nolimits^{2/3} $
при
${{t}_{1}} = \frac{{{{\varkappa }^{2}}}}{{3\mathfrak{T}{{n}_{0}}}}.$
Перейдем ко второму уравнению (7):
$\frac{{d\lambda }}{{dt}} = \left( {1 + \frac{{2\mathfrak{N}}}{{{{\varkappa }^{2}}}}} \right)\frac{{{{n}_{0}}{{t}_{1}}}}{{t + {{t}_{1}}}},$
откуда

(9)
$\lambda = {{\lambda }_{0}} + {{n}_{0}}{{t}_{1}}\left( {1 + \frac{{2\mathfrak{N}}}{{{{\varkappa }^{2}}}}} \right)ln\left( {1 + \frac{t}{{{{t}_{1}}}}} \right).$

Как и ожидалось, результаты этого параграфа совпали с соответствующими результатами [8, § 2], поскольку для круговых орбит триедр ($ - \mathfrak{N},\mathfrak{T},W$) идентичен триедру ($S,T,W$) из [8]. Поведение круговых орбит подробно описано в [8], здесь только укажем область определения $t \in ({{t}_{*}},t{\kern 1pt} *)$ решения (8), (9), которую найдем из обращения знаменателя первого уравнения (8) в нуль при $t = - {{t}_{1}}$. При $\mathfrak{T} > 0$ $({{t}_{1}} > 0)$ получим ${{t}_{*}} = - {{t}_{1}}$, $t{\kern 1pt} * = \infty $, при $\mathfrak{T} < 0$ $({{t}_{1}} < 0)$: ${{t}_{*}} = - \infty $, $t{\kern 1pt} * = - {{t}_{1}}$.

Перейдем к некруговым орбитам, т.е. в дальнейшем положим $0 < {{e}_{0}} < 1$.

4. ЭВОЛЮЦИЯ СРЕДНЕГО ДВИЖЕНИЯ И ЭКСЦЕНТРИСИТЕТА

Первые два уравнения (5) не зависят от остальных, поэтому рассмотрим их отдельно:

(10)
$\begin{array}{*{20}{c}} {\dot {n} = - \frac{{6{{n}^{2}}}}{{\pi {{\varkappa }^{2}}{{\eta }^{2}}}}[2{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]\mathfrak{T},} \\ {\dot {e} = \frac{{4n}}{{\pi {{\varkappa }^{2}}e}}[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]\mathfrak{T}.} \end{array}$
Если $\mathfrak{T} = 0$, то $n,e = {\text{const}}$.

Пусть $\mathfrak{T} \ne 0$. Разделив первое уравнение (10) на второе, получим уравнение с разделяющимися переменными

$\begin{gathered} \frac{{dn}}{n} = - \frac{{3e}}{{2{{\eta }^{2}}}}\left[ {1 + \frac{{{\mathbf{E}}(e)}}{{{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)}}} \right]de = \\ \, = - \frac{{3ede}}{{{{\eta }^{2}}}} - \frac{{3e{\mathbf{K}}(e)de}}{{2({\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e))}} \\ \end{gathered} $
и проинтегрируем
$ln\frac{n}{{{{n}_{0}}}} = 3ln\frac{\eta }{{{{\eta }_{0}}}} - \int\limits_{{{e}_{0}}}^e {\frac{{3e{\mathbf{K}}(e)de}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}} .$
Таким образом,
(11)
$\begin{array}{*{20}{c}} {n = {{n}_{0}}exp\left[ {ln\mathop {\left( {\frac{\eta }{{{{\eta }_{0}}}}} \right)}\nolimits^3 - \int\limits_{{{e}_{0}}}^e \,\frac{{3e{\mathbf{K}}(e)de}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}} \right] = } \\ {\, = {{n}_{0}}\mathop {\left( {\frac{\eta }{{{{\eta }_{0}}}}} \right)}\nolimits^3 exp\left[ { - \int\limits_{{{e}_{0}}}^e \,\frac{{3e{\mathbf{K}}(e)de}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}} \right].} \end{array}$
Здесь и ниже $e$ является и переменной интегрирования, и верхним пределом интегрирования как некоторое текущее значение эксцентриситета, что не создает путаницы.

Представим (11) в виде ряда с помощью приведенной в Приложении формулы (А11):

(12)
$n = {{n}_{0}}\mathop {\left( {\frac{\eta }{{{{\eta }_{0}}}}} \right)}\nolimits^3 exp(3{{C}_{1}})\mathop {\left( {\frac{{{{e}_{0}}}}{e}} \right)}\nolimits^3 \left( {1 - \sum {A_{k}^{3}{{e}^{{2k}}}} } \right),$
где зависящая от ${{e}_{0}}$ постоянная ${{C}_{1}}$ определена рядом (А9). Все коэффициенты $A_{k}^{3}$ положительны.

Для определения зависимости переменных от времени подставим (11) в уравнение (10) для $\dot {e}$:

(13)
$\begin{gathered} \frac{{\pi ede}}{{2{{\eta }^{3}}[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}} \times \\ \times \;exp\int\limits_{{{e}_{0}}}^e \,\frac{{3e{\mathbf{K}}(e)de}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}} = \frac{{2{{n}_{0}}\mathfrak{T}}}{{\eta _{0}^{3}{{\varkappa }^{2}}}}dt, \\ \end{gathered} $
откуда
(14)
$\begin{gathered} t = \frac{{\pi \eta _{0}^{3}{{\varkappa }^{2}}}}{{4{{n}_{0}}\mathfrak{T}}}\int\limits_{{{e}_{0}}}^e \,\frac{e}{{{{\eta }^{3}}[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}} \times \\ \times \;\left( {exp\int\limits_{{{e}_{0}}}^e \,\frac{{3x{\mathbf{K}}(x)dx}}{{2[{\mathbf{E}}(x) - (1 - {{x}^{2}}){\mathbf{K}}(x)]}}} \right)de, \\ \end{gathered} $
т.е. мы получили кинематическое уравнение (по терминологии теоретической механики), в котором эксцентриситет является независимой переменной, а время представлено функцией эксцентриситета. Подынтегральное выражение в круглых скобках в (14) мы записали как функцию от $x$, чтобы подчеркнуть, что результат интегрирования будет зависеть от переменной интегрирования $e$ внешнего интеграла.

Разложим (14) в ряд. С учетом (11) и (А10)

${{n}^{{ - 1}}} = n_{0}^{{ - 1}}\mathop {\left( {\frac{{{{\eta }_{0}}}}{\eta }} \right)}\nolimits^3 exp( - 3{{C}_{1}})\mathop {\left( {\frac{e}{{{{e}_{0}}}}} \right)}\nolimits^3 \left( {1 + \sum {a_{k}^{3}{{e}^{{2k}}}} } \right),$
где ${{C}_{1}}$ по-прежнему определено формулой (А9), коэффициенты $a_{k}^{3}$ положительны, и с помощью формул (А3) из раздела А.1 Приложения вместо (13) получим
$\frac{{{{e}^{2}}\left( {1 + \sum {a_{k}^{3}{{e}^{{2k}}}} } \right)}}{{{{\eta }^{3}}\left( {1 + \sum {{{a}_{{6k}}}{{e}^{{2k}}}} } \right)}}de = \frac{{{{n}_{0}}e_{0}^{3}}}{{\eta _{0}^{3}}}exp(3{{C}_{1}})\frac{\mathfrak{T}}{{{{\varkappa }^{2}}}}dt.$
Используя биномиальный ряд, найдем
(15)
$\begin{gathered} {{(1 - {{e}^{2}})}^{{ - 3/2}}} = 1 + \sum {{{a}_{{13,k}}}{{e}^{{2k}}}} , \\ {\text{где}}\quad {{a}_{{13,k}}} = \frac{{(2k + 1)!!}}{{(2k)!!}}, \\ \end{gathered} $
все ${{a}_{{13,k}}}$ положительны. Ряд (15) расходится при $e = 1$.

Полагая

$\begin{gathered} \frac{{{{e}^{2}}\left( {1 + \sum {{{a}_{{13,k}}}{{e}^{{2k}}}} } \right)\left( {1 + \sum {a_{k}^{3}{{e}^{{2k}}}} } \right)}}{{1 + \sum {{{a}_{{6k}}}{{e}^{{2k}}}} }} = \\ \, = {{e}^{2}}\left( {1 + \sum {{{a}_{{14,k}}}{{e}^{{2k}}}} } \right), \\ \end{gathered} $
(16)
${{a}_{{14,k}}} = {{a}_{{13,k}}} - {{a}_{{6k}}} + a_{k}^{3} + $
$\begin{gathered} + \;\sum\limits_{m = 1}^{k - 1} \,{{a}_{{13,m}}}a_{{k - m}}^{3} - \sum\limits_{m = 1}^{k - 1} \,{{a}_{{14,m}}}{{a}_{{6,k - m}}}, \\ {\text{где}}\quad {{a}_{{14,1}}} = \frac{{25}}{{16}}, \\ \end{gathered} $
вместо (14) получим кинематическое уравнение в виде ряда:
(17)
$\nu t = \frac{{{{e}^{3}}}}{3} + \sum {\frac{{{{a}_{{14,k}}}}}{{2k + 3}}} \,{{e}^{{2k + 3}}} - {{C}_{3}},$
где
$\nu = \frac{{{{n}_{0}}e_{0}^{3}}}{{\eta _{0}^{3}}}exp(3{{C}_{1}})\frac{\mathfrak{T}}{{{{\varkappa }^{2}}}},\quad {{C}_{3}} = \frac{{e_{0}^{3}}}{3} + \sum {\frac{{{{a}_{{14,k}}}}}{{2k + 3}}e_{0}^{{2k + 3}}} .$
Поскольку слева в (16) числитель и знаменатель представлены рядами с положительными коэффициентами, то ${{a}_{{14,k}}} > 0$, ряд (17) сходится при $e < 1$.

При заданном $e$ кинематическое уравнение (14) или (17) позволит получить время, за которое произойдет изменение эксцентриситета $de = e - {{e}_{0}}$. Покажем, что каждому $t \in ({{t}_{*}},t{\kern 1pt} *)$ соответствует единственное значение $e$. Так как коэффициенты ${{a}_{{14,k}}}$ положительны, то правая часть (17) монотонно возрастает в промежутке $e \in [0,1)$, следовательно, существует обратная функция. При $e = 0$ правая часть (17) равна $ - {{C}_{3}}$. При $e \to 1$ правая часть (14) стремится к бесконечности согласно (А14). Таким образом, если $\mathfrak{T} > 0$, $\nu > 0$, при росте $e$ от $0$ до $1$ левая часть (17) возрастает от ${{t}_{*}} = - {{C}_{3}}{\text{/}}\nu $ до $t{\kern 1pt} * = \infty $, и каждому $t$ отвечает единственное решение $e$. При $t \to {{t}_{*}}$ получим $e \to 0$, и согласно (12) $n \to \infty $, $a \to 0$, т.е. при движении в прошлое тело за конечное время упадет по спирали на $\mathcal{S}$. При $t \to t{\kern 1pt} *$ получим $e \to 1$, и согласно (12) $n \to 0$ и $a \to \infty $, т.е. при движении в будущее тело уйдет на бесконечность. Поскольку метод осреднения неприменим при больших $t$, на практике следует ограничиться значениями $t < {{t}_{*}}{\text{/}}2$.

При $\mathfrak{T} < 0$ решение определено при ${{t}_{*}} = - \infty $, $t{\kern 1pt} * = {{C}_{3}}{\text{/}}\nu $. В орбитальной эволюции прошлое и будущее поменяются местами.

Замечание. Так как при $e > 0.9$ ряды сходятся медленно, рекомендуем использовать кинематическое уравнение (14), вычисляя интегралы численными методами. Для упрощения задачи можно использовать комбинированное выражение

$\begin{gathered} t = \frac{{\pi \eta _{0}^{3}{{\varkappa }^{2}}}}{{4{{n}_{0}}\mathfrak{T}}}\int\limits_{{{e}_{0}}}^e \,\frac{e}{{{{\eta }^{3}}[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}} \times \\ \times \;\left( {exp\int\limits_{{{e}_{0}}}^e \,3x\left( {\frac{1}{{{{x}^{2}}}} + \frac{1}{8} + \sum\limits_{k = 1}^{200} \,a_{{11}}^{k}{{x}^{{2k}}}} \right)dx} \right)de, \\ \end{gathered} $
которое мы получили, подставив (А7) в (14). При эксцентриситетах, близких к нулю, лучше использовать решение для круговых орбит (см. раздел 3).

5. ЭВОЛЮЦИЯ НЕКРУГОВЫХ ОРБИТ ПРИ $\mathfrak{T} \ne 0$, $\mathfrak{N} = W = 0$

Если $\mathfrak{N} = W = 0$, то $i,\;\Omega ,\;\omega = {\text{const}}$. С учетом результатов раздела 4 решим последнее уравнение (5), которое примет вид

(18)
$\dot {M} = n.$
Представим $M$ как функцию от $e$, разделив (18) на второе уравнение (10):
(19)
$\frac{{dM}}{{de}} = \frac{{\pi {{\varkappa }^{2}}e}}{{4[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]\mathfrak{T}}}.$
Отсюда

(20)
$M = {{M}_{0}} + \frac{{\pi {{\varkappa }^{2}}}}{{4\mathfrak{T}}}\int\limits_{{{e}_{0}}}^e \,\frac{e}{{{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)}}de.$

Перейдем к представлению в виде ряда. Вместо (19) с помощью (А3) получим

$\frac{{dM}}{{de}} = \frac{{{{\varkappa }^{2}}}}{{\mathfrak{T}e\left( {1 + \sum {{{a}_{{6k}}}{{e}^{{2k}}}} } \right)}} = \frac{{{{\varkappa }^{2}}}}{{\mathfrak{T}e}}\left( {1 - \sum {{{a}_{{15,k}}}{{e}^{{2k}}}} } \right),$
где
${{a}_{{15,k}}} = {{a}_{{6k}}} - \sum\limits_{m = 1}^{k - 1} \,{{a}_{{6m}}}{{a}_{{15,k - m}}},\quad {{a}_{{15,1}}} = \frac{1}{8}.$
Отсюда

(21)
$\begin{gathered} M = {{M}_{0}} + \frac{{{{\varkappa }^{2}}}}{\mathfrak{T}}\left( {ln\frac{e}{{{{e}_{0}}}} - \sum {\frac{{{{a}_{{15,k}}}}}{{2k}}{{e}^{{2k}}}} + {{C}_{4}}} \right), \\ {{C}_{4}} = \sum {\frac{{{{a}_{{15,k}}}}}{{2k}}e_{0}^{{2k}}} . \\ \end{gathered} $

Интеграл в правой части (20) при $e \to 1$, $\eta \to 0$ в соответствии с (А15) стремится к $ - \eta _{0}^{2}{\text{/}}2$, что по модулю меньше единицы. Поэтому ряд в (21) сходится при $e = 1$.

В выражениях (20), (21) средняя аномалия представлена как функция эксцентриситета. Зависимость $M$ от времени установлена посредством кинематических уравнений (14) или (17). Поэтому область определения в данном случае совпадет с найденной в разделе 4.

Пусть $\mathfrak{T} > 0$. Тогда с ростом времени до $t{\kern 1pt} *$ эксцентриситет увеличивается до 1, $M$ возрастает до $M{\kern 1pt} * = {{M}_{0}} - \tfrac{{{{\varkappa }^{2}}}}{\mathfrak{T}}\left( {ln{{e}_{0}} + \sum {\tfrac{{{{a}_{{15,k}}}}}{{2k}}} - {{C}_{4}}} \right)$. При $t \to {{t}_{*}}$ эксцентриситет уменьшается до нуля, $M$ убывает до ${{M}_{*}} = - \infty $. При $\mathfrak{T} < 0$ прошлое и будущее поменяются местами.

6. ЭВОЛЮЦИЯ НЕКРУГОВЫХ ОРБИТ ПРИ $\mathfrak{N} \ne 0$, $\mathfrak{T} = W = 0$

Если $\mathfrak{T} = W = 0$, то $\dot {n} = \dot {e} = \mathop \imath \limits^ \bullet \; = \dot {\Omega } = 0$, n, a, e, i, $\Omega $ $ = {\text{const}}$, $\dot {\omega },\dot {M} = {\text{const}}$. Отсюда

$\begin{array}{*{20}{c}} {\omega = {{\omega }_{0}} + \frac{{2n}}{{\pi {{\varkappa }^{2}}}}{\mathbf{K}}(e)\mathfrak{N}t,} \\ {M = {{M}_{0}} + nt + \frac{{2n\eta }}{{\pi {{\varkappa }^{2}}}}{\mathbf{K}}(e)\mathfrak{N}t.} \end{array}$
Решение определено при всех $t$: ${{t}_{*}} = - \infty $, $t{\kern 1pt} * = \infty $. Средняя аномалия $M$ со временем равномерно возрастает, а аргумент перицентра $\omega $ равномерно возрастает или убывает в зависимости от знака $\mathfrak{N}$.

7. ЭВОЛЮЦИЯ НЕКРУГОВЫХ ОРБИТ ПРИ $W \ne 0,\;\mathfrak{T} = \mathfrak{N} = 0$

При $\mathfrak{T} = \mathfrak{N} = 0$ элементы $n,\;a,\;e = {\text{const}}$, $M = $ $ = {{M}_{0}} + nt$. Остальные уравнения (5) примут вид

$\mathop \imath \limits^ \bullet \; = - \frac{{necos\omega }}{{{{\varkappa }^{2}}\eta (1 + \eta )}}W,$
(22)
$\dot {\Omega } = - \frac{{nesin\omega }}{{{{\varkappa }^{2}}\eta (1 + \eta )sini}}W,$
$\dot {\omega } = \frac{{nesin\omega {\kern 1pt} {\kern 1pt} {\text{ctg}}{\kern 1pt} i}}{{{{\varkappa }^{2}}\eta (1 + \eta )}}W.$
Решение этих уравнений выполнено в [8, § 6].

Замечание. В статье [8] буквой $\omega $ обозначено среднее движение, а аргумент перицентра – $g$.

8. ЭВОЛЮЦИЯ НЕКРУГОВЫХ ОРБИТ ПРИ $\mathfrak{T}\mathfrak{N} \ne 0$, $W = 0$

Поведение $n,e$ исследовано в разделе 4. Элементы $i,\Omega $ постоянны. Решим уравнения для $\omega $ и $M$:

(23)
$\begin{gathered} \dot {\omega } = \frac{{2n}}{{\pi {{\varkappa }^{2}}}}{\mathbf{K}}(e)\mathfrak{N}, \\ \dot {M} = n + \frac{{2n\eta }}{{\pi {{\varkappa }^{2}}}}{\mathbf{K}}(e)\mathfrak{N}. \\ \end{gathered} $
Разделив (23) на второе уравнение (10), выразим (23) через эксцентриситет и получим уравнения с разделяющимися переменными:
$\begin{gathered} \frac{{d\omega }}{{de}} = \frac{{e{\mathbf{K}}(e)}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{\mathfrak{N}}{\mathfrak{T}}, \\ \frac{{dM}}{{de}} = \frac{{\pi {{\varkappa }^{2}}e}}{{4[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]\mathfrak{T}}} + \frac{{e\eta {\mathbf{K}}(e)}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{\mathfrak{N}}{\mathfrak{T}}, \\ \end{gathered} $
интегрирование которых даст
(24)
$\begin{gathered} \omega = {{\omega }_{0}} + \int\limits_{{{e}_{0}}}^e {\left\{ {\frac{{e{\mathbf{K}}(e)}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{\mathfrak{N}}{\mathfrak{T}}} \right\}de} , \\ M = {{M}_{0}} + \int\limits_{{{e}_{0}}}^e {\left\{ {\frac{{\pi {{\varkappa }^{2}}e}}{{4[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]\mathfrak{T}}}} \right.} + \\ + \;\left. {\frac{{e\eta {\mathbf{K}}(e)}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{\mathfrak{N}}{\mathfrak{T}}} \right\}de. \\ \end{gathered} $
Перейдем к рядам по степеням эксцентриситета. Среднее движение и время представлены рядами (12) и (17). Используя третью и последнюю формулы (А3) с учетом формул из раздела 5, получим
(25)
$\frac{{e\eta {\mathbf{K}}(e)}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}} = \frac{1}{e}\left( {1 - \sum {{{a}_{{16,k}}}{{e}^{{2k}}}} } \right),$
где
${{a}_{{16,k}}} = {{a}_{{9k}}} + {{a}_{{15,k}}} - \sum\limits_{m = 1}^{k - 1} \,{{a}_{{9,m}}}{{a}_{{15,k - m}}}.$
C помощью (А8), (25) и формул из раздела 5 получим ряды для аргумента перицентра и средней аномалии:
(26)
$\begin{array}{*{20}{c}} {\omega = {{\omega }_{0}} + \frac{\mathfrak{N}}{\mathfrak{T}}\left( {ln\frac{e}{{{{e}_{0}}}} + \sum {\frac{{{{a}_{{12,k}}}}}{{2k}}{{e}^{{2k}}}} - {{C}_{1}}} \right),} \\ {M = {{M}_{0}} + \frac{{{{\varkappa }^{2}}}}{\mathfrak{T}}\left( {ln\frac{e}{{{{e}_{0}}}} - \sum {\frac{{{{a}_{{15,k}}}}}{{2k}}{{e}^{{2k}}}} + {{C}_{4}}} \right) + } \\ {\, + \frac{\mathfrak{N}}{\mathfrak{T}}\left( {ln\frac{e}{{{{e}_{0}}}} - \sum {\frac{{{{a}_{{16,k}}}}}{{2k}}{{e}^{{2k}}}} + {{C}_{5}}} \right),} \end{array}$
где константы ${{C}_{1}}$ и ${{C}_{4}}$ определены формулой (А9) и вторым выражением (21) соответственно, а

${{C}_{5}} = \sum {\frac{{{{a}_{{16,k}}}}}{{2k}}e_{0}^{{2k}}} .$

Решение определено при ${{t}_{*}},\;t{\kern 1pt} *$, которые приведены в разделе 4. Со временем $M$ и $\omega $ либо равномерно возрастают, либо убывают в зависимости от знаков $\mathfrak{T}$ и $\mathfrak{N}$, причем при $e \to 0$ $M$ и $\omega $ стремятся к $ \pm \infty $, а при $e \to 1$ они стремятся к некоторому конечному значению согласно асимптотикам (А13), (А15), (А16). Отсюда же следует, что ряды в (26) сходятся при $e = 1$.

9. ЭВОЛЮЦИЯ НЕКРУГОВЫХ ОРБИТ ПРИ $\mathfrak{T}W \ne 0$, $\mathfrak{N} = 0$

Поведение $n,e,M$ рассмотрено в разделах 4 и 5. Для $i,\Omega ,\omega $ справедливы уравнения (22), но теперь коэффициенты уравнений зависят от переменных $n,e$.

Как и ранее, перейдем к $e$ как независимой переменной:

(27)
$\begin{gathered} \frac{{di}}{{de}} = - \frac{{\pi {{e}^{2}}cos\omega }}{{4\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{W}{\mathfrak{T}}, \\ \frac{{d\Omega }}{{de}} = - \frac{{\pi {{e}^{2}}sin\omega }}{{4\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]sini}}\frac{W}{\mathfrak{T}}, \\ \frac{{d\omega }}{{de}} = \frac{{\pi {{e}^{2}}sin\omega \operatorname{ctg} i}}{{4\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{W}{\mathfrak{T}}. \\ \end{gathered} $
Уравнения (27) аналогичны рассмотренным в [7, § 8] с точностью до зависящих только от $e$ коэффициентов. Мы не будем дублировать ход решения, приведем результирующие формулы.

Наклон и аргумент перицентра однозначно определяются с помощью соотношений

(28)
$\begin{gathered} cosi = \sqrt {1 - {{V}^{2}}} sin\varphi , \\ sini = \sqrt {1 - (1 - {{V}^{2}})si{{n}^{2}}\varphi } , \\ \end{gathered} $
(29)
$sin\omega = \frac{V}{{sini}},\quad cos\omega = \frac{{\sqrt {1 - {{V}^{2}}} cos\varphi }}{{sini}},$
где
$V = sinisin\omega = {\text{const}}$
является интегралом движения; вспомогательная функция
$\varphi (e) = \frac{{\pi W}}{{4\mathfrak{T}}}\int\limits_{{{e}_{0}}}^e {\frac{{{{e}^{2}}de}}{{\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}} + {{C}_{6}};$
константа ${{C}_{6}}$ вычисляется по формулам:
$cos{{C}_{6}} = \frac{{sin{{i}_{0}}cos{{\omega }_{0}}}}{{\sqrt {1 - {{V}^{2}}} }},\quad sin{{C}_{6}} = \frac{{cos{{i}_{0}}}}{{\sqrt {1 - {{V}^{2}}} }}.$
После подстановки (28), (29) второе уравнение (27) примет вид:
$\begin{gathered} \frac{{d\Omega }}{{de}} = - \frac{{\pi {{e}^{2}}}}{{4\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{W}{\mathfrak{T}} \times \\ \, \times \frac{V}{{1 - (1 - {{V}^{2}})si{{n}^{2}}\varphi }}. \\ \end{gathered} $
Переменные разделятся:

(30)
$\begin{gathered} \Omega = {{\Omega }_{0}} - \frac{{\pi W}}{{4\mathfrak{T}}} \times \\ \times \;\int\limits_{{{e}_{0}}}^e \,\frac{{V{{e}^{2}}de}}{{\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)][1 - (1 - {{V}^{2}})si{{n}^{2}}\varphi ]}}. \\ \end{gathered} $

Перейдем к рядам по степеням эксцентриситета. С помощью формул (А3) получим

(31)
$\begin{gathered} \frac{{\pi {{e}^{2}}}}{{4\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}} = \\ = \frac{{\tfrac{1}{2} + \sum {{{a}_{{5k}}}{{e}^{{2k}}}} }}{{1 + \sum {{{a}_{{6k}}}{{e}^{{2k}}}} }} = \frac{1}{2} + \sum {{{a}_{{17,k}}}{{e}^{{2k}}}} , \\ \end{gathered} $
где
${{a}_{{17,k}}} = {{a}_{{5k}}} - \frac{1}{2}{{a}_{{6k}}} - \sum\limits_{m = 1}^{k - 1} \,{{a}_{{6m}}}{{a}_{{17,k - m}}},\quad {{a}_{{17,1}}} = \frac{5}{{16}},$
с учетом чего
(32)
$\begin{gathered} \varphi (e) = \frac{W}{\mathfrak{T}}\int\limits_{{{e}_{0}}}^e \left( {\frac{1}{2} + \sum {{{a}_{{17,k}}}{{e}^{{2k}}}} } \right)de + {{C}_{6}} = \\ \, = \frac{W}{{2\mathfrak{T}}}\sum {{{a}_{{18,k}}}{{e}^{{2k - 1}}}} + {{C}_{7}}, \\ \end{gathered} $
где
${{a}_{{18,1}}} = 1,\quad {{a}_{{18,k}}} = \frac{{2{{a}_{{17,k - 1}}}}}{{2k - 1}}\quad {\text{при}}\quad k > 1$
и константа интегрирования
${{C}_{7}} = {{C}_{6}} - \frac{W}{{2\mathfrak{T}}}\sum {{{a}_{{18,k}}}e_{0}^{{2k - 1}}} .$
Замена $\varphi $ рядом (32) в формулах (28), (29) даст представление тригонометрических функций от наклона и аргумента перицентра в виде рядов по степеням эксцентриситета.

Обозначим

(33)
$\frac{W}{\mathfrak{T}}\sum {{{a}_{{18,k}}}{{e}^{{2k - 1}}}} = \xi $
и разложим $si{{n}^{2}}\varphi $ в ряд по степеням эксцентриситета:
(34)
$\begin{gathered} si{{n}^{2}}\varphi = \frac{1}{2} - \frac{1}{2}cos(2{{C}_{7}} + \xi ) = \\ = \frac{1}{2} - \frac{1}{2}cos2{{C}_{7}}\left( {1 + \sum {\frac{{{{{( - 1)}}^{k}}{{\xi }^{{2k}}}}}{{(2k)!}}} } \right) + \\ \, + \frac{1}{2}sin2{{C}_{7}}\sum {\frac{{{{{( - 1)}}^{{k - 1}}}{{\xi }^{{2k - 1}}}}}{{(2k - 1)!}}} , \\ \end{gathered} $
или
(35)
$si{{n}^{2}}\varphi = si{{n}^{2}}{{C}_{7}} + \sum {{{a}_{{19,k}}}{{e}^{k}}.} $
Коэффициенты ${{a}_{{19,k}}}$ находятся средствами компьютерной алгебры путем разложения в ряд по эксцентриситету выражения (34) после подстановки вместо $\xi $ ряда (33) и имеют вид:

Подставим (31) и (35) в (30):

$\begin{gathered} \Omega = {{\Omega }_{0}} - \frac{{WV}}{\mathfrak{T}}\int\limits_{{{e}_{0}}}^e \,\frac{{\left( {\tfrac{1}{2} + \sum {{{a}_{{17,k}}}{{e}^{{2k}}}} } \right)de}}{{\left[ {1 - (1 - {{V}^{2}})\left( {si{{n}^{2}}{{C}_{7}} + \sum {{{a}_{{19,k}}}{{e}^{k}}} } \right)} \right]}} = \\ = {{\Omega }_{0}} - \frac{{WV}}{{2\mathfrak{T}[1 - (1 - {{V}^{2}})si{{n}^{2}}{{C}_{7}}]}}\int\limits_{{{e}_{0}}}^e \,\left( {1 + \sum {{{a}_{{20,k}}}{{e}^{k}}} } \right)de, \\ \end{gathered} $
где
$\begin{gathered} {{a}_{{20,k}}} = {{C}_{8}}\left( {{{a}_{{19,k}}} + \sum\limits_{m = 1}^{k - 1} \,{{a}_{{20,m}}}{{a}_{{19,k - m}}}} \right)\;{\text{при}}\;{\text{нечетных}}\;k, \\ {{a}_{{20,k}}} = 2{{a}_{{17,k/2}}} + {{C}_{8}}\left( {{{a}_{{19,k}}} + \sum\limits_{m = 1}^{k - 1} \,{{a}_{{20,m}}}{{a}_{{19,k - m}}}} \right) \\ {\text{при}}\;{\text{четных}}\;k, \\ {{C}_{8}} = \frac{{1 - {{V}^{2}}}}{{1 - (1 - {{V}^{2}})si{{n}^{2}}{{C}_{7}}}}. \\ \end{gathered} $
Отсюда
$\begin{gathered} \Omega = {{\Omega }_{0}} - \frac{{WV}}{{2\mathfrak{T}[1 - (1 - {{V}^{2}})si{{n}^{2}}{{C}_{7}}]}} \times \\ \, \times \left( {e + \sum {\frac{{{{a}_{{20,k}}}{{e}^{{k + 1}}}}}{{k + 1}}} } \right) + {{C}_{9}}, \\ \end{gathered} $
где постоянная интегрирования
${{C}_{9}} = \frac{{WV}}{{2\mathfrak{T}[1 - (1 - {{V}^{2}})si{{n}^{2}}{{C}_{7}}]}}\left( {{{e}_{0}} + \sum {\frac{{{{a}_{{20,k}}}e_{0}^{{k + 1}}}}{{k + 1}}} } \right).$
В статье не приведены числовые значения коэффициентов ${{a}_{{19,k}}}$, ${{a}_{{20,k}}}$, как для других коэффициентов (см. Приложение), так как они зависят от значений компонентов возмущающего ускорения и начальных эксцентриситета, наклона и аргумента перицентра.

10. ЭВОЛЮЦИЯ НЕКРУГОВЫХ ОРБИТ ПРИ $\mathfrak{N}W \ne 0$, $\mathfrak{T} = 0$

Так как $\mathfrak{T} = 0$, то элементы $n,a,e$ постоянны, и для средней аномалии получим:

$M = {{M}_{0}} + \left\{ {n + \frac{{2n\eta }}{{\pi {{\varkappa }^{2}}}}{\mathbf{K}}(e)\mathfrak{N}} \right\}t.$
Остальные уравнения системы (5) примут вид:
(36)
$\begin{gathered} \mathop \imath \limits^ \bullet \; = - {{A}_{2}}cos\omega , \\ \dot {\Omega } = - {{A}_{2}}\frac{{sin\omega }}{{sini}}, \\ \dot {\omega } = {{A}_{3}} + {{A}_{2}}sin\omega {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{ctg}}{\kern 1pt} {\kern 1pt} i, \\ \end{gathered} $
где постоянные ${{A}_{s}}$ определены соотношениями
${{A}_{2}} = \frac{{ne}}{{{{\varkappa }^{2}}\eta (1 + \eta )}}W,\quad {{A}_{3}} = \frac{{2n}}{{\pi {{\varkappa }^{2}}}}{\mathbf{K}}(e)\mathfrak{N}.$
Уравнения (36) исследованы и решены в [9, § 8], в силу громоздкости решения мы не привели его здесь.

11. ЭВОЛЮЦИЯ НЕКРУГОВЫХ ОРБИТ ПРИ $\mathfrak{T}\mathfrak{N}W \ne 0$

В случае произвольных $\mathfrak{T}\mathfrak{N}W \ne 0$ поведение элементов $n,a,e$ останется таким же, как описано в разделе 4. Для $M$ справедливы формулы (24), (26).

Для остальных элементов $i,\Omega ,\omega $ уравнения примут вид (36), но коэффициенты ${{A}_{2}}$, ${{A}_{3}}$ уже не будут постоянными. После перехода в (36) к производной по эксцентриситету:

$\frac{{di}}{{de}} = - \frac{{\pi {{e}^{2}}cos\omega }}{{4\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{W}{\mathfrak{T}},$
(37)
$\begin{gathered} \frac{{d\omega }}{{de}} = \frac{{e{\mathbf{K}}(e)}}{{2[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{\mathfrak{N}}{\mathfrak{T}} + \\ + \;\frac{{\pi {{e}^{2}}sin\omega \,{\text{ctg}}\,i}}{{4\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]}}\frac{W}{\mathfrak{T}}, \\ \end{gathered} $
$\frac{{d\Omega }}{{de}} = - \frac{{\pi {{e}^{2}}sin\omega }}{{4\eta (1 + \eta )[{\mathbf{E}}(e) - {{\eta }^{2}}{\mathbf{K}}(e)]sini}}\frac{W}{\mathfrak{T}},$
получим неавтономную систему дифференциальных уравнений, но уравнения (37) для $i$ и $\omega $ не зависят от $\Omega $, поэтому достаточно решить лишь их, например, численно или методом малого параметра. Далее $\Omega $ получится простой квадратурой.

12. ЗАКЛЮЧЕНИЕ

Мы рассмотрели движение тела нулевой массы в центральном гравитационном поле при наличии малого возмущающего ускорения, обратно пропорционального квадрату расстояния до центрального тела, относительно неинерциальной системы отсчета с осями, направленными по вектору скорости, нормали к нему в плоскости оскулирующей орбиты и бинормали.

Для различных частных случаев получено решение осредненных по средней аномалии уравнений движения типа Эйлера в виде зависимостей элементов орбиты от времени либо времени и элементов орбиты от эксцентриситета. При $e = 0$ в начальную эпоху, а также при $(\mathfrak{T},\mathfrak{N} = 0,\;W \ne 0)$ решение представлено элементарными функциями. При $(\mathfrak{T},W = 0,\;\mathfrak{N} \ne 0)$ и $(\mathfrak{T} = 0,\;\mathfrak{N},W \ne 0)$ решение содержит полные эллиптические интегралы. В остальных случаях, если хотя бы один из компонентов $\mathfrak{T},\;\mathfrak{N},\;W$ возмущающего ускорения равен нулю, решение содержит интегралы от комбинаций полных эллиптических интегралов. В случаях, когда решение выражено в квадратурах, оно представлено как в виде замкнутых выражений, так и в виде разложений по степеням эксцентриситета, сходящихся при $e < 1$. Отмечены случаи сходимости и при $e = 1$.

В общем случае задача сведена к неавтономной системе двух дифференциальных уравнений первого порядка. Их решение можно найти методами малого параметра Ляпунова-Пуанкаре или численного интегрирования.

Список литературы

  1. W. F. Bottke Jr., D. Vokrouhlický, D. P Rubincam, and M. Broz, in: Asteroids III, edited by W. F. Bottke Jr., A. Cellino, P. Paolicchi, and R. P. Binzel (University of Arizona Press, 2002), p. 395.

  2. JPL Small-Body Database Search Engine, Jet Propulsion Laboratory NASA. https://ssd.jpl.nasa.gov/sbdb_query.cgi.

  3. М. Ф. Субботин, Введение в теоретическую астрономию (М.: Наука, 1968).

  4. Т. Н. Санникова, К. В. Холшевников, Астрон. журн. 96(5), 418 (2019).

  5. К. В. Холшевников, Асимптотические методы небесной механики (Л.: Изд-во ЛГУ, 1985).

  6. И. С. Градштейн, И. М. Рыжик, В. В. Максимов, Таблицы интегралов, рядов и произведений (СПб: БХВ-Петербург, 2011).

  7. Н. Батмунх, Т. Н. Санникова, К. В. Холшевников, Астрон. журн. 95 (4), 307 (2018).

  8. Т. Н. Санникова, К. В. Холшевников, Астрон. журн. 97(9), 747 (2020).

  9. Т. Н. Санникова, К. В. Холшевников, Астрон. журн. 92(8), 681 (2015).

  10. D. Vokrouhlický, Astron. and Astrophys. 344, 362 (1999).

  11. Н. И. Ахиезер, Элементы теории эллиптических функций (М.: Наука, Физматлит, 1970).

  12. А. Гурвиц, Теория аналитических и эллиптических функций (М.: ЛЕНАНД, Физмат. наследие, 2015).

  13. Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления. Том 2 (М.: Физматлит, 2001).

  14. М. Тихомандрицкий, Теория эллиптических интегралов и эллиптических функций (М.: Книга по Требованию, 2012).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал