Астрономический журнал, 2021, T. 98, № 2, стр. 91-101

2.1. Смещение фотоцентра двойной системы между начальным и финальным периодами наблюдений Gaia DR2

Смещение звезды в двойной системе за время наблюдений Gaia DR2 ($T = 1.8$ года) приводит к возникновению дополнительного собственного движения и дополнительной скорости, которая увеличивает дисперсию скоростей внутри ОВ-ассоциаций.

Давайте рассмотрим двойную систему, компоненты которой вращаются по круговым орбитам в плоскости небесной сферы с периодом обращения $P$ (см. рис. 1а). Обозначим главный и вторичный компоненты двойной звезды соответственно 1 и 2. Типичным представителем звезды ОВ-ассоциаций в каталоге Блаха и Хамфрис [5] является звезда с массой 10 ${{M}_{ \odot }}$, поэтому будем считать, что главный компонент имеет массу ${{M}_{1}} = 10\,{{M}_{ \odot }}$, а масса вторичного компонента равна ${{M}_{2}} = q{{M}_{1}}$:

Компоненты двойной вращаются вокруг общего центра масс $O$ по орбитам с радиусами соответственно ${{a}_{1}}$ и ${{a}_{2}}$. Радиус ${{a}_{2}}$ можно оценить из закона гравитации Ньютона: а радиус ${{a}_{1}}$ вычисляется из следующего соотношения: Смещения ${{S}_{1}}$ и ${{S}_{2}}$ компонентов двойной системы между первым и последним наблюдательными периодами Gaia DR2 равны: где $T$ – это временнáя база наблюдений Gaia DR2.

Однако проект Gaia DR2 включает много наблюдений индивидуальных звезд. Например, звезды ОВ-ассоциаций наблюдались в среднем в течение 14 наблюдательных периодов. Наблюдательные периоды (visibility periods) – это интервалы наблюдений, разнесенные друг от друга не менее, чем на 4 дня [3, 16]. В разделе 2.2 мы рассмотрим другой метод, основанный на решении $n$ уравнений, определяющих смещение ${{s}_{n}}$ в момент времени ${{t}_{n}}$.

Оказалось, что двойные системы с периодом $P = 5.9$ года дают максимальный вклад в дисперсию скоростей. В этом случае смещение компонентов двойной системы $S = {{S}_{1}} + {{S}_{2}}$ между первым и последним наблюдательными периодами имеет значение, близкое к диаметру системы $D \approx {{a}_{1}} + {{a}_{2}}$, равному $D \approx 8$ а.е., что на расстоянии $r = 1$ кпк соответствует углу $ \sim 8$ мсд. Заметим, что медианное значение расстояний от Солнца до ОВ-ассоциаций из каталога Блаха и Хамфрис [5] равно $r = 1.7$ кпк, т.е. медианное значение угла между компонентами двойной звезды должно быть в 1.7 раза меньше.

Изображения звезд в фокальной плоскости спутника Gaia имеют большой размер, что делается специально для увеличения числа пикселов, участвующих в построении изображения, и дает возможность точнее определять положение центра изображения. Медианное значение полуширины изображения, вычисленное на половине максимума линейной функции источника (full width half maximum of the line spread function), составляет $ \sim {\kern 1pt} 100$ мсд [17]. Это означает, что компоненты рассмотренной двойной системы должны быть представлены одним и тем же источником.

Таким образом, мы должны рассматривать смещение фотоцентра двойной системы, а не движение одного из ее компонентов. В целом вычисление эффекта двойных требует учета линейной функции источника, точечной функции источника и алгоритма определения источника. Здесь мы не претендуем на полное решение, а делаем приблизительную оценку, полагая, что линейная функция источника является практически плоской вблизи $ \pm 10$ мсд от положения максимума [17].

Следовательно, световой поток от обоих компонентов двойной системы, полностью, без потерь, участвует в построении изображения. Используя соотношение между светимостью звезды $L$ и ее массой $M$, например, [18]:

мы можем записать следующее выражение для смещения фотоцентра двойной системы: Подставляя переменные из (4)$ - $(7), получаем: где функция ${{F}_{q}}$ имеет вид: Рисунок 1c показывает ход функции ${{F}_{q}}$, которая равна нулю при $q = 1$. Действительно, движение двух одинаковых звезд в картинной плоскости не приводит к смещению их общего фотоцентра. С другой стороны, если один компонент очень мал, то перемещения основного компонента будут ничтожными. Оказалось, что функция ${{F}_{q}}$ достигает максимума при $q = 0.52$.

Движение фотоцентра двойной системы приводит к появлению дополнительной скорости, которая искажает скорость звезды в картинной плоскости:

где $T$ – временнáя база наблюдений Gaia DR2. Рисунок 1b показывает зависимость дополнительной скорости $\overline {{{V}_{{bn}}}} $, усредненной по параметру $q = {{M}_{2}}{\text{/}}{{M}_{1}}$, от $logP$. В целом легко понять зависимость скорости $\overline {{{V}_{{bn}}}} $ от периода обращения системы $P$: при малых периодах двойная система имеет малый диаметр и смещения фотоцентра малы; чем больше период, тем больше диаметр системы, но в этом случае скорости движения по орбите малы и за время наблюдений Gaia DR2 фотоцентр смещается на небольшое расстояние. Следовательно, существует определенный период $P$, соответствующий максимальному смещению ${{S}_{{{\text{ph}}}}}$. Максимальное смещение ${{S}_{{{\text{ph}}}}}$ и, следовательно, максимальная скорость $\overline {{{V}_{{bn}}}} $ достигаются при периоде $P = 5.9$ года. Максимальная скорость имеет значение $\overline {{{V}_{{bn}}}} = 5.4$ км/с. При малых периодах $P$ скорость $\overline {{{V}_{{bn}}}} $ демонстрирует колебания, а нулевые значения скорости $\overline {{{V}_{{bn}}}} = 0$ соответствуют периодам $P = T{\text{/}}n$, где $n$ – целое число, при которых двойная система делает несколько полных оборотов за время $T$, что приводит к нулевому смещению ${{S}_{{{\text{ph}}}}}$.

Чтобы оценить вклад двойных звезд ${{\sigma }_{{bn}}}$ в дисперсию скоростей внутри ОВ-ассоциаций ${{\sigma }_{{v}}}$, мы интегрируем $V_{{bn}}^{2}(P,q)$ по всем возможным периодам $P$ и отношениям масс $q$:

где множители ${{f}_{b}}$ и ${{f}_{j}}$ характеризуют соответственно долю двойных звезд и эффекты проекции, а функции ${{f}_{p}}(logP)$ и ${{p}_{q}}(q)$ учитывают распределение двойных систем по периодам и по отношению масс компонентов $q$ в них. Здесь мы принимаем следующие предположения. Доля двойных систем среди массивных молодых звезд составляет ${{f}_{b}} = 0.5$ [13]. Ансамбль двойных систем ориентирован случайным образом по отношению к лучу зрения, следовательно, квадрат проекции полной скорости $V$ на случайное направление, например $x$, в среднем составляет $V_{x}^{2} = 1{\text{/}}3{{V}^{2}}$, что дает фактор проекции, равный ${{f}_{j}} = 1{\text{/}}3$. Алдоретта и др. [19] показали, что распределение массивных двойных звезд по периодам является практически плоским по инкременту $logP$ (так называемый закон Эпика [20, 21]) на интервале $logP$ от –3 до +6. Поэтому мы можем принять значение ${{f}_{p}} = 1{\text{/}}9$ на единицу $logP$. Сана и Эванс [22] нашли, что распределение двойных систем по отношению масс компонентов $q$ является практически плоским на интервале $q = 0.2{\kern 1pt} - {\kern 1pt} 1.0$, поэтому мы можем принять ${{p}_{q}} = 1.25$.

Численно интегрируя (13), мы получаем среднее значение вклада двойных звезд в дисперсию скоростей внутри ОВ-ассоциаций:

что примерно в два раза превышает значение ${{\sigma }_{{bn}}} = 0.38$ км/с, полученное для временной базы наблюдений Gaia DR1, равной $T$ = 24 года [23]. Оба значения ${{\sigma }_{{bn}}}$ являются достаточно малыми по сравнению с наблюдаемой дисперсией скоростей внутри ОВ-ассоциаций ${{\sigma }_{{v}}} = 4{\kern 1pt} - {\kern 1pt} 5$ км/с. Из (14) видно, что значение ${{\sigma }_{{bn}}}$ слабо зависит от массы ${{M}_{1}}$: при уменьшении массы звезды в 10 раз (c ${{M}_{1}} = 10$ до 1 ${{M}_{ \odot }}$) значение ${{\sigma }_{{bn}}}$ уменьшается только в $ \sim {\kern 1pt} 2$ раза.

2.2. Смещение фотоцентра двойной звезды с учетом промежуточных наблюдений Gaia DR2

Предположим, что положение фотоцентра двойной системы измеряется $n$ раз за время наблюдений Gaia DR2. Для определенности рассмотрим $n = 14$ – среднее число периодов наблюдений звезд высокой светимости из каталога Блаха и Хамфрис [5]. Рисунок 2a показывает вращение компонентов двойной системы с периодом обращения $P = 5.9$ года, обеспечивающим максимальное смещение фотоцентра за время наблюдений Gaia DR2. Рисунок 2b демонстрирует вращение фотоцентра $C$ относительно центра масс системы $O$. Радиус орбиты фотоцентра равен:

Вектор $\overrightarrow S $ равен смещению между начальным и финальным периодами наблюдений. Введем локальную систему координат: ось $x$ совпадает с направлением вектора $\overrightarrow S $, а ось $y$ перпендикулярна ему. Хорда ${{c}_{n}}$ показывает смещение фотоцентра C к моменту времени ${{t}_{n}}$. Проекции хорды ${{c}_{n}}$ на направления $x$ и $y$ равны соответственно ${{x}_{n}}$ и ${{y}_{n}}$. Максимальное смещение фотоцентра происходит вдоль оси $x$, а в перпендикулярном направлении положение фотоцентра отклоняется на величину $ \sim {\kern 1pt} {\text{|}}\overrightarrow S {\text{|/}}2$ и возвращается в положение, близкое к исходному. Дополнительные скорости ${{V}_{x}}$ и ${{V}_{y}}$ в направлении осей соответственно $x$ и $y$ вычисляются из решения системы $2n$ уравнений: Так как мы вычисляем одномерную дисперсию скоростей ${{\sigma }_{{bn}}}$ и учитываем эффект проекции с помощью коэффициента ${{f}_{j}} = 1{\text{/}}3$, то нам надо найти максимально возможное смещение в одном направлении. Это означает, что Заметим, что скорость ${{V}_{y}}$ и дополнительное собственное движение (см. (32)) вычисляются с большой ошибкой, что может привести к большому размеру эллипсоида ошибок (astrometric_sigma5d_max) при определении пяти астрометрических параметров ($\alpha $, $\delta $, ${{\mu }_{\alpha }}$, ${{\mu }_{\delta }}$ и $\varpi $) данной звезды и их последующей отбраковке [3]. Эта проблема будет обсуждаться в разделе 2.5.

Рисунок 2c показывает зависимость дополнительной скорости $\overline {{{V}_{{bn}}}} $, усредненной по параметру $q$, от $logP$, полученную двумя методами: первый основан на полном смещении $S$ между начальным и конечным периодами наблюдений (раздел 2.1), а второй метод включает решение $n$ уравнений, определяющих проекцию ${{x}_{n}}$ в момент времени ${{t}_{n}}$. Максимальная скорость $\overline {{{V}_{{bn}}}} $, вычисленная первым и вторым методом, имеет значения соответственно 5.4 и 6.0 км/с. Максимальная скорость $\overline {{{V}_{{bn}}}} $, вычисленная вторым методом, имеет большее значение ($\overline {{{V}_{{bn}}}} = 6$ км/с), но при малых периодах, там где происходят колебания, она принимает меньшие значения, чем скорость, вычисленная первым методом.

Интегрируя скорость $\overline {{{V}_{{bn}}}} $ по инкременту $logP$, мы получаем средний вклад двойных систем в дисперсию скоростей, вычисленную с учетом промежуточных измерений:

Таким образом, средний вклад двойных систем в дисперсию скоростей внутри ОВ-ассоциаций, вычисленный двумя методами, отличается только на 3%.

2.3. Эллиптические орбиты

Распределение орбит массивных двойных звезд по эксцентриситету $e$ зависит от периода: долгопериодические системы ($P > 10$ лет) имеют практически равномерное распределение по эксцентриситету, а короткопериодические системы ($P < 100$ дней) показывают избыток круговых орбит [13, 15, 24, 25].

Рассмотрим двойную систему с эксцентриситетом орбит $e = 0.5$ и оценим вклад таких систем в дисперсию скоростей внутри ОВ-ассоциаций. Рисунок 3а показывает двойную систему, компоненты которой двигаются по эллиптическим орбитам, фокусы которых находятся в центре масс системы $O$. Точки $P$ и $A$ показывают положения перицентра и апоцентра орбиты вторичного компонента, углы ${{\theta }_{1}}$ и ${{\theta }_{2}}$ отсчитываются от перицентра $P$ и соответствуют положению вторичного компонента в начальный ${{t}_{1}}$ и конечный ${{t}_{2}}$ периоды наблюдений Gaia DR2.

Движение материального тела по эллиптической орбите описывается законом Кеплера:

где $E$ – эксцентрическая аномалия, а $M$ – средняя аномалия: где ${{t}_{0}}$ – время прохождения перицентра. Зная эксцентрическую аномалию $E$, мы легко можем вычислить истинную аномалию – угол $\theta $ между направлением на спутник в момент времени $t$ и направлением на перицентр [26]: Расстояние $r$ от центра масс системы до вторичного компонента в момент времени $t$ определяется соотношением: где $a$ – большая полуось орбиты вторичного компонента, которая зависит от периода системы $P$, массы основного компонента ${{M}_{1}}$ и отношения масс $q$ (см. (4)).

Величина $E$ вычислялась методом последовательных приближений по Денби [27] до точности порядка 10^–6 рад. В нулевом приближении E₀ = $ = M + 0.85e$, и каждое следующее значение равно:

Время ${{t}_{1}} \in [0,P]$ определяет значение угла ${{\theta }_{1}}$ и радиуса ${{r}_{1}}$ в начальный период наблюдений Gaia DR2. Время ${{t}_{2}}$ соответствует последнему периоду наблюдений Gaia DR2: Для каждого момента времени ${{t}_{1}}$ вычислялись значения ${{t}_{2}}$, углов ${{\theta }_{1}}$ и ${{\theta }_{2}}$, расстояний ${{r}_{1}}$ и ${{r}_{2}}$, а также смещение вторичного компонента: Смещение первичного компонента ${{S}_{1}}$ определяется выражением (7). Зная ${{S}_{1}}$ и ${{S}_{2}}$, мы можем найти смещение фотоцентра системы ${{S}_{{{\text{ph}}}}}$ (см. (9)) и дополнительную скорость ${{V}_{{bn}}}$ (см. (12)).

Рисунок 3b показывает зависимость дополнительной скорости $\overline {{{V}_{{bn}}}} $, усредненной по параметрам $q$ и ${{t}_{1}}$ (${{t}_{1}} \in [0,P]$), от $logP$, вычисленную для орбит с эксцентриситетом $e = 0.5$ (красная кривая). В этом случае максимальное значение скорости составляет $\overline {{{V}_{{bn}}}} = 4.8$ км/с. Для сравнения приведена кривая $\overline {{{V}_{{bn}}}} $ (показана синим цветом), полученная для круговых орбит методом, изложенным в разделе 2.1. Видно, что предположение об эллиптичности орбиты немного уменьшает значение дополнительной скорости $\overline {{{V}_{{bn}}}} $.

Средний вклад эллиптических орбит с $e = 0.5$ в дисперсию скоростей внутри ОВ-ассоциаций составляет:

что примерно на 10% меньше значения 0.90 км/с, полученного для круговых орбит (см. (14)). Вероятно, это связано с тем, что вторичный компонент проводит большую часть времени вблизи апоцентра своей орбиты, где вращается с низкой угловой скоростью, смещаясь на малый угол за время наблюдений Gaia DR2, и его большое расстояние $r$ от центра масс системы не может скомпенсировать низкую угловую скорость.

Оказалось, что изменение эксцентриситета $e$ орбит двойных звезд от $e = 0$ до 0.9 соответствует изменению ${{\sigma }_{{bn}}}$ от ${{\sigma }_{{bn}}} = 0.90$ до 0.58 км/с. Предполагая, что эксцентриситеты орбит двойных массивных систем распределены равномерно на интервале $e \in [0,0.9]$, мы вычислили среднее значение $\overline {{{\sigma }_{{bn}}}} $ по эксцентриситету:

которое практически совпадает со значением, полученным для эксцентриситета $e = 0.5$.

2.4. Другое распределение ${{p}_{q}}$

В предыдущих разделах мы предполагали, что массивные двойные системы распределены равномерно по $q = {{M}_{2}}{\text{/}}{{M}_{1}}$ на интервале $q \in [0.2,1]$ [20]. Но есть мнение, что распределение двойных звезд ${{p}_{q}}$ смещено в сторону малых значений $q$ и описывается степенным законом ${{p}_{q}} \sim {{q}^{\gamma }}$, где $\gamma $ лежит в диапазоне от –0.5 до –2.4 [15].

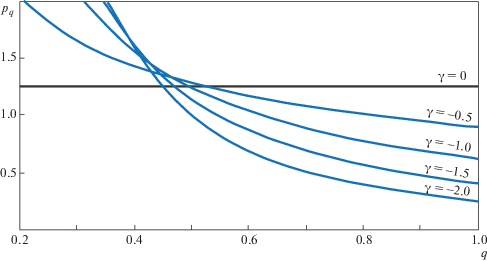
Рисунок 4 показывает плотность вероятности распределения ${{p}_{q}} = C{{q}^{\gamma }}$ для значений $\gamma = 0$ (постоянное распределение), $\gamma = - 0.5$, –1.0, –1.5 и –2.0. Значение константы $C$ выбирается из условия нормировки:

Интегрирование $V_{{bn}}^{2}$ (см. (13)) с функцией ${{p}_{q}} = C{{q}^{\gamma }}$ для показателя $\gamma = - 1.5$ дает значение дисперсии скоростей ${{\sigma }_{{bn}}}$: которое лишь на 18% больше значения ${{\sigma }_{{bn}}} = $ = 0.90 км/c, полученного для равномерного распределения ${{p}_{q}}$. В целом выбор показателя $\gamma $ мало влияет на значение ${{\sigma }_{{bn}}}$: изменение $\gamma $ от 0 до –2.0 соответствует изменению ${{\sigma }_{{bn}}}$ в диапазоне 0.90–1.07. Это связано с тем, что максимальный вклад в дисперсию скоростей дают системы с $q = 0.5$, при котором все рассмотренные функции ${{p}_{q}}$ имеют близкие значения (рис. 4).

2.5. Анализ ошибок собственных движений при движении фотоцентра двойной системы

Максимальный вклад в дисперсию скоростей, выведенную по данным Gaia DR2, дают двойные системы с периодом $P = 5.9$ года. При этом в одном направлении фотоцентр системы двигается практически линейно, а в другом совершает колебание, не имеющее ничего общего с линейным движением. В этом разделе мы анализируем ошибки собственных движений, вызванные нелинейными движениями.

Рисунок 5 показывает положения фотоцентра двойной системы в разные моменты времени и вычисленные по ним собственные движения. Моменты времени выбирались случайно на временной базе наблюдений Gaia DR2. Ось $x$ совпадает с вектором $\overrightarrow S $, соединяющим положения фотоцентра между начальным и финальным периодами наблюдений, а ось $y$ перпендикулярна оси $x$ (см. рис. 2b). Для примера выбрана система c периодом обращения $P = 5.9$ года, дающая максимальный вклад в смещение фотоцентра. Для удобства перехода к угловым единицам система расположена на расстоянии $r = 1$ кпк от Солнца. Собственные движения фотоцентра ${{\mu }_{x}}$ и ${{\mu }_{y}}$ вычисляются из решения системы линейных уравнений, определяющих положения фотоцентра на небесной сфере ($x_{n}^{'}$, $y_{n}^{'}$) в разные моменты времени:

где значения $x_{n}^{'}$, $x_{0}^{'}$, $y_{n}^{'}$ и $y_{0}^{'}$ даны в единицах мсд, а собственные движения ${{\mu }_{x}}$ и ${{\mu }_{y}}$ в единицах мсд/год: Рисунки 5а, b показывают, что смещение фотоцентра по оси x подчиняется линейному закону, а смещение по оси y описывает дугу, существенно увеличивая ошибки определения координаты ${{y}_{0}}$ и собственного движения ${{\mu }_{y}}$. В целом движение по дуге предполагает, как минимум, квадратическую зависимость от времени.

Мы также рассмотрели влияние параллактического смещения на выведенные значения собственных движений. Рисунки 5c, d показывают движение фотоцентра двойной системы, искаженное параллактическими смещениями. Для удобства амплитуды параллактических движений вдоль осей $x$ и $y$ были приняты равными ${{P}_{x}} = {{P}_{y}} = 1$ мсд.

Хорошо видно, что наклоны прямых на рис. 5а, c, а также на рис. 5b, d практически совпадают, что говорит о малом влиянии параллактического смещения на вычисленные значения собственных движений.

Таблица 1 представляет собственные движения ${{\mu }_{x}}$ и ${{\mu }_{y}}$ и их ошибки, а также ошибки определения координат ${{x}_{0}}$ и ${{y}_{0}}$ (сами координаты в нашем случае не представляют интереса), выведенные для движения фотоцентра двойной системы с учетом и без учета параллактического смещения. Видно, что точность определения координаты и собственного движения по оси $x$ примерно на порядок выше, чем по оси $y$. Так, ошибки определения значений ${{x}_{0}}$ и ${{\mu }_{x}}$ составляют 0.01 мсд и 0.01 мсд/год, а ошибки определения ${{y}_{0}}$ и ${{\mu }_{y}}$ имеют значения 0.1 мсд и 0.1 мсд/год соответственно.

Таким образом, движение фотоцентра рассмотренной двойной системы практически не увеличивает ошибку определения собственного движения в одном направлении и добавляет дополнительную погрешность в 0.1 мсд/год в определение собственного движения в другом направлении. Средняя точность собственных движений звезд ОВ-ассоциаций равна 0.1 мсд/год, поэтому рассмотренная двойная система будет иметь ошибки собственных движений в диапазоне 0.1–0.2 мсд/год.

Линдегрен и др. [3] сформулировали три условия, при которых пятипараметрическое решение, выведенное по наблюдениям Gaia GR2, не будет отброшено:

где $\gamma (G) = max[1,{{10}^{{0.2(G - 18)}}}]$.

Для звезд ОВ-ассоциаций средние значения звездной величины в полосе $G$ и числа наблюдательных периодов равны соответственно $\overline G = {{8.5}^{m}}$ и ${{n}_{{{\text{vis}}}}} = 14$. Следовательно, два первых условия легко выполняются. Третье условие состоит в том, что пятимерный эквивалент большой полуоси позиционного эллипсоида ошибок (astrometric_sigma5d_max) не должен превышать 1.2 мсд [3]. Рассмотренные выше нелинейные движения фотоцентра двойной системы создают ошибки на уровне 0.1 мсд, что примерно на порядок меньше порогового значения 1.2 мсд (см. (34)). Таким образом, выведенное пятипараметрическое решение для движения фотоцентра двойной системы не будет отброшено.

Заметим, что двойные системы других периодов создают меньшее смещение фотоцентра и, следовательно, ошибки, вызванные нелинейными движениями, также должны быть меньше.

Кроме того, медианное значение расстояния от Солнца до ОВ-ассоциаций из каталога Блаха и Хамфрис [5] составляет $r = 1.7$ кпк и, следовательно, медианное значение ошибок собственных движений должно быть в 1.7 раза меньше.