Астрономический журнал, 2021, T. 98, № 5, стр. 355-362

1. ВВЕДЕНИЕ

Еще в 1964 г. Я.Б. Зельдович обратил внимание, что свет во Вселенной распространяется так, что наблюдатель, применяющий стандартные космологические тесты для измерения угловых расстояний между объектами, получает кривизну пространства, которая оказывается несколько меньше кривизны, отвечающей средней плотности Вселенной [1]. В частности, если средняя плотность мира в точности равна критической плотности, то наблюдатель должен прийти к выводу, что Вселенная открыта. При критической плотности пространственное сечение плоское, а при меньшей плотности оно имеет отрицательную кривизну. В пространстве нулевой кривизны расстояние между близкими геодезическими увеличивается с ростом длин геодезических линейно, а в пространстве отрицательной кривизны оно растет экспоненциально. Это явление возникает из-за коллективного действия небольших пространственных неоднородностей кривизны. Именно его и должен заметить наблюдатель, конечно, если условия наблюдения позволят зафиксировать различие между линейным и экспоненциальным ростом. Сам физический эффект вполне воспринят современной космологией и в различных контекстах упоминается в работах по гравитационному линзированию, однако в количественном выражении оказывается невелик из‑за того, что флуктуации плотности малы, а плотность близка к критической [2].

Отмеченный Я.Б. Зельдовичем эффект имеет геометрическую природу и сводится к задаче о разбегании геодезических в римановом пространстве, кривизна которого вдоль геодезической может рассматриваться как случайный процесс (см. подробнее [3]). Природа этого эффекта не связана с четырехмерностью пространства-времени и с наличием временной координаты. Поскольку в данной работе мы не планируем изучать непосредственные космологические следствия идеи Я.Б. Зельдовича (они исчерпаны в его работе), мы говорим просто о разбегании геодезических на искривленном двумерном римановом пространстве. Отметим, что оригинальная работа Я.Б. Зельдовича была написана еще до формирования современной физики случайных сред, поэтому он решал задачу с помощью очень специального приема. О ее решении современными регулярными методами см. [3].

Скорость роста расстояния между геодезическими (геодезического отклонения) можно определять в различных терминах. В случайной среде можно говорить о показателе Ляпунова (выборочной скорости роста) и о скоростях роста нормированных статистических моментов геодезического отклонения. В своей работе Зельдович предположил, что эти скорости роста не должны совпадать, скорость роста статистических моментов должна быть больше показателя Ляпунова, а высшие моменты должны расти быстрее низших.

Со временем было осознано, что задача Зельдовича представляет собой удобный модельный пример для изучения развития различных неустойчивостей в случайной среде, а отмеченное Зельдовичем соотношение скоростей роста различных характеристик геодезического отклонения является проявлением общего свойства развития неустойчивостей в случайных средах, которое со временем получило название перемежаемости [4].

В своей работе Зельдович приходил к правильным ответам, используя рассуждения, не требующие явного вычисления скоростей роста. При определенных предположениях о свойствах кривизны как случайного процесса (подробнее см. ниже) методами математической теории произведения случайных матриц удается вычислить показатель Ляпунова, однако эти методы не позволяют вычислить среднеквадратическую скорость роста и скорость роста старших моментов [5]. Это удавалось сделать лишь в модели флуктуаций кривизны в виде белого шума [6]. Данная модель задания случайного процесса, определяющего кривизну, плохо совместима с представлением о свойствах сил тяготения, и ее желательно заменить на более физические предположения. Это и составляет содержание настоящей работы.

Подчеркнем, что в своей работе Зельдович высказал целый ряд плодотворных мыслей, лишь отчасти связанных с интересующей нас идеей. Они развивались в последующие годы рядом авторов, включая самого Зельдовича (см., напр., [7–10]). Хотя подробный обзор восприятия в современной науке идей, высказанных Зельдовичем в своей работе, представлял бы несомненный интерес, это не является целью данной работы.

2. ОСНОВНЫЕ УРАВНЕНИЯ

Одной из важных технических находок в работе Зельдовича было осознание того, что изучаемое явление можно свести к поведению геодезических на двумерном римановом пространстве, натянутом на проекции двух близких лучей света на пространственное сечение космологической модели, и перемасштабировать результаты для нестационарной многомерной космологической модели.

Рассмотрим две геодезические на двумерном римановом пространстве, пересекающиеся в одной точке, причем угол $\theta $ между геодезическими в точке пересечения мы считаем малой величиной. Отложим на обеих геодезических расстояние (в метрике риманова многообразия) $x$ в одну и ту же сторону от точки их пересечения. Расстояние (в той же метрике) между полученными точками в первом приближении по $\theta $ составляет $\theta y$, где величина $y$ известна в римановой геометрии как поле Якоби (а в физике $\theta y$ известно как отклонение геодезических). Оказывается (см., напр., [11]), что поле Якоби удовлетворяет уравнению

которое называется уравнением Якоби. Здесь производные берутся по переменной $x$, а $K$ – гауссова кривизна многообразия, единственная ненулевая компонента четырехмерного тензора Римана, которая рассматривается как случайный процесс. Предполагая, что движение точек по геодезическим происходит с постоянной скоростью, расстояние $x$ можно понимать и как время, за которое точки проходят данное расстояние, так что мы имеем дело с эволюцией величины $y$ в случайной среде $K$. Мы предполагаем, что случайный процесс $K$ устроен следующим образом. На каждом отрезке вида $n\Delta \leqslant x < (n + 1)\Delta $ (их называют промежутками обновления) кривизна $K$ не зависит от $x$ и рассматривается как случайная величина с нулевым средним значением и конечной дисперсией ${{\sigma }^{2}}$, а на различных отрезках эти случайные величины статистически независимы и одинаково распределены (например, по гауссовскому закону). Такая модель случайного процесса называется моделью с обновлением. Возможны и иные предположения о строении случайного процесса $K$, которые тоже можно изучать подобными методами (см., напр., [12, 13]). Предлагаемый метод не требует специального вида статистического распределения кривизны, хотя для получения конкретного результата необходимо, конечно, задать какое-то конкретное распределение. Мы это сделаем ниже.

Для решения уравнения (1) необходимо задать начальные условия. Мы будем предполагать, что $y(0) = 0$, $y{\kern 1pt} '(0) = 1$.

Перепишем уравнение (1) как систему уравнений первого порядка, введя двумерный вектор ${\mathbf{z}}$, первая координата которого равна ${{z}_{1}} = y$, вторая координата – ${{z}_{2}} = y{\kern 1pt} '\Delta $ (постоянный множитель $\Delta $, равный длине промежутка обновления, введен для согласования размерностей компонент вектора ${\mathbf{z}}$). Тогда в матричной форме

Естественно, вектор ${\mathbf{z}}(x)$ тоже является (векторным) случайным процессом.

3. УРАВНЕНИЕ ДЛЯ КОРРЕЛЯЦИОННОГО ТЕНЗОРА

Построим теперь корреляционный тензор для случайного процесса ${\mathbf{z}}$. Для этого введем двухиндексный тензор

средним значением (вычисленным по распределению $K$) которого и является корреляционный тензор. Дифференцируя произведение ${{z}_{{ij}}} = {{z}_{i}}{{z}_{j}}$ и используя (2), нетрудно показать, что ${{z}_{{ij}}}$ удовлетворяет уравнению где компоненты тензора ${{A}_{{ijkl}}}$ равны

На каждом промежутке обновления уравнение (3) является уравнением с постоянными коэффициентами, так что его решение представляет собой значение тензора ${{z}_{{ij}}}$ в точке $n\Delta $, умноженное на экспоненту от тензора ${{A}_{{ijkl}}}$, которую мы обозначим $B_{{ijkl}}^{n}$, поскольку она тоже, конечно, является тензором четвертого ранга. Нам пришлось снабдить этот тензор индексом $n$, который указывает, на каком именно промежутке обновления проведено вычисление. Естественно, что конкретные значения тензора зависят от номера промежутка и являются случайными.

Теперь мы можем усреднить уравнение (3). Сначала сделаем это на первом отрезке $0 \leqslant x < \Delta $. Для этого достаточно вычислить среднее значение тензора $B_{{ijkl}}^{0}$. Это среднее вычисляется покомпонентно.

Поскольку на концах промежутков обновления значения $K$ заменяются на независимые, мы можем провести такое же вычисление последовательно на следующих промежутках обновления, причем среднее значение тензора $B$ не зависит от $n$ в силу одинаковости распределений $K$ на различных промежутках обновления.

Для удобства дальнейших рассуждений сделаем перенумеровку переменных. Введем вспомогательную четырехмерную величину ${\mathbf{w}}$, компоненты которой равны, соответственно, ${{w}_{1}} = {{z}_{{11}}}$, ${{w}_{2}} = {{z}_{{12}}}$, ${{w}_{3}} = {{z}_{{21}}}$, ${{w}_{4}} = {{z}_{{22}}}$. Величина ${\mathbf{w}}$ удовлетворяет уравнению

где

Решение этого уравнения на каждом промежутке обновления выражается через матрицу $\hat {B} = exp(\hat {A}\Delta )$. Соответственно, эволюция осредненной величины $\left\langle {\mathbf{w}} \right\rangle $ выражается через матрицу $\left\langle {\hat {B}} \right\rangle $. Переходя от одного промежутка обновления к другому, $\left\langle {\mathbf{w}} \right\rangle $ приближается к собственному вектору матрицы $\left\langle {\hat {B}} \right\rangle $, отвечающему старшему собственному значению, которое, в свою очередь, определяет скорость роста компонент $\left\langle {\mathbf{w}} \right\rangle $. Поскольку среднее значение компоненты ${{w}_{1}} = {{z}_{{11}}}$ равно среднему значению ${{y}^{2}}$, то старшее собственное значение матрицы $\left\langle {\hat {B}} \right\rangle $ определяет и скорость роста второго момента поля Якоби.

4. ВЫЧИСЛЕНИЕ СОБСТВЕННОГО ЧИСЛА

Для начала найдем явный вид матрицы $\hat {B} = $ $ = exp(\hat {A}\Delta )$, используя определение матричной экспоненты. В силу простого устройства самой матрицы $\hat {A}$ ее степени выписываются явно. Вид матрицы $\hat {B}$ зависит от знака $K$. Для удобства записи временно введем безразмерную кривизну $k = K{{\Delta }^{2}}$. Тогда при $k \geqslant 0$ имеем:

при k < 0 матрица $\hat {B}$ имеет вид: Заметим, что было бы достаточно выписать только одну матрицу, например, для $k \geqslant 0$, тогда для отрицательных $k$ из соотношений $\sqrt k = i\sqrt { - k} $ и $sin\sqrt k = sin(i\sqrt { - k} ) = i\sqrt { - k} $ следовал бы вид второй матрицы.

Покажем далее, как в случае малых $\Delta $ можно получать приближенные оценки для собственных чисел матрицы $\left\langle {\hat {B}} \right\rangle $. Точный ответ, конечно, будет зависеть от распределения величины $K$. Нашей целью будет получить разложение собственных чисел в ряд по степеням $\Delta $.

Начнем с простого случая, в котором матрица $\left\langle {\hat {B}} \right\rangle $ вычисляется явно. Для этого предположим, что $K$ принимает всего два значения $ \pm \sigma $ с одинаковой вероятностью. Тогда $\left\langle {\hat {B}} \right\rangle $ является полусуммой матриц (4) и (5), и можно выписать явное характеристическое уравнение. Коэффициенты состоят из комбинаций $co{{s}^{2}}\sqrt {\sigma {{\Delta }^{2}}} $ и $^{2}\sqrt {\sigma {{\Delta }^{2}}} $. Мы выпишем результат их разложения по степеням $\Delta $. Приближенное характеристическое уравнение с точностью до членов порядка ${{\Delta }^{4}}$ имеет вид

Ниже мы поясним, почему более правильно смотреть на полученное разложение как на ряд по степеням $\Delta $, а не $\sigma $, но пока займемся решением уравнения (6). Нетрудно заметить, что одним из корней является $\lambda = 1$. Оставшееся кубическое уравнение имеет вид Пусть $\gamma = {{\sigma }^{2}}{{\Delta }^{4}}{\text{/}}3$, тогда (7) примет вид Стандартной заменой переменных $\lambda = y + (3 + $ $ + \;4\gamma ){\text{/}}3$ приведем кубическое уравнение к канонической форме (отметим, что теперь все преобразования делаются с точностью до $\gamma $):

Еще одна стандартная замена $y = t + 11\gamma {\text{/}}3t$, известная как подстановка Виета, с точностью до $\gamma $ приводит к уравнению

Корни последнего уравнения выражаются легко, и с учетом всех сделанных замен можно выписать решения (7): где $\delta = {{(\sigma {{\Delta }^{2}}{\text{/}}2)}^{{2/3}}}$. Старшее собственное значение ${{\lambda }_{1}}$ и определяет рост решений расширенной системы (3).

Заметим, что прийти к уравнению (6) можно было несколько иным путем, который применим для более широкого класса распределений $K$. Идея состоит в том, чтобы заменить математическое ожидание функции от случайной величины математическим ожиданием от первых нескольких слагаемых ее ряда Тейлора. Вопрос о точности подобной аппроксимации довольно сложен, поскольку нужно принимать во внимание не только локальное поведение функции вблизи точки разложения, но и характер роста моментов случайной величины. В нашей ситуации дело упрощается, поскольку мы рассматриваем произведение случайной величины и малого параметра $\Delta $. Тогда с точностью до членов порядка Δ⁴ для произвольной достаточно гладкой в окрестности нуля функции $f$ и симметричного распределения $K$ можно записать

Пользуясь данным приближением для вычисления элементов матрицы $\left\langle {\hat {B}} \right\rangle $, а также тем, что для симметричного распределения $K$ первый момент равен нулю, мы приходим в точности к выражению (6), в котором ${{\sigma }^{2}} = {\text{D}}K = \left\langle {{{K}^{2}}} \right\rangle $. Заметим, что следующие уточняющие поправки в (9) содержат моменты случайной величины $K$ более старших порядков, которые, в общем случае, не выражаются через ее дисперсию ${{\sigma }^{2}}$. По этой причине (6), вообще говоря, не является разложением по степеням $\sigma $.

Таким образом, лишь в первом приближении для симметричного распределения $K$ старшее собственное значение матрицы $\left\langle {\hat {B}} \right\rangle $ определяется всего двумя параметрами – дисперсией распределения $K$ и длиной интервала обновления $\Delta $.

Осталось в явном виде пересчитать найденное старшее собственное значение в терминах скорости роста второго статистического момента поля Якоби (1).

5. СВЯЗЬ СОБСТВЕННОГО ЗНАЧЕНИЯ И СКОРОСТИ РОСТА

Напомним (см. [4]), что скоростью роста $p$-го статистического момента называется величина

где $p$ – номер статистического момента, причем скорость роста ${{\gamma }_{p}}$ нормирована на номер момента $p$ в знаменателе уравнения (10), чтобы сделать сравнимыми результаты для моментов различного порядка.

Найденное в (8) старшее собственное число ${{\lambda }_{1}}$ по построению характеризует рост среднего квадрата поля Якоби $y$. А именно, это означает, что на расстоянии в $n$ интервалов обновления величина $\left\langle {{{y}^{2}}} \right\rangle $ увеличивается в $\lambda _{1}^{n}$ раз. С другой стороны, согласно определению скорости роста (10), это же изменение запишется как $\exp (2n\Delta {{\gamma }_{2}})$. Отсюда следует связь между собственным значением и скоростью роста второго момента:

Подставляя выражение для ${{\lambda }_{1}}$ из (8), с точностью до слагаемых порядка ${{\Delta }^{3}}$ получаем

Отметим, что при переходе к разложению (11) нужно учитывать ограниченную область сходимости ряда для логарифма, отсюда вытекают ограничения на возможные значения произведения $\sigma {{\Delta }^{2}}$. Численные оценки показывают, что для применимости формулы разложения логарифма должно выполняться условие $\sigma {{\Delta }^{2}} < 0.37$.

Конечно, мы предполагаем, что для более сложных распределений старшее собственное значение нашей матрицы и среднеквадратичная скорость роста вычисляются численно.

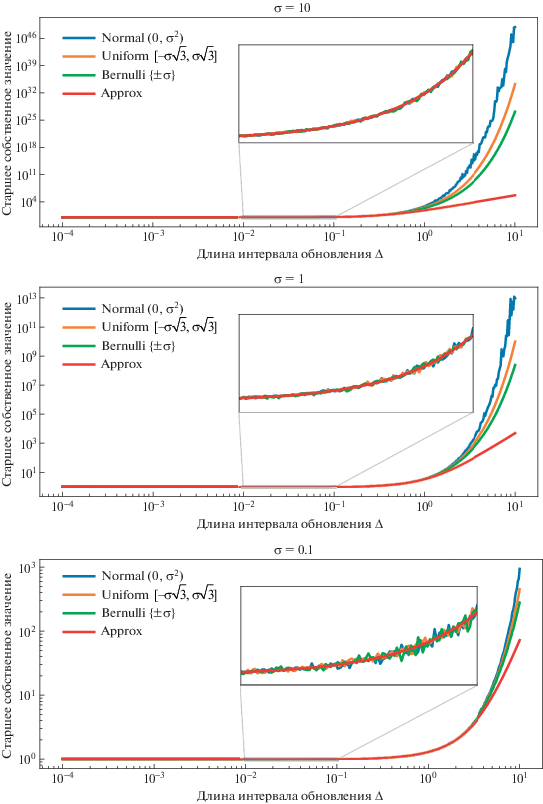
Для демонстрации согласия полученных оценок с численным экспериментом мы рассмотрим три семейства распределений $K$: Бернулли со значениями $ \pm \sigma $, равномерное на отрезке $[ - \sigma \sqrt 3 $, $\sigma \sqrt 3 ]$ и гауссовское с нулевым средним и дисперсией ${{\sigma }^{2}}$. Параметры распределений подобраны так, чтобы дисперсия $K$ в точности была ${{\sigma }^{2}}$. Дальше мы рассмотрим $\sigma = 0.1$, 1 и 10, и значения $\Delta $, пробегающие интервал от ${{10}^{{ - 4}}}$ до 10. Для каждого значения $\sigma $ и $\Delta $ смоделируем ${{10}^{4}}$ реализаций случайной величины $K$, численно оценим матрицу $\left\langle {\hat {B}} \right\rangle $ и найдем ее старшее собственное значение. Результаты изобразим на графиках зависимости старшего собственного значения от величины $\Delta $ и сравним с аппроксимацией, которую мы получили в (8). На рис. 1 можно видеть, что для малых $\Delta $ результаты практически неотличимы и хорошо согласуются с полученной аппроксимацией, для больших значений $\Delta $ появляется расхождение, поскольку начинают преобладать более старшие моменты распределения $K$.

Наконец, на рис. 2 показаны зависимости скорости роста от длины интервала обновления $\Delta $ для разных дисперсий распределения $K$. Заметим, что при малых $\Delta $ скорость роста определяется первым слагаемым ${{(\sigma {\text{/}}2)}^{{2/3}}}{{\Delta }^{{1/3}}}$, а значение $\Delta $, при котором теряется точность разложения логарифма, приблизительно совпадает с тем значением $\Delta $, на котором теряется точность аппроксимации для собственных значений (см. рис. 1). По-видимому, для малых значений произведения $\sigma {{\Delta }^{2}}$ хорошим приближением является ${{\gamma }_{2}} \approx {{(\sigma {\text{/}}2)}^{{2/3}}}{{\Delta }^{{1/3}}}$.

Отметим один частный случай, когда $\Delta = 1$ и $K$, равномерно распределенное на отрезке $[ - 1,\;1]$, рассмотренный ранее в работе [5]. Для него мы получаем приблизительное значение математического ожидания матрицы $\hat {B}$,

и старшее собственное значение ${{\lambda }_{1}} \approx 2.53$ (фор-мула (8) также дает близкое значение ${{\lambda }_{1}} \approx 2.49$). В пересчете на скорость роста получаем ${{\gamma }_{2}} \approx 0.46$. Заметим, что найденное в [5] значение для показателя Ляпунова $\lambda \approx 0.2132$ оказывается, как и должно быть, меньше скорости роста старшего момента ${{\gamma }_{2}}$. Отметим также, что прямое применение формулы (11) дает завышенное значение ${{\gamma }_{2}} \approx 0.50$. Это связано с тем, что данный случай лежит за границами применимости разложения логарифма.

6. ВЫВОДЫ И ОБСУЖДЕНИЕ

Мы показали, как вычислить среднеквадратичную скорость роста геодезического отклонения в задаче Зельдовича. Трудность вычисления состоит в том, что нас интересует квадратичная величина (квадрат геодезического отклонения), для которой ранее не удавалось получить линейного уравнения. Мы разрешаем эту трудность, вводя билинейную величину (тензор второго порядка), одна из компонент которой является квадратом геодезического отклонения. Этот прием широко применяется в теории турбулентности. Например, при изучении эволюции магнитной энергии в потоке проводящей жидкости неясно, как получить уравнение для этой квадратичной величины, но зато удается построить уравнение для корреляционного тензора магнитного поля [14].

Применяемый нами прием никак не ограничен конкретным видом уравнения геодезических отклонений, а применим к переносу произвольной физической величины, описывающейся системой обыкновенных линейных дифференциальных уравнений со случайными коэффициентами. К таким уравнениям сводятся многие задачи об исследовании развития неустойчивостей в случайных средах с помощью перехода в лагранжеву систему отсчета (см., напр., [4]).

С помощью рассмотренного приема можно изучать и рост статистических моментов более высокого порядка. Например, для исследования скорости роста четвертой степени геодезического отклонения потребуется ввести тензор четвертого порядка ${{Z}_{{ijkl}}} = {{z}_{i}}{{z}_{j}}{{z}_{k}}{{z}_{l}}$. Это, естественно, потребует рассмотрения матриц более высокого порядка и сделает вычисления более громоздкими, но принципиально не изменит их характер.

Что касается перспектив применения полученных результатов и всего имеющегося объема знаний об эффекте Зельдовича, мы еще раз отмечаем, что на близких к нам по времени этапах развития Вселенной этот эффект количественно очень невелик. В принципе, не исключена возможность того, что совместное действие многих небесных тел, находящихся вблизи одного луча зрения, которые по отдельности не приводят к гравитационному линзированию, может в совокупности привести к возникновению гравитационной линзы. Для оценки вероятности возникновения подобной линзы нужно, конечно, уметь вычислять разнообразные моменты поля Якоби. Однако это направление исследований не выглядит особенно многообещающим. Гораздо более важным выглядит эффект Зельдовича для исследования самой ранней Вселенной, поскольку он явно говорит о том, что влияние неоднородностей размывает понятие критической плотности для космологической модели и заставляет задуматься о том, как корректно сформулировать уравнения Эйнштейна для флуктуирующего пространства-времени. Представляется, что сформулированная Зельдовичем задача удачно изолирует из этой большой проблемы фрагмент, который поддается исследованию без последовательной математической проработки понятия псевдориманова многообразия со случайной метрикой и одновременно указывает на возможное направление фундаментального развития общей теории относительности. Авторы надеются в будущем внести посильный вклад в это развитие.