Астрономический журнал, 2021, T. 98, № 5, стр. 431-440
Анализ цифровой модели физической поверхности Луны, построенной на основе спутниковых альтиметрических измерений
А. О. Андреев 1, 2, 3, Е. Н. Ахмедшина 1, Л. А. Нефедьев 1, Ю. А. Нефедьев 1, *, Н. Ю. Демина 1
1 Казанский (Приволжский) федеральный университет
Казань, Россия
2 Московский государственный университет
Москва, Россия
3 Казанский государственный энергетический университет
Казань, Россия
* E-mail: star1955@yandex.ru
Поступила в редакцию 23.12.2019
После доработки 29.01.2021
Принята к публикации 29.01.2021
Аннотация
При выполнении космических миссий по исследованию Солнечной системы было получено значительное количество данных о геофизических и морфологических свойствах планет. Это позволило создать новое научное направление – сравнительную планетологию. Данное направление сосредоточено не только на развитии эволюционных и космогонических концепций, но и на описании природных явлений, происходящих на небесных телах. Целью настоящей работы является исследование цифровой модели физической поверхности Луны, построенной на измерениях, выполненных в ходе космической миссии “Kaguya”. Для построения и анализа такой модели использовался многопараметрический гармонический анализ оптических и альтиметрических данных, полученных в ходе осуществления окололунных спутниковых наблюдений. Разработанный подход предполагает создание регрессионных гармонических моделей на основе разложения альтиметрических данных и анализ их фрактальных размерностей. Для исследуемой системы получен спектр фрактальных оценок как для различных локальных зон, так и для полной модели лунной сферы.
1. ВВЕДЕНИЕ
Анализ структуры и эволюции небесных тел включает в себя различные методы статистического многопараметрического анализа [1–3]. В настоящее время одним из перспективных направлений исследования структуры, материалов и их свойств разнородных природных объектов является фрактальная геометрия. Основное свойство фрактальных объектов – подобие при масштабировании. Описание экспериментальных данных с помощью фракталов позволяет рационально представлять их.
Количественной мерой, характеризующей распределение структуры в пространстве, является фрактальная размерность $D$. Исследования фрактальной размерности позволяют изучать не только структуру, но и связь между структурой и процессами ее формирования. Фрактальные структуры были обнаружены и в динамических системах. В частности, методы фрактального анализа позволяют количественно описать модели поверхностей небесных тел. В работе [4] подробно описаны основные подходы при фрактальном анализе параметров тел Солнечной системы. Однако в отличие от предыдущих исследований, в настоящей работе использовался авторский метод более точного учета коэффициентов самоподобия и цветовых фрактальных размерностей с целью нахождения самоподобных структур на основе многопараметрического анализа.
2. ПОСТРОЕНИЕ МОДЕЛИ ФИЗИЧЕСКОЙ ПОВЕРХНОСТИ ЛУНЫ
Основным методом исследования рельефа Луны является численно-аналитический метод, который подразумевает разложение спутниковых высотных данных в гармонические ряды по сферическим функциям.
При построении цифровой модели физической поверхности Луны использовалось регрессионное моделирование. С этой целью был разработан программный комплекс “Автоматизированная система преобразования координат” (ASTC). Программные модули обеспечивают решение нормальных и переопределенных систем линейных алгебраических уравнений. Решение последних реализовано на основе МНК. В отличие от существующих специализированных программных пакетов (СПП), созданных российскими и зарубежными командами и ориентированных на обработку данных с использованием методов математической статистики, ASTC разработана конкретно для решения селенодезических задач с учетом ряда необходимых для этого условий и позволяет выполнять процедуры регрессионного моделирования селенографических и гравиметрических параметров Луны. Данный программный комплекс имеет возможность перебора большого количества вариантов решения с целью оценки ошибок неизвестных. При этом проводится сопоставление остатка с основными параметрами МНК при определении параметров модели. Величины неизвестных и их ошибок, значения элементов матрицы корреляции, внутренние и внешние показатели качества, используемые для определения надежности и получения рекомендаций по структурированию модели, могут играть роль выходных данных. В большинстве случаев программа выполняет определенную процедуру поиска наиболее надежной структуры модели. Существует возможность использования пошагового регрессионного анализа, который применяется для получения модели при меньшем количестве наблюдений $n$, чем число коэффициентов $p$. Это возможно, поскольку дополнительные члены вводятся в модель последовательно, и процедура расчета может закончиться раньше, чем появятся избыточные решения.
Модель лунного рельефа может быть построена с использованием вариаций разложения радиусов-векторов $R({{\lambda }_{i}},{{\varphi }_{i}})$ по сферическим функциям в следующем виде:
(1)
$R({{\lambda }_{i}},{{\varphi }_{i}}) = F({{\bar {C}}_{{nm}}},{{\bar {S}}_{{nm}}},{{\bar {P}}_{{nm}}}),$В результате разложений по гармоническим коэффициентам была построена цифровая модель высотных данных с точностью покрытия одна точка на один квадратный градус поверхности, что является вполне достаточным для наших исследований.
3. МЕТОД АНАЛИЗА ДАННЫХ ЦИФРОВОЙ ВЫСОТНОЙ КАРТЫ ЛУНЫ
Наибольшей чувствительностью обладают фрактальные размерности по нескольким свойствам исследуемых структур [5].
Пусть структура рассматриваемого объекта может быть представлена частично упорядоченным множеством $A({{N}^{2}})$, где ${{N}^{2}}$ – число элементов ${{a}_{{ij}}}$ в множестве ${{a}_{{ij}}} \in A({{N}^{2}})$, где $i,\;j = 1,\; \ldots ,\;N$.
Будем считать, что частичный порядок на конечном множестве задается диаграммой Хассе (рис. 1) и элементы множества обладают некоторыми свойствами ${{H}_{\xi }}(a)$ (размер, цвет, объем, форма и т.д.), присущими только элементам данного множества $\forall {{a}_{{ij}}}$ $({{a}_{{ij}}} \in \{ a\,|\,{{H}_{\xi }}(a)\} )$. Если общих свойств несколько, $\xi > 1$, то описание множества должно быть произведено с помощью нескольких фрактальных размерностей.
Представим множество $A({{N}^{2}})$ в виде
(2)
$A({{N}^{2}}) = {{Q}^{{(1)}}}({{n}^{2}}) \cup {{Q}^{{(2)}}}({{n}^{2}}) \cup \ldots {{Q}^{{({{\alpha }^{2}})}}}({{n}^{2}}),$Будем считать, что существуют верхняя и нижняя грани множества $A({{N}^{2}})$ по всем свойствам ${{H}_{\xi }}(a)$:
причем ${{G}_{\xi }} \in A({{N}^{2}})$ и ${{g}_{\xi }} \in A({{N}^{2}})$. В этом случае возможно провести шкалирование множества $A({{N}^{2}})$ по всем свойствам. Для этого сопоставим верхней ${{G}_{\xi }}$ и нижней ${{g}_{\xi }}$ грани множества $A({{N}^{2}})$ некоторые числа ${{R}_{\xi }}$ и ${{r}_{\xi }}$ соответственно. Тогда в пространстве каждого свойства все множество $A({{N}^{2}})$ может быть покрыто кубом объема ${{V}_{\xi }} = $ $ = {{({{R}_{\xi }} - {{r}_{\xi }})}^{3}}$. Причем на каждый элемент множества $A({{N}^{2}})$ будет приходиться область в пространстве свойств площадью ${{s}_{\xi }} = {{({{R}_{\xi }} - {{r}_{\xi }})}^{2}}{\text{/}}{{N}^{2}}$. Соотвественно, каждое подмножество ${{Q}^{{(k)}}}({{n}^{2}})$ можно покрыть кубами с $\vartheta = \tfrac{{{{V}_{\xi }}}}{{{{\alpha }^{3}}}}$, а их число определится величиной $sup{{Q}^{{(k)}}}({{n}^{2}}) \in {{Q}^{{(k)}}}({{n}^{2}})$ во введенной выше шкале свойств, причем площадь, занимаемая элементами подмножества, будет ${{S}_{\xi }}({{n}^{2}}) = {{s}_{\xi }}{{n}^{2}}$.Фрактальную размерность ${{D}_{\xi }}$ множества $A({{N}^{2}})$ по свойству ${{H}_{\xi }}(a)$ определим угловым коэффициентом зависимости $log{{\Gamma }_{\xi }}({{n}^{2}})$ от $log{{s}_{{{{n}^{2}}}}}$, где ${{\Gamma }_{\xi }}({{n}^{2}})$ – число несоприкасающихся поверхностей кубов, покрывающих подмножество ${{Q}^{{(k)}}}({{n}^{2}})$:
(5)
${{D}_{\xi }} = \sum\limits_\gamma \frac{{log{{\Gamma }_{\xi }}(n_{{\gamma + 1}}^{2}) - log{{\Gamma }_{\xi }}(n_{\gamma }^{2})}}{{\left| {(log{{S}_{\xi }}(n_{{\gamma + 1}}^{2}))} \right| - \left| {(log{{S}_{\xi }}(n_{\gamma }^{2}))} \right|}}\frac{{{{\alpha }_{{\gamma + 1}}} - {{\alpha }_{\gamma }}}}{{N - 1}}.$(7)
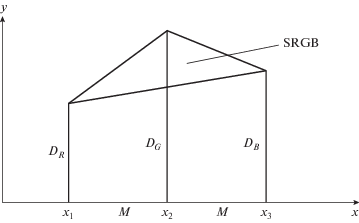
$D_{\xi }^{0} = \frac{{log{{\Gamma }_{\xi }}({{N}^{2}}) - log{{\Gamma }_{\xi }}(1)}}{{\left| {(log{{S}_{\xi }}({{N}^{2}}))} \right| - \left| {(log{{S}_{\xi }}(1))} \right|}}.$Из рис. 2 следует, что
(8)
$\begin{gathered} SRGB = \left( {\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{D}_{R}}}&1 \\ {{{x}_{2}}}&{{{D}_{G}}}&1 \\ {{{x}_{3}}}&{{{D}_{B}}}&1 \end{array}} \right) = \\ = \frac{1}{2}M[ - 2({{D}_{R}} + {{D}_{B}}) + ({{D}_{G}} + {{D}_{B}}) + ({{D}_{R}} + {{D}_{G}})], \\ \end{gathered} $Однако в случае черно-белого изображения SRGB = 0. Поэтому введем величину $S0$.
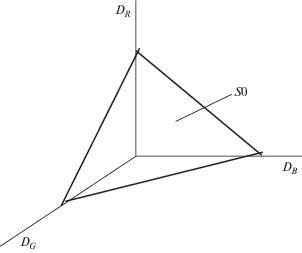
Из рис. 3 следует, что
где(10)
$\begin{gathered} a = \sqrt {D_{R}^{2} + D_{G}^{2}} ,\quad b = \sqrt {D_{R}^{2} + D_{B}^{2}} , \\ c = \sqrt {D_{B}^{2} + D_{G}^{2}} ,\quad p = \frac{1}{2}(a + b + c). \\ \end{gathered} $В случае неупорядоченного множества $A(N)$ его описание с помощью фрактальных размерностей ${{D}_{\xi }}$ по свойству ${{H}_{\xi }}(a)$ приведет к $k = 1, \ldots ,N!$ различных $D_{\xi }^{{(k)}}$. Однако набор свойств каждого элемента множества $A(N)$ может быть охарактеризован фрактальной размерностью этого множества свойств. В этом случае $k = 1, \ldots ,N$.
4. АНАЛИЗ РЕЗУЛЬТАТОВ ЦИФРОВОЙ КАРТЫ ПОВЕРХНОСТИ ЛУНЫ
Как результат работы, выполнены два вида исследований:
1. Проведен анализ 173 гистограмм распределения параметра SGRB по лунной долготе и широте с целью определения идентичных по структуре областей лунной поверхности.
2. Исследованы 253 области на лунной поверхности для определения максимальных значений коэффициентов самоподобия и распределения параметра SGRB.
Следует отметить, что физический смысл коэффициентов самоподобия заключается в том, что данные области наиболее полно соответствуют фрактальной логарифмической зависимости, в свою очередь близость параметра SGRB для двух областей подтверждает структурное подобие этих областей.
Области, имеющие одинаковые значения параметра SGRB и максимальные значения коэффициента самоподобия, обладают самоподобными свойствами, не зависящими от масштабирования, и именно эти области, по всей видимости, имеют и сходное эволюционное происхождение.
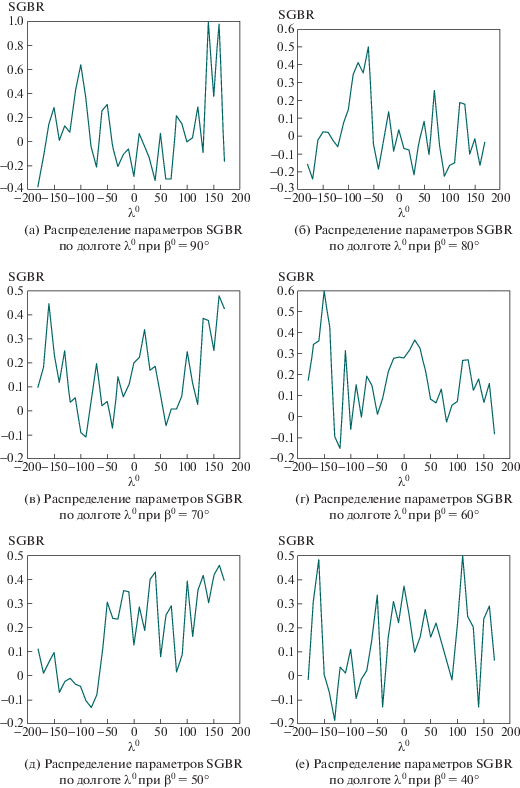
На рис. 5, как пример, показаны гистограммы распределения параметра SGRB по лунной долготе, а на рис. 6 – по широте.
Для анализа гистограмм распределения параметра SGRB по лунной поверхности введем градацию значений параметра SRGB. Так как по значениям этот параметр меняется от $0$ до $ \pm 60$, введем 6 градаций: 0 < SRGB ≤ 20, 20 < SRGB ≤ ≤ 40, 40 < SRGB ≤ 60, –60 ≤ SRGB < –40, –40 ≤ ≤ SRGB < –20, –20 ≤ SRGB < 0. То есть малые, средние и большие значения абсолютных величин параметра SRGB. Анализ соответствующих гистограмм приводит к следующим результатам (см. табл. 1).
Таблица 1.
Распределение параметра SGRB
| № | SRGB | Выделяются области | |
|---|---|---|---|
| 1 | –60 < SRGB < –40 | ($150^\circ < \lambda < 165^\circ $, | $ - 45^\circ < \beta < - 30^\circ )$ |
| ($75^\circ < \lambda < 120^\circ $, | $ - 30^\circ < \beta < - 15^\circ $) | ||
| ($75^\circ < \lambda < 90^\circ $, | $ - 15^\circ < \beta < 45^\circ $) | ||
| ($45^\circ < \lambda < 60^\circ $, | $ - 15^\circ < \beta < 0^\circ $) | ||
| ($60^\circ < \lambda < 75^\circ $, | $15^\circ < \beta < 30^\circ $) | ||
| ($45^\circ < \lambda < 60^\circ $, | $45^\circ < \beta < 60^\circ $) | ||
| ($60^\circ < \lambda < 75^\circ $, | $60^\circ < \beta < 75^\circ $) | ||
| ($30^\circ < \lambda < 45^\circ $, | $60^\circ < \beta < 75^\circ $) | ||
| ($ - 75^\circ < \lambda < - 60^\circ $, | $ - 45^\circ < \beta < - 30^\circ $) | ||
| ($ - 165^\circ < \lambda < - 150^\circ $, | $ - 45^\circ < \beta < - 15^\circ $) | ||
| ($ - 150^\circ < \lambda < - 135^\circ $, | $ - 30^\circ < \beta < 30^\circ $) | ||
| ($75^\circ < \lambda < 120^\circ $, | $ - 30^\circ < \beta < - 15^\circ $) | ||
| 2 | –40 < SRGB < –20 | ($150^\circ < \lambda < 165^\circ $, | $ - 75^\circ < \beta < - 45^\circ )$, |
| ($120^\circ < \lambda < 150^\circ $, | $ - 60^\circ < \beta < - 30^\circ $), | ||
| ($135^\circ < \lambda < 165^\circ $, | $45^\circ < \beta < 60^\circ $), | ||
| ($75^\circ < \lambda < 105^\circ $, | $60^\circ < \beta < 90^\circ $), | ||
| ($ - 120^\circ < \lambda < 0^\circ $, | $75^\circ < \beta < 90^\circ $), | ||
| ($ - 180^\circ < \lambda < - 165^\circ $, | $ - 75^\circ < \beta < - 15^\circ $) | ||
| 3 | –20 < SRGB < 40 | ($150^\circ < \lambda < 175^\circ $, | $15^\circ < \beta < 45^\circ $), |
| ($105^\circ < \lambda < 135^\circ $, | $ - 75^\circ < \beta < - 60^\circ $), | ||
| ($ - 75^\circ < \lambda < - 30^\circ $, | $ - 75^\circ < \beta < - 45^\circ $), | ||
| ($ - 180^\circ < \lambda < - 165^\circ $, | $60^\circ < \beta < 75^\circ $) | ||
| 4 | –20 < SRGB < 20 | Вся остальная поверхность лунной сферы | |
Анализ распределения параметра SRGB по лунной поверхности показывает, что сами исследуемые регионы имеют структуры, связанные с величинами перепадов высот на лунной поверхности. Это является результатом того, что параметр SRGB строится на основе информации о высотах, закодированной в цветовых характеристиках поверхности. Поэтому минимальные абсолютные значения параметра SRGB соответствуют областям с минимальным разбросом высот. Такая сложная структура поверхности может быть объяснена разными условиями формирования разных участков поверхности. Тем не менее для определенных областей присутствуют подобные структуры.
На рис. 7 построена модель распределения усредненных значений коэффициента самоподобия 〈SRGB〉 для областей 15° × 15°, а на рис. 8, соответственно, модель распределения параметра SGRB.
Рис. 7.
Модель распределения усредненных значений коэффициента самоподобия для областей 15° × 15°. Шкала соответствует изменению коэффициента самоподобия.

Рис. 8.
Модель распределения усредненных значений параметра SGRB для областей 15° × 15°. Шкала соответствует изменению параметра SGRB.

Анализ рис. 7 показывает, что распределение коэффициента самоподобия по различным областям лунной поверхности меняется в пределах от 0.8 до 1, что указывает на значительное изменение ее структуры от области к области.
В табл. 2 приведены результаты выборки самоподобных областей на поверхности Луны. Следует отметить, что параметр SRGB характеризует структурное подобие двух областей, а максимальное значение коэффициента подобия говорит об их фрактальном самоподобии. Таким образом, если для определенного значения параметра SRGB выбираются области с максимальным значением коэффициента самоподобия, мы получаем области, которые с большой долей вероятности были эволюционно сформированы при действии одинаковых селенохимических процессов. Первый столбец в табл. 2 – номер по порядку, второй столбец содержит значения 〈SRGB〉 – усредненных параметров SRGB, и в последнем столбце приведено описание самоподобных областей. Как следует из таблицы, наибольшее количество самоподобных областей наблюдается для значения параметра SRGB, равного $ - 10$. В данном случае такое значение параметра SRGB означает, что эти области имеют незначительный перепад на лунной поверхности возвышений и впадин. Также следует отметить, что параметр SGRB принимает наибольшие значения на обратной стороне Луны в основном в северной части лунной сферы. Для видимой стороны в большей части преобладают отрицательные значения SGRB, с увеличением в положительную область шкалы в южной части сферы. В результате можно сделать выводы, что при формировании лунной поверхности в северной части сферы обратной стороны Луны и южной части на видимой стороне преобладало вытеснение внутренних масс Луны. В частности, в процессе воздействия крупных плотных ударников. Остальная лунная поверхность подвергалась воздействию ударных тел более пористого содержания. Предварительным результатом можно считать, что в северной части сферы обратной стороны Луны и южной части видимой может быть сосредоточено наибольшее число полезных ресурсов, образованных падением медленных (скорость падения менее 12 км/с) твердых тел. Причем более пористых ударников в 1.5–2.0 раза больше, чем твердых. Плотные ударники содержат наибольшее количество металлических компонентов. Определенную связь полученные нами выводы имеют с результатами из работы [6] по исследованию фрактальных свойств Меркурия. Там авторы приходят к выводу, что южное полушарие Меркурия меньше подвергалось ударам астероидов и метеоритов, чем северное. Одно из объяснений данного явления заключается в разной преобладающей ориентации плоскости орбит пористых и плотных малых небесных тел относительно плоскости эклиптики в процессе эволюции Солнечной системы.
Таблица 2.
Самоподобные области на поверхности Луны
| 〈SRGB〉 | Самоподобные области |
|---|---|
| Область в районе кратера Метон ($73^\circ 34\prime $ с.ш. $19^\circ 38\prime $ в.д.) | |
| Область в районе кратера Платон ($51^\circ 37\prime $ с.ш. $9^\circ 23\prime $ з.д.) | |
| Область между кратером Аристотель ($50^\circ 14\prime $ с.ш. $17^\circ 19\prime $ в.д.) и Озером смерти ($45^\circ 00\prime $ с.ш. $27^\circ 12\prime $ в.д.) | |
| Область в районе кратера Шайн ($32.6^\circ $ с.ш. $172.5^\circ $ в.д.) | |
| Область между кратерами Аль Бируни ($18^\circ 04\prime $ с.ш. $92^\circ 37\prime $ в.д.) и Эдисон ($25.0^\circ $ с.ш. $99.1^\circ $ в.д.) | |
| Область выше кратера Ингирами ($47^\circ 29\prime $ ю.ш. $68^\circ 57\prime $ з.д.) | |
| –10 | Область в районе кратера Пуанкаре ($56^\circ 52\prime $ ю.ш. $163^\circ 59\prime $ в.д.) |
| Область выше кратера Крамера ($53.6^\circ $ с.ш. $127.6^\circ $ з.д.) | |
| Область в районе кратера Де ля Рю ($59^\circ 01\prime $ с.ш. $52^\circ 50\prime $ в.д.) | |
| Область в районе кратера Лютер ($33^\circ 12\prime $ с.ш. $24^\circ 09\prime $ в.д.) | |
| Область в районе кратера Шуберт ($2.8^\circ $ с.ш. $81.0^\circ $ в.д.) | |
| Область между кратерами Венделин ($16^\circ 28\prime $ ю.ш. $61^\circ 33\prime $ в.д.) и Каптейн ($10^\circ 47\prime $ ю.ш. $70^\circ 35\prime $ в.д.) | |
| Область в районе кратера Ридберг ($46^\circ 26\prime $ ю.ш. $96^\circ 26\prime $ з.д.) | |
| Область в районе кратера Де Руа ($55^\circ 14\prime $ ю.ш. $98^\circ 59\prime $ з.д.) | |
| Область в районе кратера Чемберлин ($58.9^\circ $ с.ш. $95.7^\circ $ в.д.) | |
| Область в районе кратера Планк ($57^\circ 23\prime $ ю.ш. $135^\circ 05\prime $ в.д.) | |
| Область в районе кратера Нансен ($81^\circ 10\prime $ с.ш. $95^\circ 23\prime $ в.д.) | |
| –25 | Область в районе кратера Сегерс ($47.1^\circ $ с.ш. $127.7^\circ $ в.д.) |
| Область в районе кратера Нильсен ($31^\circ 48\prime $ с.ш. $51^\circ 46\prime $ з.д.) | |
| Область в районе кратера Лауритсен ($27^\circ 32\prime $ ю.ш. $96^\circ 19\prime $ в.д.) | |
| –30 | Область севернее кратера Петерман ($74^\circ 21\prime $ с.ш. $67^\circ 53\prime $ в.д.) |
| Область в районе кратера Маундер ($14^\circ 31\prime $ ю.ш. $93^\circ 53\prime $ з.д.) |
Для наглядности на рис. 9 приведена 3D-модель распределения параметра SGRB по поверхности Луны. Анализ рис. 9 показывает, что параметр SGRB имеет большую чувствительность к изменению структуры лунной поверхности.
5. ЗАКЛЮЧЕНИЕ
В работе проведен анализ современных способов решения вопросов лунной селенографии на основе данных, полученных в ходе лунных космических миссий. В частности, были исследованы альтиметрические данные миссии “Kaguya” [7]. Обнаружена необходимость многократной обработки наборов космических данных из-за постоянного совершенствования методов обработки, на основе которых разрабатывается построение глобальных селенодезических опорных сетей. Это направление стало особенно важным после появления селеноцентрических систем, основанных на окололунных спутниковых наблюдениях [8]. Также в настоящее время создаются базы данных по глобальным измерениям высот лунной физической поверхности для будущих проектов, что должно повысить точность селеноцентрических опорных сетей [9], а также производится анализ динамических и геометрических моделей лунной фигуры. Такой анализ включает изучение систем координат селенографических каталогов и спутниковых наблюдений с учетом взаимного расположения центра симметрии Луны и ее центра масс [10]. На основании данных миссии “Kaguya” была построена модель лунной физической поверхности в цифровом виде и исследована методом многопараметрической фрактальной геометрии [11, 12]. Проведен анализ 173 гистограмм распределения параметра SGRB по лунной долготе и широте. В результате определена корреляция областей с максимальными значениями коэффициента самоподобия и областей с одинаковыми величинами параметра SRGB. Найденные таким образом области, по всей видимости, имеют и сходное эволюционное происхождение.
Фрактально оцененная цифровая модель распределения высот лунной поверхности может быть использована в имитационной модели для определения селенографических координат поверхности [13], для тестирования точности их определения [14], при исследовании лунных ударников [15], выполнения работ по структурному и вещественному строению Луны [16], создании теории физической либрации Луны [17, 18]. Все это является важным фактором для выбора будущей площадки для прилунения и создания роботизированных лунных баз.
Список литературы
D. L. Turcotte, J. Geophys. Res. Solid Earth 92, id. E597 (1987).
T. Stepinski, M. Collier, P. McGovern, and S. Clifford, J. Geophys. Res. Planets 109(E2), id. E02005 (2004).
A. D. Linkevich, Nonlinear Phenom. Complex Syst. 2, 93 (1999).
P. R. Massopust, Fractal functions, fractal surfaces, and wavelets (San Diego: Academic Press, 2014).
L. A. Nefed’ev, D. L. Nefed’eva, A. R. Sakhbieva, and D. R. Khasanova, Intern. J. Development Res. 06, 9760 (2016).
B. Ranguelov and R. Iliev, Russ. J. Earth Sciences 19, id. ES6001 (2019).
H. Araki, S. Tazawa, H. Noda, Y. Ishihara, et al., Science 323, 897 (2009).
Y. A. Nefedyev, A. Andreev, N. Petrova, N. Y. Demina, and A. Zagidullin, Astron. Rep. 62, 1016 (2018).
K. Churkin, A. Andreev, Y. A. Nefedyev, N. Petrova, and N. Y. Demina, Astron. Rep. 62, 1042 (2018).
Y. Nefedyev, S. Valeev, R. Mikeev, A. Andreev, and N. Varaksina, Adv. Space Res. 50, 1564 (2012).
N. Varaksina, Y. Nefedyev, K. Churkin, R. Zabbarova, and S. Demin, in J. Phys. Conf. Ser. (IOP Publishing, 2015), 661, 012014 (2015).
A. O. Andreev, Y. A. Nefed’ev, L. A. Nefed’ev, E. N. Akh-medshina, N. Y. Demina, and A. A. Zagidullin, Uchenye Zapiski Kazanskogo Universiteta. Seriya Fiziko-Matematicheskie Nauki 162, 223 (2020).
A. Andreev, Y. Nefedyev, L. Nefediev, N. Demina, A. Bag-rov, N. Petrova, and A. Zagidullin, in J. Phys. Conf. Ser. (IOP Publishing, 2020), 1697, 012016 (2010).
A. Andreev, Y. A. Nefedyev, N. Y. Demina, L. Nefediev, N. Petrova, and A. Zagidullin, Astron. Rep. 64, 795 (2020).
M. Sergienko, M. Sokolova, Y. A. Nefedyev, and A. Andreev, Astron. Rep. 64, 1087 (2020).
E. Kronrod, V. Kronrod, O. Kuskov, and Y. A. Nefedyev, Dokl. Earth Sci. (Springer, 2018), 483, 1475 (2018).
A. Zagidullin, V. Usanin, N. Petrova, Y. A. Nefedyev, A. Andreev, and T. Gudkova, Astron. Rep. 64, 1093 (2020).
N. Petrova, Y. A. Nefedyev, A. Andreev, and A. Zagidullin, Astron. Rep. 64, 1078 (2020).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал