Астрономический журнал, 2021, T. 98, № 6, стр. 443-452
Сравнительный анализ задачи об истечении атмосфер экзопланет
П. Б. Исакова 1, *, Я. Н. Павлюченков 1, Е. С. Калиничева 1, В. И. Шематович 1
1 Институт астрономии Российской академии наук
Москва, Россия
* E-mail: isakovapb@inasan.ru
Поступила в редакцию 17.11.2020
После доработки 22.01.2021
Принята к публикации 29.01.2021
Аннотация
Задача о моделировании истечений атмосфер планет важна для понимания эволюции экзопланетных систем и интерпретации их наблюдений. Современнные теоретические модели атмосфер экзопланет становятся все более детальными и многокомпонентными, что затрудняет вхождение в эту область новых исследователей. В статье впервые представлены результаты тестирования газодинамического метода, входящего в состав разработанной ранее авторами аэрономической модели. Проведенные тесты свидетельствуют о корректности метода, что подтверждает возможность его использования. Для моделирования планетного ветра предложена новая гидродинамическая модель с феноменологической функцией нагрева УФ-излучением звезды. Общая картина течения в представленной модели хорошо согласуется с результатами, полученными в более детальных аэрономических моделях. Предложенная модель может быть использована для методических целей и для тестирования газодинамических модулей самосогласованных химико-динамических моделей планетного ветра.
1. ВВЕДЕНИЕ
Открытие экзопланет, безусловно, является одним из самых значимых достижений современной астрономии. За последние десятилетия мы прошли путь от предположений об их существовании до обнаружения нескольких тысяч внесолнечных планет11 [1]. Космический телескоп Кеплер показал неожиданные конфигурации планетных систем, отличающихся от Солнечной. Наблюдаемое распределение радиусов экзопланет, определенных в транзитных наблюдениях, является непрерывным [2], простираясь от планет земного типа с размерами $ < {\kern 1pt} 1{{R}_{ \otimes }}$ до планет-гигантов с радиусами $ > {\kern 1pt} 4{{R}_{{\text{J}}}}$. Многие из них могут иметь каменные ядра, окруженные тонкими оболочками газов водорода и гелия. Недавний анализ подобных Нептуну экзопланет с низкой плотностью показал, что они не должны удерживать свои водородные оболочки из-за чрезвычайно высоких газодинамических темпов атмосферных потерь, если текущие оценки их больших радиусов или малых масс точны [3, 4]. Из этих результатов можно сделать вывод, что в некоторых случаях используемые оценки могут занижать массы или преувеличивать радиусы планет (из-за облаков на больших высотах). Или можно заключить, что горячие нептуны способны иметь более высокие альбедо, чем экзопланеты, подобные Юпитеру [3].
Атмосферы экзопланет очень разнообразны. Именно они являются ключом к пониманию физики и общих свойств экзопланет. Например, неожиданным оказалось открытие нескольких каменистых планет низкой массы с оболочками из легких газов H2 и/или H2O. Это указывает на то, что многие планеты, которые можно рассматривать как планеты земного типа, могут не полностью потерять свою первоначальную протоатмосферу из водорода и гелия [5–8]. Все это выводит на передний план вопросы моделирования наблюдательных проявлений атмосфер экзопланет в целом и биомаркеров, в частности, ведь одним из мировоззреченских аспектов изучения экзопланет является вопрос о существовании жизни на них.
Исследования планетных экзосфер не могут быть успешными без рассмотрения термосфер и ионосфер, которые обычно называются верхними атмосферами. И именно со структурой и свойствами верхних атмосфер связаны вопросы влияния родительских звезд. Верхняя атмосфера планеты под сильным звездным УФ-излучением может расширяться на большие расстояния от центра планеты. Это приводит к быстрым атмосферным потерям [9–11]. Такое явление, так называемое газодинамическое истечение (или планетный ветер), было теоретически изучено для планет Солнечной системы на ранних стадиях их эволюции [12–15]. Только в последние десятилетия появились возможности наблюдений газодинамического истечения для нескольких близких экзопланет [16–19]. Были предприняты попытки численного моделирования этого явления [20–26]. В том числе были исследованы трехмерные эффекты, связанные с влиянием звездного ветра и магнитного поля на структуру и наблюдательные проявления экзопланет [27, 28].
Как видно из этих работ, теоретическое изучение атмосфер планет активно развивается. Вместе с тем начинающему исследователю трудно разобраться в основах теории атмосфер. Классической можно считать задачу о динамике сферически-симметричной атмосферы, имеющей непосредственное отношение к вопросу о диссипации газовой оболочки. Эта задача близка к задаче о звездном ветре, аналитическое решение которой было получено еще в 60-е годы XX века в работах Паркера [29, 30]. Однако планетные атмосферы обладают своей спецификой, связанной с процессами нагрева и охлаждения. Исследования образования и эволюции первичных и вторичных атмосфер и потенциальной обитаемости экзопланет имеют первостепенное значение для ряда современных естественно-научных проблем, важнейшими из которых являются космогония Солнечной системы и происхождение жизни на Земле. В особенности это касается планет земного типа (суб-, экзо- и супер-земель) и планет класса суб-нептунов и планет-океанов, не имеющих аналогов в Солнечной системе.
Целью данной работы является тестирование метода, использованного ранее для расчета истечения атмосфер экзопланет [25, 31]. В статье рассматриваются результаты газодинамического моделирования изотермической атмосферы, а также представлена модель истечения атмосферы с простейшей функцией нагрева для приближенного воспроизведения потери атмосфер экзопланет. Статья будет полезна исследователям для тестирования газодинамических методов, предназначенных для моделирования планетного ветра.
2. ТЕСТИРОВАНИЕ ГАЗОДИНАМИЧЕСКОГО МЕТОДА
Воспроизведение динамики экзопланетной атмосферы основано на решении системы уравнений газодинамики:
(2)
$\frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}} \cdot \nabla ){\mathbf{v}} = - \frac{{\nabla P}}{\rho } - \frac{{GM{\mathbf{r}}}}{{{{r}^{3}}}},$(3)
$\frac{{\partial \varepsilon }}{{\partial t}} + ({\mathbf{v}} \cdot \nabla )\varepsilon = - \frac{P}{\rho }\nabla \cdot {\mathbf{v}} + \Gamma ,$Стационарное истечение атмосферы в случае ненулевой функции нагрева и охлаждения можно описать следующей системой уравнений для переменных $v$ и $\varepsilon $:
(6)
$\left[ {v - (\gamma - 1)\frac{\varepsilon }{v}} \right]\frac{{dv}}{{dr}} + (\gamma - 1)\frac{{d\varepsilon }}{{dr}} = (\gamma - 1)\frac{{2\varepsilon }}{r} - \frac{{GM}}{{{{r}^{2}}}},$(7)
${v}\frac{{d\varepsilon }}{{dr}} + (\gamma - 1)\varepsilon \frac{{d{v}}}{{dr}} = - (\gamma - 1)\frac{{2\varepsilon {v}}}{r} + \Gamma .$(8)
$\frac{d}{{dr}}\left[ {\frac{{{{{v}}^{2}}}}{2} + \gamma \varepsilon - \frac{{GM}}{r}} \right] = \frac{\Gamma }{{v}},$(9)
$\frac{d}{{dr}}\left[ {\varepsilon {{{v}}^{{\gamma - 1}}}{{r}^{{2\gamma - 2}}}} \right] = \frac{{\Gamma {{r}^{{2\gamma - 2}}}}}{{{{{v}}^{{2 - \gamma }}}}}.$Выбор газодинамического метода, в свою очередь, является ответственной задачей, поскольку метод должен правильно воспроизводить характерные особенности решения и не приводить к артефактам. Для моделирования динамики сферически-симметричной атмосферы в работе [25] использовался полностью консервативный лагранжевый неявный метод, описанный в книге [32]. Этот метод хорошо зарекомендовал себя при решении задачи о коллапсе протозвездного облака, см. [33]. В задаче о коллапсе облака данный метод успешно воспроизводит все особенности аналитического решения [34]. Однако корректность применения данного метода к задаче расчета истечения атмосферы в работе [25] показана не была. В данном разделе мы продемонстрируем как данный численный метод справляется с задачей изотермического истечения атмосферы, для которой известно точное решение.
Используемый численный метод основан на конечно-разностной аппроксимации исходной системы газодинамических уравнений и является лагранжевым, т.е. газ не перетекает через границы ячеек, но сами ячейки движутся и сжимаются (растягиваются) вместе с веществом. Значения всех величин, кроме скорости, задаются в центрах ячеек, а скорость – на границах ячеек. При расчетах использовалась 2001 ячейка, при этом начальная дискретная сетка имеет однородное разбиение по $r$. Левая граница расчетной области жестко зафиксирована, т.е. скорость на левой границе равна нулю. Правая граница расчетной области может двигаться, при этом в качестве граничного условия задается давление во внешней среде (во вспомогательной ячейке, прилегающей справа к границе). Положение границы атмосферы отслеживается автоматически по координате границы последней ячейки. Более подробно метод описан в работе [25].
Рассмотрим атмосферу вокруг планеты с массой $M = 0.07{{M}_{{\text{J}}}}$ и радиусом $a = 0.35{{R}_{{\text{J}}}}$. Эти значения близки к параметрам теплого нептуна GJ 436b (см. табл. 1).. Температуру искусственно выберем равной ${{T}_{0}} = 8575$ К, что соответствует безразмерному параметру Джинса $\lambda = 10$ – отношению гравитационной энергии на внутренней границе к тепловой энергии (без учета фактора $i{\text{/}}2$):
где ${{T}_{0}}$ – температура изотермической атмосферы. Пусть плотность на внутренней границе атмосферы ${{\rho }_{0}} = {{10}^{{ - 12}}}$ г/см3. Введем безразмерную плотность в виде $\eta = \rho {\text{/}}{{\rho }_{0}}$. Левая граница расчетной области жестко привязана к значению $x = 1$, где $x = r{\text{/}}a$. В начальный момент времени правая граница атмосферы находится на безразмерном расстоянии $x = 2$, а распределение плотности внутри области $1 \leqslant x \leqslant 2$ соответствует гидростатическому, за исключением условия на границе, при котором давление в последней ячейке может не совпадать с давлением во внешней среде.Рассмотрим результаты для нескольких граничных условий. В качестве первого граничного условия на правой границе было зафиксировано давление, соответствующее безразмерной плотности ${{\eta }_{{\text{b}}}} = 4 \times {{10}^{{ - 4}}}$. Данное значение меньше плотности на внешней границе первоначальной атмосферы ($\eta \approx 7 \times {{10}^{{ - 3}}}$ при $x = 2$), поэтому начальное распределение должно эволюционировать вследствие расширения внешних областей атмосферы под действием градиента давления на границе атмосферы. Значение ${{\eta }_{{\text{b}}}}$ на порядок выше значения ${{\eta }_{\infty }} \approx 4.5 \times {{10}^{{ - 5}}}$, соответствующего равновесной плотности изотермической атмосферы на бесконечности для изотермического случая, ${{\eta }_{\infty }} = {{e}^{{ - \lambda }}}$. На верхних панелях рис. 1 показаны результаты численного моделирования динамики данной атмосферы в безразмерных переменных $\eta $ и $y$, где $y$ – отношение кинетической энергии молекулы газа к ее тепловой энергии (без учета фактора $i{\text{/}}2$):
На момент времени $1.5 \times {{10}^{4}}$ с атмосфера расширяется, при этом ее правая граница достигает значения $x = 6$, а значения $y$ близки к аналитическим стационарным значениям. Достигнув $x = 6.5$ на момент $2.5 \times {{10}^{4}}$ с, атмосфера прекращает расширение – ее самые внешние слои начинают сжиматься под действием внешнего давления. Скачки на распределениях $y(x)$ и $\eta (x)$ являются следствием неравновесности начальных распределений. В дальнейшем атмосфера осциллирует, при этом ее внешняя граница колеблется возле значения $x = 4.3$. Со временем атмосфера постепенно приходит к равновесию, причем полученное распределение плотности очень близко к аналитическому гидростатическому распределению. Таким образом, при фиксированном граничном условии на плотность ${{\eta }_{{\text{b}}}} > {{\eta }_{\infty }}$, атмосфера приходит к гидростатическому равновесию, причем ее граница соответствует тому $x$, на котором плотность аналитической гидростатической атмосферы совпадает с граничным условием.Рис. 1.
Результаты газодинамического моделирования изотермической атмосферы с фиксированными внешними граничными условиями на плотность. Верхние диаграммы: для граничной безразмерной плотности ${{\eta }_{b}} = 4 \times $ 10–4, нижние диаграммы – для ${{\eta }_{b}} = 4 \times $ 10–6. Штриховые линии на левых панелях соответствуют отрицательным скоростям, непрерывные линии – положительным скоростям.
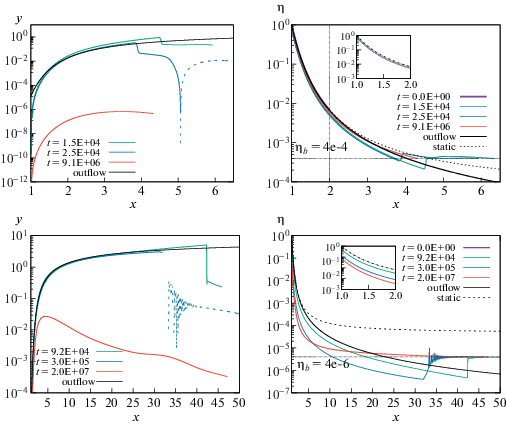
В том случае, если плотность на внешней границе выбрать ниже значения ${{\eta }_{\infty }}$, т.е. ${{\eta }_{{\text{b}}}} < {{\eta }_{\infty }}$, расширение атмосферы будет происходить до больших радиусов, но она со временем также придет к равновесию. Это связано с тем, что в использованном лагранжевом методе масса атмосферы конечна, а внутренняя граница расчетной области неподвижна. При расширении атмосферы область разрежения достигает первой ячейки, в результате чего плотность в ней падает. Со временем плотность во всей атмосфере падает настолько сильно, что внешнее граничное условие начинает соответствовать гидростатическому решению. Этот случай проиллюстрирован на нижних панелях рис. 1, где показана модель с граничным условием ${{\eta }_{{\text{b}}}} = 4 \times {{10}^{{ - 6}}}$. Отметим, что на промежуточных временах (см. кривые для $9.2 \times {{10}^{4}}$ с на нижних панелях на рис. 1) профили распределений $y(x)$ и $\eta (x)$ по форме близки к аналитическим для стационарного изотермического ветра. Осцилляции на распределениях $y(x)$ и $\eta (x)$ связаны с недостаточно эффективным подавлением численной неустойчивости искусственной вязкостью.
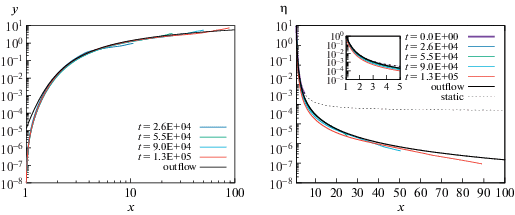
На рис. 2 показано численное решение для случая, когда плотность на внешней границе атмосферы на каждом временном шаге адаптивно меняется в соответствии с аналитическим решением для стационарного истечения. Другими словами, ${{\eta }_{{\text{b}}}}(x)$ берется из аналитической зависимости $\eta (x)$ для изотермического ветра. В данном случае полученные распределения $\eta (x)$ и $y(x)$ близки к аналитическим для изотермического ветра. Наибольшие отличия между численным и аналитическим решениями видны на распределении $y(x)$ в окрестности левой границы атмосферы. Это связано с тем, что внутренняя граница атмосферы в методе зафиксирована, т.е. скорость на границе равна нулю. В то же время в аналитическом стационарном решении скорость на левой границе не равна нулю, а соответствует конкретному значению ${{y}_{0}}$.
Рис. 2.
Газодинамическое решение с граничным условием по давлению на правой границе, взятым из стационарного решения. Решение представлено в безразмерном виде.
Проведенные тесты позволяют нам утверждать, что используемый газодинамический метод пригоден для моделирования истечения атмосфер экзопланет. Используя этот метод, в следующем разделе мы рассмотрим динамику истечения атмосферы в случае простой функции нагрева.
3. АТМОСФЕРА С ФЕНОМЕНОЛОГИЧЕСКОЙ ФУНКЦИЕЙ НАГРЕВА
Основными механизмами нагрева атмосфер экзопланет являются процессы фотоионизации и фотодиссоциации газа УФ-излучением центральных звезд (см,. напр., [25]). В то время как часть энергии УФ-квантов идет на разрушение связи электронов с атомами и атомов в молекулах, остаточная энергия уносится продуктами реакций (главным образом, электронами). Эта кинетическая энергия продуктов фотопроцессов в конечном итоге и приводит к нагреву газа. Детальное моделирование этих процессов представляет собой отдельную и сложную задачу. Здесь мы не будем моделировать процессы ионизации, диссоциации, рекомбинации и другие микрофизические процессы, ответственные за нагрев и охлаждение атмосферы. Вместо этого будет использована модельная функция нагрева, имитирующая нагрев в результате фотоионизации газа:
где ${{F}_{0}}$ – поток излучения, $\kappa $ – коэффициент поглощения, $\tau = \kappa \Sigma $ – оптическая толщина, $\Sigma $ – лучевая плотность газа, отсчитываемая от внешней границы атмосферы до текущей позиции. В рамках данного описания предполагается, что газ преимущественно нагревается в окрестности $\tau = 1$. Действительно, при $\tau \ll 1$ газ должен быть полностью ионизован и не должен участвовать в нагреве, а в области $\tau \gg 1$ излучение не проникает и, следовательно, не нагревает эту область. Отметим, что оптическая толщина $\tau $ в нашем подходе зависит от лучевой концентрации нейтральных и ионизованных компонентов, а не от лучевой концентрации только нейтрального газа. По мере истечения атмосферы газ, находящийся первоначально в области прогрева, движется наружу, расширяется и становится прозрачным к УФ-излучению. Множитель 3.57 выбран для нормировки интеграла по полной оптической толщине. Этот подход является феноменологическим приближением, однако для физически более обоснованного описания необходимо вычислять содержание нейтрального и ионизованного газа в рамках более сложной (аэрономической) модели. В описанной модели газ может охлаждаться только за счет совершения работы, т.е. за счет расширения.Описанная выше модель не требует детального моделирования кинетических процессов, но приводит (как мы увидим в дальнейшем) к качественно верной картине истечения и легко воспроизводима. Последнее представляется важным для тестирования методов расчета динамики атмосфер. Параметрами введенной функции нагрева являются ${{F}_{0}}$ и $\kappa $. Параметр ${{F}_{0}}$ описывает общий поток энергии УФ-излучения, поглощаемый атмосферой. Параметр $\kappa $ определяет пространственное положение области эффективного нагрева. Учитывая наш предыдущий вывод о важности внешнего граничного условия при моделировании истечения атмосферы, следует выделить еще один ключевой параметр для данной задачи, а именно давление на внешней подвижной границе ${{P}_{{{\text{out}}}}}$.
Рассмотрим атмосферу вокруг планеты, параметры которой близки к теплому нептуну GJ 436b (см. табл. 1). Масса и радиус планеты, приведенные в таблице, взяты с сайта http://www.exoplanet.eu, начальная температура и поток взяты такими же, как в работе [35]. Коэффициент поглощения выбирается нами как отношение сечения ионизации атома водорода ${{\sigma }_{{\text{H}}}}$ на длине волны 912 Å, к массе атома водорода ${{m}_{{\text{H}}}}$: $\kappa = {{\sigma }_{{\text{H}}}}{\text{/}}{{m}_{{\text{H}}}}$. В базовой модели предполагается, что атмосфера состоит из молекулярного водорода, при этом показатель адиабаты равен 7/5. В начальный момент времени атмосфера находится в гидростатическом равновесии, при этом давление на ее внешней границе равно давлению во внешней среде ${{P}_{{{\text{out}}}}}$.
Таблица 1.
Параметры базовой модели атмосферы с феноменологической функцией нагрева
| Параметр | Обозначение | Значение |
|---|---|---|
| Масса планеты, ${{M}_{J}}$ | $M$ | 0.07 |
| Радиус планеты, ${{R}_{J}}$ | $a$ | 0.35 |
| Начальная температура, K | ${{T}_{0}}$ | 750 |
| Поток УФ-излучения, эрг/(с см2) | ${{F}_{0}}$ | ${{10}^{3}}$ |
| Коэффициент поглощения, см2/г | $\kappa $ | $1.5 \times {{10}^{6}}$ |
| Плотность на внутренней границе, г/см3 | ${{\rho }_{0}}$ | ${{10}^{{ - 10}}}$ |
| Давление на внешней границе, дин/см2 | ${{P}_{{{\text{out}}}}}$ | ${{10}^{{ - 6}}}$ |
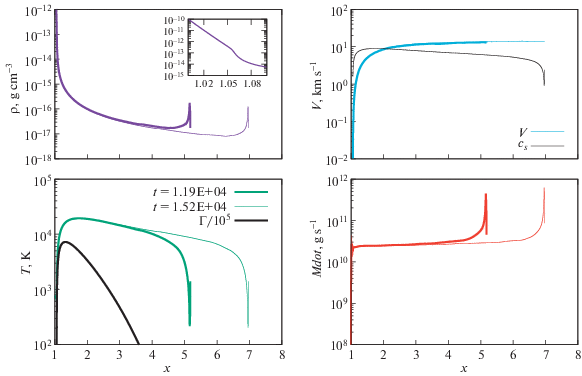
На рис. 3 показаны распределения плотности, скорости, температуры и темпа истечения в базовой модели для двух моментов времени. На момент времени $1.52 \times {{10}^{4}}$ с внешняя граница атмосферы достигла $ \sim 7$ радиусов планеты, при этом темп истечения внутри области $x < 6.5$ близок к постоянному по пространству и равен $3 \times {{10}^{{10}}}$ г/c. Кроме того, во внутренних областях истечения темп массопереноса для обоих приведенных на рис. 3 времен ($1.19 \times {{10}^{4}}$ с и $1.52 \times {{10}^{4}}$ с) совпадает – это свидетельствует об установившемся стационарном характере истечения. Структуру атмосферы можно условно разделить на несколько областей. В самой внутренней области ($x < 1.06$) атмосфера близка к гидростатическому равновесию, плотность в ней быстро падает с расстоянием, а скорость близка к нулю. В области $1.06 < x < 2$ происходит интенсивный нагрев атмосферы, это видно по распределнию $\Gamma (x)$, показанному на нижней левой панели рис. 3 черной линией. В области нагрева атмосферы скорость истечения быстро возрастает с расстоянием. Характер распределения плотности в этой области меняется, профиль становится более пологим (см. вкладку на верхней левой панели рис. 3). Температура достигает максимума $2 \times {{10}^{4}}$ K внутри области нагрева. В области $2 < x < 7$, где нагрев атмосферы является слабым, скорость истечения медленно растет с расстоянием. Температура в этой области медленно уменьшается с расстоянием из-за адиабатического расширения. В самых внешних областях истечения видны значительные градиенты всех физических величин. Эти проявления – результат начальных и граничных условий данного моделирования. Действительно, в начальный момент времени атмосфера находится в гидростатическом равновесии при постоянной температуре с монотонным распределением плотности. Однако в последующие моменты времени атмосфера начинает нагреваться внешним излучением, что повышает температуру и увеличивает давление в зоне поглощения излучения (находящейся на некотором удалении от границы). Это приводит к расширению оболочки и сжатию приграничных слоев, имеющих меньшую температуру. Это и приводит к формированию приграничных пиков на распределениях плотности. Эти особенности не влияют на распределения физических величин во внутренних слоях атмосферы. На правой верхней панели рис. 3 наряду с распределением скорости газа показано также распределение скорости звука. Видно, что течение становится сверхзвуковым на расстоянии $x = 2$. Отметим, что при полученном темпе истечения атмосферы масса планеты существенно не изменится за космологическое время.
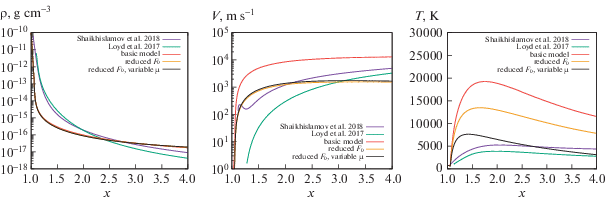
На рис. 4 показано сравнение полученных распределений с результатами аэрономических моделей для GJ 436b. Фиолетовым и зеленым цветами показаны результаты из работ [35] и [36] соответственно. В этих моделях наряду с гидродинамическими процессами рассчитываются ионизация, диссоциация, рекомбинация и другие фотохимические процессы с участием H2, H, He, H+, H$_{2}^{ + }$, H$_{3}^{ + }$ и др. Использованный нами подход в общих чертах воспроизводит морфологию распределений плотности, скорости и температуры, полученную в этих моделях, однако существенными являются количественные отличия. В частности, в газодинамической модели с феноменологической функцией нагрева получается завышенная в несколько раз температура (см. красные кривые, “basic model”). В работе [37] продемонстрировано, что эффективность нагрева атмосферы УФ-квантами должна составлять величину около 0.1. Учитывая это, мы провели дополнительный расчет с темпом нагрева ${{F}_{0}}$ в 10 раз меньше базового значения.
Рис. 4.
Сравнение результатов моделирования с аэрономическими моделями. Красным цветом показаны результаты базовой модели атмосферы c простой функцией нагрева, желтым – для модели с уменьшенным на порядок потоком излучения F0, черным – для модели с уменьшенным потоком УФ-излучения и переменным молекулярным весом, фиолетовым – результаты для аэрономической модели из работы [35], зеленым – результаты для аэрономической модели из работы [36].
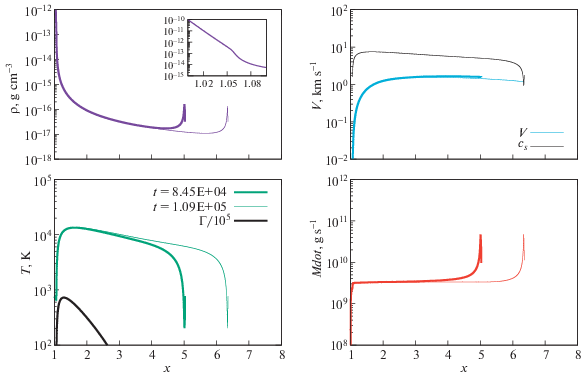
На рис. 5 показаны результаты расчета для модели с уменьшенным темпом нагрева. Морфологические особенности полученных распределений близки к тем, что наблюдаются в базовой модели, но скорость и темп истечения стали примерно на порядок величины ниже базовых. Максимальная температура в этой модели снизилась до ~13 000 К, (см. желтые кривые, “reduced ${{F}_{0}}$”, на рис. 4). Течение во всей области стало дозвуковым. Несмотря на уменьшение температуры, она в 2–3 раза превышает значения, полученные в аэрономических моделях.
В действительности для корректного воспроизведения физичеcкой структуры атмосферы (в том числе распределения температуры) необходимо учитывать большое число физических процессов. В частности, неотъемлемым элементом аэрономических моделей является расчет степени диссоциации и ионизации основных молекул. Знание ионизационной структуры позволяет корректно расcчитать поле УФ-излучения, проникающее в более внутренние слои атмосферы. Кроме того, диссоциация и ионизация молекул ведет к повышению концентрации свободных частиц. Локальное увеличение концентрации частиц (при постоянной температуре) приводит к повышению давления согласно уравнению (4). Таким образом, давление в зоне поглощения УФ-квантов растет не только за счет увеличения температуры, но и вследствие диссоциации и ионизации молекулярного водорода. Продемонстрируем влияние последнего эффекта на тепловую структуру атмосферы в рамках используемой газодинамической модели. Для этого будем считать, что средняя молекулярная масса (отношение маccы частицы к массе протона) зависит от оптической толщины $\tau $ следующим образом:
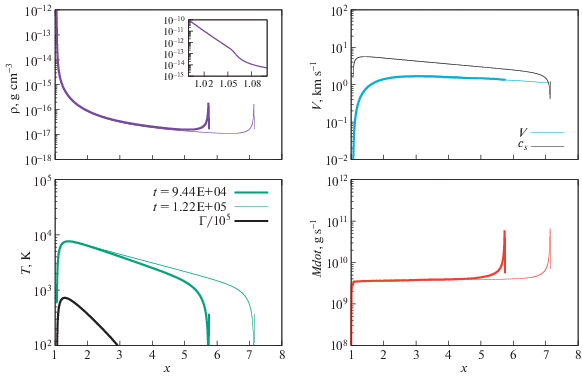
Это выражение описывает плавный переход $\mu $ от значения 1/2 в оптически-тонкой среде (где водород полностью диссоциирован и ионизован) до величины 2 при высокой оптической толщине (где водород находится в молекулярном состоянии). Соответственно, мы меняем количество степеней свободы частиц $i$ и показатель адиабаты газа $\gamma $, используя выражения: $i = 3 + \tfrac{4}{3}\left( {\mu - \tfrac{1}{2}} \right)$, $\gamma = \tfrac{{i + 2}}{i}$. Отметим, что при использовании пространственно-зависимых $\mu $ и $\gamma $ в газодинамическом коде мы сохраняем удельную тепловую энергию при преобразованиях между давлением, температурой и тепловой энергией.На рис. 4 черным цветом (“reduced ${{F}_{0}}$, variable $\mu $”) и рис. 6 показаны результаты для модели, где наряду с уменьшенным потоком излучения введены зависящие от оптической толщины средний молекулярный вес и показатель адиабаты.
Ключевой особенностью данной модели является уменьшение максимальной температуры до ~7000 К, что уже сопоставимо с результатами аэрономических моделей. Отметим также, что темп потери массы ($3 \times {{10}^{9}}$ г/c) не изменился по сравнению с моделью c постоянными значениями $\mu $, $\gamma $ и уменьшенным значением ${{F}_{0}}$.
Полезно сравнить полученный темп истечения $\dot {M}$ с оценкой, предложенной в работе [12]:
где сохранены исходные обозначения: $F$ – убегающий поток частиц в единицу времени в единичном телесном угле, $S$ – общий темп нагрева (в наших обозначениях соответствует ${{F}_{0}}$), ${{r}_{1}}$ – уровень, где оптическая толщина равна единице, ${{r}_{0}}$ – радиус планеты, $m$ – масса убегающих частиц (в нашем случае – масса атома водорода), $M$ – масса планеты. Выбирая ${{r}_{1}} \approx {{r}_{0}} = a$, ${{F}_{0}} = {{10}^{2}}$ эрг/(c см2), умножая формулу (14) на 4 $\pi $ и массу атома водорода, получим оценку для темпа истечения атмосферы $\dot {M} \approx 2 \times {{10}^{9}}$ г/с. Это значение хорошо согласуется с результатами нашего моделирования.Отметим, что динамика атмосферы, связанная с ее нагревом внешним излучением, является гораздо более сложным процессом, чем изотермический или адиабатический ветер. Именно в этой связи на первый план выходят численные методы решения задач о структуре и динамике планетных атмосфер. Представленные в данном разделе модели носят во многом иллюстративный, методический характер. Тем не менее предложенное феноменологическое описание нагрева может использоваться для приближенного моделирования истечения атмосферы без расчета ионизационно-химической структуры. Описанные модели также могут быть использованы для тестирования газодинамических методов, используемых в аэрономических моделях.
4. ЗАКЛЮЧЕНИЕ
Данная статья представляет собой своего рода введение в быстро развивающуюся область современной астрофизики, связанную с моделированием истечений планетных атмосфер. Из-за сложности получения аналитических решений даже в простейших приближениях на первый план выходят численные методы моделирования динамики атмосфер. Одним из ключевых элементов таких моделей является газодинамический метод, к которому предъявляются высокие требования в связи с большими градиентами физических величин, наличием сверхзвуковых режимов и необходимостью корректно воспроизводить квазиравновесные состояния. В данной работе продемонстрирован пример тестирования газодинамического модуля, который активно используется в программном комплексе для моделирования физической структуры атмосфер экзопланет [25, 31]. Показано, что при соответствующих граничных условиях используемый газодинамический метод воспроизводит аналитические решения для изотермической атмосферы.
Современные модели истечения атмосфер (так называемые аэрономические модели) включают в себя расчет ионизационной, химической и тепловой структуры атмосферы. В рамках таких моделей можно изучать самые тонкие физические эффекты и приблизиться к детальной интерпретации наблюдательных данных (см., напр., [35, 38]). Однако такие модели очень сложны и их трудно использовать в образовательных целях. В представленной статье показан пример того, что общую картину истечения атмосферы под воздействием УФ-нагрева со стороны звезды можно описать в рамках элементарной газодинамической модели с феноменологической функцией нагрева. В рамках данной модели продемонстрировано влияние темпа нагрева и переменного молекулярного веса на характеристики течения. Эта модель может быть полезна не только в методических целях, но и для тестирования газодинамических модулей аэрономических моделей, а также для приближенных расчетов в рамках моделей без моделирования детальной химической и ионизационной структуры.
Список литературы
L. D. Deming and S. Seager, J. Geophys. Res. Planets 122, 53 (2017).
J. F. Rowe, J. L. Coughlin, V. Antoci, T. Barclay, et al., Astrophys. J. Suppl. 217, id. 16 (2015), arXiv:1501.07286 [astro-ph.EP].
P. Cubillos, N. V. Erkaev, I. Juvan, L. Fossati, et al., Monthly Not. Roy. Astron. Soc. 466, 1868 (2017), arXiv:1611.09236 [astro-ph.EP].
L. Fossati, N. V. Erkaev, H. Lammer, P. E. Cubillos, et al., Astron. and Astrophys. 598, id. A90 (2017), arXiv:1612.05624 [astro-ph.EP].
H. Lammer, A. Stökl, N. V. Erkaev, E. A. Dorfi, et al., Monthly Not. Roy. Astron. Soc. 439, 3225 (2014), arXiv:1401.2765 [astro-ph.EP].
F. Tian and S. Ida, Nature Geoscience 8, 177 (2015).
R. Luger, R. Barnes, E. Lopez, J. Fortney, B. Jackson, and V. Meadows, Astrobiology 15, 57 (2015), arXiv:1501.06572 [astro-ph.EP].
H. Massol, K. Hamano, F. Tian, M. Ikoma, et al., Space Sci. Rev. 205, 153 (2016).
R. E. Johnson, M. R. Combi, J. L. Fox, W.-H. Ip, et al., Space Sci. Rev. 139, 355 (2008).
V. I. Shematovich, D. V. Bisikalo, and D. E. Ionov, in Characterizing Stellar and Exoplanetary Environments, edited by H. Lammer and M. Khodachenko, Astrophys. Space Sci. Library 411, 105 (2015).
V. I. Shematovich and M. Y. Marov, Physics Uspekhi 61, 217 (2018).
A. J. Watson, T. M. Donahue, and J. C. G. Walker, Icarus 48, 150 (1981).
D. M. Hunten, R. O. Pepin, and J. C. G. Walker, Icarus 69, 532 (1987).
E. Chassefiére, J. Geophys. Res. 101(E11), 26039 (1996).
A. N. Volkov, Monthly Not. Roy. Astron. Soc. 459, 2030 (2016).
A. Vidal-Madjar, A. Lecavelier des Etangs, J.-M. Désert, G. E. Ballester, R. Ferlet, G. Hébrard, and M. Mayor, Nature 422, 143 (2003).
A. Vidal-Madjar, J. M. Désert, A. Lecavelier des Etangs, G. Hébrard, et al., Astrophys. J. Letters 604, L69 (2004), astro-ph/0401457.
J. L. Linsky, H. Yang, K. France, C. S. Froning, J. C. Green, J. T. Stocke, and S. N. Osterman, Astrophys. J. 717, 1291 (2010), arXiv:1005.1633 [astro-ph.EP].
J. R. Kulow, K. France, J. Linsky, and R. O. P. Loyd, Astrophys. J. 786, id. 132 (2014), arXiv:1403.6834 [astro-ph.EP].
R. V. Yelle, Icarus 170, 167 (2004).
A. García Muñoz, Planet. Space Sci. 55, 1426 (2007).
R. A. Murray-Clay, E. I. Chiang, and N. Murray, Astrophys. J. 693, 23 (2009), arXiv:0811.0006 [astro-ph].
T. T. Koskinen, M. J. Harris, R. V. Yelle, and P. Lavvas, Icarus 226, 1678 (2013), arXiv:1210.1536 [astro-ph.EP].
I. F. Shaikhislamov, M. L. Khodachenko, Y. L. Sasunov, H. Lammer, K. G. Kislyakova, and N. V. Erkaev, Astrophys. J. 795, id. 132 (2014), arXiv:1506.03548 [astro-ph.EP].
D. E. Ionov, V. I. Shematovich, and Y. N. Pavlyuchenkov, Astron. Rep. 61, 387 (2017), arXiv:1706.02098 [astro-ph.EP].
J. E. Owen, Ann. Rev. Earth and Planet. Sciences 47, 67 (2019), arXiv:1807.07609 [astro-ph.EP].
A. A. Cherenkov, D. V. Bisikalo, and A. G. Kosovichev, Monthly Not. Roy. Astron. Soc. 475, 605 (2018).
A. G. Zhilkin and D. V. Bisikalo, Astron. Rep. 63, 550 (2019), arXiv:1903.09459 [astro-ph.EP].
E. N. Parker, Astrophys. J. 132, 821 (1960).
E. N. Parker, Astrophys. J. 139, 72 (1964).
D. E. Ionov, Y. N. Pavlyuchenkov, and V. I. Shematovich, arXiv:1803.04278 [astro-ph.EP] (2018).
A. A. Samarskii and Y. P. Popov, Differential methods of solving problems of gas dynamics (M.: Nauka, 1992).
Y. N. Pavlyuchenkov, A. G. Zhilkin, E. I. Vorobyov, and A. M. Fateeva, Astron. Rep. 59, 133 (2015), arXiv:1502.04835 [astro-ph.GA].
Y. N. Pavlyuchenkov, Emission of molecules and dust in prestellar and protostellar object (Dissertation for the degree of Doctor of Physical and Mathematical Sciences, Moscow, 2016).
I. F. Shaikhislamov, M. L. Khodachenko, H. Lammer, A. G. Berezutsky, I. B. Miroshnichenko, and M. S. Rumenskikh, Monthly Not. Roy. Astron. Soc. 481, 5315 (2018), arXiv:1811.08146 [astro-ph.EP].
R. O. P. Loyd, T. T. Koskinen, K. France, C. Schneider, and S. Redfield, Astrophys. J. Letters 834, id. L17 (2017), arXiv:1612.08962 [astro-ph.EP].
V. I. Shematovich, D. E. Ionov, and H. Lammer, Astron. and Astrophys. 571, id. A94 (2014), arXiv:1409.0730 [astro-ph.EP].
I. F. Shaikhislamov, L. Fossati, M. L. Khodachenko, H. Lammer, A. García Muñoz, A. Youngblood, N. K. Dwi-vedi, and M. S. Rumenskikh, Astron. and Astrophys. 639, id. A109 (2020), arXiv:2006.06959 [astro-ph.EP].
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал