1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 98, № 6, 2021

Астрономический журнал, 2021, T. 98, № 6, стр. 476-486

О причинах коллимированного распространения астрофизических и лабораторных джетов

И. Ю. Калашников 1, 2, *, А. В. Додин 3, И. В. Ильичев 4, В. И. Крауз 4, В. М. Чечеткин 1, 2, 4

1 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

2 Институт автоматизации проектирования РАН
Москва, Россия

3 Московский государственный университет им. М.В. Ломоносова, Государственный астрономический институт им. П.К. Штернберга
Москва, Россия

4 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

* E-mail: kalasxel@gmail.com

Поступила в редакцию 06.11.2020
После доработки 16.01.2021
Принята к публикации 29.01.2021

Полный текст (PDF)

Аннотация

Использование Z-пинчевых установок позволяет проводить хорошо управляемые и диагностируемые лабораторные эксперименты по исследованию лабораторных джетов, имеющих скейлинговые параметры, близкие к параметрам джетов молодых звезд. Это дает возможность наблюдать процессы, недоступные для астрономических наблюдений. Такие эксперименты проводятся на установке ПФ-3 (плазменный фокус, НИЦ “Курчатовский институт”), в которой испущенный плазменный выброс распространяется по пролетной камере сквозь окружающую среду на расстояние одного метра. В работе представлены результаты экспериментов с гелием, в которых наблюдался последовательный выход двух выбросов. Анализ этих результатов позволяет предположить, что после прохождения первого сверхзвукового выброса за ним образуется область с низкой концентрацией, так называемый вакуумный след, благодаря которому последующий выброс практически не испытывает сопротивления окружающей среды и распространяется коллимированно. Представленное в работе численное моделирование распространения двух выбросов подтверждает эту точку зрения. Используя масштабирующие законы и соответствующее численное моделирование астрофизических выбросов, показано, что этот эффект может также иметь значение и для джетов молодых звезд.

1. ВВЕДЕНИЕ

При исследовании процессов, происходящих в космосе, все большую роль начинает играть лабораторное моделирование. Несмотря на то что характерные пространственные и временные масштабы лабораторных экспериментов на много порядков меньше, чем у астрофизических, они могут быть масштабированы до астрофизических в той степени, в которой и те и другие подчиняются одним и тем же уравнениям, не имеющим собственного масштаба [1, 2]. При этом исследование таких течений in vitro позволяет гораздо лучше измерить имеющиеся параметры, чем это можно было бы сделать благодаря наблюдениям. К тому же лабораторные условия можно изменять, таким образом изучая отклик системы на внешние воздействия, что крайне важно для проверки предсказаний теоретических моделей.

В настоящий момент многие группы по всему миру пытаются, используя законы масштабирования, воссоздать экспериментально астрофизические условия при аккреции, коллимации и последующем распространении плазмы около молодых звезд. Как правило, в подобных экспериментах изучается динамика вещества на масштабах около нескольких сантиметров, причем генерация плазменных образований происходит обычно в условиях, близких к вакууму. Подобные опыты проводят как на плазменных установках [3, 4], так и на лазерных [5–7].

Интерес именно к лабораторному моделированию струйных выбросов молодых звезд связан с тем, что, как правило, в экспериментах удается достичь лишь нерелятивистских скоростей, которые как раз характерны для джетов молодых звезд. При этом зачастую в лабораторных условиях реализуется единичный выброс сгустка плазмы. Однако, согласно астрономическим наблюдениям [8], на некотором расстоянии от молодой звезды струйные выбросы распадаются на отдельные фрагменты, которые на заре наблюдений за межзвездным газом и были названы объектами Хербига-Аро [9]. Поэтому лабораторные эксперименты с единичными выбросами могут соответствовать космическим джетам, рассматриваемым на значительном расстоянии от центрального объекта.

Для лабораторного моделирования распространения джета в окрестности молодой звезды существенными факторами являются как пространственный масштаб течения, так и наличие окружающей среды. Существует возможность реализовать эти условия на установке ПФ-3 (плазменный фокус, НИЦ “Курчатовский институт”) [10, 11], что позволяет моделировать в лаборатории взаимодействие астрофизических джетов с окружающим веществом. При этом, в силу достаточно больших размеров получаемых джетов, удается измерять не только термодинамические и кинематические характеристики, и, используя магнитные зонды, величину и структуру магнитных полей.

В нашей предыдущей работе [12] с помощью численного моделирования было показано, что как в астрофизических, так и в лабораторных условиях после прохождения сверхзвукового плазменного выброса сквозь окружающую среду позади него остается область с пониженной концентрацией, так называемый вакуумный след. Благодаря этому последующие выбросы испытывают гораздо меньшее сопротивление окружающей среды и распространяются более коллимированно – практически все вещество такого выброса остается в его первоначальных радиальных границах. Оценки показали, что вакуумный след заполняется окружающим веществом как минимум за 10 мкс в случае лабораторного и за 70 лет в случае астрофизического джетов, т.е. такой эффект будет наблюдаться, если интервал между вылетами выбросов не превышает указанных значений. В недавних экспериментах на установке ПФ-3 удалось получить два выброса, вылетающих последовательно из области пинчевания. Настоящая работа посвящена исследованию этого результата и его значения для астрофизических приложений.

2. ЛАБОРАТОРНОЕ МОДЕЛИРОВАНИЕ

2.1. Установка ПФ-3

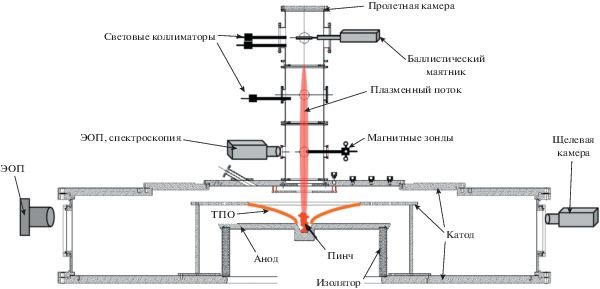
Установка ПФ-3 представляет собой плазменный фокус с плоской геометрией электродов по типу Филиппова [13]. К разрядной камере присоединена трехсекционная пролетная камера, позволяющая проводить исследования динамики плазменного выброса на расстоянии до 100 см от анода (рис. 1). Каждая секция пролетной камеры снабжена набором диагностических окон, рассчитанных на измерение различных параметров, на расстояниях 35, 65 и 95 см (центральные сечения каждого окна). Работает плазменная установка ПФ-3 следующим образом [14]: предварительно откачивается атмосферный воздух из всей установки, затем камеры заполняются каким-либо рабочим газом под давлением в несколько торр. Далее на катод и анод замыкается заряженная конденсаторная батарея, благодаря чему между анодом и катодом появляется высокое напряжение, пробивающее рабочий газ. Из-за этого образуется токонесущая плазменная оболочка (ТПО), которая за счет притяжения параллельных токов (действие силы Ампера) движется к оси разряда, вдоль которой и образуется плазменный пинч.

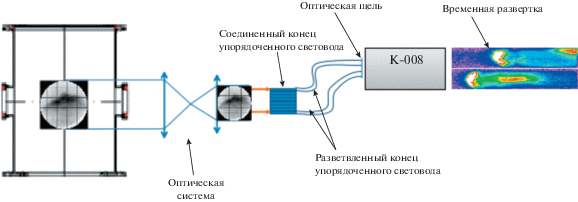
Рис. 1.

Схема эксперимента: ТПО – токово-плазменная оболочка; ЭОП – электронно-оптический преобразователь.

Образовавшийся плазменный пинч длиной несколько сантиметров характеризуется температурой порядка $T \simeq 5 \times {{10}^{2}}$ эВ и концентрацией порядка $n \simeq {{10}^{{19}}}$ см–3. На этой стадии плотность тока превышает 107 А/см2, что приводит к образованию сильных неустойчивостей, появлению турбулентного сопротивления и, как следствие, резкому обрыву тока. Таким образом происходит размыкание тока, и энергия, запасенная в магнитном поле пинча, переходит в плазму – начинается разрушение пинча и генерация плазменных потоков, распространяющихся вверх вдоль оси пролетной камеры. Начальная скорость потока составляет ~107 см/с, превышает скорость движения ТПО в аксиальном направлении и практически не зависит от типа рабочего газа.

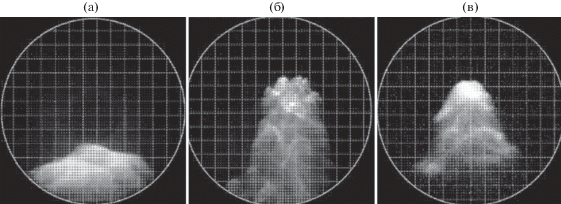
Когда уже сгенерированный поток распространяется по пролетной камере, практически вся выброшенная плазма остается в близких к первоначальным радиальных границах на расстояниях, значительно превышающих поперечные размеры потока. Это значит, что продольная скорость движения джета намного превышает скорость его поперечного расширения. На рис. 2 для примера приведены фотографии потока, полученные на разных расстояниях при экспериментах с различными газами. Видно, что структуры потока зависят от химического состава рабочего газа, что, скорее всего, связано с влиянием радиационных эффектов охлаждения и различной скоростью звука. Также хорошо видны ударные волны на фронте потока (аналог объектов Хербига-Аро). Головная часть потока даже на больших расстояниях от области пинчевания имеет поперечный размер в несколько сантиметров.

Рис. 2.

Фотографии фронта плазменного потока согласно [14] на расстоянии $z = 35$ см от анода при разряде в водороде (а) и неоне (б), а также при разряде в неоне на расстоянии 65 см (в). Масштаб одной клетки равен 1 см.

Как показала диагностика плазмы спектральными методами [15], для разряда в гелии концентрация фоновой плазмы на растоянии 35 см составляет ${{n}_{i}} \approx 2 \times {{10}^{{16}}}$ см–3 (c температурой $T \approx 1$ эВ). Это означает, что плазма ионизована на 20%. При этом сам плазменный поток имеет концентрацию ${{n}_{i}} \approx 2 \times {{10}^{{17}}}$ см–3 и температуру порядка $T \approx 5$ эВ. С помощью магнитозондового метода было показано [16], что плазменный поток распространяется с уже вмороженным магнитным полем, основным компонентом которого является тороидальный компонент с напряженностью ~103 Гс, а полоидальный, по крайне мере на некотором удалении от оси, на порядок меньше. Проведенные исследования также позволили изучить радиальное распределение тороидального поля. При $r > {{r}_{{{\text{core}}}}}$ поведение поля хорошо описывается зависимостью ${{B}_{\phi }} \sim 1{\text{/}}r$, а при $r < {{r}_{{{\text{core}}}}}$ получается ${{B}_{\phi }} \sim r$, что будет в дальнейшем использовано нами для численного моделирования.

2.2. Результаты экспериментов с гелием

В качестве основного диагностического метода в данной работе применена регистрация плазменного потока с помощью скоростной оптической камеры с щелевой разверткой К-008. Схема измерений приведена на рис. 3. Изображение плазменного потока через диагностическое окно с помощью оптической системы проецируется на торец упорядоченного световода, представляющего собой “сэндвич” из нескольких параллельных жил. Таким образом, каждая из жил передает на вход прибора изображение из определенной области наблюдения по высоте камеры. На входе прибора расположена щель шириной 0.1 мм, вырезающая из объекта узкую область вдоль диаметра камеры, которая затем электронно-оптическими методами разворачивается во времени. Пример такой развертки показан на рис. 3 и рис. 4а.

Рис. 3.

Схема измерений скоростной оптической камерой с щелевой разверткой.

Рис. 4.

Временнáя развертка изображения плазменного потока на высотах 30.5 и 39.5 см над уровнем анода (a) и преобразованное изображение развертки в пространственном масштабе (б). Полная длительность развертки 6 мкс, размер изображения вдоль диаметра камеры 9 см. Распространение потока справа налево.

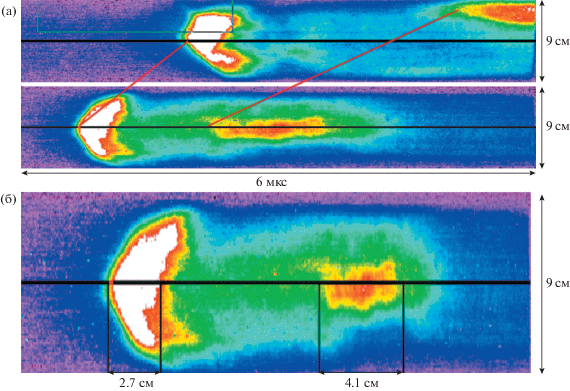
Прежде всего отметим, что на высоте $ \sim {\kern 1pt} 30$ см наблюдается компактный ярко излучающий объект диаметром $ \sim {\kern 1pt} 5{\kern 1pt} - {\kern 1pt} 6$ см (диаметр пролетной камеры $ \sim {\kern 1pt} 30$ см) и длительностью всего $ \sim {\kern 1pt} 0.5$ мкс с коническим профилем, обусловленным, по-видимому, образованием ударной волны.

Как уже отмечалось в разделе 2.1, плазменные выбросы в плазмофокусном разряде образуются на стадии развития МГД (магнитогидродинамических) неустойчивостей, приводящих к развалу пинча. Характерное время этих процессов составляет порядка сотен наносекунд, поэтому на значительном удалении от места выброса плазменный поток воспринимается как единое образование со сложной структурой (см. рис. 2). В этом случае трудно выделить области с вакуумным следом. Организовать управляемым образом повторный выброс практически невозможно. Однако физика процессов в плазменном фокусе допускает повторное сжатие токовой оболочки и формирование нового пинча и, соответственно, генерацию повторного выброса. Пример такого повторного выброса показан на рис. 4а. Видно, что через $ \sim {\kern 1pt} 1.6$ мкс на развертке появляется еще один объект длительностью $ \sim {\kern 1pt} 1.5$ мкс.

По временнóй развертке можно измерить только длительность излучения. Грубо оценить продольные пространственные масштабы можно с помощью простого преобразования. По задержке появления объектов на верхней развертке относительно нижней можно оценить среднюю скорость потока на участке пролета. Так, для головного объекта эта скорость равна $ \sim {\kern 1pt} 7 \times {{10}^{6}}$ см/с, а для второго сгустка раза в два меньше. Меньшая скорость второго сгустка обусловлена разными условиями формирования потока: повторное пинчевание обычно происходит при меньших величинах тока, меньшей скорости пинчевания и меньшей степени сжатия. Тогда в первом приближении длина сгустка будет равна произведению скорости сгустка на его длительность. Пример такого преобразования для нижней щели приведен на рис. 4б.

Прежде всего, обращает на себя внимание отсутствие ударной волны у второго сгустка, что объясняется, по-видимому, движением в вакуумном следе от первого потока. Нужно отметить также высокое аспектное отношение у второго сгустка ($ > {\kern 1pt} 2$). Причем это оценка снизу, поскольку скорость потока в области нижней щели всегда выше из-за торможения потока на длине пролета.

3. ЗАКОНЫ МАСШТАБИРОВАНИЯ

В работе [1] впервые было показано, что две системы, описываемые уравнениями идеальной МГД, эволюционируют одинаково, если обладают схожей геометрией, и выполняются некоторые масштабные соотношения. Помимо этого обсуждены условия применимости идеальной МГД и показано, что они удовлетворяются с большим запасом как в ряде астрофизических объектов, так и в специально спроектированных экспериментах с мощными лазерами. Это позволяет проводить лабораторные эксперименты, результаты которых могут быть использованы для качественной интерпретации различных астрофизических замагниченных течений.

Уравнения идеальной МГД в общепринятых обозначениях имеют вид:

(1)
$\frac{{\partial \rho }}{{\partial t}} = - \operatorname{div} \rho {\mathbf{v}},$
(2)
$\frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}},\nabla ){\mathbf{v}} = - \frac{1}{\rho }\nabla p - \frac{1}{{4\pi \rho }}[{\mathbf{B}} \times \operatorname{rot} {\mathbf{B}}],$
(3)
$\frac{{\partial {\mathbf{B}}}}{{\partial t}} = \operatorname{rot} [{\mathbf{v}} \times {\mathbf{B}}],$
(4)
$\operatorname{div} {\mathbf{B}} = 0,$
(5)
$\frac{{\partial e}}{{\partial t}} = - {\text{div}}\left( {{\mathbf{v}}\left( {e + p + \frac{{{{{\mathbf{B}}}^{2}}}}{{8\pi }}} \right) - \frac{{{\mathbf{B}}({\mathbf{v}} \cdot {\mathbf{B}})}}{{4\pi }}} \right) + S,$
(6)
$p = (\gamma - 1)\left( {e - \frac{{\rho {{{\mathbf{v}}}^{2}}}}{2} - \frac{{{{{\mathbf{B}}}^{2}}}}{{8\pi }}} \right),$
где $e = \rho \varepsilon + \rho {{{\mathbf{v}}}^{2}}{\text{/}}2 + {{{\mathbf{B}}}^{2}}{\text{/}}8\pi $ – полная внутренняя энергия, $S$ – сток энергии за счет излучения. Зная плотность и давление, температуру $T$ можно найти из уравнения состояния идеального газа: $p = \rho RT{\text{/}}M$, где $R$ – универсальная газовая постоянная, $M$ – молярная масса. Можно видеть, что при $S = 0$, вводя некий пространственный масштаб $L{\kern 1pt} *$, в единицах которого можно измерять имеющиеся в задаче длины, можно перейти к безразмерным координатам ${\mathbf{r}}{\kern 1pt} ' = {\mathbf{r}}{\text{/}}L{\kern 1pt} *$. Далее можно обезразмерить фигурирующие в уравнениях идеальной МГД величины следующим образом:
(7)
$\begin{gathered} \rho {\kern 1pt} ' = \rho {\text{/}}\rho {\kern 1pt} *,\quad p{\kern 1pt} ' = p{\text{/}}p{\kern 1pt} *, \\ {\mathbf{v}}{\kern 1pt} ' = \sqrt {\rho {\kern 1pt} *{\text{/}}p{\kern 1pt} *{\kern 1pt} } {\mathbf{v}},\quad {\mathbf{B}}{\kern 1pt} ' = {\mathbf{B}}{\text{/}}\sqrt {p{\kern 1pt} *} , \\ \end{gathered} $
где звездочкой обозначены масштабы исходных величин, а штрихом – уже безразмерные функции. Из уже имеющихся масштабных величин можно составить комбинацию с размерностью времени, с помощью которой можно перейти к безразмерному времени $t{\kern 1pt} ' = t\sqrt {{{p}_{*}}{\text{/}}\rho {\kern 1pt} *} {\text{/}}L{\kern 1pt} *$.

После указанных преобразований система уравнений идеальной МГД не изменится, но в ней будут фигурировать лишь безразмерные величины. Однако также имеются начальные условия, которые, вообще говоря, могут быть произвольными. В качестве масштабных факторов для скорости и магнитного поля выбираются комбинации из масштабных факторов давления и плотности, однако начальные значения не обязательно должны иметь такие же масштабы. Поэтому для начальных значений нужно записать:

(8)
${{\left. \rho \right|}_{{t = 0}}} = \rho {\kern 1pt} *f({\mathbf{r}}{\text{/}}L{\kern 1pt} *{\kern 1pt} ),\quad {{\left. p \right|}_{{t = 0}}} = p{\kern 1pt} *{\kern 1pt} g({\mathbf{r}}{\text{/}}L{\kern 1pt} *{\kern 1pt} ),$
(9)
${{\left. {\mathbf{v}} \right|}_{{t = 0}}} = {v}{\kern 1pt} *{\mathbf{h}}({\mathbf{r}}{\text{/}}L{\kern 1pt} *),\quad {{\left. B \right|}_{{t = 0}}} = B{\kern 1pt} *{\kern 1pt} {\mathbf{k}}({\mathbf{r}}{\text{/}}L{\kern 1pt} *).$
С учетом приведенных выше преобразований получаются следующие начальные условия для уже безразмерных величин:
(10)
${{\left. {\rho {\kern 1pt} '} \right|}_{{t{\kern 1pt} ' = 0}}} = f({\mathbf{r}}{\kern 1pt} '),\quad {{\left. {p{\kern 1pt} '} \right|}_{{t{\kern 1pt} ' = 0}}} = g({\mathbf{r}}{\kern 1pt} '),$
(11)
${{\left. {{\mathbf{v}}{\kern 1pt} '} \right|}_{{t' = 0}}} = Eu{\mathbf{h}}({\mathbf{r}}{\kern 1pt} '),\quad {{\left. {B{\kern 1pt} '} \right|}_{{t{\kern 1pt} ' = 0}}} = \sqrt {8\pi {\text{/}}\beta } {\mathbf{k}}({\mathbf{r}}{\kern 1pt} '),$
где $Eu = {v}{\kern 1pt} *\sqrt {\rho {\kern 1pt} *{\kern 1pt} {\text{/}}p{\kern 1pt} *} $ – число Эйлера, $\beta = 8\pi p{\kern 1pt} *{\text{/}}B{\kern 1pt} {{*}^{2}}$ – отношение газокинетического давления плазмы к магнитному давлению.

Таким образом, если две какие-либо системы имеют одинаковые значения $Eu$ и $\beta $, а также сходные начальные условия, описываемые функциями $f({\mathbf{r}}{\kern 1pt} ')$, $g({\mathbf{r}}{\kern 1pt} ')$, ${\mathbf{h}}({\mathbf{r}}{\kern 1pt} ')$ и ${\mathbf{k}}({\mathbf{r}}{\kern 1pt} ')$, то их эволюция будет происходить одинаковым образом. Зная поведение системы “1”, поведение системы “2” может быть восстановлено с помощью указанного масштабирования. Например, значение плотности системы “2” выражается через значение плотности системы “1” следующим образом:

(12)
${{\rho }_{2}}({\mathbf{r}},t) = \frac{{\rho _{2}^{*}}}{{\rho _{1}^{*}}}{{\rho }_{1}}\left( {\frac{{L_{2}^{*}}}{{L_{1}^{*}}}{\mathbf{r}},\frac{{t_{2}^{*}}}{{t_{1}^{*}}}t} \right).$
Казалось бы, имея результаты моделирования лабораторных выбросов, достаточно применить описанные выше законы масштабирования и получить описание динамики распространения астрофизичесикх выбросов. Однако эти законы не учитывают, возможно, разные излучательные характеристики обоих систем. Поэтому, прежде чем утверждать, что обнаруженный эффект образования вакуумного следа – области с низкой концентрацией, оставшейся позади пролетевшего сверхзвукового выброса, – имеет место быть в случае джетов молодых звезд, необходимо удостовериться, что поведение системы качественно не изменится при задании другого закона объемной скорости остывания $S$.

Исходя из данных лабораторных опытов и астрономических наблюдений были выбраны масштабные коэффициенты, отображенные в табл. 1. Плотности и давления брались соответствующими состоянию фоновой плазмы – гелиевой в лабораторной установке и с так называемым космическим обилием элементов [17] в астрофизическом случае.

Таблица 1.  

Выбранные масштабные параметры, соответствующие фоновой плазме

Среда $L{\kern 1pt} *$, см $\rho {\kern 1pt} *$, г/см3 $p{\kern 1pt} *$, дин/см2 $t{\kern 1pt} *$, с
Лабораторная 5 $5.4 \times {{10}^{{ - 7}}}$ $1.3 \times {{10}^{5}}$ ${{10}^{{ - 5}}}$
Астрофизическая $5 \times {{10}^{{15}}}$ $2 \times {{10}^{{ - 21}}}$ $4.9 \times {{10}^{{ - 10}}}$ ${{10}^{{10}}}$

4. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

4.1. Моделирование лабораторных выбросов

Уравнения (1)–(6) решались с использованием нашей собственной программы с численной схемой годуновского типа в осесимметричной цилиндрической системе координат с использованием хорошо зарекомендовавшего себя солвера HLLD (Harten-Lax-van Leer Discontinuities) [18]. Радиационное охлаждение учитывалось посредством вычисления объемной скорости остывания плазмы как оптически тонкого тела $S = 2k\rho \sigma {{T}^{4}}$, где $\sigma $ – постоянная Стефана–Больцмана, $k$ – коэффициент непрозрачности, рассчитанный в ЛТР (локальное термодинамическое равновесие) приближении с использованием атомных данных из TOPbase [19].

Для корректного сравнения результатов МГД моделирования с экспериментом был произведен расчет выходящего оптического излучения. Уравнение переноса излучения решалось для цилиндрической геометрии методом коротких характеристик вдоль лучей, перпендикулярных оси распространения выброса. Непрозрачность в линиях и континууме рассчитывалась в ЛТР приближении с использованием атомных данных NIST и TOPbase.

В начальный момент выбросы задавались как сферические сгустки плазмы с радиусом ${{R}_{{{\text{clot}}}}}$ (см. табл. 2), погруженные в фоновую плазму меньшей плотности и температуры. Магнитное поле задавалось только тороидальное: оно растет линейно от нуля и до границы сгустка, а далее падает как ${{r}^{{ - 1}}}$. Такая конфигурация магнитного поля хотя и соответствует измерениям, проведенным на установке ПФ-3, однако не учитывает обратные токи замыкания и реальное направление вектора магнитной индукции. Но этого вполне достаточно для исследования совместного влияния азимутального поля, радиационного охлаждения и внешней среды, а также влияния образованного первым выбросом вакуумного следа на  коллимированность последующего выброса. Учет полоидального магнитного поля представляет из себя более сложную задачу хотя бы из-за необходимости задания самосогласованной начальной конфигурации плазменного выброса. С другой стороны, в эксперименте, описанном в разделе 2.2, не производилась спектральная диагностика плазмы, поэтому значительная часть параметров осталась неизвестной. Из-за этого и из‑за несогласованной начальной конфигурации токов не стояло цели детально воспроизвести результаты эксперимента численно, предполагалось лишь качественно изучить динамику вакуумного следа и получить схожую морфологию двух выбросов. Поэтому представленные в табл. 2 значения могут несколько отличаться от значений, которые были при эксперименте.

Таблица 2.  

Отличные от нуля начальные условия при моделировании лабораторных и астрофизических выбросов

Параметр Лабораторный Астрофизический
${{R}_{{{\text{clot}}}}}$, см 2 $2 \times {{10}^{5}}$
n, см–3 выброс $1.8 \times {{10}^{{17}}}$ 3582
  фон $6 \times {{10}^{{16}}}$ 1195
T, эВ выброс 6 1.52
  фон 1 0.26
$B_{\varphi }^{{max}}$, Гс $7 \times {{10}^{5}}$ $4.3 \times {{10}^{{ - 4}}}$
$V_{z}^{{(1)}}$, км/с 55 55.55
$V_{z}^{{(2)}}$, км/с 45 45.45
${{t}_{{{\text{launch}}}}}$, с $5 \times {{10}^{{ - 6}}}$ $5 \times {{10}^{9}}$

Всему плазменному выбросу придается продольная скорость, и он начинает распространяться вдоль оси. По прошествии времени ${{t}_{{{\text{launch}}}}}$ в том же самом месте появляется точно такой же выброс, однако имеющий немного меньшую скорость, что, по-видимому, имело место при проведении лабораторных экспериментов с гелием.

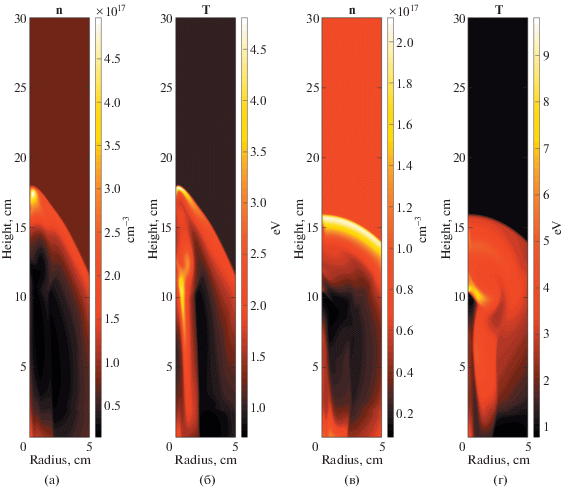
Для начала сравним динамику распространения одиночного выброса с учетом радиационного охлаждения и без оного. Это поможет выяснить, насколько правомерно масштабирование систем с различным слагаемым $S$ в выражении (5). Как можно видеть на рис. 5, динамика выбросов значительно различается. Из-за того, что плазма излучает, происходит уменьшение температуры и, соответственно, давления. Поэтому постепенно давление тороидального магнитного поля, сжимающего плазму, начинает доминировать. Благодаря такому сжатию на рис. 5а видно распространение компактного, относительно холодного, плазменного сгустка, в то время как на рис. 5в начальный выброс практически полностью распался, образовав грибовидную ударную волну. При этом стоит заметить, что в обоих случаях позади прошедшего выброса образуется полость с низкой концентрацией и повышенной температурой – тот самый вакуумный след. Таким образом, конкретный вид закона излучения $S$ оказался не столь важным для исследуемого эффекта.

Рис. 5.

Слева направо (a, б, в, г ): распределение концентрации (а) и температуры (б) излучающей и не излучающей плазмы ((в) и (г) соответственно) в момент времени 4.46 мкс в случае лабораторной плазмы (рабочий газ – гелий).

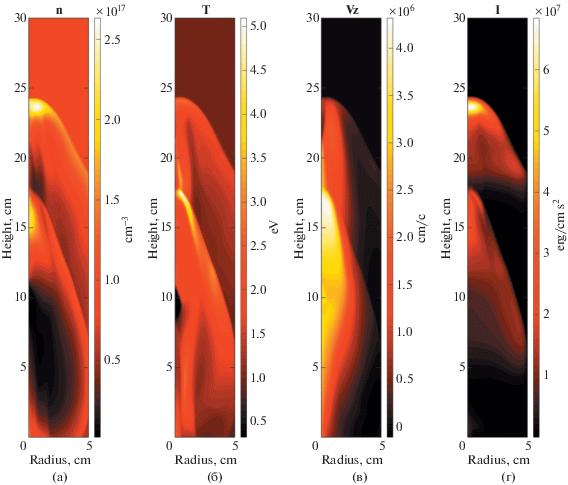
Обратимся к случаю последовательного испускания выбросов и сравним первый выброс, находящийся на расстоянии 16 см в момент $t = 4.46$ мкс (рис. 5а, б), со вторым, прилетевшим в эту же область в момент $t = 8.4$ мкс (рис. 6). Видно, что второй выброс, по сравнению с первым, более прижат к оси и образует ударную волну примерно в три раза менее плотную. Это происходит потому, что выброс, следующий за первым, оказывается в вакуумном следе и испытывает меньшее сопротивление со стороны окружающей среды. Как можно видеть на рис. 5б и рис. 6б, температура внутри вакуумного следа в несколько раз выше температуры фоновой плазмы. Следует отметить, что продольная скорость вещества, оставшегося в следе, повышена (рис. 6г), что уменьшает ударное сжатие. Судя по рассчитанной интенсивности излучения в видимом диапазоне (рис. 6г), нам удалось удовлетворительно воспроизвести морфологию выбросов, наблюдавшуюся в эксперименте (рис. 4).

Рис. 6.

Слева направо (a, б, в, г ): распределение концентрации (а), температуры (б), продольной скорости (в) и интенсивности излучения (г) в момент времени 8.4 мкс в случае лабораторной плазмы (рабочий газ – гелий).

Таким образом, о возникновении вакуумного следа позади сверхзвукового выброса и его влиянии на последующие выбросы свидетельствуют как лабораторные эксперименты, описанные в разделе 2.2, так и результаты численного моделирования для водорода, аргона, представленные в нашей предыдущей работе [12], и гелия, содержащиеся в настоящем разделе. Согласно масштабирующим законам (9)–(12) и результатам моделирования распространения одиночного выброса с учетом радиационного охлаждения и без него, аналогичного поведения стоило бы ожидать и от выбросов, чьи параметры близки к астрофизическим. Проверим это, выбирая обезразмеривающие параметры согласно табл. 1.

4.2. Моделирование астрофизических выбросов

Описанная выше процедура моделирования была выполнена для астрофизических выбросов с начальными условиями, приведенными в табл. 2, которые соответствуют масштабированию по законам (9)–(12) согласно табл. 1. Однако объемная скорость остывания плазмы рассчитывалась как $S = {{n}_{e}}{{n}_{i}}\Lambda $, где ${{n}_{e}}$, ${{n}_{i}}$ – объемные концентрации электронов и ионов соответственно, $\Lambda (T)$ – функция охлаждения, рассчитанная в пакете CHIANTI [20] в предположении о стандартном содержании химических элементов в веществе джета [17].

Результаты расчетов для астрофизических выбросов к моменту $t = 78.01$ лет (рис. 7а, б) свидетельствуют о том, что полученные распределения плотности и температуры плазмы значительно отличаются от таковых для лабораторной излучающей плазмы (рис. 6а, б), и структура головной ударной волны более походит на неизлучающую (рис. 5в, г). Это связано, очевидно, с более плохой излучательной способностью астрофизической плазмы по сравнению с лабораторной. Видно, что практически все вещество разошлось по грибовидной ударной волне. Далее заметим, что позади выброса сформировался вакуумный след – область с пониженной концентрацией и повышенной температурой. Как и в лабораторных условиях, в вакуумном следе высока продольная скорость плазмы.

Рис. 7.

Слева направо (a, б, в, г ): распределение концентрации (а), температуры (б) и продольной скорости (в) в момент времени 78.01 лет и концентрации в момент времени 268.26 лет (г) в случае астрофизической плазмы.

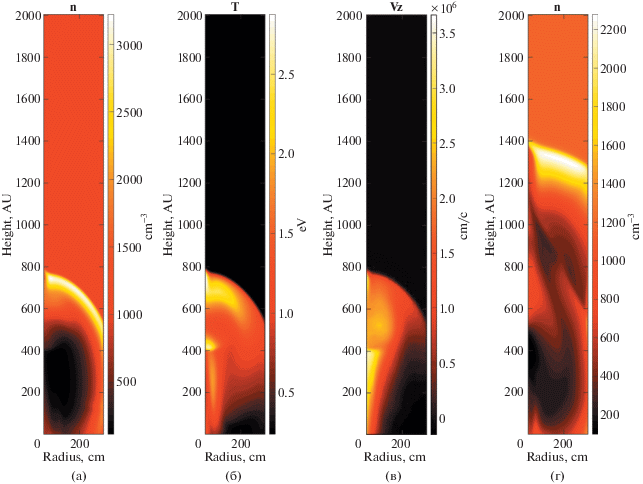
В момент $t = 268.26$ лет, что соответствует 8.4 мкс для лабораторных условий, оба выброса успели распространиться на значительные расстояния (рис. 7г). При этом второй выброс, находясь на месте первого, демонстрирует гораздо большую коллимированность – он образует крайне слабую ударную волну и сильно прижат к оси. Это связано с распространением выброса в области с низкой концентрацией и повышенной температурой, которая к тому же обладает значительной продольной скоростью. Таким образом, эффект образования вакуумного следа и его влияния на последующий выброс хорошо масштабируется от лабораторных к астрофизическим условиям, несмотря на различные законы радиационного охлаждения.

5. БАЛАНС СИЛ НА УДАРНОЙ ВОЛНЕ

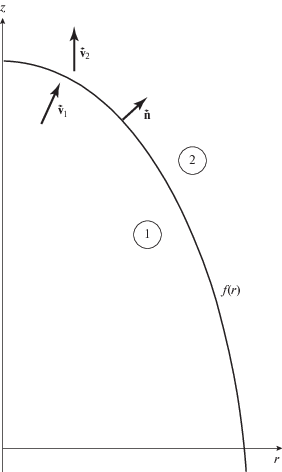
Проанализируем силы, действующие на фронте ударной волны джета, набегающего на внешнюю среду, имеющую только продольную скорость, что достаточно хорошо согласуется с нашими расчетами. Для простоты ограничимся лишь гидродинамическим случаем. В осесимметричном случае форма такого фронта есть фигура вращения, описываемая некоей функцией $z = f(r)$ (рис. 8), нормаль к которой есть ${\mathbf{n}} = \{ - f{\kern 1pt} ',0,1\} $, где штрих обозначает производную. Обозначим величины, относящиеся к джету индексом “1”, а к внешней среде индексом “2”. Скорость вещества джета перед ударной волной обозначим как ${{{\mathbf{v}}}_{2}} = \{ u,0,v\} $, а скорость окружающего вещества как ${{{v}}_{1}} = \{ 0,0,w\} $, скорость самого ударного фронта обозначим так: ${\mathbf{U}}\{ C,0,D\} $.

Рис. 8.

Схематический рисунок фронта ударной волны, описывающегося функцией $z = f(r)$.

Поток вещества на поверхности разрыва должен быть непрерывен, поэтому имеем: $[\rho ({\mathbf{v}} - $ $ - \;{\mathbf{U}}) \cdot {\mathbf{n}}] = 0$, где квадратными скобками обозначена разность величин по обе стороны ударной волны. Отсюда имеем:

(13)
$({{\rho }_{1}} - {{\rho }_{2}})(f{\kern 1pt} 'C - D) = {{\rho }_{2}}w + {{\rho }_{1}}(f{\kern 1pt} 'u - {v}).$
Далее, должны уравновешиваться силы, с которыми оба газа действуют друг на друга, т.е. должен быть непрерывен поток импульса через ударную волну: $[{{\Pi }_{{ik}}}{{n}_{k}}] = 0$, где ${{\Pi }_{{ik}}} = \rho ({{v}_{i}} - {{U}_{i}})({{v}_{k}} - $ $ - \;{{U}_{k}}) + p{{\delta }_{{ik}}}$. С учетом (13) $r$ и $z$ проекции имеют вид:
(14)
$({{p}_{1}} - {{p}_{2}})f{\kern 1pt} ' = {{\rho }_{2}}u(w + f{\kern 1pt} 'C - D),$
(15)
$({{p}_{1}} - {{p}_{2}}) = {{\rho }_{2}}(w - v)(w + f{\kern 1pt} 'C - D).$
Из этих соотношений сразу следует:
(16)
$f{\kern 1pt} ' = \frac{u}{{w - v}}.$
Подставляя (16) в (13), (14) (или в (13), (15)), приходим к хорошо известному соотношению [21]:
(17)
${{\rho }_{1}}{{\rho }_{2}}({{u}^{2}} + {{(v - w)}^{2}}) = ({{\rho }_{1}} - {{\rho }_{2}})({{p}_{1}} - {{p}_{2}}).$
Из (16), (17) получаем следующее соотношение:
(18)
$f{\kern 1pt} ' = - \sqrt {1 - \frac{{{{\rho }_{1}} - {{\rho }_{2}}}}{{{{\rho }_{1}}{{\rho }_{2}}}}\frac{{{{p}_{1}} - {{p}_{2}}}}{{{{{(v - w)}}^{2}}}}} ,$
где знак минус перед корнем был выбран для соответствия формы фигуры грибовидной ударной волне.

Из (18) видно, что уменьшение плотности или деления внешней среды приводит к уменьшению величины под корнем, а значит к более крутому поведению функции $f(r)$. К этому же приводит увеличение продольной скорости внешней сре-ды w. То есть уменьшение плотности и давления, а так же увеличение продольной скорости внешней среды делают ударную волну более поджатой поперечно, т.е. увеличивают коллимированность выброса.

6. ЗАКЛЮЧЕНИЕ

Результаты моделирования, проведенные в нашей предыдущей работе [12], предсказали образование вакуумного следа вслед за прохождением первого выброса и его критическое влияние на коллимированность последующих в случае, если рабочим газом в лабораторной установке является аргон. Последовавшие опыты с гелием в качестве рабочего газа подтвердили этот эффект, что отражено в разделе 2.2. С помощью численного моделирования, на этот раз уже с гелиевой плазмой, удалось воссоздать морфологию выбросов, наблюдавшуюся в экспериментах, и получить пространственные распределения основных величин (рис. 6).

Используя масштабирующие законы (9)–(12), были выбраны параметры, соответствующие астрофизическим (табл. 1, 2). Получившиеся значения не вполне соответствуют обычным космическим условиям. А именно, отношение плотностей выброса и окружающей среды в астрофизических условиях значительно превышает таковую в лабораторных. Помимо этого, лабораторная и астрофизическая плазма теряют энергию благодаря излучению по разным законам. Для параметров, близких к наблюдаемым у объекта HH 229, численное моделирование последовательных выбросов нами уже производилось [12], и эффект, связанный с вакуумным следом, был подтвержден. Чтобы узнать, насколько обнаруженный в лаборатории эффект применим для астрофизики, было произведено численное моделирование с получившимися в результате масштабирования параметрами. Его результаты свидетельствуют об образовании вакуумного следа и о коллимированности плазменного выброса, следующего по нему (рис. 7).

Проведенные расчеты с различными параметрами и простые оценки скачков величин на ударной волне заставляют думать, что эффект образования вакуумного следа и его влияние на последующие выбросы весьма универсален. Можно выделить две основных характеристики вакуумного следа, благодаря которым распространяющиеся в нем плазменные выбросы остаются коллимированными:

• низкая концентрация, благодаря чему выбросы испытывают меньшее сопротивление;

• значительная продольная скорость, из-за которой уменьшается относительная скорость среды и набегающего потока.

Таким образом, эксперименты на установке ПФ-3 продемонстрировали возможность воспроизведения отдельных астрофизических эффектов, происходящих вдали от центрального объекта. Благодаря этому становится возможным изучать в лаборатории вопросы, связанные с внутренней структурой астрофизических выбросов, и делать обоснованные выводы об их устойчивости.

Изучение возможности образования вакуумного следа в астрофизических условиях требует дальнейшего, более точного теоретического исследования, учитывающего причины образования джетов. По крайней мере, как было показано в настоящей работе, есть основания полагать возможным образование вакуумного следа в выбросах молодых звезд.

Список литературы

  1. D. Ryutov, R. P. Drake, J. Kane, E. Liang, B. A. Remington, and W. M. Wood-Vasey, Astrophys. J. 518, 821 (1999).

  2. D. D. Ryutov and B. A. Remington, Plasma Phys. Control. Fusion 44, 407 (2002).

  3. S. V. Lebedev, A. Ciardi, D. J. Ampleford, S. N. Bland, et al., Monthly Not. Roy. Astron. Soc. 361, 97 (2005).

  4. S. C. Hsu and P. M. Bellan, Phys. Plasmas 12, id. 032103 (2005), arXiv:physics/0411089 [physics.plasm-ph].

  5. R. F. Coker, B. H. Wilde, J. M. Foster, B. E. Blue, et al., Astrophys. Space Sci. 307, 57 (2007).

  6. B. Albertazzi, A. Ciardi, M. Nakatsutsumi, T. Vinci, et al., Science 346, 325 (2014).

  7. В. С. Беляев, Г. С. Бисноватый-Коган, А. И. Громов, Б. В. Загреев, А. В. Лобанов, А. П. Матафонов, С. Г. Моисеенко, О. Д. Торопина, Астрон. журн. 95, 171 (2018).

  8. P. Hartigan, J. A. Morse, B. Reipurth, S. Heathcote, and J. Bally, Astrophys. J. 559, L157 (2001).

  9. G. H. Herbig, Astrophys. J. 111, 11 (1950).

  10. К. Н. Митрофанов, В. И. Крауз, В. В. Мялтон, Е. П. Ве-лихов, В. П. Виноградов, Ю. В. Виноградова, ЖЭТФ 146, 1035 (2014).

  11. V. I. Krauz, V. S. Beskin, and E. P. Velikhov, Intern. J. Modern Physics D 27, id. 1844009 (2018).

  12. I. Kalashnikov, P. Chardonnet, V. Chechetkin, A. Dodin, and V. Krauz, Phys. Plasmas 25(6), id. 062901 (2018).

  13. N. V. Filippov, T. I. Filippova, and V. P. Vinogradov, Nuclear Fusion Suppl. 2, 577 (1962).

  14. В. С. Бескин, Я. Н. Истомин, А. М. Киселев, В. И. Крауз, и др., Изв. ВУЗов. Радиофизика 59, 1004 (2016).

  15. С. С. Ананьев, С. А. Данько, В. В. Мялтон, А. И. Жужунашвили, Ю. Г. Калинин, В. И. Крауз, М. С. Ладыгина, А. К. Марченко, Физика плазмы 42, 282 (2016).

  16. К. Н. Митрофанов, В. И. Крауз, В. В. Мялтон, В. П. Виноградов, А. М. Харрасов, Ю. В. Виноградова, Астрон. журн. 94(2), 152 (2017).

  17. M. Asplund, N. Grevesse, A. J. Sauval, and P. Scott, Ann. Rev. Astron. Astrophys. 47(1), 481 (2009), arXiv:0909.0948 [astro-ph.SR].

  18. T. Miyoshi and K. Kusano, J. Comput. Phys. 208, 315 (2005).

  19. W. Cunto and C. Mendoza, Revista Mexicana Astron. Astrof. 23, 107 (1992).

  20. K. P. Dere, E. Landi, H. E. Mason, B. C. Monsignori Fossi, and P. R. Young, Astron. and Astrophys. Suppl. Ser. 125, 149 (1997).

  21. Л. Д. Ландау, Е. М. Лифшиц, Теоретическая физика: учебное пособие в 10 т., VI. Гидродинамика (М.: Наука. Гл. ред. физ.-мат. лит., 1986).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал