Астрономический журнал, 2021, T. 98, № 6, стр. 497-505
Новая оценка наилучшего значения расстояния от Солнца до центра галактики
В. В. Бобылев 1, *, А. Т. Байкова 1
1 Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия
* E-mail: vbobylev@gaoran.ru
Поступила в редакцию 05.02.2021
После доработки 28.02.2021
Принята к публикации 28.02.2021
Аннотация
С использованием данных из литературы составлен список индивидуальных оценок расстояния от Солнца до галактического центра ${{R}_{0}}$, которые сделаны после 2017 г. разными методами. Эти значения пока не использовались для вычисления наилучшего среднего значения ${{R}_{0}}$. По выборке, содержащей 21 оценку, на основе стандартного подхода мы нашли среднее взвешенное значение ${{\bar {R}}_{0}} = 8.14$ кпк с дисперсией $\sigma = 0.16$ кпк, а с применением медианной статистики получили оценку ${{R}_{0}} = 8.15 \pm 0.11$ кпк. Для практического использования можно рекомендовать значение ${{R}_{0}} = 8.1 \pm 0.1$ кпк.
1. ВВЕДЕНИЕ
Расстояние от Солнца до центра Галактики ${{R}_{0}}$ является одним из важнейших фундаментальных астрономических параметров, точность знания которого имеет большое значение для астрофизики и космологии. Рекомендованные Международным астрономическим союзом (МАС) “стандартные” значения этой величины заметно различаются, составляя ${{R}_{0}} = 10$ кпк (МАС, 1964) и ${{R}_{0}} = 8.5$ кпк (МАС, 1986). Современные оценки дают значение, близкое к $8.0$ кпк [1–6].
Известны разнообразные способы оценки ${{R}_{0}}$, для которых предложены различные виды классификации. Рид [7] разделил все такие измерения на три класса: прямые, вторичные и непрямые. Близкой классификации придерживаются Бланд-Хотторн и Герхард [3], разделившие все измерения на три класса: прямые, модельно зависимые и вторичные. Никифоров [1] предложил особую трехмерную классификацию. Он разделил измерения на три класса в зависимости от типа измерений, типа оценки ${{R}_{0}}$ и типа опорных объектов.
По-настоящему прямым является метод определения абсолютного тригонометрического параллакса объекта, находящегося близко к центру Галактики. По РСДБ наблюдениям нескольких источников мазерного излучения в области Sgr B2 этим методом была получена оценка ${{R}_{0}} = 7.9_{{ - 0.7}}^{{ + 0.8}}$ кпк [8]. Высокой точностью и надежностью обладает также метод динамического параллакса. Из совместного анализа орбитального движения 28 звезд вокруг центральной сверхмассивной черной дыры Жиллесен и соавт. [9] нашли этим методом ${{R}_{0}} = 8.33 \pm 0.31$ кпк с одновременной оценкой массы черной дыры (4.31 ± 0.38) × $ \times \;{{10}^{6}}\;{{M}_{ \odot }}$. За время высокоточных астрометрических наблюдений этих звезд только одна звезда, S2, имеющая период обращения около 16 лет, совершила полный оборот. Значения периодов обращения остальных 27 звезд составляют 45 лет и более, вплоть до 1000 лет [9]. Поэтому с целью уточнения оценки ${{R}_{0}}$ обычно анализируют именно движение звезды S2 [10–13]. К настоящему моменту применение этого метода позволяет оценивать ${{R}_{0}}$ с относительной погрешностью около 0.3% [12, 13].
Важное значение для оценки ${{R}_{0}}$ представляют переменные звезды – классические цефеиды, цефеиды типа II и переменные типа RR Лиры. Высокая точность оценок расстояния до цефеид возможна благодаря соотношениям “период–светимость” [14, 15] и “период-функция Весенхейта” [16, 17]. Эти соотношения хорошо откалиброваны с помощью высокоточных тригонометрических параллаксов звезд [18]. Их использование позволяет оценивать расстояния до цефеид с относительными ошибками менее 10% [19, 20]. Более того, согласно [21], ошибки в расстояниях до цефеид составляют ~5%. Хотя не исключена систематика локального характера, где могут иметь место сильные различия в металличности звезд, нестандартное отношение полного поглощения к селективному и т.д. Согласно оценкам Маджаеса с соавторами [22], расстояния до переменных типа RR Лиры в настоящее время могут быть измерены в среднем с относительными ошибками около 4%. Для оценки ${{R}_{0}}$ требуется выделить группу таких переменных звезд, которые расположены в галактическом диске, балдже или гало, и симметрично распределены относительно центра Галактики.
Отметим мазерные источники с измеренными тригонометрическими параллаксами [23, 24]. В настоящее время опубликованы результаты наблюдений в радиодиапазоне РСДБ-методом более 200 таких источников. Расстояния до них измерены в среднем с относительными ошибками около 6%. Оценки ${{R}_{0}}$ по этим данным получены главным образом кинематическим способом [23–25]. Никифоров и Веселова [26] предложили интересный метод оценки ${{R}_{0}}$ по распределению мазеров в спиральных рукавах.
Целью настоящей работы является получение новой оценки среднего значения ${{R}_{0}}$ из анализа новейших индивидуальных определений. Для практического использования важно знать наиболее вероятное значение ошибки определения ${{R}_{0}}$, которое мы планируем оценить. Объективное значение такой ошибки необходимо, в частности, при оценке линейной скорости вращения Галактики ${{V}_{0}}$ по измеренному значению угловой скорости ее вращения ${{\Omega }_{0}}$ (${{V}_{0}} = {{R}_{0}}{{\Omega }_{0}}$), а также при оценке, например, неопределенности постоянных Оорта $A = - 0.5\Omega _{0}^{'}{{R}_{0}}$ и $B = - {{\Omega }_{0}} + A$.
2. ДАННЫЕ
К настоящему моменту имеется ряд исследований, в которых среднее значение “наилучшего” расстояния ${{R}_{0}}$ выводится на основе индивидуальных определений этой величины, полученных независимыми методами в течение определенного длительного интервала времени. Такие результаты приведены в табл. 1. В первом столбце таблицы дано среднее значение ${{R}_{0}}$ с оценкой ошибки, во втором – количество независимых измерений $n$, использованных для вычисления среднего, в третьем – временной интервал в течение которого были получены индивидуальные оценки ${{R}_{0}}$, в последнем столбце дана ссылка на авторов индивидуальной оценки.
В табл. 1 приведены средние значения ${{R}_{0}},$ полученные из анализа индивидуальных оценок, опубликованных на временном отрезке от 6 до 20 лет. Особого внимания заслуживает результат из работы [5], в которой проанализированы 162 индивидуальные оценки на столетнем временном интервале. При этом видно, что все представленные в таблице средние значения ${{R}_{0}}$ находятся между собой в очень хорошем согласии. Отметим, что не все результаты являются полностью независимыми. Например, наборы исходных данных в работах [4] и [6] практически являются общими. Но Валле [4] и Камарильо с соавторами [6] применяют разные статистические методы анализа данных.
Главный вывод, который можно сделать из анализа табл. 1, заключается в том, что значение ${{R}_{0}}$ близко к 8.0 кпк. И это значение сильно отличается от ${{R}_{0}} = 8.5$ кпк, рекомендованного МАС в 1986 г.
В табл. 2 приведены индивидуальные результаты определения расстояния ${{R}_{0}}$, которые были получены после публикации работы [6]. Таким образом, они никем еще не были использованы для вывода среднего значения ${{R}_{0}}$. В первом столбце таблицы дано значение ${{R}_{0}}$ с оценкой ошибки, соответствующей уровню $1\sigma $, во втором столбце – тип использованных звезд или метод оценки ${{R}_{0}}$, в третьем – количество объектов $n$, использованных для вычисления ${{R}_{0}}$, в последнем столбце дана ссылка на авторов оценки ${{R}_{0}}$.
Таблица 2.
Индивидуальные результаты определения расстояния ${{R}_{0}}$
| ${{R}_{0}} \pm {{\varepsilon }_{R}}(1\sigma )$, кпк | Тип звезд/Метод | $n$ | Ссылка |
|---|---|---|---|
| $7.99 \pm 0.49$ | переменные типа RR Лиры | 850 | [31] |
| $8.27 \pm 0.10$ | классические цефеиды | ~800 | [38] |
| $8.275 \pm 0.033$ | S2 | 1 | [27] |
| $8.15 \pm 0.12$ | мазеры и радиозвезды | 256 | [25] |
| $8.2 \pm 0.6$ | ветвь голубых гигантов | ~2500 | [36] |
| $8.28 \pm 0.14$ | переменные типа RR Лиры | 16 221 | [30] |
| $7.92 \pm 0.30$ | мазеры программы VERA | 99 | [24] |
| $8.15 \pm 0.15$ | мазеры программы BeSSeL | 199 | [23] |
| $7.971 \pm 0.032$ | S2 | 1 | [13] |
| $8.1 \pm 0.2$ | переменные типа RR Лиры | 2016 | [29] |
| $8.2 \pm 0.1$ | классические цефеиды | 218 | [37] |
| $7.9 \pm 0.3$ | мириды | 1863 | [34] |
| $7.6 \pm 0.7$ | шаровые скопления | 119 | [39] |
| $8.05 \pm 0.024{\kern 1pt} * $ | переменные типа RR Лиры | 960 | [28] |
| $8.30 \pm 0.36$ | переменные типа RR Лиры | 4194 | [22] |
| $8.46 \pm 0.11$ | цефеиды II | 894 | [33] |
| $8.10 \pm 0.22$ | классические цефеиды | 4 | [35] |
| $7.93 \pm 0.13$ | S2 | 1 | [11] |
| $8.8 \pm 0.5$ | отрезки спиральных рукавов | 2 | [26] |
| $8.34 \pm 0.41$ | цефеиды II | 264 | [32] |
| $8.32 \pm 0.14$ | S2 | 1 | [10] |
Отметим, что некоторые авторы оценивают как статистическую, так и систематическую погрешность результата. Например, в работе [5] получено ${{R}_{0}} = 8.3$ кпк с погрешностью $ \pm 0.2$ (стат.) и $ \pm 0.4$ (сист.), далее будем записывать как R0 = = $8.3 \pm 0.2 \pm 0.4$ кпк. В настоящей работе мы обычно при цитировании оценки ${{R}_{0}}$ берем в качестве ошибки систематическую погрешность. В таком случае, как и для ${{R}_{0}} = 7.93 \pm 0.13 \pm 0.04$ кпк [11], берем максимальное значение ошибки.
Таблица 2 содержит 21 оценку ${{R}_{0}}$. Четыре оценки получены из анализа орбитального движения звезды S2 вокруг сверхмассивной черной дыры в центре Галактики [10, 11, 13, 27]. Во всех этих четырех случаях имеются частично общие астрометрические измерения положений звезды S2, но имеются различия, например, в количестве и качестве лучевых скоростей этой звезды. Действительно, в работах коллаборации GRAVITY [12, 27] наблюдения выполнены в Европейской Южной Обсерватории в Чили с использованием оптического интерферометра VLTI (Very Large Telescope Interferometer). Результаты Чу с соавторами [11[, а также Ду с соавторами [13] получены в основном на основе наблюдений в обсерватории Кека, расположенной на горе Мауна-Кеа в Гавайях.
Совсем недавно была опубликована работа [12], где была получена оценка ${{R}_{0}} = 8.178 \pm 0.013 \pm $ $ \pm \;0.022$ кпк. Но в самой последней публикации Абутера с соавторами [27] показано наличие инструментальных аберраций. Поэтому все предыдущие оценки коллаборации, начиная с 2018 г. (в частности результат [12]), были пересмотрены, и предложено значение ${{R}_{0}} = 8.275 \pm 0.009 \pm 0.033$ кпк. Именно его мы используем в настоящей работе.
Видно, что среди всех этих результатов оценки [27, 13 ] получены с наименьшими случайными ошибками, поэтому должны иметь наибольшие веса при вычислении средневзвешенного. Отметим, что случайные ошибки представленных оценок ${{R}_{0}}$ различаются на порядок. В таком случае необходимо использовать систему весов.
Девять оценок ${{R}_{0}}$ получены из анализа пространственного распределения переменных звезд. Четыре оценки получены по переменным типа RR Лиры [22, 28–31], две по цефеидам II типа [32, 33], одна по миридам [34] и одна по классическим цефеидам [35]. По схожести подхода к ним примыкает результат, полученный по звездам ветви голубых гигантов [36].
В работах [32, 33] использованы цефеиды II типа. Они являются маломассивными звездами, бедными металлами. Встречаются в шаровых скоплениях, галактическом диске и галактическом балдже. Цефеиды II типа более чем на величину слабее, чем классические цефеиды с аналогичными периодами, и следуют несколько другому соотношению “период–светимость”. В работе [32] скомбинированы данные из обзоров OGLE-III (Optical Gravitational Lensing Experiment [40]) и VVV (VISTA Variables in the Via Lactea [41]). Были отобраны 264 звезды с кривыми блеска хорошего качества. В работе [33] такое исследование было повторено с использованием гораздо большей выборки цефеид. Оценки ${{R}_{0}}$ были получены исходя из предположения о том, что отобранные звезды распределены симметрично относительно галактического центра.
Переменные типа RR Лиры принадлежат горизонтальной ветви гигантов на диаграмме Герцшпрунга–Рассела. Это старые звезды, принадлежащие населению II, содержащие мало тяжелых элементов и расположенные в сферической подсистеме Галактики. Обычно встречаются в шаровых скоплениях. В работе [22] отбор переменных типа RR Лиры был осуществлен из обзора VVV [41]. Индивидуальные расстояния до этих звезд оценивались с применением ближней инфракрасной фотометрии ($JH{{K}_{s}}$). ${{R}_{0}}$ было вычислено с использованием высокоширотной подвыборки отобранных звезд $({\kern 1pt} {\text{|}}b{\kern 1pt} {\text{|}} > 4^\circ )$. В работе [28] также был осуществлен отбор кандидатов из каталога VVV [41], но индивидуальные расстояния до звезд оценивались ими с использованием других калибровок. В работе [29] для отбора переменных типа RR Лиры был использован обзор SEKBO (Southern Edgeworth–Kuiper Belt Object [42]). В работе [30] для этих целей были использованы обзоры программы OGLE [43]. В работе [31] для оценки ${{R}_{0}}$ были использованы новые спектральные и фотометрические наблюдения на телескопе SALT (Southern African Large Telescope), а также новая калибровка для 850 звезд типа RR Лиры. Согласно оценкам [22], дисперсия при определении абсолютной величины звезд типа RR Лиры составляет ${{M}_{{{{K}_{s}}}}} = {{0.08}^{m}}$. Это означает, что в среднем случайная ошибка определения индивидуального расстояния до таких переменных звезд составляет около 4%.
В работе [35] была изучена выборка из 55 классических цефеид, принадлежащих галактическому балджу. Для учета поглощения использованы их фотометрические наблюдения в семи диапазонах $J$, $H$, ${{K}_{s}},$ 3.6 мкм, 4.5 мкм, 5.8 мкм и 8.0 мкм. В этих диапазонах значение межзвездного поглощения существенно меньше по сравнению с оптическим диапазоном. Как известно, от правильного учета поглощения сильно зависит оценка индивидуального расстояния до звезды, цефеиды в частности. В итоге, согласно [35], ошибка оценки расстояний до этих цефеид составила в среднем около 4–5%. Относительно центра Галактики они распределены неравномерно. Основная масса находится за центром Галактики на среднем расстоянии около 12 кпк. И только 4 звезды расположены в центре Галактики, по которым и была получена оценка ${{R}_{0}}.$
В работе [34] изучена большая выборка мирид. Эти звезды являются пульсирующими переменными, которые находятся на поздних эволюционных стадиях асимптотической ветви гигантов. Они характеризуются длительными периодами пульсаций (более 100 дней) и высокой ближней инфракрасной и болометрической светимостью. Принадлежат галактическому гало. В работе [34] сформирована большая выборка, скомпилированная из данных нескольких наблюдательных программ (SAAO, MACHO, OGLE). Калибровки и учет поглощения выполнены с использованием фотометрии $JH{{K}_{s}}$ из каталога 2MASS [44]. Оценка ${{R}_{0}}$ была получена исходя из предположения, что отобранные звезды распределены симметрично относительно галактического центра.
В работе [36] использованы звезды ветви голубых гигантов, которые также являются объектами гало. Оценка ${{R}_{0}}$ была получена путем анализа их кинематики на основе метода статистических параллаксов.
По сравнению со случайными ошибками ${{R}_{0}}$, полученными по другим выборкам звезд типа RR Лиры, случайные ошибки в работе [28] слишком малы. Поэтому при вычислении средневзвешенного мы их увеличили в 10 раз, т.е. сделали сопоставимыми с оценками [22, 29].
Пять оценок ${{R}_{0}}$ получены из анализа кинематики мазерных источников с измеренными тригонометрическими параллаксами [23, 24], мазерных источников и радиозвезд [25], а также по различным выборкам классических цефеид [37, 38]. Данные о 199 мазерах, наблюдавшихся на различных частотах (метанольных на частоте 8.4 ГГц и H2O-мазеров на частоте 22 ГГц) в рамках проекта BeSSeL (The Bar and Spiral Structure Legacy Survey11) описаны в [23]. В работе [24] проанализированы 99 источников мазерного излучения, которые наблюдались на частоте 22 ГГц в рамках японской программы VERA (VLBI Exploration of Radio Astrometry22). Отметим, что чем больше частота, тем точнее получаются РСДБ наблюдения параллаксов и собственных движений радиообъектов. Большая часть данных из работы [24] входила в выборку [23]. В работе [25] выборка [23] была дополнена РСДБ наблюдениями радиозвезд, которые, правда, лежат очень близко к Солнцу в области пояса Гулда. В работе [38] были использованы новейшие данные о классических цефеидах из работ [45, 21 ]. Эти цефеиды принадлежат дисковой составляющей Галактики, распределены практически по всему диску. Во всех пяти отмеченных здесь случаях ${{R}_{0}}$ входило в качестве неизвестного при решении основных кинематических уравнений, описывающих галактическое вращение. По классификации Рида [7] такой подход относится к непрямым методам, а согласно классификации Бланд-Хотторна и Герхарда [3] он относится к модельно зависимым методам.
Кинематическим способом получена также оценка ${{R}_{0}}$ в работе [39]. Для этого были проанализированы пространственные скорости 119 шаровых скоплений. Причем для них были вычислены оригинальные значения собственных движений, полученные с разностью эпох около 65 лет.
Наконец, в табл. 2 имеется оценка ${{R}_{0}}$, полученная в [26] из анализа распределения мазеров с измеренными тригонометрическими параллаксами в спиральных рукавах. Они использовали мазеры, лежащие в двух ближайших к Солнцу отрезках спиральных рукавов – Персея и Киля–Стрельца. Пока, впрочем, мало данных для уверенного применения метода, поэтому ошибка оценки ${{R}_{0}}$ получилась большой.
Для статистического анализа и сопоставления полученных результатов с другими авторами мы сформировали выборку из 35 измерений, выполненных в период 2011–2017 гг. Эти данные описаны в работе [6], где также указаны некоторые результаты из работы [4], которые Камарильо с соавторами [6] не включили в свою выборку. Мы же включили, создав таким образом более полный список измерений за этот период времени.
При этом в выборку не была включена очень неточная оценка ${{R}_{0}} = 7.6 \pm 1.35$ кпк, полученная статистическим методом по планетарным туманностям в работе [46]. Наконец, в выборку был добавлен один наш результат, полученный по 73 мазерам, ${{R}_{0}} = 8.3 \pm 0.3$ кпк [47].
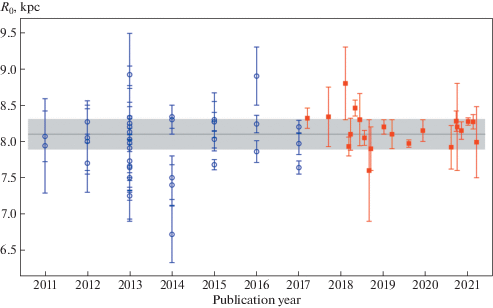
Все используемые в настоящей работе индивидуальные оценки ${{R}_{0}}$ в зависимости от года публикации показаны на рис. 1. Они покрывают десятилетний диапазон с 2011 по 2021 г., на котором совершенно не заметен так называемый “bandwagon” эффект. Этот эффект был замечен Ридом [7]. Он проявляется в тенденции к получению новой оценки, близкой к текущему стандартному значению.
Рис. 1.
Значения ${{R}_{0}},$ полученные различными авторами в последнем десятилетии: открытые синие кружки – данные из обзора [6], красные квадраты – данные из табл. 2 настоящей работы. Приведены среднее ${{\bar {R}}_{0}} = 8.090$ кпк (серая горизонтальная линия) и доверительная область, соответствующая дисперсии $1\sigma = 0.225$ кпк (серая заливка).
3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
3.1. Традиционный подход
Этот подход заключается в вычислении среднего арифметического, среднего взвешенного значения параметра ${{R}_{0}}$, а также оценки ошибок, исходя из предположения об их гауссовом распределении. (Отметим, что среднее арифметическое значение получается при единичных весах.)
В табл. 3 приведены значения среднего расстояния ${{R}_{0}}$. Вычисления проведены для трех выборок. Во-первых, для выборки из 21 индивидуальной оценки, которые даны в табл. 2. Во-вторых, для выборки из 35 индивидуальных оценок, которую мы сформировали по данным из работы [6]. В третьих, для объединенной выборки из 56 индивидуальных оценок, которая содержит результаты с 2011 по 2021 г. Среднее ${{\bar {R}}_{0}}$ вычислено в соответствии с известной формулой:
(1)
${{\bar {R}}_{0}} = \frac{{\sum\limits_{i = 1}^n \,{{w}_{i}}\mathop {{{R}_{0}}}\nolimits_i }}{{\sum\limits_{i = 1}^n \,{{w}_{i}}}},$(2)
$\sigma = \sqrt {\frac{{\sum\limits_{i = 1}^n \,{{w}_{i}}{{{(\mathop {{{R}_{0}}}\nolimits_i - {{{\bar {R}}}_{0}})}}^{2}}}}{{\sum\limits_{i = 1}^n \,{{w}_{i}}}}} .$Таблица 3.
Оценки среднего ${{R}_{0}}$ и его ошибки, полученные стандартным методом
| $n$ | ${{\bar {R}}_{0}}$, кпк | Дисперсия, кпк | Ошибка среднего, кпк | Вес $w$ | Значки на рис. 1 |
|---|---|---|---|---|---|
| 21 | 8.157 | 0.239 | 0.052 | 1 | красные |
| 21 | 8.139 | 0.157 | 0.034 | $1{\text{/}}\varepsilon _{R}^{2}$ | красные |
| 35 | 7.977 | 0.422 | 0.071 | 1 | синие |
| 35 | 7.973 | 0.304 | 0.051 | $1{\text{/}}\varepsilon _{R}^{2}$ | синие |
| 56 | 8.044 | 0.374 | 0.050 | 1 | все |
| 56 | 8.090 | 0.225 | 0.030 | $1{\text{/}}\varepsilon _{R}^{2}$ | все |
В нашем случае имеем чуть большее количество членов в выборке $n5$ из интервала 2011–2017 гг. по сравнению с выборкой, проанализированной Камарильо и др. [6], где $n = 28$. Несмотря на это, найденный нами результат, ${{\bar {R}}_{0}} = 7.973 \pm 0.051$ кпк (четвертая строка сверху в табл. 3), находится в хорошем согласии с оценкой [6] ${{\bar {R}}_{0}} = 7.93 \pm 0.03$ кпк (среднее взвешенное, с весами вида ${{w}_{i}} = 1{\text{/}}\varepsilon _{R}^{2}$ и дисперсией $\sigma = 0.40$ кпк). Можно также отметить хорошее согласие нашей оценки с результатом работы [2], который получен на основе аналогичного метода ${{\bar {R}}_{0}} = 7.967 \pm 0.048$ кпк (ошибка среднего взвешенного) из анализа совершенно другого набора индивидуальных оценок ${{R}_{0}}$.
Наиболее интересным мы считаем среднее взвешенное ${{\bar {R}}_{0}} = 8.139 \pm 0.034$ кпк, найденное по выборке из интервала 2017–2021 гг. ($n!$, вторая строка сверху в табл. 3). Эта оценка является новой, получена по независимым данным. Видно, что значения дисперсии в этой выборке выгодно отличаются в меньшую сторону от значений дисперсии, вычисленных для предшествующего периода.
На рис. 1 проведено среднее значение ${{\bar {R}}_{0}} = $ $ = 8.090$ кпк, найденное по выборке из 56 измерений, и указана доверительная область, соответствующая найденному по всей этой выборке стандартному отклонению ($1\sigma = 0.225$ кпк). При этом хорошо видно, что доверительная область для красных точек должна быть примерно в два раза более узкой.
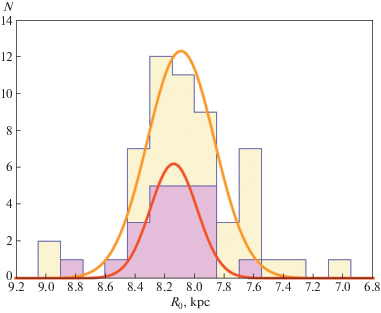
На рис. 2 приведены две гистограммы. Одна построена по выборке из 56 индивидуальных определений ${{R}_{0}}$ (светлая заливка) со средним ${{\bar {R}}_{0}} = 8.090$ кпк и $\sigma = 0.225$ кпк. Другая построена по выборке из 21 индивидуального определения ${{R}_{0}}$ (темная заливка) со средним ${{\bar {R}}_{0}} = 8.139$ кпк и $\sigma = 0.157$ кпк. В работе Камарильо и др. [6] отмечено, что распределение использованных ими 28 оценок ${{R}_{0}}$ шире гауссового и имеет другие небольшие отклонения от гауссианы. Такие проявления можно видеть на рис. 2 (уширены крылья распределения, вторичный максимум при $R \sim $ ~ 7.6 кпк на распределении из 56 оценок), хотя они и невелики.
Рис. 2.
Гистограммы распределения выборок из 56 значений (светлая заливка) и 21 значения ${{R}_{0}}$ (темная заливка) с соответствующими гауссианами, подробности см. текст.
В работе [6] негауссовость в распределении ошибок была доказана с применением распределения Стьюдента. Подход, использованный для определения наиболее вероятного значения ошибки среднего ${{R}_{0}}$ в работе [6] представляет интерес, мы также решили его применить.
3.2. Медианная статистика
Описание подхода можно найти в работах [6, 48, 49], которые применяли его при поиске наиболее вероятных значений ряда астрономических параметров. Камарильо с соавторами называют свой подход “медианной статистикой”. При этом он совершенно отличается от медианного метода, применяемого, например, в работах [2, 50].
Медиана – это центральное значение в отсортированном наборе данных, которое делит набор данных на две половины, каждая из которых содержит равное количество элементов. Медианная статистика предполагает статистическую независимость всех измерений и отсутствие систематических ошибок. Она не использует погрешности измерений, что является преимуществом, если ошибки оцениваются неправильно или являются негауссовыми. Расплатой за это служит то, что центральная медианная оценка имеет относительно большую неопределенность. Чтобы найти ошибки, связанные с медианной величиной, мы следуем работе [48].
Для набора данных из $N$ независимых измерений ${{M}_{i}}$ определяем вероятность $P$ медианы ${{M}_{{{\text{med}}}}}$, лежащей между ${{M}_{i}}$ и ${{M}_{{i + 1}}},$ как биномиальное распределение:
Ошибки на медиане ${{M}_{{{\text{med}}}}}$ определяются следующим образом. От значения ${{M}_{{{\text{med}}}}}$, имеющей наибольшую вероятность, производится интегрирование в обе стороны. Остановка происходит при достижении кумулятивной вероятности значения 0.6827 от полной вероятности, что соответствует стандартному отклонению $1\sigma $. Далее берется разность между медианой ${{M}_{{{\text{med}}}}}$ и двумя значениями $M$, соответствующими концам интегралов, чтобы получить погрешность в одно стандартное отклонение, $1\sigma _{ - }^{ + }$. Далее мы продолжаем это интегрирование до тех пор, пока кумулятивная вероятность не достигнет 0.9545 от полной вероятности, чтобы получить ошибки стандартного отклонения в $2\sigma _{ - }^{ + }$. Отметим, что распределение не обязательно должно быть симметричным, поэтому оценки граничных значений $2\sigma _{ - }^{ + }$ не обязательно в два раза больше значений $1\sigma _{ - }^{ + }$.В табл. 4 даны оценки ${{R}_{0}}$ и его ошибки, полученные только что описанным методом. Как показано в работе [6], оценки ошибок не симметричные, поэтому в табл. 4 даны оценки ${{R}_{0}}$ как для уровня $1\sigma _{ - }^{ + }$, так и для $2\sigma _{ - }^{ + }$. Отметим, что среднее в этом методе не вычисляется, а берется медианное из имеющегося упорядоченного списка (поэтому здесь не ставим значок среднее).
Таблица 4.
Оценки ${{R}_{0}}$ и его ошибки, полученные методом “медианной статистики”
| $n$ | ${{R}_{0}} \pm 1\sigma $, кпк | ${{R}_{0}} \pm 2\sigma $, кпк | Интервал $ \pm 1\sigma $, кпк | Интервал $ \pm 2\sigma $, кпк |
|---|---|---|---|---|
| 21 | $8.15_{{ - 0.10}}^{{ + 0.12}}$ | $8.15_{{ - 0.18}}^{{ + 0.13}}$ | 8.05–8.27 | 7.97–8.28 |
| 35 | $8.03_{{ - 0.12}}^{{ + 0.10}}$ | $8.03_{{ - 0.33}}^{{ + 0.17}}$ | 7.91–8.13 | 7.70–8.20 |
| 56 | $8.08_{{ - 0.09}}^{{ + 0.12}}$ | $8.08_{{ - 0.11}}^{{ + 0.12}}$ | 7.99–8.20 | 7.97–8.20 |
Вторая строка в таблице дана для сопоставления с результатом работы [6], где для выборки из 28 оценок с применением медианной статистики было найдено ${{R}_{0}} = 7.96_{{ - 0.23}}^{{ + 0.11}}$ для уровня $1\sigma $ и ${{R}_{0}} = 7.96_{{ - 0.30}}^{{ + 0.24}}$ для уровня $2\sigma .$ С учетом сделанного замечания о среднем, видим очень хорошее согласие в полученных нами и Камарильо и др. [6] оценках, сделанным по очень близким выборкам.
Метод проиллюстрирован на рис. 3. На рис. 3а показаны три упорядоченные по возрастанию последовательности измерений для трех выборок, которые содержат 21 (красный цвет), 35 (песочный цвет) и 56 (голубой цвет) измерений соответственно. Вертикальные линии на этом рисунке отмечают медианное значение. Распределение вероятности $P$ (см. выражение (4)) для этих же выборок приведено на рис. 3b.
Рис. 3.
Упорядоченные последовательности измерений с указанием медианных значений (a) и распределения вероятности $P$ (b) в зависимости от номера последовательности $i$ для трех выборок.
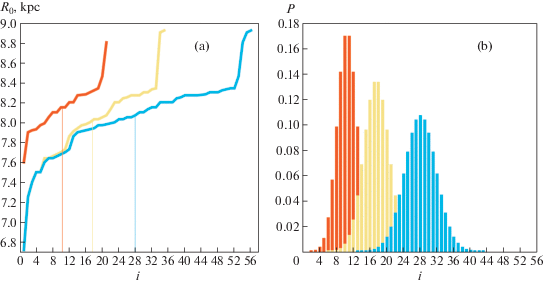
В табл. 4 наиболее интересным, конечно, является результат, полученный по выборке, содержащей 21 оценку. В предположении о симметричности ошибок, можем записать ${{R}_{0}} = 8.15 \pm 0.11$ кпк. Как можно видеть из рис. 3а, последовательность для выборки из 56 измерений (голубая линия) имеет наименьший наклон к горизонтальной оси по сравнению с другими двумя последовательностями. Поэтому для этой выборки получены близкие ошибки, как для уровня $1\sigma _{ - }^{ + }$, так и для $2\sigma _{ - }^{ + }$.
Согласно второй и последней строкам табл. 3 имеем наиболее вероятное значение среднего ${{R}_{0}} = 8.1$ кпк. В качестве наиболее вероятной оценки ошибки ${{R}_{0}}$ можно взять значение $0.1$ кпк, которое находится в согласии как со значением, полученным при стандартном подходе, так и при использовании медианной статистики. Тогда для практического использования можно рекомендовать значение ${{R}_{0}} = 8.1 \pm 0.1$ кпк. Отметим, что это значение находится в хорошем согласии с результатами, которые даны в табл. 1.
4. ЗАКЛЮЧЕНИЕ
Выполнен статистический анализ оценок расстояния ${{R}_{0}}$ от Солнца до центра Галактики. Для этого использованы результаты, полученные различными авторами в течение последнего десятилетия, с 2011 по 2021 г. По всей этой выборке, содержащей 56 измерений, на основе стандартного подхода мы нашли среднее взвешенное значение ${{\bar {R}}_{0}} = 8.090$ кпк с дисперсией $\sigma = 0.225$ кпк и ошибкой среднего взвешенного ${{\varepsilon }_{R}} = 0.030$ кпк. По этой же выборке на основе медианной статистики мы нашли ${{R}_{0}} = 8.08 \pm 0.10$ кпк.
В нашем списке имеется 21 индивидуальная оценка ${{R}_{0}}$, сделанная после 2017 г. Эти результаты никем еще не использовались для вычисления наилучшего среднего значения ${{R}_{0}}$. По этой выборке на основе стандартного подхода мы нашли среднее взвешенное значение ${{\bar {R}}_{0}} = 8.14$ кпк с дисперсией $\sigma = 0.16$ кпк и ошибкой среднего взвешенного ${{\varepsilon }_{R}} = 0.03$ кпк. По этой же выборке, содержащей 21 оценку, на основе медианной статистики мы нашли ${{R}_{0}} = 8.15 \pm 0.11$ кпк в предположении о симметричности ошибок.
Как мы уже отмечали, медианная статистика не дает совершенно точного значения среднего (медиана назначается из имеющегося списка измерений), но хорошо оценивает ошибки результата. Поэтому мы используем комбинированный результат, а именно, берем среднее взвешенное значение ${{R}_{0}},$ а ошибки – оцененные на основе медианной статистики.
В итоге мы пришли к заключению, что для практического использования можно рекомендовать значение ${{R}_{0}} = 8.1 \pm 0.1$ кпк.
Список литературы
I. I. Nikiforov, Order and Chaos in Stellar and Planetary Systems, Proc. Conf. 17–24 August 2003, at St. Petersburg State University, Russia; edited by G. G. Byrd, K. V. Kholshevnikov, A. A. Myllari, I. I. Nikiforov, and V. V. Orlov (San Francisco: Astron. Soc. Pacific), ASP Conf. Ser. 316, 199 (2004).
Z. Malkin, Advancing the Physics of Cosmic Distances, edited by R. de Grijs and G. Bono, Proc. IAU Symp. 289, 406 (2013).
J. Bland-Hawthorn and O. Gerhard, Ann. Rev. Astron. Astrophys. 54, 529 (2016).
J. P. Vallée, Astrophys. Space Sci. 362, 79 (2017).
R. de Grijs and G. Bono, Astrophys. J. Suppl. 232, id. 22 (2017).
T. Camarillo, V. Mathur, T. Mitchell, and B. Ratra, Publ. Astron. Soc. Pacific 130, 4101 (2018).
M. J. Reid, Ann. Rev. Astron. Astrophys. 31, 345 (1993).
M. J. Reid, K. M. Menten, X. W. Zheng, A. Brunthaler, and Y. Xu, Astrophys. J. 705, 1548 (2009).
S. Gillessen, F. Eisenhauer, S. Trippe, T. Alexander, R. Genzel, F. Martins, and T. Ott, Astrophys. J. 692, 1075 (2009).
S. Gillessen, P. M. Plewa, F. Eisenhauer, R. Sari, et al., Astrophys. J. 837, id. 30 (2017).
D. S. Chu, T. Do, A. Hees, A. Ghez, et al., Astrophys. J. 854, id. 12 (2018).
R. Abuter, A. Amorim, M. Bauböck, J. P. Berger, et al., Astron. and Astrophys. 625, id. L10 (2019).
T. Do, A. Hees, A. Ghez, G. D. Martinez, et al., Science 365, 664 (2019).
H. S. Leavitt, Ann. Harvard College Observ. 60, 87 (1908).
H. S. Leavitt and E. C. Pickering, Harvard College Observ. Circ. 173, 1 (1912).
B. F. Madore, Astrophys. J. 253, 575 (1982).
F. Caputo, M. Marconi, and I. Musella, Astron. and Astrophys. 354, 610 (2000).
V. Ripepi, R. Molinaro, I. Musella, M. Marconi, S. Leccia, and L. Eyer, Astron. and Astrophys. 625, id. A14 (2019).
L. N. Berdnikov, A. K. Dambis, and O. V. Vozyakova, Astron. and Astrophys. Suppl. Ser. 143, 211 (2000).
A. Sandage and G. A. Tammann, Ann. Rev. Astron. Astrophys. 44, 93 (2006).
D. M. Skowron, J. Skowron, P. Mróz, A. Udalski, et al., Science 365, 478 (2019).
D. Majaess, I. Dékány, G. Hajdu, D. Minniti, D. Turner, and W. Gieren, Astrophys. Space Sci. 363, 127 (2018).
M. J. Reid, K. M. Menten, A. Brunthaler, X. W. Zheng, et al., Astrophys. J. 885, id. 131 (2019).
T. Hirota, T. Nagayama, M. Honma, Y. Adachi, et al., Publ. Astron. Soc. Japan 72, 50 (2020).
V. V. Bobylev, O. I. Krisanova, and A. T. Bajkova, Astron. Letters 46, 439 (2020).
I. I. Nikiforov and A. V. Veselova, Astron. Letters 44, 81 (2018).
R. Abuter, A. Amorim, M. Bauböck, J. P. Berger, et al., arXiv:2101.12098 [astro-ph.GA] (2021).
R. Contreras Ramos, D. Minniti, F. Gran, M. Zoccali, et al., Astrophys. J. 863, id. 79 (2018).
E. Griv, M. Gedalin, and I.-G. Jiang, Monthly Not. Roy. Astron. Soc. 484, 218 (2019).
E. Griv, M. Gedalin, P. Pietrukowicz, D. Majaess, and I.‑G. Jiang, Monthly Not. Roy. Astron. Soc. 499, 1091 (2020).
T. D. Muhie, A. K. Dambis, L. N. Berdnikov, A. Y. Kniazev, and E. K. Grebel, Monthly Not. Roy. Astron. Soc. 502, 4074 (2021), arXiv:2101.03899 [astro-ph.GA].
A. Bhardwaj, M. Rejkuba, D. Minniti, F. Surot, et al., Astron. and Astrophys. 605, id A100 (2017).
V. F. Braga, A. Bhardwaj, R. Contreras Ramos, D. Minniti, G. Bono, R. de Grijs, J. H. Minniti, and M. Rejkuba, Astron. and Astrophys. 619, id. A51 (2018).
W. Qin, D. M. Nataf, N. Zakamska, P. R. Wood, and L. Casagrande, Astrophys. J. 865, id. 47 (2018).
X. Chen, S. Wang, L. Deng, and R. de Grijs, Astrophys. J. 859, id. 137 (2018).
N. D. Utkin and A. K. Dambis, Monthly Not. Roy. Astron. Soc. 499, 1058 (2020).
D. Kawata, J. Bovy, N. Matsunaga, and J. Baba, Monthly Not. Roy. Astron. Soc. 482, 40 (2019).
V. V. Bobylev, A. T. Bajkova, A. S. Rastorguev, and M. V. Zabolotskikh, Monthly Not. Roy. Astron. Soc. 502, 4377 (2021).
A. D. Klinichev, E. V. Glushkova, A. K. Dambis, and L. N. Yalalieva, Astron. Rep. 62, 986 (2018).
I. Soszyński, A. Udalski, M. K. Szymański, M. Kubiak, et al., Acta Astronomica 58, 293 (2008).
D. Minniti, P. W. Lucas, J. P. Emerson, R. K. Saito, et al., New Astronomy 15, 433 (2010).
R. Moody, B. Schmidt, C. Alcock, J. Goldader, T. Axelrod, K. Cook, and S. Marshall, Earth, Moon, and Planets 92, 125 (2003).
I. Soszyński, A. Udalski, M. Wrona, M. Szymański, et al., Acta Astronomica 69, 321 (2019).
M. F. Skrutskie, R. M. Cutri, R. Stiening, M. D. Weinberg, et al., Astron. J. 131, 1163 (2006).
P. Mróz, A. Udalski, D. M. Skowron, J. Skowron, et al., Astrophys. J. 870, id. L10 (2019).
A. Ali, H. A. Ismail, and Z. Alsolami, Astrophys. Space Sci. 357, 21 (2015).
V. V. Bobylev and A. T. Bajkova, Astron. Letters 40, 389 (2014).
J. R. Gott, M. S. Vogeley, S. Podariu, and B. Ratra, Astrophys. J. 549, 1 (2001).
H. Yu, A. Singal, J. Peyton, S. Crandall, and B. Ratra, Astrophys. Space Sci. 365, 146 (2020).
Z. Malkin, arXiv:1202.6128 [astro-ph.GA] (2012).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


