Астрономический журнал, 2021, T. 98, № 7, стр. 550-561
Затменно-двойные системы со сложными изменениями орбитальных периодов XZ Per и BO VuL
1 Московский государственный университет им. М.В. Ломоносова,
Государственный астрономический институт им. П.К. Штернберга
Москва, Россия
* E-mail: khaliullinkhf@yandex.ru
Поступила в редакцию 31.01.2021
После доработки 27.02.2021
Принята к публикации 28.02.2021
Аннотация
Проведено исследование изменений орбитального периода в затменно-двойных системах XZ Per и BO Vul. Показано, что изменения орбитального периода затменно-двойной системы XZ Per одинаково хорошо представляются как суперпозицией векового уменьшения и циклических изменений, так и суммой двух циклических изменений. В первом случае монотонная составляющая может быть следствием потери системой углового момента за счет магнитного торможения, а циклические изменения можно объяснить присутствием в системе третьего тела или магнитной активностью вторичного компонента, имеющего конвективную оболочку. Во втором случае можно предположить присутствие двух дополнительных тел в системе, либо отнести одно из колебаний периода на счет светового уравнения, а другое – на счет магнитной активности вторичного компонента. Изменения орбитального периода затменно-двойной системы BO Vul можно представить суперпозицией векового уменьшения и циклических изменений. Наблюдаемые циклические изменения периода могут происходить из-за присутствия в системе третьего тела или из-за магнитной активности вторичного компонента, имеющего конвективную оболочку.
1. ВВЕДЕНИЕ
Изучение периодов затменно-двойных звезд является удобным инструментом для изучения процессов, происходящих в тесных двойных системах. Вековые изменения периода (монотонное увеличение или уменьшение) связывают с процессами обмена веществом между компонентами и потерей вещества системой в целом [1–3]. Количественные оценки скорости уменьшения (или увеличения) периода могут помочь сделать выбор среди имеющихся теоретических моделей. Циклические изменения орбитального периода тесных двойных систем могут вызываться вращением линии апсид (при эксцентричной орбите) или присутствием в системе третьего тела (или нескольких дополнительных тел). Однако световое уравнение не всегда подходит для объяснения циклических изменений орбитального периода из-за неприемлемых параметров третьего тела или данных, противоречащих гипотезе о движении в долгопериодической орбите. В настоящее время при изучении циклических изменений периодов затменно-двойных систем все чаще рассматривается влияние магнитных циклов, когда речь идет о системах с компонентами поздних спектральных классов, имеющих конвективную оболочку. Довольно часто изменения орбитального периода являются суперпозицией нескольких изменений различной природы.
Для затменно-двойных систем, рассматриваемых в настоящей работе, графики зависимости от времени разностей между наблюдаемыми моментами минимумов и вычисленными с линейными элементами имеют довольно сложный вид. Форма всех диаграмм указывает на вековое уменьшение периода, при этом соответствующая обратная парабола искажается дополнительными изменениями, и если наличие обратной параболы было очевидно для всех исследователей этих систем, то дополнительные изменения периода вызывали трудности при их интерпретации.
2. ИЗМЕНЕНИЯ СО ВРЕМЕНЕМ ОРБИТАЛЬНОГО ПЕРИОДА XZ PER
Изучение звезды XZ Per (HV 03553, GSC 3328.03186, Vmax = 11.4m, P = 1.15163d) началось с визуальных наблюдений Дубяго и Мартынова, на основе которых была построена визуальная кривая блеска [4]. Лавров [5] получил фотометрические элементы орбиты XZ Per из решения этой кривой блеска. Используя эти же визуальные наблюдения и добавив к ним свои более поздние данные, Цесевич [6, 7] изучил поведение периода XZ Per и обнаружил его плавное изменение. Спектральный класс главного компонента, F2-5 определил Поппер [8]. Кривой лучевых скоростей для этой системы нет. В работе [9] было проведено подробное фотометрическое исследование XZ Per. Из ПЗС наблюдений в нескольких спектральных полосах были получены фотометрические элементы орбиты и определены абсолютные характеристики звезд-компонентов. Изменения периода XZ Per изучались многими авторами, однако достаточно большое количество моментов минимумов было рассмотрено в работах [9, 10]. В обеих этих работах изменения периода XZ Per были представлены в виде суперпозиции векового уменьшения периода и его скачков. Подобная интерпретация изменений орбитального периода предлагалась в свое время для затменно-двойных систем RW Tau, TU Her, TY Peg, однако в дальнейшем было показано, что эти изменения можно представить плавными кривыми, соответствующими световому уравнению или магнитным колебаниям [11, 12].
Для исследования изменений периода затменно-двойной системы XZ Per были использованы моменты минимумов из базы данных B. R. N. O. [13] и не вошедшие в эту базу данных моменты минимумов из работы [9]. Всего имеется 498 моментов главного минимума: 414 визуальных, 9 фотографических и 75 из фотоэлектрических и ПЗС наблюдений и 3 момента вторичного минимума. На рис. 1 приведены отклонения (O – C)1 наблюдаемых (О) моментов минимумов XZ Per от вычисленных (C) с линейными элементами, полученными методом наименьших квадратов с использованием всех имеющихся моментов главного минимума:
(1)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2443507.4630(8) + \\ + \;1.15163143{{(11)}^{{\text{d}}}}T, \\ \end{gathered} $(2)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2443507.4746(6) + \\ + \;1.15163079{{(7)}^{{\text{d}}}}T--2.17{{(7)}^{{\text{d}}}} \times {{10}^{{--10}}}{{T}^{2}}. \\ \end{gathered} $(3)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2443507.4761(9) + \\ + \;1.15163140{{(4)}^{{\text{d}}}}T--1.01{{(6)}^{{\text{d}}}} \times {{10}^{{--10}}}{{T}^{2}} + \\ + \;\frac{{{{a}_{3}}\sin {{i}_{3}}}}{c}(1--{{e}_{3}}\cos E)\sin ({v} + {{\omega }_{3}}). \\ \end{gathered} $Рис. 1.
Отклонения (O–C)1 наблюдаемых моментов минимумов XZ Per от вычисленных с линейными элементами (1). Фотографические наблюдения представлены в виде треугольников, визуальные – маленькими точками, фотоэлектрические и из ПЗС наблюдений – большими точками.

Таблица 1.
Параметры гипотетического светового уравнения в изменениях орбитального периода XZ Per для квадратичного представления моментов минимумов
| Параметр | Значение |
|---|---|
| P3 | (23 300 ± 150) сут = (63.8 ± 0.4) лет |
| A3 | (0.019 ± 0.001) сут |
| e3 | 0.67 ± 0.04 |
| ω3 | 147° ± 2° |
| JD3 | 2 447 500 ± 70 |
| ${{a}_{3}}\sin {{i}_{3}}$ | (4.9 ± 0.2) × 108 км = (3.29 ± 0.17) а.е. |
| f(M3) | 0.00877 ${{M}_{ \odot }}$ |
| ${{M}_{3}}\sin {{i}_{3}}$ | 0.402 ${{M}_{ \odot }}$ |
Рис. 2.
Зависимость от времени значений (O–C)2, полученных вычитанием из наблюдаемых значений моментов минимумов XZ Per теоретической параболы (3). Сплошной кривой показана теоретическая кривая для светового уравнения с параметрами из табл. 1.

Остатки после вычитания из наблюдаемых моментов минимумов теоретических, вычисленных по формуле (3), приведены в верхней части рис. 5. На этом графике фотографические и визуальные точки расположены довольно хаотично, но можно заметить некоторые “всплески”. Данные же, полученные из фотоэлектрических и ПЗС наблюдений, показывают хорошо выраженные изменения. Построить теоретическую кривую, которая представляла бы все данные на этом графике, не удалось. Поэтому был испробован другой подход к интерпретации изменений периода XZ Per. Они были представлены непосредственно световым уравнением. Поскольку зависимость от времени остатков после вычитания из наблюдений теоретической кривой для светового уравнения также показывает колебания, изменения периода XZ Per были представлены суперпозицией двух световых уравнений:
(4)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2443507.4652(1) + \\ + \;1.15163121{{(1)}^{{\text{d}}}}T + LTE1 + LTE2. \\ \end{gathered} $Таблица 2.
Параметры гипотетических световых уравнений в изменениях орбитального периода XZ Per для линейного представления моментов минимумов
| Параметр | Значение | Параметр | Значение |
|---|---|---|---|
| PG | (33 000 ± 600) сут = (90.3 ± 1.6) лет | PL | (10 700 ± 110) сут = (29.3 ± 0.3) лет |
| AG | (0.023 ± 0.001) сут | AL | (0.0058 ± 0.0003) сут |
| eG | 0.23 ± 0.01 | eL | 0.33 ± 0.03 |
| ωG | 81° ± 7° | ωL | 77° ± 18° |
| JDG | 2 443 500 ± 620 | JDL | 2 456 350 ± 500 |
| ${{a}_{G}}\sin {{i}_{G}}$ | (5.96 ± 0.03) × 108 км = (3.98 ± 0.17) а.е. | ${{a}_{L}}\sin {{i}_{L}}$ | (1.50 ± 0.08) × 108 км = (1.00 ± 0.05) а.е. |
| f(M3) | 0.00776 ${{M}_{ \odot }}$ | f(M3) | 0.00118 ${{M}_{ \odot }}$ |
| $M\sin {{i}_{3}}$ | 0.385 ${{M}_{ \odot }}$ | ${{M}_{3}}\sin {{i}_{3}}$ | 0.196 ${{M}_{ \odot }}$ |
На рис. 3 приведены изменения со временем разностей, полученных вычитанием теоретической кривой для волны с меньшим периодом из отклонений наблюдаемых моментов минимумов XZ Per от вычисленных с линейными элементами (4). Сплошная линия на этом рисунке – теоретическая кривая для волны с бóльшим периодом с параметрами из табл. 2. На рис. 4 приведены изменения со временем разностей, полученных вычитанием теоретической кривой для волны с бóльшим периодом из отклонений наблюдаемых моментов минимумов XZ Per от вычисленных с линейными элементами (4). Сплошная линия на этом рисунке – теоретическая кривая для волны с меньшим периодом с параметрами из табл. 2.
Рис. 3.
Изменения со временем разностей, полученных вычитанием теоретической кривой для волны с меньшим периодом из отклонений наблюдаемых моментов минимумов XZ Per от вычисленных с линейными элементами (4). Сплошная линия на этом рисунке – теоретическая кривая для волны с бóльшим периодом с параметрами из табл. 2. Обозначения такие же, как на рис. 1.

Рис. 4.
Изменения со временем разностей, полученных вычитанием теоретической кривой для волны с бóльшим периодом из отклонений наблюдаемых моментов минимумов XZ Per от вычисленных с линейными элементами (4). Сплошная линия на этом рисунке – теоретическая кривая для волны с меньшим периодом с параметрами из табл. 2. Обозначения такие же, как на рис. 1.
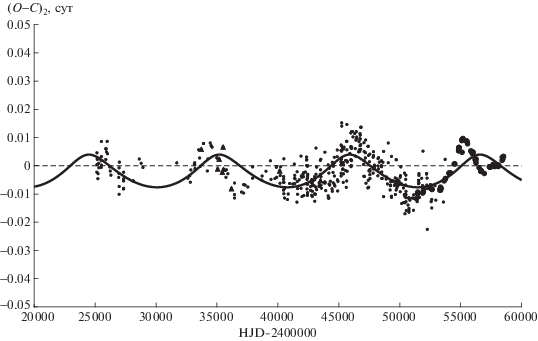
Рис. 5.
Остатки после вычитания из наблюдаемых моментов минимумов а) параболы и светового уравнения согласно формуле (3); б) двух световых уравнений согласно формуле (4). Сплошные линии – теоретические кривые для световых уравнений, полученные по фотоэлектрическим и ПЗС наблюдениям. Обозначения такие же, как на рис. 1.

Остатки после вычитания из наблюдаемых моментов минимумов теоретических, вычисленных по формуле (4), приведены в нижней части рис. 5. Этот график почти не отличается от полученного для квадратичного представления. То есть можно представить изменения периода XZ Per либо суперпозицией параболы и светового уравнения, либо суммой двух световых уравнений, в остатке получается практически одна и та же картина. Сплошные линии на этом рисунке – теоретические кривые для световых уравнений, полученные по фотоэлектрическим и ПЗС наблюдениям: для первого случая период равен 13 лет, амплитуда 0.0059 сут; для второго – период 12 лет, амплитуда 0.0055 сут. К сожалению, ни в одном из двух случаев эти кривые не отражают визуальные наблюдения. Для уточнения характера этих остаточных изменений периода нужны дальнейшие высокоточные наблюдения.
3. ВОЗМОЖНЫЕ ПРИЧИНЫ ИЗМЕНЕНИЙ ОРБИТАЛЬНОГО ПЕРИОДА XZ PER
Скорость векового уменьшения периода вычисляется по формуле: dP/dt = 2Q/P, где Q – коэффициент при квадратичном члене в представлении моментов минимумов. Для XZ Per мы получили Q = –1.01(6)d × 10–10, откуда dP/dt = –6.41 × × 10–8 сут/год. Вековое уменьшение периода может быть вызвано потерей углового момента системы, наиболее эффективный механизм потери углового момента – магнитное торможение [17–19].
Полученные параметры долгопериодических орбит позволяют вычислить функцию масс для каждого светового уравнения в предположении, что в системе имеется только одно дополнительное тело:
(5)
$f({{M}_{3}}) = \frac{{a_{3}^{3}{{{\sin }}^{3}}{{i}_{3}}}}{{P_{3}^{2}}} = \frac{{M_{3}^{3}{{{\sin }}^{3}}{{i}_{3}}}}{{{{{({{M}_{1}} + {{M}_{2}} + {{M}_{3}})}}^{2}}}}.$В случае квадратичных элементов предполагается существование только одного дополнительного тела. В случае линейных элементов могут быть разные случаи. 1) Одно из циклических изменений периода вызвано присутствием третьего тела, а второе (или оба) – другими причинами (см. ниже). 2) Оба циклических изменения периода вызваны световыми уравнениями. Тогда мы имеем четырехкратную систему. Для иерархической четырехкратной системы функция масс связана с массами компонентов следующим соотношением:
(6)
$f({{M}_{4}}) = \frac{{a_{4}^{3}{{{\sin }}^{3}}{{i}_{4}}}}{{P_{4}^{2}}} = \frac{{M_{4}^{3}{{{\sin }}^{3}}{{i}_{4}}}}{{{{{({{M}_{1}} + {{M}_{2}} + {{M}_{3}} + {{M}_{4}})}}^{2}}}}.$Во всех рассмотренных случаях минимальная масса дополнительных компонентов получается небольшой. Действительную массу вероятных дополнительных тел нельзя узнать, пока неизвестны наклонности их орбит. Полезно было бы попытаться найти долю третьего света в общем блеске системы. В работе [9] при решении кривой блеска не ставилась задача определить долю третьего света в системе, поскольку автор не предполагал наличие в системе третьего тела.
В качестве альтернативы гипотезе о третьем теле может служить предположение, что наблюдаемые циклические изменения периода являются проявлением магнитной активности. Вторичный компонент в затменно-двойной системе XZ Per имеет спектральный класс K4 [9], и должен иметь конвективную оболочку. В работе [20] была предложена модель, в которой гравитационное квадрупольное взаимодействие обеспечивает механизм, посредством которого орбита реагирует на изменения внутренней структуры активной звезды. В этой модели амплитуда модуляций орбитального периода ΔP и амплитуда осцилляций Δ(О – С) на диаграмме О – С связаны соотношением: ΔP/P0 = 2π Δ(О – С)/Pmod. Принимая для радиусов и масс компонентов значения согласно [9], из третьего закона Кеплера находим величину большой полуоси относительной орбиты двойной системы, a = 6.12 ${{R}_{ \odot }}$. Затем, используя последовательность формул, приведенную в [20], находим оценки величины переносимого (от ядра звезды к ее оболочке и обратно) углового момента ΔJ, количества энергии, необходимого для переноса углового момента во внешнюю часть звезды, ΔE, напряженности магнитного поля B активного компонента и изменений его светимости ΔL. Эти величины приведены в табл. 3 для каждого модулирующего периода.
Таблица 3.
Величины, характеризующие циклы магнитной активности вторичного компонента затменно-двойной системы XZ Per
| Величина | С параболой | Без параболы | |
|---|---|---|---|
| Рmod | 23 300 сут | 33 000 сут | 10 700 сут |
| Δ(О – С) | 0.019 сут | 0.023 сут | 0.0058 сут |
| ΔP | 0.51 с | 0.44 с | 0.34 с |
| ΔJ | 3.48 × 1047 г см2/с | 2.98 × 1047 г см2/с | 2.31× 1047 г см2/с |
| ΔE | 9.52 × 1040 эрг | 6.93 × 1040 эрг | 4.19 × 1040 эрг |
| B | 3.26 × 103 Гаусс | 2.53 × 103 Гаусс | 3.92 × 103 Гаусс |
| ΔL | 1.48 × 1032 эрг/с = = 0.039 ${{L}_{ \odot }}$ = 0.032 L2 |
7.64 × 1031 эрг/с = = 0.020 ${{L}_{ \odot }}$ = 0.017 L2 |
1.42 × 1032 эрг/с = 0.037 ${{L}_{ \odot }}$ = 0.031 L2 |
Полученные оценки магнитных и энергетических величин для всех модулирующих периодов вполне укладываются в допустимые рамки. Возможные колебания светимости вторичного компонента невелики. Следовательно, магнитные колебания могут быть причиной циклических изменений орбитального периода XZ Per.
4. ИЗМЕНЕНИЯ СО ВРЕМЕНЕМ ОРБИТАЛЬНОГО ПЕРИОДА BO VUL
Звезда BO Vul (HD 187949, Vmax = 10.5m, P = = 1.9458d) была открыта Хоффмайстером [21] из фотографических наблюдений как затменно-переменная типа Алголя. Первые эфемериды были определены в работе [22] из визуальных наблюдений. Две фотографические кривые блеска были построены в работах [23, 24]. Шафранец [25] построила кривую блеска BO Vul в главном минимуме по визуальным наблюдениям. Однако фотометрические элементы орбиты были определены только из фотографической кривой блеска [23] и в этой же работе были оценены спектральные классы компонентов как F2 + K3. Для этой системы нет ни кривой лучевых скоростей, ни современных высокоточных наблюдений кривой блеска. Имеются только приближенные значения абсолютных характеристик компонентов [26].
То, что период системы меняется, впервые заметил Анерт [27], который нашел два набора эфемерид для двух диапазонов Юлианских дней и заявил о невозможности вывести средние эфемериды. Болдуин [28] отметил, что в BO Vul произошли несколько изменений орбитального периода. Первый подробный анализ изменений орбитального периода этой системы был проведен в работе [29]. Авторы представили изменения орбитального периода BO Vul суперпозицией векового уменьшения и внезапных скачков. Они предположили, что вековое изменение может быть вызвано магнитным звездным ветром, а внезапные скачки – неустойчивостью аккреционного диска вокруг главной звезды. Эрдем [30] исследовал изменения орбитального периода BO Vul на основе большого количества моментов минимумов, в основном, визуальных, и представил их суперпозицией векового уменьшения периода и светового уравнения. Заше [31] исследовал те же самые моменты минимумов с использованием также фотографических данных и получил результат, почти не отличающийся от результата, полученного в работе [30]. С тех пор было получено довольно много моментов минимумов из фотоэлектрических и ПЗС наблюдений. На рис. 6 приведены отклонения (O – C) наблюдаемых (О) моментов минимумов BO Vul от вычисленных (C) c квадратичными элементами из работы [30]. Сплошная линия на этом рисунке – теоретическая кривая для светового уравнения, посчитанного с параметрами из той же работы. Из этого рисунка видно, что результаты из работы [30] хорошо удовлетворяют ранним наблюдениям и совсем не согласуются с последними фотоэлектрическими и ПЗС наблюдениями. Аналогичная картина наблюдается, если использовать результаты из работы [31]. Исходя из новых данных, изменения периода OB Vul следует пересмотреть.
Рис. 6.
Отклонения (O–C) наблюдаемых (О) моментов минимумов BO Vul от вычисленных (C) c квадратичными элементами из работы [30]. Сплошная линия на этом рисунке – теоретическая кривая для светового уравнения, посчитанного с параметрами из той же работы. Визуальные наблюдения представлены маленькими точками, фотоэлектрические и из ПЗС наблюдений – большими точками.

Для исследования изменений периода затменно-двойной системы BO Vul были использованы моменты минимумов из базы данных B. R. N. O. [13]. Всего имеется 359 моментов главного минимума: 260 визуальных, 67 фотографических и 32 из фотоэлектрических и ПЗС наблюдений и 1 момент вторичного минимума. На рис. 7 приведены отклонения (O – C)1 наблюдаемых (О) моментов минимумов BO Vul от вычисленных (C) с линейными элементами, полученными методом наименьших квадратов с использованием всех имеющихся моментов главного минимума:
(7)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2435989.436(2) + \\ + \;1.9458690{{(4)}^{{\text{d}}}}T, \\ \end{gathered} $(8)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2435989.416(2) + \\ + \;1.9458795{{(9)}^{{\text{d}}}}T--10.0{{(8)}^{{\text{d}}}} \times {{10}^{{--10}}}{{T}^{2}}. \\ \end{gathered} $Рис. 7.
Отклонения (O–C)1 наблюдаемых моментов минимумов BO Vul от вычисленных с линейными элементами (7). Фотографические наблюдения представлены в виде треугольников, визуальные – маленькими точками, фотоэлектрические и из ПЗС наблюдений – большими точками.

Рис. 8.
Отклонения (O–C)2 наблюдаемых моментов минимумов BO Vul от вычисленных с линейными элементами из представления (8). Теоретическая парабола с параметрами из этого же представления показана на рисунке сплошной кривой. Обозначения такие же, как на рис. 6.

Рис. 9.
Зависимость от времени значений (O–C)3, полученных вычитанием из наблюдаемых значений моментов минимумов BO Vul теоретической параболы. Сплошной кривой показана теоретическая кривая для светового уравнения с параметрами из табл. 4. Внизу приведена зависимость от времени значений (O – C)4, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом квадратичных элементов и светового уравнения с параметрами из табл. 4. Обозначения такие же, как на рис. 6.

Считая, что циклические изменения периода вызваны присутствием в системе третьего тела, можно выразить их через параметры долгопериодической орбиты посредством светового уравнения. Параметры долгопериодической орбиты BO Vul были определены таким же способом, как для XZ Per. При этом уточнялись и квадратичные элементы. При расчетах визуальным данным был приписан вес 1, а полученным из фотоэлектрических и ПЗС наблюдений – вес 10. В табл. 4 приведены полученные нами значения параметров светового уравнения и квадратичных элементов: орбитального периода двойной системы P2, начальной эпохи JD2 и коэффициента при квадратичном члене Q. Сплошная линия на рис. 9 – теоретическая кривая для светового уравнения с параметрами из табл. 4. В нижней части рис. 9 приведены остатки после вычитания из наблюдаемых моментов минимумов параболы и светового уравнения с параметрами из табл. 4. На этом рисунке видно, что теоретическая кривая для светового уравнения хорошо удовлетворяет наблюдениям, для которых JD > 2 445 000 и не очень хорошо проходит среди более ранних точек. В работе [30] были рассмотрены точки с JD < 2 452 000, и полученная теоретическая кривая хорошо проходила по всем таким точкам, однако, как было показано на рис. 6, представление, полученное в этой работе, совершенно не согласуется с более поздними данными. Могут быть две причины такого расхождения: 1) в системе действительно наблюдается световое уравнение, но из-за низкой точности старых визуальных наблюдений теоретическая кривая, полученная с участием фотоэлектрических и ПЗС данных, плохо согласуется с ранними наблюдениями; 2) циклические изменения периода вызваны не световым уравнением, а другими причинами, например, магнитными колебаниями, в таком случае колебания не следуют строгой кривой.
Таблица 4.
Параметры гипотетической долгопериодической орбиты BO Vul
| Параметр | Значение |
|---|---|
| P3 | (11 400 ± 40) сут = (31.2 ± 0.1) лет |
| A3 | (0.0233 ± 0.0004) сут |
| e3 | 0.50 ± 0.02 |
| ω3 | 342° ± 2° |
| JD3 | 2 445 600 ± 70 |
| ${{a}_{3}}\sin {{i}_{3}}$ | (6.0 ± 0.1) × 108 км = (4.03 ± 0.07) а.е. |
| P2 | 1.9458817(3) сут |
| JD2 | 2 435 989.4064(1) |
| Q | (−1.19 ± 0.02) × 10−9 |
5. ВОЗМОЖНЫЕ ПРИЧИНЫ ИЗМЕНЕНИЙ ОРБИТАЛЬНОГО ПЕРИОДА BO VUL
Если циклические колебания периода BO Vul представляют собой световое уравнение, то используя найденные нами параметры долгопериодической орбиты, приведенные в табл. 4, можно вычислить функцию масс тройной системы: f(M3) = = 0.068 ${{M}_{ \odot }}$. Используя значения масс компонентов затменно-двойной системы из [26]: М1 = = 1.45 ${{M}_{ \odot }}$, М2 = 0.64 ${{M}_{ \odot }}$, получаем ${{М}_{3}}\sin {{i}_{3}}$ = = 0.83 ${{M}_{ \odot }}$. Считая третий компонент звездой Главной последовательности, из соотношения масса–светимость в соответствующем диапазоне масс [32] найдем светимость третьего тела: L3 = = 0.38 ${{L}_{ \odot }}$. Светимости компонентов затменно-двойной системы определим, исходя из оценок массы и относительной светимости главного компонента, приведенных в [26]. Главный компонент затменно-двойной системы является звездой Главной последовательности, и его светимость можно найти из соотношения масса–светимость в соответствующем диапазоне масс [32]: L1 = 4.97 ${{L}_{ \odot }}$. Согласно [26], его относительная светимость равна 0.81, тогда абсолютная светимость вторичного компонента получается равной L2 = 1.16 ${{L}_{ \odot }}$. Теперь можно найти относительную светимость предполагаемого третьего тела: L3/(L1+ L2+ L3) = 0.06. Такое количество третьего света можно было бы найти из решения кривой блеска. Возможность присутствия третьего тела в этой системе нельзя исключить, тем более что нет ни точной кривой блеска, ни кривой лучевых скоростей, так что для абсолютных характеристик компонентов имеются лишь приближенные оценки.
Вторичный компонент в затменно-двойной системе BO Vul имеет спектральный класс G0 IV [26] и должен иметь конвективную оболочку, следовательно, наблюдаемые циклические изменения периода могут являться проявлением магнитной активности. Для приведенных выше оценок масс компонентов из 3-го закона Кеплера находим величину большой полуоси относительной орбиты двойной системы: a = 8.38 ${{R}_{ \odot }}$. Из каталога [26] берем величину радиуса вторичного компонента R2 = 2.55 ${{R}_{ \odot }}$. Далее, используя те же формулы и обозначения, что и в предыдущем разделе, находим оценки величин, характеризующих магнитные циклы. Они приведены в табл. 5. Из этой таблицы видно, что магнитные колебания могут быть причиной циклических изменений периода BO Vul.
Таблица 5.
Величины, характеризующие циклы магнитной активности вторичного компонента затменно-двойной системы BO Vul
| Величина | Значение |
|---|---|
| Рmod | 11 400 сут |
| Δ(О − С) | 0.023 сут |
| ΔP | 2.13 с |
| ΔJ | 7.44 × 1047 г см2/с |
| ΔE | 4.14 × 1041 эрг |
| B | 5.046 × 103 Гаусс |
| ΔL | 1.32 × 1033 эрг/с = 0.34 ${{L}_{ \odot }}$ = 0.29 L2 |
Обратная парабола в зависимости от времени отклонений наблюдаемых моментов минимумов от вычисленных с линейными элементами означает, что происходит вековое уменьшение периода. Для BO Vul Q = –1.19 × 10–9 и dP/dt = –4.47 × × 10–7 сут/год. Уменьшение периода может быть вызвано потерей углового момента системы за счет магнитного торможения.
6. ЗАКЛЮЧЕНИЕ
Изменения орбитального периода затменно-двойной системы XZ Per одинаково хорошо представляются как суперпозицией обратной параболы и циклических изменений, так и суммой двух циклических изменений. В первом случае монотонная составляющая может быть следствием потери системой углового момента за счет магнитного торможения. Циклические изменения периода могут быть следствием либо присутствия в системе третьего тела, либо проявления магнитной активности вторичного компонента, имеющего конвективную оболочку. Во втором случае можно предположить присутствие двух дополнительных тел в системе, либо отнести одно из колебаний периода на счет светового уравнения, а другое – на счет магнитной активности вторичного компонента. В обоих случаях после исключения из наблюдаемых моментов минимумов соответствующих теоретических кривых остаются почти одинаковые колебания периода, природа которых пока не ясна. Для выяснения природы этих колебаний нужны дальнейшие высокоточные наблюдения моментов минимумов.
Изменения орбитального периода затменно-двойной системы BO Vul можно представить суперпозицией обратной параболы и циклических изменений. Наблюдаемые циклические изменения периода могут быть следствием присутствия в системе третьего тела или проявлением магнитной активности вторичного компонента, имеющего конвективную оболочку. Для этой системы имеется очень небольшое количество высокоточных фотоэлектрических и ПЗС наблюдений моментов минимумов, основную массу составляют визуальные наблюдения. Полученная нами по остаткам после исключения параболы теоретическая кривая для светового уравнения хорошо представляет наблюдения для JD > 2 446 000, в то время как для более ранних наблюдений расхождение между теорией и наблюдениями довольно заметно. Результаты предыдущих авторов, наоборот, хорошо согласуются с ранними наблюдениями и совсем не согласуются с фотоэлектрическими и ПЗС наблюдениями. Не исключено, что эти колебания нельзя представить регулярной кривой, в этом случае их следует отнести на счет магнитной активности. Возможно также наличие дополнительных колебаний периода. Решить этот вопрос помогут только дальнейшие наблюдения.
Список литературы
Х. Ф. Халиуллин, Астрон. журн. 51, 395 (1974).
N. Nanouris, A. Kalimeris, E. Antonopolou, and H. Rjvithis-Livaniou, Astron. and Astrophys. 535, 126 (2011).
N. Nanouris, A. Kalimeris, E. Antonopolou, and H. Rjvithis-Livaniou, Astron. and Astrophys. 575, 64 (2015).
Д. Я. Мартынов, Изв. АО им. Энгельгардта 20, 154 (1938).
М. И. Лавров, Астрон. журн. 48, 301 (1971).
В. П. Цесевич, Изв. Одесской АО 4, 304 (1954).
В. П. Цесевич, Переменные звезды 11, 403 (1957).
D. M. Popper, Astrophys. J. Supp. 106, 133 (1996).
E. J. Michaels, JAAVSO 45, 43 (2017).
S. Qian, Astron. J. 121, 1614 (2001).
А. И. Халиуллина, Астрон. журн. 95, 280 (2018).
А. И. Халиуллина, Астрон. журн. 95, 550 (2018).
B. R. N. O. Project – Eclipsing Binaries database, http://var2.astro.cz/EN/brno/index.php
Д. Я. Мартынов, в кн. М. С. Зверев, Б. В. Кукаркин, Д. Я. Мартынов, П. П. Паренаго, Н. Ф. Флоря, В. П. Цесевич, Переменные звезды, т. 3, Гостехиздат (1947), стр. 464–490.
А. И. Халиуллина, Х. Ф. Халиуллин, Астрон. журн. 61, 393 (1984).
А. И. Халиуллина, Астрон. журн. 96, 196 (2019).
S. Rappaport, F. Verbunt, and P. C. Joss, Astrophys. J. 275, 713 (1983).
N. Ivanova, and R. E. Taam, Astrophys. J. 599, 516 (2003).
C. Knigge, I. Baraffe, and J. Patterson, Astrophys. J. Suppl. 194, 28 (2011).
J. H. Applegate, Astrophys. J. 385, 621 (1992).
C. Hoffmeister, Astron. Nachr. 255, 401 (1935).
J. Piegza, Acta Astron. ser. c, 2, 125 (1935).
J. J. Nassau, Astron. J. 48, 89 (1939).
S. Gaposchkin, Harv. Ann. 113, 69 (1954).
R. Szafraniec, Acta Astron. 26, 25 (1976).
М. А. Свечников, Э. Ф. Кузнецова Каталог приближенных фотометрических и абсолютных элементов затменных переменных звезд (Свердловск, Изд-во Урал. ун-та, 1990).
P. Ahnert, Inform. Bull. Var. Stars, № 786, 1 (1973).
M. E. Baldwin, JAAVSO 24, 92 (1996).
L. Li, D. Jiang, F. Zhang, New Astron. 11, 415 (2006).
A. Erdem, S. S. Doğru, V. Bakış, and O. Demircan, Astron. Nachr. 328, 543 (2007).
P. Zasche, “Multiple stellar systems under photometric and astrometric analysis”, Doctoral Thesis, The Astronomical Institute of Charles University, Prague (2008).
Z. Eker, F. Soudugan, E. Soydugan, S. Bilir, E. Yaz Gökçe, I. Steer, M. Tüysüz, T. Şenyüz, and O. Demircan, Astron. J. 149, 131 (2015).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


