Астрономический журнал, 2021, T. 98, № 9, стр. 754-779

1. ВВЕДЕНИЕ

Рентгеновские новые – мягкие рентгеновские транзиенты, принадлежащие к классу маломассивных рентгеновских двойных систем, в которых оптическая звезда-донор вещества имеет сравнительно малую массу, менее $1\;{{M}_{ \odot }}$ (см. книгу [1], где приведены все необходимые ссылки). Оптическая звезда заполняет свою полость Роша и истекает через внутреннюю точку Лагранжа ${{L}_{1}}$ на релятивистский объект – нейтронную звезду (НЗ) или черную дыру (ЧД). Рентгеновские новые показывают мощные (светимость в максимуме $ \sim {\kern 1pt} {{10}^{{38}}}$ эрг/с) вспышки рентгеновского излучения, которые длятся несколько месяцев. Эти вспышки обусловлены усилением темпа аккреции на релятивистский объект, вызванным увеличением вязкости вещества аккреционного диска. Ввиду прогрева рентгеновским излучением звезды-донора и аккреционного диска, рентгеновские вспышки сопровождаются вспышками оптического излучения. Вспышки происходят раз в несколько лет или несколько десятков лет. В перерывах между вспышками реализуется так наэываемое спокойное состояние системы, при котором рентгеновская светимость очень мала (менее 10³³ эрг/с). Главная причина оптической переменности в этом случае – эффект эллипсоидальности оптической звезды [2, 3], кроме того, на регулярную орбитальную “эллипсоидальную” переменность блеска амплитудой в несколько десятых звездной величины накладываются дополнительные типы переменности блеска, обусловленные вкладом незвездного компонента – аккреционного диска и области взаимодействия между газовой струей и внешней границей диска. При этом возможно также проявление пятнистой структуры звезды-донора (см., напр., [4, 5]).

Рентгеновские двойные системы, в том числе рентгеновские новые, до последнего времени были основным источником сведений о массах ЧД. К настоящему времени по движению звезд-доноров измерены массы около трех десятков звездных ЧД в рентгеновских двойных системах, которые лежат в интервале ($(4{\kern 1pt} - {\kern 1pt} 21)\;{{M}_{ \odot }}$). Эти массы в среднем существенно меньше масс ЧД, измеренных в гравитационно-волновых (ГВ) наблюдениях в двойных системах, $(7{\kern 1pt} - {\kern 1pt} 80)\;{{M}_{ \odot }}$ (см. каталоги [6, 7], где опубликованы сведения о массах около 100 ЧД, измеренных по гравитационно-волновым сигналам от слияния ЧД в двойных системах). Можно заключить, что “пальма первенства” в измерениях масс звездных ЧД в последние годы перешла от рентгеновских двойных систем к ГВ системам.

Тем не менее исследование рентгеновских двойных систем не потеряло своей актуальности. Во-первых, исследование рентгеновских двойных позволяет изучать спектр масс ЧД со стороны малых масс, что важно как для теории звездной эволюции, так и для релятивистской астрофизики. Во-вторых, в рентгеновских двойных системах, особенно в рентгеновских новых, происходят сложные и разнообразные физические процессы, изучение которых важно для астрофизики высоких энергий и релятивистской астрофизики. В частности в оптических спектрах рентгеновских новых в спокойном состоянии наблюдаются мощные и широкие двугорбые эмиссионные линии водорода от вращающегося вокруг релятивистского объекта газового диска. Другими словами, излучение диска доминирует в оптическом диапазоне, в то время как в рентгеновском близко к нулю. Предложены различные модели такого феномена, например адвекционно-доминированный диск, ламинарный диск – накопитель вещества и т.п., однако полной ясности в этом вопросе пока нет.

В спокойном состоянии у рентгеновских новых также наблюдаются аномалии в проявлениях оптической переменности [1, 8–10]. Средний блеск системы испытывает медленные изменения с амплитудой в несколько десятых звездной величины, что сравнимо с амплитудой регулярной орбитальной переменности, кроме того у многих систем (А0620-00, V404 Cyg и др.) на кривых блеска рентгеновских новых в спокойном состоянии появляются быстрые и иррегулярные флуктуации оптического блеска – фликкеринг (фликкер-шум).

Амплитуда фликкеринга также бывает сравнимой с амплитудой регулярной орбитальной переменности. У некоторых рентгеновских новых в спокойном состоянии в последние годы обнаружена переменная линейная поляризация инфракрасного излучения, связанная, по-видимому, с синхротронным излучением релятивистских джетов, которые, как оказалось, существуют даже в спокойном состоянии рентгеновских новых [11, 12]. Кроме того, у ряда рентгеновских новых в спокойном состоянии, в том числе и у системы А0620-00, недавно было обнаружено аномально быстрое укорочение орбитальных периодов [13–15], что отражает сложную эволюционную историю этих систем.

Все указанные аномалии связаны с наличием излучения от незвездных компонентов в суммарном излучении двойной системы. В настоящий момент для объяснения фликкеринга предложено несколько различных физических механизмов: (1) магнитогидродинамические процессы в области взаимодействия струи и диска, (2) неустойчивости в процессах аккреции вещества в диске и т.п.

Исследования фликкер-шума проводились в работах [12, 13, 16]. Отметим, что в новой статье [17] был проведен сравнительный анализ различных параметров фликкеринга для более чем 100 катаклизмических звезд, что представляет большой интерес и для исследователей, занимающихся статистическими свойствами этого явления. Также в статье [19] был дан обзор по исследованию фликкеринга у этого класса звезд. В работе [20] показано, как во время затмения компактного компонента двойной системы (белого карлика) фликкер-шум практически исчезает.

В предлагаемой работе изучаются статистические и спектральные характеристики явления фликкеринга в оптическом излучении рентгеновской новой с ЧД А0620-00 [9], находящейся в спокойном состоянии. Соответствующий анализ выполнен для данной системы по наблюдениям, полученным в период 2016 и 2017 г., что важно для понимания механизмов формирования и природы этого интересного явления.

Физическая природа фликкер-шума является до конца неизученной, и его исследование представляется актуальным для широкого класса астрофизических задач, в том числе для задач о двойных системах, а также задач космологии.

В задачах астрофизики фликкеринг представляет собой апериодическую изменчивость (мерцание) блеска звезды, что наблюдается в большинстве типов аккрецирующих компактных объектов [21]. В настоящий момент на физическую природу фликкеринга нет единой точки зрения. Предположительно его причиной могут служить вспышечные процессы в сочетании с процессами, носящими случайный характер. На практике такие процессы моделируются эмпирически подобранными кривыми, имеющими, например, степенную зависимость от частоты [9]. Таким образом, становится актуальной задача выявления единой структурной модели фликкер-шума, которая может быть априорно включена в общую модель построения кривой блеска для произвольных астрофизических объектов, параметры которой можно находить путем оптимизации реальных данных с расширенной моделью.

Рассмотренный в работе набор методов спектрального и статистического исследования фликкеринга позволяет выявить некоторые общие свойства и особенности такого процесса, причем как для пассивной стадии (2016 г.) так и для активной стадии (2017 г.).

2. НАБЛЮДАТЕЛЬНЫЙ МАТЕРИАЛ

Наблюдательный материал по А0620-00 и его анализ подробно описаны в статье [9]. Кратко приведем результаты этих наблюдений. Оптические наблюдения А0620-00 = V616 Mon проводились С.Ю. Шугаровым и Н.А. Катышевой в течение двух зимних сезонов 2015–2016 и 2016–2017 гг. Поскольку в спокойном состоянии система А0620-00 очень слаба ($V \sim {{18}^{m}}$), то для повышения точности кривых блеска наблюдения были выполнены в белом интегральном свете без фильтров: эффективная полоса пропускания лежит в диапазоне $\lambda \;4300{\kern 1pt} - {\kern 1pt} 8300$ Å с центральной длиной волны $\lambda = 6400$ Å. Для наблюдений использовался 125-см телескоп ЗТЭ Южной станции ГАИШ МГУ им. М.В. Ломоносова, а также 60-см телескоп обсерватории астрономического института Словацкой Академии наук. Время экспозиции при регистрации изображения звезды на ПЗС-приемнике составляло 1–2 мин. Обработка ПЗС-изображений А0620-00 проводилось стандартным методом апертурной фотометрии с привязкой к нескольким звездам сравнения. Точность индивидуального наблюдения А0620-00 составляет 0.01–0.02^m. Всего было получено 1037 индивидуальных наблюдений в сезоне наблюдений 2015–2016 гг. и 2347 наблюдений в сезоне 2016–2017 гг.

Более подробную информацию о наблюдательном материале см. в статье [9], где проведена интерпретация кривых блеска А0620-00. Наблюдения, выполненные в обоих сезонах, показали, что оптическая кривая блеска А0620-00 представляет собой двойную волну за орбитальный период амплитудой примерно 0.3^m с неравными максимумами. Причем в сезон 2016 г. (для краткости будем обозначать сезоны наблюдений, как 2016 г. и 2017 г.) амплитуда фликеринга на кривой блеска оказалась сравнительно небольшой (средняя квадратичная амплитуда $ \sim {\kern 1pt} {{0.045}^{m}}$), а в сезоне 2017 г. эта амплитуда резко возросла и достигла величины ${{0.093}^{m}}$. Эти величины значительно больше ошибок наблюдений, ${{(0.01{\kern 1pt} - {\kern 1pt} 0.02)}^{m}}$. Средний блеск системы А0620-00 в сезон 2017 г. также возрос по сравнению с 2016 г. на величину ${{0.2}^{m}}$, что сравнимо с амплитудой орбитальной переменности. Таким образом, находясь в спокойном состоянии по рентгеновскому излучению (L_x < 10³¹ эрг/с) система А0620-00 за время порядка 1 г. перешла от пассивной стадии к активной (средний блеск возрос, и возросла амплитуда фликкеринга).

Все указанные особенности наблюдательных проявлений А0620-00 (кроме двойной волны за период) отражают физику процессов, происходящих в незвездных компонентах излучения системы. В результате интерпретации кривых блеска А0620-00 в рамках модели взаимодействующей двойной системы с горячей линией и горячим пятном [9] были получены остаточные отклонения индивидуальных точек на кривых блеска от оптимальной теоретической кривой блеска. При этом минимизация невязок между наблюдаемой и теоретической кривыми блеска проводилась таким образом, что математическое ожидание остаточных отклонений было несмещенным, т.е. близким к нулю. В этих отклонениях содержатся фликкеринг и ошибки наблюдений ${{(0.01{\kern 1pt} - {\kern 1pt} 0.02)}^{m}}$, которые существенно меньше средней амплитуды фликкеринга.

В работе анализируются такие несмещенные остаточные отклонения.

Как отмечено в работах [22–24], фликкеринг в системе А0620-00 проявляется в большинстве случаев в виде отдельных вспышек, называемых “поярчаниями” блеска длительностью 15–30 мин и амплитудой от 3 до 20–40% от регулярной орбитальной кривой блеска, которая может рассматриваться как нижняя огибающая для индивидуальных наблюдательных точек. Методика выделения нижней огибающей описана в работах [22, 23]. Она содержит ряд субъективных моментов, что не позволяет полностью формализовать процедуру определения параметров модели А0620-00. При использовании нижней огибающей математическое ожидание остаточных отклонений будет смещенным, не равным нулю.

Отметим, что фликкер-шум наблюдается у большинства катаклизматических звезд [17, 25]. Оценки характерного времени вспышек в работе [26] также дают сходные значения порядка десятков минут. Подобные вспышки наблюдаются и в симбиотических звездах [27–29]. Таким образом, предлагаемый анализ применим к большому классу звезд с компактным компонентом (для катаклизматических и симбиотических звезд это белый карлик).

Для учета описанной вспышечной природы фликкеринга на втором этапе нашего исследования в остаточные отклонения с нулевым математическим ожиданием было введено систематическое смещение на величину, равную среднеквадратичному разбросу остаточных отклонений, который, как показано в работе [9], составляет ${{0.045}^{m}}$ для пассивной стадии системы (2016 г.) и ${{0.093}^{m}}$ для активной стадии (2017 г.). Тем самым в среднем был учтен односторонний, вспышечный характер фликкеринга. Поскольку вспышки длятся десятки минут, а характерное время экспозиций при наблюдениях порядка 1–2 мин, усреднение амплитуды вспышек при наблюдениях не происходит, и в распределении остаточных отклонений даже при нулевом математическом ожидании должен сохраняться негауссов компонент. Последнее и показал проведенный в текущей работе статистический анализ.

Однако использование остаточных отклонений со смещенным математическим ожиданием с точностью до погрешности метода дало те же статистические негауссовы распределения фликкеринга (гамма-распределение и распределение Вейбулла). Попытки ввести в модель дополнительный гауссов шум и различить его от фликкер-шума путем смещения математического ожидания результатов не дали; оптимизация приводит к исходному гамма-распределению (или распределению Вейбулла), что указывает на отсутствие во фликкеринге компонентов гауссовой природы и родственных им, а также на трудность выделения дополнительных неучтенных шумов на фоне фликкеринга.

Такие распределения указывают на то, что одно из объяснений природы фликкеринга – это атмосферные вспышечные явления.

Подчеркнем, что в работах [22–24] исследовались характеристики индивидуальных вспышек. В нашей работе мы изучаем характеристики вспышек как статистического ансамбля.

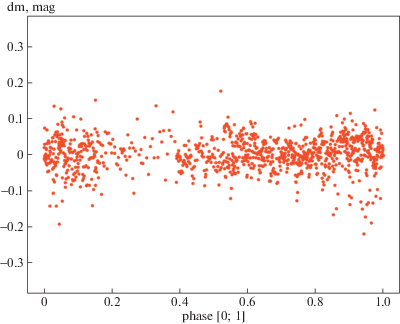
Итак, анализируются две выборки наблюдений $\Delta m(\phi )$ (см. рис. 1, 2), где $\Delta m = {{m}_{{{\text{obs}}}}} - {{m}_{{{\text{mod}}}}}$ есть отличие модельной кривой блеска [9] от кривой наблюдений, $\phi $ – орбитальная фаза системы.

Рис. 1.

Исходные данные фликкер-шума объекта A0620–00 $\Delta m(\phi )$ (2016 г.).

Рис. 2.

Исходные данные фликкер-шума объекта A0620–00 $\Delta m(\phi )$ (2017 г.).

3. ПЕРИОДИЧНОСТЬ И СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ

3.1. Численный метод получения спектра

Данные были проанализированы на наличие выраженного периодического тренда. С этой целью было необходимо получить спектр сигнала,

(1)

$S(\omega ) = \int\limits_{ - \infty }^{ + \infty } \,\Delta m(t){{e}^{{ - i\omega t}}}dt,$

и его спектральную мощность $\rho (\omega ) = {\text{|}}S(\omega ){\kern 1pt} {{{\text{|}}}^{2}}$.

В силу дискретности данных, а также из-за того, что $t$ известно только по модулю $T$ (фаза), определим ${{\omega }_{k}} = 2\pi k{\text{/}}T$, $k \in \mathbb{Z}$. Тогда ${{e}^{{ - i{{\omega }_{k}}t}}} = {{e}^{{ - i{{\omega }_{k}}T\phi }}}$. Далее, можно вычислить значение спектра численно с точностью до константы в точках ${{\omega }_{k}}$ следующим способом:

(2)

$S({{\omega }_{k}}) = \sum\limits_{n \in \mathbb{Z}} \,\int\limits_{nT}^{(n + 1)T} \,\Delta m(t){{e}^{{ - i{{\omega }_{k}}T\phi }}}dt \sim \int\limits_0^1 \,\Delta m(\phi ){{e}^{{ - i{{\omega }_{k}}T\phi }}}d\phi ,$

или

(3)

$S(k) \sim \int\limits_0^1 \,\Delta m(\phi ){{e}^{{ - i2\pi k\phi }}}d\phi .$

Для вычисления последнего интеграла его можно привести к виду:

(4)

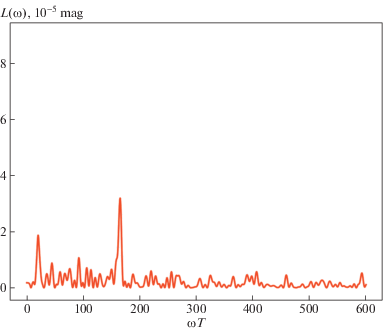
$S(k) \sim \sum\limits_n \,\Delta m({{\phi }_{n}}){{e}^{{ - i2\pi k{{\phi }_{n}}}}}\frac{{{{\phi }_{{n + 1}}} - {{\phi }_{{n - 1}}}}}{2}.$

На рис. 3, 4 представлены вычислимые участки спектра для данных 2016 и 2017 г. Они изображены на промежутке $k$, не превышающем длины массива наблюдений. Это делается, потому что на большем промежутке будет заметен так называемый элайзинг (хорошо заметный уже в спектре 2017 г.).

Рис. 3.

Спектр $\Delta m(\phi )$ (2016 г.).

Рис. 4.

Спектр $\Delta m(\phi )$ (2017 г.).

За исключением пиков элайзинга спектры мощности представляют собой характерный спектр шума, см. рис. 3, 4. Следовательно, явной периодичности сигнала нет, что подтверждает свойство апериодичности фликкер-шума. Бинировать полученный спектр для удаления шума не представляется возможным, поскольку известен только дискретный набор точек, следовательно, есть вероятность пропустить резкий пик на характерной частоте.

3.2. LS-спектр

Для неравномерного временного ряда случайного процесса $\Delta m({{\phi }_{k}})$, $k = 1 \ldots N$ его периодограмма связана с реальным спектром мощности $\rho (\omega )$ через спектральное окно $W(\omega )$:

(5)

$\left\langle {\frac{1}{{{{N}^{2}}}}{{{\left| {\sum\limits_{k = 1}^N \,\Delta m({{\phi }_{k}}){{e}^{{ - i\omega {{\phi }_{k}}}}}} \right|}}^{2}}} \right\rangle = \int\limits_\mathbb{R} \,\rho (\omega {\kern 1pt} ')W(\omega - \omega {\kern 1pt} ')d\omega {\kern 1pt} '.$

Вычислим спектральное окно для суммы дельта-функций (см. рис. 5, 6), которое можно явно представить в виде:

(6)

$W(\omega ) = \frac{1}{{{{N}^{2}}}}{{\left| {\sum\limits_{k = 1}^N \,{{e}^{{ - i\omega {{\phi }_{k}}}}}} \right|}^{2}}.$

Рис. 5.

Спектральное окно (2016 г.).

Рис. 6.

Спектральное окно (2017 г.).

Заметим, что при наличии одного временнóго ряда, а не двух, как в рассматриваемой задаче, была бы возможна аппроксимация процесса полигармонической функцией.

Легко видеть, что спектральные окна очень “чистые”, т. е. не содержат никаких дополнительных пиков на больших расстояниях от нулевой частоты. Следовательно, сигнал с высокой плотностью совпадает с реальным спектром (ошибка составляет величину $O(1{\text{/}}{{N}^{2}})$, где $N$ – количество точек в одной серии наблюдений.

При обработке, в общем случае, неравномерных временны́х рядов возникает проблема, связанная с тем, что величины периодограммы не подчиняются экспоненциальному распределению [30]. Обобщением периодограммы, которое сохраняет ее свойства, является среднеквадратический спектр (LS-спектр), который позволяет оценить значимость максимумов спектральной плотности.

Для анализа LS-спектра сигнала введем скалярное произведение на множестве моментов наблюдений {t_k}:

$({{f}_{1}},{{f}_{2}}) = \frac{1}{N}\sum\limits_{k = 1}^N \,{{f}_{1}}({{t}_{k}}){{f}_{2}}({{t}_{k}}).$

Основная идея данного метода – представление функции сигнала $\Delta m(t)$ в виде гармонической функции с неизвестными амплитудами:

$\Delta m(t) = {{a}_{1}}(\omega )cos(\omega t) + {{a}_{2}}(\omega )sin(\omega t).$

Далее применяется метод МНК для нахождения величин ${{a}_{1}}$ и ${{a}_{2}}$ при фиксированном $\omega $. В силу громоздкости получающихся формул используем разложение временнóго ряда по базису (представление Ломба):

$\begin{gathered} \Delta m(t) = {{a}_{1}}(\omega )cos[\omega (t - \tau (\omega ))] + \\ \, + {{a}_{2}}(\omega )sin[\omega (t - \tau (\omega ))] = {{a}_{1}}{{\phi }_{1}} + {{a}_{2}}{{\phi }_{2}}, \\ \end{gathered} $

где функция $\tau (\omega )$ – сдвиг по фазе, делающий перекрестные скалярные произведения функций нулевыми (аналог процедуры ортогонализации). Этот сдвиг по фазе дается формулой:

$\tau (\omega ) = \frac{1}{{2\omega }}arctan\frac{{\sum\nolimits_k \,sin2\omega {{t}_{k}}}}{{\sum\nolimits_k \,cos2\omega {{t}_{k}}}}.$

Спектр мощности после всех вычислений есть:

$L(\omega ) = \frac{1}{2}\left[ {\frac{{(\Delta m,{{\phi }_{1}})}}{{{{{\left\| {{{\phi }_{1}}} \right\|}}^{2}}}} + \frac{{(\Delta m,{{\phi }_{2}})}}{{{{{\left\| {{{\phi }_{2}}} \right\|}}^{2}}}}} \right],$

где норма понимается в евклидовом смысле.

Моделирование показывает, что периодограмма и спектр Ломба совпадают (последний представлен на рис. 7, 8).

Рис. 7.

Спектр Ломба (2016 г.).

Рис. 8.

Спектр Ломба (2017 г.).

Заметим, что они содержат частоты с большой мощностью относительно фонового шума.

Спектр Ломба – наиболее точная спектральная характеристика рассматриваемых данных. Отметим существенное различие спектров для активной и пассивной стадий.

Для определения по периодограмме, содержит ли сигнал периодическую составляющую, важным фактором является значимость пика периодограммы. Значимость обычно выражается в терминах вероятности так называемой “ложной тревоги” (FAP, False Alarm Probability). FAP есть вероятность измерения пика заданной высоты либо превышающего заданную высоту. Вероятность обусловлена априорным предположением, что данные представляют собой гауссовый шум без периодической составляющей.

Для анализа периодограммы была использована библиотека astropy в python. При анализе максимальных пиков по данным 2016 и 2017 г., соответственно, было получено

${\text{FA}}{{{\text{P}}}_{{2016}}} = 0.19{\text{\% }},$

${\text{FA}}{{{\text{P}}}_{{2017}}} = 0.0013{\text{\% }}.$

Другими словами, при априорном предположении, что в данных нет периодического сигнала, будет наблюдаться пик такого высокого или более высокого уровня примерно в 0.19 и 0.0013% времени. Малость этих величин указывает на подтверждение отсутствия в данных периодического сигнала [31].

4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ

4.1. Анализ функции плотности вероятности

Исследуем статистические характеристики двух выборок. Для того, чтобы определить функцию плотности вероятности, достаточно построить гистограммы (использовалась библиотека seaborn в python) (см. рис. 9, 10).

Рис. 9.

Гистограмма $\Delta m(\phi )$ (2016 г.).

Рис. 10.

Гистограмма $\Delta m(\phi )$ (2017 г.).

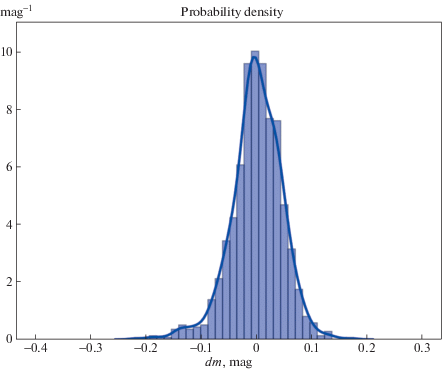
Полученные функции плотности вероятности представлены на рис. 11, 12. Для их построения использовался метод ядерной оценки плотности вероятности (с простейшим гауссовым ядром).

Рис. 11.

Плотность вероятности $dP{\text{/}}dm(m)$ (2016 г.).

Рис. 12.

Плотность вероятности $dP{\text{/}}dm(m)$ (2017 г.).

Отметим схожесть функций плотности вероятности. Обе содержат ненулевой коэффициент асимметрии одного знака, который может быть явно вычислен в обоих случаях:

${{\left. {\frac{{{{\mu }_{3}}}}{{{{\sigma }^{3}}}}} \right|}_{{2016}}} = - 0.52,$

${{\left. {\frac{{{{\mu }_{3}}}}{{{{\sigma }^{3}}}}} \right|}_{{2017}}} = - 0.33.$

Из полученной оценки асимметрии очевидна негауссовость обоих распределений.

Вспышечные процессы во многом носят индивидуальный характер и в деталях зависят уже от конкретной исследуемой астрофизической системы. Однако вспышечные процессы с необходимостью должны обладать той общей чертой, что они, очевидно, представляются неотрицательными случайными величинами. Таким образом, особое внимание следует уделить подсемейству экспоненциальных распределений, определенных для неотрицательных случайных величин. К таковым (помимо равномерного, которое, очевидно, не рассматривается для нашей задачи) относятся собственно экспоненциальное распределение, гамма-распределение (или распределение Эрланга) и его обобщения (такие как нормированное гамма-распределение, гиперэкспоненциальное, гипергамма-распределение) [32].

Мы остановимся на исследовании простого гамма-распределения, распределения Вейбулла, как очень простого для моделирования и также представляющего собой распределение неотрицательной случайной величины. Кроме того, рассмотрим модель, которая сочетает распределение неотрицательной случайной величины (распределение модуля нормального распределения) с естественным для подавляющего большинства физических процессов гауссовым шумом.

Используя статистику ${{\chi }^{2}}$, приведем количественное сравнение обоих выборок на соответствие сочетанию нормального и модуля нормального распределений, гамма-распределению и распределению Вейбулла.

Далее, для понимания общей структуры наблюдающегося распределения, построим диаграмму Херста для данных активной стадии (2017 г.) и для синтезированных распределений с заданными законами.

4.2. Критерий ${{\chi }^{2}}$ для различных видов распределений

4.2.1. Модуль нормального распределения. В  этом случае очевидно, что вычислить χ² не представляется возможным, потому что он станет бесконечным из-за малых значений $\Delta m$, где точек теоретически не должно быть (${{p}_{k}} = 0$). Однако к исходной модели можно добавить случайный шум. Тогда если исходные плотности вероятности имеют вид:

${{f}_{s}}(x) = \sqrt {\frac{2}{\pi }} \frac{1}{s}exp\left( {\frac{{{{{(x - {{\mu }_{s}})}}^{2}}}}{{2{{s}^{2}}}}} \right)\quad (x \geqslant {{\mu }_{s}}),$

${{f}_{n}}(x) = \frac{1}{{n\sqrt {2\pi } }}exp\left( {\frac{{{{{(x - {{\mu }_{n}})}}^{2}}}}{{2{{n}^{2}}}}} \right)\quad (x \in \mathbb{R}),$

то плотность вероятности для соответствующей им суммы случайных величин является сверткой:

$f(x) = \int\limits_\mathbb{R} \,{{f}_{s}}(u){{f}_{n}}(x - u)du.$

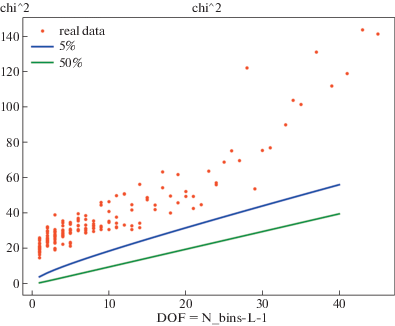
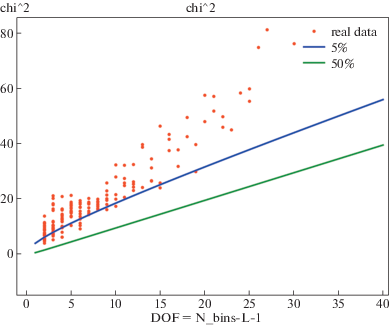
Это распределение имеет 4 параметра, которые сводятся к трем параметрам при преобразовании математического ожидания к нулю (центрировании). Минимизируя отклонение одной функции распределения от другой при помощи МНК, получим ${{\chi }^{2}}$ в зависимости от количества степеней свободы (фактически от количества бинов) (см. рис. 13, 14, где синяя и зеленая линии указывают границы, ниже которых распределение удовлетворяется с доверительной вероятностью 0.05 и 0.5 соответственно).

Рис. 13.

${{\chi }^{2}}({\text{DOF}})$ для модели совместной функции распределения: модуль нормального распределения и шум, заданный нормальным распределением (2016 г.).

Рис. 14.

${{\chi }^{2}}({\text{DOF}})$ для модели совместной функции распределения: модуль нормального распределения и шум, заданный нормальным распределением (2017 г.).

Как можно видеть, данные обеих стадий согласуются с моделью менее чем на 5%.

Для оптимального [33] числа разбиений величина ${{\chi }^{2}}$ есть, соответственно, ${{\chi }^{2}}(5) = 13.55$ ($\gamma < 2.5{\text{\% }}$, 2017 г.) и ${{\chi }^{2}}(4) = 20.58$ ($\gamma < 1{\text{\% }}$, 2016 г.)

На рис. 15, 16 представлено сравнение данных с соответствующей модельной функцией распределения.

Рис. 15.

Гистограмма реальных данных и плотность вероятности для модели совместной функции распределения: модуль нормального распределения и шум, заданный нормальным распределением, с параметрами, полученными по результатам МНК (2016 г.).

Рис. 16.

Гистограмма реальных данных и плотность вероятности для модели совместной функции распределения: модуль нормального распределения и шум, заданный нормальным распределением, с параметрами, полученными по результатам МНК (2017 г.).

Попытка фитировать данные спокойной стадии нормальным распределением положительных результатов не дала (см. рис. 17). Параметры, полученные в результате сравнения модели с реальными данными, получаются нефизичными, так как модель стремится сойтись к гауссовому шуму.

Рис. 17.

${{\chi }^{2}}({\text{DOF}})$для модели гауссового распределения, данные 2016 г.

4.2.2. Гамма-распределение. Гамма-распределение – двухпараметрическое и имеет вид:

$\begin{gathered} \Gamma (k,\theta ,x - {{x}_{0}}) = \\ \, = \frac{1}{{{{\theta }^{k}}\Gamma (k)}}{{(x - {{x}_{0}})}^{{k - 1}}}{{\left. {exp\left( { - \frac{{x - {{x}_{0}}}}{\theta }} \right)} \right|}_{{x - \Delta m}}}. \\ \end{gathered} $

Из первых трех моментов легко получить параметры $k,\theta ,{{x}_{0}}$. Они равны:

$\begin{gathered} {{k}_{{2016}}} = 14.8,\quad {{\theta }_{{2016}}} = 0.012\;{\text{mag}}, \\ {{x}_{{0,\;2016}}} = k\theta = 0.178\;{\text{mag}}, \\ \end{gathered} $

$\begin{gathered} {{k}_{{2017}}} = 57.7,\quad {{\theta }_{{2017}}} = 0.013\;{\text{mag}}, \\ {{x}_{{0,\;2017}}} = k\theta = 0.821\;{\text{mag}}. \\ \end{gathered} $

Далее данные были разбиты на равные по количеству точек промежутки. Зависимость ${{\chi }^{2}}({\text{DOF}})$ представлена на рис. 18, 19. Таким образом, спокойную стадию гамма-распределение не описывает, в то время как с доверительной вероятностью 0.5 активная стадия может быть описана этим распределением.

Рис. 18.

${{\chi }^{2}}({\text{DOF}})$для гамма-распределения (2016 г.).

Рис. 19.

${{\chi }^{2}}({\text{DOF}})$для гамма-распределения (2017 г.).

Для оптимального числа разбиений величина ${{\chi }^{2}}$ есть ${{\chi }^{2}}(6) = 6.42$ ($\gamma \approx 38{\text{\% }}$, 2017 г.) и ${{\chi }^{2}}(5) = 31.40$ ($\gamma < 0.1{\text{\% }}$, 2016 г.) соответственно.

На рис. 20, 21 представлено сравнение данных с соответствующей модельной функцией распределения.

Рис. 20.

Гистограмма реальных данных и плотность вероятности гамма-распределения, с параметрами, полученными по результатам МНК (2016 г.).

Рис. 21.

Гистограмма реальных данных и плотность вероятности гамма-распределения, с параметрами, полученными по результатам МНК (2017 г.).

4.2.3. Распределение Вейбулла. Распределение Вейбулла случайной величины $\xi $ также двухпараметрическое, и его функция распределения (намного более удобная для анализа) имеет аналитический вид:

${{F}_{{{\text{weibull}}}}}(\xi < x) = 1 - exp\left( { - {{{\left( {\frac{{x - {{x}_{0}}}}{\lambda }} \right)}}^{k}}} \right).$

С помощью библиотеки lmfit в python были получены следующие параметры для аппроксимации:

${{k}_{{2016}}} = 4.84,\quad {{\lambda }_{{2016}}} = 0.19\;{\text{mag}},$

${{k}_{{2017}}} = 5.04,\quad {{\lambda }_{{2017}}} = 0.45\;{\text{mag}}.$

Далее данные были разбиты на равные по количеству точек промежутки. Зависимость ${{\chi }^{2}}({\text{DOF}})$ представлена на рис. 22, 23.

Рис. 22.

${{\chi }^{2}}({\text{DOF}})$для распределения Вейбулла (2016 г.).

Рис. 23.

${{\chi }^{2}}({\text{DOF}})$для распределения Вейбулла (2017 г.).

Для оптимального числа разбиений величина ${{\chi }^{2}}$ есть ${{\chi }^{2}}(6) = 7.29$ ($\gamma \approx 30{\text{\% }}$, 2017 г.) и ${{\chi }^{2}}(5) = 20.3$ ($\gamma < 1{\text{\% }}$, 2016 г.) соответственно.

На рис. 24, 25 представлено сравнение данных с соответствующей модельной функцией распределения.

Рис. 24.

Гистограмма реальных данных и плотность вероятности распределения Вейбулла, с параметрами, полученными по результатам МНК (2016 г.).

Рис. 25.

Гистограмма реальных данных и плотность вероятности распределения Вейбулла, с параметрами, полученными по результатам МНК (2017 г.).

Заметим, что возможные ошибки в вычислении параметров распределений и оценке вероятности гипотезы могут быть связаны с тем фактом, что исходное распределение не является чистым фликкерингом, а суммой фликкеринга и ошибок инструмента ($\sigma = 0.015\;{\text{mag}}$ [9]). Однако точный закон распределения ошибок неизвестен. Кроме того, для исследуемых выборок распределение Вейбулла носило ряд аномалий, что также могло привести к ухудшению общей статистической картины.

4.3. Корреляционные функции и их физический смысл

Чтобы понять динамику рассматриваемого процесса, следует вычислить его корреляционную функцию:

$K(s) = \frac{1}{{\left\| {\Delta m(t)} \right\|_{\mathbb{R}}^{2}}}\int\limits_\mathbb{R} \,\Delta m(t)\Delta m(t + s)dt.$

Для данной задачи:

$\hat {K}(\xi ) = \frac{1}{{\left\| {\Delta m(\phi )} \right\|_{{[0;1]}}^{2}}}\int\limits_0^1 \,\Delta m(\phi )\Delta m(\phi + \xi )d\phi .$

Поскольку известен только дискретный набор точек, предложим процедуру для установления связи между $\hat {K}(\xi )$ и $K(s)$. Разобьем первый интеграл по периодам и примем $s < T$, потому что на большем промежутке времени данных нет. Таким образом,

$K(s) = \frac{1}{{\left\| {\Delta m(t)} \right\|_{\mathbb{R}}^{2}}}\sum\limits_{k - \infty }^{ + \infty } \,\int\limits_{kT}^{(k + 1)T} \,\Delta m(t)\Delta m(t + s)dt.$

Далее, представим интеграл в виде:

$\int\limits_\mathbb{R} \, \ldots = \mathop {lim}\limits_{N \to + \infty } \int\limits_{ - NT}^{NT} \, \ldots .$

Поскольку данные обладают трансляционной симметрией во времени, то после всех усреднений получим:

$\hat {K}(\phi ) = K(T\phi ),\quad \phi \in [0,1].$

Есть три варианта вычислить $\hat {K}(\phi )$:

1) свертка $\Delta {{m}_{{{\text{real}}}}}$, но тогда мы получим заведомо заниженное значение автокорреляции (рис. 26, 27);

Рис. 26.

Автокорреляция методом 1 (2016 г.), см. текст.

Рис. 27.

Автокорреляция методом 1 (2017 г.), см. текст.

2) бинирование графика (в данном случае оставить шаг $\Delta \phi = 0.01$), тогда у нас будет меньше точек, меньше шума, но опять же заниженная корреляция (рис. 28, 29);

Рис. 28.

Автокорреляция методом 2 (2016 г.), см. текст.

Рис. 29.

Автокорреляция методом 2 (2017 г.), см. текст.

3) учесть, что у любой физической системы есть некая задержка по времени и восстановить промежуточные точки до равномерного временного ряда неким малым затуханием (или просто оставляя предыдущее значение) (рис. 30, 31).

Рис. 30.

Автокорреляция методом 3 (2016 г.), см. текст.

Рис. 31.

Автокорреляция методом 3 (2017 г.), см. текст.

Наиболее физически оправданным с нашей точки зрения является третий метод (рис. 30, 31). На рисунках серыми прерывистыми линиями показана 99% вероятность, что процесс случайный. Видно, что данные 2017 г. намного лучше представляют процесс, потому что на них есть явный тренд. Данные 2016 г. ничего не говорят о процессе.

4.4. Экспонента Херста

Многие процессы в природе могут быть рассмотрены как самоподобные себе с неким коэффициентом:

$x(\lambda t) = {{\lambda }^{H}}x(t).$

Параметр $H$ называется параметром Херста, аналогичный нашему анализ был выполнен в [34]. При $H > 0.5$ процесс называется персистентным, т.е. он повторяет прошлые тренды, при $H = 0.5$ это просто шум, при $H < 0.5$ процесс стремится нарушить тренд. Для периодических процессов $H$ около нуля. Рассматривая фликкеринг на одном периоде системы, мы хотим понять, есть ли там скрытая периодичность. Для большинства природных процессов $H \sim 0.7$. Оценка $H$ производится следующим образом:

Мы выделяем из временнóго ряда на $[0,T]$ отрезок $\Theta $ длиной $\tau < T$ и вычисляем для него отношение $R{\text{/}}S$, где:

$R(\tau ) = \max X(t,\tau ) - \min X(t,\tau ),$

$X(t,\tau ) = \sum\limits_{{{t}_{k}} < t} \,(x({{t}_{k}}) - {{\bar {x}}_{\tau }}),$

$S(\tau ) = \sqrt {\frac{1}{\tau }\sum\limits_{{{t}_{k}} \in \Theta } \,{{{(x({{t}_{k}}) - {{{\bar {x}}}_{\tau }})}}^{2}}} .$

После этого, усредняя по всем промежуткам $\Theta $, мы получаем зависимость:

${{\left\langle {R{\text{/}}S} \right\rangle }_{\Theta }} \sim {{\tau }^{H}}.$

Проделав все вычисления с исходными данными, мы получим экспоненты Херста для активной и неактивной стадий.

В неактивной стадии наблюдается типичное поведение с $H = 0.668 \pm 0.008$.

В активной стадии на малом масштабе наблюдается шум, имеющий нормальное распределение с ${{H}_{1}} = 0.520 \pm 0.006$, в то время как на большом временн’ом масштабе проявляется некий дополнительный процесс, их сумма дает экспоненту Херста ${{H}_{2}} = 1.432 \pm 0.014$. Это является дополнительным подтверждением того, что надо рассматривать фликкеринг как некую вспышечную активность на фоне шума (рис. 32, 33). Отметим, что величина $1.432$ дает очень сильное подтверждение гипотезы вспышечной активности (последняя была бы значима уже даже для значения экспоненты Херста, равной единице).

Рис. 32.

Диаграммы $log{{\left\langle {R{\text{/}}S} \right\rangle }_{\Theta }}{\kern 1pt} - {\kern 1pt} log\tau $ (2016 г.).

Рис. 33.

Диаграммы $log{{\left\langle {R{\text{/}}S} \right\rangle }_{\Theta }}{\kern 1pt} - {\kern 1pt} log\tau $ (2017 г.).

4.5. Моделирование экспоненты Херста и сравнение с данными

Дополнительно было проведено моделирование процессов, имеющих: (1) закон распределения модуля Гаусса в сочетании с дополнительным гауссовым шумом, а также (2) гамма-распределение. Оба модельных процесса содержат неотрицательные случайные величины, ассоциирующиеся с предполагаемой вспышечной структурой фликкер-шума на фоне дополнительных шумов как самого источника, так и инструментального шума, и связанного, возможно, с неучтенными ошибками модели самой кривой блеска, что вносит дополнительные случайные ошибки в результирующий фликкер-шум.

Моделирование показало схожесть структуры реального и модельного сигналов как на малых, так и больших масштабах (рис. 34), что снова указывает в пользу вспышечного характера фликкер-шума, описываемого неотрицательными случайными величинами. Однако несмотря на схожесть структур присутствует сдвиг, который может быть объяснен как наличием всего лишь одной реализации данных (аналогичный эффекту селекции), так и наличием дополнительных неучтенных шумов, которые в первом приближении могут быть описаны нормальным законом.

Рис. 34.

Сравнение диаграмм Херста (см. рис. 32, 33 для данных (2017 г.) для модели модуля нормального распределения в сочетании со случайным шумом, имеющим нормальный закон распределения (синие кривые) и для модели гамма-распределения (зеленые кривые).

Таким образом, в модель кривой блеска рекомендуется включать случайный процесс, обладающей функцией распределения неотрицательной случайной величины, а также комбинации гауссовых шумов.

5. ЗАКЛЮЧЕНИЕ

Полученные несколькими независимыми методами результаты обработки фликкер-шума активной стадии рентгеновской новой A0620–00 дают статистически значимые указания на гипотезу атмосферных процессов на звезде, носящих вспышечный характер.

Статистически значимые модели, хорошо согласующиеся с наблюдательными данными, это модель, имеющая гамма-функцию распределения и функцию распределения Вейбулла. Оба распределения применимы для неотрицательных случайных величин. Обе модели находят подтверждение по критерию ${{\chi }^{2}}$ с доверительной вероятностью около $50\% $, что существенно превышает доверительные вероятности других моделей, в том числе моделей, являющихся комбинациями гауссовых шумов и родственных распределений. Так, модель суперпозиции двух распределений – модуля нормального и нормального – не проходит по статистическим критериям, что означает, что фликкер-шум, скорее всего, не описывается никакими модификациями нормального распределения.

Модели гамма-распределения и распределения Вейбулла выглядят физически предпочтительными и обнаруживают тесную связь с физическими процессами в метеорологии и геофизике (землетрясения, см., напр., [35]).

Кроме того, структура фликкер-шума, представленная в виде диаграммы Херста, также хорошо соответствует гамма-распределению, указывая, однако, на наличие в данных дополнительных неучтенных шумов. Последние носят предположительно гауссовый характер и могут быть связаны с инструментальным шумом либо с погрешностями модельной кривой блеска (с помощью которой были получены исходные данные по фликкер-шуму и которая не рассматривается в данной работе).

Приведенные методы исследования периодичности и спектральных характеристик могут быть использованы для изучения фликкеринга любых астрофизических систем. Так, для фликкер-шума рентгеновской новой A0620-00 показано отсутствие периодичности.

Помимо катаклизмических и симбиотических звезд, проделанный анализ может быть также применим к большой группе полуправильных SR-звезд, несмотря на другой физический механизм переменности: пульсации красного гиганта с циклом в сотни дней. Таким образом, предложенный подход охватывает все основные квазипериодические процессы в астрофизике.

Проделанный статистический анализ и анализ диаграмм Херста для фликкер-шума на примере активной и спокойной стадии объекта A0620-00 дает статистически значимые указания на использование в основной модели для кривой блеска дополнительного вклада неотрицательных случайных величин (гамма-распределение, распределение Вейбулла).

Полученные результаты имеют значение для интерпретации наблюдений различных астрофизических объектов. Например, в случае рентгеновских двойных систем, как уже упоминалось, “зашумленность” орбитальных кривых блеска связана как с ошибками наблюдений (которые распределены по нормальному закону), так и с иррегулярной физической переменностью, в том числе, с фликкерингом. Во многих случаях амплитуда физической переменности много больше ошибок наблюдений. В таких случаях поиск точечных оценок параметров модели и их ошибок разумно проводить не с использованием статистики нормального распределения для возмущений средних кривых блеска, а с применением рассмотренных нами распределений Вейбулла и гамма-распределения. Это позволит получить более надежные значения параметров модели и их ошибок.

В дальнейшем представляется перспективным рассмотрение фликкер-шума как суперпозиции нескольких случайных распределений, например, распределений Вейбулла, лог-Вейбулла в сочетании с гауссовыми шумами. Отметим, однако, что увеличение количества параметров сопряжено с техническими трудностями из-за неустойчивости процесса счета. На текущем этапе исследований выделить дополнительный случайный шум на фоне фликкер-сигнала не представляется возможным.